2019探究理数(北师大版)练习:第四章 第三节 平面向量的数量积含解析
2019版高考数学(理)一轮复习:平面向量的数量积及应用举例含解析

由于 · =2a·(2a+b)=4|a|2+2a·b=4+2×1×2× =2,
所以2a·b=2-4|a|2=-2,
所以a·b=-1,故B,C错误;
又因为(4a+b)· =(4a+b)·b=4a·b+|b|2=4×(-1)+4=0,
所以(4a+b)⊥ .
二、填空题(每小题5分,共15分)
所以 · = ·
= ·
= · + · + + ·
=1+ + - = .
答案:
5.(2015·安徽高考)△ABC是边长为2的等边三角形,已知向量a,b满足 =2a, =2a+b,则下列结论正确的是()
A.|b|=1B.a⊥b
C.a·b=1D.(4a+b)⊥
【解析】选D.因为 = - =(2a+b)-2a=b,
4.已知△ABC为等边三角形,AB=2,设点P,Q满足 =λ , =(1-λ) ,λ∈R,若 · =- ,则λ=()
A. B.
C. D.
【解析】选A.因为 · =- ,
所以- = ·
= ·
=- -λ + ·
=-4 -4λ+2 =-2λ2+2λ-2,
解得λ= .
【一题多解】
选A.如图建立平面直角坐标系,
6.若非零向量a,b满足|a|=3|b|=|a+2b|,则a,b夹角θ的余弦值为________.
【解析】|a|=|a+2b|,两边平方得,|a|2=|a|2+4|b|2+4a·b
=|a|2+4|b|2+4|a||b|·cosθ.
2019年高考数学(理)热点题型和提分秘籍专题20平面向量的数量积(题型专练)含解析

【答案】 C 【解析】因为点 C(- 1,0),D (4,5),所以 C→D =(5,5) ,又 A→B= (2,1),所以向量 A→B在
C→D 方向上的投影为
|A→B
|cos〈
A→B,
C→D
〉=
A→B·C→D |C→D |
=
15 =3 52
2
2.
11.若向量 a= (2,- 1), b= (3- x,2), c= (4, x)满足 (6a- b) ·c= 8,则 x 等于 ( )
2
=8
x0+
1 4
-
1 2≥-
1, 2
14.若非零向量 a,b 满足 |a|= 1,|b|= 2,且 (a+ b)⊥ (3a- b),则 a 与 b 夹角的余弦值为 ________.
【答案】 1 4
【解析】由 (a+ b)⊥(3 a- b)可得 (a+ b) ·(3a- b)= 0,又 |a|= 1, |b |= 2,则可得 a·b= 1,设 a, b 2
且 O→A⊥ O→B,则 tan α的值为 (
)
4
4
A .- 3 B.- 5
4 C. 5
3 D.4
【答案】A 【解析】由题意知 6sin2α+ cos α·(5sin α- 4cos α)= 0,即 6sin2α+ 5sin αcos α- 4cos2α
= 0,上述等式两边同时除以
cos2α,得
6tan2α+ 5tan α- 4=0,由于
2.已知 e1, e2 是单位向量, m=e1+2e2, n=5e1 -4e2 ,若 m⊥ n,则 e1 与 e2 的夹角为 ( )
A.
B.
C. π
【解 析】选 B.因为 m⊥ n,|e1|=|e2|=1,
2019大一轮高考总复习文数(北师大版)讲义第5章 第03节 平面向量的数量积及应用 Word版含答案
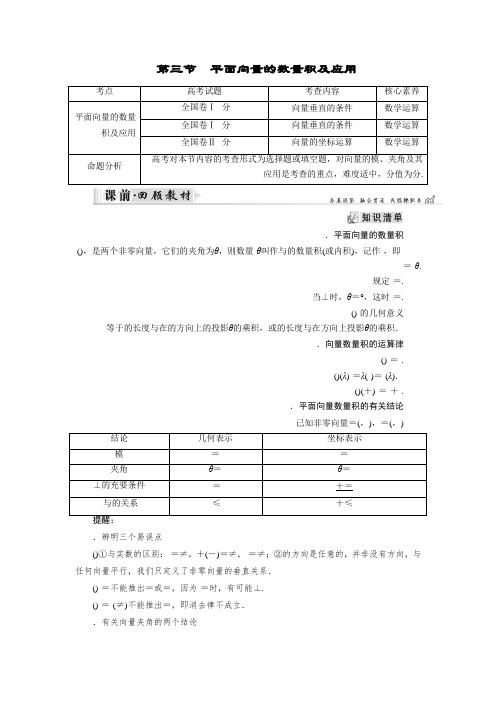
第三节 平面向量的数量积及应用.平面向量的数量积(),是两个非零向量,它们的夹角为θ,则数量·θ叫作与的数量积(或内积),记作·,即·=·θ.规定·=.当⊥时,θ=°,这时·=.()·的几何意义·等于的长度与在的方向上的投影θ的乘积,或的长度与在方向上投影θ的乘积..向量数量积的运算律()·=·.()(λ)·=λ(·)=·(λ).()(+)·=·+·..平面向量数量积的有关结论 已知非零向量=(,),=(,).辨明三个易误点()①与实数的区别:·=≠,+(-)=≠,·=≠;②的方向是任意的,并非没有方向,与任何向量平行,我们只定义了非零向量的垂直关系.()·=不能推出=或=,因为·=时,有可能⊥. ()·=·(≠)不能推出=,即消去律不成立. .有关向量夹角的两个结论()两个向量与的夹角为锐角,则有·>,反之不成立(因为夹角为时不成立);()两个向量与的夹角为钝角,则有·<,反之不成立(因为夹角为π时不成立)..判断下列结论的正误(正确的打“√”,错误的打“×”)()向量在另一个向量方向上的投影为数量,而不是向量.( )()两个向量的数量积是一个实数,向量的加、减、数乘运算的运算结果是向量.( ) ()由·=,可得=或=.( )()两向量⊥的充要条件:·=⇔+=.( )()若·>,则和的夹角为锐角;若·<,则和的夹角为钝角.( )()(·)·=·(·).( )()·=·(≠),则=.( )答案:()√()√()×()×()×()×()×.向量=(,- ),=(-),则(+)·=( ).-...解析:选方法一∵=(,-),=(-),∴=,·=-,从而(+)·=+·=-=.方法二∵=(,-),=(-),∴+=(,-)+(-)=(),从而(+)·=()·(,-)=,故选..设,是非零向量,“·=”是“∥”的( ).充分而不必要条件.必要而不充分条件.充分必要条件.既不充分也不必要条件解析:选若·=·,则〈,〉=,∴〈,〉=°,∴∥,充分.若∥,则〈·〉=°或°,∴·=或·=-,不必要..(教材习题改编)若=,=,且+=,则与的夹角为.解析:因为+=+·+=,即+·+=,所以·=-,设与的夹角为θ,则θ===-,∴θ=.答案:.(·北京卷)已知向量=(,),=(,),则与夹角的大小为.解析:设与夹角为θ,则θ===,又θ∈[,π],故θ=.答案:。
2018-2019学年高中(北师大版)数学必修4:17平面向量数量积的坐标表示 含解析

平面向量数量积的坐标表示来自时间:45 分钟 满分:80 分 班级________ 姓名________ 分数________ 一、选择题:(每小题 5 分,共 5×6=30 分) 1.已知 a=(-3,4),b=(5,2),则 a·b=( ) A.23 B.7 C.-23 D.-7 答案:D 2.若向量 a=(2,0),b=(1,1),则下列结论正确的是( ) A.a·b=1 B.|a|=|b| C.(a-b)⊥b D.a∥b 答案:C 解析:a·b=2,选项 A 错误;|a|=2,|b|= 2,选项 B 错误;(a-b)·b=(1,-1)·(1,1)=0,选项 C 正确, 故选 C. 3.已知向量 a=(0,-2 3),b=(1, 3),则向量 a 在 b 方向上的投影为( ) A. 3 B.3 C.- 3 D.-3 答案:D a·b -6 解析:向量 a 在 b 方向上的投影为 = =-3.选 D. |b| 2 4.若 A(1,2),B(2,3),C(-3,5),则△ABC 为( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.不等边三角形 答案:C 解析:∵A(1,2),B(2,3),C(-3,5), → → ∴AB=(1,1),AC=(-4,3), → → AB·AC 1×-4+1×3 1 cosA= = =- <0,∴∠A 为钝角,△ABC 为钝角三角形. → → 5 2 2× 25 |AB||AC| → → → 5.若向量AB=(3,-1),n=(2,1),且 n·AC=7,那么 n·BC等于( ) A.-2 B.2 C.-2 或 2 D.0 答案:B → → → → → → 解析:n·(AB+BC)=n·AB+n·BC=7,所以 n·BC=7-n·AB=7-(6-1)=2. 7 1 1 7 6.与向量 a=( , ),b=( ,- )的夹角相等,且模为 1 的向量是( ) 2 2 2 2 4 3 A.( ,- ) 5 5 4 3 4 3 B.( ,- )或(- , ) 5 5 5 5 2 2 1 C.( ,- ) 3 3 2 2 1 2 2 1 D. ( ,- )或(- , ) 3 3 3 3 答案:B 7 1 1 7 解析:设与向量 a=( , ),b=( ,- )的夹角相等,且模为 1 的向量为 e=(x,y),则 2 2 2 2 4 4 x= , x=- , x2+y2=1 5 5 7 1 1 7 ,解得 或 故选 B. 3 3 x+ y= x- y y=- , y= , 2 2 2 2 5 5
2019版+全国版+高考数学一轮复习第4章平面向量第3讲平面向量的数量积及应用增分练.doc

第3讲 平面向量的数量积及应用板块四 模拟演练•提能增分[A 级基础达标]1. [2018 •许昌模拟]设丛 yGR,向量 a= (x 1), b= (1, y), c= (2, —4),且日丄 c, b// c,则 a+b\ =( )ApB.帧C. 2书D. 10答案 B1 yJOT-ITT田0丄c, 得日• c —2x 4 — 0,解得x —2. E0 b// c,得?一 乍 解得y — 2.刃「以a= (2, 1), b= (1, —2), a+b= (3, —1), | a+b\ =y[10.故选 B.2. [2015 •广东高考]在平面直角坐标系 已知四边形加尬9是平行四边形,AB=(1, -2), AD= (2, 1),则AD-AC={)A. 5B. 4C. 3D. 2 答案A解析 AC=AB+AD=仃,一2) + (2, 1) = (3, -1),所以〃・ AC= (2, 1)・(3, -1)=2X3 + 1X (-1)=5.故选 A.A. 30°B. 45°C. 60°D. 120°答案A解析 cosZABC=J t =¥,所以.故选 A.\BA\ - \BC\4. 己知|a|=2|b|H0,且关于x 的方程^+\a\x+a-b= 0有实根,则a 与b 的夹角的 取值范围是()H ・•兀A. 0, 日B.C. 'JI 2兀]D.■兀 云’71 _答案B解析 由于\a\ =2\b\ ^0,且关于x 的方程x + \a\x+a • b=0有实根,则|a|2 —1a.b 引列14曰•方$0,即a b^-\a\2.设向量a 与方的夹角为贝0 cos 0=— W ------ :■ 0创SI 丄1 12 2e y, Ji ・故选B.—► —► —► —►2|a3. [2016・全国卷III]已知向量胡=JI则 ZABC=(5.在中,ZC=90° ,且CA=CB=3,点、M满足则少・CA={ )A. 18 B・ 3 C. 15 D・ 12答案A—► —► ―► ―►―► ―►—►解析由题意可得△必7是等腰直角三角形,仙=3型,AM=BA,故他・CA= (64+M・CA—► —► —►―► ―► —►―► —► —►= C^+AM・ C4=9+(以一C% ・CA=9+C/f —CB・以=9 + 9 — 0=18.故选A.―► ―►―► ―►—►6.[2018・济宁模拟]平面四边形外况卩中,AB+CD=0, {AB-AD)・AC=0,则四边形畀彩是()A.矩形B.正方形C.菱形D.梯形答案C―► ―►—►—► —►—►解析因为/1B+CA0,所以AB= _CD= DC,所以四边形/况刀是平行四边形.又(仍一AD・AC=DB・/片0,所以四边形对角线互相垂直,所以四边形力如是菱形.故选C.7.[2018 •重庆模拟]已知非零向量日,b满足\b\=4\a\,且日丄(2a+/>),则日与方的夹角为()答案C解析・・・£丄(2a+Z>), ・・・$• (2a+A)=0,/.2 a 2 + a• 6=0,即2\a\~+ \a\ \ b\cos〈a, b) =0. V | b\ =41 a\, /.21 a|2+4| a|2cos〈a, b〉=0,1 2 n・*.cos 〈£, b).:〈曰,ti) =~-•故选C.8.[2018・南宁模拟]己知平面向量S 0,且|a|=l, |Q=2, a丄(a—20),则| 2 a + 0 = _________ .答案A/T O解析由a丄(a —2 0)得a・(a—2 0)= a2—2 a・0=0,所以a・0=£,所以(2 a+ 0严=4 ^+02+4 a ・=4X l2+22+4x|= 10,所以|2。
2019高三数学理北师大版一轮课时分层训练28 平面向量的数量积与平面向量应用举例 含解析 精品

课时分层训练(二十八) 平面向量的数量积与平面向量应用举例(对应学生用书第252页)A 组 基础达标一、选择题1.在边长为1的等边△ABC 中,设BC →=a ,CA →=b ,AB →=c ,则a ·b +b ·c +c ·a =( )A .-32 B .0 C.32D .3A [依题意有a ·b +b ·c +c ·a =⎝ ⎛⎭⎪⎫-12+⎝ ⎛⎭⎪⎫-12+⎝ ⎛⎭⎪⎫-12=-32.] 2.已知AB →=(2,1),点C (-1,0),D (4,5),则向量AB →在CD →方向上的投影为 ( )A .-322B .-3 5 C.322D .35C [因为点C (-1,0),D (4,5),所以CD =(5,5),又AB →=(2,1),所以向量AB →在CD →方向上的投影为|AB →|cos 〈AB →,CD →〉=AB →·CD →|CD →|=1552=322.]3.(2018·海口调研)若向量a =(2,-1),b =(3-x,2),c =(4,x )满足(6a -b )·c =8,则x 等于( )A .4B .5C .6D .7D [因为6a -b =(9+x ,-8),所以(6a -b )·c =36+4x -8x =8,解得x =7,故选D.]4.已知O 为坐标原点,向量OA →=(3sin α,cos α),OB →=(2sin α,5sin α-4cos α),α∈⎝ ⎛⎭⎪⎫3π2,2π,且OA →⊥OB →,则tan α的值为( )【导学号:79140158】A .-43B .-45C .45D .34A [由题意知6sin 2α+cos α·(5sin α-4cos α)=0,即6sin 2α+5sin αcos α-4cos 2α=0,上述等式两边同时除以cos 2α,得6tan 2α+5tan α-4=0,由于α∈⎝ ⎛⎭⎪⎫3π2,2π,则tan α<0,解得tan α=-43,故选A.]5.(2016·山东高考)已知非零向量m ,n 满足4|m |=3|n |,cos 〈m ,n 〉=13.若n ⊥(t m +n ),则实数t 的值为( ) A .4 B .-4 C.94D .-94B [∵n ⊥(t m +n ),∴n ·(t m +n )=0, 即t m ·n +|n |2=0,∴t |m ||n |cos 〈m ,n 〉+|n |2=0. 又4|m |=3|n |,∴t ×34|n |2×13+|n |2=0, 解得t =-4.故选B.] 二、填空题6.(2016·全国卷Ⅰ)设向量a =(m,1),b =(1,2),且|a +b |2=|a |2+|b |2,则m =________.-2 [∵|a +b |2=|a |2+|b |2+2a·b =|a |2+|b |2, ∴a·b =0.又a =(m,1),b =(1,2),∴m +2=0,∴m =-2.]7.(2018·合肥一检)若非零向量a ,b 满足|a |=1,|b |=2,且(a +b )⊥(3a -b ),则a 与b 夹角的余弦值为________.14 [由(a +b )⊥(3a -b )可得(a +b )·(3a -b )=0,又|a |=1,|b |=2,则可得a·b=12,设a ,b 的夹角为θ,θ∈[0,π],则cos θ=a·b |a |·|b |=14.]8.已知向量a =⎝ ⎛⎭⎪⎫-12,32,OA →=a -b ,OB →=a +b ,若△OAB 是以O 为直角顶点的等腰直角三角形,则△OAB 的面积为________.【导学号:79140159】1 [由题意得,|a |=1,又△OAB 是以O 为直角顶点的等腰直角三角形,所以OA →⊥OB →,|OA →|=|OB →|.由OA →⊥OB →得(a -b )·(a +b )=|a |2-|b |2=0,所以|a |=|b |,由|OA →|=|OB →|得|a -b |=|a +b |,所以a·b =0. 所以|a +b |2=|a |2+|b |2=2,所以|OB →|=|OA →|=2,故S △OAB =12×2×2=1.] 三、解答题9.已知|a |=4,|b |=8,a 与b 的夹角是120°.(1)计算:①|a +b |,②|4a -2b |; (2)当k 为何值时,(a +2b )⊥(k a -b ). [解] 由已知得,a ·b =4×8×⎝ ⎛⎭⎪⎫-12=-16.(1)①∵|a +b |2=a 2+2a ·b +b 2=16+2×(-16)+64=48,∴|a +b |=4 3. ②∵|4a -2b |2=16a 2-16a ·b +4b 2=16×16-16×(-16)+4×64=768, ∴|4a -2b |=16 3.(2)∵(a +2b )⊥(k a -b ),∴(a +2b )·(k a -b )=0, ∴k a 2+(2k -1)a ·b -2b 2=0,即16k -16(2k -1)-2×64=0,∴k =-7. 即k =-7时,a +2b 与k a -b 垂直.10.如图4-3-2,已知O 为坐标原点,向量OA →=(3cos x,3sin x ),OB →=(3cos x ,sin x ),OC →=(3,0),x ∈⎝ ⎛⎭⎪⎫0,π2.图4-3-2(1)求证:(OA →-OB →)⊥OC →;(2)若△ABC 是等腰三角形,求x 的值. [解] (1)证明:OA →-OB →=(0,2sin x ), ∴(OA →-OB →)·OC →=0×3+2sin x ×0=0, ∴(OA →-OB →)⊥OC →.(2)若△ABC 是等腰三角形,则AB =BC , ∴(2sin x )2=(3cos x -3)2+sin 2x , 整理得2cos 2x -3cos x =0, 解得cos x =0,或cos x =32. ∵x ∈⎝ ⎛⎭⎪⎫0,π2,∴cos x =32,x =π6.B 组 能力提升11.(2018·广州综合测试(二))已知两点A (-1,1),B (3,5),点C 在曲线y =2x 2上运动,则AB →·AC →的最小值为( ) A .2 B .12 C .-2D .-12D [设C (x 0,2x 20),因为AB →=(4,4),AC →=(x 0+1,2x 20-1),所以AB →·AC →=8x 20+4x 0=8⎝ ⎛⎭⎪⎫x 0+142-12≥-12,即AB →·AC →的最小值为-12,故选D.] 12.(2017·全国卷Ⅱ)已知△ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则P A →·(PB →+PC →)的最小值是( )A .-2B .-32C .-43D .-1B [法一:(解析法)(1)建立坐标系如图(1)所示,则A ,B ,C 三点的坐标分别为A (0,3),B (-1,0),C (1,0).设P 点的坐标为(x ,y ),则P A →=(-x ,3-y ),PB →=(-1-x ,-y ),PC →=(1-x ,-y ),∴P A →·(PB →+PC →)=(-x ,3-y )·(-2x ,-2y )=2(x 2+y 2-3y )=2⎣⎢⎡⎦⎥⎤x 2+⎝⎛⎭⎪⎫y -322-34≥2×⎝ ⎛⎭⎪⎫-34=-32. 当且仅当x =0,y =32时,P A →·(PB →+PC →)取得最小值,最小值为-32. 故选B. 法二:(几何法)(2)如图(2)所示,PB →+PC →=2PD →(D 为BC 的中点),则P A →·(PB →+PC →)=2P A →·PD →.要使P A →·PD →最小,则P A →与PD →方向相反,即点P 在线段AD 上,则(2P A →·PD →)min =-2|P A →||PD →|,问题转化为求|P A →||PD →|的最大值.又|P A →|+|PD →|=|AD →|=2×32=3, ∴|P A →||PD →|≤⎝⎛⎭⎪⎫|P A →|+|PD →|22=⎝ ⎛⎭⎪⎫322=34,∴[P A →·(PB →+PC →)]min =(2P A →·PD →)min =-2×34=-32. 故选B.]13.(2017·山东高考)已知e 1,e 2是互相垂直的单位向量.若3e 1-e 2与e 1+λe 2的夹角为60°,则实数λ的值是________. 33 [由题意知|e 1|=|e 2|=1,e 1·e 2=0,|3e 1-e 2|=(3e 1-e 2)2=3e 21-23e 1·e 2+e 22=3-0+1=2.同理|e 1+λe 2|=1+λ2. 所以cos 60°=(3e 1-e 2)·(e 1+λe 2)|3e 1-e 2||e 1+λe 2|=3e 21+(3λ-1)e 1·e 2-λe 2221+λ2=3-λ21+λ2=12, 解得λ=33.]14.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足(2a -c )BA →·BC →=cCB →·CA →.(1)求角B 的大小;(2)若|BA →-BC →|=6,求△ABC 面积的最大值.【导学号:79140160】[解] (1)由题意得(2a -c )cos B =b cos C .根据正弦定理得(2sin A -sin C )cos B =sin B cos C , 所以2sin A cos B =sin(C +B ),即2sin A cos B =sin A ,因为A ∈(0,π),所以sin A >0, 所以cos B =22,又B ∈(0,π),所以B =π4. (2)因为|BA →-BC →|=6,所以|CA →|=6,即b =6,根据余弦定理及基本不等式得6=a 2+c 2-2ac ≥2ac -2ac =(2-2)ac (当且仅当a =c 时取等号),即ac≤3(2+2),故△ABC的面积S=12ac sin B≤3(2+1)2,即△ABC的面积的最大值为32+32.。
最新-2021版同步理数北师大版课件:第四章 第三节 平面向量的数量积 精品
a·b等于( A )
A. 3
3 B. 2
C.2 3
1 D.2
解析:a·b=|a|·|b|cos 30°=2sin 15°×4sin 75°× 23=
4 3sin 15°cos 15°=2 3sin 30°= 3,故选A.
2.在菱形ABCD中,对角线AC=4,E为CD的中点,则 A→E·A→C=( C ) A.8 B.10 C.12 D.14 解析:特殊化处理,用正方形代替菱形,边 长为2 2,以A为原点,建立如图所示坐标 系,则A(0,0),C(2 2,2 2),E( 2,2 2), 所以A→C=(2 2,2 2),A→E=( 2,2 2),所以A→C·A→E=2 2 × 2+2 2×2 2=12,故选C.
4.若向量a与b的夹角为60°,a=(2,0),|a+2b|=2 3,
则|b|=( B )
A. 3
B.1
C.4
D.3
解析:因为|a+2b|2=(a+2b)2=|a|2+4a·b+4|b|2=22+
8·|b|·cos 60°+4|b|2=(2 3)2,所以|b|2+|b|-2=0,
解得|b|=1.故选B.
利用坐标式a·b=x1x2+y1y2解题. 坐标式的特点是具有明显的代数特 坐标 征,解题时需要引入直角坐标系, 法 明确向量的坐标进行求解,即向量
问题“坐标化”.
求较复杂的向量数量积的运算时, 转化
可先利用向量数量积的运算律或相 法
关公式进行化简,然后进行计算.
适合题型
适用于已知相应向 量的坐标求解数量 积的有关计算问题
第四章 平面向量 第三节 平面向量的数量积
C目录 ONTENTS
高考·导航 主干知识 自主排查 .理解平面向量数量积的含义及其物理意义. 2.了解平面向量的数量积与向量投影的关系. 3.掌握数量积的坐标表达式,会进行平面向量数量积的运 算. 4.能运用数量积表示两个向量的夹角,会用数量积判断两个 平面向量的垂直关系. 5.会用向量的方法解决某些简单的平面几何问题. 6.会用向量方法解决简单的力学问题与其他一些实际问题.
2019届高考数学(理)一轮复习讲练测:专题5.3 平面向量的数量积(测)(解析版)
【答案】
Байду номын сангаас【解析】
试题分析:设 ,由 ,即有 ,得 ,点 是 的中点,则 ,
.当且仅当 取得最小值,且为 .则 的最小值为 .
18.已知向量 , .
(1)若 , ,且 ,求 ;
(2)若 ,求 的取值范围.
【答案】
【解析】因为 , ,
因此 ,
16.【江苏省淮安市高三上学期第一次摸底】如图,已知 中, , , 是 的中点,若向量 ,且 的终点 在 的内部(不含边界),则 的取值范围是.
【答案】
【解析】以A为坐标原点,AB所在直线为x轴建立直角坐标系,则 且 ,
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
【答案】C.
【解析】根据题意,可画出如下示意图,设 , , ,
则 ,从而可知 的值为以 , 为邻边的平行四边形的面积.
11.【重庆卷】若非零向量a,b满足|a|= |b|,且(a-b) (3a+2b),则a与b的夹角为()
A、 B、 C、 D、
【答案】A
12.【【百强校】2019届福建省泉州市高三5月】已知 是圆 的一条直径,点 在圆 上,则 的最小值为()
【答案】A
2.【福建卷】设 , , .若 ,则实数 的值等于()
A. B. C. D.
【答案】A
【解析】由已知得 ,因为 ,则 ,因此 ,解得 ,故选A.
3.【2019湖北省优质高中联考】已知向量 ,若 ,则向量 与向量 的夹角的余弦值是()
A. B. C. D.
【答案】A
【解析】 ,因为 ,所以 ,解得 ,当 时, ,故选A.
北师大版(2019)高中数学《向量数量积的坐标表示》课件(完整版)1
平面向量数量积的坐标运算
[例 1] (1)设 a =(1,-2),b =(-3,4),c=(3,2),则(a +
2b )·c= A.12 C.-3
B.0 D.-11
()
北 师 大 版 ( 2019) 高中数 学《向 量数量 积的坐 标表示 》课件 (完整 版)1
北 师 大 版 ( 2019) 高中数 学《向 量数量 积的坐 标表示 》课件 (完整 版)1于 A.11 C-14B.5 D.10
()
解析: a +b =(4,-1),a -c=(2,-3). 所以(a +b )·(a -c)
=4×2+(-1)×(-3)=11.故选A.
答案:A
北 师 大 版 ( 2019) 高中数 学《向 量数量 积的坐 标表示 》课件 (完整 版)1
3.已知向量 m =(1,1),向量 n 与向量 m 的夹角为34π,且 m ·n
[系统归纳]
1.关于平面向量数量积的坐标表示 (1)两向量a 与b 的数量积是一个实数,不是一个向量,其值可
以为正(当a ≠0,b ≠0,0°≤θ<90°时),也可以为负(当a ≠0,
b ≠0,90°<θ≤180°时),还可以为0(当a =0或b =0或θ=90°时).
(2)公式a ·b =|a ||b |cos〈a ,b 〉与a ·b =x1x2+y1y2都是用来求 两向量的数量积的,没有本质区别,只是书写形式上的差异,两 者可以相互推导.
=-1,则|n |= A.-1 C.2
B.1 D.-2
()
解析:
cos34π=|mm
·n =
||n |
-1 =- 2|n |
22,|n |=1.故选
B.
答案:B
北 师 大 版 ( 2019) 高中数 学《向 量数量 积的坐 标表示 》课件 (完整 版)1
2019年高考数学(理)热点题型和提分秘籍专题20平面向量的数量积(教学案)含解析
1.理解平面向量数量积的含义及其几何意义2.了解平面向量的数量积与向量投影的关系3.掌握数量积的坐标表达式,会进行平面向量数量积的运算4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系热点题型一 平面向量的数量积运算例1、(2018年全国I 卷理数)设抛物线C :y 2=4x 的焦点为F ,过点(–2,0)且斜率为的直线与C 交于M ,N 两点,则=A. 5B. 6C. 7D. 8 【答案】D【变式探究】【2017课标II ,理12】已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则的最小是( )A.2-B.32-C. 43- D.1- 【答案】B【解析】如图,以BC 为x 轴, BC 的垂直平分线DA 为y 轴, D 为坐标原点建立平面直角坐标系,则(3A , ()1,0B -, ()1,0C ,设(),P x y ,所以,,,所以,,当0,2P ⎛⎫⎪ ⎪⎝⎭时,所求的最小值为32,故选B .【变式探究】 (1)已知两个单位向量a ,b 的夹角为60°,c =t a +(1-t )b ,若b ·c =0,则t =__________。
(2)已知正方形ABCD 的边长为1,点E 是AB 边上的动点.则DE →·CB →的值为__________,DE →·DC →的最大值为__________。
【答案】(1)2 (2)1 1【解析】(1)由c =t a +(1-t )b 得,b ·c =t a ·b +(1-t )b 2=0,整理得t |a ||b |c os60°+(1-t )|b |2=0,化简得12方法二:选取{AB →,AD →}作为基底,设AE →=tAB →,0≤t ≤1,则DE →·CB →=(tAB →-AD →)·(-AD →) =-tAB →·AD →+AD →2=0+1=1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业
A组——基础对点练
1.已知|a|=6,|b|=3,向量a在b方向上的投影是4,则a·b为( )
A.12 B.8
C.- 8 D.2
解析:∵|a|cos〈a,b〉=4,|b|=3,∴a·b=|a||b|·cos〈a,b〉=3×4=12.
答案:A
2.已知向量a=(1,m),b=(3,-2),且(a+b)⊥b,则m=( )
A.-8 B.-6
C.6 D.8
解析:由向量的坐标运算得a+b=(4,m-2),由(a+b)⊥b,(a+b)·b=12
-2(m-2)=0,解得m=8,故选D.
答案:D
3.(2018·云南五市联考)在如图所示的矩形ABCD中,AB=4,AD=2,E
为线段BC上的点,则AE→·DE→的最小值为( )
A.12 B.15
C.17 D.16
解析:以B为坐标原点,BC所在直线为x轴,BA所在直线为y轴,建立
如图所示的平面直角坐标系,则A(0,4),D(2,4),设E(x,0)(0≤x≤2),所以AE→·DE
→
=(x,-4)·(x-2,-4)=x2-2x+16=(x-1)2+15,于是当x=1,即E为BC
的中点时,AE→·DE→取得最小值15,故选B.
答案:B
4.(2018·昆明市检测)已知a,b为单位向量,设a与b的夹角为π3,则a
与a-b的夹角为( )
A.π6 B.π3
C.2π3 D.5π6
解析:由题意,得a·b=1×1×cosπ3=12,所以|a-b|2=a2-2a·b+b2=1
-2×12+1=1,所以cos〈a,a-b〉=a·〈a-b〉|a||a-b|=a2-a·b1×1=1-12=12,
所以〈a,a-b〉=π3,故选B.
答案:B
5.在△ABC中,BC=5,G,O分别为△ABC的重心和外心,且OG→·BC→=5,
则△ABC的形状是( )
A.锐角三角形
B.钝角三角形
