线速度公式
线速度的计算公式

"计算线速度的公式及应用"一、介绍线速度的概念线速度是指物体在一定时间内从一点移动到另一点的平均速度,它是求取运动路线的一个重要指标,是运动路线的有效表示。
它是通过测量物体在一段时间内从一点到另一点的距离来计算的,因此它可以用来衡量物体的速度。
以北京到上海的高铁为例,从北京出发,经过多个站点,最终到达上海,它的线速度就是指它在一定时间内从北京出发到上海的平均速度。
假设它在8个小时内从北京出发到上海,那么它的线速度就是每小时行驶800公里。
另一个例子是汽车,假设一辆汽车从北京出发,在5小时内到达上海,那么它的线速度就是每小时行驶600公里。
线速度是衡量物体运动速度的重要指标,它不仅可以用来衡量物体的速度,而且可以用来衡量物体的距离,它是运动路线的有效表示。
通过计算物体在一段时间内从一点到另一点的距离,可以得到它的线速度,从而可以更好地了解物体的运动轨迹。
二、介绍线速度的计算公式线速度是指物体在一定时间内从一点移动到另一点的速度,它可以用来衡量物体的移动速度。
线速度的计算公式为:线速度=距离/时间,即:v=s/t。
以跑步为例,一个人从A点跑到B点,跑了10分钟,距离为2公里,那么他的线速度就是:v=2km/10min=0.2km/min,即每分钟他可以跑0.2公里。
再以汽车行驶为例,一辆汽车从A点开到B点,行驶了2小时,距离为200公里,那么它的线速度就是:v=200km/2h=100km/h,即每小时它可以行驶100公里。
线速度的计算公式是一个简单但十分有用的公式,它可以帮助我们更好地了解物体的运动状态,并作出更准确的判断。
例如,我们可以根据线速度来估算一辆汽车行驶到一个地点所需要的时间,或者估算一个人从一个地点跑到另一个地点所需要的时间。
此外,我们也可以利用线速度来比较不同物体的运动状态,例如比较汽车、自行车和步行者的线速度,以及比较不同时间段的线速度。
三、讲解计算公式中的参数参数是计算公式中的重要因素,它们可以用来确定最终的结果。
线速度与直径计算公式(一)

线速度与直径计算公式(一)线速度与直径计算公式1. 线速度公式•线速度(V)是指物体单位时间内在一条直线上所移动的距离,通常用米/秒(m/s)表示。
计算公式如下:V = π × d × n其中,V表示线速度,d表示直径,n表示转速。
例如,如果一个物体的直径为米,转速为10转/秒,则可以计算出其线速度:V = π × × 10 = m/s2. 直径公式•直径(d)是指通过物体中心的两个相互平行的线段的长度,通常用米(m)表示。
计算公式如下:d = C / π其中,d表示直径,C表示周长。
例如,如果一个物体的周长为2π米,则可以计算出其直径:d = (2π) / π = 2 米3. 周长公式•周长(C)是指物体封闭曲线的长度,通常用米(m)表示。
计算公式如下:C = π × d其中,C表示周长,d表示直径。
例如,如果一个物体的直径为米,则可以计算出其周长:C = π × = 米4. 转速公式•转速(n)是指单位时间内物体绕某一轴旋转的圈数,通常用转/秒表示。
计算公式如下:n = V / (π × d)其中,n表示转速,V表示线速度,d表示直径。
例如,如果一个物体的线速度为20 m/s,直径为1米,则可以计算出其转速:n = 20 / (π × 1) = 转/秒以上是线速度与直径计算公式的相关内容。
通过这些公式,我们可以便捷地计算物体的线速度、直径、周长和转速。
这些计算对于工程、物理等领域中的问题解决十分重要。
高三复习-转速与线速度公式

转速与线速度公式
线速度就是周长乘以转速(每分钟转多少圈),又有线速度=角速度×半径=转速*π*半径*2,所以有角速度=转速*2π。
线速度的公式在匀速圆周运动中,线速度的大小等于运动质点通过的弧长(S)和通过这段弧长所用的时间(△t)的值。
即v=S/△t,也是v=2πr/T,在匀速圆周运动中,线速度的大小虽不改变,但它的方向时刻在改变。
它和角速度的关系是v=ω*r、v=ωr=2πrf=2πnr=2πr/T
当运动质点做圆周运动的同时也做另一种平动时,例如汽车车轮上的某一定点,此时该质点的线速度为做圆周运动的线速度(w*r)与平动运动的速度(v
)的矢量之和:v=w*r+v
、v=Δl/Δt。
转速的公式当单位为r/S时,数值上与频率相等,即n=f=1/T,T为作圆周运动的周期。
圆周上某点对应的线速度为:v=2π*R*n,R为该点对应的旋转半径。
常见的转速有:额定转速和最大转速等。
离心机的国际单位是g,转速r/min变为g的公式:RCF=1.12*10^(-5)*r*(r/min)^2。
线速度和频率的关系公式

线速度和频率的关系公式在物理学中,线速度通常指的是线性运动的速度,是一个矢量量,可以用公式v=Δs/Δt来表示,其中v是线速度,Δs是物体在Δt时间内经过的距离。
线速度的单位通常是米/秒(m/s),也可以是其他长度单位除以时间单位的组合。
而频率表示事件发生的频率或周期性。
频率的定义是单位时间内事件发生的次数。
频率可以用公式f=1/T来表示,其中f是频率,T是周期。
频率的单位通常是赫兹(Hz),表示每秒发生的事件次数。
假设有一辆汽车行驶在直线上,已知汽车的速度是20米/秒(m/s),这个速度就是汽车的线速度。
如果汽车通过一个测速点的频率为10赫兹(Hz),表示汽车每秒通过测速点10次。
可以看出,线速度并不直接决定频率,而是和频率一起决定了通过测速点的次数。
根据线速度公式v=Δs/Δt,可以推导出通过测速点的距离Δs和通过测速点的时间间隔Δt之间的关系,即Δs=v*Δt。
假设通过测速点的时间间隔是0.1秒(s),那么通过测速点的距离就是2米(m),这意味着汽车在通过测速点时每次行驶2米的距离。
所以,当汽车通过测速点的频率为10赫兹(Hz)时,汽车每秒行驶20米的线速度,通过测速点的距离为2米。
另一个例子是声音传播。
声音的速度在空气中大约是343米/秒(m/s),而声音的频率决定了声音的音调。
根据声音的频率可以判断出声音是高音还是低音。
例如,当声音的频率为1000赫兹(Hz)时,表示每秒振动1000次。
这个频率对应的是中高音,而当声音的频率为100赫兹(Hz)时,表示每秒振动100次,这个频率对应的是低音。
所以,在声音传播中,线速度和频率的关系可以用来解释不同音调的声音。
总结来说,线速度和频率是两个不同的物理量,线速度是表示物体其中一点在单位时间内通过的距离,频率是单位时间内发生的事件次数。
线速度和频率的关系取决于具体的物理过程和条件。
在特定的情况下,线速度可以影响频率,例如汽车通过测速点的次数取决于汽车的线速度。
转速和线速度的转换公式
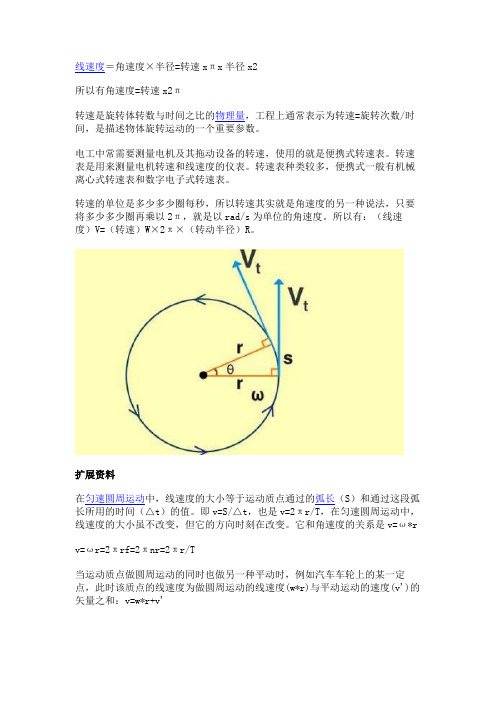
线速度=角速度×半径=转速xπx半径x2
所以有角速度=转速x2π
转速是旋转体转数与时间之比的物理量,工程上通常表示为转速=旋转次数/时间,是描述物体旋转运动的一个重要参数。
电工中常需要测量电机及其拖动设备的转速,使用的就是便携式转速表。
转速表是用来测量电机转速和线速度的仪表。
转速表种类较多,便携式一般有机械离心式转速表和数字电子式转速表。
转速的单位是多少多少圈每秒,所以转速其实就是角速度的另一种说法,只要将多少多少圈再乘以2π,就是以rad/s为单位的角速度。
所以有:(线速度)V=(转速)W×2π×(转动半径)R。
扩展资料
在匀速圆周运动中,线速度的大小等于运动质点通过的弧长(S)和通过这段弧长所用的时间(△t)的值。
即v=S/△t,也是v=2πr/T,在匀速圆周运动中,线速度的大小虽不改变,但它的方向时刻在改变。
它和角速度的关系是v=ω*r
v=ωr=2πrf=2πnr=2πr/T
当运动质点做圆周运动的同时也做另一种平动时,例如汽车车轮上的某一定点,此时该质点的线速度为做圆周运动的线速度(w*r)与平动运动的速度(v')的矢量之和:v=w*r+v'。
线速度计算公式

线速度计算公式线速度是物体在单位时间内所走过的距离,也可以理解为物体在单位时间内的速度。
线速度计算公式可以根据物体在运动过程中的位置变化和时间间隔来求得。
线速度 = 距离 / 时间其中,线速度的单位通常为米/秒(m/s)或者千米/小时(km/h)。
在物体做匀速直线运动的情况下,可以使用下列公式来计算线速度:线速度 = 位移 / 时间间隔位移是指物体从起点到终点的位置变化,可以用x表示,时间间隔可以用t表示。
假设物体在时间t0时刻位于起点A,在时间t1时刻位于终点B,则位移可以计算为:位移 = 终点位置 - 起点位置 = B - A = x线速度 = 位移 / 时间间隔 = x / (t1 - t0)这个公式适用于物体做匀速直线运动的情况,即物体以恒定的速度从起点运动到终点。
在这种情况下,位移可以看作是物体在做匀速直线运动过程中所走过的距离。
在物体做变速直线运动的情况下,线速度的计算稍微复杂一些。
可以通过物体在各个时刻的瞬时速度来求得。
瞬时速度是指物体在某一时刻的瞬时速率,可以用v表示。
速率是速度的大小,只有大小没有方向。
在作直线运动时,速度的大小等于线速度。
假设物体运动过程中在时间t0时刻的速度为v0,在时间t1时刻的速度为v1,时间间隔为Δt = t1 - t0,则平均速度可以计算为:平均速度 = (v1 + v0) / 2在时间间隔Δt内,物体的速度可能是变化的,那么可以将Δt按照若干小的时间段分割,然后求出每个小时间段内的平均速度,再取这些平均速度的极限值,即可得到瞬时速度。
瞬时速度可以根据物体的位置随时间的变化来求得。
假设物体在时间t0时刻的位置为x0,在时间t1时刻的位置为x1,则瞬时速度可以计算为:瞬时速度 = (x1 - x0) / Δt 考虑到时间间隔Δt趋近于0时,瞬时速度趋近于平均速度,所以可以写成:瞬时速度 = dx / dt其中,dx表示位置的微小变化,dt表示时间的微小变化。
线速度、角速度、速度关系

线速度、角速度与转速线速度、角速度与转速线速度V就是物体运动的速率。
那么物理运动360度的路程为:2πR这样可以求出它运动一周所需的时间,也就是圆周运动的周期:T=2πR/V角速度ω就是物体在单位时间内转过的角度。
那么由上可知,圆周运动的物体在T(周期)时间内运动的路程为2πR ,也就可以求出它的角速度:ω=2π / T =V / R线速度与角速度是解决圆周运动的重要工具,解题时要灵活运用。
高一物理公式总结匀速圆周运动1.线速度V=s/t=2πR/T2.角速度ω=Φ/t=2π/T=2πf ω×r=V3.向心加速度a=V2/R=ω2R=(2π/T)2r4.向心力F心=mV2/r=mω2r=mr(2π/T)2=mωv=F合5.周期与频率:T=1/f6.角速度与线速度的关系:V=ω r7.角速度与转速的关系ω=2 π n (此处频率与转速意义相同)8.主要物理量及单位:弧长(s):米(m);角度(Φ):弧度(rad);频率(f):赫(Hz);周期(T):秒(s);转速(n):r/s;半径(r):米(m);线速度(V):m/s;角速度(ω):rad/s;向心加速度:m/s2。
注:(1)向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供,方向始终与速度方向垂直,指向圆心;(2)做匀速圆周运动的物体,其向心力等于合力,并且向心力只改变速度的方向,不改变速度的大小,因此物体的动能保持不变,向心力不做功,但动量不断改变。
转速、线速度与角速度:v = (2 π r)/Tω = 2 π/Tv = 2 π r/60ω = 2 πn/60(T为周期,n为转速,即每分钟物体的转数)。
线速度v与转速n的公式

线速度v与转速n的公式线速度和转速的关系,有时候真让人头大。
想象一下,你在车里,坐着,一路飞驰,耳边的风呼啸而过,仿佛自己是个风驰电掣的赛车手。
这个过程背后有个不简单的公式在悄悄作祟。
哎,听说过线速度v和转速n吗?这俩小家伙就像好朋友一样,形影不离。
线速度v就是我们说的物体在运动中,单位时间内走的距离。
这玩意儿,简单点说,就是“快”和“慢”的区别。
想想你在马路上骑自行车,风驰电掣的时候,感觉像是飞起来了一样。
这个时候,线速度可不是一般的快。
线速度的公式是v = r × ω,这里r是半径,ω就是角速度,换句话说,就是转速。
这个公式就像是说,咱们想知道速度多快,得先知道转的圈数和半径有多大。
说到转速n,那真是个热闹的家伙,简单点说,它就是每分钟转多少圈。
比方说,电风扇开到最大,那声音咕噜噜的转个不停,这个转速就是在和你打招呼。
转速越高,线速度也就越快,像是比赛跑步一样,你想想,那些运动员,脚步轻快,风驰电掣,那就是转速给力的效果。
不过,有趣的是,转速和线速度的关系,并不是一成不变的,得看半径。
你想啊,半径大了,转一圈的距离就变长,线速度自然也就快了,真是一举两得。
想象一下,转个小圈,跟转个大圈,那感觉真是大相径庭。
就像是你在一个小篮球场上打球和在一个大球场上打球,跑动的距离可大不一样了。
再说说这线速度和转速在生活中的应用。
比如说,汽车轮胎的转速和车速,都是紧密相连的。
轮胎转得快,车子就跑得快,谁不想当个飙车手呢?开车可不能只看转速,还得看路况,要不然真是“飞上天,摔个跟头”。
所以说,这玩意儿可不止是理论,实打实地影响我们的日常生活。
还有个例子,转速在机械上也很重要,像电机工作的时候,转速不对,机器可就罢工了。
你想,哪个机器不怕“失业”呢?转速得稳定,才能保证工作效率。
换句话说,转速就像是机器的心脏,跳得稳,机器才能稳。
不过,大家常常忽略了,线速度和转速其实是相辅相成的。
就像老话说的,“一荣俱荣,一损俱损”,其中一个出问题,另一个也难逃干系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线速度公式
“线速度”是物体上任一点对定轴作圆周运动时的速度。
它的一般定义是质点(或物体上各点)作曲线运动(包括圆周运动)时所具有的即时速度。
计算公式是:v=S/△t,也是v=2πr/T。
在匀速圆周运动中,线速度的大小等于运动质点通过的弧长(S)和通过这段弧长所用的时间(△t)的值。
即v=S/△t,也是v=2πr/T,在匀速圆周运动中,线速度的大小虽不改变,但它的方向时刻在改变。
它和角速度的关系是v=ω*r
v=ωr=2πrf=2πnr=2πr/T
当运动质点做圆周运动的同时也做另一种平动时,例如汽车车轮上的某一定点,此时该质点的线速度为做圆周运动的线速度(w*r)与平动运动的速度(v')的矢量之和:v=w*r+v'
v=Δl/Δt。
