固体物理练习题(1)
固体物理题库

固体物理题库一、填空题第一章1.一些晶体的物理性质是各向异性的:原因是晶体中的原子排列(在不同方向上具有不同的周期性)2.按结构划分,晶体可分为大晶系,共布喇菲格子?3、面心立方原胞的体积为;第一布里渊区的体积为。
4.简单立方原始单元的体积为;第一布里渊区的体积为。
5.BCC原细胞的体积为;第一个布里渊区的体积是。
6、对于立方晶系,有、和三种布喇菲格子。
7.钻石晶体是一种晶格,由两个子晶格沿空间对角线位移1/4的长度组成。
晶胞中有一个碳原子。
8.原胞是的晶格重复单元。
对于布喇菲格子,原胞只包含个原子。
9.具有规则对称晶面的固体,以及具有长程有序特性的固体称为;在没有结晶(即有序化)的缩合过程中,原子的排列是长程无序固体。
10.由完全相同的一种原子构成的格子,格子中只有一个原子,称为布喇菲格子。
满足关系的b1,b2,b3为基矢,由gh=h1b1+h2b2+h3b3构成的格子,称为。
由若干个布喇菲格子相套而成的格子,叫做,其原胞中有以上的原子。
11.CSCL晶体是一种晶格,由两个子晶格组成,对角线位移为1/2的长度套构而成。
12.对于晶格常数为a的SC晶体,与正晶格向量r=AI+2aj+2ak正交的逆晶格平面族面指数为,其面间距为。
122,2.3a13。
晶体有一定的熔点,晶体的熔化热实际上是能量(破坏晶体结构或将晶体从结晶状态转变为非晶状态)14、一个面心立方晶格单元(晶胞)包含有个面心原子和个顶点原子,其原胞拥有个原子(3,1,1)15.晶胞是一种能反射晶体的结构单元。
在固体物理学中,理解单胞的结构(晶格的对称性和周期性)很重要16、根据晶胞对称性,晶体分为晶系;根据晶格特点,晶格分为bravais格子(7种,14种)18.格分为简单格和复合格。
NaCI是复合晶格,CSCI是复合晶格(面心立方,简立方)19.晶格常数是晶胞的边长,可通过实验(X射线衍射)测量20、常用的x射线衍射方法主要有、和转动单晶法(劳厄法、粉末法)21.单晶具有规则的几何形状,这是(晶体中原子排列具有周期性)22.根据原子排列特征,固体分为:、和准晶(晶体和非晶)23、晶体分为单晶和多晶,单晶是长程有序,具有规则的和物理性质(几何外形、各向异性)24.金属晶体是典型的多晶,多晶的单晶晶粒尺寸为m(10-6~10-5)25、晶体结构的基本特征是原子排列的周期性,原胞是能够反映的最小单元,一个原胞拥有一个原子(晶格周期性)26.单中心立方晶格单元(单元)包含一个顶点原子和一个单中心原子,其原始单元包含原子(1,1,1)28.晶格是晶体中原子排列的结构特征,称为布拉瓦晶格。
固体物理学习题课-1
1.12 利用转动对称操作,证 明六角晶系介电常数矩阵为. 解:若 A是一旋转对称操作,则晶体的介电常数 满足 = AT A., 对六角晶系,绕x(即a)轴旋转180o和绕z(即c)轴旋转120o都 是对称操作,坐标变换矩阵分别为
假 设 六 角晶系统的介电常数为 x= Ax' Ax得
可见 即有
=
00 0 0
00 0 0
00
0
=
0
= Az' Az得
可见
,=
于是得到六角晶系的介电常数
=
1.12 比较面心立方晶格、金刚石晶格、闪锌矿晶格、N acl晶格 的晶系、布拉伐格子、点群、空间群。
补充习题 01 做出简单立方晶格、面心立方晶格和体心 立方晶格的维格纳 — 塞茨原胞 (Wingner-Seitz)
体心立方
面心立方
1.9 指出立方晶格(111)面与(100)面(111)面与(110)面的交线的晶 向
(111)面与(100)面的交线的AB
—— AB平移,A与O点重合
B点位矢 ⇀
⇀⇀
(111)面与(100)面的交线的晶向 ⇀ ⇀ —— 晶向指数
(111)面与(110)面的交线的AB
—— 将AB平移,A与原点O重合,B点位矢
⇀
⇀⇀
(111)面与(110)面的交线的晶向 ⇀⇀
—— 晶向指数 110
1.10 找出立方体中保持x 轴不变的所有对称操作,并指出他们中 任意两个操作乘积的结果 解:立方体中保持x轴不变,可有绕x轴转 , , ,加上不动 C1,所有对称操作构成群C4=(C1 C2 C3 C4),群中任意两 元素乘积仍是群中元。
a
3 2 –( )2= ( )2
大学固体物理试题及答案

大学固体物理试题及答案一、选择题(每题5分,共20分)1. 下列关于晶体结构的描述,错误的是:A. 晶体具有规则的几何外形B. 晶体内部的原子排列是无序的C. 晶体具有各向异性D. 晶体具有固定的熔点答案:B2. 固体物理中,描述电子在晶格中运动的方程是:A. 薛定谔方程B. 牛顿运动方程C. 麦克斯韦方程D. 热力学第一定律答案:A3. 固体中,电子能带的宽度与下列哪个因素有关?A. 电子的电荷B. 电子的质量C. 晶格的周期性D. 电子的自旋答案:C4. 金属导电的原因是:A. 金属内部存在自由电子B. 金属内部存在空穴C. 金属内部存在离子D. 金属内部存在分子答案:A二、填空题(每题5分,共20分)1. 晶体的周期性结构可以用_________来描述。
答案:晶格常数2. 能带理论中,电子在能带之间跃迁需要吸收或释放_________。
答案:光子3. 根据泡利不相容原理,一个原子轨道内最多可以容纳_________个电子。
答案:24. 半导体的导电性介于金属和绝缘体之间,其原因是半导体的_________较窄。
答案:能带间隙三、简答题(每题10分,共30分)1. 简要说明什么是费米能级,并解释其在固体物理中的重要性。
答案:费米能级是指在绝对零度时,电子占据的最高能级。
在固体物理中,费米能级是描述电子分布状态的重要参数,它决定了固体的导电性、磁性等物理性质。
2. 解释为什么金属在常温下具有良好的导电性。
答案:金属具有良好的导电性是因为其内部存在大量的自由电子,这些电子可以在电场作用下自由移动,形成电流。
3. 什么是超导现象?请简述其物理机制。
答案:超导现象是指某些材料在低于某一临界温度时,电阻突然降为零的现象。
其物理机制与电子之间的库珀对形成有关,这些库珀对在低温下能够无阻碍地流动,从而实现零电阻。
四、计算题(每题15分,共30分)1. 假设一个一维晶格,晶格常数为a,电子的有效质量为m*,求电子在第一能带的最低能级。
固体物理第一章习题

15
得到:
d 1 h 2 k l a 2 s h i n 2 2 b k 2 2 c 2 s l i n 2 2 a 2 c h s c i o n s 2 s i n 1 2 a h 2 2 c l 2 2 2 h l a c c o s b k 2 2
即:
1
1 h2 l2 2hlcos k22 dhkl sin2a2c2 ac b2
bc
•
ca
0
b*•c* 42 2
ca
•
ab
0
将以上诸式代入:
d 1 h 2 k l 4 1 2 h 2 a 2 k 2 b 2 l 2 c 2 2 h k a * • b * 2 k lb * • b * 2 h la * • c *
编辑版pppt
1
1
2p K h 1 h 2h 32p (h 1 b 1h 2 b 2h 3 b 3)
Kh1h2h3 与晶面族(h1h2h3)正交。
因此,若已知晶面族的密勒指数(hkl),则原胞坐标 系中的面指数
(h1h2h3)1 p{(kl)(lh)(hk)} 其中p是(k+l)(l+h)(h+k)的公约数。
编辑版pppt
只有当 n(4 3h2 3kl)奇数时才出现衍射消光
编辑版pppt
23
(a)n为奇数时:若l是偶数,nl也是偶数 为保证n(4/3h+2/3k+l)=奇数成立, 须n(4/3h+2/3k)=奇数 由此,2n(2h+k)=3奇数=奇数。 由于h, k为整数,上式左端是偶数,右端为奇数,显
然不成立。
矛盾的产生是l为偶数的条件导致的,所以l不能为偶 数,只能为奇数。因而n(4/3h+2/3k)=偶数,即(2h+k)=3 整数/n=整数。
固体物理学习题答案(朱建国版)汇编

《固体物理学》习题参考第一章1.1 有许多金属即可形成体心立方结构,也可以形成面心立方结构。
从一种结构转变为另一种结构时体积变化很小.设体积的变化可以忽略,并以R f 和R b 代表面心立方和体心立方结构中最近邻原子间的距离,试问R f /R b 等于多少?答:由题意已知,面心、体心立方结构同一棱边相邻原子的距离相等,都设为a :对于面心立方,处于面心的原子与顶角原子的距离为:R f=2 a 对于体心立方,处于体心的原子与顶角原子的距离为:R b=2a 那么,Rf Rb1.2 晶面指数为(123)的晶面ABC 是离原点O 最近的晶面,OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,除O 点外,OA ,OB 和OC 上是否有格点?若ABC 面的指数为(234),情况又如何?答:根据题意,由于OA 、OB 和OC 分别与基失a 1,a 2和a 3重合,那么 1.3 二维布拉维点阵只有5种,试列举并画图表示之。
答:二维布拉维点阵只有五种类型:正方、矩形、六角、有心矩形和斜方。
分别如图所示:1.4 在六方晶系中,晶面常用4个指数(hkil )来表示,如图所示,前3个指数表示晶面族中最靠近原点的晶面在互成120°的共平面轴a 1,a 2,a 3上的截距a 1/h ,a 2/k ,a 3/i ,第四个指数表示该晶面的六重轴c 上的截距c/l.证明:i=-(h+k ) 并将下列用(hkl )表示的晶面改用(hkil )表示:(001)(133)(110)(323)(100)(010)(213)答:证明设晶面族(hkil )的晶面间距为d ,晶面法线方向的单位矢量为n °。
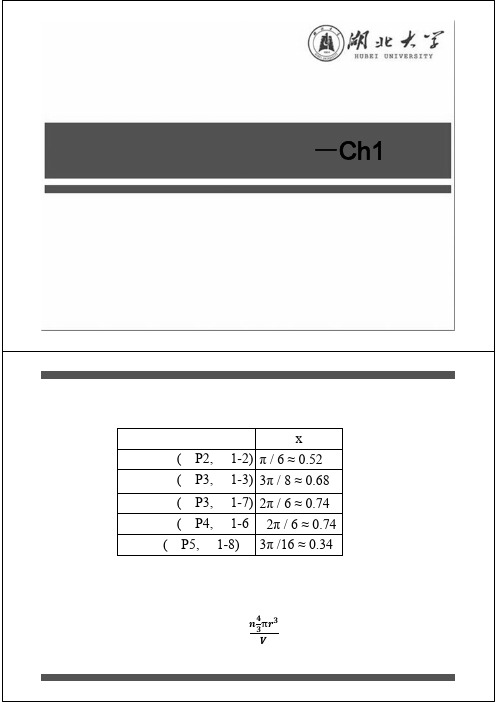
因为晶面族(hkil )中最靠近原点的晶面ABC 在a 1、a 2、a 3轴上的截距分别为a 1/h ,a 2/k ,a 3/i ,因此123o o o a n hda n kd a n id=== ……… (1) 正方 a=b a ^b=90° 六方 a=b a ^b=120° 矩形 a ≠b a ^b=90° 带心矩形 a=b a ^b=90° 平行四边形 a ≠b a ^b ≠90°由于a 3=–(a 1+ a 2)313()o o a n a a n =-+把(1)式的关系代入,即得()id hd kd =-+ ()i h k =-+根据上面的证明,可以转换晶面族为(001)→(0001),(133)→(1323),(110)→(1100),(323)→(3213),(100)→(1010),(010)→(0110),(213)→(2133)1.5 如将等体积的硬球堆成下列结构,求证球可能占据的最大面积与总体积之比为(1)简立方:6π(2(3)面心立方:6(4)六方密堆积:6(5)金刚石:。
2010-2011(1)《固体物理》试卷A附答案

宝鸡文理学院试题课程名称 固体物理 适 用 时 间 2011年1月 试卷类别 A 适用专业、年级、班 2008级物理教育专业一、简答题(每题6分,共6×5=30分)1、试述离子键、共价键、金属键、范德瓦尔斯和氢键的基本特征.2、试述晶态、非晶态、准晶、多晶和单晶的特征性质。
3、什么叫声子?对于一给定的晶体,它是否拥有一定种类和一定数目的声子?4、周期性边界条件的物理含义是什么?引入这个条件后导致什么结果?如果晶体是无限大,q 的取值将会怎样?5、倒格子的实际意义是什么?一种晶体的正格矢和相应的倒格矢是否有一一对应的关系?二、试证明体心立方格子和面心立方格子互为正倒格子。
(20分)三、一维晶格,晶格由两种离子组成,间距为R 0,计算晶格的Madelung 常数α。
(15分)四、用钯靶αK X 射线投射到NaCl 晶体上,测得其一级反射的掠射角为5。
9°,已知NaCl 晶胞中Na +与Cl -的距离为2.82×10—10m ,晶体密度为2.16g/cm 3.求:(1)X 射线的波长;(2)阿伏加德罗常数。
(20分)五、写出量子谐振子系统自由能,证明在经典极限,自由能为:(15分) ⎪⎪⎭⎫ ⎝⎛+≈∑KT hw KT U F q q o ln宝鸡文理学院试题参考答案与评分标准课程名称 固体物理 适 用 时 间 2011年1月 试卷类别 A 适用专业、年级、班07物理教育一、简答题(每小题6分,5×6=30分)1、试述离子键、共价键、金属键、范德瓦尔斯和氢键的基本特征。
解:(1)离子键:无方向性,键能相当强;(2)共价键:饱和性和方向性,其键能也非常强;(3)金属键:有一定的方向性和饱和性,其价电子不定域于2个原子实之间,而是在整个晶体中巡游,处于非定域状态,为所有原子所“共有”;(4)范德瓦尔斯键:依靠瞬时偶极距或固有偶极距而形成,其结合力一般与7r 成反比函数关系,该键结合能较弱;(5)氢键:依靠氢原子与2个电负性较大而原子半径较小的原子(如O,F,N 等)相结合形成的。
固体物理题库第一章晶体的结构

固体物理题库第⼀章晶体的结构第⼀章晶体的结构⼀、填空体(每空1分)1. 晶体具有的共同性质为长程有序、⾃限性、各向异性。
2. 对于简⽴⽅晶体,如果晶格常数为a,它的最近邻原⼦间距为 a ,次近邻原⼦间,原胞与晶胞的体积⽐1:1 ,配位数为 6 。
3. 对于体⼼⽴⽅晶体,如果晶格常数为a a2,次近邻原⼦间距为 a ,原胞与晶胞的体积⽐1:2 ,配位数为8 。
4. 对于⾯⼼⽴⽅晶体,如果晶格常数为a邻原⼦间距为 a ,原胞与晶胞的体积⽐1:4 ,配位数为12 。
5. ⾯指数(h1h2h3)所标志的晶⾯把原胞基⽮a1,a2,a3分割,其中最靠近原点的平⾯在a1,a2,a3上的截距分别为__1/h1_,_1/h2__,__1/h3_。
6. 根据组成粒⼦在空间排列的有序度和对称性,固体可分为晶体、准晶体和⾮晶体。
7. 根据晶体内晶粒排列的特点,晶体可分为单晶和多晶。
8. 常见的晶体堆积结构有简⽴⽅(结构)、体⼼⽴⽅(结构)、⾯⼼⽴⽅(结构)和六⾓密排(结构)等,例如⾦属钠(Na)是体⼼⽴⽅(结构),铜(Cu)晶体属于⾯⼼⽴⽅结构,镁(Mg)晶体属于六⾓密排结构。
9. 对点阵⽽⾔,考虑其宏观对称性,他们可以分为7个晶系,如果还考虑其平移对称性,则共有14种布喇菲格⼦。
10.晶体结构的宏观对称只可能有下列10种元素:1 ,2 ,3 ,4 ,6 ,i ,m ,3,4,6,其中3和6不是独⽴对称素,由这10种对称素对应的对称操作只能组成32个点群。
11. 晶体按照其基元中原⼦数的多少可分为复式晶格和简单晶格,其中简单晶格基元中有 1 个原⼦。
12. 晶体原胞中含有 1 个格点。
13. 魏格纳-塞茨原胞中含有 1 个格点。
⼆、基本概念1. 原胞原胞:晶格最⼩的周期性单元。
2. 晶胞结晶学中把晶格中能反映晶体对称特征的周期性单元成为晶胞。
3. 散射因⼦原⼦内所有电⼦在某⼀⽅向上引起的散射波的振幅的⼏何和,与某⼀电⼦在该⽅向上引起的散射波的振幅之⽐。
固体物理:第一章典型习题

FGIHGK: E
(111)
I A
H B
消光现象
• 点阵消光 • 起源于体心或者面心上有附加点阵而引起的结构因子F=0
的消光现象。如对于体心晶格,衍射hkl中,h+k+l=奇数的 衍射将系统消失;对于面心晶格,hkl为异性数(非同奇同 偶的数)时衍射线消失。这一类消光称为点阵消光。
1.6证明简立方的(hkl)晶面系的面间距:
d2
a2
h2 k 2 l 2
证明思路: d 2
G
证明:设正格子基矢为
倒格子基矢易计算得到:
a1 ai
a2 a j
a3 ak
b1 b2 b3
2
a
2
a
2
a
i
j
k
G hb1 kb2
2 (hi k j
a
l b3 lk)
代入公式可得:
(hkl)晶面系的面间距
d
2
G
2
a
2
h2 k 2 l 2
a h2 k 2 l 2
1.7立方格子的特征
项目 晶胞体积
每个晶胞所含格点数
原胞体积 最近邻数 最近邻距离 次近邻数 次近邻距离
简立方 体心立方
面心立方
a3
a3
a3
1
2
4
(即1+8×1/8) (即 8 × 1/8+6 × 1/2)
a3
简立方体心立方面心立方晶胞体积18612原胞体积12最近邻距离次近邻数1218画出体心立方和面心立方晶格结构在100110111面上的原子排列1001101111体心立方晶格2面心立方晶格10011011119指出立方晶格111面与100面111面与110面交线的晶向写出晶列
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题
1.晶体中的原子排列的最大特点是 ,这种有序排列至少是在 量
级范围内。由晶格的周期性,晶体不允许有 度旋转对称轴。
2.晶体中可以独立存在的8种对称元素是1、2、3、4、6、 、 、 。
晶体的点群类型有32种,空间对称群类型有 种,立方晶格的对称操作一共
有48个,故而立方晶系晶体的独立介电常数有 个。
3.半导体材料Si和Ge单晶的晶体空间点阵类型是 ,倒易空间点阵类型
为 。第一布里渊区的形状为 ,每个原子的最近邻原子数
为 。
4.共价键的共同特点是 和 ,但是对大多数晶体而言,其结合是混
合型,比如石墨晶体,即有共价结合,还有 和 结合。
5. 金刚石是复式格子,应该有 支格波,其中声学支有 。右图
是实验测量得到的金刚石的沿[111]方向的振动谱,从该频谱图中,光学波
和声学波的两支横波都是简并的,所以只能测出四条频谱曲线,最高一只
是 ,最低的是 。
二、若一晶体两个离子间的相互作用能可以表示为:
8
)(rrru
)(0,0
,请完成如下问题。
1. 试求出原子间的平衡间距r0;
2. 请问,平衡态下吸引能是排斥能的多少倍?
3. 请证明,当两原子被拉开至711/36r(临界距离)时,两个原子将被拉
开。
三、推导简立方晶格中由原子S态波函数形成的能带
(1)写出最近邻近似作用近似下,由紧束缚近似法求出晶体s态的电子能量表
达式E(k)。
(2)指出能带底和能带顶晶体的电子能量,其能带宽度等于多少
(3)画出原子能级分裂成能带示意图
(4)近自由电子模型和紧束缚模型各有何特点,其适用对象各是什么
四、请回答如下声子和热容理论的相关问题。
1.声子是否为真实粒子,请说明原因?
2.晶体中声子的数目是否守恒?按照德拜模型,声子数目与温度的变化关系是什
么
3.若温度一定时,一个光学波的声子数目多,还是一个声学波的声子数目多,为
什么?
4. 请简述爱因斯坦模型的成功之处和不足之处?
5. 试说明德拜模型在晶格比热温度关系上有那些成功和不足并说明原因。
五、设有一维双原子链,两种原子的质量分别为M和m,且M >m,相邻原子间
的平衡间距为a,作用力常数为β,考虑原子沿链的一维振动;分子间相邻原子
的力系数为β2,分子的两原子间距为d,晶格常数为a。
1.求格波简正模的频率与波矢间的关系ω(q)。
2.证明波矢q和𝑞+
𝜋
𝑎
𝑛(其中n为整数),描述的格波是全同的。
4.在20oC时铜粉末样品的一级衍射角是47.75o,在1000oC时是46.60
o
,求铜的
线性膨胀系数(6分)
