第5章-轴心受压构件
合集下载
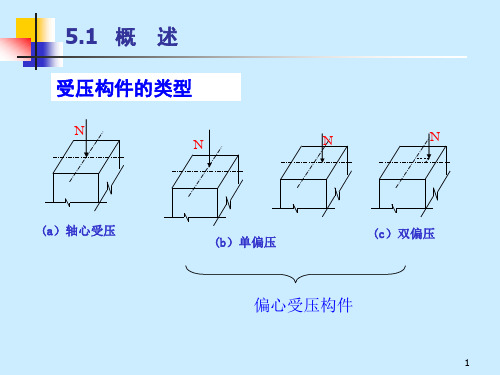
第五章受压构件计算
8 f y Ass1 s dcor
Acor
20
2 、 正截面受压承载力计算
(a) (b)
2
s
(c)
Ass 1 Acor S d cor
Ass 1
2 d cor
S d cor
4
Ass 1 d cor 4S
箍筋的换算纵筋面积:
dcor
按体积相等原则换算
s
1.0l
0.7l 0.5l 实际结构按 规范规定取值
一端固定,一端自由
2.0l
4、公式应用
• 截面设计:
已知:fc, f y, l0, N, 求As、A
A N 0.9 ( f c ' f y' )
设ρ’(0.6%~2%), φ=1
N -f c Ac ) 0.9 As f y (
27
受拉破坏时的截面应力和受拉破坏形态 (a)截面应力 (b)受拉破坏形态
N
cu
e0 N
fyAs
f yAs
(a)
N
(b)
2、受压破坏
产生受压破坏的条件有两种情况: ⑴当相对偏心距e0/h0较小,截面全部受压或大部分受压 ⑵或虽然相对偏心距e0/h0较大,但受拉侧纵向钢筋配置较多时
N N
As 太 多
17
混凝土圆柱体三向受压状态的纵向抗压强度
1 f c 4 2
2 、 正截面受压承载力计算
(a) (b)
2
s
(c)
dcor fyAss1
s
2
fyAss1
1 f c 4 2
达到极限状态时(保护层已剥落,不考虑)
Nu 1 Acor f y As
建筑结构:第五章

面积与其中心到给定轴距离的乘积)。
南京林业大学《建筑结构》授课教师: 王志强博士
第五章 木结构构件计算
5.3 受弯构件
试求宽为b、高为h的矩形,截面如图,在中性轴X-X处的 最大水平剪应力。
解:中性轴以上的面积为(b*d/2),其形心到中性轴的 距离为d/4,则
S = (b × h) × h = bh2 24 8
fv
=
VS Ib
=
V × bh2 8 bh3 12× b
=
3× 2
V bd
这就是通常用于计算矩形截面的最大水平单
位剪应力的公式。
南京林业大学《建筑结构》授课教师: 王志强博士
第五章 木结构构件计算
5.3 受弯构件
例1:如右图所示,箱形梁上的最大竖向 剪力为4000 lb,试确定其胶合线上的单 位剪应力。
计算长度l0 =0.8×3000=2400mm
i = 1 × b = 1 ×150 = 43.35mm
12
12
λ = l0 = 2400 = 55.36〈75
i 43.35
ϕ
=
1+
1
(λ
)2
=
1
1+ (55.36)2
= 0.676
80
80
N = 240000 = 13.15N / mm〈14.3N / mm
②有缺口时,根据缺口的不同位置确 定Ao。
缺口不在边缘时,取Ao=0.9A; 缺口在边缘且对称时,取Ao=An; 缺口在边缘但不对称时,应按偏心受
压构件计算。 验算稳定时,螺栓孔不作为缺口考虑。
南京林业大学《建筑结构》授课教师: 王志强博士
第五章 木结构构件计算
南京林业大学《建筑结构》授课教师: 王志强博士
第五章 木结构构件计算
5.3 受弯构件
试求宽为b、高为h的矩形,截面如图,在中性轴X-X处的 最大水平剪应力。
解:中性轴以上的面积为(b*d/2),其形心到中性轴的 距离为d/4,则
S = (b × h) × h = bh2 24 8
fv
=
VS Ib
=
V × bh2 8 bh3 12× b
=
3× 2
V bd
这就是通常用于计算矩形截面的最大水平单
位剪应力的公式。
南京林业大学《建筑结构》授课教师: 王志强博士
第五章 木结构构件计算
5.3 受弯构件
例1:如右图所示,箱形梁上的最大竖向 剪力为4000 lb,试确定其胶合线上的单 位剪应力。
计算长度l0 =0.8×3000=2400mm
i = 1 × b = 1 ×150 = 43.35mm
12
12
λ = l0 = 2400 = 55.36〈75
i 43.35
ϕ
=
1+
1
(λ
)2
=
1
1+ (55.36)2
= 0.676
80
80
N = 240000 = 13.15N / mm〈14.3N / mm
②有缺口时,根据缺口的不同位置确 定Ao。
缺口不在边缘时,取Ao=0.9A; 缺口在边缘且对称时,取Ao=An; 缺口在边缘但不对称时,应按偏心受
压构件计算。 验算稳定时,螺栓孔不作为缺口考虑。
南京林业大学《建筑结构》授课教师: 王志强博士
第五章 木结构构件计算
第五章1 钢筋混凝土受压构件正截面承载力计算w

柱的破坏形态
5-6弯曲变形
5-7轴心受压长柱的破坏形态
试验结果表明长柱的承载力低于相同条件短柱的承载 试验结果表明长柱的承载力低于相同条件短柱的承载 力,目前采用引入稳定系数Ψ的方法来考虑长柱纵向 挠曲的不利影响, 挠曲的不利影响,Ψ值小于1.0,且随着长细比的增大 而减小。 而减小。
表5-1 钢筋混凝土轴心受压构件的稳定系数面承载力计
5.2.1 受力过程及破坏特征 轴心受拉构件从开始加载到破坏, 轴心受拉构件从开始加载到破坏,其受力过程可 分为三个不同的阶段: 分为三个不同的阶段: 1.第I阶段 开始加载到混凝土开裂前, 属于第I 阶段。 从 开始加载到混凝土开裂前 , 属于第 I 阶段 。 此 纵向钢筋和混凝土共同承受拉力, 时 纵向钢筋和混凝土共同承受拉力,应力与应变大致 成正比,拉力 N与截面平均拉应变 ε 之间基本上是线 成正比, 性关系, 性关系,如图5-2a中的OA段。
当现浇钢筋混凝土轴心受压构件截面长边或直径 小于300㎜时 ,式中混凝土强度设计值应乘以系数0.8 (构件质量确有保障时不受此限)。 4. 构造要求 (1)材料 混凝土强度对受压构件的承载力影响较大, 混凝土强度对受压构件的承载力影响较大,故宜 采用强度等级较高的混凝土 强度等级较高的混凝土, 采用强度等级较高的混凝土,如C25,C30,C40等。 在高层建筑和重要结构中, 在高层建筑和重要结构中,尚应选择强度等级更高的 混凝土。 混凝土。 钢筋与混凝土共同受压时, 钢筋与混凝土共同受压时 , 若钢筋强度过高 ( 如 则不能充分发挥其作用, 高于 0.002Es) , 则不能充分发挥其作用 , 故 不宜用高 强度钢筋作为受压钢筋。同时, 强度钢筋作为受压钢筋。同时,也不得用冷拉钢筋作 为受压钢筋。 为受压钢筋。
5-6弯曲变形
5-7轴心受压长柱的破坏形态
试验结果表明长柱的承载力低于相同条件短柱的承载 试验结果表明长柱的承载力低于相同条件短柱的承载 力,目前采用引入稳定系数Ψ的方法来考虑长柱纵向 挠曲的不利影响, 挠曲的不利影响,Ψ值小于1.0,且随着长细比的增大 而减小。 而减小。
表5-1 钢筋混凝土轴心受压构件的稳定系数面承载力计
5.2.1 受力过程及破坏特征 轴心受拉构件从开始加载到破坏, 轴心受拉构件从开始加载到破坏,其受力过程可 分为三个不同的阶段: 分为三个不同的阶段: 1.第I阶段 开始加载到混凝土开裂前, 属于第I 阶段。 从 开始加载到混凝土开裂前 , 属于第 I 阶段 。 此 纵向钢筋和混凝土共同承受拉力, 时 纵向钢筋和混凝土共同承受拉力,应力与应变大致 成正比,拉力 N与截面平均拉应变 ε 之间基本上是线 成正比, 性关系, 性关系,如图5-2a中的OA段。
当现浇钢筋混凝土轴心受压构件截面长边或直径 小于300㎜时 ,式中混凝土强度设计值应乘以系数0.8 (构件质量确有保障时不受此限)。 4. 构造要求 (1)材料 混凝土强度对受压构件的承载力影响较大, 混凝土强度对受压构件的承载力影响较大,故宜 采用强度等级较高的混凝土 强度等级较高的混凝土, 采用强度等级较高的混凝土,如C25,C30,C40等。 在高层建筑和重要结构中, 在高层建筑和重要结构中,尚应选择强度等级更高的 混凝土。 混凝土。 钢筋与混凝土共同受压时, 钢筋与混凝土共同受压时 , 若钢筋强度过高 ( 如 则不能充分发挥其作用, 高于 0.002Es) , 则不能充分发挥其作用 , 故 不宜用高 强度钢筋作为受压钢筋。同时, 强度钢筋作为受压钢筋。同时,也不得用冷拉钢筋作 为受压钢筋。 为受压钢筋。
第5章轴心受压构

φ--稳定系数,按附录表4-3、4-4、4-5、5-6采用。
5.6实腹式轴心受压构件的局部稳定
5.6.1概述 组成构件的板件出现鼓曲 称为板件失稳,即局部失 稳。 板件的局部失稳并不一定 导致整个构件丧失承载能 力,但由于失稳板件退出 工作,将使能承受力的截 面(称为有效截面)面积 减少,同时还可能使原本 对称的截面变得不对称, 促使构件整体破坏。
N
2 cr , x 1 cr , y
I e, x Ix
2 (k b) t (h / 2) k 2 2 b t ( h / 2)
2
N N
I e, y Iy
2 cr , y
t (k b) 3 / 12 k3 t b 3 / 12
焊接工字钢残余应力分布
由于k小于1,对这样的残余应力分布,其对y轴稳定承 载力的影响比对x轴要大的多。
对板件的稳定目前有两种处理方法,一是不容许出现 板件失稳,二是板件可以失稳,利用其屈曲后强度, 但要求板件受到的轴力小于板件发挥屈曲后强度的极 限承载力。考虑屈曲后强度的轴压杆设计目前用于薄 壁型钢轴压杆。 5.6.2实腹轴心压杆中板件的临界应力 1、板件的分类 根据板件两边支承情况将其分为加劲板件、部分加劲 板件和非加劲板件三种。 加劲板件为两纵边均与其他板件相连接的板件; 部分加劲板件即为一纵边与其他板件相连,另一纵边 为卷边加劲的板件,在薄壁型钢中普片存在;
5.4.1格构式轴心受压构件绕实轴(y-y轴)的整体稳定
格构式轴心受压构件绕实轴(y-y轴)的整体稳定承载力 计算和实腹式轴心受压构件完全相同。 5.4.2格构式轴心受压构件绕虚轴(x-x轴)的整体稳定 构式轴心受压构件绕虚轴发生弯曲失稳时,所产生的 剪力由缀材承担,缀材抵抗剪变形的能力小,剪力产 生的剪切变形大,对整体稳定承载力的不利影响必须 予以考虑。 2 EI 1 即 N
轴心受压构件

其中,4、5、6均属于初始缺陷。
以上各因素都不是孤立的。
第13页/共77页
5.3.3 轴心压杆的弯曲失稳、扭转失稳、弯扭失稳
(1) 具有初始缺陷的任意非对称开口薄壁轴心 压杆弯扭失稳弹性微分方程,对任一截面取:
Z ( ) N
Y(v)
X(u)
M x 0, M y 0, M z 0
第14页/共77页
第9页/共77页
a)理想轴心压杆欧拉临界应力
l/2
p 2 EI
Ncr NE l 2
NE — 欧拉(Euler)临界力
欧拉临界应力
scr
sE
NE A
pl
2EI 2A
pl
2E(
2
I A
)2
p2E
l2
i
2
(pl/2iE)2pl2E2
l/2
图 有初弯曲的 轴心压杆
λ——杆件长细比,λ=l/i;
i ——截面对应于屈曲的回转半径, i = I/A。
3.不对称截面均的弯扭失稳
当压杆的截面无对称轴时,微分方程即为公式。 这三个微分方程是互相联立的,因此,杆件失稳时必 定是弯扭变形状态,属于弯扭失稳。
EI EI
x y
(v(4) (u ( 4 )
v0(4) ) u0(4) )
Nv'' Nu
Nx0 '' '' Ny0
''
0 0
EI (
(4)
弯曲屈曲:双轴对称截面,单轴对称截面绕非对称轴; 扭转屈曲:十字形截面; 弯扭屈曲:单轴对称截面(槽钢,等边角钢)。
第6页/共77页
第7页/共77页
5.2 轴心受压构件的强度 以净截面的平均应力强度为准则,即
以上各因素都不是孤立的。
第13页/共77页
5.3.3 轴心压杆的弯曲失稳、扭转失稳、弯扭失稳
(1) 具有初始缺陷的任意非对称开口薄壁轴心 压杆弯扭失稳弹性微分方程,对任一截面取:
Z ( ) N
Y(v)
X(u)
M x 0, M y 0, M z 0
第14页/共77页
第9页/共77页
a)理想轴心压杆欧拉临界应力
l/2
p 2 EI
Ncr NE l 2
NE — 欧拉(Euler)临界力
欧拉临界应力
scr
sE
NE A
pl
2EI 2A
pl
2E(
2
I A
)2
p2E
l2
i
2
(pl/2iE)2pl2E2
l/2
图 有初弯曲的 轴心压杆
λ——杆件长细比,λ=l/i;
i ——截面对应于屈曲的回转半径, i = I/A。
3.不对称截面均的弯扭失稳
当压杆的截面无对称轴时,微分方程即为公式。 这三个微分方程是互相联立的,因此,杆件失稳时必 定是弯扭变形状态,属于弯扭失稳。
EI EI
x y
(v(4) (u ( 4 )
v0(4) ) u0(4) )
Nv'' Nu
Nx0 '' '' Ny0
''
0 0
EI (
(4)
弯曲屈曲:双轴对称截面,单轴对称截面绕非对称轴; 扭转屈曲:十字形截面; 弯扭屈曲:单轴对称截面(槽钢,等边角钢)。
第6页/共77页
第7页/共77页
5.2 轴心受压构件的强度 以净截面的平均应力强度为准则,即
第五章 受压构件的截面承载力

12
3.受压短柱承载力
N 混凝土压碎 钢筋凸出
钢筋屈服
混凝土压碎
N
达到最大承载力时混凝土压坏。 o
l
c' f c 应变 c' 0
如果 y 0则钢筋已经屈服 s' f y' 如果 y 0则钢筋未屈服但 f
' s ' y
fc f y As
(注意f y' 取值原则)
6e0 N 弹性材料 ( 1 ) A h
钢筋混凝土偏心受压构件的破坏形态与 偏心距e0和纵向钢筋配筋率有关
20
一、偏心受压短柱的破坏形态
(一)受拉破坏(大偏心受压破坏)
条件:偏性距较大且As不过多。 靠近纵向力一侧受压,远离纵向力一侧受拉。截面受拉侧混 凝土较早出现裂缝,As的应力随荷载增加发展较快,首先达 到屈服强度。此后,裂缝迅速开展,受压区高度减小,压区 混凝土压碎而达到破坏。受压侧钢筋A‘s 一般能受压屈服。
普通箍筋柱:
螺旋箍筋柱:箍筋的形状为圆形, 且间距较密,其对混凝土的约束作 用较强。
9
纵筋的作用:
◆ ◆ ◆
协助混凝土受压减小截面尺寸、改善截面延性。
承担弯矩作用
减小持续压应力下混凝土收缩和徐变的影响。
箍筋的作用: 与纵筋组成空间骨架,避免纵筋受压外凸。
10
一、配有纵向钢筋和普通箍筋柱
1.试验分析
混凝土:混凝土强度等级对受压构件的承载影响较大,一 般应采用强度等级较高的混凝土。目前我国一般结构中柱 的混凝土强度等级常用C30~C40,在高层建筑中, C50~C60级混凝土也经常使用。 钢筋:纵筋:HRB400 HRB500。箍筋:HRB400 HPB300。
钢结构第五章_轴心受力构件详解

得欧拉临界力和临界应力:
Ncr
NE
2 EI l2
2 EA
2
cr
E
2E 2
(4 7) (4 8)
上式中,假定材料满足虎克定律,E为常量,因此当
截面应力超过钢材的比例极限 fp 后,欧拉临界力公式不 再适用。
第五章 钢柱与钢压杆
3、初始缺陷、加工条件和截面形式对压杆稳定都有影响
初
力学缺陷:残余应力、材料不均匀等
钢结构中理想的轴心受压构件的失稳,也叫发生屈 曲。理想的轴心受压构件有三种屈曲形式,即:弯曲屈 曲,扭转屈曲,弯扭屈曲。
第五章 钢柱与钢压杆
(1)弯曲屈曲——只发生弯曲变形,截面只绕一个 主轴旋转,杆纵轴由直线变为曲线,是双轴对称截面常 见的失稳形式。
图14
第五章 钢柱与钢压杆
图15整体弯曲屈曲实例
图1桁架
第五章 钢柱与钢压杆
图2 网架
图3 塔架
第五章 钢柱与钢压杆
图4 临时天桥
第五章 钢柱与钢压杆
图5 固定天桥
第五章 钢柱与钢压杆
图6 脚手架
第五章 钢柱与钢压杆
图7 桥
第五章 钢柱与钢压杆
5.1.2 轴心受力构件类型 轴心受力构件包括轴心受压杆和轴心受拉杆。 轴心受拉 :桁架、拉杆、网架、塔架(二力杆) 轴心受压 :桁架压杆、工作平台柱、各种结构柱
第五章 钢柱与钢压杆
5.1钢柱与钢压杆的应用和构造形式
本节目录
1. 轴心受力构件的应用 2. 轴心受力构件类型 3. 轴心受力构件的截面形式 4. 轴心受力构件的计算内容
基本要求
了解轴心受力构件的类型、应用。
掌握计算内容
第五章 钢柱与钢压杆
5.1.1 轴心受力构件的应用
《钢结构设计原理》苏州科技学院教材配套第5章轴心受力构件

对普通钢结构 ,通常只考虑两种缺陷: ①初弯曲(L/1000), ②残余应力。
最大强度准则:以有 初始缺陷的压杆为模型, 考虑截面的塑性发展, 以最终破坏的最大荷载 为其极限承载力。
第5章 轴心受力构件
1. 轴心受压构件的柱子曲线
Suzhou University of Science & Technology
y
t
h
x
x
kb b
t
第5章 轴心受力构件
Suzhou University of Science & Technology
对x x轴屈曲时:
crx
2E 2x
I ex Ix
2E 2x
2t ( kb)h2 2tbh2 4
4
2E 2x
k
对y y轴屈曲时:
cry
2E 2y
I ey Iy
2 E 2t(kb)3 12 2y 2tb3 12
λ l0 [ λ] i
l0 构件的计算长度; i I A 截面的回转半径;
[ λ] 构件的容许长细比
第5章 轴心受力构件
5.2 轴心受压构件的整体稳定
Suzhou University of Science & Technology
所谓的稳定是指结构或构件受载变形后,所处平 衡状态的属性。
使构件整体屈曲前其板件不发生局部屈曲,即局部屈曲 临界应力大于或等于整体临界应力,称作等稳定性准则。
σcr f y
第5章 轴心受力构件
板件宽厚比限值
Suzhou University of Science & Technology
工字形截面:
翼缘为三边简支、一边自由的均匀受压板 腹板为四边支承板
最大强度准则:以有 初始缺陷的压杆为模型, 考虑截面的塑性发展, 以最终破坏的最大荷载 为其极限承载力。
第5章 轴心受力构件
1. 轴心受压构件的柱子曲线
Suzhou University of Science & Technology
y
t
h
x
x
kb b
t
第5章 轴心受力构件
Suzhou University of Science & Technology
对x x轴屈曲时:
crx
2E 2x
I ex Ix
2E 2x
2t ( kb)h2 2tbh2 4
4
2E 2x
k
对y y轴屈曲时:
cry
2E 2y
I ey Iy
2 E 2t(kb)3 12 2y 2tb3 12
λ l0 [ λ] i
l0 构件的计算长度; i I A 截面的回转半径;
[ λ] 构件的容许长细比
第5章 轴心受力构件
5.2 轴心受压构件的整体稳定
Suzhou University of Science & Technology
所谓的稳定是指结构或构件受载变形后,所处平 衡状态的属性。
使构件整体屈曲前其板件不发生局部屈曲,即局部屈曲 临界应力大于或等于整体临界应力,称作等稳定性准则。
σcr f y
第5章 轴心受力构件
板件宽厚比限值
Suzhou University of Science & Technology
工字形截面:
翼缘为三边简支、一边自由的均匀受压板 腹板为四边支承板
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中换算长细比为:
弯扭失稳临界力公式
2
1 2
2x 2
1 2
2x 2
2
41
x02 r02
2x2
采用换算长细比后,理想轴心压杆的弯
扭失稳临界应力的计算公式与弯曲失稳临界 应力的计算公式完全一样。
单轴对称截面弯扭失稳极限承载力计算过程:
计算换算长细比
2
1 2
2x 2
1 2
计算相对长细比 f y E
也称柱子曲线
二、实际轴心压杆的整体稳定
实际轴心压杆有多种初始缺陷,如初始弯曲、 初始偏心、残余应力、材料不均匀,使得实际轴心 压杆与理想轴心压杆之间存在很大区别。
初始缺陷使得压杆在受力一开始就出现弯曲变 形,压杆失稳为极值型失稳。
实际轴心压杆的稳定极限承载力不再是长细比 的唯一函数。
实际轴心压杆整体稳定计算公式:
2E 2
绕x轴长细比: 绕y轴长细比: 扭转长细比:
x
l0 x Ix
A
y
l0 y Iy
A
l0
I Ar02
l02
2
GIt R EAr02
双轴对称截面的弯曲失稳和扭转失稳
对于一般的双轴对称截面,弯曲失稳的 极限承载力小于扭转失稳,因此不会出现扭 转失稳现象,但对某些特殊截面形式如十字 形等,扭转失稳的极限承载力会低于弯曲失 稳的极限承载力。
C2
sin
nz
l
C1
2 EI l2
x
N C2 Nx0
0
C1Nx0
C2
2 EI l2
GIt
R
1 r02
N
r02
0
将以下关系代入上式
N Ex
2 EI x l02x
N E
2 EI l02
GIt
R
1 r02
C1 C1
NEx N
Nx0 C2
C2 Nx0
NE N
r02
0
0
由v
C1 sin
EI
x
EIy
v4 v04 u4 u04
Nv2 Nx0 2
Nu2 0
0
EI
4
4
0
GIt
2 02
Nx0v2 r02 N 2 R 2
0
(1)和(3)式相关,(2)式独立
r02
Ix
Iy A
x02
假定两端铰支时,上述微分方程的通解为:v
C1 sin
nz
l
令n=1,代入到上述微分方程得:
均匀弹性。
欧拉临界压力:
NE
2EA 2
cr
2E 2
N NE压杆维持直线平衡 N NE压杆维持曲线平衡,临界状态 N NE压杆失稳
1947年,香莱(Shanley)研究了理想轴心压 杆的非弹性稳定问题,临界压力与临界应力为:
Nt
2Et A 2
t
2Et 2
crd
欧拉双曲线
切线模量 临界应力
或
d2y dz 2
k
2
y
0
l
k2
N
EIx 1 1N
将通解代入下式:
d 2 y k 2 y 0 y Asin z
dz 2
l
A
k
2
2
l2
0
代入下式:
k2
N
EIx 1 1N
Ncr
2x
2EA 2EA1
令:0x 2x 2EA1
Ncr
2EA 2
0x
剪应变考虑了缀条或缀板剪切变形的影响,与缀条的截面 尺寸、缀条布置方式和缀板的截面尺寸、缀板间距等有关,可 以采用以下方法计算:
L
x y1
N
y2
由边缘屈服准则得:
初偏心率
0
A0 Wx
x
cr
平
N A
均 应
cr
fy
N A
N m Wx
fy
m
0 1 N
N Ex
1 0 Ex 欧拉应力
2
联 合 两 式 佩 利
y
N
m
力
fy
1 0 Ex
2
2
f y Ex
公 式
上式给出了关系 cr
给定 0即可求得 cr 关系,我国《冷弯薄
欧拉扭转失 稳临界力:
N E
2 EI l02
GIt
R
1 r02
r02
Ix
Iy A
x02
y02
R T x2 y2 dA
A
计算长度系数
l0x xl l0 y yl l0 l 查P101表5-1
欧拉弯曲失 稳临界应力:
欧拉扭转失稳 临界应力:
Ex
2E 2x
Ey
2E 2y
E
稳定极限承载力理论:轴心构件的压力达到极值 型失稳的顶点。
2、按边缘纤维屈服准则计算临界应力
弯曲变形的微分方程:
N
EIx v4 v04 Nv2 0
假定压杆为两端简支,杆轴具有正弦
Lx y1
y2
曲线的初弯曲,即
v0 0 sin
z
l
x
压杆中点最大初挠度
y
N
m
m
0 1 N
压杆中点的最大挠度
N Ex
先计算缀条的伸长量: 当V 1时,斜缀条的伸长量为:
d Ndld
1
a
EA1x sin cos EA1x
1
1
ld 缀条的长度
ld
Nd 前后两根缀条内力总和
a
V 1 d
Nd
1
sin
ld
a
cos
1 d / sin
N
z N
L
C
z a
y
N
y
N
N
V
虚轴
C
1
1
ld
a
V 1 d
Nd
1
sin
1 d / sin
EI
4 04
GIt
2
2
0
r02 N 2 R 2
0
绕z轴扭转失稳
此时,三个微分方程变为相互独立,可以单独分析。
双轴对称截面的弯曲失稳和扭转失稳
对于理想压杆,对方程组的三式分别求解可以得到失稳临界力
u0 v0 0 0
欧拉弯曲失 稳临界力:
N Ex
2 EI x l02x
N Ey
2EI y l02y
相对长细比计算: f y E
稳定系数计算:
公 式
当
0.215时, cr
fy
11 2
计 当 0.215时,
算
cr
fy
1
2 2
2
3
2
2
3
2
2
4 2
查 按表5-4确定截面类型(a、b、c、d) 表
计 算
查附表4-3~附表4-6
单轴对称截面绕对称轴弯扭失稳
换算长细比计算
3、按极限承载力理论计算临界应力
实际轴心受压构件存在初始弯曲、残余应力、初始偏心 等缺陷,我国《钢结构设计规范》将其作为压弯构件来处理。
实际轴心受压构件的柱子曲线分布在一个相当宽的带状 范围内,因此,用单一的柱子曲线来反映构件的整体稳定, 显然是不合理的。
柱子曲线见P105图5-5
我国《钢结构设计规范》方法:
查表找初偏心率
2x 2
2 41
x02 r02
2x2
按边缘纤维屈服准则计算稳定系数
cr
fy
1 2
1
1
2
1 0
1
1
2
1
0
2
4
2
公式(5-32)
或按稳定极限承载力理论计算稳定系数
当
0.215时,
cr
fy
11 2
当 0.215时,
公式(5-34)
cr fy
1
以初弯曲为l/1000,选用不同的截面形式,不同的残余应 力模式计算出200条柱子曲线,这些曲线呈相当宽的带状分布。
根据数理统计原理,将这些柱子曲线分成a、b、c、d四组
这四条曲线具有如下形式:
当
0.215时,
cr
fy
11 2
当 0.215时,
cr fy
1
2 2
2
3
2
2
Nx0v2 Ny0u2 r02 N 2 R 2
0
三个微分方程是相互联系的
双轴对称截面的弯曲失稳和扭转失稳
双轴对称截面因其剪力中心与形心重合,有
x0 y0 0
故双轴对称截面弹性微分方程简化为:
EI
x
EIy
v4 v04 u4 u04
Nv2 0 Nu2 0
绕x轴平面内弯曲失稳 绕y轴平面内弯曲失稳
壁型钢结构技术规范》采用了这个方法,并用下式
计算 cr / f y ,称为轴心压杆稳定系数 :
cr
fy
1 2
1
1
2
1 0
1
1
2
1
0
2
4
2
fy E
相对长细比
0
初偏心率见 P104表5-2
附表4-1与4-2给出了我国《冷弯薄壁型钢结构技术规范》 对Q235与Q345钢计算得到的稳定系数表,设计时直接查表。
任一点的变形由两部分组成:
L y1
y2 z
弯曲变形y1,剪切变形y2 y y1 y2
y N
y
Hale Waihona Puke 弯曲变形由下式计算:d 2 y1 M Ny
z
dz 2
弯扭失稳临界力公式
2
1 2
2x 2
1 2
2x 2
2
41
x02 r02
2x2
采用换算长细比后,理想轴心压杆的弯
扭失稳临界应力的计算公式与弯曲失稳临界 应力的计算公式完全一样。
单轴对称截面弯扭失稳极限承载力计算过程:
计算换算长细比
2
1 2
2x 2
1 2
计算相对长细比 f y E
也称柱子曲线
二、实际轴心压杆的整体稳定
实际轴心压杆有多种初始缺陷,如初始弯曲、 初始偏心、残余应力、材料不均匀,使得实际轴心 压杆与理想轴心压杆之间存在很大区别。
初始缺陷使得压杆在受力一开始就出现弯曲变 形,压杆失稳为极值型失稳。
实际轴心压杆的稳定极限承载力不再是长细比 的唯一函数。
实际轴心压杆整体稳定计算公式:
2E 2
绕x轴长细比: 绕y轴长细比: 扭转长细比:
x
l0 x Ix
A
y
l0 y Iy
A
l0
I Ar02
l02
2
GIt R EAr02
双轴对称截面的弯曲失稳和扭转失稳
对于一般的双轴对称截面,弯曲失稳的 极限承载力小于扭转失稳,因此不会出现扭 转失稳现象,但对某些特殊截面形式如十字 形等,扭转失稳的极限承载力会低于弯曲失 稳的极限承载力。
C2
sin
nz
l
C1
2 EI l2
x
N C2 Nx0
0
C1Nx0
C2
2 EI l2
GIt
R
1 r02
N
r02
0
将以下关系代入上式
N Ex
2 EI x l02x
N E
2 EI l02
GIt
R
1 r02
C1 C1
NEx N
Nx0 C2
C2 Nx0
NE N
r02
0
0
由v
C1 sin
EI
x
EIy
v4 v04 u4 u04
Nv2 Nx0 2
Nu2 0
0
EI
4
4
0
GIt
2 02
Nx0v2 r02 N 2 R 2
0
(1)和(3)式相关,(2)式独立
r02
Ix
Iy A
x02
假定两端铰支时,上述微分方程的通解为:v
C1 sin
nz
l
令n=1,代入到上述微分方程得:
均匀弹性。
欧拉临界压力:
NE
2EA 2
cr
2E 2
N NE压杆维持直线平衡 N NE压杆维持曲线平衡,临界状态 N NE压杆失稳
1947年,香莱(Shanley)研究了理想轴心压 杆的非弹性稳定问题,临界压力与临界应力为:
Nt
2Et A 2
t
2Et 2
crd
欧拉双曲线
切线模量 临界应力
或
d2y dz 2
k
2
y
0
l
k2
N
EIx 1 1N
将通解代入下式:
d 2 y k 2 y 0 y Asin z
dz 2
l
A
k
2
2
l2
0
代入下式:
k2
N
EIx 1 1N
Ncr
2x
2EA 2EA1
令:0x 2x 2EA1
Ncr
2EA 2
0x
剪应变考虑了缀条或缀板剪切变形的影响,与缀条的截面 尺寸、缀条布置方式和缀板的截面尺寸、缀板间距等有关,可 以采用以下方法计算:
L
x y1
N
y2
由边缘屈服准则得:
初偏心率
0
A0 Wx
x
cr
平
N A
均 应
cr
fy
N A
N m Wx
fy
m
0 1 N
N Ex
1 0 Ex 欧拉应力
2
联 合 两 式 佩 利
y
N
m
力
fy
1 0 Ex
2
2
f y Ex
公 式
上式给出了关系 cr
给定 0即可求得 cr 关系,我国《冷弯薄
欧拉扭转失 稳临界力:
N E
2 EI l02
GIt
R
1 r02
r02
Ix
Iy A
x02
y02
R T x2 y2 dA
A
计算长度系数
l0x xl l0 y yl l0 l 查P101表5-1
欧拉弯曲失 稳临界应力:
欧拉扭转失稳 临界应力:
Ex
2E 2x
Ey
2E 2y
E
稳定极限承载力理论:轴心构件的压力达到极值 型失稳的顶点。
2、按边缘纤维屈服准则计算临界应力
弯曲变形的微分方程:
N
EIx v4 v04 Nv2 0
假定压杆为两端简支,杆轴具有正弦
Lx y1
y2
曲线的初弯曲,即
v0 0 sin
z
l
x
压杆中点最大初挠度
y
N
m
m
0 1 N
压杆中点的最大挠度
N Ex
先计算缀条的伸长量: 当V 1时,斜缀条的伸长量为:
d Ndld
1
a
EA1x sin cos EA1x
1
1
ld 缀条的长度
ld
Nd 前后两根缀条内力总和
a
V 1 d
Nd
1
sin
ld
a
cos
1 d / sin
N
z N
L
C
z a
y
N
y
N
N
V
虚轴
C
1
1
ld
a
V 1 d
Nd
1
sin
1 d / sin
EI
4 04
GIt
2
2
0
r02 N 2 R 2
0
绕z轴扭转失稳
此时,三个微分方程变为相互独立,可以单独分析。
双轴对称截面的弯曲失稳和扭转失稳
对于理想压杆,对方程组的三式分别求解可以得到失稳临界力
u0 v0 0 0
欧拉弯曲失 稳临界力:
N Ex
2 EI x l02x
N Ey
2EI y l02y
相对长细比计算: f y E
稳定系数计算:
公 式
当
0.215时, cr
fy
11 2
计 当 0.215时,
算
cr
fy
1
2 2
2
3
2
2
3
2
2
4 2
查 按表5-4确定截面类型(a、b、c、d) 表
计 算
查附表4-3~附表4-6
单轴对称截面绕对称轴弯扭失稳
换算长细比计算
3、按极限承载力理论计算临界应力
实际轴心受压构件存在初始弯曲、残余应力、初始偏心 等缺陷,我国《钢结构设计规范》将其作为压弯构件来处理。
实际轴心受压构件的柱子曲线分布在一个相当宽的带状 范围内,因此,用单一的柱子曲线来反映构件的整体稳定, 显然是不合理的。
柱子曲线见P105图5-5
我国《钢结构设计规范》方法:
查表找初偏心率
2x 2
2 41
x02 r02
2x2
按边缘纤维屈服准则计算稳定系数
cr
fy
1 2
1
1
2
1 0
1
1
2
1
0
2
4
2
公式(5-32)
或按稳定极限承载力理论计算稳定系数
当
0.215时,
cr
fy
11 2
当 0.215时,
公式(5-34)
cr fy
1
以初弯曲为l/1000,选用不同的截面形式,不同的残余应 力模式计算出200条柱子曲线,这些曲线呈相当宽的带状分布。
根据数理统计原理,将这些柱子曲线分成a、b、c、d四组
这四条曲线具有如下形式:
当
0.215时,
cr
fy
11 2
当 0.215时,
cr fy
1
2 2
2
3
2
2
Nx0v2 Ny0u2 r02 N 2 R 2
0
三个微分方程是相互联系的
双轴对称截面的弯曲失稳和扭转失稳
双轴对称截面因其剪力中心与形心重合,有
x0 y0 0
故双轴对称截面弹性微分方程简化为:
EI
x
EIy
v4 v04 u4 u04
Nv2 0 Nu2 0
绕x轴平面内弯曲失稳 绕y轴平面内弯曲失稳
壁型钢结构技术规范》采用了这个方法,并用下式
计算 cr / f y ,称为轴心压杆稳定系数 :
cr
fy
1 2
1
1
2
1 0
1
1
2
1
0
2
4
2
fy E
相对长细比
0
初偏心率见 P104表5-2
附表4-1与4-2给出了我国《冷弯薄壁型钢结构技术规范》 对Q235与Q345钢计算得到的稳定系数表,设计时直接查表。
任一点的变形由两部分组成:
L y1
y2 z
弯曲变形y1,剪切变形y2 y y1 y2
y N
y
Hale Waihona Puke 弯曲变形由下式计算:d 2 y1 M Ny
z
dz 2
