二次函数动点问题中面积最值的解法策略
二次函数中面积的最值问题(六大题型)学生版-2024年中考数学压轴题专项训练
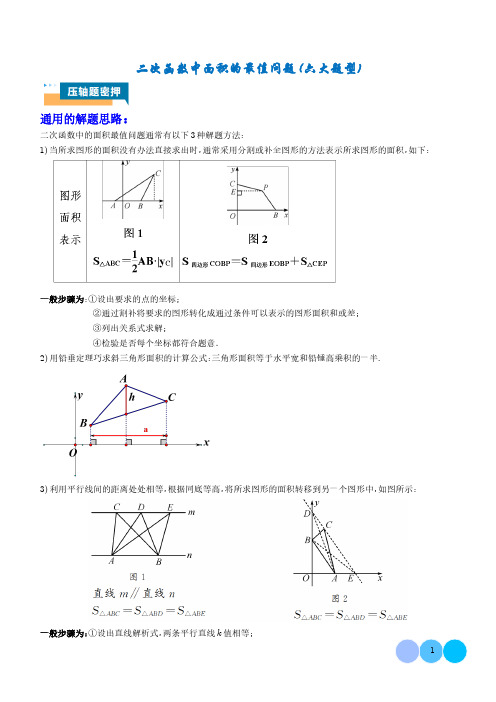
二次函数中面积的最值问题(六大题型)通用的解题思路:二次函数中的面积最值问题通常有以下3种解题方法:1)当所求图形的面积没有办法直接求出时,通常采用分割或补全图形的方法表示所求图形的面积,如下:一般步骤为:①设出要求的点的坐标;②通过割补将要求的图形转化成通过条件可以表示的图形面积和或差;③列出关系式求解;④检验是否每个坐标都符合题意.2)用铅垂定理巧求斜三角形面积的计算公式:三角形面积等于水平宽和铅锤高乘积的一半.3)利用平行线间的距离处处相等,根据同底等高,将所求图形的面积转移到另一个图形中,如图所示:一般步骤为:①设出直线解析式,两条平行直线k值相等;②通过已知点的坐标,求出直线解析式;③求出题意中要求点的坐标;④检验是否每个坐标都符合题意.题型01三角形面积最值问题1(2024·宁夏银川·一模)如图,二次函数y =-x 2+6x 的图象与x 轴的正半轴交于点A ,经过点A 的直线与该函数图象交于点B 1,5 ,与y 轴交于点C .(1)求直线AB 的函数表达式及点C 的坐标;(2)点P 是二次函数图象上的一个动点,且在直线AB 上方,过点P 作直线PE ⊥x 轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m .①当PD =12OC 时,求m 的值;②设△PAB 的面积为S ,求S 关于m 的函数表达式,并求出S 的最大值.2(2024·新疆克孜勒苏·二模)如图,抛物线y =x ²+bx +c (b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,A 2,0 ,AB =6,点P 为线段AB 上的动点,过P 作PQ ∥BC 交AC 于点Q .(1)求抛物线的解析式;(2)求△CPQ 面积的最大值,并求此时P 点坐标.3(23-24九年级下·湖北武汉·开学考试)如图,抛物线y =ax 2-4ax +3a 交x 轴于A ,B 两点(点A 在点B 的左侧),交y 轴正半轴于点C ,OB =OC ,点P 在抛物线上.(1)求抛物线的解析式;(2)若tan∠ACP=2,求点P的横坐标.(3)平面上有两点M m,-m-3,求△PMN的面积的最小值.,N m+2,-m-54(23-24九年级下·辽宁沈阳·阶段练习)△ABC中,∠BAC=90°,AB=2,AC=4,点P从点C出发,沿射线CA方向运动,速度为每秒1个单位长度,同时点Q以相同的速度从点B出发,沿射线BA方向运动.设运动时间为x(x≠2且x≠4)秒,△APQ的面积为S.(1)当0<x<2时,如图①,求S与x的函数关系式;(2)当2<x<4时,如图②,求S的最大值;(3)若在运动过程中,存在两个时刻x1,x2,对应的点P和点Q分别记为P1,P2和Q1,Q2,对应的△AP1Q1和△AP2Q2的面积分别记为S1和S2,且当CP1=P1P2时,S1=S2,请求出x1的值.5(2023·山东聊城·二模)如图,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),点A 的坐标为-1,0,直线CD:y=2x-3与x轴交于点D.动点M在抛物线上运动, ,与y轴交于点C0,-3过点M作MP⊥x轴,垂足为点P,交直线CD于点N.(1)求抛物线的表达式;(2)当点P在线段OD上时,△CDM的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;(3)点M在运动过程中,能否使以C,N,M为顶点的三角形是以NM为腰的等腰直角三角形?若存在,请直接写出点M的坐标.6(2024·浙江宁波·模拟预测)如图,一次函数y=33x+3的图象与坐标轴交于点A、B,抛物线y=-33x2+bx+c的图象经过A、B两点.(1)求二次函数的表达式;(2)若点P为抛物线上一动点,在直线AB上方是否存在点P使△PAB的面积最大?若存在,请求出△PAB 面积的最大值及点P的坐标,请说明理由.7(2024·甘肃陇南·一模)如图,在平面直角坐标系xOy中,已知直线y=-x-3与x轴交于点A,与y轴交于点C,过A,C两点的抛物线y=ax2+bx+c与x轴交于另一点B1,0,抛物线对称轴为直线l.(1)求抛物线的解析式;(2)点M为直线AC下方抛物线上一点,当△MAC的面积最大时,求点M的坐标;(3)点P是抛物线上一点,过点P作l的垂线,垂足为D,E是l上一点.要使得以P,D,E为顶点的三角形与△BOC全等,请直接写出点P的坐标.8(2024·江苏盐城·模拟预测)已知抛物线y=x2+bx-3与x轴交于A,B(点A在点B的左侧),与y轴交于点C,且OB=OC.(1)求抛物线的解析式和点A的坐标;(2)如图1,点P为直线BC下方抛物线上一点,求△PBC的最大面积;(3)如图2,M、N是抛物线上异于B,C的两个动点,若直线BN与直线CM的交点始终在直线y=2x-9上,求证:直线MN必经过一个定点,并求该定点坐标.9(2024·四川广元·二模)如图,在平面直角坐标系中,抛物线y1=-x2+bx+c与x轴交于点B,A(-3, 0),与y轴交于点C(0,3).(1)求直线AC和抛物线的解析式.(2)若点M是抛物线对称轴上的一点,是否存在点M,使得以M,A,C三点为顶点的三角形是以AC为底的等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.(3)若点P是第二象限内抛物线上的一个动点,求△PAC面积的最大值.10(2024·安徽安庆·一模)如图,抛物线y=ax2+bx+3与x轴交于点A1,0两点,与y轴交于、B3,0点C.(1)求此抛物线对应的函数表达式;(2)点E为直线BC上的任意一点,过点E作x轴的垂线与此抛物线交于点F.①若点E在第一象限,连接CF、BF,求△CFB面积的最大值;②此抛物线对称轴与直线BC交于点D,连接DF,若△DEF为直角三角形,请直接写出E点坐标.11(2024·安徽合肥·一模)如图,直线y=x-3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c 经过B、C两点,抛物线与x轴负半轴交于点A.(1)求抛物线的函数表达式;(2)直接写出当x-3>x2+bx+c时,x的取值范围;(3)点P是位于直线BC下方抛物线上的一个动点,过点P作PE⊥BC于点E,连接OE.求△BOE面积的最大值及此时点P的坐标.12(2024·天津西青·一模)已知抛物线y=-x2-4ax-12a(a<0)与x轴交于A,B两点(点A在点B左边),与y轴交于点C.(1)若点D4,12在抛物线上.①求抛物线的解析式及点A的坐标;②连接AD,若点P是直线AD上方的抛物线上一点,连接PA,PD,当△PAD面积最大时,求点P的坐标及△PAD面积的最大值;(2)已知点Q的坐标为-2a,-8a,连接QC,将线段QC绕点Q顺时针旋转90°,点C的对应点M恰好落在抛物线上,求抛物线的解析式.13(2024·山东临沂·二模)如图,抛物线y=ax2+32x+c与x轴交于点A和点B4,0,与y轴交于点C0,2,连接BC,点D在抛物线上.(1)求抛物线的解析式;(2)小明探究点D位置时发现:如图1,点D在第一象限内的抛物线上,连接BD,CD,△BCD面积存在最大值,请帮助小明求出△BCD面积的最大值;(3)小明进一步探究点D位置时发现:如图2,点D在抛物线上移动,连接CD,存在∠DCB=∠ABC,请帮助小明求出∠DCB=∠ABC时点D的坐标.14(2024·广东深圳·二模)如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与轴交于A,B 点,与y轴交于点C0,3,点B的坐标为3,0,点P是抛物线上一个动点.(1)求二次函数解析式;(2)若P点在第一象限运动,当P运动到什么位置时,△BPC的面积最大?请求出点P的坐标和△BPC面积的最大值;(3)连接PO,PC,并把△POC沿CO翻折,那么是否存在点P,使四边形POP C为菱形;若不存在,请说明理由.15(2024·湖北·模拟预测)如图,抛物线y=x-12+k与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C0,-3.设P点在抛物线上运动,横坐标为m.(1)求此抛物线的解析式;(2)当P点位于第四象限时,求△BCP面积的最大值,并求出此时P点坐标;(3)设此抛物线在点C与点P之间部分(含点C和点P)最高点与最低点的纵坐标之差为h.① 求h关于m的函数解析式,并写出自变量m的取值范围;② 根据h的不同取值,试探索点P的个数情况.16(22-23九年级下·重庆·阶段练习)抛物线y=ax²+bx+5经过点A1,0和点B5,0.该抛物线与直线y=12x+5相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.(1)求该抛物线所对应的函数解析式;(2)连接PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;(3)连接PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.17(2024·江苏宿迁·一模)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+3与x轴分别相交于A、B两点,与y轴相交于点C,已知点A的坐标为(-1,0),点B的坐标为(3,0).(1)求出这条抛物线的函数表达式;(2)如图2,点D是第一象限内该抛物线上一动点,过点D作直线l∥y轴,直线l与△ABD的外接圆相交于点E.①仅用无刻度直尺找出图2中△ABD外接圆的圆心P.②连接BC、CE,BC与直线DE的交点记为Q,如图3,设△CQE的面积为S,在点D运动的过程中,S是否存在最大值?如果存在,请求出S的最大值;如果不存在,请说明理由.18(2024·新疆乌鲁木齐·一模)如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m 从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C,点P与直线m同时停止运动,设运动时间为t秒t>0.(1)AH=,EF=(用含t的式子表示).(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.19(2024·重庆·模拟预测)如图,在平面直角坐标系中,抛物线y=ax2+bx+c过点(3,-4),交x轴于点A(-1,0),B两点,交y轴于点C(0,2).(1)求抛物线的表达式;(2)连接AC ,BC ,M 为线段AB 上一动点,过点M 作MD ∥BC 交直线AC 于点D ,连接MC ,求△MDC 面积的最大值及此时M 点的坐标;(3)在(2)中△MDC 面积取得最大值的条件下,将该抛物线沿射线BC 方向平移2个单位长度,P 是平移后的抛物线上一动点,连接CP ,当∠PCM 与△OBC 的一个内角相等时,请直接写出所有符合条件的点P 的坐标.20(2024·湖南衡阳·一模)如图,已知抛物线y =ax 2+bx +c 经过A 1,0 ,B -3,0 ,C 0,3 三点.(1)求抛物线的解析式;(2)若点D 为第二象限内抛物线上一动点,求△BCD 面积的最大值;(3)设点P 为抛物线的对称轴上的一个动点,求使△BPC 为直角三角形的点P 的坐标.21(2024·甘肃天水·一模)如图,在平面直角坐标系中,开口向下的抛物线与x 轴交于A ,B 两点,D 是抛物线的顶点.O 为坐标原点.A ,B 两点的横坐标分别是方程x 2-4x -12=0的两根,且cos ∠DAB =22.(1)求抛物线的函数解析式;(2)作AC ⊥AD ,AC 交抛物线于点C ,求点C 的坐标及直线AC 的函数解析式;(3)在(2)的条件下,在x 轴上方的抛物线上是否存在一点P ,使△APC 的面积最大?如果存在,请求出点P 的坐标和△APC 的最大面积;如果不存在,请说明理由.22(2024·山东聊城·一模)在平面直角坐标系中,抛物线y =ax 2+bx -3与x 轴交于点A -1,0 和点B 3,0 ,与y 轴交于点C .(1)求抛物线的解析式及顶点坐标;(2)若点P 为第四象限内抛物线上一点,当△PBC 面积最大时,求点P 的坐标;(3)若点P 为抛物线上一点,点Q 是线段BC 上一点(点Q 不与两端点重合),是否存在以P 、Q 、O 为顶点的三角形是等腰直角三角形,若存在,请直接写出满足条件的点P 的坐标;若不存在,请说明理由.23(2024·吉林长春·一模)如图,在平面直角坐标系中,直线y =x +2分别交x 轴、y 轴于A 、B 两点,过点C 2,2 作x 轴垂线,垂足为D ,连接BC .现有动点P 、Q 同时从A 点出发,分别沿AB 、AD 向终点B 和终点D 运动,若点P 的运动速度为每秒2个单位长度,点Q 的运动速度为每秒2个单位长度.设运动的时间为t 秒.(1)求A、B两点的坐标;(2)当CQ∥AB时,t=;(3)设△CPQ的面积为y,写出y与t的函数关系式,并求△CPQ面积的最大值;(4)当△CPQ为轴对称图形时,直接写出t的值.24(2023·湖南娄底·中考真题)如图,抛物线y=x2+bx+c过点A-1,0,交y轴于点C.、点B5,0(1)求b,c的值.(2)点P x0,y0是抛物线上的动点0<x0<5①当x0取何值时,△PBC的面积最大?并求出△PBC面积的最大值;②过点P作PE⊥x轴,交BC于点E,再过点P作PF∥x轴,交抛物线于点F,连接EF,问:是否存在点P,使△PEF为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.25(2024·河南安阳·模拟预测)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与抛物线y=-x2+x-1的形状相同,且与x轴交于点-1,0.直线y=kx+2分别与x轴、y轴交于点A,B,和4,0与y=ax2+bx+c于点C,D(点C在点D的左侧).(1)求抛物线的解析式;(2)点P是直线y=kx+2上方抛物线上的任意一点,当k=2时,求△PCD面积的最大值;(3)若抛物线y=ax2+bx+c与线段AB有公共点,结合函数图象请直接写出k的取值范围.26(2024·湖南长沙·一模)如图,抛物线y=x2-bx+c与x轴交于A-1,0两点,与y轴交于,B m,0点C0,-3,顶点为D,直线BD交y轴于点E.(1)求抛物线的解析式.(2)设点P为线段BD上一点(点P不与B,D两点重合),过点P作x轴的垂线与抛物线交于点F,连接DF,BF,求△BDF面积的最大值.(3)连接CD,在线段BD上是否存在点Q,使得∠BDC=∠QCE?若存在,求出点Q的坐标;若不存在,请说明理由.27(2024·江西萍乡·一模)如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A3,0,连接AC,BC.,C0,3(1)求抛物线的函数解析式;(2)在抛物线的对称轴上找一点P,使得以A、D、P为顶点的三角形与△OBC相似,求出点P的坐标;(3)若点M是抛物线上的一个动点,且位于第一象限内,连接MC,MA.设△ACM的面积为S,试求S的最大值.28(2024·四川广元·二模)如图1,抛物线y=ax²+bx+c与x轴交于A,B两点,且点B的坐标为5,0,与y轴交于点C,该抛物线的顶点坐标为(3,-4).(1)求抛物线和直线BC的解析式.(2)在抛物线上是否存在点M,使得△BCM是以BC为底边的等腰三角形?若存在,求出所有点M的坐标;若不存在,请说明理由.(3)如图2,以点B 为圆心,画半径为2的圆,点P 为⊙B 上的一个动点,连接AC ,求△ACP 面积的最大值.29(2023·山东青岛·中考真题)如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,AB =10cm ,BD =45cm .动点P 从点A 出发,沿AB 方向匀速运动,速度为1cm/s ;同时,动点Q 从点A 出发,沿AD 方向匀速运动,速度为2cm/s .以AP ,AQ 为邻边的平行四边形APMQ 的边PM 与AC 交于点E .设运动时间为t s 0<t ≤5 ,解答下列问题:(1)当点M 在BD 上时,求t 的值;(2)连接BE .设△PEB 的面积为S cm 2 ,求S 与t 的函数关系式和S 的最大值;(3)是否存在某一时刻t ,使点B 在∠PEC 的平分线上?若存在,求出t 的值;若不存在,请说明理由.30(2023·湖南怀化·中考真题)如图一所示,在平面直角坐标系中,抛物线y =ax 2+bx -8与x 轴交于A (-4,0)、B (2,0)两点,与y 轴交于点C .(1)求抛物线的函数表达式及顶点坐标;(2)点P 为第三象限内抛物线上一点,作直线AC ,连接PA 、PC ,求△PAC 面积的最大值及此时点P 的坐标;(3)设直线l 1:y =kx +k -354交抛物线于点M 、N ,求证:无论k 为何值,平行于x 轴的直线l 2:y =-374上总存在一点E ,使得∠MEN 为直角.31(2024·海南省直辖县级单位·一模)如图,已知抛物线y =ax 2+2x +c a ≠0 ,与x 轴交于点A -1,0 和点B 3,0 ,与y 轴交于点C ,E 为抛物线的顶点.图1图2(1)求该抛物线的函数表达式;(2)如图1,点P 是第一象限内抛物线上一动点,连接PC 、PB 、BC ,设点P 的横坐标为t .①当t 为何值时,△PBC 的面积最大?并求出最大面积;②当t 为何值时,△PBC 是直角三角形?(3)如图2,过E 作EF ⊥x 轴于F ,若M m ,0 是x 轴上一动点,N 是线段EF 上一点,若∠MNC =90°,请直接写出实数m 的取值范围.32(2024·四川成都·一模)如图,直线y =-x -4分别交x 轴,y 轴于A ,C 两点,点B 在x 轴正半轴上.抛物线y =15x 2+bx +c 过A ,B ,C 三点.(1)求抛物线的解析式;(2)过点B 作BD ∥AC 交y 轴于点D ,交抛物线于点F .若点P 为直线AC 下方抛物线上的一动点,连接PD 交AC 于点E ,连接EB ,求S △PEB 的最大值及最大值时点P 的坐标;(3)如图2,将原抛物线进行平移,使其顶点为原点,进而得到新抛物线,直线y =-2x 与新抛物线交于O ,G 两点,点H 是线段OG 的中点,过H 作直线RQ (不与OG 重合)与新抛物线交于R ,Q 两点,点R 在点Q 左侧.直线GR 与直线OQ 交于点T ,点T 是否在某条定直线上?若是,请求出该定直线的解析式,若不是,请说明理由.33(2024·江苏苏州·一模)如图,在平面直角坐标系中,抛物线y =ax 2-8ax +10a -1a <0 与x 轴的交点分别为A x 1,0 ,B x 2,0 ,其中(0<x 2<x 1),且AB =4,与y 轴的交点为C ,直线CD ∥x 轴,在x 轴上有一动点E t ,0 ,过点E 作直线l ⊥x 轴,与抛物线、直线CD 的交点分别为P 、Q .(1)求抛物线的解析式;(2)当0<t ≤8时,求△APC 面积的最大值;(3)当t >2时,是否存在点P ,使以C 、P 、Q 为顶点的三角形与△OBC 相似?若存在,求出此时t 的值;若不存在,请说明理由.题型02四边形面积最值问题1(2024·安徽阜阳·一模)如图,抛物线y =ax 2+bx +3与x 轴交于A -1,0 ,B 3,0 两点,与y 轴交于点C .(1)求抛物线的解析式;(2)在抛物线的对称轴上找一点P ,使△PAC 的周长最小,求△PAC 的周长的最小值及此时点P 的坐标;(3)若M 为抛物线在第一象限内的一动点,求出四边形OCMB 的面积的最大值及此时点M 的坐标.2(2024·山东临沂·一模)如图,在平面直角坐标系中,抛物线y =-14x 2+bx +c 与x 轴交于点A (-2,0)和点B ,与y 轴交于点C (0,4),点P 是直线BC 上方的抛物线上一点(点P 不与点B ,C 重合),过点P 作PD ∥y 轴交直线BC 于点D .(1)求抛物线的函数表达式;(2)求线段PD 长的最大值;(3)连接CP ,BP ,请直接写出四边形ABPC 的面积最大值为.3(2024·山西运城·一模)综合与探究如图,抛物线y=ax2+bx-3a≠0与x轴交于A-1,0、B两点,与y轴交于点C,点D-2,9 2在抛物线上,点P是抛物线在第四象限内的一个动点,过点P作PQ∥y轴交直线BD于点Q,连接PA、PB、QA,设点P的横坐标为m.(1)求抛物线的函数表达式;(2)求四边形PAQB面积的最大值及此时点P的坐标;(3)若点M是抛物线上任意一点,是否存在点M,使得∠MAB=2∠ACO,若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.4(2024·安徽合肥·一模)在平面直角坐标系中,点O是坐标原点.抛物线y=ax2+bx-3a≠0与x轴交于A,B两点,直线l:y=kx+2与抛物线交于A,C两点,且A-1,0,B3,0.(1)求a,b,k的值;(2)点M是线段OB上的动点,点N在x轴上,MN=2,且点N在M的左边.过点M作MP⊥x轴,交抛物线于点P.过点N作x轴的垂线,交抛物线于点Q,交直线l于点R.①当以P,Q,R,M为顶点的四边形是平行四边形时,求点M的坐标.②记以P,Q,R,M为顶点的四边形面积为S,求S的最大值.5(2024·安徽蚌埠·一模)如图1,已知直线y=-x+5与坐标轴相交于A、B,点C坐标是-1,0,抛物线经过A、B、C三点.点P是抛物线上的一点,过点P作y轴的平行线,与直线AB交于点D,与x轴相交于点F.(1)求抛物线的解析式;(2)当点P在第一象限时,连接CP交OA于点E,连接EF,如图2所示;①求AE+DF的值;②设四边形AEFB的面积为S,则点P在运动过程中是否存在面积S的最大值,若存在,请求出此时点P的坐标;若不存在,请说明理由.6(2024·安徽马鞍山·一模)如图,过原点的二次函数y=ax2+bx的图象与x轴正半轴交于点A,经过点A的直线与该函数交于B1,-3,与y轴交于点C0,-4.(1)分别求此二次函数与直线AB的解析式.(2)点P是第四象限内二次函数图象上的一个动点,过点P作直线PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为t.①当PD=12OC时,求t的值;②当点P在直线AB下方时,连接OP,过点B作BQ⊥x轴于点Q,BQ与OP交于点F,连接DF,求四边形FQED面积的最大值.7(2024·山东济南·一模)如图,直线y=-12x+3交y轴于点A,交x轴于点C,抛物线y=-14x2+bx+c经过点A,点C,且交x轴于另一点B.(1)求抛物线的解析式;(2)在直线AC上方的抛物线上有一点M,求四边形ABCM面积的最大值及此时点M的坐标;(3)将线段OA绕x轴上的动点P m,0顺时针旋转90°得到线段O A ,若线段O A 与抛物线只有一个公共点,请结合函数图象,求m的取值范围.8(2024·四川广元·二模)如图,二次函数y=ax2+bx+c的图象与x轴交于原点O和点A4,0,经过点A的直线与该函数图象交于另一点B1,3,与y轴交于点C.(1)求直线AB的函数解析式及点C的坐标.(2)点P是抛物线上位于直线AB上方的一个动点,过点P作直线PE⊥x轴于点E,与直线AB交于点D,过点B作BF⊥x轴于点F,连接OP,与BF交于点G,连接DG.求四边形GDEF面积的最大值.(3)抛物线上是否存在这样的点Q,使得∠BOQ=45°?若存在,请求出点Q的坐标;若不存在,请说明理由.9(2024·广东珠海·一模)如图,抛物线y=-x2+3x+4和直线y=x+1交于A-1,0点,点B,B3,4在直线x=3上,直线x=3与x轴交于点C.(1)求∠BAC的度数.(2)点P从点A出发,以每秒2个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒t>0.以PQ为边作矩形PQNM,使点N在直线x=3上.①当t为何值时,矩形PQNM的面积最小?并求出最小面积;②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.10(2024·安徽宿州·二模)如图1,抛物线y=ax2+bx-3(a,b是常数且a>0)与x轴交于点A-1,0和点B(点B在点A的右侧),点D是抛物线的顶点,CD是抛物线的对称轴且交x轴于点C1,0.(1)求a,b的值;(2)点P是抛物线上一点且位于点A和点D之间.(i)如图2,连接AP,DP,BD,求四边形ABDP面积的最大值;(ii)如图3,连接AP并延长交CD延长线于点Q,连接BP交CD于点E,求CE+CQ的值.11(2024·安徽·二模)如图1,在平面直角坐标系中,抛物线y=ax2+bx-4交x轴于点A-1,0,B4,0,交y轴于点C,点M在该抛物线上,横坐标为m,将该抛物线M,C两点之间(包括M,C两点)的部分记为图象W.(1)求抛物线的解析式;(2)图象W的最大值与最小值的差为4时,求m的值;(3)如图2,若点M位于BC下方,过点A作AE∥BC交拋物线于点E,点D为直线AE上一动点,连接CM, CD,BM,BD,求四边形CDBM面积的最大值及此时点M的坐标.12(2024·四川广安·二模)如图,抛物线y=-x2+bx+c交x轴于A-4,0.,B两点,交y轴于点C0,4(1)求抛物线的函数解析式.(2)点D在线段OA上运动,过点D作x轴的垂线,与AC交于点Q,与抛物线交于点P,连接AP、CP,求四边形AOCP的面积的最大值.(3)在抛物线的对称轴上是否存在点M,使得以点A、C、M为顶点的三角形是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.13(23-24九年级上·重庆渝北·期末)二次函数y=ax2+bx+4经过点A-1,0,点C,点D,点B4,0分别二次函数与y轴的交点和顶点,点M为二次函数图象上第一象限内的一个动点.(1)求二次函数的解析式;(2)如图1,连接BC ,过点A 作BC 的平行线交二次函数于点E ,连接CM ,BM ,BE ,CE .求四边形CMBE 面积的最大值以及此时点M 的坐标;(3)如图2,过点M 作MN ∥y 轴,交BC 于点N (点M 不与点D 重合),过点D 作DH ∥y 轴,交BC 于点H ,当DM =HN 时,直接写出点M 的坐标.题型03面积比最值问题14(2024·安徽合肥·一模)在平面直角坐标系xOy 中,已知抛物线y =a x +1 x -4 与x 轴交于A 、 B 两点,与y 轴交于点C 0,-2 .(1)求a 的值;(2)点D 为第四象限抛物线上一点①求△BCD 的面积最大值②连接AD ,BC 交于点E ,连接BD ,记△BDE 的面积为S 1,△ABE 的面积为S 2,求S 1S 2的最大值;15(2023·四川遂宁·中考真题)在平面直角坐标系中,O 为坐标原点,抛物线y =14x 2+bx +c 经过点O (0,0),对称轴过点B (2,0),直线l 过点C 2,-2 ,且垂直于y 轴.过点B 的直线l 1交抛物线于点M 、N ,交直线l 于点Q ,其中点M 、Q 在抛物线对称轴的左侧.(1)求抛物线的解析式;(2)如图1,当BM :MQ =3:5时,求点N 的坐标;(3)如图2,当点Q 恰好在y 轴上时,P 为直线l 1下方的抛物线上一动点,连接PQ 、PO ,其中PO 交l 1于点E ,设△OQE 的面积为S 1,△PQE 的面积为S 2.求S2S 1的最大值.16(2024·湖北省直辖县级单位·一模)抛物线y =x 2-4x 与直线y =x 交于原点O 和点B ,与x 轴交于另一点A ,顶点为D .(1)求出点B 和点D 的坐标;(2)如图①,连接OD ,P 为x 轴的负半轴上的一点,当tan ∠PDO =12时,求点P 的坐标;(3)如图②,M 是点B 关于抛物线的对称轴的对称点,Q 是抛物线上的动点,它的横坐标为m 0<m <5 ,连接MQ ,BQ ,MQ 与直线OB 交于点E ,设△BEQ 和△BEM 的面积分别为S 1和S 2,求S1S 2的最大值.17(2023·湖南永州·中考真题)如图1,抛物线y =ax 2+bx +c (a ,b ,c 为常数)经过点F 0,5 ,顶点坐标为2,9 ,点P x 1,y 1 为抛物线上的动点,PH ⊥x 轴于H ,且x 1≥52.(1)求抛物线的表达式;(2)如图1,直线OP :y =y 1x 1x 交BF 于点G ,求S △BPG S △BOG的最大值;(3)如图2,四边形OBMF 为正方形,PA 交y 轴于点E ,BC 交FM 的延长线于C ,且BC ⊥BE ,PH =FC ,求点P 的横坐标.18(2024·四川南充·一模)抛物线y =-38x 2+bx +c b >0 与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C 0,3 ,抛物线对称轴为x =1,点P 是抛物线在第一象限上动点,连接CB ,PB .(1)求抛物线和直线BC 的解析式;(2)如图,连接PA ,交BC 于点M ,设△ABM 的面积为S 1,△PBM 的面积为S 2,求S 1S 2的最小值及此时点P的坐标.19(2024·湖北孝感·一模)如图1,已知抛物线y=ax2+bx+3与x轴交于点A-1,0,B3,0,与y轴交于点C,连接BC.(1)求a,b的值及直线BC的解析式;(2)如图1,点P是抛物线上位于直线BC上方的一点,连接AP交BC于点E,过P作PF⊥x轴于点F,交BC于点G,(ⅰ)若EP=EG,求点P的坐标,(ⅱ)连接CP,CA,记△PCE的面积为S1,△ACE的面积为S2,求S1S2的最大值;(3)如图2,将抛物线位于x轴下方面的部分不变,位于x轴上方面的部分关于x轴对称,得到新的图形,将直线BC向下平移n个单位,得到直线l,若直线l与新的图形有四个不同交点,请直接写出n的取值范围.题型04面积和最值问题1(2024·吉林长春·一模)在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于点A(-1,0)、B(3,0),交y轴于点C,连结AC、BC.点D在该抛物线上,过点D作DE∥AC,交直线BC于点E,连结AD、AE、BD.设点D横坐标为m(m>0),△DAE的面积为S1,△DBE的面积为S2.(1)求a,b的值;(2)设抛物线上D、B两个点和它们之间的部分为图象G,当图象G的最高点的纵坐标与m无关时,求m的取值范围;(3)当点D在第一象限时,求S1+S2的最大值;(4)当S1:S2=2:1时,直接写出m的值.题型05面积差最值问题1(2024·安徽合肥·一模)如图1,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=。
二次函数中的面积最值问题

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
二次函数动点面积最值专题
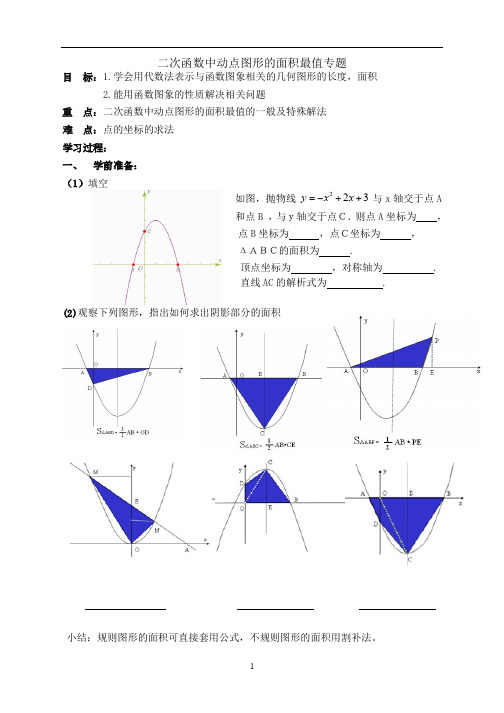
二次函数中动点图形的面积最值专题目 标:1.学会用代数法表示与函数图象相关的几何图形的长度,面积2.能用函数图象的性质解决相关问题重 点:二次函数中动点图形的面积最值的一般及特殊解法难 点:点的坐标的求法学习过程:一、 学前准备:(1)填空如图,抛物线 与x轴交于点A和点B ,与y轴交于点C.则点A坐标为 ,点B坐标为 ,点C坐标为 ,ΔABC的面积为 .顶点坐标为 ,对称轴为 . 直线AC的解析式为 .(2)观察下列图形,指出如何求出阴影部分的面积小结:规则图形的面积可直接套用公式,不规则图形的面积用割补法。
322++−=xxy二、“二次函数中动点与图形面积”试题解析例题:如图二次函数434312−−=x x y 与x 轴交于点C,与y 轴交于点A,过点A 作一条直线与x 轴平行,与抛物线交于点B.(1)求直线AC 的解析式;(2)连接BC,求ΔABC 的面积.变式1:若抛物线的顶点为B,求ΔABC 的面积.变式2:若点B 是线段AC 下方的抛物线上的动点,那么,ΔABC 的面积有最大值吗?如果有,请求出.最大面积和此时点B 的坐标.变式3:若B、C 是抛物线与x 轴的交点,A是抛物线与y 轴的交点,点D 是线段AC 上的动点,求四边形ABCD 面积的最大 过点D 作x 轴的垂线与抛物线相交于点E,当点D运动到什么位置时,四边形ABCE 的面积最大?求最大面积及此时点D 的坐标.学后反思:归纳“二次函数中动点图形的面积最值”试题解析一般规律:这类问题的特征是要以静代动解题,首先找面积关系的函数解析式,关键是用含x 的代数式表示出相关的线段的长度,若是规则图形则套用公式或用割补法,若为不规则图形则用割补法. 三、自我检测1.若抛物线y=-x ²-X+6与x 轴交于A、B 两点,则AB= ,抛物线与y 轴交于点C,则C 点的坐标为 ,△ABC 的面积为 .2.已知二次函数23212−−=x x y 与x 轴交于A、B 两点,顶点为C,则△ABC 的面积为 . 3. 已知抛物线322−+=x x y 与x 轴交于A(-3,0),B(1,0)两点,与y 轴交于点C,直线y=x+1与抛物线交于E,F 两点.点P是直线EF 下方抛物线上的动点,求△PEF面积的最大值及点P 的坐标.4.抛物线4524542+−=x x y 在平面直角坐标系中的位置如图,直线454−−=x y 与x 轴交于点A(-5,0),与y 轴交于点B.在抛物线上是否存在一点P,使得△PAB 的面积最小?若存在,求出点P 的坐标及△PAB 面积的最小值;若不存在,请说明理由.综合题:1、如图,已知抛物线y=﹣x 2+bx+c 与x 轴交于A(﹣1,0)、B(3,0)两点,与y 轴交于点C,抛物线的对称轴与抛物线交于点P、与直线BC 相交于点M,连接PB.(1)求该抛物线的解析式;(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD 的面积最大?若存在,求出D 点坐标及△BCD 面积的最大值;若不存在,请说明理由.(3)在(1)中的抛物线上是否存在点Q,使得△QMB 与△PMB 的面积相等?若存在,求出点Q 的坐标;若不存在,请说明理由.2、如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.(1)求抛物线的解析式和对称轴;(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.。
二次函数动点问题解答方法技巧(含例解标准答案)

下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
二、抛物线上动点
5、(湖北十堰市)如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当 为何值时,四边形 的面积 有最大值,并求出此最大值;
(4)在运动过程中,四边形 能否形成矩形?若能,求出此时 的值;若不能,请说明理由.
[解](1)点 ,点 ,点 关于原点的对称点分别为 , , .
设抛物线 的解析式是
,
则
解得
所以所求抛物线的解析式是 .
(2)由(1)可计算得点 .
过点 作 ,垂足为 .
⑶ 根据图象的位置判断二次函数ax²+bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式ax²+bx+c﹙a≠0﹚本身就是所含字母x的二次函数;下面以a>0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:
当运动到时刻 时, , .
根据中心对称的性质 ,所以四边形 是平行四边形.
所以 .
所以,四边形 的面积 .
因为运动至点 与点 重合为止,据题意可知 .
所以,所求关系式是 , 的取值范围是 .
(3) ,( ).
二次函数中考压轴题研究——兼谈动点三角形的面积解题策略

二次函数中考压轴题研究——兼谈动点三角形的面积解题策略
在高中数学中,二次函数通常是一个考试的难点,也是考压轴题的常见题型之一。
在考压轴题的时候,做题正确率高低是很重要的因素。
为了更好地解决二次函数的考压轴题,可以先从动点三角形的面积解题策略做起,把一些克服这类考压轴题的方法总结出来,弥补
一些可能存在的不足。
首先,要明白动点三角形的面积是如何求出来的,并熟悉三角形的面积的基本原理和公式,如海伦公式,简单三角形公式等。
再次,可以把题中涉及到的二次函数表示为椭圆,是椭圆中间两个拉错线中相交地点,这
三个点构成由虚线构成的动点三角形,应该考虑把题目中的三角形面积求出来,可以用公
式求出。
最后,还可以结合图形解决问题,通过图形来分析函数的大小、极点的位置等,加深对二
次函数的理解。
总的来说,熟悉动点三角形的面积解题策略,对于二次函数的考压轴题的解决和理解都有很大的帮助,是一个拓宽数学思路的不错的方法,都有可能获得较高的分数。
二次函数面积最值问题解题思路

二次函数面积最值问题解题思路分析题意,列表如下:先看最值点,要使一个函数在某点取得最值,必须使该点的横坐标最小。
3、函数的最值应满足三个条件:(1)在闭区间[0, 2],(2)开区间[-1, 1],(3)过(-1, 1)。
(上述已排除C、 D两点)。
4、有二次函数f(x)满足,则在该点处必有一条切线(f(x)=0)与一条抛物线x=y-2交于C(C不能为1/2),而在切线(C)、抛物线y-2的焦点上都有0,这样, f(C)=f(0)=f(-1),从而有f(0)为f(-1)的最小值,故C点为一次函数y-2最小值,即为抛物线的顶点C。
3、“可去”“可进”(“进”指的是大于最小值的某一定点,“去”是去掉最小值)。
①用函数y=x+1,求出x和最小值C的距离,即C 为最小值。
②令y=0,因此有y>0,在抛物线y-2的上方不可能取得最小值,所以去掉了最小值。
综合以上几点,此题答案为C。
4、若函数有一次、二次两个极值,要保证使函数在第一个极值处取得最值,就必须保证在第二个极值处取得最小值。
(因为在第一个极值处取得最小值的同时,也在第二个极值处取得最小值,若选C,将在第一个极值处取得最小值,但在第二个极值处取得最小值时,将会使这个最小值减小;若选B,将在第一个极值处取得最小值,但在第二个极值处取得最小值时,将会使这个最小值增大。
)因此本题选A。
3、假设,则当x=2时,方程(1)(x)=0;当x=3时,方程(1)(x)=-4;4、选项A、 B两个点,都可以。
点评:学习二次函数面积最值问题的解法,要抓住关键:一是确定二次函数的顶点和对称轴;二是明确两个性质点。
二次函数在一个点处的最值问题,重点是把握两个性质点,一是函数图象上二次函数的最值点;二是性质点的坐标范围或者说“最小值”。
有了二次函数的图象和性质点,再考虑各个性质点是否过直线外一点。
要想“最值”问题解得最好,一般都是按照这样的思路来完成解答的。
4、若函数有一次、二次两个极值,要保证使函数在第一个极值处取得最值,就必须保证在第二个极值处取得最小值。
《二次函数综合——动点、面积最值问题》教学设计

二次函数综合教学目标:1.通过学习,进一步熟练待定系数法求函数解析式的方法2.设置问题,让学生经历思考、讨论、对比等过程,使学生了解解决二次函数中因动点产生的几何图形面积的表示方法,以及利用二次函数的性质解决最值问题3.在学生解决问题的过程中,锻炼学生的计算能力、观察能力,了解数形结合的数学思想教学重点:1.动点产生的几何图形面积的表示方法2.利用二次函数的性质解决最值问题教学难点:1.动点产生的几何图形面积的表示方法2.利用二次函数的性质解决最值问题教学过程:回忆复习•二次函数的基本形式、基本性质•若求二次函数的最值,常用的方法是什么?•配方后,如何判断y在什么情况下取到最值?y取最值和谁有关?考纲例证1.如图:二次函数 的图像经过点B(2,4)与A (6,0)(1).求 的值(2).点C 是该二次函数图像上A,B 两点间的一动点,横坐标为 ,写出四边形OACB 的面积S 关于点C 的横坐标 的函数表达式,并求S 的最大值本题师生一起讨论、一起完成2y ax bx =+,a b x(2<x<6)x2.已知:如图,抛物线 经过点O (0,0)(1).求 的值和抛物线与 轴的另一个交点A 的坐标(2).用配方法求该抛物线的顶点B 的坐标(3).若点P 是位于该抛物线点B 至点A 之间的一个动点,则四边形OBPA 的面积S 能否等于10?若能,请求出点P 的坐标;若不能,请说明理由本题有学生完成,对疑难点给出指导,完成之后,让学生将两题中的最后一问进行对比,点B 的位置有什么不同?解法上有什么区别?以后碰到类似的题,应该从哪些方面考虑?243y x x m =-++-m x已知:抛物线 的对称轴为 ,与 轴交于A ,B 两点,与 轴交于点C ,其中A(-3,0),C(0,-2)1.求这条抛物线的函数解析式2.已知在对称轴上存在一点P ,使得 PBC 的周长最小,请求出点P 的坐标3.在2的条件下,若点D 是线段OC 上一个动点。
如何求解二次函数中的面积最值问题

如何求解二次函数中的面积最值问题从近几年的各地中考试卷来看,求面积的最值问题在压轴题中比较常见,而且通常与二次函数相结合•使解题具有一定难度,本文以一道中考题为例,介绍几种不同的解题方法,供同学们在解决这类问题时参考.题目(重庆市江津区)2如图1抛物线y = —x + bx+ c与x轴交于A(1 , 0) , B( —3, 0)两点.(1) 求该抛物线的解析式;(2) 设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q使得△ QAC 的周长最小若存在,求出Q点的坐标;若不存在,请说明理由;(3) 如图2,在(1)中的抛物线上的第二象限上是否存在一点P,使厶PBC的面积最大若存在,求出点P的坐标及厶PBC的面积最大值;若没有,请说明理由.解答(1)抛物线解析式为2y=—x —2x + 3;(2)Q( —1 , 2);下面着重探讨求第(3)小题中面积最大值的几种方法.一、补形、割形法几何图形中常见的处理方式有分割、补形等,通过对图形的这些直观处理,一般能辅助解题,使解题过程简捷、明快.此类方法的要点在于把所求图形的面积进行适当的补或割,变成有利于表示面积的图形.方法一2如图3,设P 点(x,—x —2x + 3) ( —3<x<0).~2^x + 3)( - x - It + 3) + —(-x)( - JC3 -2r + 3 + 3}=• PE卡yOE(P£ + 0C}3J 3 / 9 27^T(I + T)+T + T当工时,SiWfig呆大值=*轨・c 总亠加9 ± 27 9 27 ―恵应*PC最大值二丕+二g此叭-a1* 2x + 3 =罠4:•点户坐标为卜寻占).2 方法二如图4,设P点(x , - x - 2x-$吐皿=5&fW i + S杜柑匚p ** 5也叱=y x3(-x2-2^ + 3} +y x3(-x)-y x 3 x 33 I3『丄9丄27 •'Tl"+7)+T + T(下略•)二、“铅垂高,水平宽”面积法如图5,过厶ABC的三个顶点分别作出与力的距离叫厶ABC的“水平宽” (a),中间的这I“铅垂高(h)”,我们可得出一种计算三角形面积面积等于水平宽与铅垂高乘积的一半.=^-PF(BE + OE) = ~PF * OB& 寻[-'-2* + 3 * (x + 3)]根据上述方法,本题解答如下:解如图6,作PE±x轴于点E,交BC设P 点(x,- x2- 2x + 3)(- 3<x<0). 直的三条直线,外侧两条直线之间仏ABC 内部线段的长度叫厶ABC的1种方法:S A ABG= _ ah,即三角形3 15•••点P坐标为(一一,一)2 4三、切线法若要使△ PBC的面积最大,只需使BC上的高最大.过点P作BC的平行线I ,当直线I 与抛物线有唯一交点(即点P)时,BC上的高最大,此时△ PBC的面积最大,于是,得到下面的切线法.解如图7,直线BC的解析式是y = x + 一,过点P作BC的平行线I,从而可设直线I的解析式为:y= x + b.ly = - x ~2x + 3.x + 6 二-2 —2 耳 + ? 丫即? + 3x + t - 3 = 0,(4i d = 3J-4(t - 3) = 0T此时RC±L的曲h垠大, h =应伽" HP=MC * sin ^_oca9 v j2 9^24 2 «TSgac h +肮* h洛曲普=278 .四、三角函数法本题也可直接利用三角函数法求得.解如图8,作PE±x轴交于点E,交BC于点F,怍PM L BC于点M设P 点(x,—x2—2x + 3) (- 3<x<0),则F(x , x + 3).=y X37? X PF 'IS 7乂警【(-卫-2^ +3> - +3)] x=攀-加十3} xsin L OCB* 它* 9 2? 9 27「仏雌饋大=y +j-y s F「当直=-?时"~ x1 -2^+3 m 孕.2 4*■-点p坐标为(-从以上四种解法可以看到,本题解题思路都是过点出各元素之间的关系进行求解.如此深入挖掘一道题的多种解法,可使我们摆脱题海战术, 提高解题能力•同时,善于总结一道题的多种解法能加快解题速度,提高解题效率,也有利于培养我们的钻研能力和创新精神.P作辅助线,然后利用相关性质找。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数动点问题中面积最值的解法策略摘要:我国正在实施新的基础教育课程改革,《义务教育数学课程标准(2022年版)》指出要培养学生的数学核心素养,而二次函数和几何图形的综合应用题,能充分的考查学生的数学抽象,逻辑推理,数学运算以及数学建模等综合能力。
这种类型的综合题,通常出现在中考的压轴题中,综合性强,计算强度大,具有较大的难度,在二次函数与几何图形的综合题中,求二次函数面积的最值问题比较常见,本文就此问题解法进行探讨。
关键词:二次函数与几何图形;函数动点问题;二次函数面积最值二次函数动点问题就是通过点的运动生成一种函数关系及函数图象,抛物线上点的运动与直线相结合而产生的三角形面积问题,就是将几何图形与函数图象有机地融合在一起,解决的关键是结合图形通过点坐标衔接函数、方程找到函数关系。
本文就求解二次函数面积最值的问题,浅谈几种解决此类问题的方法策略。
一、割补法在解决二次函数面积最值问题时,不规则多边形的面积往往可以通过割补法把多边形分为几个三角形或者是规则的四边形的面积来求解,当三角形中有一边是在坐标轴上,或者在以坐标轴平行的直线上,那么就可以把这一条边当作三角形的底边,第三个点到这一条边的距离,作为三角形的高,直接利用三角形的面积公式求解,或者过图形的各端点作两坐标轴的平行线,构造与轴平行的最小矩形对所要求面积的图形进行覆盖,然后所求图形的面积即为矩形面积减去多余的几个直角三角形的面积。
最终把多边形面积的最值问题,转化为求三角形面积的最值问题,这也体现了一种“化归”的思想方法。
题目1、(2019枣庄)已知抛物线y=ax2+x+4的对称轴是直线x=3,与x轴相交于A,B两点(点B在点A右侧),与y轴交于点C.(1)求抛物线的解析式和A,B两点的坐标;(2)如图①,若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),是否存在点P,使四边形PBOC的面积最大?若存在,求点P的坐标及四边形PBOC面积的最大值;若不存在,请说明理由.[思路分析](1)由抛物线的对称轴是直线x=3,解出a的值,即可求得抛物线的表达式,再令其y值为0,解一元二次方程即可求出A和B的坐标。
(2)易求出点C的坐标为(0,4)。
连接OP,则不规则的四边形PBOC的面积等于△OPC的面积加上△OPB的面积,在平面直角坐标系中,解决函数动点问题的方法是设带有参数的动点坐标,本题可设动点P的坐标为(x,-x2+x+4),因△OPC、△OPB中各有一边是在坐标轴上,可直接利用三角形的面积公式求解。
经计算得到四边形PBOC的面积是一个关于x的二次函数,把二次函数配方为顶点式,根据x的取值范围,可以求得四边形PBOC面积的最大值。
解:(1)∵抛物线y=ax2+x+4的对称轴是直线x=3,∴-=3,解得a=-.∴抛物线的解析式为y=-x2+x+4.令y=0,则-x2+x+4=0,解得x1=-2,x2=8,∴点A的坐标为(-2,0),点B的坐标为(8,0);(2)存在,如右图,连接OP.∵当x=0时,y=-x2+x+4=4,∴点C的坐标为(0,4).设点P的坐标为(x,-x2+x+4),∴S四边形PBOC=S△POC+S△POB=×4×x+×8×(-x2+x+4)=-x2+8x+16=-(x-4)2+32.∵-1<0,0<x<8.∴当x=4时,四边形PBOC的面积最大,最大面积是32,此时y=-x2+x+4=-×42+×4+4=6.∴点P的坐标是(4,6).故存在点P,使四边形PBOC的面积最大,点P的坐标是(4,6),四边形PBOC面积的最大值是32;点评:对于二次函数中不规则四边形面积最值的求法,我们常规的方法是把它转化为规则的图形去解决。
从而达到简化计算过程和计算难度的目的。
二、铅垂高法如图,过△ABC的三个顶点,分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫做△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫做△ABC的“铅垂高”(h),则S△ABC=ah,即三角形的面积等于水平宽与铅垂高乘积的一半。
公式证明如下:S△ABC=S△ABD+S△ADC=h+h =(+)= ah铅垂高度,实际上就是横坐标相同的两个点的纵坐标差的绝对值,即AD= |-| , 为了保证这个差值是正数,用铅垂线上方点的纵坐标减去下方点的纵坐标,因此,求出点A、 D 的坐标,是求铅垂高度 AD 的关键。
即,S△ABC=AD|-| =|-||-|题目 2、在平面直角坐标系中,直线y=x-2与x轴交于点B,与y轴交于C,二次函数y=x2+bx+c的图象经过B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.(1)求二次函数的解析式及点A的坐标;(2)如图,连接DC,DB,设△BCD的面积为S,求S的最大值;[思路分析](1)令关系式y=x-2中的y、x的值分别为0,求出对应的x,y的值,可求得B、C两点坐标,然后利用待定系数法可求得抛物线解析式,再令其y值为0,解一元二次方程即可求出点A的坐标。
(2)△BCD是一个斜三角形,它没有任何一条边在坐标轴上或者在与坐标轴平行的直线上,可以考虑用铅垂法求它的面积。
过点D作DE∥y轴,交BC于点E, 则△BCD的铅垂高就是DE,水平宽就是OB, 因动点D在抛物线上,可设动点D的坐标为(x,x2-x-2),点E在直线BC上,且与D点的横坐标相等,故可设E的坐标为 (x,x-2) ,则DE= |-| =(x-2)-(x2-x-2)=-x2+2x,再利用三角形的面积等于水平宽与铅垂高乘积的一半即可求出△BCD的面积。
2. 解:(1)令y=x-2=0,解得x=4,令x=0,则y=x-2=-2,∴点B(4,0),C(0,-2),将点B(4,0),C(0,-2)代入y=x2+bx+c中得解得∴二次函数的表达式为y=x2-x-2.令y=x2-x-2=0,解得x1=-1,x2=4,∴点A的坐标为(-1,0).(2)如解图①,过点D作DE∥y轴,交BC于点E,设点D的坐标为(x,x2-x-2),则点E(x,x-2),∴DE=x-2-(x2-x-2)=-x2+2x,第2题解图①∴S=S△CDE+S△BDE=DE×OB =DE×4=×(-x2+2x)×4=-x2+4x=-(x-2)2+4,∵-1<0,0<x<4,∴当x=2时,S有最大值,最大值为4;点评:用铅垂法解决斜三角形面积最值问题,先通过设立带有参数的点的坐标来确定线段长,进而求斜三角形面积的最值,体现了建模思想,数形结合思想和转化思想在二次函数中的应用。
三、平移法当三角形的底边已经确定,要求三角形面积的最大值,只有当高最大时,三角形的面积才是最大的。
平移三角形底边所在的直线,当这条直线与抛物线只有唯一的一个公共点的时候,能使得三角形的面积最大。
这个公共点就是能使得三角形面积最大的动点位置。
题目 3、直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.(1)求该抛物线的解析式;(2)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值.[思路分析](1)由直线解析式可求得B、C坐标,利用待定系数法可求得抛物线解析式。
(2)以 BC作为三角形的底边,只要求出高的最大值就可以求出面积的最值.将直线 BC平移,与抛物线存在唯一的一个交点时,两直线的距离就是高的长度,此时三角形的面积最大。
解(1)∵直线y =﹣x+3与x轴、y轴分别交于点B、点C,∴B(3,0),C(0,3),把B、C坐标代入抛物线解析式可得,解得,∴ 抛物线解析式为y = x2﹣4x+3;(2)把直线BC平移与抛物线仅有唯一的一个交点时,两条平行线间的距离最大,此时△CBE的面积最大,这个交点就是点E的位置,如图所示。
∵直线BC 的解析式为y =﹣x+3,直线DE与直线BC平行∴设直线DE 的解析式为y =﹣x+m ,直线DE与抛物线仅有一个交点,联立直线DE、抛物线解析式,得{,消去y得:-3+3-m=0,由△=-4×(3-m)=0 解得:m=,即当 m=时,点E到BC的距离最大,△CBE的面积最大,此时x=,y =﹣+=﹣∴E(,﹣)即当E点坐标为(,﹣)时,△CBE的面积最大.点评:平移三角形底边所在的直线,当直线与抛物线有且只有一个交点时,三角形的面积最大,联立直线与抛物线两个函数,消去y,得关于x一元二次函数,使其判别式为0,最终求出交点坐标,平行线法解决二次函数中面积最值十分方便,使得二次函数压轴题面积最值迎刃而解。
二次函数动点问题中的综合题,一般借助函数图像上点的坐标建立与几何图形、图形运动的关系,总结解题策略是突破函数和几何图形综合题的关键,抓住知识之间的纽带,利用数形结合研究方法,依据点坐标的衔接作用对问题进行转化, 基于函数方程思想,构建研究模型,解决二次函数和几何图形综合题实际上就是策略运用和模型构建的过程,掌握解题策略即可显著提升解题能力,与此同时,在课堂解题教学中,还需要突出数学基本活动经验的积累,可采取由学生总结归纳,教师进行完善提炼,强调解决问题的思路策略,通过例题运用进行巩固和强化,切实提升学生解决问题和分析问题能力。
参考文献:[1]王唯一. 解二次函数中三角形面积最值问题. 数理化解题研究,2016 (35)[2] 熊猛. 二次函数中三角形面积问题的解法例析. 数理化解题研究2014(01)[3]杨洛瑞. “双轨平行线”破解二次函数面积最值. 教学改革2019 (9)[4] 陈艳. 关于二次函数综合题的探究与思考. 数学教学通讯试题研究2018(12)。
