1 用表格表示变量之间的关系 & 2 用表达式表示变量之间的关系
4.1《用表格表示变量间关系》 课件(北师大版) (9)

课堂小结:
• 通过今天的学习,你能用自己的话说说你的 收获和体会吗? • 1.在具体情境中理解什么是变量、常量、 • 自变量、因变量. • 2.能从表格中获得变量之间关系的信息, 能用表格表示变量之间的关系,尝试对变 化趋势进行初步的预测.
布置作业
• • • • • 1.习题4.1:P100-问题解决4、5 2、计算: ①0.2510×220 ②(yx3)2÷x2 ③【(x+y)2-(x-y)2】÷2xy
土豆产量/ 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75 吨/公顷
• (3)根据表格中的数据,你认为氮肥的施用量 是多少时比较适宜?说说你的理由. • (4)粗略说一说氮肥的施用量对土豆产量的影 响.
当施用量小于336时,施的越多产量越高,当 施用量大于336时施的越多产量反而下降。
概念介绍
• 在“小车下滑的时间”中,支撑物的高度 h和小车下滑的时间t都在变化,它们叫做 变量(variable).其中支撑物高度h的变化 导致小车下滑的时间t随之发生变化.支撑 物的高度h叫自变量,小车下滑的时间t叫 因变量
自变量就是自身主动发生变 化的量,而因变量则是随着自 变量的变化而变化的!
(1)支撑物高度为70厘米时,小车下滑时间 是多少? (2)如果用h表示支撑物高度,t表示小车下 滑时间,随着h逐渐变大,t的变化趋势是 什么? (3)h每增加10厘米,t的变化情况相同吗? (4)估计当h=110厘米时,t的值是多少.你 是怎样估计的? (5)随着支撑物高度h的变化,有哪些量发 生变化?哪些量始终不发生变化?
用表格表示的变量间关系
进入变化的世界
• 我们生活在一个变化的世界中, 万事 万物都在发生变化. • 你能从生活中举出一些发生变化的例 子吗?
初中数学_用表格表示变量之间的关系教学设计学情分析教材分析课后反思

第三章变量之间的关系第一节用表格表示的变量间关系一、学生知识状况分析本节课是本章的起始课,与后面三个课时合起来分别呈现的是表示变量之间关系的三种方式——表格法、解析式法和图象法。
本章作为研究变量和函数的起始章节,重在让学生感受和体会生活中的“变量”。
同时,在第一课时还要教给学生用表格呈现实验中变量的数据的方法。
但“数量推理所得到的结果远比那些单纯用数刻画的事实更具威力,这种数量推理稳固地根植于数和有关计算的一般模式之中。
(James Fey)”所以,依据变量之间关系的数学表示(表格、解析式和图象)进行预测或推测已知中没有给出的量,也是研究变量之间关系的重要目标之一。
知识基础:本节课是学生在七年级上册教材中学习了探索规律,从统计图中获取信息的基础上,通过表格形式来理解变量、自变量、因变量这些概念。
我们生活在变化的世界中,变量与变量的关系,在生活生产中无处不在,通过对实际问题的理解,在表格信息中发现两个变化的量,通过了解哪一个是主动变化的,哪一个是随着变化的,来识别自变量和因变量,这对今后学习函数知识是非常重要的。
活动经验基础:在以前的学习中,学生已经经历了分组学习、合作交流等形式,可以解决一些实际问题,具备了合作学习的能力。
二、教学任务分析在学生现有的知识基础上,本节的教学及学习任务是鼓励学生用表格整理数据并充分地从表格中获取信息,运用自己的语言进行描述,与同伴进行交流,提高学生合作交流的意识。
学生通过对表格中数据的分析,进一步体会变量之间的关系,明确自变量与因变量,并能通过资料分析进行预测。
教学目标:1.经历探索具体情境中两个变量之间关系的过程,获得探索变量之间关系的体验,进一步发展符号感。
2.在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子。
3.学会用表格整理试验得出的数据,能从表格中获得变量之间关系的信息,并根据表格中的资料尝试对变化趋势进行初步的预测。
三、教学过程设计本节课设计了九个教学环节:情景导入,探究篇,认知篇,升级探究篇,闯关篇,生活链接篇,课堂小结、课堂检测、布置作业。
《用表格表示的变量间关系》教案 (公开课)2022年(1)
用表格表示变量之间的关系一.学习目标1.在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子.2.能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,并根据表格中的数据尝试对变化趋势进行初步的预测.二.学习导航活动——交流——探索相结合三.探究新知1.具体情境:今天早上一起床,我就到厨房烧上了一壶水,10分钟后,水烧开了.在这一过程中,什么在发生变化?2.你能从生活中找到一些发生变化的例子吗?自变量:因变量:生活中有哪些例子也反映了变量之间的关系?并指出哪一个是自变量?哪一个是因变量?四.运用新知下面我们来做一个试验:小车下滑.每个小组利用同一块木板,测量小车从不同高度下滑的时间.然后将得到的〔1〕支撑物高度为70厘米时,小车下滑时间是多少?〔2〕指出表中的变量,谁是自变量,谁是因变量?〔3〕如果用h表示支撑物高度,t表示小车下滑时间,随着h逐渐变大,t变化趋势如何?〔4〕h每增加10厘米,t的变化情况相同吗?思考:根据我们做的实验和经验,为什么会有支撑物h越高,小车下滑时间t越短呢?议一议〔2〕如果用x表示时间,y表示我国人口总数,那么随着x的变化,y 的变化趋势是什么?〔3〕从1949年起,时间每向后推移10年,我国人口是怎样变化的?五.反响练习研究说明,当钾肥和磷肥的施用量一定时,土豆的产量与氮服的施用量有如〔2〕当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?〔3〕根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.〔4〕粗略说一说氮肥的施用量对土豆产量的影响.六.拓展与应用在北京市“危旧房改造〞中,小强一家搬进了回龙观小区.这个小区冬季用家庭燃气炉取暖.为了估算冬季取暖第一个月使用天然气的开支情况,从11月1 5日起,小强连续八天每天晚上记录了天然气表显示的读数,如下表〔注:天然3小强的妈妈11月15日买了一张面值600元的天然气使用卡,每立方米天然气1.70元,请你估算这张卡够小强家用一个月〔按30天计算〕吗?为什么?〔平行四边形的性质总体说明〔1〕本节的主要内容包含平行四边形的性质。
人教版-初二-七下1、暑假教案-用表格表示的变量间关系、用关系式表示的变量间关系

知识典例(注意咯,下面可是黄金部分!)知识清单(一)变量、自变量、因变量1、在某一变化过程中,不断变化的量叫做变量。
2、如果一个变量y随另一个变量x的变化而变化,则把x叫做自变量,y叫做因变量。
3、自变量与因变量的确定:(1)自变量是先发生变化的量;因变量是后发生变化的量。
(2)自变量是主动发生变化的量,因变量是随着自变量的变化而发生变化的量。
(3)利用具体情境来体会两者的依存关系(二)表格法1、表格是表达、反映数据的一种重要形式,从中获取信息、研究不同量之间的关系。
2、绘制表格表示两个变量之间关系(1)列表时首先要确定各行、各列的栏目;(2)一般有两行,第一行表示自变量,第二行表示因变量;(3)写出栏目名称,有时还根据问题内容写上单位;(4)在第一行列出自变量的各个变化取值;第二行对应列出因变量的各个变化取值。
(5)一般情况下,自变量的取值从左到右应按由小到大的顺序排列,这样便于反映因变量与自变量之间的关系。
(三)关系式法1、用关系式表示因变量与自变量之间的关系时,通常是用含有自变量(用字母表示)的代数式表示因变量(也用字母表示),这样的数学式子(等式)叫做关系式。
2、关系式的写法不同于方程,必须将因变量单独写在等号的左边。
3、关系式的应用:(1)利用关系式能根据任何一个自变量的值求出相应的因变量的值;(2)同样也可以根据任何一个因变量的值求出相应的自变量的值;(3)根据关系式求值的实质就是解一元一次方程(求自变量的值)或求代数式的值(求因变量的值)。
(四)图象法1、图象是刻画变量之间关系的又一重要方法,其特点是非常直观、形象。
2、图象能清楚地反映出因变量随自变量变化而变化的情况。
3、用图象表示变量之间的关系时,通常用水平方向的数轴(又称横轴)上的点表示自变量,用竖直方向的数轴(又称纵轴)上的点表示因变量。
4、图象上的点:(1)对于某个具体图象上的点,过该点作横轴的垂线,垂足的数据即为该点自变量的取值;(2)过该点作纵轴的垂线,垂足的数据即为该点相应因变量的值。
用表格表示变量之间的关系
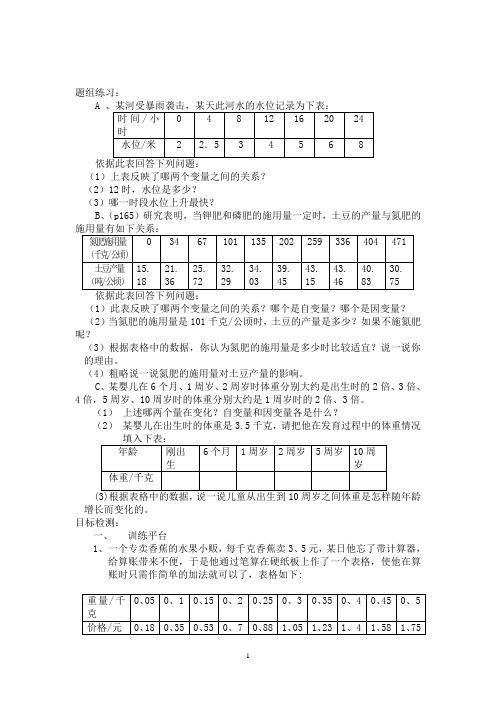
题组练习:A 、某河受暴雨袭击,某天此河水的水位记录为下表:时间/小时0 4 8 12 16 20 24水位/米 2 2.5 3 4 5 6 8 依据此表回答下列问题:(1)上表反映了哪两个变量之间的关系?(2)12时,水位是多少?(3)哪一时段水位上升最快?B、(p165)研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:氮肥施用量(千克/公顷)0 34 67 101 135 202 259 336 404 471土豆产量(吨/公顷)15.1821.3625.7232.2934.0339.4543.1543.4640.8330.75依据此表回答下列问题:(1)此表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说一说你的理由。
(4)粗略说一说氮肥的施用量对土豆产量的影响。
C、某婴儿在6个月、1周岁、2周岁时体重分别大约是出生时的2倍、3倍、4倍,5周岁、10周岁时的体重分别大约是1周岁时的2倍、3倍。
(1)上述哪两个量在变化?自变量和因变量各是什么?(2)某婴儿在出生时的体重是3.5千克,请把他在发育过程中的体重情况填入下表:年龄刚出生6个月1周岁2周岁5周岁10周岁体重/千克(3)根据表格中的数据,说一说儿童从出生到10周岁之间体重是怎样随年龄增长而变化的。
目标检测:一、训练平台1、一个专卖香蕉的水果小贩,每千克香蕉卖3、5元,某日他忘了带计算器,给算账带来不便,于是他通过笔算在硬纸板上作了一个表格,使他在算账时只需作简单的加法就可以了,表格如下:重量/千克0、05 0、1 0、15 0、2 0、25 0、3 0、35 0、4 0、45 0、5价格/元0、18 0、35 0、53 0、7 0、88 1、05 1、23 1、4 1、58 1、75(1)当买香蕉0、5千克时,价格是多少?(2)如果用x表示质量,y表示价格,那么x随着的变化,y的变化趋势时什么?(3)请你估计当x=3千克时,y的值是多少?2、爷爷告诉小强:“距离地面越高,温度越低”,并给小强出示了下面的表格:距离地面高度/千米0 1 2 3 4 5温度/摄氏度20 14 8 2 —4 —10 根据上表,爷爷还给小强出了下面几个问题,请你和小强一起来回答。
初中数学-变量之间的关系

变量之间的关系第一节用表格表示变量之间的关系知识点一变量、自变量、因变量、常量的定义一般地,在某一变化过程中,数值发生变化的量成为变量. 如果有两个变量,当其中一个变量在一定范围内取一个数值时,两一个变量也有唯一的一个数值与其对应,那么,通常前一个变量叫自变量,后一个变量叫做因变量. 在变化过程中数值始终不变的的那个量叫做常量.注意:(1)常亮与变量往往是相对的,相当于某个变化过程.(2)在某一变化过程中,可能有一个或几个常量,不可能没有变量,也不可能只有一个变量,一般有两个变量.知识点二自变量与因变量的区别与联系自变量与因变量共同存在于一个变化过程中,它们既有区别又有联系.因变量随自变量的变化情况:知识点三从表格中获取信息对变化趋势进行初步预测借助表格可以表示两个变量之间的关系.表示两个变量之间关系的表格,一般第一行表示自变量,第二行表示因变量,从表格中发现因变量随自变量变化存在一定的规律——或者增加或者减少或者呈规律性的起伏变化,从而利用变化趋势对结果作出预测.用列表法表示两个变量之间的关系时,表格只能提供自变量与因变量对应的部分数据,不能全面反映两个变量之间的关系,想要知道表格中没有出现的自变量与因变量的对应数据,需要对表格中的数据进行分析,从已知部分数据中观察变量的变化规律并依此估计未在表格中出现的数据.例题1. 某人要在规定时间内加工100个零件,则工作效率y与时间t之间的关系中,下列说法正确的是()A.y,t和100都是变量 B.100和y都是常量C.y和t是变量D.100和t都是常量练习1. 下表是某报纸公布的世界人口数情况:上表中的变量是()A.仅有一个,是年份B.仅有一个,是人口数C.有两个变量,一个是人口数,另一个是年份D.一个变量也没有在这三个量中,__________是常量,__________是自变量,__________是因变量.练习4. 在利用太阳能热水器给水加热的过程中,热水器里水的温度随所晒太阳光时间的长短而变化,这个问题中因变量是()A.太阳光的强弱B.热水器里水的温度C.所晒太阳光的时间D.热水器练习5. 一个圆柱的高h为10 cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中()A.r是因变量,V是自变量B.r是自变量,V是因变量C.r是自变量,h是因变量D.h是自变量,V是因变量练习6. 明明从广州给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个过程中,因变量是()。
(五四制) 鲁教版数学 6年级下册 配套练习册 一课一练 基本功训练_36
第九章变量之间的关系1用表格表示变量之间的关系王波学习小组利用同一块木板,测量了小车从不同高度沿斜放的木板从顶部下滑到底部所用的时间,得到如下数据:表 1(1)支撑物高度为 70 cm 时,小车下滑时间是多少?(2)如果用 h 表示支撑物高度,t 表示小车下滑时间,随着 h 逐渐变大,t 的变化趋势是什么?(3)h 每增加 10 cm ,t 的变化情况相同吗?(4)估计当 h = 110 cm 时,t 的值是多少.你是怎样估计的?(5)随着支撑物高度 h 的变化,还有哪些量发生变化?哪些量始终不发生变化?1用表格表示变量之间的关系随堂练习我国从 1949 年到 2009 年的人口统计数据如下(精确到 0.01 亿):表 2(1)如果用 x 表示时间,y 表示我国人口总数,那么随着 x 的变化,y 的变化趋势是什么?(2)从 1949 年起,时间每向后推移 10 年,我国人口是怎样变化的?在表 1 中,支撑物高度 h 和小车下滑时间 t 都在变化,它们都是变量(variable ). 其中 t 随 h 的变化而变化,h 是自变量(independent variable ),t 是因变量(dependent variable ).在这一变化过程中,小车下滑的距离(木板长度)一直没有变化. 像这种在变化过程中数值始终不变的量叫做常量(constant ).在表 2 中,我国人口总数 y 随时间 x 的变化而变化, x 是自变量, y 是因变量.借助表格,我们可以表示因变量随自变量的变化而变化的情况.1. 生活中有哪些例子反映了变量之间的关系?与同伴进行交流.2. 研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)当氮肥的施用量是 101 千克/公顷时,土豆的产量是多少?如果不施氮肥呢?议一议第九章变量之间的关系3. 举出生活中包含变量的例子,分析变量之间的关系,并与同伴进行交流. 如分析烧水过程中水的温度随时间变化的情况.4. 小明在课余时间找了几副度数不同的老花镜,让镜片正对着太阳光,并上下移动镜片,直到地上的光斑最小. 此时他测量了镜片与光斑的距离,得到如下数据:1. 据世界人口组织公布,地球上的人口 1600 年为 5 亿,1830 年为 10 亿,1930 年为 20 亿,1960 年为 30 亿,1974 年为 40 亿,1987 年为 50 亿,1999 年为 60亿,而到 2011 年地球上的人口达到了 70 亿. 用表格表示上面的数据,并说一说世界人口是怎样随时间推移而变化的.2. 婴儿在 6 个月、1 周岁、2 周岁时体重分别大约是出生时的 2 倍、3 倍、4 倍,6 周岁、10 周岁时体重分别约是 1 周岁时的 2 倍、3 倍.(1)上述的哪些量在发生变化?自变量和因变量各是什么?(2)某婴儿在出生时的体重是 3.5 kg ,请把他在发育过程中的体重情况填入下表:年龄刚出生6 个月1 周岁2 周岁6 周岁10 周岁体重/ kg(3)根据表格中的数据,说一说儿童从出生到 10 周岁之间体重是怎样随年龄增长而变化的.(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由;(4)粗略说一说氮肥的施用量对土豆产量的影响.习题 9.1知识技能数学理解问题解决。
3.1用表格表示变量之间的关系
3.1用表格表示的变量间关系【学习目标】我要做到:在探索具体情境中两个变量之间关系的过程中,获得探索变量之间关系的体验,进一步发展符号感。
我要突破:在具体情境中理解什么是变量、自变量、因变量,能举出反映变量之间关系的例子。
进而用表格表示变量之间的关系,根据表格中的资料尝试对变化趋势进行初步的预测。
【预习导航】学法指导:请同学们结合学习目标自学课文第62-63页的“用表格表示的变量间关系”的内容。
1.什么是变量、自变量、因变量?在一个变化过程中数值保持不变的量叫做______,可以取不同数值的量叫做______,如果一个量随着另外一个量的变化而变化,那么把这个量叫做______,另一个量叫做______。
2.本节是通过______形式来表示两个变量之间的关系的。
尝试对变化趋势进行初步的预测吗? 知识链接:1.某电影院地面的一部分是扇形,座位按下列方式设置: (1)第5排有 个 座位,第6排有 个座位; (2)第n 排有 个 座位。
(3)若电影院一共有13排座位,则电影院共有 个 座位。
2.我们的世界无时无刻地发生着变化的,请举出一些发生变化的例子:【合作探究】问题1:与同伴交流下列问题,理解变量之间的关系?并找出哪是自变量?哪是因变量 ?1、 完成课本62页表1并回答问题:2、 在“小车下滑的时间” 中,支撑物的高度h 和小车下滑的时间t 都在变化,它们都是 ,其中小车下滑的时间t 随支撑物的高度h 的变化而变化,支撑物的高度h 是 ,小车下滑的时间t 是 ,小车下滑的距离是 。
(填“变量”、“常量”、“自变量”或“因变量”) 问题2:你能结合下列具体问题进一步体会变量之间的关系,从表格中获取信息,预测我国人口将会有怎样的变化吗?1、我国从1949年到1999年的人口统计数据如下(精确到0.01亿):(1)如果用x 表示时间,y 表示我国人口总数,那么随着x 的变化,则y 会 , (2)X 和y 中 是自变量, 是因变量。
北师大版七年级数学下册第三章变量之间的关系PPT导学课件
1 用表格表示的变量间关系
知识点二 借助表格表示两个变量之间的关系
把自变量的一系列值和因变量的对应值列成一个表来表示变量 之间的关系,像这种表示变量之间关系的方法叫做表格法. 用表格表示两个变量,一般第一栏表示自变量,第二栏表示因 变量,从表格中可以发现因变量随自变量的变化存在一定的规律, 或增加或减少或呈现规律性的起伏变化,从而利用变化趋势对结果 做出预测.
1 用表格表示的变量间关系
解:他的答案不正确,因为π表示一个常量,所以常量是 2,π而不是 2,所以正确答案是 B.
第三章 变量之间的关系
第三章 变量之间的关系
2 用关系式表示的变量间关系
知识目标 目标突破 总结反思
2 用关系式表示的变量间关系
知识目标
1.通过对几何图形的分析,能用关系式表示出两个变量之间
ቤተ መጻሕፍቲ ባይዱ
例 2 教材补充例题 某同学用弹簧做试验,在弹簧上挂不同质 量的物体时弹簧的长度就会发生变化, 但所挂物体的质量不能超过 1000 克,试验数据如下表: 物体质量(克) 100 200 300 400 12 13 14 弹簧长度(厘米) 11 关系?
(1) 此题中哪个是自变量?哪个是因变量?它们之间有什么
1 用表格表示的变量间关系
[注意] 自变量是在一定范围内主动发生变化的量;因变量是 随着自变量的变化而发生变化的量. [点拨] (1)变量与常量是相对的,自变量与因变量是相对的, 在不同的研究过程中,二者可以互相转化. (2)一般情况下, 在某一变化过程中, 可能有一个或几个常量, 不可能没有变量,也不可能只有一个变量.
1 用表格表示的变量间关系
【归纳总结】自变量和因变量的联系和区别: 自变量 区别 因变量 先发生变化或自 后发生变化或随着自变量 主发生变化的量 的变化而发生变化的量 1.两者都是某一变化过程中的变量; 联系 2.两者因研究的侧重点或先后顺序不同而可 以相互转化
第四章-变量之间的关系 同步练习题-七年级下册(北师大版)
七年级数学下第三章变量之间的关系§3.1用表格表示变量间的关系➢知识导航一、变量、自变量、因变量1、在某一变化过程中,不断变化的量叫做变量。
2、如果一个变量y随另一个变量x的变化而变化,则把x叫做自变量,y叫做因变量。
二、列表法采用数表相结合的形式,运用表格可以表示两个变量之间的关系。
列表时要选取能代表自变量的一些数据,并按从小到大的顺序列出,再分别求出因变量的对应值。
列表法最大的特点是直观,可以直接从表中找出自变量与因变量的对应值,但缺点是具有局限性,只能表示因变量的一部分。
➢同步练习1.小明和他爸爸做了一个实验:由小明从一幢245m高的楼顶随手扔下一只苹果,由他爸爸测量有关数据,得到苹果下落的路程和下落的时间有下面的关系:则下列说法错误的是( ) A、苹果每秒下落的路程不变; B.苹果每秒下落的路程越来越长C.苹果下落的速度越来越快;D.可以推测,苹果下落7s后到达地面2、赵先生手中有一张记录他从出生到24岁期间的身高情况表: 下列说法错误的是( )A.赵先生的身高增长速度总体上先快后慢;B.赵先生的身高在21岁以后基本不长了;C.赵先生的身高从0岁到24岁平均每年增高7.1cm;D.赵先生的身高从0岁到24岁平均每年增高5.1cm.3.小明的妈妈自小明出生时起每隔一段时间就给小明称一下体重,得到下面的数据: 从表中可以得到:小明体重的变化是随小明的________的变化而变化的,这两个变量中,________是自变量,_________是因变量,虽然随着年龄的增大,•小明的体重__________,但体重增加的速度越来越_________.4.据国家统计局统计,解放以来至2000年我国各项税收收入合计如下表:从表中可以得出:•解放以来我国的税收收入总体趋势是__________,•其中,_______年与5年前相比,增长百分数最大,_________年与5•年前相比增长百分数最小,算一算,2000年与1950年相比,税收收入增长了________倍.(保留一位小数)5.随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势年 份 2006 2007 2008 … 入学儿童人数2 5202 3302 140…(1)上表中_____是自变量,_____是因变量.(2)你预计该地区从_____年起入学儿童的人数不超过1 000人. 6.2012年1~12月某地大米的平均价格如下表表示?月份 123456789101112平均价格(元/kg)2.3 2.4 2.4 2.5 2.4 2.2 2.0 1.9 1.8 1.8 1.9 2.0(1)表中列出的是哪两个变量之间的关系?哪个是自变量,哪个是因变量? (2)自变量是什么值时,因变量的值最小?自变量是什么值时,因变量的值最大? (3)该地哪一段时间大米平均价格在上涨?哪一段时间大米平均价格在下落?(4)从表中可以得该地大米平均价格变化方面的哪些信息?平均比年初降低了还是涨价了?体重(kg)515 20 23.5 26.3 293132.834.53637年份 1950 1955 1960 1965 1970 1975 1980 1985 1990 19952000税收收入(亿)48127203204281402571 •204028216038 125817.下表是佳佳往妹妹家打长途电话的几次收费记载:时间/分 1 2 3 4 5 6 7电话费/元0.6 1.2 1.8 2.4 3.0 3.6 4.2(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)你能帮佳佳预测一下,如果她打电话用时间是10分钟,则需付多少电话费?8.如图,是一个形如六边形的点阵,它的中心是一个点,算第一层;第二层每边两个点;第三层每边有三个点,依此类推:(1)填写下表:层数 1 2 3 4 5 6 ……该层的点数……所有层的点数……(2)每层点数是如何随层数的变化而变化的?所有层的总点数是如何随层数的变化而变化的?(3)此题中的自变量和因变量分别是什么?(4)写出第n层所对应的点数,以及n层的六边形点阵的总点数;(5)如果某一层的点数是96,它是第几层?(6)有没有一层,它的点数是100?为什么?9.下表是明明商行某商品的销售情况,该商品原价为560元,随着不同幅度的降价(单位:元),日销量(单位:件)发生相应变化如下表:降价(元) 5 10 15 20 25 30 35日销量(件)780 810 840 870 900 930 960(1)上表反映了哪两个变量之间的关系?其中那个是自变量,哪个是因变量?P DCB A(2)每降价5元,日销量增加多少件?请你估计降价之前的日销量是多少? (3)如果售价为500元时,日销量为多少?§3.2用关系式表示的变量间关系➢ 知识导航:关系式法关系式是利用数学式子来表示变量之间关系的等式,利用关系式,可以根据任何一个自变量的值求出相应的因变量的值,也可以已知因变量的值求出相应的自变量的值。
