(完整)机械波的多解问题-
2022-2023高中物理--机械波--专题:波动问题的多解

波动问题的多解一、知识点梳理机械波传播过程中在时间和空间上的周期性、传播方向上的双向性、质点振动方向的不确定性都是形成波动问题多解的主要原因.解题时常出现漏解,现归类分析1.波的空间周期性沿波的传播方向,在x 轴上任取一点)(x P ,如图所示.P 点的振动完全重复波源O 点的振动,只是时间上比O 点要落后t ∆时间,且T xv x t λ==∆.在同一列波上,凡坐标与P 点坐标x 之差为波长整数倍的质点,在同一时刻t 的振动位移都与坐标为x 的质点的振动位移相同,其振动速度、加速度也都与坐标为x 的质点相同,或者说它们的振动“相貌”完全相同.因此在同一列波上,某一振动“相貌”势必会不断地重复出现,这就是机械波的空间周期性.波的空间周期性说明,在同一列波上,相距为波长整数倍的多个质点的振动情况完全相同.2.波的时间周期性在x 轴上取一给定质点,在kT t +时刻的振动情况与它在t 时刻的振动情况(位移、速度、加速度等)相同.因此在t 时刻的波形,在kT t +时刻必然多次重复出现,这就是机械波的时间周期性,波的时间周期性表明,波在传播过程中,经过整数倍周期时,其波形图线相同.3.波的双向性双向性是指波沿正、负两方向传播时,若沿正、负两方向传播的时间之和等于周期的整数倍,则沿正、负两方向传播到那一时刻的波形图相同.4.波的对称性波源的振动,要带动它左、右相邻质点的振动,波要向左、右两方向传播.对称性是指波在向左、右同时传播时,关于波源对称的左、右两质点的振动情况完全相同.5.介质中两质点间的距离与波长关系未定在波的传播方向上,如果两个质点相距的距离不确定,就会形成多解,学生若不能联想到所有可能的情况,则易出现漏解.6.介质中质点的振动方向未定在波的传播过程中,质点振动方向与传播方向相联系,若某一质点振动方向未确定,则波的传播方向有两种,这样会形成多解.例1.一列简谐横波在0=t 时刻的波形如图中的实线所示,s 02.0=t 时刻的波形如图中虚线所示.若该波的周期T 大于s 02.0,则该波的传播速度可能是( ) A .2m/s B .3m/s C .4m/s D .5m/s例2.如图所示,一列简谐横波在x 轴上传播,图甲和图乙分别为x 轴上a 、b 两质点的振动图象,且m 6=ab x ,下列判断正确的是( )A .此波一定沿x 轴正方向传播B .波长一定是8mC .波速可能是2m/sD .波速一定是6m/s二、技巧总结1.波动问题的解题技巧(1)波动图象的周期性形成的多解分析方法求解波动图象多解问题,关键是分析时间和空间的周期性,注意以下两点:①写关系式时,先找出两个状态下的最小时间间隔或最小距离,再引入整数n 写出通式.x n x ∆+=λ,t T n t ∆+=',tT n xn t x v ∆+∆+=='λ,其中n 、 3,2,1,0'=n ②如果有限制条件再根据限制条件确定n 的取值(2)解决由周期性及双向性带来的多解问题的般思路是: ①首先考虑传播方向的双向性,如果题目未告知波的传播方向或没有其他条件暗示,应首先按波传播方向(x +和x -两个方向)的可能性进行讨论.②对设定的传播方向,确定t ∆和T 的关系,一般先确定最简单的情况,即一个周期内的情况,然后在此基础上加nT .③应注意题日是否有限制条件,如有的题目限制波的传播方向,或限制时间t ∆大于或小于一个周期等所以解题时应综合考虑,加强多解意识,认真分析题意.④空间的周期性和时间的周期性是一致的,实质上是波形平移规律的应用,所以解题时我们可以针对不同题目选择其中一种方法求解 (3)波形的不确定造成的多解问题在波动问题中,往往只给出完整波形的一部分,或给出几个特殊点,而其余信息均处于隐含状态,这样,波形就有多种情况,形成相关波动问题的多解. 实际上这类题型主要有两种命题形式:一是已知同一时刻波动中两质点所处的位置求解可能的波长.我们应先确定这两点间可能出现的小于一个波长的所有可能性,再利用波的空间的周期性,判断出所有可能的波形.二是告诉同一质点在不同时刻所处的位置.例如0t 时A 质点处于波峰,1t 时刻A 质点处于平衡位置,此时就应利用振动时间的周期性来确定周期.由于A 质点振动方向不明确,先确定A 质点在一个周期内发生这一运动的两种可能性即T t 41=∆或T 43. 再由时间的周期性可得到,T nT t t 4101+=-或T nT t t 4301+=-,即可求出所有可能的周期值,解决此类问题的关键是:①分析题目给定的关键状态. ②确定两状态点可能存在的波形,只需画出一个周期内的可能波形.③利用波的周期性,确定所有可能出现的波形.④结合题日的限制条件,选择正确的值.(4)两质点间关系不确定形成多解的分析方法 在波的传播方向上,如果两个质点间距离不确定或者两者相位之间关系不确定,就会形成多解,若不能联想到所有可能的情况,就会出现漏解.例3.一列简谐横波沿水平直线向右传播. M 、N 为介质中相距为s ∆的两质点,M 在左,N 在右. t 时刻,M 、N 两质点正好振动经过平衡位置,而且M 、N 之间只有一个波峰,经过t ∆时间N 质点恰好在波峰位置,求这列波的波速.2.图象互推问题分析要点(1)1t 时刻波形图⇔2t 时刻波形图:将“波形图平移”,即波形沿传播方向平移.平移的距离t v x ∆⋅=∆(2)振动图象与波动图象:通常取振动图象上的特殊时刻或波动图象上的特殊质点,利用波的传播方向和振动方向关联分析,任一质点的振动状态(如位移,振动方向)在波形图和振动图上应该一致.(3)1x 振动图象⇔2x 振动图象:将“振动图象平移”,即被带动的质点的振动状态(或振动图象)延迟了t ∆时间,延迟的时间vx t ∆=∆.例4.多选一列简谐横波沿x 轴正方向传播,图(a )是t =0时刻的波形图,图(b )和图(c )分别是x 轴上某两处质点的振动图象.由此可知,这两质点平衡位置之间的距离可能是( ) A .m 31B .m 32C .m 1D .m 43三、针对训练1.(多选)一列简谐横波沿直线传播,该直线上的a 、b 两点相距4.42m. 图中实、虚两条曲线分别表示平衡位置在a 、b 两点处质点的振动曲线. 从图示可知( ) A .此列波的频率一定是10Hz B .此列波的波长一定是0.1mC .此列波的传播速度可能是34m/sD .a 点一定比b 点距波源近2. 一列简谐横波沿直线由a 向b 传播,相距10.5m 的a 、b 两处的质点振动图象如图中a 、b 所示,则( )3. A .该波的振幅可能是20cm4. B .该波的波长可能是8.4m5. C .该波的波速可能是10.5m/s6. D .该波由a 传播到b 可能历时7s3.(多选)一列在竖直方向振动的简谐横波,波长为λ,沿正x 方向传播.某一时刻,在振动位移向上且大小等于振幅一半的各点中,任取相邻的两点1P 、2P ,已知1P 的x 轴坐标小于2P 的x 轴坐标,则( ) A .若221λ<P P ,则1P 向下运动,2P 向上运动 B .若221λ<P P ,则1P 向上运动,2P 向下运动 C .若221λ>P P ,则1P 向上运动,2P 向下运动 D .若221λ>P P ,则1P 向下运动,2P 向上运动4.(多选)M 、N 为介质中波的传播方向上的两点,间距s =1.5m ,它们的振动图象如图所示,这列波的波速的可能值为( )A .15 m/sB .7.5m/sC .5 m/sD .3 m/s5. 在波传播的直线上有两个质点A 、B ,它们相距60cm ,当A 质点在平衡位置处向上振动时,B 质点处在波谷位置. 已知波的速度是24m/s ,则此列波的频率可能是( ) ①30Hz ②410Hz ③400Hz ④430HzA .①②③B .②③④C .①②④D .①③④6. (多选)(2019·天津高考)一列简谐横波沿x 轴传播,已知x 轴上m 11=x 和m 72=x 处质点的振动图象分别如图1、图2所示,则此列波的传播速率可能是( )图1 图2A .7 m/sB .2 m/sC .1.2 m/sD .1 m/s7. (多选)如图所示,一根张紧的水平弹性长绳的a 、b 两点相距14.0m ,b 点在a 点右方. 当一列简谐波沿此绳向右传播时,若a 点位移达到正向极大时,b 点位移恰好为零,且向下运动,经过1.00s 后,a 点位移第一次变为零,且向下运动,而b 点的位移恰好达到负向极大,则这列简谐波的波速可能等于( ) A .4.67m/s B .6 m/s C .2 m/s D .14 m/s8. 一列简谐横波向右传播,波速为v ,沿波传播方向上有相距为L 的P 、Q 两质点,如图所示,某时刻P 、Q 两质点都处于平衡位置,且P 、Q 间仅有一个波峰,经过时间t ,Q 质点第一次运动到波谷,则t 的可能值有( ) A .1个 B .2个 C .3个 D .4个9.(多选 )一列横波以10 m/s 的速率沿水平方向传播,某时刻的波形如图中的实线所示,经时间t ∆后的波形如图中的虚线所示,已知T t T >∆>2(T 为这列波的周期). 由此可知t ∆可能是( )A .0.3sB .0.5sC .0.6sD .0.7s10. 一列简谐横波沿直线由A 向B 传播,A 、B 相距0.45m ,如图是A 处质点的振动图象,当A 处质点运动到波峰位置时,B 处质点刚好到达平衡位置且向y 轴正方向运动,这列波的波速可能是( )A .4.5m/sB .3.0m/sC .1.5m/sD .0.7m/s11. 如图所示,一简谐横波在x 轴上传播,轴上a 、b 两点相距12m ,t=0时a 点为波峰,b 点为波谷,t=0.5s 时,a 点为波谷,b 点为波峰. 则下列判断中正确的是( ) A .波一定沿x 轴正方向传播 B .波长可能是8m C .周期可能是0.5s D .波速一定是24m/s12. 如图所示,实线是一列简谐横波在01=t 时刻的波形,虚线是这列波在s 5.02 t 时刻的波形. (1)写出这列波的波速表达式;(2)若波速大小为74 m/s ,波速方向如何?13. 如图所示,实线是某时刻的波形图象,虚线是0.2s 后的波形图 (1)若波向左传播,求它的可能周期和最大周期, (2)若波向右传播,求它的可能传播速度. (3)若波速是45m/s ,求波的传播方向.14. 在波的传播方向上有两个质点P 和Q ,它们的平衡位置相距s=1.2m ,且大于一个波长,介质中的波速为v =2m/s ,P 和Q 的振动图线如图所示,求振动周期的最大值,并画出t=0时的波的图象.答案例题例1.B 解析:由图λ=0.08m ,该波的周期T 大于0.02s,波传播的距离小于波长,则据题意,由两个时刻的波形得到:T t 41=或T t 43=,解得s 08.01=T , s 308.01=T由波速公式Tv λ=,得m/s 11=v ,m/s 32=v , 故选:B例2.C 解答:解:A 、由振动图象无法比较a 、b 两质点振动的先后,所以无法判断波的传播方向,故A 错误。
波的多解问题(201912)

a
b
变化三:若把原题中“a点的位移第一次为零”改为“a
点的位移为零”,并取消“波长λ>14m”的条件,
原题:如图,一根张紧的水平弹性长绳上的a、b两点, 相距为14.0m,b点在a点的右方,波长λ>14m。当 一列简谐横波沿此长绳向右传播时,若a点的位移达到 正极大时,b点的位移为零,且向下运动,经过1.00s后, a点的位移第一次为零,且向下运动,而b点的位移达到 负极大,则这列简谐波的波速等于多少?
a
b
变化二:若把原题中“a点的位移第一次为零”改为“a
点的位移为零”。问这列简谐波的波速可能等于:
A:4.67m/s B:6m/s C:10m/s D:14m/s 解答:由题意知,3 λ/4=14m,考虑时间上的周期性, 即:(n+1/4)T=1s ,故波速:V=λ/T=14(4n+1)/3
当n=0时,V= 4.67m/s A答案正确
原题:如图,一根张紧的水平弹性长绳上的a、b两点, 相距为14.0m,b点在a点的右方,波长λ>14m。当 一列简谐横波沿此长绳向右传播时,若a点的位移达到 正极大时,b点的位移为零,且向下运动,经过1.00s后, a点的位移第一次为零,且向下运动,而b点的位移达到 负极大,则这列简谐波的波速等于多少?
波的多解问题
原题:如图,一根张紧的水平弹性长绳上的a、b两点, 相距为14.0m,b点在a点的右方,波长λ>14m。当 一列简谐横波沿此长绳向右传播时,若a点的位移达到 正极大时,b点的位移为零,且向下运动,经过1.00s后, a点的位移第一次为零,且向下运动,而b点的位移达到 负极大,则这列简谐波的波速等于多少?
a
b
变化一:若把原题中“波长λ>14m”的条件取消,
破解机械波中的多解问题

为零, 且向下运动 , 点的位移恰好 达到 负向极大 , 而6 则这列简谐波的波速可能等 于
A .4. 7 m / 6 s
C 1 / 0m s
芹
(
)
B.6 m / s
D . 1 / 4m s
右
6
图3
图1
足题设条件的n 6 、两点可以有无数个可能位置 , 如图4 对波向 + 轴, 轴方向传播两种情况分别讨论. 一 由于 中 的 6、 6… … 等 . 可 以 写 出 。 6 距 的通 式 ; 6、, 只 、间 。6 、间距离小于一个波长. 因此n 6 、 间不足一个波长 , 3 s + 入 ( =0 l2 . 而波速的答案也有多 n n 、、…) 从 其图像如图2 所示 , 为波向 + 传播时的波形 ; ① 时由 ②
2 …) 通 过求解 可知 A、 D答案是 正确 的. , B、
乙
图7
、
题 目中所 给定 的时 间条件不 充分 , 可能 比一 个
周 期 长 , 能 比一 个 周 期 短 , 而 导 致 了 多 解 问 题 的 可 从
出现.
…
解析 题目 j 只给定了两个质点振动图像还揭
示 了质 点 的 关 系 质 点 在 0 刻 位 于 正 的最 大 位 时 移 处 ,2 点 此 时 位 于平 衡 位 置 且 向上 振 动 . 满 足此 X质 但 条 件 的 位 置 有 许 多 个 , 图 乙 中 的A、 C … 等. 如 B、 因此 , 械波 的波长有 多个答案. 、 间距要遵循 机
图4
t l  ̄ j -
ቤተ መጻሕፍቲ ባይዱ
问 间 隔 与 周 期 关 系 不 确 定 . > ’Af 都 可 能 , J At 7 、 < 只
高中物理第二章机械波小专题研究(三)波的多解问题教学案教科版选修3-4(new)

小专题研究(三) 波的多解问题1.方向性不确定出现多解波总是由波源发出并由近及远地向前传播,波在介质中传播时,介质各质点的振动情况根据波的传播方向是可以确定的,反之亦然。
因此,根据题中的已知条件不能确定波的传播方向或者不能确定质点的振动方向,就会出现多解,然而同学们在解题中往往凭着主观臆断,先入为主地选定某一方向为波的传播方向或是质点的振动方向,这样就会漏掉一个相反方向的可能性解.2.时间、距离不确定形成多解沿着波的传播方向,相隔一个波长的连续两个相邻的质点振动的步调是完全相同的;在时间上相隔一定周期的前后两个相邻时刻的波形图线是完全相同的,所以,当题中已知条件没有给定传播的时间(波传播的时间Δt与周期T之间的大小关系不确定)或是没有给定波的传播距离(波的传播距离Δs与波长λ之间的大小关系不确定),就会出现多解现象。
同学们在解题时经常只分析传播时间Δt小于T(或传播距离Δs小于波长λ)的特解情况,从而造成特解代替通解的漏解现象。
3.两质点间关系不确定形成多解在波的传播方向上,如果两质点间距离不确定或相位之间关系不确定,会形成多解,若不会联想所有的可能性,就会出现漏解。
[例证] 一列简谐横波沿直线传播,在传播方向上有P、Q两个质点,它们相距8 m,当t=0时,P、Q的位移恰好是正最大值,且P、Q之间只有一个波谷。
t=0.6 s末时,P、Q两点正好都处在平衡位置,且P、Q之间只有一个波峰和一个波谷,且波峰距Q点的距离第一次为错误!,试求:(1)波由P传至Q,波的周期;(2)波由Q传到P,波的速度;(3)波由Q传到P,从t=0时开始观察,哪些时刻P、Q间(P、Q除外)只有一个质点的位移大小等于振幅.[解析](1)由题意,t=0时的波形如图1(a)所示,t=0.6 s时的波形如图(b)所示:图1若波从P传向Q,则t=错误!T,从而得T=0。
8 s。
(2)若波从Q传向P,则t=错误!T,从而得T=2.4 s,波速v=错误!=3。
高二物理机械波波的多解问题学案

第4讲波的多解问题[目标定位] 1.掌握波在传播过程中的周期性和双向性特点.2.能分析和处理波动图像的多解问题。
一、波的多解问题1.波具有时间和空间的周期性,传播具有双向性,所以关于波的问题更容易出现多解.造成多解的主要因素有:(1)时间间隔Δt与周期T的关系不明确;(2)波的传播距离Δx与波长λ的关系不明确;(3)波的传播方向不确定.2.在解决波的问题时,对题设条件模糊,没有明确说明的物理量,一定设法考虑其所有的可能性:(1)质点达到最大位移处,则有正向和负向最大位移两种可能;(2)质点由平衡位置开始振动,则有起振方向相反的两种可能;(3)只告诉波速不指明波的传播方向,应考虑沿两个方向传播的可能;(4)只给出两时刻的波形,则有多次重复出现的可能.【例1】一列横波在x轴上传播,t1=0和t2=0.005 s时的波形如图12-3-2中的实线和虚线所示.图12-3-2(1)设周期大于(t2-t1),求波速;(2)设周期小于(t2-t1),并且波速为6 000 m/s.求波的传播方向.解析当波传播时间小于周期时,波沿传播方向前进的距离小于一个波长;当波传播的时间大于周期时,波沿传播方向前进的距离大于波长.这时从波形的变化上看出的传播距离加上n个波长才是波实际传播的距离.(1)因Δt=t2-t1<T,所以波传播的距离可以直接由图读出.若波向右传播,则在0.005 s内传播了2 m,故波速为v=2 m0.005 s=400 m/s.若波向左传播,则在0.005 s内传播了6 m,故波速为v=6 m0.005 s=1 200 m/s.(2)因Δt=t2-t1>T,所以波传播的距离大于一个波长,在0.005 s内传播的距离为Δx=vΔt=6 000×0.005 m=30 m,Δxλ=308=334,即Δx=3λ+34λ.因此,可得波的传播方向沿x轴的负方向.答案(1)波向右传播时,v=400 m/s;波向左传播时,v=1 200 m/s(2)x轴负方向借题发挥解决周期性及双向性带来的多解问题的一般思路如下:(1)首先考虑传播方向的双向性,如果题目未说明波的传播方向或没有其他条件暗示,应首先按波传播的可能性进行讨论.(2)对设定的传播方向,确定Δt和T的关系,一般先确定最简单的情况,即一个周期内的情况,然后在此基础上加nT.(3)应注意题目是否有限制条件,如有的题目限制波的传播方向,或限制时间Δt 大于或小于一个周期等.所以解题时应综合考虑,加强多解意识,认真分析题意.(4)空间的周期性和时间的周期性是一致的,实质上是波形平移规律的应用,所以解题时我们可以针对不同题目选择其中一种方法求解.波的多解问题1.一列横波在t=0时刻的波形如图12-3-4中实线所示,在t=1 s时的波形如图中虚线所示.由此可以判定此波的()A.波长一定是4 cmB.周期一定是4 sC.振幅一定是2 cmD.传播速度一定是1 cm/s1.一列简谐横波在t=0时刻的波形如图12-3-10中的实线所示,t=0.02 s时刻的波形如图中虚线所示.若该波的周期T大于0.02 s,则该波的传播速度可能是()图12-3-10A.7 m/s B.3 m/s C.1 m/s D.5 m/s2.如图12-3-12所示,一列简谐横波沿x轴传播,实线为t1=0时的波形图,此时P质点向y轴负方向运动,虚线为t2=0.01 s时的波形图.已知周期T>0.01 s.(1)波沿x轴________(填“正”或“负”)方向传播;(2)求波速.3.一列简谐横波沿x轴正方向传播,t=0时刻的波形如图12-3-13所示.经0.6 s时间质点a第一次到达波峰位置,求:(1)波的传播速度大小;(2)质点b第一次出现波峰的时刻.4.一列简谐横波t1时刻的波形如图12-3-14中实线所示,t2时刻的波形如图中虚线所示,已知Δt=t 2-t1=0.5 s.问:(1)这列波的传播速度是多少?(2)若波向左传播,且3T<Δt<4T,波速是多大?(3)若波速等于68 m/s,则波向哪个方向传播?5. 如图实线是某时刻的波形图象,虚线是经过0.2s时的波形图象。
机械振动与机械波:振动图像与波的图像及多解问题
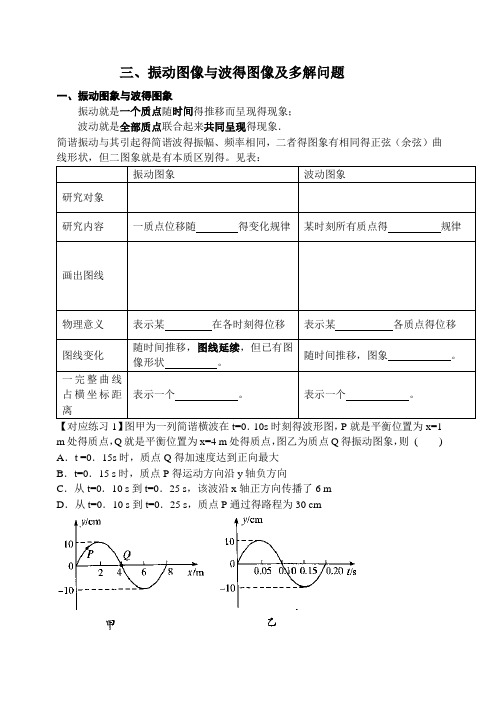
三、振动图像与波得图像及多解问题一、振动图象与波得图象振动就是一个质点随时间得推移而呈现得现象;波动就是全部质点联合起来共同呈现得现象.简谐振动与其引起得简谐波得振幅、频率相同,二者得图象有相同得正弦(余弦)曲振动图象波动图象研究对象研究内容一质点位移随得变化规律某时刻所有质点得规律画出图线物理意义表示某在各时刻得位移表示某各质点得位移图线变化随时间推移,图线延续,但已有图像形状。
随时间推移,图象。
一完整曲线占横坐标距离表示一个。
表示一个。
m处得质点,Q就是平衡位置为x=4 m处得质点,图乙为质点Q得振动图象,则( ) A.t =0.15s时,质点Q得加速度达到正向最大B.t=0.15 s时,质点P得运动方向沿y轴负方向C.从t=0.10 s到t=0.25 s,该波沿x轴正方向传播了6 mD.从t=0.10 s到t=0.25 s,质点P通过得路程为30 cm【对应练习2】如图甲所示,为一列横波在t=0时刻得波动图像,图乙为质点P得振动图像,下列说法正确得就是()A.波沿x轴正方向传播B.波沿x轴负方向传播C.波速为6m/sD.波速为4m/s【对应练习3】一列横波沿x轴正方向传播,a、b、c、d为介质中得沿波传播方向上四个质点得平衡位置。
某时刻得波形如图1所示,此后,若经过3/4周期开始计时,则图2描述得就是()A.a处质点得振动图象B.b处质点得振动图象C.c处质点得振动图象D.d处质点得振动图象【对应练习4】图甲表示一简谐横波在t=20 s时得波形图,图乙就是该列波中得质点P得振动图象,由甲、乙两图中所提供得信息可知这列波得传播速度以及传播方向分别就是( ).A.v=25cm/s,向左传播B.v=50cm/s,向左传播C.v=25 cm/s.向右传播D.v=50 cm/s,向右传播.二、波动图象得多解1、波得空间得周期性:相距为得多个质点振动情况完全相同.2、波得时间得周期性:波在传播过程中,经过时,其波得图象相同.3、波得双向性:波得传播方向及质点得振动方向不确定,要全面考虑。
波的多解问题(教学图文课件分享)

外汇维权;
;外汇经验心得-外汇投资心得 https:///xinde/
外汇经验心得;
;每日最新外汇新闻-今日实时全球外汇新闻 https:///yaowen/
外汇新闻网;
;外汇今天行情-黄金原油行情走势分析 https:///hangqing/ 外汇今天行情;
原题:如图,一根张紧的水平弹性长绳上的a、b两点, 相距为14.0m,b点在a点的右方,波长λ>14m。当 一列简谐横波沿此长绳向右传播时,若a点的位移达到 正极大时,b点的位移为零,且向下运动,经过1.00s后, a点的位移第一次为零,且向下运动,而b点的位移达到 负极大,则这列简谐波的波速等于多少?
a
b
变化二:若把原题中“a点的位移第一次为零”改为“a
点的位移为零”。问这列简谐波的波速可能等于:
A:4.67m/s B:6m/s C:10m/s D:14m/s 解答:由题意知,3 λ/4=14m,考虑时间上的周期性, 即:(n+1/4)T=1s ,故波速:V=λ/T=14(4n+1)/3
当n=0时,V= 4.67m/s A答案正确
https:///zigzag/ ZIGZAG指标;
;外汇ADX指标-ADX平均趋向指数下载 https:///adx/
ADX指标;
;外汇BOLL指标-布林线BOLL指标下载 https:///boll/
;外汇技术分析 /jishufenxi/ 外汇技术分析方法;
;外汇技术指标 /jishufenxi/jishuzhibiao/ 外汇常用技术指标;
;外汇图表形态 /jishufenxi/tbxingtai/ 外汇图表分析;
a
b
变化一:若把原题中“波长λ>14m”的条件取消,
专题42 机械波(解析版)

2023届高三物理一轮复习多维度导学与分层专练专题42 机械波导练目标导练内容目标1机械波的传播和波的图像目标2波的图像与振动图像目标3波的多解问题目标4波的干涉目标5波的衍射目标6多普勒效应一、机械波的传播和波的图像1.机械波的传播特点(1)波传到任意一点,该点的起振方向都和波源的起振方向相同。
(2)介质中每个质点都做受迫振动,因此,任一质点的振动频率和周期都和波源的振动频率和周期相同。
(3)波从一种介质进入另一种介质,由于介质不同,波长和波速可以改变,但频率和周期都不会改变。
(4)波源经过一个周期T完成一次全振动,波恰好向前传播一个波长的距离。
2.波速公式v=λT=λf的理解(1)波速v:机械波在介质中的传播速度,由介质本身的性质决定,与波源的周期T无关。
(2)频率f:由波源决定,等于波源的振动频率。
各个质点振动的频率等于波源的振动频率。
3.波的图像的特点(1)时间间隔Δt=nT(波传播nλ,n=0,1,2,3,…)时,波形不变。
(2)在波的传播方向上:①当两质点平衡位置间的距离Δx=nλ (n=1,2,3,…)时,它们的振动步调总相同,在波形图上的对应位移一定相同;①当两质点平衡位置间的距离Δx=(2n+1)λ2 (n=0,1,2,3,…)时,它们的振动步调总相反,在波形图上的对应位移一定等值反向。
(3)波源质点的起振方向决定了它后面的质点的起振方向,各质点的起振方向与波源的起振方向相同。
4.根据波的图像、波的传播方向判定质点的振动方向的方法内容图像“上下坡”法沿波的传播方向,“上坡”时质点向下振动,“下坡”时质点向上振动“同侧”法波形图上某点表示传播方向和振动方向的箭头在图线同侧“微平移”法将波形沿传播方向进行微小的平移,再由对应同一x坐标的两波形曲线上的点来判断振动方向注意:波的图像、波的传播方向与质点振动方向三者之间可以互相判定。
【例1】战绳训练是当下流行的一种健身方式,健身者通过晃动战绳的一端使其上下振动从而让手臂和肩部的肌肉得到良好的锻炼。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题机械波的多解问题一.造成多解的原因以及处理方法1 原因:波的传播方向不确定。
解决方法:分两种情况分别讨论2.原因:时间与周期的关系不确定造成多解。
解决方法:找出时间与周期的对应关系。
常见题型:波形变化题3.原因:一列波上不同的两个振动质点之间的距离与波长的关系不确定造成多解解决方法:画某一时刻(如t=0时刻)的波形图,找出两质点可能的位置,确定距离与波长的对应关系。
常见题型:题目中会给出两个质点的振动情况二.确定时间与周期或者距离与波长的关系时,有两个思路:其一是根据质点振动确定关系;其二是根据波的平移确定关系。
注意:灵活运用对应关系:振动一个周期的时间,波传播一个波长的距离.振动半个周期的时间,波传播半个波长的距离。
振动1/4个周期的时间,波传播1/4个波长的距离.振动几分之几个周期的时间,波传播几分之几个波长的距离。
三.例题:1.如图所示,一列简谐波在x轴上传播,实线和虚线分别表示前后间隔1s的两个时刻的波形图,则这列简谐波的波速可能是A.0.60m/sB. 0。
75m/sC. 1。
05m/s D。
1.15m/s2.如图所示,实线是一列简谐横波某时刻的波形,虚线是经过0。
5s后的波形.已知波的周期为T,而且0。
25s<T<0.5s,下列说法中正确的是A。
当波向x轴的正方向传播时,该波的波速为7m/sB。
当波向x轴的正方向传播时,在这0.5s内,x=1。
5m处的质点通过的路程为50cmC. 当波向x轴负方向传播时,x=1。
5m的质点M比x=1。
75m的质点N在0.5s内通过的路程少D. 当t=0.1s时.x=1.5m处的质点的位移一定是03.一列沿x轴正方向传播的简谐横波,t=0时刻的波形如图中实线所示,t=0。
2s时刻的波形如图中的虚线所示,则正确的是( )A。
质点P的运动方向沿y轴正方向B。
波的周期可能为0.27sC。
波的频率可能为8.75HzD。
波的传播速度可能为150m/s4.一列简谐横波沿x轴正方向传播,在x=12m处的质点的振动图线如图1所示,在x=18m处的质点的振动图线如图2所示。
下列说法正确的是A。
该波的周期为12sB. x=12m处的质点在平衡位置向上振动时,x=18m处的质点在波峰C. 在0~4s内x=12m处和x=18m处的质点通过的路程均为6cmD。
该波的波长可能为8mE. 该波的传播速度可能为2m/s5.一列简谐横波沿z轴正方向传播,在t秒与(t+0.2)秒两个时刻,x轴上(—3 m,3 m)区间的波形完全相同,如图所示为£秒时刻的波形图.并且图中M、N两质点在t秒时位移均为2。
5 cm,下列说法正确的是A。
(t+0.1)秒时刻,x= —2 m处的质点位移大小一定是5 cmB. 质点M随波一起沿z轴正方向传播C。
从t秒时刻起,x=2 m处的质点比x=2.5 m的质点先回到平衡位置D。
从t秒时刻起,在质点M第一次到达平衡位置时,质点N恰好到达波峰E。
从t秒时刻起经过0.15 s,x=l m处的P点通过的路程可能为45 cm6.在简谐横波的传播直线上有两个介质质点A、B,它们相距60cm,当A质点在平衡位置处向上振动时,B质点处于波谷位置,若波速的大小为24m/s,则波的频率可能是( )A。
30Hz B. 410Hz C。
400Hz D. 490Hz7.简谐横波在均匀介质中沿直线传播,P、Q是传播方向上相距为16 m的两个质点,波先传到P点,从波传到Q点开始计时,P、Q两质点的振动图象如图所示。
下列说法正确的是 .A. 质点P开始振动的方向沿y轴正方向B. 该波从P传到Q的时间可能为10 sC. 该波的波长可能为16 m D 。
该波的传播速度可能为1 m/sE 。
在一个周期内,P 、Q 两点振动方向相同的时间为1s8.一列简谐横波沿直线传播,该直线上平衡位置相距9 m 的a 、b 两质点的振动图象如图所示,下列描述该波的图象可能正确的是A. B 。
C 。
D 。
9.一列简谐波沿直线传播,该直线上的A 、B 两点相距3.5m,图中两条曲线分别表示平衡位置在A 、B 两点处质点的震动曲线。
从图示可知,下列说法正确的是 。
A 。
此列波的频率一定是0。
5Hz B. 此列波的波长可能是2m C. 此列波的传播速度可能是7m/s D 。
A 点一定比B 点距波源近E 。
若该波由A 传播到B ,可能历时0.5S 四.巩固练习10.如图所示,实线为一列沿x 轴正方向传播的简谐横波在0t =时刻的波形,虚线是该波在0.20s t =时刻的波形,则此列波的周期可能为( )A. 0.16sB. 0.20s B. 0.32s D. 0.40s11.一列横波沿x 轴传播,在0x =与1cm x =处的两质点的振动图线分别如图中实线与虚线所示.由此可以得出( )A 。
波一定沿X 轴正方向传播B 。
波的周期可能是2sC 。
波的传播速度可能是12cm/s . D. 波的传播速度可能是02cm/s .12.有一列沿水平绳传播的简谐横波,频率为10 Hz 。
振动方向沿竖直方向,当绳上的质点P 到达其平衡位置且向下运动时,在其平衡位置右方相距0.6 m 处的质点Q 刚好到达最高点,由此可知波速和传播方向不可能的是( )A. 4.8 m/s ,向右传播B. 8 m/s ,向左传播C. 24 m/s,向右传播 D 。
24 m/s,向左传播13.如图所示,实线是沿x 轴传播的一列简谐横波在t =0时刻的波形图,虚线是这列波在t =0.2s 时刻的波形图.则下列说法正确的是____________A.这列波的周期可能是1.2s B 。
这列波的波长为12m C 。
这列波可能向左传播4mD.这列波的波速可能是40m /s E 。
t =0时刻x =4m 的质点沿x 轴正方向运动14.如图所示,实线为简谐波在t 时刻的图线,虚线为波在()0.01s t +时刻的图线. (1)若波向左传播,求它可能传播的距离. (2)若波向右传播,求它的最大周期.(3)若波速为500m/s ,指出简谐波的传播方向.15.一列简谐波沿x 轴方向传播,已知x 轴上1x =0和2x =1m 两处质点的振动图象分别如图(甲)、(乙)所示,求此波的传播速度。
(甲) (乙)16.如图中实线是一列简谐横波在t 1=0时刻的波形图,虚线是这列波在t 2=0。
5时刻的波形图。
(1) 若t l =0时刻,x = 2m 处的质点向y 轴正方向振动,且T>0.5s ,则这列波的波速多大; (2)若波速大小为58m/s,波速方向如何?试通过计算说明理由。
参考答案1.BC 【解析】由图可知波长为: 60cm λ=。
若波沿x 轴正方向,传播的距离为: 114x n λ⎛⎫=+ ⎪⎝⎭ n =0,1,2,…,波速为: ()1114/0.60.15/1n x v m s n m s t λ⎛⎫+ ⎪⎝⎭===+ n =0,1,2,…,当n=1时, 10.75/v m s =,故B 正确;若波沿x 轴负方向,传播的距离为: 234x n λ⎛⎫=+ ⎪⎝⎭ n =0,1,2,…,波速为:()2234/0.60.45/1n x v m s n m s t λ⎛⎫+ ⎪⎝⎭===+ n =0,1,2,…,当n =1时, 2 1.05/v m s =,故C 正确所。
所以选BC 。
2.AC 【解析】由图线可直接读出波长λ=4m.∵0。
25s <T <0。
5s ,∴当波向+x 方向传播时,0。
5s=(0.75+n )T ,当n=1时符合条件,解得T=s ,所以,选项A 正确;因,则 在0.5s 内,x=1。
5m处的质点通过的路程为7A=70cm,选项B错误;当波向-x方向传播时,0。
5s=(0。
25+n)T,当n=1时符合条件,解得T=0.4s,所以0.5s=1T,则在T内,x=1.75m 处的质点向上振动的速度大于x=1。
5m处质点的速度,故x=1。
75m处的质点的路程比x=1.5m处质点的路程较大,故C正确;若波沿+x传播,则从t=0。
1s到t=0。
5s的时间内,0。
4s=1.4T,因t=0。
5s时,x=1.5m 处的质点在波谷,则t=0。
1s时刻不在平衡位置,即位移不为,选项D错误;故选AC。
3.AD【解析】由波形图可知,质点P的运动方向沿y轴正方向,选项A正确;由图,得到t=(n+)T,n=0,1,2,、则周期,因为n为整数,T不可能为0.27s.故B 错误.由上,频率,因为n为整数,f不可能为8.75Hz,选项C错误;若波速v=150m/s,则在t=0。
2s内波传播的路程x=vt=30m,根据波形图象,波向右传播的最短距离6m,故D正确.故选AD。
4.ABD【解析】由图知,振动周期为12s,A正确;3s、15s时,x=12m处的质点在平衡位置向上振动,而此时x=18m处的质点在波峰,所以B正确;由图知,在t=2s时,x=18m处质点的位移为零,在平衡位置向上振动,在t=4s时,x=18m处质点的位移大于2cm,所以C错误;两质点间的距离为x,3x nλ4⎛⎫=+⎪⎝⎭所以424λ4343xn n==++,n=0、1、2、3、……当n=0时,波长最长为8m,所以D正确;波速2v/43m sT nλ==+,当n=0时,速度最大2v/3m s=,所以E错误。
5.ACE【解析】由图知波长λ=4m.由于t秒与(t+0。
2)秒两个时刻的波形相同,经过了整数倍周期的时间,则得:△t=0.2s=nT,n=1,2…,由于周期不确定,时间0。
1s等于半个周期的整数倍,则(t+0。
1)秒时刻,x=—2m 处的质点可能在波峰,也可能在波谷,位移的大小是5cm.故A正确.机械波传播的过程中,质点不随波迁移,选项B错误;质点沿x轴正向传播,在t=0时刻x=2。
5 m的质点向下振动,故从t秒时刻起,x=2 m 处的质点比x=2.5 m的质点先回到平衡位置,选项C正确;根据数学知识得知质点M和N之间的距离等于,由波形得知,质点M第一次到达平衡位置时,质点N不在波峰.故D错误.当n=3时, ,此时 ,则x=1m处的质点运动的路程为,选项E正确;6.AB【解析】若这列波的传播方向是由A向B,据题有:(n+14)λ=0.6m,(n=0,1,2,3…)则得λ=2.441n+m,由v=λf得:242.441vfnλ==+Hz=10(4n+1)Hz,(n=0,1,2,3…)①若这列波的传播方向是由B向A,则有:(n+34)λ=0。
6m,(n=0,1,2,3…)则得λ=2.443n+m,(n=0,1,2,3…);频率为 f=vλ=10(4n+3)Hz,(n=0,1,2,3…) ②当n=0时,由②式得f=30Hz;当n=10时,由①式得f=410Hz;由于n是整数,f不可能等于400Hz和490Hz;故选AB.7.ABD【解析】根据振动图象的斜率表示速度,可知质点Q的起振方向,即t=0时刻的速度方向沿y轴正方向,则质点P开始振动的方向沿y轴正方向.故A正确.由题可知,简谐横波的传播方向从P到Q,由图可知,周期为 T=6s,质点 Q的振动图象向左4s、后与P点的振动重合,意味着Q点比P点振动滞后了4s,即P 传到Q的时间△t可能为4s,同时由周期性可知,从P传到Q的时间△t=(4+nT)s=(4+6n),n=0、1、2、3…,即△t=4s,10s,16s…,选项B正确.波的传播速度16/46xv m st n∆==∆+,当n=2时,v=1m/s.选项D正确;由λ=vT可知,波长为9646mnλ=+,n是整数,λ不可能是16m,故C错误.由振动图像可知,在一个周期内,P、Q两点振动方向相同的时间为2s,选项E错误;故选ABD.8.AD【解析】由振动图象可知,在t=0时刻,a位于波峰,b经过平衡位置向下运动。
