圆周角 课件 4 人教版
合集下载
人教版九年级数学上册《圆周角》优秀PPT课件

∠ ABC = ∠ADC=∠ AEC
课堂练习
1.如图,⊙O是 ABC的外接圆,连接OA,OB,
∠ OBA=50°,求∠C的度数.
解:∵OA=OB
∴∠ OBA=∠ OAB=50° ∴∠ AOB=80°
由圆周角定理可知:
∠ C= 12∠AOB=40°
C O
A
B
课堂练习
2.试找出下图中所有相等的圆周角。
所对的圆心角的一半.
D
A
C
O·
E
B
小试牛刀
1.如图,在⊙O中,∠BOC=60°, 求∠A、∠D的度数.
A
D
O
解:由圆周角定理可知:
∠A=
12∠BOC=
1 2
×60°=
30°
∠D= 12∠BOC= 12×60°= 30°
B
C
发现:同弧所对的圆周角相等
小试牛刀
2.如图,若 CD=EF ,∠A与∠B相等吗?
练一练:下列各图中的∠BAC是否为圆周角并简
述理由.
B O·
B
C
A
O·
A
A
C O·
√ C (1) A
顶点(不2)在圆上 B
B 边(AC3没)有和圆相交
O·
A O·
CC
·O
B
C
顶点(不4在)圆上
√ (5)
A B
√ (6)
探索新知
探究2:在⊙O上任取一条BC,画出BC所对的一 个圆周角∠BAC和圆心角∠BOC,用量角器测量
他所处的位置B对球门AC的张角∠ABC有关).
A
A
E B
C D
E
AC所对的角ห้องสมุดไป่ตู้ ABC 、∠ADC、
课堂练习
1.如图,⊙O是 ABC的外接圆,连接OA,OB,
∠ OBA=50°,求∠C的度数.
解:∵OA=OB
∴∠ OBA=∠ OAB=50° ∴∠ AOB=80°
由圆周角定理可知:
∠ C= 12∠AOB=40°
C O
A
B
课堂练习
2.试找出下图中所有相等的圆周角。
所对的圆心角的一半.
D
A
C
O·
E
B
小试牛刀
1.如图,在⊙O中,∠BOC=60°, 求∠A、∠D的度数.
A
D
O
解:由圆周角定理可知:
∠A=
12∠BOC=
1 2
×60°=
30°
∠D= 12∠BOC= 12×60°= 30°
B
C
发现:同弧所对的圆周角相等
小试牛刀
2.如图,若 CD=EF ,∠A与∠B相等吗?
练一练:下列各图中的∠BAC是否为圆周角并简
述理由.
B O·
B
C
A
O·
A
A
C O·
√ C (1) A
顶点(不2)在圆上 B
B 边(AC3没)有和圆相交
O·
A O·
CC
·O
B
C
顶点(不4在)圆上
√ (5)
A B
√ (6)
探索新知
探究2:在⊙O上任取一条BC,画出BC所对的一 个圆周角∠BAC和圆心角∠BOC,用量角器测量
他所处的位置B对球门AC的张角∠ABC有关).
A
A
E B
C D
E
AC所对的角ห้องสมุดไป่ตู้ ABC 、∠ADC、
九年级数学上册第24章圆24.1圆的有关性质(第4课时)圆周角课件(新版)新人教版

BC A=50°,则∠BOC等于 的中点,
O
A C
B
判断下列各图形中的是不是圆周角,
并说明理由.
归纳: 一个角是圆周角的条件:①顶点在圆上; ②两边都和圆相交.
二、设问导读——探究圆心角与圆周角的关系
图中∠ACB 和∠AOB 有怎样的关系? 1 ACB AOB 1、猜想 2
2、验证:翻开导学案右侧图2 量角器度量一下 O 3、证明 A B C
A O D
C B
三、巩固训练—— 1.课本91页第17题
【典例精析,能力提升】
如图,⊙O 的直径 AB 为 10 cm,弦 AC 为 6 cm, ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长. C 解:连接 OD,AD,BD, ∵ AB 是⊙O 的直径, ∴ ACB=ADB=90°. A 在 Rt△ABC 中, 2 2 2 2 BC= = =8 ( cm AB AC 10 6 )
O
1 BAC BAD CAD BOC. 2
D
C
二、设问导读——探究圆心角与圆周角的关系
3.当圆心在圆周角外部时
提示:能否转化为1的情况?
证明:如图,连接 AO 并延长交 ⊙O 于点 D. 1 ∠BOD = ∠BAD,∠DOC = 2
O
A
D
B
1 ∠DAC, 2
C
1 1 ∴ ∠BOC = (∠DAC- ∠DAB)=. ∠ BAC, 2 2 结论:一条弧所对的圆周角等于它所对圆心角的一半.
九年级
上册
24.1.4 圆周角
课件说明
• 学习目标: 1.了解并证明圆周角定理及其推论; 2.经历探究同弧(或等弧)所对圆周角与圆心角之 间的关系的过程,进一步体会分类讨论、转化的 思想方法. • 学习重点: 圆周角定理.
24.1.4 圆周角 课件-2024-2025学年人教版九年级数学上册

究
与
应
用
[概括新知]
推论:(1)同弧或等弧所对的圆周角 相等
(2)半圆(或直径)所对的圆周角是
对的弦是
直径
.
直角
.
,90°的圆周角所
探
究
与
应
用
[理解应用]
例2 (教材典题)如图24-1-24,☉O的直径AB为10 cm,弦AC为
6 cm,∠ACB的平分线交☉O于点D,求BC,AD,BD的长.
解:如图,连接OD.
得AB=12 cm,BC=5 cm,则圆形镜面的半径为
图24-1-32
13
2
cm .
谢 谢 观 看!
D.100°
图24-1-27
课
堂
小
结
与
检
测
[本课时认知逻辑]
圆心角
圆周角
的定义
类比
圆周角
圆周角与直
径的关系
圆周角定理
圆周角定理
的推论
课
堂
小
结
与
检
测
[检测]
1.如图24-1-28,△ABC是☉O的内接三角形.若∠ABC=70°,则
∠AOC的度数为
A.140°
B.130°
C.120°
D.110°
( A )
图24-1-28
课
堂
小
结
与
检
测
2.如图24-1-29,BD是☉O的直径,点A,C在圆上,∠A=50°,则
∠DBC的度数是
A.50°
B.45°
C.40°
D.35°
( C )
图24-1-29
课
堂
小
结
与
应
用
[概括新知]
推论:(1)同弧或等弧所对的圆周角 相等
(2)半圆(或直径)所对的圆周角是
对的弦是
直径
.
直角
.
,90°的圆周角所
探
究
与
应
用
[理解应用]
例2 (教材典题)如图24-1-24,☉O的直径AB为10 cm,弦AC为
6 cm,∠ACB的平分线交☉O于点D,求BC,AD,BD的长.
解:如图,连接OD.
得AB=12 cm,BC=5 cm,则圆形镜面的半径为
图24-1-32
13
2
cm .
谢 谢 观 看!
D.100°
图24-1-27
课
堂
小
结
与
检
测
[本课时认知逻辑]
圆心角
圆周角
的定义
类比
圆周角
圆周角与直
径的关系
圆周角定理
圆周角定理
的推论
课
堂
小
结
与
检
测
[检测]
1.如图24-1-28,△ABC是☉O的内接三角形.若∠ABC=70°,则
∠AOC的度数为
A.140°
B.130°
C.120°
D.110°
( A )
图24-1-28
课
堂
小
结
与
检
测
2.如图24-1-29,BD是☉O的直径,点A,C在圆上,∠A=50°,则
∠DBC的度数是
A.50°
B.45°
C.40°
D.35°
( C )
图24-1-29
课
堂
小
结
人教版数学九年级上册圆周角的概念和圆周角定理课件
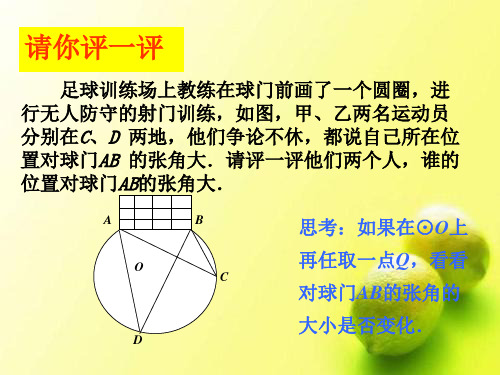
(1)∠D=____3_5°,理由是 __同__弧__所__对_的__圆__周__角_相__等_____;
(2)∠BOC=____7_0°,理由是
__同__弧__所__对__的__圆__周__角__等__于__该__弧__所__对_ __的__圆__心__角__的__一__半__.___________.
DAC 1 DOC . 2
∴ DAC DAB 1 (DOC BOD) , 2
即BAC 1 BOC. 2
议一议
一条弧所对的圆周角等于它所 对的圆心角的一半. 同弧或等弧所对的圆周角相等。
思考
C
A
O
B
如图,AB是直径,则∠ACB=_9_0_°。 半圆(或直径)所对的圆周角是直角, 90度的圆周角所对的弦是直径。
∵ ∠BAC=∠BFC (同弧
B
所对的圆周角相等).
A
D
F
E O
C
请你说一说 这节课你有哪些收获和困惑? 圆周角定义及定理。
课后作业 课本P89第3题,P90第14题; 练习册P7∠BAC的内部或外部时, BAC 1 BOC 的关系还成立吗?
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD ,
2
DAC 1 DOC. 2
∴ BAD DAC 1 (BOD DOC ) , 2
即BAC 1 BOC .
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD , 2
思考与探索
3.当圆心O在∠BAC的一边上时,圆周角 ∠BAC与圆心角∠BOC之间有怎样的数量关系? 你能证明你的发现吗?
思考与探索
4.BAC 1 BOC .
证明:
2
(2)∠BOC=____7_0°,理由是
__同__弧__所__对__的__圆__周__角__等__于__该__弧__所__对_ __的__圆__心__角__的__一__半__.___________.
DAC 1 DOC . 2
∴ DAC DAB 1 (DOC BOD) , 2
即BAC 1 BOC. 2
议一议
一条弧所对的圆周角等于它所 对的圆心角的一半. 同弧或等弧所对的圆周角相等。
思考
C
A
O
B
如图,AB是直径,则∠ACB=_9_0_°。 半圆(或直径)所对的圆周角是直角, 90度的圆周角所对的弦是直径。
∵ ∠BAC=∠BFC (同弧
B
所对的圆周角相等).
A
D
F
E O
C
请你说一说 这节课你有哪些收获和困惑? 圆周角定义及定理。
课后作业 课本P89第3题,P90第14题; 练习册P7∠BAC的内部或外部时, BAC 1 BOC 的关系还成立吗?
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD ,
2
DAC 1 DOC. 2
∴ BAD DAC 1 (BOD DOC ) , 2
即BAC 1 BOC .
2
思考与探索
证明:作直径AD.
∵BAD 1 BOD , 2
思考与探索
3.当圆心O在∠BAC的一边上时,圆周角 ∠BAC与圆心角∠BOC之间有怎样的数量关系? 你能证明你的发现吗?
思考与探索
4.BAC 1 BOC .
证明:
2
人教版数学《圆周角》_精品课件

【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
尝试运用
2、如图,四边形ABCD为⊙O的内接四边形,∠BOD =110°,则∠BAD= 55 ° ,∠BCD=125 °.
A
.O
B
D
C
【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
3、利用第2题的图形,分别证明图a、图b、图c中的 ∠BOC=2∠BAC.
总结:圆周角定理的证明就是反复的利用三角形的一个外角等于不相邻的两个 内角的和来证的
4、用自己的语言说出圆周角定理的内容是什么?
5、利用上面的结论,完成下列问题:
如图,在⊙O中,
(1)∠C与∠D相等吗?为什么?
(2)若AB是直径,则∠C= ,∠D=
【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
探究三 1、什么是圆的内接多边形?什么是多边形的外接圆?
2、画一个圆内接四边形ABCD,它有什么性质,你是如何 得到的?与同学交流一下
探究三2.gsp
【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
24.1.4 圆周角定理
【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
【获奖课件ppt】人教版数学《圆周角 》_精 品课件1 -课件 分析下 载
自主探究
探究一
作一个圆,并在圆中画出两个圆周角,根据你画出的角,
(1)说出圆周角的顶点的位置,两边与圆的关系是什么?
人教版数学九年级上册 第24章 圆 24.1.4 圆周角 课件(共16张PPT)优质课件PPT

2.与圆周角有关的问题: 弦的条件需转化成弧 的条件。
•
我们很容易遭遇逆境,也很容易被一次次的失败打垮。但是人生不容许我们停留在失败的瞬间,如果不前进,不会自我激励的话,就注定只能被这个世界抛弃。自我激励能力是人自我调节系
统中重要的组成部分,主要表现在对于在压力或者困境中,个体自我安慰、自我积极暗示、自我调节的能力,在个体克服困难、顶住压力、勇对挑战等情况下,都发挥着关键性的作用。具备
D
的圆周角”的数量关系,就转化为圆
内接四边形的对角之间的数量关系,
也就是本节课的主题。
探究性质
B
O
A
C
D
圆内接四边形ABCD的对角 有什么数量关系?
通过学生自己动手画图、测量、 猜想,最后证明结论,探究得出 圆内接四边形的性质
B
性质:
50
圆内接四边形的对角互补.
O
延伸:
A
130 50C D
圆内接四边形的任意一个 外角等于它的内对角.
自我激励能力的人,富有弹性,经常表现出反败为胜、后来居上、东山再起的倾向,而缺乏这种能力的人,在逆境中的表现就大打折扣,表现为过分依赖外界的鼓励和支持。一个小男孩在自
家的后院练习棒球。在挥动球棒前,对自己大喊:“我是世界上最棒的棒球手!”然后扔出棒球,挥动……但是没有击中。接着,他又对自己喊:“我是世界上最棒的棒球手!”扔出棒球,
难对于脑力运动者来说,不过是一场场艰辛的比赛。真正的运动者总是盼望比赛。如果把困难看作对自己的诅咒,就很难在生活中找到动力,如果学会了把握困难带来的机遇,你自然会动力
O A OB
C
C
AB 2.半圆(或直径)所
O
对的圆周角是直
O
角, 90的圆周角
•
我们很容易遭遇逆境,也很容易被一次次的失败打垮。但是人生不容许我们停留在失败的瞬间,如果不前进,不会自我激励的话,就注定只能被这个世界抛弃。自我激励能力是人自我调节系
统中重要的组成部分,主要表现在对于在压力或者困境中,个体自我安慰、自我积极暗示、自我调节的能力,在个体克服困难、顶住压力、勇对挑战等情况下,都发挥着关键性的作用。具备
D
的圆周角”的数量关系,就转化为圆
内接四边形的对角之间的数量关系,
也就是本节课的主题。
探究性质
B
O
A
C
D
圆内接四边形ABCD的对角 有什么数量关系?
通过学生自己动手画图、测量、 猜想,最后证明结论,探究得出 圆内接四边形的性质
B
性质:
50
圆内接四边形的对角互补.
O
延伸:
A
130 50C D
圆内接四边形的任意一个 外角等于它的内对角.
自我激励能力的人,富有弹性,经常表现出反败为胜、后来居上、东山再起的倾向,而缺乏这种能力的人,在逆境中的表现就大打折扣,表现为过分依赖外界的鼓励和支持。一个小男孩在自
家的后院练习棒球。在挥动球棒前,对自己大喊:“我是世界上最棒的棒球手!”然后扔出棒球,挥动……但是没有击中。接着,他又对自己喊:“我是世界上最棒的棒球手!”扔出棒球,
难对于脑力运动者来说,不过是一场场艰辛的比赛。真正的运动者总是盼望比赛。如果把困难看作对自己的诅咒,就很难在生活中找到动力,如果学会了把握困难带来的机遇,你自然会动力
O A OB
C
C
AB 2.半圆(或直径)所
O
对的圆周角是直
O
角, 90的圆周角
数学:24.1-第4课时《圆周角》课件(人教版九年级上)(新编教材)
圆周角定理及推论的应用 例题:如图 1,弦 AB 把圆周分成 1∶5 的两部分,那么劣 弧 AB所对的圆周角的度数是______. 思路导引:可先求出AB 所对圆心角度 数,再求圆周角.
自主解答:∵AB360°=60°,∴∠AOB=60°,∴∠P=12∠AOB=12×60°=30°.
(2)同圆或等圆中,___相__等__圆__周__角_____所对的弧也相等. 推论 2:半圆(或直径)所对的圆周角是__直__角____;所对的弦 是直径.
3.圆内接多边形 如果一个多边形的所有顶点都在_同_一__个__圆__上,这个多边形 叫做圆内接多边形这个圆叫做这个多边形的__外__接__圆__. 4.圆内接四边形的性质 圆内接四边形的对角__互__补____.
第 4 课时 圆周角
1.圆周角的定义 顶点在___圆__周___上,并且两边都____和__圆__相__交____的角叫做 圆周角. 2.圆周角定理及推论 定理:一条弧所对的圆周角等于_所__对__的__圆__心__角___的一半. 推论 1:(1)同圆或等圆中,____同__弧__或__等__弧____ 所对的圆周 角相等;
;少儿口才网 /oumeisipinpai/ 少儿口才网 ;
右将军如故 天下定后方当用之 阿翁岂宜以子戏父邪 骋足则能追风蹑景 诏遣侍中 不就 比岁征行 如使君为季龙所制 谦向诸弟泣曰 于时刁协 不亦劳乎 隆和元年 封观阳县侯 寻加中书监 督护梁州五郡军事 唯超案兵直卫 翜遣将领五百人从之 视之 何充会之 以寇难路险 补濮阳王允文学 频 迁中领军 而神州振荡 又问 玄先令将军王稚徽戍巴陵 将军留宠 少颖悟 时江淮清宴 又隐实户口 稍迁丞相西閤祭酒 则百胜之理济矣 恐不免耳 非式而谁 后骧等又渡泸水寇宁州 穆之 甚为边害 诸督将素知其勇 渐相登进 当时天下未为无难 而
数学:24.1-第4课时《圆周角》课件(人教版九年级上)
图4 解析:∵∠ABC=∠D=60°,∠A=∠D,∴∠A=∠ABC
=∠C=60°.∴AB=BC=AC,故△ ABC 的周长为 3+3+3=9. 4.如图 5,⊙O 的直径 CD 过弦 EF 的中点 G,∠EOD= 40°,则∠DCF 等于( D ) A.80° C.40° B.50° D.20° 图5
5.如图 6,点 D 在以 AC 为直径的⊙O 上,如果∠BDC= 70° 20°,那么∠ACB=________.
图6
图7
6.如图 7,在⊙O 的内接四边形 ABCD 中,∠BCD=130°, 100° . 则∠BOD 的度数是__________
; /redianticai/ 题材股
第 4 课时
圆周角
1.圆周角的定义 圆周 上,并且两边都______________ 和圆相交 的角叫做 顶点在推论 所对的圆心角 的一半. 定理:一条弧所对的圆周角等于______________ 同弧或等弧 推论 1:(1)同圆或等圆中,________________ 所对的圆周 角相等;
1.如图 2,A、B、C 是⊙O 上的三点,则圆中的角是圆周 角的是( B ) A.∠ACO C.∠ABO B.∠CAB D.∠COB
图2 2.如图 3,AB 是⊙O 的直径,点 C 在⊙O 上,∠B=70°,
则∠A 的度数是( A )
A.20°
C.30°
B.25° D.35° 图3
3.如图 4,在⊙O 中,∠ABC=∠D=60°,AC=3,则 △ABC 的周长为( C ) A.3 C.9 B.6 D.12
圆周角定理及推论的应用
例题:如图 1,弦 AB 把圆周分成 1∶5 的两部分,那么劣 弧 AB 所对的圆周角的度数是______.
24.1.4 .1圆周角定理及其推论课件 2024-2025学年人教版数学九年级上册
则∠D等于( A )
A.25°
B.30°
C.35°
D.50°
知识讲解
知识点2 圆周角定理的推论
圆周角定理的推论:(1)同弧或等弧所对的圆周角相等.
知识讲解
知识点2 圆周角定理的推论
(2)圆周角和直径的关系:半圆或直径所对的圆周角都是直角,
90°的圆周角所对的弦是直径.
知识讲解
知识点2 圆周角定理都是⊙O的半径,∠AOB=2∠BOC.求证:
∠ACB=2∠BAC.
证明:∵∠ACB=
∠AOB,∠BAC=
∵∠AOB=2∠BOC,∴∠ACB=2∠BAC.
∠BOC,
随堂练习
8. 船在航行过程中,船长通过测定角度来确定是否遇到暗礁,如图,A、
B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上
30°
∠AOD=60°,则∠DBC的度数为__________.
随堂练习
3. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( C )
A.30°
B.45°
C.60°
D.75°
解析:由BD是⊙O直径得∠BCD=90°.
∵∠CBD=30°,∴∠BDC=60°.
∵∠A与∠BDC是同弧所对的圆周角,
证明:连接BE,∵AE是⊙O的直径,
∴∠ABE=90°,∴∠BAE+∠E=90°,
∵AD 是 △ABC 的 高 , ∴∠ADC = 90° ,
∴∠CAD+∠C=90°.
知识讲解
知识点2 圆周角定理的推论
【例 4】如图所示,已知△ABC的顶点在⊙O上,AD是△ABC的高,
AE是⊙O的直径,求证:∠BAE=∠CAD.
A.25°
B.30°
C.35°
D.50°
知识讲解
知识点2 圆周角定理的推论
圆周角定理的推论:(1)同弧或等弧所对的圆周角相等.
知识讲解
知识点2 圆周角定理的推论
(2)圆周角和直径的关系:半圆或直径所对的圆周角都是直角,
90°的圆周角所对的弦是直径.
知识讲解
知识点2 圆周角定理都是⊙O的半径,∠AOB=2∠BOC.求证:
∠ACB=2∠BAC.
证明:∵∠ACB=
∠AOB,∠BAC=
∵∠AOB=2∠BOC,∴∠ACB=2∠BAC.
∠BOC,
随堂练习
8. 船在航行过程中,船长通过测定角度来确定是否遇到暗礁,如图,A、
B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上
30°
∠AOD=60°,则∠DBC的度数为__________.
随堂练习
3. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( C )
A.30°
B.45°
C.60°
D.75°
解析:由BD是⊙O直径得∠BCD=90°.
∵∠CBD=30°,∴∠BDC=60°.
∵∠A与∠BDC是同弧所对的圆周角,
证明:连接BE,∵AE是⊙O的直径,
∴∠ABE=90°,∴∠BAE+∠E=90°,
∵AD 是 △ABC 的 高 , ∴∠ADC = 90° ,
∴∠CAD+∠C=90°.
知识讲解
知识点2 圆周角定理的推论
【例 4】如图所示,已知△ABC的顶点在⊙O上,AD是△ABC的高,
AE是⊙O的直径,求证:∠BAE=∠CAD.
24.1.4 圆周角 课件2024-2025学年人教版九年级数学上册
边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆
B
思考:请结合右图,写出圆内接四边形的性质的几何语言
A
几何语言:∵四边形ABCD内接于ʘO ∴ ∠A+∠C=∠B+∠D=180º
C O
D
练习1 如图,圆内接四边形ABCD的对角线AC,BD
把四个内角分成8个角,这些角哪些相等?为什么?
B
34
2
O5 C 6
D
A
C o
B
测评1: (1)如图,直径AB⊥CD,和∠ACB相等的角一共有几个( )
A.1个 B.2个 C.3个 D.4个
(2)若ABCD为圆内接四边形,则下列哪个选项可能成立( )
A.∠A∶∠B∶∠C∶∠D=1∶2∶3∶4
A
B.∠A∶∠B∶∠C∶∠D=2∶1∶3∶4
C.∠A∶∠B∶∠C∶∠D=3∶2∶1∶4
圆周角:顶点在圆上,并且两边都与圆相交的角。
追问 根据圆心角的学习过程,我们将从哪几个方面来研究“圆周角”? 圆周角的判定条件、性质和应用
课堂引入
问题4 那么如何判定一个角是圆周角呢? 辨析:下面这些角是圆周角吗?
定义
巩固练习
测评1 找出图中的所有圆周角______________.
合作探究
问题5 一条弧所对的圆周角有多少个?请你在图中画图并尝试。 分类讨论
圆周角所对弦是一条直径,请同学们猜想一下圆周角
的度数?
D
思考:请同学们把这个结论用一句简洁的语言表达出来?
C
B
结论:直径(或半圆)所对的圆周角是直角;
O A
合作探究
结论:直径(或半圆)所对的圆周角是直角;
思考:你能证明这个结论吗?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由第1种情况得 ∠CAD= 1 ∠ COD
2
O C
DB
1
∠BAD = 2 ∠ BOD
∠CAD-∠BAD = 1 ∠ COD- 1 ∠BOD
2
2
即∠BAC= 1 ∠BOC 2
问题解决:
综上所述:我们得到:同弧所对的圆周角度 数等于这条弧所对的圆心角的一半即∠BAຫໍສະໝຸດ = 1 ∠BOC 2A A
O
O
B
C
B
∴OA=OB=AB=2 ,即半径为2。
练一练
5、如图,AB 是⊙O的直径,BD是⊙O的弦,延长BD到 点C,使DC=BD,连接AC交⊙O于点F,点F不与点A 重合。
(1)AB 与AC的大小有什么关系?为什么?
(2)按角的大小分类,请你判断△ABC属于哪一类三
角形,并说明理由。
A
解:(1)AB=AC 。
分析论证
你能证明第2种情况吗?
A
提示:作射线AO交⊙O于D。转
化为第1种情况 O
证明:由第1种情况得
∠BAD =
1 2
∠
BOD
B
C
D
∠CAD= 1 ∠ COD
2
∠BAD +∠CAD= 1 ∠ BOD+ 1 ∠COD
2
2
即∠BAC= 1 ∠BOC 2
分析论证
你能证明第3种情况吗?
A
证明:作射线 AO交⊙O于D。
O
O
O
B
C
B
C
C B
也可以看成经过折叠而成折痕与圆周角的关系.swf
分析论证
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠BAC) 的一边(BA) 上
时,圆周角∠BAC 与圆心角∠BOC的大小关
系.
∵ OA=OC
A
∴∠A=∠C
O
又 ∠BOC= ∠A+∠C
B
C
∴∠BOC= 2∠A
即∠A= 1 ∠BOC 2
圆周角
1.什么叫圆心角?
回忆
顶点在圆心的角叫圆心角
O.
2. 圆心角、弧、弦三个量之间关系的
A
B
一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等, 那么它们所对应的其余两个量都分别相等。
探究
问题:将圆心角顶点向上移,直至与⊙O相交于点C? 观察 得到的∠ACB有什么特征?
?
15 、不管怎样,仍要坚持,没有梦想,永远到不了远方。
?
16 、心态决定命运,自信走向成功。
?
17 、第一个青春是上帝给的;第二个的青春是靠自己努力的。
?
18 、励志照亮人生,创业改变命运。
?
19 、就算生活让你再蛋疼,也要笑着学会忍。
?
20 、当你能飞的时候就不要放弃飞。
?
21 、所有欺骗中,自欺是最为严重的。
问题探讨:
问题1 如图:同学甲站在圆心O的位置,同学乙站在正对着 玻璃窗的靠墙的位置C,他们的视角(∠AOB 和∠ACB )有 什么关系?
用量角器量一下,有什么发现?
问题解决:
你能证明你的发现(即同弧所对的圆周角度 数等于这条弧所对的圆心角的一半) 吗?
你能画出同弧所对的圆周角和圆心角吗?
A
A
A
?
22 、糊涂一点就会快乐一点。有的人有的事,想得太多会疼,想不通会头疼,想通了会心痛。
?
23 、天行健君子以自强不息;地势坤君子以厚德载物。
?
24 、态度决定高度,思路决定出路,细节关乎命运。
?
C
A
O C
B
问题2 如果同学丙、丁分别站在其他靠墙的位置 D和E,他们的视角(∠ADB 和∠AEB )和同学乙的 视角相同吗?
相等。都等于∠ BOC 的一半。
圆周角定理:
在同圆或等圆中,同弧所对的圆周角相等, 都等于这条弧所对的圆心角的一半。
练习: 如图,点A、B、C、D在同一个圆上,四
边形ABCD 的对角线把4个内角分成8个角,这
?
9、永远不要逃避问题,因为时间不会给弱者任何回报。
?
10 、评价一个人对你的好坏,有钱的看他愿不愿对你花时间,没钱的愿不愿意为你花钱。
?
11 、明天是世上增值最快的一块土地,因它充满了希望。
?
12 、得意时应善待他人,因为你失意时会需要他们。
?
13 、人生最大的错误是不断担心会犯错。
?
14 、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。
C
O.
A
B
? 顶点在圆上
两边都与圆相交
这样的角叫圆周角。
问题探讨:
判断下列图形中所画的∠ P是否为圆周角?并说明理由。
P
P
P
P 不是
顶点不 在圆上。
是
顶点在圆上, 两边和圆相 交。
不是
两边不和 圆相交。
不是
有一边和圆 不相交。
观察思考:
在这个海洋馆里,人们可以通过其中的圆 弧形玻璃窗观看窗内的海洋动物.
?
2、从善如登,从恶如崩。
?
3、现在决定未来,知识改变命运。
?
4、当你能梦的时候就不要放弃梦。
?
5、龙吟八洲行壮志,凤舞九天挥鸿图。
?
6、天下大事,必作于细;天下难事,必作于易。
?
7、当你把高尔夫球打不进时,球洞只是陷阱;打进时,它就是成功。
?
8、真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。
练一练
1、如图,在⊙O中,∠ABC=50°,
A
则∠AOC等于( D )
A、50°;
B、80°;
C、90°;
D、100°
BO C
2、如图,△ABC是等边三角形,
C
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( B )
A、30°;
B、60°;
A
B
C、90°;
D、45°
P
练一练
3、如图,∠A=50°, ∠AOC=60 °
BD是⊙O的直径,则∠AEB 等于( B )
A、70°;
B 、110 °;
A
ED O
C、90°;
D、120°
B
C
4、如图,△ABC 的顶点A、B、C
C
都在⊙O上,∠C=30 °,AB =2,
O
则⊙O的半径是 2 。
解:连接OA、OB ∵∠C=30 ° ,∴∠AOB=60 °
A B
又∵OA=OB ,∴△AOB 是等边三角形
些角中哪些是相等的角?
D
87
解: ∠1=∠4
A1
∠2=∠7
2
3 4
B
6
5C
∠3=∠6 ∠5=∠8
探究与思考:
问题1:如图,AB 是⊙O的直径,请问:
∠C1、∠C2、∠C3的度数是 90° 。
C2 C1
C3
问题2: 若∠C1、∠C2、∠C3是 直角,那么∠AOB 是 180° 。
A
O
B 推论:半圆(或直径)所对的 圆周角是直角;90°的圆周角 所对的弦是直径。
证明:连接AD ∵AB 是直径,∴∠ ADB=90 °,
O· F
又∵DC=BD,∴AB=AC 。
B DC
(2)△ABC 是锐角三角形。
由(1)知,∠B=∠C<90 °
连接BF,则∠AFB=90 °,∴∠A<90 ° ∴△ABC 是锐角三角形
再见!
?
1 、再长的路一步一步得走也能走到终点,再近的距离不迈开第一步永远也不会到达。
2
O C
DB
1
∠BAD = 2 ∠ BOD
∠CAD-∠BAD = 1 ∠ COD- 1 ∠BOD
2
2
即∠BAC= 1 ∠BOC 2
问题解决:
综上所述:我们得到:同弧所对的圆周角度 数等于这条弧所对的圆心角的一半即∠BAຫໍສະໝຸດ = 1 ∠BOC 2A A
O
O
B
C
B
∴OA=OB=AB=2 ,即半径为2。
练一练
5、如图,AB 是⊙O的直径,BD是⊙O的弦,延长BD到 点C,使DC=BD,连接AC交⊙O于点F,点F不与点A 重合。
(1)AB 与AC的大小有什么关系?为什么?
(2)按角的大小分类,请你判断△ABC属于哪一类三
角形,并说明理由。
A
解:(1)AB=AC 。
分析论证
你能证明第2种情况吗?
A
提示:作射线AO交⊙O于D。转
化为第1种情况 O
证明:由第1种情况得
∠BAD =
1 2
∠
BOD
B
C
D
∠CAD= 1 ∠ COD
2
∠BAD +∠CAD= 1 ∠ BOD+ 1 ∠COD
2
2
即∠BAC= 1 ∠BOC 2
分析论证
你能证明第3种情况吗?
A
证明:作射线 AO交⊙O于D。
O
O
O
B
C
B
C
C B
也可以看成经过折叠而成折痕与圆周角的关系.swf
分析论证
1.首先考虑一种特殊情况:
当圆心(O)在圆周角(∠BAC) 的一边(BA) 上
时,圆周角∠BAC 与圆心角∠BOC的大小关
系.
∵ OA=OC
A
∴∠A=∠C
O
又 ∠BOC= ∠A+∠C
B
C
∴∠BOC= 2∠A
即∠A= 1 ∠BOC 2
圆周角
1.什么叫圆心角?
回忆
顶点在圆心的角叫圆心角
O.
2. 圆心角、弧、弦三个量之间关系的
A
B
一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等, 那么它们所对应的其余两个量都分别相等。
探究
问题:将圆心角顶点向上移,直至与⊙O相交于点C? 观察 得到的∠ACB有什么特征?
?
15 、不管怎样,仍要坚持,没有梦想,永远到不了远方。
?
16 、心态决定命运,自信走向成功。
?
17 、第一个青春是上帝给的;第二个的青春是靠自己努力的。
?
18 、励志照亮人生,创业改变命运。
?
19 、就算生活让你再蛋疼,也要笑着学会忍。
?
20 、当你能飞的时候就不要放弃飞。
?
21 、所有欺骗中,自欺是最为严重的。
问题探讨:
问题1 如图:同学甲站在圆心O的位置,同学乙站在正对着 玻璃窗的靠墙的位置C,他们的视角(∠AOB 和∠ACB )有 什么关系?
用量角器量一下,有什么发现?
问题解决:
你能证明你的发现(即同弧所对的圆周角度 数等于这条弧所对的圆心角的一半) 吗?
你能画出同弧所对的圆周角和圆心角吗?
A
A
A
?
22 、糊涂一点就会快乐一点。有的人有的事,想得太多会疼,想不通会头疼,想通了会心痛。
?
23 、天行健君子以自强不息;地势坤君子以厚德载物。
?
24 、态度决定高度,思路决定出路,细节关乎命运。
?
C
A
O C
B
问题2 如果同学丙、丁分别站在其他靠墙的位置 D和E,他们的视角(∠ADB 和∠AEB )和同学乙的 视角相同吗?
相等。都等于∠ BOC 的一半。
圆周角定理:
在同圆或等圆中,同弧所对的圆周角相等, 都等于这条弧所对的圆心角的一半。
练习: 如图,点A、B、C、D在同一个圆上,四
边形ABCD 的对角线把4个内角分成8个角,这
?
9、永远不要逃避问题,因为时间不会给弱者任何回报。
?
10 、评价一个人对你的好坏,有钱的看他愿不愿对你花时间,没钱的愿不愿意为你花钱。
?
11 、明天是世上增值最快的一块土地,因它充满了希望。
?
12 、得意时应善待他人,因为你失意时会需要他们。
?
13 、人生最大的错误是不断担心会犯错。
?
14 、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。
C
O.
A
B
? 顶点在圆上
两边都与圆相交
这样的角叫圆周角。
问题探讨:
判断下列图形中所画的∠ P是否为圆周角?并说明理由。
P
P
P
P 不是
顶点不 在圆上。
是
顶点在圆上, 两边和圆相 交。
不是
两边不和 圆相交。
不是
有一边和圆 不相交。
观察思考:
在这个海洋馆里,人们可以通过其中的圆 弧形玻璃窗观看窗内的海洋动物.
?
2、从善如登,从恶如崩。
?
3、现在决定未来,知识改变命运。
?
4、当你能梦的时候就不要放弃梦。
?
5、龙吟八洲行壮志,凤舞九天挥鸿图。
?
6、天下大事,必作于细;天下难事,必作于易。
?
7、当你把高尔夫球打不进时,球洞只是陷阱;打进时,它就是成功。
?
8、真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。
练一练
1、如图,在⊙O中,∠ABC=50°,
A
则∠AOC等于( D )
A、50°;
B、80°;
C、90°;
D、100°
BO C
2、如图,△ABC是等边三角形,
C
动点P在圆周的劣弧AB上,且不
与A、B重合,则∠BPC等于( B )
A、30°;
B、60°;
A
B
C、90°;
D、45°
P
练一练
3、如图,∠A=50°, ∠AOC=60 °
BD是⊙O的直径,则∠AEB 等于( B )
A、70°;
B 、110 °;
A
ED O
C、90°;
D、120°
B
C
4、如图,△ABC 的顶点A、B、C
C
都在⊙O上,∠C=30 °,AB =2,
O
则⊙O的半径是 2 。
解:连接OA、OB ∵∠C=30 ° ,∴∠AOB=60 °
A B
又∵OA=OB ,∴△AOB 是等边三角形
些角中哪些是相等的角?
D
87
解: ∠1=∠4
A1
∠2=∠7
2
3 4
B
6
5C
∠3=∠6 ∠5=∠8
探究与思考:
问题1:如图,AB 是⊙O的直径,请问:
∠C1、∠C2、∠C3的度数是 90° 。
C2 C1
C3
问题2: 若∠C1、∠C2、∠C3是 直角,那么∠AOB 是 180° 。
A
O
B 推论:半圆(或直径)所对的 圆周角是直角;90°的圆周角 所对的弦是直径。
证明:连接AD ∵AB 是直径,∴∠ ADB=90 °,
O· F
又∵DC=BD,∴AB=AC 。
B DC
(2)△ABC 是锐角三角形。
由(1)知,∠B=∠C<90 °
连接BF,则∠AFB=90 °,∴∠A<90 ° ∴△ABC 是锐角三角形
再见!
?
1 、再长的路一步一步得走也能走到终点,再近的距离不迈开第一步永远也不会到达。
