2017版高考数学一轮总复习第七章立体几何第一节空间几何体的结构及其三视图和直观图练习文
高考数学(立体几何)第一轮复习
高考数学(立体几何)第一轮复习资料知识点小结:高考立体几何知识点总结一 、空间几何体 (一) 空间几何体的类型1 多面体:由若干个平面多边形围成的几何体。
围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点。
2 旋转体:把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。
其中,这条直线称为旋转体的轴。
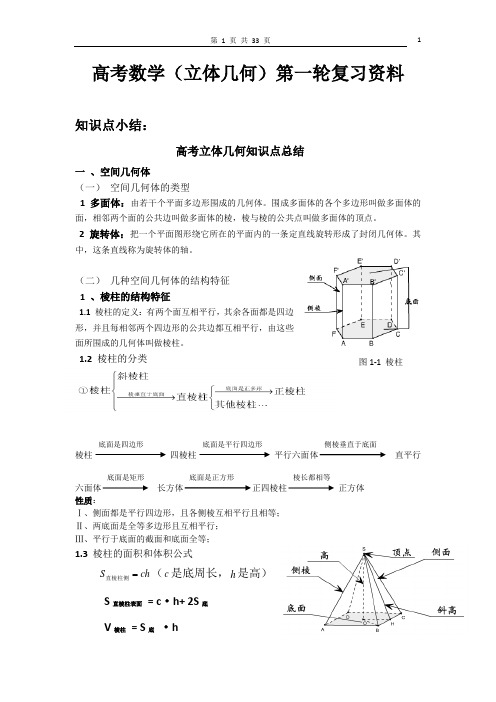
(二) 几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2 棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体 性质:Ⅰ、侧面都是平行四边形,且各侧棱互相平行且相等; Ⅱ、两底面是全等多边形且互相平行; Ⅲ、平行于底面的截面和底面全等;1.3 棱柱的面积和体积公式ch S 直棱柱侧(c 是底周长,h 是高) S 直棱柱表面 = c ·h+ 2S 底 V 棱柱 = S 底 ·h棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形图1-1 棱柱2 、棱锥的结构特征2.1 棱锥的定义(1) 棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
(2)正棱锥:如果有一个棱锥的底面是正多边形,并且顶点在底面的投影是底面的中心,这样的棱锥叫做正棱锥。
2.2 正棱锥的结构特征Ⅰ、 平行于底面的截面是与底面相似的正多边形,相似比等于顶点到截面的距离与顶点到底面的距离之比;它们面积的比等于截得的棱锥的高与原棱锥的高的平方比;截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比;Ⅱ、 正棱锥的各侧棱相等,各侧面是全等的等腰三角形;正棱锥侧面积:1'2S ch =正棱椎(c 为底周长,'h 为斜高) 体积:13V Sh =棱椎(S 为底面积,h 为高)正四面体:对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。
(新课标)2017高考数学一轮复习 第七章 立体几何 第2讲.

四面体的棱长);
面体的棱长).
●双基自测
1 . 下 列 结 论 正 确 的 打 “√” , 错 误 的 打 “×”. 导学号 25401614 (1)圆柱的一个底面积为 S,侧面展开图是一个正方形,那 么这个圆柱的侧面积是 2πS.( ) ) ) (2)设长方体的长、宽、高分别为 2a,a,a,其顶点都在一 个球面上,则该球的表面积为 3πa2( (3)若一个球的体积为 4 3π,则它的表面积为 12π.(
体积
Sh V=____________
1 V=3Sh
1 1 正棱台 S 侧= (c+c′)h′ V= (S 上+S 下+ S上· S下)h 2 3 球
4πR2 S 球面=______
4 3 V=3πR
2.几何体的表面积 各面面积之和. (1)棱柱、棱锥、棱台的表面积就是____________ 矩形 、_____ 扇形 、 (2)圆柱、圆锥、圆台的侧面展开图分别是_____ 扇环形 ;它们的表面积等于_______ 侧面积 与底面面积之和. ____________
3.几何体的外接球与内切球 (1)长方体的外接球:
a2+b2+c2 2 ①球心:体对角线的交点;②半径:r=____________( a,
b,c为长方体的长、宽、高). (2)正方体的外接球、内切球及与各条棱相切的球: 3 a为正方体的 ①外接球:球心是正方体中心;半径r=____( 2a 棱长); a ②内切球:球心是正方体中心;半径r=____( 2 a为正方体的 棱长);
[ 答案]
1:47
5.(必修 2P36T10 改编)一直角三角形的三边长分别为 6 cm,8 cm,10 cm , 绕 斜 边 旋 转 一 周 所 得 几 何 体 的 表 面 积 为 _______________. 导学号 25401618
全国版2017版高考数学一轮复习第七章立体几何7.1空间几何体的结构及其三视图和直观图课件理

的转化.
【规范解答】选B.将三视图还原为几何体即可.如图所
示,几何体为三棱柱.
【技法感悟】
1.已知几何体,识别三视图的技巧
已知几何体画三视图时,可先找出各个顶点在投影面上
的投影,然后再确定线在投影面上的实虚.
2.已知三视图,判断几何体的技巧 (1)对柱、锥、台、球的三视图要熟悉. (2)明确三视图的形成原理,并能结合空间想象将三视 图还原为直观图. (3)遵循“长对正、高平齐、宽相等”的原则. 易错提醒:对于简单组合体的三视图,应注意它们的交 线的位置,区分好实线和虚线的不同.
直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),
(0,1,1),(0,0,0),画该四面体三视图中的正视图时, 以zOx平面为投影面,则得到正视图可以是 ( )
【解题导引】在空间直角坐标系中找出四个点,然后作
出这四个点在平面zOx中的投影,要注意线的实虚.
【规范解答】选A.由已知可作出示意图,以zOx平面为
半圆
_______________所在的直线 垂直于底边的腰 _____所在的直线 直径
3.空间几何体的三视图 (1)三视图的形成与名称:
①形成:空间几何体的三视图是用平行投影得到的,在
这种投影之下,与投影面平行的平面图形留下的影子, 与平面图形的_____和_____是完全相同的; 形状 _______ 大小 、_______、_______. ②名称:三视图包括
2.(必修2P19练习T3改编)利用斜二测画法得到的: ①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形; ④菱形的直观图一定是菱形. 以上结论正确的个数是________.
2017年高考数学(理)一轮总复习课件:第七章 立体几何

模型,有些问题可以利用它们举特例解决或者学会利用反例对概念类的命 题进行辨析.
第十一页,编辑于星期六:二点 四十七分。
【变式训练】 1.给出下列命题: ①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线; ②四棱锥的四个侧面都可以是直角三角形;
平行
_全___等如各__侧_图_.棱:之平间面的A关BC系与是平__面__平__A行_1B__且1C__1相_间_等_的__关__系__是.________,△ABC 与△A1B1C1 的关系是
第三页,编辑于星期六:二点 四十七分。
(如2)图棱:锥一(以个四底棱面锥是为四例边) 形,四个侧面是有一个_公___共__顶___点______的三角形.
但不一定全等;②正确,若三棱锥的三条侧棱两两垂直,则三个侧面构 成的三个平面的二面角都是直二面角;③正确,因为两个过相对侧棱的 截面的交线平行于侧棱,又垂直于底面;④正确,如图,正方体AC1中
的三棱锥C1-ABC,四个面都是直角三角形;⑤正确,由棱台的概念 可知. 答案:②③④⑤
第十页,编辑于星期六:二点 四十七分。
其余两边旋转形成的面所围成的几何体不是圆锥,如图3所示,它是由两个同底圆
锥组成的几何体;⑤错误,棱台的上、下底面相似且是对应边平行的多边形,各侧棱 延长线交于一点,但是侧棱长不一定相等.
答案:B
第十三页,编辑于星期六:二点 四十七分。
探究点二 几何体的三视图
第十四页,编辑于星期六:二点 四十七分。
(1)一个几何体的三视图如图所示,则该几何体的直观图可以是( )
(2)(2015·济宁模拟)点 M,N 分别是正方体 ABCD-A1B1C1D1 的棱 A1B1,A1D1 的中点,
高考数学大一轮复习配套课时训练:第七篇 立体几何 第1节 空间几何体的结构及三视图和直观图(含答案)

第七篇立体几何(必修2)第1节空间几何体的结构及三视图和直观图课时训练练题感提知能【选题明细表】A组一、选择题1.(2013山东烟台模拟)如图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,则该组合体的侧(左)视图的面积为( C )(A)8π(B)6π(C)4+(D)2+解析:该组合体的侧(左)视图为其中正方形的边长为2,三角形为边长为2的三角形,所以侧(左)视图的面积为22+×22×=4+,故选C.2.(2013山东莱州模拟)一个简单几何体的正(主)视图,侧(左)视图如图所示,则其俯视图不可能为①长方形;②直角三角形;③圆;④椭圆.其中正确的是( C )(A)①(B)② (C)③ (D)④解析:当该几何体的俯视图为圆时,由三视图知,该几何体为圆柱,此时,正(主)视图和侧(左)视图应相同,所以该几何体的俯视图不可能是圆,其余都有可能.故选C.3.(2013韶关市高三调研)某几何体的三视图如图所示,根据图中标出的数据,可得这个几何体的表面积为( B )(A)4+4 (B)4+4(C) (D)12解析:由三视图知该几何体为正四棱锥P ABCD,底面边长为2,高PO=2,如图所示,取CD的中点E,连接OE、PE,则PE==,因此几何体的表面积为2×2+×2×4×=4+4,故选B.4.如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( A )(A)2+(B)(C)(D)1+解析:由题意画出斜二测直观图及还原后原图,由直观图中底角均为45°,腰和上底长度均为1,得下底长为1+,所以原图上、下底分别为1,1+,高为2的直角梯形.所以面积S=(1++1)×2=2+.故选A.5.(2013北京东城区模拟)已知一个三棱锥的三视图如图所示,其中三个视图都是直角三角形,则在该三棱锥的四个面中,直角三角形的个数为( D )(A)1 (B)2 (C)3 (D)4解析:由题意可知,几何体是三棱锥,其放置在长方体中形状如图所示,利用长方体模型可知,此三棱锥A BCD的四个面中,全部是直角三角形.故选D.6.(2013广州市毕业班测试(二))一个圆锥的正(主)视图及其尺寸如图所示,若一个平行于圆锥底面的平面将此圆锥截成体积之比为1∶7的上、下两部分,则截面的面积为( C )(A)π(B)π (C)π(D)4π解析:由题意知,该几何体是底面半径为3,高为4的圆锥.由截面性质知截面圆半径为×3=,故截面的面积为π·()2=,故选C.7.下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若过两个相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱.其中真命题为( D )(A)①②(B)①③(C)②③(D)②④解析:对于①,平行六面体的两个相对侧面与底面垂直且互相平行,而另两个相对侧面可能与底面不垂直,则不是直棱柱,故①假;对于②,两截面的交线平行于侧棱,且垂直于底面,故②真;对于③,作正四棱柱的两个平行菱形截面,可得满足条件的斜四棱柱(如图(1)所示),故③假;对于④,四棱柱一个对角面的两条对角线,恰为四棱柱的对角线,故对角面为矩形,于是侧棱垂直于底面的一条对角线,同样侧棱也垂直于底面的另一条对角线,故侧棱垂直于底面,故④真.故选D.二、填空题8.如图所示的Rt△ABC绕着它的斜边AB旋转一周得到的图形是.解析:过Rt△ABC的顶点C作线段CD⊥AB,垂足为D,所以Rt△ABC绕着它的斜边AB旋转一周后应得到的是以CD作为底面圆的半径的两个圆锥的组合体.答案:两个圆锥的组合体9.一个几何体的正(主)视图为一个三角形,则这个几何体可能是下列几何体中的(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.解析:显然①②⑤均有可能;当三棱柱放倒时,其正(主)视图可能是三角形,所以③有可能,④不可能.答案:①②③⑤10.如图,点O为正方体ABCD A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是(填出所有可能的序号).解析:空间四边形D′OEF在正方体的平面DCC′D′上的投影是①;在平面BCC′B′上的投影是②;在平面ABCD上的投影是③,而不可能出现投影为④的情况.答案:①②③11.(2013山东烟台模拟)如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正(主)视图是边长为2的正方形,俯视图为正三角形,则侧(左)视图的面积为.解析:因为俯视图为正三角形,所以俯视图的高为,侧视图为两直角边分别为2、的矩形,所以侧(左)视图的面积为2.答案:2三、解答题12.(2013西工大附中模拟)已知四棱锥P ABCD的三视图如图所示,求此四棱锥的四个侧面的面积中最大值.解:由三视图可知该几何体是如图所示的四棱锥,顶点P在底面的射影是底面矩形的顶点D.底面矩形边长分别为3,2,△PDC是直角三角形,直角边为3与2,所以S△PDC=×2×3=3.△PBC是直角三角形,直角边长为2,,三角形的面积为×2×=.△PAB是直角三角形,直角边长为3,2;其面积为×3×2=3.△PAD也是直角三角形,直角边长为2,2,三角形的面积为×2×2=2. 所以四棱锥P ABCD的四个侧面中面积最大的是前面三角形的面积为3.13.圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角为45°,求这个圆台的高、母线长和底面半径.解:圆台的轴截面如图.设圆台的上、下底面半径分别为x cm和3x cm,延长AA1交OO1的延长线于点S.在Rt△SOA中,∠ASO=45°,则∠SAO=45°.所以SO=AO=3x,OO1=2x.又×(6x+2x)×2x=392,解得x=7.所以圆台高OO母线长l=OO1=14 cm,底面半径分别为7 cm和21 cm.B组14.(2013广州高三调研)已知四棱锥P ABCD的三视图如图所示,则四棱锥P ABCD的四个侧面中面积最大的是( C )(A)3 (B)2(C)6 (D)8解析:四棱锥如图所示,PM=3,×4×=2,S△PDC=S△PAB=×4×3=6,S△PBC=S△PAD=×2×3=3,故四个侧面中面积最大的是6.15.(2013北京西城检测)三棱锥D ABC及其三视图中的正视图和侧视图如图所示,则棱BD的长为.解析:取AC的中点E,连结BE,DE,由正(主)视图可知BE⊥AC,BE⊥DE.DC⊥平面ABC且DC=4,BE=2,AE=EC=2.所以BC====4,即BD====4.答案:416.三棱锥V ABC的底面是正三角形,顶点在底面ABC上的射影为正△ABC的中心,其三视图如图所示:(1)画出该三棱锥的直观图;(2)求出侧(左)视图的面积.解:(1)直观图如图所示.(2)根据三视图间的关系可得BC=2,作AM⊥BC于M,连结VM,过V作VO⊥AM于O,过O作EF∥BC交AB,AC于F、E,则△VEF即侧(左)视图.由=,得EF=.又VA=4,AM==3.则AO=2,VO===2.××2=4.所以S即侧(左)视图的面积为4.。
2017年高考数学人教版理科一轮复习课件第7章 立体几何 1 空间几何体的结构及其三视图和直观图

4.正棱柱、正棱锥的结构特征 23________ 24 (1)正棱柱:侧棱○ 垂直 于底面的棱柱叫做直棱柱,底面是○ 正多边形 25正多边形 ________的直棱柱叫做正棱柱。反之,正棱柱的底面是○ ________, 垂直 于底面,侧面是矩形。 26________ 侧棱○ (2)正棱锥:底面是正多边形,顶点在底面的射影是底面正多边形 的中心的棱锥叫做正棱锥。特别地,各棱均相等的正三棱锥叫正四面 体。
考纲要求 1.认识柱、锥、台、球及其简单组合体的结构特征,并能运用这 些特征描述现实生活中简单物体的结构。 2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简 易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二测 法画出它们的直观图。 3.会用平行投影方法画出简单空间图形的三视图与直观图,了解 空间图形的不同表示形式。
解析:根据正视图与俯视图,我们可以将选项 A、C 排除,根据 侧视图,可以将 D 排除,故选 B。 答案:B
1.空间几何体的结构特征 (1)多面体的结构特面 相似
(2)旋转体的结构特征: 几何体 旋转图形 旋转轴 任一边所在的直线 圆柱 矩形 ⑦______ 任一直角边所在的直线 圆锥 直角三角形 ⑧__________ ⑨________________ 垂直于底边的腰 圆台 直角梯形 所在的直线 直径 所在的直线 球 半圆 ⑩______
考情分析 1.本部分内容是高考中的重点考查内容,涉及到空间几何体的结 构特征、空间几何体的三视图与直观图等内容。 2.命题形式主要以选择题、填空题为主,主要考查空间几何体的 三视图的确认与应用,同时这类题目也重点考查了空间几何体的结构 特征,解题要求有较强的空间想象能力。
[小题热身] 1.思考辨析(正确的打“√”,错误的打“×”) (1)底面是正方形的四棱柱为正四棱柱。( × ) (2)有一个面是多边形,其余各面都是三角形的几何体是棱锥。 (× ) (3)夹在圆柱的两个平行截面间的几何体还是圆柱。( × ) (4)用斜二测画法画水平放置的∠A 时,若∠A 的的两边分别平行 于 x 轴和 y 轴,且∠A=90° ,则在直观图中,∠A=45° 。( × ) (5)正方体、球、圆锥各自的三视图中,三视图均相同。( × )
高考数学一轮复习 第七章 第1讲 空间几何体的结构特征及三视图和直观图课件 文
ppt精选
14
[做一做] 3.(2014·高考江西卷)一几何体的直观图如图,下列给出的 四个俯视图中正确的是( B )
ppt精选
15
解析:该几何体是组合体,上面的几何体是一个五面体, 下面是一个长方体,且五面体的一个面即为长方体的一个 面,五面体最上面的棱的两端点在底面的射影距左右两边 距离相等,因此选 B.
ppt精选
7
3.直观图 (1)画法:常用斜二测画法. (2)规则: ①原图形中x轴、y轴、z轴两两垂直,直观图 中,x′轴,y′ 轴的夹角为4_5°__(_或__1_3_5°__)____,z′轴与x′轴和y′轴 所在 平 面垂 直. ②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴. 平行于x轴和z轴的线段在直观变图为中原保来持的原一长半度不变,平行于 y轴的线段长度在直观图中_________________________.
ppt精选
3
知识点
第七章 立体几何
考纲下载
空间中的 以立体几何的定义、公理和定理为出发点,认识和 平行关系 理解空间中线面平行的判定定理与有关性质.
空间中的 以立体几何的定义、公理和定理为出发点,认识和 垂直关系 理解空间中线面垂直的判定定理与有关性质.
ppt精选
4
第七章 立体几何
第1讲 空间几何体的结构特征及三视图和直 观图
ppt精选
16
4.如图所示的直观图,其表示的平面图形是( D )
A.正三角形 C.钝角三角形
B.锐角三角形 D.直角三角形
ppt精选
17
考点一 考点二 考点三
空间几何体的结构特征 空间几何体的三视图(高频考点)
空间几何体的直观图
【创新课堂】高考数学总复习 专题07 第1节 空间几何体的结构及其三视图和直观图课件 文
()
A. ①② B. ②③ C. ①③ D. ②④
4. 如图,几何体的正视图和侧视图都正确的是 ( )
5. 如图是利用斜二测画法画出的△ABO的直观图,已知O′B′=4, A′B′∥y′轴,且△ABO的面积为16,过A′作A′C′⊥x′轴,则A′C′的 长为________.
答案:
1. C 解析:由棱柱定义可判断,最简单的棱柱为三棱柱,故C
答案:2 3 解析:由正视图和俯视图可知几何体是正方体切割后的一部分
(四棱锥C1ABCD),还原在正方体中,如图所示.
多面体最长的一条棱即为正方体的体对角线,
由正方体棱长AB=2知最长棱的长为2 3
9.若一个底面是正三角形的直三棱柱的正视图如图所示,
则其侧面积等于
()
A. 3
B.2
C.2 3
D.6
图1
图2
高考体验
(2012 高考浙江文 3)已知某三棱锥的三视图(单位:cm)如图 所示,则该三棱锥的体积是
A.1cm3 B.2cm3 C.3cm3 D.6cm3
【答案】C
【解析】由题意判断出,底面是一个直角三角形,两个直角
边分别为 1 和 2,整个棱锥的高由侧视图可得为 3,所以三棱
锥的体积为
1 3
3. D 解析:由母线的定义可知①、③错.
4. B 解析:注意实、虚线的区别.
5.2 2 解析:由题意知,在△ABO中,边OB上的高AB=16/4*2=8,
则在直观图中A′B′=4,∴A′C′=A′B′sin 45°=4*
2 2 2. 2
6.如图所示,矩形O′A′B′C′是水平放置的一个平面图形的直观 图,其中O′A′=6 cm,O′C′=2 cm,则原图形是 ( )
高考数学(理)一轮复习精品课件:专题《立体几何》
2.正棱柱与正棱 锥的结构特征 3.旋转体的 结构特征 4.三视图
考点42
空间几何体的结构、三视图
1.多面体的结构特征
2.正棱柱与正棱 锥的结构特征 3.旋转体的 结构特征 4.三视图
考点42
空间几何体的结构、三视图
定义:从一个几何体的正前方、正左方、正上方三个 不同的方向看这个几何体,描绘出的平面图形,分别 称为正(主)视图、侧(左)视图、俯视图.
2.外接球、内切 球的计算问题
在Rt△OO′M中,OM2=OO′2+O′M2,即R2=d2+
r2.
8
9
10
11
12
13Байду номын сангаас
14
考法2 空间几何体的三视图
1.识别三视 图的步骤
(1)弄清结构,明确位置 (2)先画正视图,再画俯视图,最后画侧视图 (3)被遮住的轮廓线要画成虚线
2.判断余下视图
1.计算有关 线段的长
当球内切于正方体时,切点为正方体各个 面的中心,正方体的棱长等于球的直径;
2.外接球、内切 球的计算问题
7
考法1
空间几何体的结构特征
球与旋转体的组合通常作轴截面解题. 球与多面体的组合,通过多面体的一条侧棱
1.计算有关 线段的长
和球心(或“切点”“接点”)作出截面图解题. 设球O的半径为R,截面圆O′的半径为r,M为截 面圆上任一点,球心O到截面圆O′的距离为d,则
专题8
第1 节
立体几何
空间几何体的三视图、表面积和体积
第2 节
质 第3 节
空间直线、平面平行与垂直的判定及其性
空间中的计算问题
1
考点42
空间几何体的结构、三视图
高三一轮复习第七讲 立体几何
第七讲立体几何1.三视图的定义光线从几何体的前面向后面正投影,得到的投影图叫做几何体的正视图(或主视图);光线从几何体的左面向右面正投影,得到的投影图叫做几何体的侧视图(左视图);光线从几何体的上面向下面正投影,得到的投影图叫做几何体的俯视图;正视图、侧视图、俯视图统称为三视图.2.三视图长度特征“长对正,宽相等,高平齐”,即正视图和俯视图长对正,侧视图和俯视图宽相等,正视图和侧视图高平齐.3.空间几何体的结构特征:(1)计算几何体中有关线段的长的常见思路:根据几何体的特征,利用一些常用定理与公式,结合题目的已知条件求解;(2)有关几何体的外接球、内切球的计算问题的常见思路:与球有关的组合体有两种:一种是外接,一种是内切,解题时要认真分析图形,明确切点和接点的位置,确定有关“元素”间的数量关系,并作出合适的截面图.如球内切于正方体各个面的中心正方体的棱长相等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线等于球的直径.(3)对于球与旋转体的组合,通常作它们的轴截面解题,对于球与多面体的组合,通过多面体的一条侧棱和球心作出截面图解题.例题1如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为()A. B.6 C. D.4例题2若空间中n个不同的点两两距离都相等,则正整数n的取值()A.至多等于3B.至多等于4C.等于5D.大于5例题3观察分析下表中的数据,猜想一般凸多面体中F V E ,,所满足的等式是__________.例题4如图,已知平面四边形3ABCD AB BC ==,,1CD =,AD =90ADC ∠=︒,沿直线AC 将ACD △翻折成ACD '△,直线AC 与BD '所成角的余弦的最大值是__________.如图,在长方体1111ABCD A B C D -中,111712AB AD AA ===,,.一质点从顶点A 射向点()4312E ,,,遇长方体的面反射(反射服从光的反射原理),将第1i -次到第i 次反射点之间的线段记为1(234)i l i l AE ==,,,,将线段1234l l l l ,,,竖直放置在同一水平线上,则大致的图形是( )练习在梯形ABCD 中,2ABC π∠=,222AD BC BC AD AB ===,∥ ,将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.23π B.43π C.2π D.53π如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为.O D E F,,为圆O上的点,DBC ECA FAB△△△,,分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC CA AB,,为折痕折起DBC ECA FAB△△△,,,使得D E F,,重合,得到三棱锥.当ABC△的边长变化时,所得三棱锥体积单位:3cm)的最大值为__________.例题7a b,为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a b,都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;②当直线AB与a成60°角时,AB与b成60°角;③直线AB与a所成角的最小值为45°;④直线AB与a所成角的最大值为60.其中正确的是__________.(填写所有正确结论的编号)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节空间几何体的结构及其三视图和直观图
【最新考纲】 1.认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.2.能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二测法画出它们的直观图.3.会用平行投影方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.
1.多面体的结构特征
(1)棱柱的侧棱都互相平行,上下底面是全等的多边形.
(2)棱锥的底面是任意多边形,侧面是有一个公共顶点的三角形.
(3)棱台可由平行于底面的平面截棱锥得到,其上下底面是相似多边形.
2.旋转体的形成
直角三角形
(1)三视图的名称
几何体的三视图包括:正视图、侧视图、俯视图.
(2)三视图的画法
①在画三视图时,重叠的线只画一条,挡住的线要画成虚线.
②三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体的正投影图.
4.空间几何体的直观图
空间几何体的直观图常用斜二测画法来画,其规则是
(1)原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴,y′轴的夹角为45°或135°,z′轴与x′轴和y′轴所在平面垂直.
(2)原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴;平行于x轴和z轴的线段在直观图中保持原长度不变;平行于y轴的线段在直观图中长度为原来的一半.
1.(质疑夯基)判断下列结论的正误.(正确的打“√”,错误的打“×”)
(1)有两个面平行,其余各面都是平行四边形的几何体是棱柱.( )
(2)有一个面是多边形,其余各面都是三角形的几何体是棱锥.( )
(3)用斜二测画法画水平放置的∠A时,若∠A的两边分别平行于x轴和y轴,且∠A=90°,则在直观图中,∠A=45°.( )
(4)正方体、球、圆锥各自的三视图中,三视图均相同.( )
答案:(1)×(2)×(3)×(4)×
2.如图,长方体ABCD A′B′C′D′中被截去一部分,其中EH∥A′D′.剩下的几何体是( )
A.棱台
B.四棱柱
C.五棱柱
D.简单组合体
解析:由几何体的结构特征,剩下的几何体为五棱柱.
答案:C
3.(2016·邯郸调研)一几何体的直观图如图所示,下列给出的四个俯视图中正确的是( )
解析:由于组合体的上部分(五面体)与下部分(长方体)有相同的底面,则几何体在下底面的投影为图形B.
答案:B
4.(2015·课标全国Ⅱ卷)一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )
A.18
B.17
C.16
D.15
解析:如图所示,由条件知,截去部分是正三棱锥D
ABC.
设正方体的棱长为a ,则V D
ABC =a 3
6
,
因此剩余部分的体积V 剩=56a 3
,
故它们的体积之比为1
5.
答案:D
5.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于________.
解析:由题意得圆柱的底面半径r =1,母线l =1. 所以圆柱的侧面积S =2πrl =2π. 答案:2π
一种思想
棱台和圆台是分别用平行于棱锥和圆锥的底面的平面截棱锥和圆锥后得到的,所以在解决棱台和圆台的相关问题时,常“还台为锥”,体现了转化的数学思想.
两点注意
1.注意空间几何体的不同放置对三视图的影响. 2.画直观图注意平行性、长度两个要素.
(1)平行性不变;(2)平行于y 轴的线段长度减半,平行于x 轴、z 轴的线段长度不变. 三条规则——画三视图应遵循的三条规则 1.画法规则:“长对正,宽相等,高平齐”.
2.摆放规则:侧视图在正视图的右侧,俯视图在正视图的正下方.
3.实虚线的画法规则:可见轮廓线和棱用实线画出,不可见线和棱用虚线画出.
一、选择题
1.(2014·福建卷)某空间几何体的正视图是三角形,则该几何体不可能是( ) A .圆柱 B .圆锥 C .四面体 D .三棱柱
解析:由三视图知识知圆锥、四面体、三棱柱(放倒看)都能使其正视图为三角形,而圆柱的正视图不可能为三角形.
答案:A
3.已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为2的矩形,则该正方体的正视图的面积等于( )
A.
32 B .1 C.2+1
2
D. 2 解析:由于该正方体的俯视图是面积为1的正方形,侧视图是一个面积为2的矩形,因此该几何体的正视图是一个长为2,宽为1的矩形,其面积为 2.
答案:D
4.(2014·北京卷)在空间直角坐标系O xyz 中,已知A(2,0,0),B(2,2,0),C(0,
2,0),D(1,1,2).若S 1,S 2,S 3分别是三棱锥D ABC 在xOy ,yOz ,zOx 坐标平面上的
正投影图形的面积,则( )
A .S 1=S 2=S 3
B .S 2=S 1且S 2≠S 3
C .S 3=S 1且S 3≠S 2
D .S 3=S 2且S 3≠S 1
解析:如右图所示。
根据题目条件,在空间直角坐标系O xyz
中作出该三棱锥D ABC ,显然S 1=S △ABC =12×2×2=2,S 2=S 3=1
2
×2×2= 2.
答案:D
二、填空题
7.某几何体的正视图和侧视图均为图甲所示,则在图乙的四个图中可以作为该几何体
的俯视图的是________.(填上所有正确的序号)
图甲
图乙
解析:若图(2)是俯视图,则正视图和侧视图中矩形的竖边延长线有一条和圆相切,故图(2)不合要求;若图(4)是俯视图,则正视图和侧视图不相同,故图(4)不合要求.显然图(1),(3)可作为几何体的俯视图.
答案:(1)(3)
8.如图所示,在正方体ABCD A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P ABC的正视图与侧视图的面积的比值为________.
解析:三棱锥P ABC的正视图与侧视图为底边和高均相等的三角形,故它们的面积相等,面积比值为1.
答案:1
9.已知等腰梯形ABCD,上底CD=1,腰AD=CB=2,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为________.
解析:如图所示:
因为OE =(2)2
-1=1,所以O′E′=12,E ′F =24,
则直观图A′B′C′D′的面积S′=1+32×24=2
2.
答案:
2
2
10.某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为________.
解析:由题中三视图可知,三棱锥的直观图如图所示,其中PA⊥
平面ABC ,M 为AC 的中点,且BM⊥AC. 故该三棱锥的最长棱为PC. 在Rt △PAC 中,
PC =PA 2
+AC 2
=22
+22
=2 2. 答案:2 2。
