中考数学复习指导;如何构造特殊四边形解决相关计算证明问题
中考数学专题复习题型七 特殊四边形课件

例 1 (2018· 张家界 )在矩形 ABCD 中,点 E 在 BC 上,AE=AD,DF⊥AE, 垂足为点 F. (1)求证:DF=AB; (2)若∠FDC=30° ,且 AB=4,求 AD.
【分析】(1)利用“AAS”证△ADF≌△EAB 即可; (2)由直角三角形和矩形的性质可得∠FDC=∠DAF=30° ,AD=2DF,根 据(1)中结论可求得 AD 的长.
3. (兰州模拟)如图,菱形 ABCD 的对角线 AC、BD 相交于点 O,过点 D 作 1 DE∥AC 且 DE= AC,连接 AE 交 OD 于点 F,连接 CE、OE. 2 (1)求证:OE=CD; (2)若菱形 ABCD 的边长为 2,∠ABC=60° ,求 AE 的长. (1)证明:∵四边形 ABCD 是菱形, 1 ∴OA=OC= AC,AD=CD, 2 1 ∵DE∥AC 且 DE= AC,∴DE=OA=OC, 2 ∴四边形 OADE、 四边形 OCED 都是平行四边形, ∴OE=AD, ∴OE=CD; (2)解:∵AC⊥BD,∴四边形 OCED 是矩形,∵在菱形 ABCD 中,∠ABC =60° ,∴AC=AB=2,∴在矩形 OCED 中,CE=OD= = 3. ∴在 Rt△ACE 中,AE= = 7.
【分析】(1)根据平行四边形的性质及△AGF≌△DGC 分别证明 AB=CD, AF=CD 即可; (2)结论:四边形 ACDF 是矩形.先证明△AFG 是等边三角形,再证明四 边形 ACDDF 是矩形.
(1)证明:∵四边形 ABCD 是平行四边形, ∴AF∥CD,AB=CD,∴∠FAG=∠CDG. ∵点 G 为 AD 的中点,∴GA=GD. 又∵∠AGF=∠DGC,∴△AGF≌△DGC(ASA),∴AF=CD. 又∵AB=CD,∴AB=AF; (2)解:四边形 ACDF 是矩形.证明如下: ∵四边形 ABCD 是平行四边形,∴∠BAD=∠BCD=120° , ∴∠FAG=60° .由(1)得 AB=AF,∴AB=AG=AF, ∴△AFG 是等边三角形,∴AG=GF.∵AF=CD,AF∥CD, ∴四边形 ACDF 是平行四边形, ∵AD=2AG,CF=2FG,∴AD=CF,∴四边形 ACDF 是矩形.
中考数学考点复习 类型五 特殊四边形存在性问题 课件(共33张PPT)

第2题图
类型五 特殊四边形存在性问题 3.如图,在平面直角坐标系中,点A(-1,0),M(1,4),直线AM交y轴 于点N.点P是y轴上一动点,点Q是平面内任意一点,若以A、P、M、Q 为顶点的四边形是矩形,求点Q的坐标.
第3题图
类型五 特殊四边形存在性问题
解:①当 AM 为矩形的对角线时,如解图①, ∵A(-1,0),M(1,4), ∴AM 的中点坐标为(0,2), 易知点 N 为 AM 的中点,则 N(0,2), ∴MN= (1-0)2+(4-2)2= 5. ∴NQ1=NQ2= 5, ∴Q1(0,2+ 5),Q2(0,2- 5);
图⑤
图⑥
类型五 特殊四边形存在性问题 满分技法
②AB 为对角线时:如图⑦,作 AB 的垂直平分线;
图⑦
类型五 特殊四边形存在性问题 满分技法
(4)求作正方形 ①AB 为边时:如图⑧,过点 A,B 分别作垂直于 AB 的直线;
图⑧
类型五 特殊四边形存在性问题
当 AB 为平行四边形的对角线时,如解图②,
y
则4-1=xP3+0,2-3=0+yQ3,
2
2
2
2
A
∴xP3=3,yQ3=-1,即 P3(3,0),Q3(0,-1).
QO3
P3 x
综上所述,点 P 的坐标为(-5,0)或(5,0)或(3,0),
B 对应的点 Q 的坐标为(0,5)或(0,-5)或(0,-1).
P1
P2
P3
第1题图
类型五 特殊四边形存在性问题 2.如图,在平面直角坐标系中,已知点A(4,2),B(-1,-3),P是x轴 上的一点,Q是y轴上的一点.若以点A,B,P,Q四点为顶点的四边形 是平行四边形,求点P和点Q的坐标.
中考总复习:特殊的四边形--知识讲解(基础)
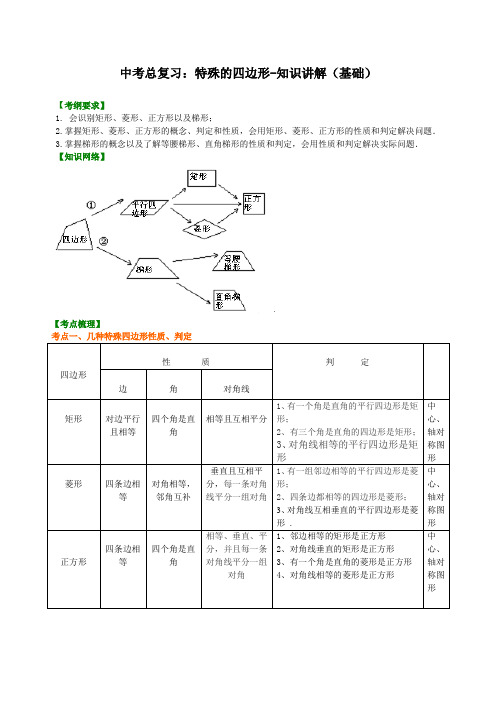
中考总复习:特殊的四边形-知识讲解(基础)【考纲要求】1. 会识别矩形、菱形、正方形以及梯形;2.掌握矩形、菱形、正方形的概念、判定和性质,会用矩形、菱形、正方形的性质和判定解决问题.3.掌握梯形的概念以及了解等腰梯形、直角梯形的性质和判定,会用性质和判定解决实际问题.【知识网络】【考点梳理】考点一、几种特殊四边形性质、判定四边形性质判定边角对角线矩形对边平行且相等四个角是直角相等且互相平分1、有一个角是直角的平行四边形是矩形;2、有三个角是直角的四边形是矩形;3、对角线相等的平行四边形是矩形中心、轴对称图形菱形四条边相等对角相等,邻角互补垂直且互相平分,每一条对角线平分一组对角1、有一组邻边相等的平行四边形是菱形;2、四条边都相等的四边形是菱形;3、对角线互相垂直的平行四边形是菱形.中心、轴对称图形正方形四条边相等四个角是直角相等、垂直、平分,并且每一条对角线平分一组对角1、邻边相等的矩形是正方形2、对角线垂直的矩形是正方形3、有一个角是直角的菱形是正方形4、对角线相等的菱形是正方形中心、轴对称图形等腰梯形两底平行,两腰相等同一底上的两个角相等相等1、两腰相等的梯形是等腰梯形;2、在同一底上的两个角相等的梯形是等腰梯形;3、对角线相等的梯形是等腰梯形.轴对称图形【要点诠释】矩形、菱形、正方形都是特殊的平行四边形,它们具有平行四边形的一切性质.考点二、梯形1.解决梯形问题常用的方法:(1)“平移腰”:把梯形分成一个平行四边形和一个三角形(图1);(2)“作高”:使两腰在两个直角三角形中(图2);(3)“平移对角线”:使两条对角线在同一个三角形中(图3);(4)“延腰”:构造具有公共角的两个三角形(图4);(5)“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形(图5).图1 图2 图3 图4 图5【要点诠释】解决梯形问题的基本思想和方法就是通过添加适当的辅助线,把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决.在学习时注意它们的作用,掌握这些辅助线的使用对于学好梯形内容很有帮助.2.特殊的梯形1)等腰梯形:两腰相等的梯形叫做等腰梯形.性质:(1)等腰梯形的同一底边上的两个角相等;等腰梯形的两条对角线相等.(2)同一底边上的两个角相等的梯形是等腰梯形.(3)等腰梯形是轴对称图形,它的对称轴是经过两底中点的一条直线.2)直角梯形:有一个角是直角的梯形叫做直角梯形.考点三、中点四边形相关问题1.中点四边形的概念:把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.2.若中点四边形为矩形,则原四边形满足条件对角线互相垂直;若中点四边形为菱形,则原四边形满足条件对角线相等;若中点四边形为正方形,则原四边形满足条件对角线互相垂直且相等.【要点诠释】中点四边形的形状由原四边形的对角线的位置和数量关系决定.【典型例题】类型一、特殊的平行四边形的应用【高清课堂:多边形与特殊平行四边形例2】1. 在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.(1)如图①,试判断四边形EGFH的形状,并说明理由;(2)如图②,当EF⊥GH时,四边形EGFH的形状是;(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是;(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.【思路点拨】中点四边形的形状由原四边形的对角线的位置和数量关系决定.【答案与解析】(1)四边形EGFH是平行四边形;证明:∵平行四边形ABCD的对角线AC、BD交于点O,∴点O是平行四边形ABCD的对称中心;∴EO=FO,GO=HO;∴四边形EGFH是平行四边形;(2)菱形;(提示:菱形的对角线垂直平分)(3)菱形;(提示:当AC=BD时,对四边形EGFH的形状不会产生影响,故结论同(2))(4)四边形EGFH是正方形;证明:∵AC=BD,∴平行四边形ABCD是矩形;又∵AC⊥BD,∴平行四边形ABCD是正方形,∴∠BOC=90°,∠GBO=∠FCO=45°,OB=OC;∵EF⊥GH,∴∠GOF=90°;∴∠BOG=∠COF;∴△BOG≌△COF(ASA);∴OG=OF,∴GH=EF;由(3)知四边形EGFH是菱形,又EF=GH,∴四边形EGFH是正方形.【总结升华】主要考查了平行四边形、菱形、矩形、正方形的判定和性质以及全等三角形的判定和性质;熟练掌握各特殊四边形的联系和区别是解答此类题目的关键.2.动手操作:在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小明同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).(1)你能说出小颖、小明所折出的菱形的理由吗?(2)请你通过计算,比较小颖和小明同学的折法中,哪种菱形面积较大?【思路点拨】(1)、要证所折图形是菱形,只需证四边相等即可.(2)、按照图形用面积公式计算S=30和S=35.21,可知方案二小明同学所折的菱形面积较大. 【答案与解析】(1)小颖的理由:依次连接矩形各边的中点所得到的四边形是菱形, 小明的理由:∵ABCD 是矩形, ∴AD ∥BC ,则∠DAC=∠ACB ,又∵∠CAE=∠CAD ,∠ACF=∠ACB , ∴∠CAE=∠CAD=∠ACF=∠ACB , ∴AE=EC=CF=FA ,∴四边形AECF 是菱形. (2)方案一:S 菱形=S 矩形-4S △AEH =12×5-4×12×6×52=30(cm )2, 方案二:设BE=x ,则CE=12-x ,∴AE=22BE AB +=225x +由AECF 是菱形,则AE 2=CE 2∴x 2+25=(12-x )2, ∴x=11924, S 菱形=S 矩形-2S △ABE =12×5-2×12×5×11924≈35.21(cm )2,比较可知,方案二小明同学所折的菱形面积较大.【总结升华】本题考查了矩形的性质和菱形的判定,以及图形面积的计算与比较. 举一反三:【高清课堂: 多边形与特殊平行四边形 例6】【变式】如图,点O 是矩形ABCD 的中心,E 是AB 上的点,沿CE 折叠后,点B 恰好与点O 重合,若BC=3,则折痕CE 的长为 ( ).A.B .C.4 D .5【答案】A.类型二、梯形的应用3.(2014•黄州区校级模拟)如图,△ABC中,∠BAC=90°,延长BA至D,使AD=AB,点E、F分别是边BC、AC的中点.(1)判断四边形DBEF的形状并证明;(2)过点A作AG∥BC交DF于G,求证:AG=DG.【思路点拨】(1)利用梯形的判定首先得出四边形DBEF为梯形,进而得出四边形HFEB是平行四边形,得出BE=FD进而得出答案;(2)利用四边形DBEF为等腰梯形,得出∠B=∠D,利用AG∥BG,∠B=∠DAG,得出答案.【答案与解析】(1)解:四边形DBEF为等腰梯形,理由如下:如图,过点F作FH∥BC,交AB于点H,∵FH∥BC,点F是AC的中点,点E是BC的中点,∴AH=BH=AB,EF∥AB,显然EF<AB<AD,∴EF≠AD,∴四边形DBEF为梯形,∵AD=AB,∴AD=AH,∵CA⊥AB,∴CA是DH的中垂线,∴DF=FH,∵FH∥BC,EF∥AB,∴四边形HFEB是平行四边形,∴FH=BE,∴BE=FD,故四边形DBEF为等腰梯形;(2)证明:∵四边形DBEF为等腰梯形,∴∠B=∠D,∵AG∥BG,∠B=∠DAG,∴∠D=∠DAG,∴AG=DG.【总结升华】此题主要考查了等腰梯形的判定以及其性质和平行四边形的判定与性质等知识,得出BE=FD 是解题关键.举一反三:【变式】如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,则CE的长为().C. 2.5D.2.3A.22B. 231【答案】D.类型三、特殊四边形与其他知识结合的综合运用4. (2015•北京)在▱ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.【思路点拨】(1)根据平行四边形的性质,可得AB与CD的关系,根据平行四边形的判定,可得BFDE是平行四边形,再根据矩形的判定,可得答案;(2)根据平行线的性质,可得∠DFA=∠FAB,根据等腰三角形的判定与性质,可得∠DAF=∠DFA,根据角平分线的判定,可得答案.【答案与解析】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.∵BE∥DF,BE=DF,∴四边形BFDE是平行四边形.∵DE⊥AB,∴∠DEB=90°,∴四边形BFDE是矩形;(2)解:∵四边形ABCD是平行四边形,∴AB∥DC,∴∠DFA=∠FAB.在Rt△BCF中,由勾股定理,得BC===5,∴AD=BC=DF=5,∴∠DAF=∠DFA,∴∠DAF=∠FAB,即AF平分∠DAB.【总结升华】本题考查了平行四边形的性质,利用了平行四边形的性质,矩形的判定,等腰三角形的判定与性质,利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键.5.已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.(1)若CE=1,求BC的长;(2)求证:AM=DF+ME.【思路点拨】(1)根据菱形的对边平行可得AB∥CD,再根据两直线平行,内错角相等可得∠1=∠ACD,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM,再根据等腰三角形三线合一的性质可得CE=DE,然后求出CD的长度,即为菱形的边长BC的长度;(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G,然后证明∠1=∠G,根据等角对等边的性质可得AM=GM,再利用“角角边”证明△CDF和△BGF 全等,根据全等三角形对应边相等可得GF=DF,最后结合图形GM=GF+MF即可得证.【答案与解析】(1)解:∵四边形ABCD是菱形,∴AB∥CD,∴∠1=∠ACD,∵∠1=∠2,∴∠ACD=∠2,∴MC=MD,∵ME⊥CD,∴CD=2CE,∵CE=1,∴CD=2,∴BC=CD=2;(2)证明:如图,∵F为边BC的中点,∴BF=CF=12 BC,∴CF=CE,在菱形ABCD中,AC平分∠BCD,∴∠ACB=∠ACD,在△CEM和△CFM中,∵CE CFACB ACD CM CM=⎧⎪∠=∠⎨⎪=⎩,∴△CEM≌△CFM(SAS),∴ME=MF,延长AB交DF于点G,∵AB∥CD,∴∠G=∠2,∵∠1=∠2,∴∠1=∠G,∴AM=MG,在△CDF和△BGF中,∵2GBFG CFD BF CF∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△CDF≌△BGF(AAS),∴GF=DF,由图形可知,GM=GF+MF,∴AM=DF+ME.【总结升华】本题考查了菱形的性质,全等三角形的判定与性质,等角对等边的性质,作出辅助线构造出全等三角形是解题的关键.6 . 如图,己知ABC的顶点B、C为定点,A为动点(不在直线BC上).是点B关于直线AC的对称点,是点C关于直线AB的对称点.连结、、、.(1)猜想线段与'的数量关系,并证明你的结论;(2)当点A运动到怎样的位置时,四边形为菱形?这样的位置有几个?请用语言对这样的位置进行描述;(不用证明)(3)当点A在线段BC的垂直平分线l(BC的中点及到BC的距离为的点除外)上运动时,判断以点B、C、、为顶点的四边形的形状,画出相应的示意图.(不用证明)【思路点拨】本题考查轴对称的基本性质,综合考查菱形、正方形、等腰梯形的判定.在运动变化过程中,认识图形之间的内在联系.【答案与解析】(1)猜想:BC′=CB′∵B′是点B关于直线AC的对称点∴AC垂直平分B B′∴BC= CB′同理BC= BC′∴B C′=C B′(2)要使BCB′C′是菱形,根据菱形的性质,对角线互相垂直平分∵B′是点B关于直线AC的对称点,C′是点C关于直线AB的对称点∴AC垂直平分B B′,AB垂直平分C C′,∴B B′、C C′应该同时过A点∴∠BAC=90°∴只要AB⊥AC即可满足要求,这样的位置有无数个.(3)如图,当A是BC的中点时,没有形成四边形;当A到BC的距离为36BC时,∵l是BC的垂直平分线,∴∠ACB=∠ABC=30°,∴∠BAC=120°,∴∠BOC=60°,∴BC=C B′= B′C′=B C′. ∴BC B′C′为菱形,当BC的中点及到BC的距离为36BC的点除外时,∵∠BOC= B′O C′,OB=OC O B′=O C′, ∴∠OBC=∠OCB=∠O B′C′=∠O C′B′, ∴BC∥B′C′.∵B C′不平行C B′,B C′=C B′,四边形BC B′ C′为等腰梯形.【总结升华】本题可以很好的培养观察推理能力,按照要求画出图形可以更清楚的解题.举一反三:【变式】(2012•襄阳)如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED=2,AC与ED相交于点F.(1)求证:梯形ABCD是等腰梯形;(2)当AB与AC具有什么位置关系时,四边形AECD是菱形?请说明理由,并求出此时菱形AECD的面积.【答案】(1)证明:∵AD∥BC,∴∠DEC=∠EDA,∠BEA=∠EAD,又∵EA=ED,∴∠EAD=∠EDA,∴∠DEC=∠AEB,又∵EB=EC,∴△DEC≌△AEB,∴AB=CD,∴梯形ABCD是等腰梯形.(2)当AB⊥AC时,四边形AECD是菱形.证明:∵AD∥BC,BE=EC=AD,∴四边形ABED和四边形AECD均为平行四边形.∴AB=ED,∵AB⊥AC,∴AE=BE=EC,∴四边形AECD是菱形.过A作AG⊥BE于点G,∵AE=BE=AB=2,∴△ABE是等边三角形,∴∠AEB=60°,∴AG=3,∴S菱形AECD=EC•AG=2×3=23.。
2025年中考数学总复习专题16 特殊的平行四边形(附答案解析)

2025年中考数学总复习专题16
特殊的平行四边形
一、矩形的性质与判定
1.矩形的性质:
1)四个角都是直角;2)对角线相等且互相平分;3)面积=长×宽=2S△ABD=4S△AOB
.(如图)
2.矩形的判定:
1)定义法:有一个角是直角的平行四边形;2)有三个角是直角;3)对角线相等的平行四边形.
二、菱形的性质与判定
1.菱形的性质:
1)四边相等;2)对角线互相垂直、平分,一条对角线平分一组对角;3)面积=底×高=对角线乘积的一半.2.菱形的判定:
1)定义法:有一组邻边相等的平行四边形;2)对角线互相垂直的平行四边形;3)四条边都相等的四边形.三、正方形的性质与判定
1.正方形的性质:
1)四条边都相等,四个角都是直角;2)对角线相等且互相垂直平分;3)面积=边长×边长=2S△ABD=4S△AOB.2.正方形的判定:
1)定义法:有一个角是直角,且有一组邻边相等的平行四边形;2)一组邻边相等的矩形;
3)一个角是直角的菱形;4)对角线相等且互相垂直、平分.
四、联系
第1页(共36页)。
中考数学复习方案 题型突破(03)三角形、四边形的有关计算与证明课件

图Z3-3
解:(3)证明:(方法一)如图②,延长BM交CF于点D,连接BE,DE.
∵∠BCE=45°,∴∠BCF=∠BCE+∠ECF=45°+45°=90°.
∵∠ABC=90°,∴∠ABC=∠BCF,
∴AB∥CF,∴∠1=∠2,∠ABM=∠FDM.
又∵AM=FM,∴△ABM≌△FDM,
∴AB=DF,∴BC=DF.
∵F 为 BC 的中点,DB=DC,∴DF 垂直平分线段 BC,∴BG=CG.
∵BE⊥AC,∴∠AEB=∠CEB.
∠ = ∠,
在△ABE 和△CBE 中, = ,
∠ = ∠,
∴△ABE≌△CBE,∴EC=EA.
在 Rt△CGE 中,由勾股定理,得 CG2-GE2=EC2.
(3)若 AG=6,EG=2 5,求 BE 的长.
图Z3-6
解:(1)证明:由折叠知,
∠EFA=∠DFA,EG=GD,EF=DF.
∵EG∥DC,∴∠DFA=∠EGF,
∴∠EFA=∠EGF,
∴EF=EG,∴EF=EG=FD=GD.
∴四边形EFDG是菱形.
3.如图 Z3-6,将矩形 ABCD 沿 AF 折叠,使点 D 落在 BC 边上的点 E 处,过点 E 作
∴AM=10 10.
1.[2019·绍兴]如图Z3-1①是实验室中的一种摆动装置,BC在地面上,支架ABC是
底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,
AD=30,DM=10.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,
连接D1D2,如图Z3-1②,此时∠AD2C=135°,CD2=60,求BD2的长.
中考数学“特殊四边形的存在性问题”题型解析

中考数学“特殊四边形的存在性问题”题型解析由抛物线上的点构成特殊四边形的问题,需要根据特殊四边形的性质与判定去确定点的坐标,然后求解 . 具体而言,解该类题时,我们要根据题目中的条件,科学地进行分类,然后画出图形,再根据这个四边形的性质或判定求出这点的坐标,若这一点是根据特殊四边形的特性得到的坐标,我们还应将这一点代入到抛物线的解析式中去验证是否是抛物线上的点 .本节主要来讨论下特殊四边形:平行四边形、菱形、矩形的存在性问题 .类型一:平行四边形问题【例题1】如图,抛物线y = 1/2 x^2 + bx + c 经过点A(-1,0)和点B(3,0),同时交y 轴于点C .(1)求抛物线的解析式;(2)若点Q 在y 轴上,点P 在抛物线上,且以A , B , Q , P 为顶点的四边形是平行四边形,求满足条件的点P 的坐标 .【分析】(1)根据抛物线经过A , B 两点即可求得b , c 的值,可解题;(2)以A , B , Q , P 为顶点的四边形是平行四边形,则点P 横坐标为4 或- 4,将x = 4 或- 4 代入抛物线解析式即可求得y 的值,即可解题 .【解析】(1)把A(-1,0),B(3,0)代入y = 1/2 x^2 + bx + c 中,∴抛物线的解析式是y = 1/2 x^2 - x - 3/2 .(2)①当AB 为边时,只要PQ∥AB 且PQ = AB = 4 即可 .又知点Q 在y 轴上,∴点P 的横坐标为4 或- 4 ,这时符合条件的点P 有两个,分别记为P1 , P2,把x = 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 5/2 ,把x = - 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 21/2 ,此时P1(4 , 5/2),P2(- 4 , 21/2);②当AB 为对角线时,只要线段PQ 与线段AB 互相平分即可 .又知点Q 在y 轴上,且线段AB 中点的横坐标为1,∴点P 的横坐标为2,这时符合条件的P 只有一个记为P3 ,而且当x = 2 时,y = - 3/2 ,此时P3(2,- 3/2),综上,满足条件的P 为P1(4 , 5/2),P2(- 4 , 21/2),P3(2,-3/2).类型二:菱形问题【例题2】如图,在平面直角坐标系中,点O 为坐标原点,直线y = -x + b 与坐标轴交于C,D 两点,直线AB 与坐标轴交于A , B 两点,线段OA , OC 的长是方程x^2 - 3x + 2 = 0 的两个根(OA > OC).(1)求点A , C 的坐标;(2)直线AB 与直线CD 交于点E,若点E 是线段AB 的中点,反比例函数y = k/x (k ≠0 )的图象的一个分支经过点E,求k 的值;(3)在(2)的条件下,点M 在直线CD 上,坐标平面内是否存在点N,使以点B , E , M , N 为顶点的四边形是菱形?若存在,请直接写出满足条件的点N 的坐标;若不存在,请说明理由 .【分析】(1)利用分解因式法解一元二次方程x^2 - 3x + 2 = 0 即可得出OA , OC 的值,再根据点所在的位置即可得出A , C 的坐标;(2)根据点C 的坐标利用待定系数法即可求出直线CD 的解析式,根据点A , B 的横坐标结合点E 为线段AB 的中点即可得出点E 的横坐标,将其代入直线CD 的解析式中即可求出点E 的坐标,再利用待定系数法即可求出k 的值;(3)假设存在,设点M 的坐标为(m , - m + 1), 分别以BE 为边、BE 为对角线来考虑 .根据菱形的性质找出关于m 的方程,解方程即可得出点M 的坐标,再结合点B , E 的坐标即可得出点N 的坐标 .【解析】(1)x^2 - 3x + 2 = (x - 1)(x - 2)= 0 ,∴x1 = 1 , x2 = 2 ,∵OA > OC ,∴OA = 2 , OC = 1 ,∴A(-2,0),C(1,0);(2)将C(1,0)代入y = - x + b 中,得0 = - 1 + b , 解得b = 1 ,∴直线CD 的解析式为y = - x + 1 .∵点E 为线段AB 的中点,A(-2,0),B 的横坐标为0 ,∴点E 的横坐标为- 1 .∵点E 为直线CD 上一点,∴E(-1,2).将点E(-1,2)代入y = k/x (k ≠0 )中,得2 = k / -1 , 解得k = -2 ;(3)假设存在,设点M 的坐标为(m , - m + 1),以点B , E , M , N 为顶点的四边形是菱形分两种情况(如上图所示)类型三:矩形问题【例题3】【解题策略】这三道例题分别呈现了运动变化过程中的平行四边形、菱形、矩形的存在性问题,三道例题的思路都是要依据特殊四边形的性质构图并建立方程求点的坐标 .特别地,由于菱形任意三个顶点组成的三角形都是等腰三角形,因此可将菱形问题转化为等腰三角形的存在性问题;而矩形问题则可转化为直角三角形的问题,要注意体会相关知识之间的联系 .。
中考总复习:特殊的四边形--知识讲解(提高)
中考总复习:特殊的四边形—知识讲解(提高)【考纲要求】1. 会识别矩形、菱形、正方形以及梯形;2.掌握矩形、菱形、正方形的概念、判定和性质,会用矩形、菱形、正方形的性质和判定解决问题.3.掌握梯形的概念以及了解等腰梯形、直角梯形的性质和判定,会用性质和判定解决实际问题.【知识网络】【考点梳理】考点二、中点四边形相关问题1. 中点四边形的概念:把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形.2. 若中点四边形为矩形,则原四边形满足条件对角线互相垂直;若中点四边形为菱形,则原四边形满足条件对角线相等;若中点四边形为正方形,则原四边形满足条件对角线互相垂直且相等. 【要点诠释】中点四边形的形状由原四边形的对角线的位置和数量关系决定. 考点三、重心1.线段的中点是线段的重心;三角形三条中线相交于一点,这个交点叫做三角形的重心;三角形的重心与顶点的距离等于它与对边中点的距离的2倍.平行四边形对角线的交点是平行四边形的重心。
【典型例题】类型一、特殊的平行四边形的应用1.(湛江)如图,设四边形ABCD 是边长为1的正方形,以对角线AC 为边作第二个正方形ACEF 、再以对角线AE 为边作笫三个正方形AEGH ,如此下去….若正方形ABCD 的边长记为a 1,按上述方法所作的正方形的边长依次为a 2,a 3,a 4,…,a n ,则a n =___________.【思路点拨】求a 2的长即AC 的长,根据直角△ABC 中AB 2+BC 2=AC 2可以计算,同理计算a 3、a 4.由表达式.【解析】∵a 2=AC ,且在直角△ABC 中,AB 2+BC 2=AC 2,【总结升华】考查了正方形的性质,以及勾股定理在直角三角形中的运用,考查了学生找规律的能力,本题中找到a n 的规律是解题的关键. 举一反三:【高清课堂: 多边形与特殊平行四边形 例4】 【变式】(德州)长为1,宽为a 的矩形纸片(121<<a ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n 此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a 的值为________.【答案】5或4. 2.(2015秋•宝安区校级期中)如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,AC=6,BD=8,点P 是AC 延长线上的一个动点,过点P 作PE⊥AD,垂足为E ,作CD 延长线的垂线,垂足为E ,则|PE ﹣PF|= .【思路点拨】延长BC 交PE 于G ,由菱形的性质得出AD ∥BC ,OA=OC=AC=3,OB=OD=BD=4,AC ⊥BD ,∠ACB=∠ACD ,由勾股定理求出AD ,由对顶角相等得出∠PCF=∠PCG ,由菱形的面积的两种计算方法求出EG ,由角平分线的性质定理得出PG=PF ,得出PE ﹣PF=PE ﹣PG=EG 即可. 【答案】4.8.【解析】解:延长BC 交PE 于G ,如图所示: ∵四边形ABCD 是菱形,∴AD ∥BC ,OA=OC=AC=3,OB=OD=BD=4,AC ⊥BD ,∠ACB=∠ACD , ∴AD==5,∠PCF=∠PCG ,∵菱形的面积=AD •EG=AC •BD=×6×8=24, ∴EG=4.8, ∵PE ⊥AD , ∴PE ⊥BG , ∵PF ⊥DF , ∴PG=PF ,∴PE ﹣PF=PE ﹣PG=EG=4.8. 故答案为:4.8.【总结升华】本题考查了菱形的性质、勾股定理、角平分线的性质定理、菱形面积的计算等知识;本题综合性强,有一定难度,通过作辅助线证出PG=PF是解决问题的关键.类型二、梯形的应用3.(资阳)如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC 上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.(1)若点F与B重合,求CE的长;(2)若点F在线段AB上,且AF=CE,求CE的长;(3)设CE=x,BF=y,写出y关于x的函数关系式(直接写出结果可).【思路点拨】(1)先证明四边形ABED为矩形,CE=BC-AD,继而即可求出答案;(2)设AF=CE=x,则HE=x-3,BF=7-x,再通过证明△BEF∽△HDE,根据对应边成比例,然后代入求解即可;(3)综合(1)(2)两种情况,然后代入求出解析式即可.【答案与解析】(1)∵F与B重合,且EF⊥DE,∴DE⊥BC,∵AD∥BC,∠B=90°,∴∠A=∠B=90°,∴四边形ABED为矩形,∴BE=AD=9,∴CE=12-9=3.(2)作DH⊥BC于H,则DH=AB=7,CH=3.设AF=CE=x,∵F在线段AB上,∴点E在线段BH上,CH=3,CE=x,∴HE=x-3,BF=7-x,∵∠BEF+90°+∠HED=180°,∠HDE+90°+∠HED=180°,∴∠BEF=∠HDE,又∵∠B=∠DHE=90°,∴△BEF∽△HDE是一道小的综合题,注意对这些知识的熟练掌握并灵活应用.举一反三:【变式】(台湾)如图为菱形ABCD与正方形EFGH的重迭情形,其中E在CD上,AD与GH相交于I 点,且AD∥HE.若∠A=60°,且AB=7,DE=4,HE=5,则梯形HEDI的面积为().A.B.C.10-D.10+【答案】B.类型三、特殊四边形与其他知识结合的综合运用【高清课堂:多边形与特殊平行四边形例7】4.(莒南县期末)正方形ABCD边长为2,点E在对角线AC上,连接DE,将线段DE绕点D 顺时针旋转90°至DF的位置,连接AF,EF.(1)证明:AC⊥AF;(2)设AD2=AE×AC,求证:四边形AEDF是正方形;(3)当E点运动到什么位置时,四边形AEDF的周长有最小值,最小值是多少?【思路点拨】(1)由已知条件及正方形的性质易证△CDE≌△ADF,所以可得∠ECD=∠DAF=45°,CE=AF,进而可得∠CAF=90°,即AC⊥AF;(2)若AD2=AE×AC,再由条件∠CAD=∠EAD=45°,易证△EAD∽△DAC,所以∠AED=∠ADC=90°,即有∠AED=∠EDF=∠EAF=90°,又DE=DF,继而证明四边形AEDF为正方形;(3)当E点运动到AC中点位置时,四边形AEDF的周长有最小值,由(2)得CE=AF,则有AE+AF=AC=2,又DE=DF,所以四边形AEDF的周长l=AE+AF+DE+DF=4+2DE,则DE最小四边形的周长最小,问题得解.【答案与解析】解:(1)∵四边形ABCD是正方形,∴∠CDA=90°,CD=AD,ED=FD,∠CAD=45°,∵将线段DE绕点D顺时针旋转90°至DF的位置,∴∠EDF=90°,∴∠CDE=∠ADF,在△CDE和△ADF中,,∴△CDE≌△ADF,∴∠ECD=∠DAF=45°,CE=AF,∴∠CAF=90°,即AC⊥AF;(2)∵AD2=AE×AC,∴∵∠CAD=∠EAD=45°,∴△EAD∽△DAC,∴∠AED=∠ADC=90°,即有∠AED=∠EDF=∠EAF=90°,又DE=DF,∴四边形AEDF为正方形(3)当E点运动到AC中点位置时,四边形AEDF的周长有最小值,理由如下:由(2)得CE=AF,则有AE+AF=AC=2,又DE=DF,则当DE最小时,四边形AEDF的周长l=AE+AF+DE+DF=4+2DE最小,当DE⊥AC时,E点运动到AC中点位置时,此时DE=2四边形AEDF的周长最小值为8.【总结升华】本题用到的知识点有正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及四边形周长最小值的问题、动点问题,题目的综合性较强,难度中等,是一道不错的中考题压轴题.5.(2016•如皋市一模)如图,等腰三角形ABC中,AB=AC,AD平分∠BAC交BC于点D,在线段AD上任取一点P(点A除外),过点P作EF∥AB,分别交AC,BC于点E和点F,作PQ∥AC,交AB于点Q,连接QE.(1)求证:四边形AEPQ为菱形;(2)当点P在何处时,菱形AEPQ的面积为四边形EFBQ面积的一半?【思路点拨】(1)先证出四边形AEPQ为平行四边形,关键是找一组邻边相等,由AD平分∠BAC和PE∥AQ可证∠EAP=∠EPA,得出AE=EP,即可得出结论;(2)S菱形AEPQ=EP•h,S平行四边形EFBQ=EF•h,若菱形AEPQ的面积为四边形EFBQ面积的一半,则EP=EF,因此P为EF中点时,S菱形AEPQ=S四边形EFBQ.【答案与解析】(1)证明:∵EF∥AB,PQ∥AC,∴四边形AEPQ为平行四边形,∴∠BAD=∠EPA,∵AB=AC,AD平分∠CAB,∴∠CAD=∠BAD,∴∠CAD=∠EPA,∴EA=EP,∴四边形AEPQ为菱形.(2)解:P为EF中点时,S菱形AEPQ=S四边形EFBQ∵四边形AEPQ为菱形,∴AD⊥EQ,∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴EQ∥BC,又∵EF∥AB,∴四边形EFBQ为平行四边形.作EN⊥AB于N,如图所示:则S菱形AEPQ=EP•EN=EF•EN=S四边形EFBQ.【总结升华】此题主要考查了菱形的判定与性质、平行四边形的判定与性质、等腰三角形的判定与性质;熟练掌握等腰三角形的性质,证明四边形是平行四边形是解决问题的关键.6.(苏州)如图,正方形ABCD的边AD与矩形EFGH的边FG重合,将正方形ABCD以1cm/s的速度沿FG方向移动,移动开始前点A与点F重合,在移动过程中,边AD始终与边FG重合,连接CG,过点A作CG的平行线交线段GH于点P,连接PD.已知正方形ABCD的边长为1cm,矩形EFGH的边FG,GH的长分别为4cm,3cm,设正方形移动时间为x(s),线段GP的长为y (cm),其中0≤x≤2.5.(1)试求出y关于x的函数关系式,并求当y=3时相应x的值;(2)记△DGP的面积为S1,△CDG的面积为S2.试说明S1-S2是常数;(3)当线段PD所在直线与正方形ABCD的对角线AC垂直时,求线段PD的长.举一反三:【变式】如图,E是矩形ABCD边BC的中点,P是AD边上一动点,PF⊥AE,PH⊥DE,垂足分别为F,H.(1)当矩形ABCD的长与宽满足什么条件时,四边形PHEF是矩形?请予以证明;(2)在(1)中,动点P运动到什么位置时,矩形PHEF变为正方形?为什么?【答案】(1)AD=2AB.证明:∵四边形ABCD是矩形,∴AD=BC,AB=CD;∵E是BC的中点,∴AB=BE=EC=CD;则△ABE、△DCE是等腰Rt△;∴∠AEB=∠DEC=45°;∴∠AED=90°;四边形PFEH中,∠PFE=∠FEH=∠EHP=90°,故四边形PFEH是矩形;(2)点P是AD的中点时,矩形PHEF变为正方形;理由如下:由(1)可得∠BAE=∠CDE=45°;∴∠FAP=∠HDP=45°;又∵∠AFP=∠PHD=90°,AP=PD,∴Rt△AFP≌Rt△DHP;∴PF=PH;在矩形PFEH中,PF=PH,故PFEH是正方形..。
中考数学专题复习:特殊的平行四边形
特殊的平行四边形
返回目录
例1 练习1
例2 练习2
例3 练习3
(3)如图,当点F是BD的中点时,则BF=DF, ∴AF⊥BD,∠BAF=∠DAF=12 ∠BAD=45°. ∵∠EAF=45°,∴∠EAF=∠BAF, ∴AE与AB重合,点E与点B重合, ∴∠AEF=∠ABD=45°,∠AFE=∠AFB=90°. 由旋转,得∠AEQ=∠ADF=45°,∠Q=∠AFD=90°, ∴∠FEQ=90°, ∴四边形AFEQ是矩形. ∵AQ=AF, ∴四边形AFEQ是正方形.
(3)对称性:既是中心对称图形,又是轴对称图形,有⑳ 4 条对称轴.
(4)面积:S= ○21 a2 (a表示正方形边长)=○22
1AC2(或 1BD2)
2
2
。
(用对角线计算).
特殊的平行四边形
返回目录
1.有一个角是直角的○23 菱 形是正方形.菱∠形ABACB=CD90° 菱形ABCD是正方形
2.有一组邻边相等的○24 矩 形是正方形.矩形ABCD
返回目录
例1
三、正方形的性质与判定 例3. 如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=
练习1 45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
例2
(1)由旋转的特征可得AQ= ,∠BAQ=∠ ,由正方形的性质可得
∠BAD= °,进而可证明△AEQ ≌ ,证明依据:
解析:如图,连接FC,AE,设AC,EF交于点O.∵EF为AC的垂直平分线,∴AF =FC,AE=EC,AO=OC.∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,
∠FAC=∠ECA, ∴∠FAC=∠ECA.在△AFO和△CEO中, AO=CO,
2023年中考数学特殊四边形问题精讲
中考特殊四边形问题【考纲解读】1.了解:多边形的概念,平行四边形的相关概念,多边形的内角和与外角和定理;矩形、菱形、正方形的概念及其之间的相互关系.2.理解:多边形的内角和定理,平行四边形的性质与判定;矩形、菱形、正方形及梯形的性质与判定定理.3.会:求一个多边形的内角和;用判定定理方法证明一个四边形是平行四边形(特殊的平行四边形);会从边、角、对角线方面通过合情推理提出性质猜想,并用演绎推理加以证明.4.掌握:多边形的外角和定理,平行四边形的性质定理与判定定理;矩形、菱形、正方形及梯形的性质与判定定理.5.能:用多边形的外角和定理来解决相关问题;能运用平行四边形、矩形、菱形、正方形及梯形的性质解决相关线段或角的问题;熟练运用特殊四边形的判定及性质定理对中点四边形进行判断,并能对自己的猜想进行证明;能综合运用特殊四边形的性质和判定定理解决问题,发现决定中点四边形形状的因素.【命题形式】1.从考查的题型来看,主要以选择题或解答题的形式进行考查,属于中、高档题,难度比较大,综合性比较强.2.从考查的内容来看,重点涉及的有:多边形的内外角和定理,平行四边形的性质与判定定理,多边形与平行四边形的应用;平行四边形、矩形、菱形、正方形、梯形的性质与判定定理及其综合应用.3.从考查的热点来看,主要涉及的有:多边形的内外角和定理,平行四边形的性质与判定定理,多边形与平行四边形的实际综合应用;平行四边形、矩形、菱形、正方形及梯形的性质与判定定理;特殊四边形的图形平移、轴对称、旋转与生产实际相结合的综合问题一、十字架模型:例1.正方形ABCD中,点E、F在BC、CD上,且BE=CF,AE与BF交于点G.(1)如图1,求证AE⊥BF;(2)如图2,在GF上截取GM=GB,∠MAD的平分线交CD于点H,交BF于点N,连接CN,求证:AN+CN BN;【答案】(1)见解析;(2)见解析;【解析】【分析】(1)根据正方形的性质得AB =BC ,90ABC BCD ∠=∠=︒,用SAS 证明ABE BCF △△≌,得BAE CBF ∠=∠,根据三角形内角和定理和等量代换即可得;(2)过点B 作BH BN ⊥,交AN 于点H ,根据正方形的性质和平行线的性质,用SAS 证明AGB AGM ≌,得BAG MAG ∠=∠,根据角平分线性质得45BHA GAN ∠=∠=︒,则HBN 是等腰直角三角形,用SAS 证明ABH CBN ≌,得AH =CN ,在Rt HBN 中,根据勾股定理即可得;【详解】解:(1)∵四边形ABCD 是正方形,∴AB =BC ,90ABC BCD ∠=∠=︒,在ABE △和BCF △中,AB BC ABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩∴ABE BCF △△≌(SAS ),∴BAE CBF ∠=∠,∵1801809090AEB BAE ABC ∠+∠=︒-∠=︒-︒=︒,∴90AEB CBF ∠+∠=︒,∴180()1809090EGB AEB CBF ∠=︒-∠+∠=︒-︒=︒,∴AE BF ⊥;(2)如图所示,过点B 作BH BN ⊥,交AN 于点H,∵四边形ABCD 是正方形,∴AB =AC ,90ABC HBN ∠=∠=︒,∵90HBN HBA ABN ∠=∠+∠=︒,90ABC CBN ABN ∠=∠+∠=︒,∴HBA CBN ∠=∠,由(1)得,AE BF ⊥,∴90AGB AGM ∠=∠=︒,∴90HBG AGM ∠=∠=︒,∴//HB AE ,∴BHA EAN ∠=∠,在AGB 和AGM 中,AG AG AGB AGM GB GM =⎧⎪∠=∠⎨⎪=⎩∴AGB AGM ≌(SAS ),∴BAG MAG ∠=∠,∵AN 平分DAM ∠,∴DAN MAN ∠=∠,∴90BAG MAG MAN DAN ∠+∠+∠+∠=︒,2290MAG MAN ∠+∠=︒,45MAG MAN ∠+∠=︒,45GAN ∠=︒,∴45BHA GAN ∠=∠=︒,∴180180904545BNH HBN BHA ∠=︒-∠-∠=︒-︒-︒=︒,∴HBN 是等腰直角三角形,∴BH =BN ,在ABH 和CBN 中,BH BN HBA CBN AB CB =⎧⎪∠=∠⎨⎪=⎩∴ABH CBN ≌(SAS ),∴AH =CN ,在Rt HBN中,根据勾股定理HN ==,∴AN CN AN AH HN +=+=;【点睛】本题考查了正方形的性质,全等三角形的判定与性质,三角形内角和定理,角平分线,等腰直角三角形的判定与性质,勾股定理和锐角三角函数,解题的关键是掌握并灵活运用这些知识点.例2.已知四边形ABCD 和四边形CEFG 都是正方形,且AB CE >.(1)如图1,连接BG 、DE ,求证:BG DE =;(2)如图2,将正方形CEFG 绕着点C 旋转到某一位置,恰好使得//CG BD ,BG BD =.①求BDE ∠的度数;②若正方形ABCDCEFG 的边长的值.【答案】(1)证明见解析;(2)∠BDE =60°;(3【解析】【分析】(1)根据正方形的性质可以得出BC =DC ,CG =CE ,∠BCD =∠GCE =90°,再证明△BCG ≌△DCE 就可以得出结论;(2)①根据平行线的性质可以得出∠DCG =∠BDC =45°,可以得出∠BCG =∠BCE ,可以得出△BCG ≌△BCE ,得出BG =BE 得出△BDE 为正三角形就可以得出结论;②延长EC 交BD 于点H ,通过证明△BCE ≌△BCG 就可以得出∠BEC =∠DEC ,就可以得出EH ⊥BD ,BH =12BD ,由勾股定理就可以求出EH 的值,从而求出结论.【详解】(1)证明:∵四边形ABCD 和CEFG 为正方形,∴BC =DC ,CG =CE ,∠BCD =∠GCE =90°.∴∠BCD +∠DCG =∠GCE +∠DCG ,∴∠BCG =∠DCE .在△BCG 和△DCE 中,BC DC BCG DCE CG CE =⎧⎪∠=∠⎨⎪=⎩,∴△BCG ≌△DCE (SAS ).∴BG =DE ;(2)①连接BE .由(1)可知:BG =DE .∵CG //BD ,∴∠DCG =∠BDC =45°.∴∠BCG =∠BCD +∠GCD =90°+45°=135°.∵∠GCE =90°,∴∠BCE =360°−∠BCG −∠GCE =360°−135°−90°=135°.∴∠BCG =∠BCE .∵BC =BC ,CG =CE ,在△BCG 和△BCE 中,BC BC BCG BCE GC EC =⎧⎪∠=∠⎨⎪=⎩,∴△BCG ≌△BCE (SAS ).∴BG =BE .∵BG =BD =DE ,∴BD =BE =DE .∴△BDE 为等边三角形.∴∠BDE=60°.②延长EC 交BD 于点H ,在△BCE 和△DCE 中,DE BE DC BC CE CE =⎧⎪=⎨⎪=⎩,∴△BCE ≌△BCG (SSS ),∴∠BEC =∠DEC ,∴EH ⊥BD ,BH =12BD .∵BC =CD Rt △BCD 中由勾股定理,得∴BD 2.∴BE =2∴BH =1.∴CH =1.在Rt △BHE 中,由勾股定理,得EH==∴CE∴正方形CEFG【点睛】此题考查四边形综合题,全等三角形的判定与性质,等边三角形的判定,勾股定理,正方形的性质,解题关键在于作辅助线和掌握判定定理.二、对角互补模型:例3.已知:90,ABC ADC AD DC ∠=∠=︒=,求证:BC AB +.【答案】见解析【解析】【分析】过点D 作BA 的垂线交BA 的延长线于点E ,过点D 作BC 的垂线交BC 于点F ,根据AAS 证明DEA DFC ≌△△得,EA FC ED FD ==,再证明四边形EBFD 是正方形,由勾股定理进一步得出结论.【详解】证明:过点D 作BA 的垂线交BA 的延长线于点E ,过点D 作BC 的垂线交BC 于点F ,如图.易知360DAB ABC BCD ADC ∠+∠+∠+∠=︒.∵90ABC ADC ∠=∠=︒,∴180DAB BCD ∠+∠=︒.又180DAB DAE ∠+∠=︒,∴DAE BCD ∠=∠.∵,DE AB DF BC ⊥⊥,∴90DEB DFC ∠=∠=︒.又AD CD =,∴()DEA DFC AAS ≌,∴,EA FC ED FD==又,DE AB DF BC ⊥⊥,90ABC ∠=︒,∴四边形EBFD 是正方形,∴222,ED BF FD EB EB ED BD ===+=,∴222EB BD =,∴EB BD =,∴EB BF +=.∵,EB BA EA BF BC CF =+=-,∴BA EA BC CF ++-=.∵EA FC =,∴BA BC +=.【点睛】此题主要考查了全等三角形的判定与性质,正方形的判定,勾股定理等知识,由勾股定理得出2EB BD =是解答本题的关键.例4.把两个完全相同的正2n 边形拼一起,其中一个正多边形的顶点在另一个正多边形的中心O 处,如图所见和如图所见分别为2n =和3n =的情形,(1)求如图所见中重叠部分与阴影部分的面积比;(2)求如图所见中重叠部分与阴影部分的面积比;(3)请直接写出正2n 边形重叠部分与阴影部分的面积比.【答案】(1)1:3;(2)1:2;(3)11n n -+【解析】【分析】利用正多边形性质,如图所见中重叠部分面积转化为AOB ∆,如图所见中重叠部分面积转化为四边形ABCO ,由此归纳正2n 边形重叠部分与阴影部分的面积比为正2n 边形内角与360︒减去内角的差的比.【详解】(1)连结AO ,BOO 为正方形ABCD 的中心,90AOB ∠=︒∴,45ABO CBO BAO ∠=∠=∠=︒AO BO ∴=90MON ∠=︒,AOM BON∴∠=∠AOM BON ∴∆≅,AOB MONB S S ∆∴=四边形,又14AOB ABCD S S ∆=正方形∴重叠部分面积和阴影部分面积比为1:3(2)连结OA ,OB ,OCO 为正六边形ABCDEF 的中心OA OB OC ∴==60AOB BOC ∠=∠=︒又120MON ∠=︒60AOM BOM ∴∠+∠=︒60BOM NOC ∠+∠=︒AOM CON ∴∆≅∆∴重叠部分面积为2AOBS ∆∴重叠部分与阴影部分的面积比为1:2(3)由(1)、(2)可得,正2n 边形重叠部分与阴影部分的面积比为11n n -+.【点睛】面积割补法经常将不规则图形转化为规则图形,让问题得解,本问题体现从特殊到一般规律的探寻,注意第三问对一般结论的探求.正多边形的计算一般要经过中心作边的垂线,并连接中心与一个端点构造直角三角形,把正多边形的计算转化为解直角三角形.本题的解决思路是需要掌握的内容.三、与正方形有关的三垂线例5.四边形ABCD 为正方形,点E 为线段AC 上一点,连接DE ,过点E 作EF ⊥DE ,交射线BC 于点F ,以DE 、EF 为邻边作矩形DEFG ,连接CG .(1)如图,求证:矩形DEFG 是正方形;(2)若AB =4,CE =CG 的长度;(3)当线段DE 与正方形ABCD 的某条边的夹角是40°时,直接写出∠EFC 的度数.【答案】(1)见解析;(2)(3)∠EFC =130°【解析】【分析】(1)作EP ⊥CD 于P ,EQ ⊥BC 于Q ,证明Rt △EQF ≌Rt △EPD ,得到EF =ED ,根据正方形的判定定理证明即可;(2)通过计算发现E 是AC 中点,点F 与C 重合,△CDG 是等腰直角三角形,由此即可解决问题;(3)分两种情形:①如图3,当DE 与AD 的夹角为40°时,求得∠DEC =45°+40°=85°,得到∠CEF =5°,根据角的和差得到∠EFC =130°,②如图4,当DE 与DC 的夹角为40°时,根据三角形的内角和定理即可得到结论.【详解】(1)证明:如图1,作EP ⊥CD 于P ,EQ ⊥BC 于Q,∵∠DCA =∠BCA ,∴EQ =EP ,∵∠QEF +∠FEC =45°,∠PED +∠FEC =45°,∴∠QEF =∠PED ,在△EQF 和△EPD 中,QEF PED EQ EP EOF EPD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△EQF ≌△EPD (ASA ),∴EF =ED ,∴矩形DEFG 是正方形;(2)如图2中,在Rt △ABC 中,AC=∵CE =∴AE =CE ,∴点F 与C 重合,此时△DCG 是等腰直角三角形,∴四边形DECG是正方形,∴CG=CE=(3)①如图3,当DE与AD的夹角为40°时,∠DEC=45°+40°=85°,∵∠DEF=90°,∴∠CEF=5°,∵∠ECF=45°,∴∠EFC=130°,②如图4,当DE与DC的夹角为40°时,∵∠DEF=∠DCF=90°,∴∠EFC=∠EDC=40°,综上所述,∠EFC=130°或40°.【点睛】此题考查了正方形的判定以及性质,涉及了全等三角形的证明、等腰直角三角形等性质,熟练掌握相关基本性质是解题的关键.例6.探究证明:(1)如图1,正方形ABCD中,点M、N分别在边BC、CD上,AM⊥BN.求证:BN=AM;(2)如图2,矩形ABCD中,点M在BC上,EF⊥AM,EF分别交AB、CD于点E、F.求证:EF BC AM AB;(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M、N分别在边BC、AB上,求DNAM的值.【答案】(1)证明见解析;(2)证明见解析;(3)4 5.【解析】【分析】(1)由矩形的性质结合等角的余角相等,可证明∠NBC=∠MAB,进而证明△BCN∽△ABM,最后根据相似三角形对应边成比例解题即可;(2)过点B作BG∥EF交CD于G,由两组对边分别平行判定四边形BEFG是平行四边形,再根据平行四边形的性质,可证明△GBC∽△MAB,最后根据相似三角形对应边成比例解题即可;(3)过点D作平行于AB的直线交过点A平行于BC的直线于R,交BC的延长线于S,连接AC,可得四边形ABSR是平行四边形,再由含有一个90°角的平行四边形是矩形,证明四边形ABSR是矩形,进而得到∠R=∠S=90°,RS=AB=10,AR=BS.,结合(2)中结论可证明△ACD≌△ACB,由全等三角形对应角相等得到∠ADC=∠ABC,再由等角的余角相等,证明△RAD∽△SDC,根据相似三角形对应边成比例,设SC=x,解得DR、DS 的长,再结合勾股定理解题即可.【详解】(1)证明∵四边形ABCD是矩形,∴∠ABC=∠C=90°∴∠NBA+∠NBC=90°.∵AM⊥BN,∴∠MAB+∠NBA=90°,∴∠NBC=∠MAB,∴△BCN∽△ABM,∴BNAM=BCAB(2)结论:EFAM=BCAB理由:如图2中,过点B作BG//EF交CD于G,∵四边形ABCD是矩形,∴AB∥CD,∴四边形BEFG是平行四边形,∴BG=EF.∵EF⊥AM,∴BG⊥AM,∴∠GBA+∠MAB=90°.∵∠ABC=∠C=90°,∴∠GBC+∠GBA=90°,∴∠MAB=∠GBC,∴△GBC∽△MAB,∴BGAM=BCAB,∴EFAM=BCAB(3)过点D作平行于AB的直线交过点A平行于BC的直线于R,交BC的延长线于S,连接AC,则四边形ABSR是平行四边形.∵∠ABC=90°,∴四边形ABSR是矩形,∴∠R=∠S=90°,RS=AB=10,AR=BS.∵AM⊥DN,∴由(2)中结论可得:DNAM=BSAB∵AB=AD,CB=CD,AC=AC,∴△ACD≌△ACB,∠ADC=∠ABC=90°,∴∠SDC+∠RDA=90°.∵∠RAD+∠RDA=90°,∴∠RAD=∠SDC,∴△RAD∽△SDC,∴CD AD =SC RD,设SC=x ,∴510=x RD∴RD=2x ,DS=10-2x ,在Rt △CSD 中,∵222CD DS SC =+,∴52=(10-2x )2+x2,∴x=3或5(舍弃),∴BS=5+x=8,∴DN AM =BS AB =810=45【点睛】本题考查全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、矩形的判定与性质、平行四边形的判定与性质等知识,是重要考点,难度一般,正确作出辅助线、掌握相关知识是解题关键.四、正方形与45°的基本图:例7.已知正方形ABCD 中,∠MAN =45°,∠MAN 绕点A 顺时针旋转,它的两边分别交CB ,DC (或它们的延长线)于点M ,N ,AH ⊥MN 于点H .(1)如图①,当∠MAN 绕点A 旋转到BM =DN 时,请你直接写出AH 与AB 的数量关系:;(2)如图②,当∠MAN 绕点A 旋转到BM ≠DN 时,(1)中发现的AH 与AB 的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN =45°,AH ⊥MN 于点H ,且MH =2,AH =6,求NH 的长.(可利用(2)得到的结论)【答案】(1)AB =AH ;(2)成立,证明见解析;(3)3【解析】【分析】(1)由BM =DN 可得Rt △ABM ≌Rt △ADN ,从而可证∠BAM =∠MAH =22.5°,Rt △ABM ≌Rt △AHM ,即可得AB =AH ;(2)延长CB 至E ,使BE =DN ,由Rt △AEB ≌Rt △AND 得AE =AN ,∠EAB =∠NAD ,从而可证△AEM ≌△ANM ,根据全等三角形对应边上的高相等即可得AB =AH ;(3)分别沿AM ,AN 翻折△AMH 和△ANH ,得到△ABM 和△AND ,分别延长BM 和DN 交于点C ,可证四边形ABCD 是正方形,设NH =x ,在Rt △MCN 中,由勾股定理列方程即可得答案.【详解】解:(1)∵正方形ABCD ,∴AB =AD ,∠B =∠D =∠BAD =90°,在Rt △ABM 和Rt △ADN 中,AB AD B D BM DN ⎧=⎪∠=∠⎨⎪=⎩,∴Rt △ABM ≌Rt △ADN (SAS ),∴∠BAM =∠DAN ,AM =AN ,∵∠MAN =45°,∴∠BAM +∠DAN =45°,∴∠BAM =∠DAN =22.5°,∵∠MAN =45°,AM =AN ,AH ⊥MN∴∠MAH =∠NAH =22.5°,∴∠BAM =∠MAH ,在Rt △ABM 和Rt △AHM 中,BAM MAH B AHMAM AM ⎧∠=∠⎪∠=∠⎨⎪=⎩,∴Rt △ABM ≌Rt △AHM (AAS ),∴AB =AH ,故答案为:AB =AH ;(2)AB =AH 成立,理由如下:延长CB 至E ,使BE =DN,如图:∵四边形ABCD 是正方形,∴AB =AD ,∠D =∠ABE =90°,∵BE=DN,∴Rt△AEB≌Rt△AND(SAS),∴AE=AN,∠EAB=∠NAD,∵∠MAN=45°,∴∠DAN+∠BAM=45°,∴∠EAB+∠BAM=45°,∴∠EAM=45°,∴∠EAM=∠NAM=45°,又AM=AM,∴△AEM≌△ANM(SAS),∵AB,AH是△AEM和△ANM对应边上的高,∴AB=AH.(3)分别沿AM,AN翻折△AMH和△ANH,得到△ABM和△AND,分别延长BM和DN交于点C,如图:∵沿AM,AN翻折△AMH和△ANH,得到△ABM和△AND,∴AB=AH=AD=6,∠BAD=2∠MAN=90°,∠B=∠AHM=90°=∠AHN=∠D,∴四边形ABCD是矩形,∵AB=AD,∴四边形ABCD是正方形,∴AH=AB=BC=CD=AD=6.由(2)可知,设NH=x,则MC=BC﹣BM=BC﹣HM=4,NC=CD﹣DN=CD﹣NH=6﹣x,在Rt△MCN中,由勾股定理,得MN2=MC2+NC2,∴(2+x)2=42+(6﹣x)2,解得x=3,∴NH=3.【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,熟练掌握正方形的性质定理,全等三角形的判定定理和性质定理是解题的关键.例8.分层探究(1)问题提出:如图1,点E、F别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF.求证:EF=BE+DF,解题思路:把△ABE绕点A逆时针旋转度至△ADG,可使AB与AD重合.由∠FDG=ADG+∠ADC=180°,则知F、D、G三点共线,从而可证△AFG≌(),从而得EF=BE+DF,阅读以上内容并填空.(2)类比引申:如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°.探究:若∠B、∠D都不是直角,当∠B、∠D满足什么数量关系时,仍有EF=BE+DF?(3)联想拓展:如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,并且∠DAE=45°.猜想BD、CE、DE的数量关系,并给出理由.【答案】(1)90,△AFE,SAS;(2)∠B+∠D=180°;(3)EF2=BE2+FD2,理由见解析【解析】【分析】(1)把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,再证明△AFG≌△AFE进而得到EF=FG,即可得EF=BE+DF;(2)∠B+∠D=180°时,EF=BE+DF,与(1)的证法类同;(3)把△AFD绕点A顺时针旋转90°得到△ABE′,连接EE′,根据旋转的性质,可知△AFD≌△ABE′得到BE′=FD,AE′=AF,∠D=∠ABE′,∠EAD=∠E′AB,在Rt△ABD中的,AB=AD,可求得∠E′BD=90°,所以E′B2+BE2=E′E2,证△AE′E≌△AE′F,利用FE=EE′得到EF2=BE2+FD2.【详解】解:(1)∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.∴∠BAE=∠DAG,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠EAF=∠FAG,∵∠ADC=∠B=90°,∴∠FDG=180°,∴点F、D、G共线,在△AFE和△AFG中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴△AFG ≌△AFE (SAS ),∴EF =FG ,即EF =BE +DF ,故答案为:90,△AFE ,SAS ;(2)当∠B +∠D =180°时,EF =BE +DF ,如图2∵AB =AD ,∴把△ABE 绕点A 逆时针旋转90°至△ADG ,可使AB 与AD 重合,∴∠BAE =∠DAG ,∵∠BAD =90°,∠EAF =45°,∴∠BAE +∠DAF =45°,∴∠EAF =∠FAG ,∵∠ADC +∠B =180°,∴∠FDG =180°,∴点F 、D 、G 共线,在△AFE 和△AFG 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△AFG (SAS ),∴EF =FG ,即EF =BE +DF ,故答案为:∠B +∠D =180°;(3)猜想:EF 2=BE 2+FD 2,证明:把△AFD 绕点A 顺时针旋转90°得到△ABE ′,连接EE ′,如图3,∴△AFD ≌△ABE ′,∴BE ′=FD ,AE ′=AF ,∠D =∠ABE ′,∠EAD =∠E ′AB ,∵AB =AD ,∴∠ABD =∠ADB =45°,∴∠ABD +∠ABE ′=90°,即∠E ′BD =90°,∴E ′B 2+BE 2=E ′E 2,又∵∠FAE =45°,∴∠BAE +∠EAD =45°,∴∠E ′AB +∠BAE =45°,即∠E ′AE =45°,在△AEE ′和△AEF 中,AE AE E AE FAE AE AF ⎧=⎪'∠=∠⎨⎪'=⎩,∴△AEE ′≌△AEF (SAS ),∴EE ′=FE ,∴EF 2=BE 2+DF 2.【点睛】本题主要考查了几何变换综合,结合全等三角形的性质与判定计算是关键.。
中考数学复习方案第五单元四边形第24课时特殊平行四边形一课件
A.6
B.3 3
C.2 6
图24-10
D.4.5
(
)
[答案] C
[解析]作 M 关于 AC 的对称点 M',显然 E,P,M'三点在同一直线上,当 EM'⊥AD
时,EM'最短,此时 PM+PE 最小,如图.
依题意,sin∠DAC=
AM,MC,CN,NA,添加一个条件,使四边形 AMCN 是矩形,这个条件是 (
1
A.OM=2AC
B.MB=MO
C.BD⊥AC
D.∠AMB=∠CND
图24-2
)
[答案] A
[解析]∵四边形 ABCD 是平行四边形,∴OA=OC,OB=OD.
∵对角线 BD 上的两点 M,N 满足 BM=DN,∴OB-BM=OD-DN,即 OM=ON,
(1)求证:△ABE≌△CDF.
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
图24-6
例1 [2019·青岛]如图24-6,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长
AE至G,使EG=AE,连结CG.
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
3
32 +(3 2)2
3
=3,
所以 EM'=AC·sin∠DAC=6 2 ×
3
3
=2 6.
即 PM+PE 的最小值为 2 6,故选 C.
考向三 正方形的性质与判定的应用
例3 [2019·长沙]如图24-11,正方形ABCD中,点E,F分别在AD,CD上,且DE=CF, AF与BE相交于点G.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何构造特殊四边形解决相关计算证明问题
特殊的四边形在生活中有非常广泛的应用,也是现行教材中的一个重点和难点。
学生在运用特殊四边形的性质,特别是构造四边形来解决有关的计算,证明问题时,存在严重缺陷。
我认为构造特殊的四边形来解决相关问题时,能够另擗佳径,减少繁难的计算和证明,同时能够开阔学生视野,增强学生观察图形,分解图形,构造基本图形的能力。
一、数形结合,巧妙构造特殊的四边形。
1、如图,点A 、B 是反比例函数y=x
k (k>0,x>0)的图象上两点,过点A 作x 轴的垂线,过点B 作y 轴的垂线,垂足分别为C 、D,AC 、BD 交于点F,则( )
A 、S △ADE >S △BEC
B 、 S △ADE =S △BE
C C 、S △ADE <S △BEC
D 、无法确定 解析:过点A 作AM ⊥y 轴,过点B 作BN ⊥x 轴,垂足分别为M 、N,
则S 矩形AMOC =S 矩形BNOD =k ,即S 矩形MADE =S 矩形BNCE ,
又S △ADE = 21 S 矩形MADE ,S △BEC =2
1S 矩形BNCE, ∴S △ADE =S △BEC 。
解决此类问题一般的同学采用参数法通过计算三角形的面积来解,计算量比较大,同时引入的参数个数也别较多,给学生造成较大的障碍,而我们采用数形结合,转化的思想,利用矩形的性
质就很巧妙地加以解决。
二、培养数感,从直觉出发,构造特殊的四边形。
2、如图,AB=8,DB ⊥AB ,EA ⊥AB ,BD=6AE=12, 点M 是DE 的中点,求BM 的长。
解析:AE 和BD 的位置关系为平行,数量关系为BD=6 , AE=12 , BD=
21AE , 延长DB 至F 点,使DF=12, 连接EF 、AD ,
则四边形ADFE 是平行四边形。
MB 分别是DE DF 的中点,
∴BM=2
1EF,EF=AD , 通过勾股定理可求出AD ,从而解决BM 长的计算问题。
我们利用学生对数字的敏感程度,对图形中相应边的位置关系和数量关系进行分析,利用我们的直觉来构图,同时进行思维的发散,通过构造平行四边形将边的关系进行转化,联系三角形的中位线和勾股定理来进行计算。
这是一道解法灵活多变的综合性较高的习题,学生没有现成的模式可以套用,也不能简单依靠知识的叠加来实现解题,需要进行细致的观察。
对数学敏感的程度......和较好的构造......图.
形的能力。
B P
练习:如图所示,已知六边形ABCDEF,其中∠A=∠B=∠C=∠D=∠E=∠F=120°, AB=10㎝,BC=70㎝,CD=20㎝,DE=40㎝ 。
求AF 、 EF 的长度。
解析:延长FA 、CB 交于点P ,延长FE 、 CD 交于点Q,△APB △DEQ 均为等边三角形,从而可以证明四边形PCQF 为平行四边形,利用方程思想可求出AF 、 EF 的长。
三、生活问题数学化,建立数学模型,构造特殊的四边形。
G
F
B C E
4、如图,是某城市部分街道示意图,AF ∥BC BA ∥DE BD ∥AE EC ⊥BC,甲乙两人同时从B 站乘车到F 站,甲乘1路车,路线是B→A→E→F,乙乘2路车,路线是B→D→C→F,假设两车速度相同,途中耽误的时间相同,那么谁先到达F 站?请说明理由!
解析:1路车路程:BA+AE+EF ,2路车路程:BD+DC+CF,
谁先到达F 站,即比较BA+AE+EF 与BD+DC+CF 的大小。
延长ED 交BC 于G 点,则四边形ABGD 为平行四边形,
∴DG=AB 又四边形ABDE 是平行四边形
∴DE=AB ∴D 为直角三角形ECG 斜边上的中点
∴CD=DG=AB,
∵DF ∥CG,D 为EG 的中点 ∴EF=CF
∴1路车2路车同时到达F 站.
这是一些立意新颖的情景性习题,充满浓厚的生活气息,它强化了学生对文字、图形、符号语言的理解,并能将生活实际问题纯数学化,建立相应的数学模型,来解决问题。
它让学生感受到数学来源于生活,又能指导我们的生活生产。
从而培养学生运用数学的意识,体现数学在生活中的价值,同时体验成功的快感,感觉学有所获。
四、构造特殊的四边形解决探究性问题
D
5、如图,E 是平行四边形ABCD 边DC 的延长线上的一点,且CE=DC=AC ,连AE 分别交BC 、BD 于F 、G ,连AC 交BD 于点O ,则下列结论:
(1)AE ⊥BC ;(2)AB=2OF ;(3)S △CEF =4
1S 平行四边形ABCD (4)四边形AOFB 为等腰梯形,其中正确的是___________,若将条件改为CE=CD ,那么正确的结论呢?
解析:连接BE ,则四边形ABEC 为菱形。
∴AE ⊥BC,F 为BC 中点 ∵O 为AC 中点 ∴S △CEF =21S △ABC =4
1S 平行四边形, 而(4)只有在AB=AD 时才成立。
我们设计一些探究性练习,给学生提供资助探索的机会,使其经历观察 实验 猜想 证明 比较 推理 反设 验证 等数学思考,体验数学问题的探索性和挑战性,培养提高学生的探究能力,
并通过变换命题,变换条件,变换图形来引发学生的认知冲突,从而进一步探索新问题,发现新见解。
