人教版八年级下册特殊四边形的证明与计算专题(无答案)
人教版八年级数学下册特殊平行四边形课后练习及详解

第十九章特殊平行四边形练习题题一:以下说法中,正确的选项是( )A.对角线相互垂直且相等的四边形是正方形B.对角线相等的四边形是平行四边形C.四条边相等的四边形是菱形D.矩形的对角线必然相互垂直题二:如图,四边形ABCD中,AB∥CD.那么以下说法中,不正确的选项是( )A.当AB=CD,AO=DO时,四边形ABCD为矩形B.当AB=AD,AO=CO时,四边形ABCD为菱形C.当AD∥BC,AC=BD时,四边形ABCD为正方形D.当AB≠CD,AC=BD时,四边形ABCD为等腰梯形题三:如图,已知四边形ABCD中,E、F、G、H别离为AB、BC、CD、DA的中点,题四:①求证:四边形EFGH是平行四边形.题五:②探索下列问题,并选择一个进行证明.题六:a.原四边形ABCD的对角线AC、BD知足________时,四边形E FGH是矩形.题七:b.原四边形ABCD的对角线AC、BD知足________时,四边形EFGH是菱形.题八:c.原四边形ABCD的对角线AC、BD知足________时,四边形EFGH是正方形.题九:如下图,在△ABC中,别离以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.(1)求证:四边形DAEF是平行四边形;(2)探究下列问题:(只填满足的条件,不需证明)①当△ABC知足_________条件时,四边形DAEF是矩形;②当△ABC知足_________条件时,四边形DAEF是菱形;③当△ABC知足_________条件时,以D、A、E、F为极点的四边形不存在.题十:如下图,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=FD.题十一:(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;题十二:(2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?什么缘故?题十三:(3)若四边形AECF是矩形,试判定四边形ABCD是不是为矩形,没必要写理由.题十四:如图,任意四边形ABCD,对角线AC、BD交于O点,过各极点别离作对角线AC、BD的平行线,四条平行线围成一个四边形EFGH.试想当四边形ABCD的形状发生改变时,四边形EFGH 的形状会有哪些转变?完成以下题目:题十五:(1)①当ABCD为任意四边形时,EFGH为___________;题十六:②当ABCD为矩形时,EFGH为___________;③当ABCD为菱形时,EFGH为___________;④当ABCD为正方形时,EFGH为___________;(2)请对(1)中①②你所写的结论进行证明.(3)反之,当用上述方法所围成的平行四边形EFGH别离是矩形、菱形时,相应的原四边形ABCD必需知足如何的条件?题十七:如图,在矩形ABCD中,M、N别离是AD、BC的中点,P、Q别离是BM、DN的中点.题十八:(1)求证:△MBA≌△NDC;题十九:(2)四边形MPNQ是什么样的特殊四边形?请说明理由.题二十:在折纸这种传统手工艺术中,包括许多数学思想,咱们能够通过折纸取得一些特殊图形.把一张正方形纸片依照图①~④的进程折叠后展开.(1)猜想四边形ABCD是什么四边形;(2)请证明你所得到的数学猜想.题二十一:如图,在梯形ABCD中,AD∥BC,AD=5cm,BC=8cm,M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.题二十二:(1)试说明△PCM≌△QDM;题二十三:(2)当P在B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.题二十四:如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D动身,按折线D-C-B方向以2cm/s的速度运动,动点N从点D动身,沿DA方向以1cm/s的速度向点A运动.动点M、N 同时动身,当一个点抵达终点时,另一个点也随即停止运动.题二十五:(1)若点E在线段BC上,且BE=4cm,通过几秒钟,点A、E、M、N组成平行四边形?题二十六:(2)动点M、N在运动的进程中,线段MN是不是通过矩形ABCD的两条对角线的交点?若是线段MN过此交点,请求出运动的时刻;若是线段MN只是此交点,请说明理由.题二十七:如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD= 4,∠ABC=∠DCB,求BC的长.题二十八:已知:如图,四边形ABCD中,AD∥BC,AB= 4,BC=6,CD=5,AD=3.求:四边形ABCD的面积.特殊平行四边形课后练习参考答案题一:C.详解:A.对角线相互垂直且相等的四边形不能判定正方形,故本选项错误;B.对角线互相平分的四边形是平行四边形,故本选项错误;C.四边相等的四边形是菱形,故本选项正确;D.矩形的对角线互相平分且相等,不一定垂直,故本选项错误;故选C.题二:C.详解:选项A的结论正确,AB=CD可判定为平行四边形,AO=DO可判定对角线相等,故是矩形;选项B的结论正确,AB=AD可判定△ABD为等边三角形,AO=CO可判定△CDB也为等边三角形,故是菱形;选项C的结论错误,判定结果为矩形,不必然是正方形;选项D的结论正确,对角线相等的梯形是等腰梯形;故选C.题三:见详解.详解:①连接AC,BD,∵四边形ABCD中,E、F、G、H别离为AB、BC、CD、DA的中点,∴EH∥BD,FG∥BD,∴EH∥FG,同理:GH∥EF,∴四边形EFGH是平行四边形.②a.当AC⊥BD时,四边形EFGH是矩形.∵由①得:四边形MONH是平行四边形,∴当AC⊥BD时,四边形MONH是矩形,∴∠EH G=90°,∴四边形EFGH是矩形.b.当AC=BD时,四边形EFGH是菱形.∵HG=12AC,EH=12BD,∴EH=GH,∴四边形EFGH是菱形;c.由a与b可得:原四边形ABCD的对角线AC、BD知足AC⊥BD且AC=BD时,四边形EFGH是正方形.故答案为:a.AC⊥BD,b.AC=BD,c.AC⊥BD且AC=BD.题四:见详解.详解:(1)∵△ABD和△FBC都是等边三角形,∴BD=BA,BF=BC,∠DBA=∠FBC=60°,∴∠DBA-∠FBA=∠FBC-∠FBA,∴∠DBF=∠ABC.在△ABC和△DBF中,BA=BD,∠ABC=∠DBF,BC=BF,∴△ABC≌△DBF.∴AC=DF=AE.同理△ABC≌△EFC.∴AB=EF=AD.∴四边形ADFE是平行四边形.(2)当∠BAC=150°,∠DAE=360°-60°-60°-150°=90°,∴平行四边形DAEF是矩形.当AB=AC≠BC,有AD=AE,∴平行四边形DAEF是菱形.当∠BAC=60°,△FBC与△ABC重合,故以D、A、E、F为极点的四边形不存在.题五:见详解.详解:连AC,设AC、BD相交于点O,(1)∵四边形AECF是平行四边形,∴OE=OF,OA=OC,∵BE=FD,∴OB=OD.∴四边形ABCD是平行四边形;(2)∵四边形AECF是菱形,∴OE=OF,OA=OC,AC⊥BD.∵BE=FD,∴OB=OD.∴四边形ABCD是菱形;(3)四边形ABCD不是矩形.题六:见详解.详解:(1)平行四边形;菱形;矩形;正方形;(2)结合图形,联想特殊四边形的特点及识别很容易发觉,其中的桥梁为AC、BD.①当ABCD为任意四边形时,EFGH为平行四边形.∵EH∥AC∥FG,EF∥BD∥GH,∴四边形EFGH为平行四边形.②若ABCD为矩形,那么EFGH为菱形.∵EH∥AC∥FG,EF∥BD∥GH.∴四边形EACH,ACGF,EFBD,BDHG,EFGH均为平行四边形.∴EH=AC=FG,EF=BD=GH.∵四边形ABCD为矩形.∴AC=BD.∴EH=AC=FG=EF=BD=GH.∴四边形EFGH为菱形.(3)当平行四边形EFGH是矩形时,四边形ABCD必需知足:对角线相互垂直.当平行四边形EFGH是菱形时,四边形ABCD必需知足:对角线相等.题七:见详解.详解:(1)∵四边形ABCD是矩形,∴AB=CD,AD=BC,∠A=∠C=90°,∵在矩形ABCD中,M、N别离是AD、BC的中点,∴AM=12AD,CN=12BC,∴AM=CN,在△MAB和△NDC中,∵AB=CD,∠A=∠C=90°,AM=CN,∴△MBA≌△NDC;(2)四边形MPNQ是菱形.理由如下:连接AP,MN,那么四边形ABNM是矩形,∴AN和BM相互平分,那么A,P,N在同一条直线上,易证:△ABN≌△BAM,∴AN=BM,∵△MAB≌△NDC,∴BM=DN,∵P、Q别离是BM、DN的中点,∴PM=NQ,∵DM=BN,DQ=BP,∠MDQ=∠NBP,∴△MQD≌△NPB,∴四边形MPNQ是平行四边形,∵M是AD中点,Q是DN中点,∴MQ=12AN,∴MQ=12BM,∵MP=12BM,∴MP=MQ,∴平行四边形MQNP是菱形.题八:见详解.详解:(1)四边形ABCD是菱形;(2)∵△AMG沿AG折叠,使AM落在AC上,∴∠MAD=∠DAC=12∠MAC,同理可得∠CAB=∠NAB=12∠CAN,∠DCA=∠MCD=12∠ACM,∠ACB=∠NCB=12∠ACN,∵四边形AMCN是正方形,∴∠MAC=∠MCA=∠NAC=∠NCA,∴∠DAC=∠BAC=∠BCA=∠DCA,∴AD∥BC,AB∥DC,∴四边形ABCD为平行四边形,∵∠DAC=∠DCA,∴AD=CD,∴四边形ABCD为菱形.题九:见详解.详解:(1)∵AD∥BC,∴∠QDM=∠PCM,∵M是CD的中点,∴DM=CM,∵∠DMQ=∠CMP,∴△PCM≌△QDM;(2)当四边形ABPQ是平行四边形时,PB=AQ,∵BC-CP=AD+QD,∴8-CP=5+CP,∴CP=(8-5)÷2=,∴当PC=时,四边形ABPQ是平行四边形.题十:见详解.详解:(1)∵点N只在AD上运动,∴当点M运动到BC边上的时候,点A、E、M、N才可能组成平行四边形,即<t<,设经过t秒,四点可组成平行四边形.分两种情形:①当M点在E点右边,如图:此时AN=EM,那么四边形AEMN是平行四边形,∵DN= t,CM=2t -5,∴AN=10- t,EM=10- 4-(2t -5),∴10- t =10- 4-(2t -5),解得:t =1,∵<t<,∴t =1舍去;②当M点在B点与E点之间,如图,那么MC=2t -5,BM=10-(2t -5)=15-2t,∴ME= 4-(15-2t)=2t -11,2t-11=10-t,解得t =7,现在符合,∴当t =7秒时,点A、E、M、N组成平行四边形;(2)动点M、N在运动的进程中,线段MN能通过矩形ABCD的两条对角线的交点,现在M在BC上,如图,∵四边形ABCD是矩形,∴OA=OC,AD∥BC,∴∠NAO=∠MCO,在△ANO和△CMO中,∠NAO=∠MCO,AO=OC,∠AON=∠COM,∴△ANO≌△CMO(ASA),∴AN=CM,设N运动的时刻是t秒,那么10-t=2t -5,解得:t =5,即动点M、N在运动的进程中,线段MN能通过矩形ABCD 的两条对角线的交点,现在运动的时刻是5秒.题十一:8.详解:∵AD∥BC,∠A=120°,∴∠ABC=180°-120°=60°,∵BD平分∠ABC,∴∠DBC=12∠ABC=12×60°=30°,又∵∠ABC=∠DCB=60°,∴∠BDC=180°-30°-60°=90°,∴BC=2CD=2×4=8.题十二:18.详解:过D作DE∥AB,交CB于E点,又∵AD∥CB,∴四边形ABED是平行四边形,∴EB=AD=3,DE=AB=4,∵CB=6,∴EC=BC-BE=6-3=3,∵CD=5,∴CD2=DE2+CE2,∴△DEC是直角三角形,∴∠DEC=90°,∴四边形ABCD的面积是:12(AD+CB)•DE=12(3+6)×4=18.。
专题训练(四) 特殊平行四边形的证明与计算

12.(2017·六盘水)如图,在正方形ABCD中,等边三角形AEF的顶点E, 75° . F分别在边BC和CD上,则∠AEB=_____ 13 .(2017·绍兴) 如图为某城市部分街道示意图,四边形ABCD 为正方形, 点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线 为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 4600 100 m,则小聪行走的路程为_______m.
5.(导学号 69654100)(2017· 苏州)如图,在菱形 ABCD 中,∠A=60° , AD=8,F 是 AB 的中点.过点 F 作 FE⊥AD,垂足为点 E. 将△AEF 沿点 A 到点 B 的方向平移,得到△A′E′F′. 设 P,P′分别是 EF,E′F′的中点,当点 A′与点 B 重合时, 四边形 PP′CD 的面积为( A ) A.28 3 C.32 3 B.24 3 D.32 3-8
ቤተ መጻሕፍቲ ባይዱ
(2)作 AH⊥BD 于点 H,由题意知∠AGB=60° ,∠ABG=45° , ∴△ABH 为等腰直角三角形,△AGH 为含 30° 角的直角三角形. 2 6 2 6 ∵AB=1,∴AH=BH= 2 ,HG= 6 .∴BG= 2 + 6 .
解:(1)证明:如图①,根据折叠,∠DBC=∠DBE. 又AD∥BC,∴∠DBC=∠ADB.∴∠DBE=∠ADB. ∴DF=BF.∴△BDF是等腰三角形. (2)①∵四边形ABCD是矩形,∴AD∥BC.∴FD∥BG.又DG∥BE, ∴四边形BFDG是平行四边形.∵DF=BF,∴四边形BFDG是菱形.
解: (1)AG2 = GE2 + GF2. 证明:连接 GC ,由正方形的性质知 AD = CD ,
八年级下学期-特殊平行四边形的判定与性质专题

(1)求证:四边形 ADCE 为矩形; (2)当△ABC 满足什么条件时,四边形 ADCE 是一个正方形?并 给出证明.
12.(1)证明:在△ABC 中,AB=AC,AD⊥BC,∴∠BAD=∠DAC.∵AN 是△ABC 的外角∠CAM 的平分线,∴∠MAE=∠CAE,∴∠DAE= ∠DAC+∠CAE=12×180°=90°.又∵AD⊥BC,CE⊥AN,∴∠ADC =∠CEA=90°,∴四边形 ADCE 为矩形;
(1)求证:BF=DE; (2)当点 E 运动到 AC 的中点时(其他条件都不变),四边形 AFBE 是 什么特殊四边形?说明理由.
13.(1)证明:∵正方形 ABCD,∴AB=AD,∠BAD =90°.∵AF⊥AC,∴∠EAF=90°,∴∠BAF=∠EAD. 在△ADE 和△ABF 中,AD=AB,∠DAE=∠BAF,AE =AF,∴△ADE≌△ABF(SAS),∴BF=DE;
(A ) A.3 个
B.2 个
C.1 个
D.0 个
4.如图,正方形 ABCD 的边长为 2,以对角线 AC 为一边作菱形
AEFC,AF 与 BC 交于点 G,则∠BCE 的度数与 BE 的长分别为( C )
A.30°,2 2-2
B.30°,2 2-1
C.22.5°,2 2-2
D.22.5°,2 2-1
(2)解:当△ABC 满足∠BAC=90°时,四边形 ADCE 是一个正方形.证 明如下:∵AB=AC,∠BAC=90°,∴∠ACB=∠B=45°.∵AD⊥ BC,∴∠CAD=∠ACD=45°,∴DC=AD.∵四边形 ADCE 为矩形, ∴矩形 ADCE 是正方形.
人教版八年级数学下册18.2 专题训练 特殊平行四边形的性质和判定(含答案)

18.2 专题训练特殊平行四边形的性质与判定1.如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE 是平行四边形,求证:四边形ADBE是矩形.2.在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB 的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.4.如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF =AE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.5.如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD 的中点.(1)当四边形ABCD是矩形时,四边形EFGH是菱形,请说明理由;(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.6.如图,等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.(1)求证:四边形EBFC是菱形;(2)如果∠BAC=∠ECF,求证:AC⊥CF.7.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN是菱形.8.如图,在矩形ABCD中,AB=2,BC=5,E,P分别在AD,BC上,且DE=BP=1.(1)判断△BEC的形状,并说明理由;(2)判断四边形EFPH是什么特殊四边形?并证明你的判断.9.如图,在▱ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.10.如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD 上一动点(不与点D重合),PO的延长线交BC于Q点.(1)求证:四边形PBQD为平行四边形;(2)若AB=3 cm,AD=4 cm,点P从点A出发,以1 cm/s的速度向点D匀速运动.设点P运动时间为t s,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.11.如图1,在▱ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.图1 图2(1)求证:四边形AFCE是平行四边形;(2)如图2,若BE⊥EC,求证:四边形ABFE是菱形.12.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.13.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.(1)求证:CE=AD;(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.14.如图,菱形ABCD 的对角线AC,BD 相交于点O,分别延长OA,OC 到点E,F,使AE =CF,依次连接B,F,D,E各点.(1)求证:△BAE≌△BCF;(2)若∠ABC =50°,则当∠EBA=20° 时,四边形BFDE是正方形.15.已知:如图,在菱形ABCD 中,点E,O,F 分别是边AB,AC,AD 的中点,连接CE,CF,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么条件时,四边形AEOF是正方形?请说明理由.16.如图,在四边形ABCD中,AB∥CD,AB≠CD,BD=AC.(1)求证:AD=BC;(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分.17.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.18.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE. 求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.19.如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点;(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.20.已知:如图,在▱ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.参考答案18.2 专题训练特殊平行四边形的性质与判定1.如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE 是平行四边形,求证:四边形ADBE是矩形.解:∵AB=AC,AD是BC边上的中线,∴AD⊥BC.∴∠ADB=90°.又∵四边形ADBE是平行四边形,∴四边形ADBE是矩形.2.在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.证明:∵AB∥DM,∴∠BAM=∠AMD.由折叠性质得:∠CAB=∠CAD,AB=AD,BM=DM.∴∠DAM=∠AMD.∴DA=DM=AB=BM.∴四边形ABMD是菱形.3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB 的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.解:(1)证明:∵点O为AB的中点,∴OA=OB.又∵OE=OD,∴四边形AEBD是平行四边形.∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,即∠ADB=90°.∴四边形AEBD是矩形.(2)当∠BAC=90°时,矩形AEBD是正方形.理由:∵AB=AC,AD是△ABC的角平分线,∴BD=CD.又∵∠BAC=90°,∴AD=BD.∴矩形AEBD是正方形.4.如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF =AE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.又∵CF=AE,∴BE=DF.又∵BE∥DF,∴四边形BFDE为平行四边形.∵DE⊥AB,∴∠DEB=90°.∴四边形BFDE是矩形.(2)∵四边形BFDE是矩形,∴∠BFD=90°.∴∠BFC=90°.在Rt△BFC中,由勾股定理,得BC=CF2+BF2=62+82=10.∴AD=BC=10.又∵DF=10,∴AD=DF.∴∠DAF=∠DFA.∵AB∥CD,∴∠DFA=∠FAB.∴∠DAF=∠FAB.∴AF是∠DAB的平分线.5.如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD 的中点.(1)当四边形ABCD是矩形时,四边形EFGH是菱形,请说明理由;(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.解:(1)理由:∵四边形ABCD是矩形,∴AC=BD.由题意,得EF=12AC,EH=12BD,GH=12AC,GF=12BD,∴EF=EH=GH=GF.∴四边形EFGH是菱形.(2)当四边形ABCD满足AC=BD且AC⊥BD时,四边形EFGH为正方形.理由:∵E,F分别是四边形ABCD的边AB,BC的中点,∴EF∥AC,EF=12AC.同理:EH∥BD,EH=12BD,GF=12BD,GH=12AC.又∵AC=BD,∴EF=EH=GH=GF.∴四边形EFGH是菱形.∵AC⊥BD,∴EF⊥EH.∴四边形EFGH是正方形.6.如图,等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.(1)求证:四边形EBFC是菱形;(2)如果∠BAC=∠ECF,求证:AC⊥CF.证明:(1)∵AB=AC,AH⊥BC,∴BH=HC.又∵FH=EH,∴四边形EBFC是平行四边形.又∵AH⊥BC,∴四边形EBFC是菱形.(2)∵四边形EBFC是菱形,∴∠ECH=∠FCH=12∠ECF.∵AB=AC,AH⊥BC,∴∠CAH=12∠BAC.∵∠BAC=∠ECF,∴∠CAH=∠FCH.∵AH⊥BC,∴∠CAH+∠ACH=90°.∴∠FCH+∠ACH=∠ACF=90°.∴AC⊥CF.7.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN是菱形.证明:∵MG∥AD,NF∥AB,∴四边形AMEN是平行四边形.∵四边形ABCD是菱形,∴AB=AD.∵BM=DN,∴AB-BM=AD-DN,即AM=AN.∴四边形AMEN是菱形.8.如图,在矩形ABCD中,AB=2,BC=5,E,P分别在AD,BC上,且DE=BP=1.(1)判断△BEC的形状,并说明理由;(2)判断四边形EFPH是什么特殊四边形?并证明你的判断.解:(1)△BEC是直角三角形.理由:∵四边形ABCD为矩形,∴∠ADC=∠BAD=90°,AD=BC=5,AB=CD=2.由勾股定理,得CE=CD2+DE2=22+12=5,BE=AB2+AE2=22+(5-1)2=2 5.∴CE2+BE2=5+20=25.∵BC2=52=25,∴BE2+CE2=BC2.∴∠BEC=90°.∴△BEC是直角三角形.(2)四边形EFPH为矩形.证明:∵四边形ABCD为矩形,∴AD=BC,AD∥BC.又∵DE=BP,∴四边形DEBP是平行四边形.∴BE∥DP.∵AD=BC,DE=BP,∴AE=CP.∴四边形AECP是平行四边形.∴AP∥CE.又∵BE∥DP,∴四边形EFPH是平行四边形.又∵∠BEC=90°,∴四边形EFPH是矩形.9.如图,在▱ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.证明:∵四边形ABCD是平行四边形,∴AD∥BC,CD∥AB.∴∠CDB=∠ABD.∵BE平分∠ABD,DF平分∠CDB,∴∠FDB=12∠CDB,∠EBD=12∠ABD.∴∠FDB=∠EBD.∴DF∥EB.又∵AD∥BC,∴四边形DFBE是平行四边形.∵AB=DB,BE平分∠ABD,∴BE⊥AD.∴∠DEB=90°.∴四边形DFBE是矩形.10.如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD 上一动点(不与点D重合),PO的延长线交BC于Q点.(1)求证:四边形PBQD 为平行四边形;(2)若AB =3 cm ,AD =4 cm ,点P 从点A 出发,以1 cm/s 的速度向点D 匀速运动.设点P 运动时间为t s ,问四边形PBQD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由.解:(1)证明:∵四边形ABCD 是矩形,∴AD ∥BC ,OD =OB .∴∠PDO =∠QBO .在△POD 和△QOB 中,⎩⎨⎧∠PDO =∠QBO ,OD =OB ,∠POD =∠QOB ,∴△POD ≌△QOB (ASA).∴OP =OQ .又∵OB =OD ,∴四边形PBQD 为平行四边形.(2)点P 从点A 出发运动t s 时,AP =t cm ,PD =(4-t )cm.当四边形PBQD 是菱形时,PB =PD =(4-t )cm.∵四边形ABCD 是矩形,∴∠BAP =90°.在Rt △ABP 中,AB =3 cm ,AP 2+AB 2=PB 2,即t 2+32=(4-t )2,解得t =78.∴点P 运动时间为78 s 时,四边形PBQD 为菱形.11.如图1,在▱ABCD 中,AF 平分∠BAD 交BC 于点F ,CE 平分∠BCD交AD 于点E.图1 图2(1)求证:四边形AFCE 是平行四边形;(2)如图2,若BE ⊥EC ,求证:四边形ABFE 是菱形.证明:(1)∵AF 平分∠BAD ,CE 平分∠BCD ,∴∠FAE =12∠BAE ,∠FCE =12∠FCD.∵四边形ABCD 是平行四边形,∴∠BAE =∠FCD ,AD ∥BC.∴∠FAE =∠FCE ,∠FCE =∠CED.∴∠FAE =∠CED.∴AF ∥EC.又∵AE ∥CF ,∴四边形AFCE 为平行四边形.(2)∵AF ∥EC ,BE ⊥EC ,∴∠AOE =∠BEC =90°.∴∠AOE =∠AOB =90°.在△ABO 和△AEO 中,⎩⎨⎧∠BAO =∠EAO ,AO =AO ,∠AOB =∠AOE ,∴△ABO ≌△AEO(ASA ).∴BO =EO.同理可得△ABO ≌△FBO ,∴AO =FO.∴四边形ABFE 是平行四边形.又∵AF ⊥BE ,∴平行四边形ABFE 是菱形.12.如图,矩形ABCD 中,AB =6,BC =4,过对角线BD 中点O 的直线分别交AB ,CD 边于点E ,F.(1)求证:四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,求EF 的长.解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴∠A =90°,AD =BC =4,AB ∥DC ,OB =OD .∴∠OBE =∠ODF .在△BOE 和△DOF 中,⎩⎨⎧∠OBE =∠ODF ,OB =OD ,∠BOE =∠DOF ,∴△BOE ≌△DOF (ASA).∴EO =FO .又∵OB =OD .∴四边形BEDF 是平行四边形.(2)∵四边形BEDF是菱形,∴BD⊥EF.设BE=x,则DE=x,AE=6-x.在Rt△ADE中,DE2=AD2+AE2,∴x2=42+(6-x)2.解得x=13 3.∵BD=AD2+AB2=213,∴OB=12BD=13.∵BD⊥EF,∴EO=BE2-OB2=213 3.∴EF=2EO=413 3.13.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.(1)求证:CE=AD;(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.解:(1)证明:∵DE⊥BC,∴∠DFB=90°.又∵∠ACB=90°,∴∠ACB=∠DFB.∴AC∥DE.又∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形.∴CE=AD.(2)四边形BECD是菱形.理由:∵D为AB中点,∴AD=BD.又由(1)得CE=AD,∴BD=CE.又∵BD∥CE,∴四边形BECD是平行四边形.又∵DE⊥BC,∴四边形BECD是菱形.(3)当∠A=45°时,四边形BECD是正方形.理由:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°.∴AC=BC.又∵D为AB中点,∴CD⊥AB,即∠CDB=90°.又∵四边形BECD是菱形,∴四边形BECD是正方形.∴当∠A=45°时,四边形BECD是正方形.14.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,分别延长OA ,OC 到点E ,F ,使AE =CF ,依次连接B ,F ,D ,E 各点.(1)求证:△BAE ≌△BCF ;(2)若∠ABC =50°,则当∠EBA =20° 时,四边形BFDE 是正方形. 证明:∵在菱形ABCD 中,BA =BC ,∴∠BAC =∠BCA .∴∠BAE =∠BCF .在△BAE 和△BCF 中,⎩⎨⎧BA =BC ,∠BAE =∠BCF ,AE =CF ,∴△BAE ≌△BCF (SAS).15.已知:如图,在菱形ABCD 中,点E ,O ,F 分别是边AB ,AC ,AD 的中点,连接CE ,CF ,OF.(1)求证:△BCE ≌△DCF ;(2)当AB 与BC 满足什么条件时,四边形AEOF 是正方形?请说明理由.解:(1)证明:∵四边形ABCD 为菱形,∴AB =BC =CD =DA ,∠B =∠D.又∵E ,F 分别是AB ,AD 的中点,∴BE =DF.在△BCE 和△DCF 中,⎩⎨⎧BC =DC ,∠B =∠D ,BE =DF ,∴△BCE ≌△DCF(SAS ).(2)当AB 与BC 满足AB ⊥BC 时,四边形AEOF 为正方形.理由如下: ∵E ,O 分别是AB ,AC 的中点,∴EO ∥BC.又∵BC ∥AD ,∴OE ∥AD ,即OE ∥AF.同理可证OF ∥AE ,∴四边形AEOF 为平行四边形.∵在菱形ABCD 中,点E ,F 分别是边AB, AD 的中点,∴AE =AF.∴四边形AEOF 为菱形.∵AB ⊥BC ,∴∠BAD =∠B =90°.∴四边形AEOF 为正方形.16.如图,在四边形ABCD 中,AB ∥CD ,AB≠CD ,BD =AC.(1)求证:AD =BC ;(2)若E ,F ,G ,H 分别是AB ,CD ,AC ,BD 的中点,求证:线段EF 与线段GH 互相垂直平分.证明:(1)延长DC 至K ,使CK =AB.连接BK.∵AB CK ,∴四边形ABKC 是平行四边形.∴AC BK.∴∠ACD =∠K.∵BD =AC ,AC =BK ,∴BD =BK.∴∠BDC =∠K.∴∠ACD =∠BDC.在△ACD 和△BDC 中,⎩⎨⎧AC =BD ,∠ACD =∠BDC ,CD =DC ,∴△ACD ≌△BDC(SAS ).∴AD =BC.(2)分别连接EH ,HF ,FG 和GE.∵E ,H 分别是AB ,BD 的中点,∴EH 为△ABD 的中位线.∴EH =12AD.同理:GF =12AD ,EG =12BC ,HF =12BC.又由(1)知AD =BC ,∴EH =HF =FG =GE.∴四边形EHFG 是菱形.∴线段EF 与线段GH 互相垂直平分.17.如图,在Rt △ABC 中,∠B =90°,点E 是AC 的中点,AC =2AB ,∠∥∥BAC 的平分线AD 交BC 于点D ,作AF ∥BC ,连接DE 并延长交AF 于点F ,连接FC.求证:四边形ADCF 是菱形.证明:∵AF ∥CD ,∴∠AFE =∠CDE.在△AFE 和△CDE 中,⎩⎨⎧∠AFE =∠CDE ,∠AEF =∠CED ,AE =CE ,∴△AFE ≌△CDE(AAS ).∴AF =CD.∵AF ∥CD ,∴四边形ADCF 是平行四边形.∵点E 是AC 的中点,AC =2AB ,∴AE =AB.∵AD 平分∠BAC ,∴∠EAD =∠BAD.又∵AD =AD ,∴△AED ≌△ABD(SAS ).∴∠AED =∠B =90°,即DF ⊥AC.∴四边形ADCF 是菱形.18.如图,△ABC ≌△ABD ,点E 在边AB 上,CE ∥BD ,连接DE. 求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.证明:(1)∵△ABC≌△ABD,∴∠ABC=∠ABD.∵CE∥BD,∴∠CEB=∠ABD.∴∠CEB=∠CBE.(2)∵△ABC≌△ABD,∴BC=BD.由(1)得∠CEB=∠CBE,∴CE=CB.∴CE=BD.又∵CE∥BD,∴四边形BCED是平行四边形.又∵BC=BD,∴四边形BCED是菱形.19.如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点;(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.解:(1)证明:∵AF∥BC,∴∠AFC=∠FCB.又∵∠AEF=∠DEC,AE=DE,∴△AEF≌△DEC(AAS).∴AF=DC.又∵AF=BD,∴BD=DC,即D是BC的中点.(2)四边形AFBD是矩形.证明:∵AF∥BC,AF=BD,∴四边形AFBD是平行四边形.∵AB=AC,D是BC的中点,∴AD⊥BC,即∠ADB=90°.∴四边形AFBD是矩形.20.已知:如图,在▱ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.证明:∵四边形ABCD是平行四边形,∴∠DAB+∠ADC=180°.∵AF,DF分别平分∠DAB,∠ADC,∴∠FAD=∠BAF=12∠DAB,∠ADF=∠CDF=12∠ADC.∴∠FAD+∠ADF=90°.∴∠AFD=90°.同理可得:∠BHC=∠HEF=90°.∴四边形EFGH是矩形.。
人教八年级数学特殊平行四边形相关知识归纳总结与例题精讲
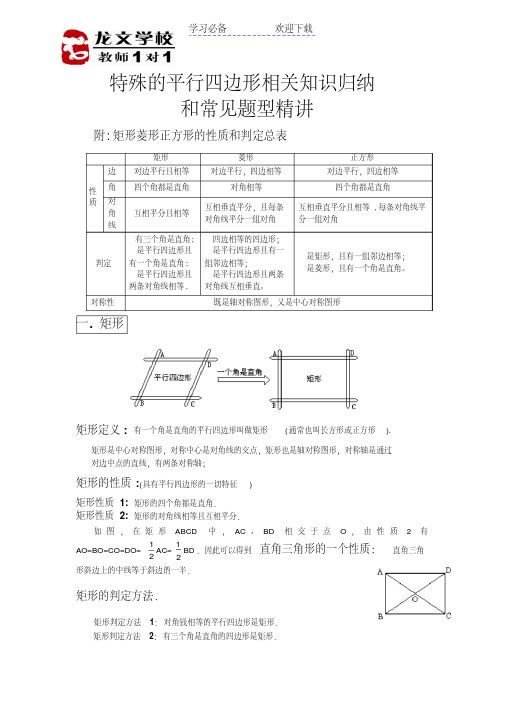
菱形的性质
性质 1 菱形的四条边都相等; 性质 2 菱形的对角线互相平分,并且每条对角线平分一组对角;
菱形的判定
菱形判定方法 1:对角线互相垂直的平行四边形是菱形.
注意此方法包括两个条件: (1)是一个平行四边形;(2)两条对角线互相垂 直.
菱形判定方法 2:四边都相等的四边形是菱形.
例 1 已知:如图,四边形 ABCD 是菱形, F 是 AB 上一点, DF 交 AC 于 E. 求证:∠ AFD= ∠CBE .
例 2 已知:如图 ABCD 的对角线 AC 的垂直平分线与边 AD 、 BC 分别交于 E、 F. 求证:四边形 AFCE 是菱形.
然后再加上相
学习必备
欢迎下载
例 1 已知:如图,正方形 ABCD 中,对角线的交点为 OB 上的一点, DG ⊥ AE 于 G,DG 交 OA 于 F. 求证: OE=OF .
O, E 是
例 2 已知:如图,四边形 ABCD 是正方形,分别过点 A 、 C 两点作 l 1∥ l2,作 BM ⊥ l 1 于 M , DN ⊥ l1 于 N ,直线 MB 、DN 分别交 l 2 于 Q、P 点.
求证:四边形 PQMN 是正方形.
例 3、( 2008 海南) 如图, P 是边长为 1 的正方形 ABCD 对角线 AC 上一动点( P 与 A、C 不重合),点 E 在射线 BC 上,且 PE=PB .
( 1)求证:① PE=PD ; ② PE⊥ PD ; ( 2)设 AP=x, △PBE 的面积为 y.
A
B
E
D
C
图5
例题讲解 例一 .分析:( 1)因为矩形四个角都是直角,因此矩形中的计算经常要用到直角三角形
人教版数学八年级下册专题训练:特殊平行四边形中的解题方法.doc

学校班级姓名解题技巧专题:特殊平行四边形中的解题方法◆类型一特殊四边形中求最值、定值问题一、利用对称性求最值【方法10】1.(2017·青山区期中)如图,四边形ABCD是菱形,AC=8,DB=6,P,Q分别是AC,AD上的动点,连接DP,PQ,则DP+PQ的最小值为________.第1题图第2题图2.(2017·安顺中考)如图,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________.二、利用面积法求定值3.如图,在矩形ABCD中,点P是线段BC上一动点,且PE⊥AC,PF⊥BD,AB=6,BC=8,则PE+PF的值为________.【变式题】矩形两条垂线段之和→菱形两条垂线段之和→正方形两条垂线段之和(1)(2017·眉山期末)如图,菱形ABCD的周长为40,面积为25,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于________.变式题(1)图变式题(2)图(2)如图,正方形ABCD的边长为1,E为对角线BD上一点且BE=BC,点P为线段CE 上一动点,且PM⊥BE于M,PN⊥BC于N,则PM+PN的值为________.◆类型二正方形中利用旋转性解题4.如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是__________.5.如图,在正方形ABCD中,点E,F分别在BC,CD上,∠EAF=45°.求证:S△AEF =S△ABE+S△ADF.6.如图,在正方形ABCD中,对角线AC,BD交于点O,P为正方形ABCD外一点,且BP⊥CP,连接OP.求证:BP+CP=2OP.参考答案与解析1.245解析:如图,过点Q 作QE ⊥AC 交AB 于点E ,则PQ =PE .∴DP +PQ =DP +PE .当点D ,P ,E 三点共线的时候DP +PQ =DP +PE =DE 最小,且DE 即为所求.当DE ⊥AB 时,DE 最小.∵四边形ABCD 是菱形,∴AC ⊥BD ,OA =12AC =4,OB =12BD =3,∴AB =5.∵S 菱形ABCD =12AC ·BD =AB ·DE ,∴12×8×6=5·DE ,∴DE =245.∴DP +PQ 的最小值为245.2.6 解析:如图,设BE 与AC 交于点P ,连接BD .∵点B 与D 关于AC 对称,∴PD =PB ,∴PD +PE =PB +PE =BE ,即P 为AC 与BE 的交点时,PD +PE 最小,为BE 的长度.∵正方形ABCD 的边长为6,∴AB =6.又∵△ABE 是等边三角形,∴BE =AB =6.故所求最小值为6.故答案为6.3.245解析:∵四边形ABCD 为矩形,∴∠ABC =90°.∵AB =6,BC =8,∴AC =10,∴OB =OC =12AC =5.如图,连接OP ,∵S △OBP +S △OCP =S △OBC ,∴OB ·PF 2+OC ·PE2=S △OBC ,∴5·PF 2+5·PE 2=S △OBC .∵S △OBC =14S矩形ABCD =14AB ·BC =14×6×8=12,∴5·PF 2+5·PE 2=12,∴PE +PF =245.【变式题】(1)52 解析:∵菱形ABCD 的周长为40,面积为25,∴AB =AD =10,S △ABD=252.连接AP ,则S △ABD =S △ABP +S △ADP ,∴12×10(PE +PF )=252,∴PE +PF =52. (2)22 解析:连接BP ,过点E 作EH ⊥BC 于H .∵S △BPE +S △BPC =S △BEC ,∴BE ·PM2+BC ·PN 2=BC ·EH 2.又∵BE =BC ,∴PM 2+PN 2=EH 2,即PM +PN =EH .∵△BEH 为等腰直角三角形,且BE =BC =1,∴EH =22,∴PM +PN =EH =22. 4.3 25.证明:延长CB 到点H ,使得HB =DF ,连接AH .∵四边形ABCD 是正方形,∴∠ABH =∠D =90°,AB =AD .∴△ADF 绕点A 顺时针旋转90°后能和△ABH 重合,∴AH =AF ,∠BAH =∠DAF .∵∠HAE =∠HAB +∠BAE =∠DAF +∠BAE =90°-∠EAF =90°-45°=45°,∴∠HAE =∠EAF =45°.又∵AE =AE ,∴△AEF 与△AEH 关于直线AE 对称,∴S △AEF =S △AEH =S △ABE +S △ABH =S △ABE +S △ADF .6.证明:∵四边形ABCD 是正方形,∴OB =OC ,∠BOC =90°.将△OCP 顺时针旋转90°至△OBE (如图所示),∴OE =OP ,BE =CP ,∠OBE =∠OCP ,∠BOE =∠COP .∵BP ⊥CP ,∴∠BPC =90°.∵∠BOC +∠OBP +∠BPC +∠OCP =360°,∴∠OBP +∠OCP =180°,∴∠OBP +∠OBE =180°,∴E ,B ,P 在同一直线上.∵∠POC +∠POB =∠BOC =90°,∠BOE =∠COP ,∴∠BOE +∠POB =90°,即∠EOP =90°.在Rt △EOP 中,由勾股定理得PE =OE 2+OP 2=OP 2+OP 2=2OP .∵PE =BE +BP ,BE =CP ,∴BP +CP =2OP .中考数学知识点代数式 一、 重要概念分类:1.代数式与有理式用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
特殊四边形的计算与证明问题(真题10道+模拟30道)-中考数学重难题型押题培优导练案【原卷版】

专题14特殊四边形的计算与证明问题(北京真题10道+模拟30道)【方法归纳】题型概述,方法小结,有的放矢考点考查年份考查频率十年8考特殊四边形的计算与证明(大题)2013.2014.2015.2016.2017.2020.2021.2022以四边形为载体的计算与证明是北京市中考数学常考的一类解答题,要求学生理解和掌握平行四边形、矩形、菱形、正方形的性质定理和判定定理,会画出四边形全等变换后的图形,并会结合其他知识解答一些有探索性、开放性的问题,提高解决问题的能力.解决此类问题的关键是要牢牢把握四边形的性质与特征,挖掘相关图形之间的联系,利用所给图形及图形之间形状、大小、位置关系,进行观察、实验、比较、联想、类比、分析、综合等.常用到的矩形、菱形、正方形的解题策略有:(1)对于矩形:①判定四边形是矩形,一般先判定是平行四边形,然后再判定是矩形;②矩形的内角是直角和对角线相等,相对于平行四边形来说是矩形特殊的性质;③利用矩形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解.(2)对于菱形:①判定四边形是菱形,一般先判定是平行四边形,然后再判定是菱形;②菱形的邻边相等和对角线垂直,相对于平行四边形来说是菱形特殊的性质;③利用菱形的性质计算或证明时,常常运用勾股定理,锐角三角函数或相似三角形求解;④求线段和的最小值时,往往运用菱形的轴对称的性质转化为求线段的长度.(3)对于正方形:①判定四边形是正方形,一般先判定是平行四边形,然后再判定是矩形或菱形,最后判定这个四边形是正方形;②正方形是最特殊的四边形,在正方形的计算或证明时,要特别注意线段或角的等量转化.【典例剖析】典例精讲,方法提炼,精准提分【例1】(2021·北京·中考真题)如图,在四边形ABCD中,∠ACB=∠CAD=90°,点E在BC上,AE//DC,EF⊥AB,垂足为F.(1)求证:四边形AECD是平行四边形;,求BF和AD的长.(2)若AE平分∠BAC,BE=5,cosB=45【例2】(2022·北京·中考真题)如图,在▱ABCD中,AC,BD交于点O,点E,F在AC上,AE=CF.(1)求证:四边形EBFD是平行四边形;(2)若∠BAC=∠DAC,求证:四边形EBFD是菱形.【真题再现】必刷真题,关注素养,把握核心1.(2014·北京·中考真题)如图,在平行四边形ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.(1)求证:四边形ABEF是菱形;(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.2.(2016·北京·中考真题)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.(1)求证:BM=MN;(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.3.(2017·北京·中考真题)如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.(1)求证:四边形BCDE为菱形;(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.4.(2017·北京·中考真题)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.,(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)请根据上图完成这个推论的证明过程.证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),S矩形EBMF=S△ABC-(____________+____________).易知,S△ADC=S△ABC,_____________=______________,______________=_____________.可得S矩形NFGD= S矩形EBMF.5.(2013·北京·中考真题)如图,在▱ABCD中,F是AD的中点,延长BC到点E,使CE=1BC,连结DE,2CF.(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长.6.(2015·北京·中考真题)在▱ABCD,过点D作DE∠AB于点E,点F在边CD上,DF=BE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.7.(2020·北京·中考真题)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF∠AB,OG∠EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.8.(2016·北京·中考真题)如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E.求证:DA=DE.【模拟精练】押题必刷,巅峰冲刺,提分培优一、解答题1.(2022·北京房山·二模)已知:如图,在四边形ABCD中,AB∥DC,AC⊥BD,垂足为M,过点A作AE⊥AC,交CD的延长线于点E.(1)求证:四边形ABDE是平行四边形;(2)若AC=8,sin∠ABD=4,求BD的长.52.(2022·北京西城·二模)如图,菱形ABCD的对角线AC,BD交于点O,点E,F分别在DA,BC的延长线上,且BE∠ED,CF=AE.(1)求证:四边形EBFD是矩形;(2)若AB=5,cos∠OBC=4,求BF的长.53.(2022·北京朝阳·二模)如图,在菱形ABCD中,O为AC,BD的交点,P,M,N分别为CD,OD,OC 的中点.(1)求证:四边形OMPN是矩形;(2)连接AP,若AB=4,∠BAD=60∘,求AP的长.4.(2022·北京东城·二模)如图,在平行四边形ABCD中,DB=DA,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.(1)求证:四边形AEBD是菱形;(2)若DC=√10,tan∠DCB=3,求菱形AEBD的边长.5.(2022·北京平谷·二模)如图,在□ABCD中,连接AC,点E是AB中点,点F是AC的中点,连接EF,过E作EG∥AF,交DA的延长线于点G.(1)求证:四边形AGEF是平行四边形;(2)若sin∠G=3,AC=10,BC=12,连接GF,求GF的长.56.(2022·北京北京·二模)如图,在等边△ABC中,D是BC的中点,过点A作AE∥BC,且AE=DC,连接CE.(1)求证:四边形ADCE是矩形;(2)连接BE交AD于点F,连接CF.若AB=4,求CF的长.7.(2022·北京丰台·二模)如图,在∠ABC中,∠BAC=90∘,AD∠BC,垂足为D,AE∠BC,CE∠DA.(1)求证:四边形AECD是矩形;(2)若AB=5,cosB=3,求AE的长.58.(2022·北京密云·二模)如图,在平行四边形ABCD中,AC平分∠BAD,点E为AD边中点,过点E作AC的垂线交AB于点M,交CB延长线于点F.(1)求证:平行四边形ABCD是菱形;(2)若FB=2,sinF=3,求AC的长.59.(2022·北京市十一学校模拟预测)如图,在四边形ABCD中,AD=CD,BD⊥AC于点O,点E是DB延长线上一点,OE=OD,BF⊥AE于点F.(1)求证:四边形AECD是菱形;(2)若AB平分∠EAC,OB=3,tan∠CED=3,求EF和AD的长.410.(2022·北京昌平·二模)如图,在矩形ABCD中,对角线AC,BD交于点O,分别过点C,D作BD,AC的平行线交于点E,连接OE交AD于点F.(1)求证:四边形OCED是菱形;(2)若AC=8,∠DOC=60°,求菱形OCED的面积.11.(2022·北京海淀·二模)如图,在Rt∠ABC中,∠A =90°,点D,E,F分别为AB,AC,BC的中点,连接DF,EF.(1)求证:四边形AEFD是矩形;(2)连接BE,若AB = 2,tan C =1,求BE的长.212.(2022·北京东城·一模)如图,在正方形ABCD中,E为对角线AC上一点(AE>CE),连接BE,DE.(1)求证:BE=DE;(2)过点E作EF⊥AC交BC于点F,延长BC至点G,使得CG=BF,连接DG.∠依题意补全图形;∠用等式表示BE与DG的数量关系,并证明.13.(2022·北京东城·一模)如图,在四边形ABCD中,AC与BD相交于点O,且AO=CO,点E在BD上,∠EAO=∠DCO.(1)求证:四边形AECD是平行四边形;(2)若AB=BC,CD=5,AC=8,tan∠ABD=2,求BE的长.314.(2022·北京市十一学校二模)如图,在平行四边形ABCD中,CE⊥AD于点E,延长DA至点F,使得AF=DE,连接BF,CF.(1)求证:四边形BCEF是矩形;(2)若AB=6,CF=8,DF=10,求EF的长.15.(2022·北京石景山·一模)如图所示,△ABC中,∠ACB=90°,D,E分别为AB,BC的中点,连接DE 并延长到点F,使得EF=DE,连接CD,CF,BF.(1)求证:四边形BFCD是菱形;(2)若cos A=5,DE=5,求菱形BFCD的面积.1316.(2022·北京大兴·一模)如图,在平面四边形ABCD中,点E,F分别是AB,CD上的点,CF=BE.(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AD=2,AB=4,求BD的长.17.(2022·北京丰台·一模)如图,在四边形ABCD中,∠DCB=90°,AD∥BC,点E在BC上,AB∥DE,AE 平分∠BAD.(1)求证:四边形ABED为菱形;(2)连接BD,交AE于点O.若AE=6,sin∠DBE=3,求CD的长.518.(2022·北京市师达中学模拟预测)如图,四边形ABCD是平行四边形,AE∠BC,AF∠CD,垂足分别为E,F,且BE=DF.(1)求证:四边形ABCD是菱形;(2)连接EF并延长,交AD的延长线于点G,若∠CEG=30°,AE =2,求EG的长.19.(2022·北京四中模拟预测)如图,在四边形ABCD中,AD=CD,BD∠AC于点O,点E是DB延长线上一点,OE=OD,BF∠AE于点F.(1)求证:四边形AECD是菱形;(2)若AB平分∠EAC,OB=3,BE=5,求EF和AD的长.20.(2021·北京丰台·一模)如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE∠BC于E,延长BC到点F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)连接OE,若AD=10,EC=4,求OE的长度.21.(2022·北京市燕山教研中心一模)如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD 交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若BD=4,AC=3,求sin∠CDE的值.22.(2022·北京平谷·一模)如图,∠ABC中,∠ACB=90°,点D为AB边中点,过D点作AB的垂线交BC 于点E,在直线DE上截取DF,使DF=ED,连接AE、AF、BF.(1)求证:四边形AEBF是菱形;(2)若cos∠EBF=3,BF=5,连接CD,求CD的长.523.(2022·北京市第一六一中学分校一模)在矩形ABCD中,AC,BD相交于点O,过点C作CE∠BD交AD的延长线于点E.(1)求证:∠ACD=∠ECD;(2)连接OE,若AB=2,tan∠ACD=2,求OE的长.24.(2022·北京房山·一模)如图,在平行四边形ABCD中,过点B作BE∠CD交CD的延长线于点E,过点C作CF∥EB交AB的延长线于点F.(1)求证:四边形BFCE是矩形;(2)连接AC,若AB=BE=2,tan∠FBC=1,求AC的长225.(2022·北京朝阳·一模)如图,在矩形ABCD中,AC,BD相交于点O,AE//BD,BE//AC.(1)求证:四边形AEBO是菱形;(2)若AB=OB=2,求四边形AEBO的面积.26.(2022·北京·中国人民大学附属中学分校一模)如图,正方形ABCD中,P为BD上一动点,过点P作PQ⊥AP 交CD边于点Q.(1)求证:PA=PQ;(2)用等式表示PB、PD、AQ之间的数量关系,并证明;(3)点P从点B出发,沿BD方向移动,若移动的路径长为4,则AQ的中点M移动的路径长为(直接写出答案).BC,27.(2022·北京市三帆中学模拟预测)已知:△ABC中,AB=AC,AD⊥BC于点D,过点A作AE,且AE=12连结DE.(1)求证:四边形ABDE是平行四边形;(2)作FG⊥AB于点G,AG=4,cos∠GAF=4,求FG和FD的长.528.(2022·北京西城·一模)如图,在∠ABC中,BA=BC,BD平分∠ABC交AC于点D,点E在线段BD上,点F在BD的延长线上,且DE=DF,连接AE,CE,AF,CF.(1)求证:四边形AECF是菱形;(2)若BA∠AF,AD=4,BC=4√5,求BD和AE的长.29.(2022·北京顺义·一模)如图,在四边形ABCD中,AD∥BC,AC⊥BD,垂足为O,过点D作BD的垂线交BC的延长线于点E.(1)求证:四边形ACED是平行四边形;(2)若AC=4,AD=2,cos∠ACB=4,求BC的长.530.(2022·北京通州·一模)如图.在∠ABC中,AB=BC,BD平分∠ABC交AC于点D.点E为AB的中点,连接DE,过点E作EF∥BD交CB的延长线于点F.(1)求证:四边形DEFB是平行四边形;(2)当AD=4,BD=3时,求CF的长.。
特殊四边形的证明与计算

特殊四边形的证明与计算1.如图,△ABC 是等边三角形,点E 在线段AC 上,连接BE ,以BE 为边作等边三角形BEF ,将线段CE 绕点C 顺时针旋转60°,得到线段CD ,连接AF 、AD 、ED .(1)求证:△BCE ≌△ACD ;(2)求证:四边形ADEF 是平行四边形.第1题图证明:(1)∵△ABC 是等边三角形,∴BC =AC ,∠BCE =60°,由题意得CE =CD ,∠ECD =60°.在△BCE 和△ACD 中,⎩⎪⎨⎪⎧BC =AC ∠BCE =∠ACD =60°CE =CD, ∴△BCE ≌△ACD (SAS);(2)∵△BCE ≌△ACD ,∴AD =BE ,∠DAE =∠CBE ,∵△BEF 是等边三角形,∴BE=EF=BF,∠EBF=60°,∴AD=EF,∵△ABC与△BEF均是等边三角形,∴∠BCE=∠BEF=60°,∵∠BCE+∠CBE=∠BEF+∠AEF,∴∠CBE=∠AEF,∴∠DAE=∠AEF,∴AD∥EF,∴四边形ADEF是平行四边形.2.如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE 平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.(1)求证:四边形BDEF是平行四边形;(2)线段BF、AB、AC之间具有怎样的数量关系?证明你所得到的结论.第2题图(1)证明:如解图,延长CE交AB于点G,第2题解图∵AE ⊥CE ,∴∠AEG =∠AEC =90°,∵AE 平分∠BAC ,∴∠GAE =∠CAE ,在△AGE 和△ACE 中,⎩⎪⎨⎪⎧∠GAE =∠CAE AE =AE∠AEG =∠AEC, ∴△AGE ≌△ACE (ASA),∴GE =EC .∵点D 是边BC 的中点,∴BD =CD ,DE 为△CGB 的中位线,∴DE ∥BF .又∵EF ∥BC ,∴四边形BDEF 是平行四边形;(2)解:BF =12(AB -AC ).理由如下:由(1)可知,△AGE ≌△ACE ,四边形BDEF 是平行四边形,∴AG =AC ,BF =DE =12BG ,∴BF =12BG =12(AB -AG )=12(AB -AC ).3.如图,已知边长为22的正方形ABCD中,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交线段BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)设AE=x,四边形DEFG的面积为S,当x为何值时,S的值最小,求出最小值.第3题图(1)证明:如解图①,过点E作EM⊥BC于点M,EN⊥CD于点N,第3题解图①∴∠MEN=90°,∴∠MEF+∠FEN=90°,∵点E是正方形ABCD对角线上的点,∴EM=EN,∵∠DEF=90°,∴∠DEN+∠FEN=90°,∴∠DEN =∠MEF ,在△DEN 和△FEM 中,⎩⎪⎨⎪⎧∠DNE =∠FME =90°EN =EM∠DEN =∠FEM, ∴△DEN ≌△FEM (ASA),∴DE =EF ,∵四边形DEFG 是矩形,∴矩形DEFG 是正方形;(2)解:∵在正方形ABCD 中,AB =22,∴AC =4,∠DAE =45°,如解图②,过点E 作EH ⊥AD 于点H ,第3题解图②∵AE =x (0<x <4),∴AH =EH =22x ,在Rt △DHE 中,DH =AD -AH =22-22x ,EH =22x ,根据勾股定理得,DE2=DH2+EH2=(22-22x)2+(22x)2=x2-4x+8,∵四边形DEFG为正方形,∴S=DE2=x2-4x+8=(x-2)2+4,∴当x=2时,S有最小值,即为4.4.如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB =CD,延长CA至点E,使AE=AC;延长CB至点F,使BF=BC,连接AD、AF、DF、EF.延长DB交EF于点N.(1)求证:AD=AF;(2)试判断四边形ABNE的形状,并说明理由.第4题图(1)证明:∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∴∠ABF=180°-∠ABC=135°,∵∠BCD=90°,∴∠ACD=90°+∠ACB=135°,∴∠ABF=∠ACD,∵CB=CD,CB=BF,∴BF =CD ,在△ABF 和△ACD 中,⎩⎪⎨⎪⎧AB =AC ∠ABF =∠ACD BF =CD,∴△ABF ≌△ACD (SAS),∴AD =AF ;(2)解:四边形ABNE 是正方形.理由如下:∵CD =CB ,∠BCD =90°,∴∠CBD =45°,∵∠ABC =45°,∴∠ABD =90°,∴∠ABN =90°,由(1)知△ABF ≌△ACD ,∴∠F AB =∠CAD ,∴∠F AB +∠BAD =∠CAD +∠BAD =90°,∵∠EAF +∠F AB =90°,∴∠EAF =∠BAD ,∵AB =AC =AE ,AF =AD ,∴△AEF ≌△ABD (SAS).∴∠AEF =∠ABD =90°,∵∠EAB=90°,∴四边形ABNE是矩形,又∵AE=AB,∴四边形ABNE是正方形.5.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB 的中点,F是AC延长线上的一点.(1)若ED⊥EF,求证:ED=EF;(2)在(1)的条件下,若DC的延长线与FB交于点P,试判断四边形ACPE是否为平行四边形?并证明你的结论.(请先补全图形,再解答)第5题图(1)证明:∵四边形ABCD是平行四边形,AD=AC,AD⊥AC.∴AC=BC,AC⊥BC,如解图,连接CE,第5题解图∵E为AB的中点,∴AE =EC ,CE ⊥AB ,∴∠ACE =∠CAE =45°,∴∠DAE =∠ECF =135°,又∵∠AED +∠CED =∠CEF +∠CED =90°,∴∠AED =∠CEF ,∴△AED ≌△CEF (ASA),∴ED =EF ;(2)解:补全图形如解图,四边形ACPE 是平行四边形;证明:∵由(1)得△AED ≌△CEF ,∴AD =CF ,∴AC =CF ,又∵CP ∥AE ,∴CP 为△F AB 的中位线,∴CP =12AB =AE ,∵CP ∥AE ,∴四边形ACPE 是平行四边形.6.如图,已知Rt △ABC 中,∠ABC =90°,先把△ABC 绕点B 顺时针旋转90°至△DBE ,再把△ABC 沿射线AB 平移至△FEG ,DE 、FG 相交于点H .(1)判断线段DE 、FG 的位置关系,并说明理由;(2)连接CG,求证:四边形CBEG是正方形.第6题图(1)解:FG⊥DE.理由如下:∵△ABC绕点B顺时针旋转90°至△DBE,∴∠DEB=∠ACB,∵把△ABC沿射线AB平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,∴∠A+∠ACB=90°,∴∠GFE+∠DEB=90°,∴∠FHE=90°,∴FG⊥DE;(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,∵CG∥EB,∴∠BCG+∠CBE=180°,∴∠BCG=90°,∴四边形BCGE是矩形,∵CB=BE,∴四边形CBEG 是正方形.7.如图①,BD 是矩形ABCD 的对角线,∠ABD =30°,AD =1.将△BCD 沿射线BD 方向平移到△B ′C ′D ′的位置,使B ′为BD 中点,连接AB ′,C ′D ,AD ′,BC ′.如图②.(1)求证:四边形AB ′C ′D 是菱形; (2)四边形ABC ′D ′的周长为________.第7题图(1)证明:∵四边形ABCD 是矩形, ∴AD ∥BC ,AD =BC .由平移性质可知AD ∥B ′C ′,AD =B ′C ′, ∴四边形AB ′C ′D 为平行四边形, ∵∠DAB =90°,∠ABD =30°, ∴AD =12BD . ∵B ′为BD 中点, ∴AB ′=12BD , ∴AD =AB ′,∴四边形AB ′C ′D 是菱形;(2)解:4 3.【解法提示】如解图,连接AC′交B′D于点O,第7题解图∵四边形AB′C′D是菱形,∴AC′⊥BD′,OA=OC′,OD=OB′,又∵BD=B′D′,∴BB′=DD′,∴OB=OD′,∴四边形ABC′D′是菱形,∴tan∠ABD=tan30°=33=ADAB=1AB,得AB=3,∴四边形ABC′D′的周长是4 3.8.边长为22的正方形ABCD中,P是对角线AC上的一个动点(点P 与A、C不重合).连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP的延长线与AD(或AD延长线)交于点F.(1)连接CQ,证明:CQ=AP;(2)设AP=x,CE=y,试写出y关于x的函数关系式,并求当x为何值时,CE=38BC;(3)猜想PF 与EQ 的数量关系,并证明你的结论.第8题图(1)证明:由题意知BP =BQ ,∠PBQ =90°, 在正方形ABCD 中,AB =CB ,∠ABC =90°, ∴∠ABC =∠PBQ ,∴∠ABC -∠PBC =∠PBQ -∠PBC ,即∠ABP =∠CBQ , 在△ABP 和△CBQ 中, ⎩⎪⎨⎪⎧AB =CB ∠ABP =∠CBQ BP =BQ, ∴△ABP ≌△CBQ (SAS), ∴CQ =AP ;(2)解:在正方形ABCD 中,AC 为对角线, ∴∠BAP =∠PCE =45°,由旋转可知△PBQ 为等腰直角三角形, ∴∠BPQ =∠PQB =45°,在△ABP 中,∠BPC =∠BAP +∠ABP =45°+∠ABP , 又∵∠BPC =∠BPQ +∠CPE =45°+∠CPE ,∴∠ABP =∠CPE , 又∵∠BAP =∠PCE , ∴△BAP ∽△PCE , ∴AB CP =AP CE ,在等腰直角△ABC 中,AB =22, ∴AC =4,又∵AP =x ,CE =y ,∴CP =4-x , ∴224-x=x y ,即y =-24x 2+2x ,(0<x <4) 当CE =38BC 时,即CE =y =38×22=324, ∴324=-24x 2+2x , 解得x 1=1,x 2=3,∴y =-24x 2+2x (0<x <4),当x =1或3时,CE =38BC ; (3)解:猜想:PF =EQ .证明:①当点F 在线段AD 上时,如解图①,在CE 上取一点H ,使HQ =EQ ,则∠QEH =∠QHE ,第8题解图①在正方形ABCD 中,∵AD ∥BC , ∴∠DFE =∠QEH , ∴∠DFE =∠QHE , ∴∠AFP =∠CHQ ,由(1)知△ABP ≌△CBQ ,AP =CQ ,∠BAP =∠BCQ =45°, ∴∠F AP =∠BAP =∠BCQ =45°, 在△AFP 和△CHQ 中, ⎩⎪⎨⎪⎧∠F AP =∠HCQ ∠AFP =∠CHQ AP =CQ, ∴△AFP ≌△CHQ (AAS), ∴PF =HQ , 又∵HQ =EQ , ∴PF =EQ ;②当点F 在线段AD 延长线上时,如解图②,在BE 上取一点H ,使HQ =EQ ,第8题解图②同理可证△AFP ≌△CHQ (AAS),得FP =HQ =EQ.9.如图,在△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG 沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE 和DF相交于点C.(1)求证:四边形ABCD是正方形;(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.第9题图(1)证明:∵△AEB由△AEG翻折得到,∴∠ABE=∠AGE=90°,∠BAE=∠EAG,AB=AG,∵△AFD由△AFG翻折得到,∴∠ADF=∠AGF=90°,∠DAF=∠F AG,AD=AG,∵∠EAG+∠F AG=∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠ABE=∠AGE=∠BAD=∠ADC=90°,∴四边形ABCD是矩形,又∵AB=AG=AD,∴四边形ABCD是正方形;(2)解:MN 2=ND 2+DH 2, 理由:如解图,连接NH ,第9题解图∵△ADH 由△ABM 旋转得到, ∴△ABM ≌△ADH ,∴AM =AH ,∠BAM =∠DAH ,∠ADH =∠ABM =45°,∴∠HAN =∠DAH +∠DAN =∠BAM +∠DAN =∠EAG +∠F AG =∠EAF ,∵在△AMN 和△AHN 中, ⎩⎪⎨⎪⎧AM =AH ∠MAN =∠NAH AN =AN, ∴△AMN ≌△AHN (SAS), ∴MN =NH , 由(1)知∠ADB =45°,∴∠HDN =∠ADH +∠ADN =90°, ∴在Rt △DHN 中,DH 2+DN 2=NH 2,∴MN2=ND2+DH2.10.如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD 于点E,N,M,连接EO.(1)已知EO=2,求正方形ABCD的边长;(2)猜想线段EM与CN的数量关系并加以证明.第10题图解:(1)∵正方形ABCD的对角线AC,BD相交于点O,∴O是线段AC的中点,∵CF=AC,∴△ACF是等腰三角形,又∵CE平分∠ACF,∴E是AF的中点,∴EO是△ACF的中位线,∴CF=2EO=22,∴AC=22,∵四边形ABCD是正方形,∴∠ACB=45°,∴在Rt △ABC 中,AB =AC ·sin45°=22×22=2, ∴正方形ABCD 的边长为2. (2)猜想:EM =12CN . 证明:如解图,连接BE ,第10题解图由(1)知,E 是AF 的中点, ∴在Rt △ABF 中,EB =AE =12AF , ∴∠ABE =∠BAF ,∵AC =CF ,CE 平分∠ACF , ∴CE ⊥AF ,∴∠F +∠BCN =90°, 又∵∠F +∠BAF =90°, ∴∠BCN =∠BAF ,∵AB =BC ,∠ABF =∠CBN =90°, ∴△ABF ≌△CBN (ASA), ∴AF =CN ,∴EB =12AF =12CN ,又∵∠EBM =∠ABE +∠ABO =∠BAF +∠OBC =∠BCE +∠OBC =∠EMB ,∴EB =EM ,∴EM =12CN .11.(1)如图①,在矩形ABCD 中,对角线AC 与BD 相交于点O ,过点O 作直线EF ⊥BD 交AD 于点E ,交BC 于点F ,连接BE ,DF ,且BE 平分∠ABD .求证:四边形BFDE 是菱形;(2)把(1)中菱形BFDE 进行分离研究,如图②,G ,I 分别在BF ,BE 边上,且BG =BI ,连接GD ,H 为GD 的中点,连接FH 并延长交ED 于点J ,连接IJ ,IH ,IF ,IG .试探究线段IH 与FH 之间满足的数量关系,并说明理由;第11题图(1)证明:如解图①,第11题解图①∵四边形ABCD 是矩形, ∴AD ∥BC ,OB =OD , ∴∠EDO =∠FBO , 在△DOE 和△BOF 中, ⎩⎪⎨⎪⎧∠EDO =∠FBO OD =OB∠EOD =∠BOF, ∴△DOE ≌△BOF (ASA), ∴EO =OF , ∵OB =OD ,∴四边形BFDE 是平行四边形, ∵EF ⊥BD ,∴四边形BFDE 是菱形; (2)解:IH =3FH .理由:如解图②,延长BE 到点M ,使得EM =EJ ,连接MJ .第11题解图②如解图①,∵四边形BFDE 是菱形, ∴∠EBO =∠FBO ,又∵BE 平分∠ABD , ∴∠ABE =∠EBO ,∴∠ABE =∠EBO =∠FBO =30°, ∴∠EBF =60°,如解图②,由四边形BFDE 是菱形可得EB =BF =ED ,DE ∥BF , ∴∠JDH =∠FGH , 在△DHJ 和△GHF 中, ⎩⎪⎨⎪⎧∠DHJ =∠GHF DH =GH∠JDH =∠FGH, ∴△DHJ ≌△GHF (ASA), ∴DJ =FG ,JH =HF , ∴EJ =BG =EM =BI , ∴BE =IM =BF , ∵∠MEJ =∠B =60°, ∴△MEJ 是等边三角形,∴MJ =EM =BI ,∠M =∠EBF =60°, 在△BIF 和△MJI 中, ⎩⎪⎨⎪⎧BI =MJ ∠B =∠M BF =IM, ∴△BIF ≌△MJI (SAS),∴IJ=IF,∠BFI=∠MIJ,∵HJ=HF,∴IH⊥JF,∵∠BFI+∠BIF=120°,∴∠MIJ+∠BIF=120°,∴∠JIF=60°,∴△JIF是等边三角形,在Rt△IHF中,∵∠IHF=90°,∠IFH=60°,∴IH=3FH.12.如图①,两个全等的等边三角形纸片ABC和DEF,其中点C和点F重合,点A、D均在直线l上,且AB⊥l,DE⊥l.如图①,保持纸片DEF不动,将△ABC沿l向右平移,直到AB与DE重合时停止,如图②,设BC与EF相交于点G,AC与DF相交于点H.(1)证明:四边形CGFH是菱形;(2)当AD=AB时,直接写出S△AHD与S菱形CGFH的关系;第12题图(1)证明:根据平移性质可知,GF∥HC,GC∥FH,∴四边形CGFH是平行四边形,∵AB⊥l,DE⊥l,∴∠BAD=∠EDA=90°,∵△ABC和△DEF都是等边三角形,∴∠BAC=∠EDF=60°,∴∠CAD=∠FDA=30°,∴HA=HD,∵△ABC≌△DEF,∴AC=DF,∴AC-AH=DF-DH,∴HC=HF,∴四边形CGFH是菱形;(2)解:S菱形CGFH=(8-43)S△AHD.【解法提示】如解图,过点H作HM⊥AD于点M,连接GH,设AB=AD=6a,第12题解图∵HA=HD,HM⊥AD,∴AM=MD=3a,∵∠HAM=30°,∴HM=33AM=3a,AH=2HM=23a,∴HC =AC -AH =6a -23a , ∵∠C =60°,四边形CGFH 是菱形, ∴△CGH 和△FGH 都是等边三角形,∴S 菱形CGFH =2S △CHG =2×34CH 2=32(6a -23a )2=(243-36)a 2, ∵S △ADH =12AD ·HM =12·6a ·3a =33a 2, ∴S △AHDS 菱形CGFH =33a 2(243-36)a 2=18-43, 即S 菱形CGFH =(8-43)S △AHD .13.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,△COD 关于CD 的对称图形为△CED . (1)求证:四边形OCED 是菱形;(2)连接AE ,若AB =6 cm ,BC = 5 cm.求sin ∠EAD 的值.第13题图(1)证明:∵四边形ABCD 是矩形, ∴AC =BD ,且AC 、BD 互相平分, ∴DO =CO .∵△COD 与△CED 关于CD 对称, ∴△COD ≌△CED ,∴CO=CE,DO=DE,∴CE=CO=DO=DE,∴四边形OCED是菱形;(2)解:如解图,连接EO交CD于点F,延长交AB于点H.第13题解图∵四边形ABCD是矩形,AB=6 cm,∴BC⊥CD,CD=AB=6 cm.∵四边形OCED是菱形,∴EO⊥CD,且EO、CD互相平分,∴EF=FO,DF=FC=3 cm,FO∥BC,即EH∥BC,又∵CE∥OB,∴四边形OBCE为平行四边形.又∵BC= 5 cm,∴EF=FO=12BC=52cm.∵FO∥BC,在矩形ABCD中,AB∥CD,∠ABC=90°,∴四边形FHBC是矩形,∴FH=BC= 5 cm,HB=FC=3 cm,∴AH=AB-HB=3 cm,EH=EF+FH=352cm.∵AB ∥CD ,EH ⊥CD , ∴EH ⊥AB ,∴在Rt △AEH 中,AE 2=AH 2+EH 2=32+(352)2=814 cm 2, ∴AE =92 cm ,∴sin ∠AEH =AH AE =392=23,∵EH ∥BC ,AD ∥BC ,∴AD ∥EH ,∴∠EAD =∠AEH ,∴sin ∠EAD =sin ∠AEH =23. 14.如图,在矩形ABCD 中,E 为AB 边上一点,EC 平分∠DEB ,F 为CE 的中点,连接AF ,BF ,过点E 作EH ∥BC 分别交AF ,CD 于G ,H 两点. (1)求证:DE =DC ; (2)求证:AF ⊥BF ;(3)当AF ·GF =28时,请直接写出CE 的长.第14题图(1)证明:∵四边形ABCD 为矩形,∴AB ∥DC ,∴∠DCE =∠CEB , ∵EC 平分∠DEB , ∴∠DEC =∠CEB , ∴∠DEC =∠DCE , ∴DE =DC ;(2)证明:如解图,连接DF ,第14题解图∵DE =DC ,F 为CE 的中点, ∴DF ⊥EC , ∴∠DFC =90°, 在矩形ABCD 中, AB =DC ,∠ABC =90°, ∴BF =CF =EF =12EC , ∴∠ABF =∠CEB , ∵∠DCE =∠CEB , ∴∠ABF =∠DCE , ∴△ABF ≌△DCF (SAS),∴∠AFB =∠DFC =90°,∴AF ⊥BF ;(3)解:CE =47.【解法提示】∵∠AFB =90°,∴∠BAF +∠ABF =90°, ∵EH ∥BC ,∠ABC =90°,∴∠BEH =90°, ∴∠FEH +∠CEB =90°,∵∠ABF =∠CEB ,∴∠BAF =∠FEH , ∵∠EFG =∠AFE ,∴△EFG ∽△AFE , ∴EF AF =GFEF ,∴EF 2=AF ·GF ,∵AF ·GF =28,∴EF =28=27,∴CE =2EF =47.15.如图,四边形ABCD 是正方形,AB =4,E 是边CD 上的点,F 是DA 的延长线上的点,且CE =AF .将△BCE 沿BE 折叠,得到△BC ′E ,延长BC ′交AD 于点G . (1)求证:△BCE ≌△BAF ; (2)①若DG =1,求FG 的长;②若∠CBE =30°,点B 和点H 关于DF 对称,求证:四边形FHGB 是菱形.第15题图(1)证明:∵四边形ABCD 为正方形,∴AB=BC,∠F AB=∠C=90°,第15题解图又∵CE=AF,∴△BCE≌△BAF(SAS);(2)①解:如解图,连接EG,∵四边形ABCD为正方形,AB=4,∴AD=AB=BC=4,∴AG=AD-GD=3,在Rt△ABG中,依据勾股定理可知BG=5.由翻折的性质可知EC′=EC,BC′=BC=4,∴C′G=BG-BC′=1,∴C′G=DG=1.在Rt△C′GE和Rt△DGE中,C′G=DG,EG=EG,∴Rt△C′GE≌Rt△DGE(HL),∴C′E=DE,∴EC=DE=2,∴AF=CE=2,∴FG=AF+AG=2+3=5;②证明:由翻折的性质可知∠C ′BE =∠CBE =30°. ∵∠ABC =90°,∴∠ABG =30°,∴AG =AB ·tan30°=433.∵在Rt △BCE 中,∠EBC =30°,∴EC =BC ·tan30°=433,∴AG =CE ,又∵CE =AF ,∴AF =AG .又∵点B 和点H 关于DF 对称,∴BH ⊥FG ,AH =AB .∵AF =AG ,AH =AB ,∴四边形FHGB 是平行四边形,又∵BH ⊥FG ,∴四边形FHGB 是菱形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊四边形的证明与计算
一. 一组对边平行+一组对角相等=平行四边形
1. 四边形ABCD 中,AB//CD,D B ∠=∠,BC=6,AB=3,求四边形ABCD 的周长。
二. 平行四边形的性质与判定的贡献
2.如图,四边形ABCD 中,BD 垂直平分AC ,垂足为点F ,E 为四边形ABCD 外一点,且∠ADE=∠BAD ,AE∠AC
(1)求证:四边形ABDE 是平行四边形;
(2)如果DA 平分∠BDE ,AB=5,AD=6,求AC 的长。
3.已知:如图,D,E,F 分别是∠ABC 各边上的点,且DE∠AC,DF∠AB.延长FD 至点G ,使DG=FD ,连接AG.
求证:ED 和AG 互相平分。
三.菱形四边相等为全等提供了可能
4.如图1,菱形ABCD中,点E.F分别为AB、AD的中点,连接CE、CF.
(1)求证:CE=CF;
(2)如图2,若H为AB上一点,连接CH,使∠CHB=2∠ECB,求证:CH=AH+AB.
四. 含60︒的菱形与等边三角形结合在一起
5.(1)如图,菱形ABCD 中,︒
=∠60C ,O 为BD 的中点,点E 在AD 上,点F 在AB 的延长线上,且︒=∠120EOF ,求证:AB BF AE 21=+.
(2)如图,菱形ABCD 中,︒
=∠60C ,O 为BD 的中点,E ,F 分别在DA ,AB 的延长线上,︒=∠120EOF ,试探究AE ,BF ,AB 之间的数量关系.
五. 从对称的角度考虑菱形问题。
6. 如图,在菱形ABCD 中,对角线AC=6,BD=8,点E. F 分别是边AB 、BC 的中点,点P 在AC 上运动,在运动过程中,存在PE+PF 的最小值,则这个最小值是 。
7.如图,已知菱形ABCD的周长为16,面积为83,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为___.
六.利用矩形对角线分得的四个等腰三角形进行角度计算
8.如图所示,矩形ABCD中,AE∠BD,∠DAE:∠BAE=3:1,求∠BAE,∠EAO的度数.
七.利用矩形对边平行且相等,邻边垂直解决问题
EF⊥.
9.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,ED
∠.
求证:AE平分BAD
10.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
八.平移矩形的一组对角线,得到等腰三角形
∆中,AB=AC,D为BC中点,四边形ABDE是平行四边形。
求证:四边11.如图,在ABC
形ADCE是矩形。
九.利用直角三角形的“斜中”解决问题
2+,12.如图,在Rt∠ABC中,∠ACB=90°,斜边AB上的中线CD=1,∠ABC的周长为6
求∠ABC的面积.
十.矩形的判定思路:平行四边形+矩形特征
十一.矩形的折叠问题(折叠的基本方法试运用勾股定理建立方程)
13.如图,在矩形ABCD中,AB=3,BC=4,点E是AD上一个动点,把∠BAE沿BE向矩形内部折
CA的长为______.
叠,当点A的对应点A1恰落在∠BCD的平分线上时,则
1。
