第5章定积分及其应用
定积分理论

y f ( x) B
A
a x1 x2 xi-1 i xi
图4
xn-1 b
x
A A1 A2 An Ai
i 1
n
第 2 步 积零为整
在每个小区间 [ xi 1 , xi ] (i 1,2,, n) 上任取一点 i ( xi 1 i xi ) (如图 4) , 过 点 i 作 x 轴 的 垂 线 , 以 [ xi 1 , xi ] 为 底 的 小 曲 边梯 形 的 面 积 Ai 用 底 为
求曲边梯形面积的思想
第 1 步 化整为零
如图 4 所示,在区间 [a, b] 内任意插入若干个分点
a x0 x1 xn1 xn b ,
将 [a, b] 分成 n 个小区间
[ x0 , x1 ] , [ x1 , x 2 ] ,…, [ xn1 , xn ] ,
各小区间的长度依次为
o
1 x1
图5
1
x
a
o
图6
b
x
3 定积分的几何意义
根据定积分的定义,定积分
b
a
f ( x)dx 表示如下几何意义:
y y = f (x)
⑴
则
如果连续的被积函数 f ( x) 0 ,
b
a
f ( x)dx 表示由曲线 y f ( x) ,x 轴
o a
图7
及直线 x a , x b 所围成的曲边梯形的 面积(如图 7) ;
第5.3节 常用积分法
第5.4节 广义积分
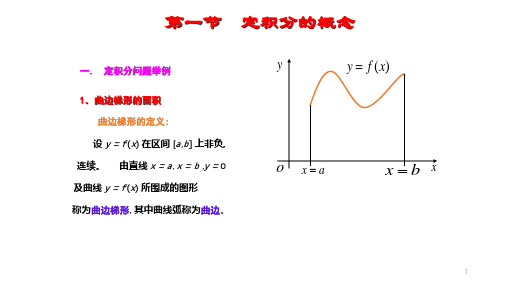
第 5.1 节
1 曲边梯形的面积
定积分的基本概念和性质
如图 1 所示, 由连续曲线 y f ( x) ( f ( x) 0 ), x 轴及直线 x a ,x b 所围成一曲边梯形 AabB ,如何计算 它的面积呢? 众所周知,矩形的面积等于底乘 以高,而与曲边梯形最相近且最易计 算面积的平面图形就是矩形,但由于 曲边梯形在底边各点处的高 f ( x) 在 区间 [ a, b] 上是变动的, 所以不能直接 按矩形的面积公式计算曲边梯形的面 积。
高等数学 第5章 第一节 定积分的概念
定积分存在的两个充分条件:
定理1 设 f ( x) 在区间 [a, b]上连续, 则 f ( x)在区间 [a, b] 上可积. 定理2 设 f ( x)在区间 [a, b] 上有界, 且只有有限个间断点,则
f ( x)在区间 [a, b]上可积.
6
定积分的几何意义
y y f (x)
A
o xa xb x
lim
n
6n 2
3
10
1 i n
i
},
0,
n
A lim 0 i1
f ( i )xi
An
x xn1 nxn b
3
2. 变速直线运动的路程
设物体作直线运动,
已知速度 v v(t )是时间间隔 [T1 ,T2 ]上 的
连续函数, 且 v(t ) 0, 计算在这段时间内物体所经过的路程。
匀速直线运动:
路程=速度×时间.
(1) 分割
T1 t0 t1 ti1 ti tn T2 ,
v( i )
ti ti ti1
(i 1,2,, n)
(2) 近似代替
si v( i )t i
T1
i
T2
t t0 t1 t2 ti1 ti tn1 tn
(3) 求和 (4) 取极限
s
n i 1
s
i
n v(
i 1
i )t i
每 个小区间的长度 xi xi xi1 (i 1,2,n).
2
(2)近似代替
y Ai f (i )xi
(i 1,2,, n)
(3)求和
y f (x)
A1 A2
Ai
A
n i 1
Ai
n
数学积分第五章

b xn x
A lim f ( i ) x i
0 i 1
n
二、定积分的定义 定义:设函数 f(x) 在闭区间 [a, b] 上有界,在 (a, b) 内任意
插入 n - 1 个分点
a x 0 x1 x 2
… xn 1 xn b
把区间 [a, b] 分成了 n 个小区间 [ x i 1 , x i ] ,其长度为
( i 1, 2 ,
… , n)
小区间的长度 x i x i x i 1 ⑵ 取近似 A i f ( i ) x i ⑶ 求和
A A i f ( i ) x i
i 1 i 1 n n
⑷ 取极限:设 为小区间长 度的最大值,则 o x0 a x 1 x 2 x i 1 i x i
b b
⑵ a [ f ( x) g ( x) ] d x a f ( x) d x a g ( x) d x ; 性质 ⑵ 可以推广到有限个可积函数的情形。 ⑶ 对任意常数 a , b , c,总有
b
b
b
a
b
f ( x) d x
a
c
f ( x) d x
c
b
f ( x) d x .
y
y f ( x)
y
y f ( x)
y
y f ( x)
。 .
o a c b x o a
。 .
.
c
。
.
c
b
x
o
a
b
x
三、定积分的几何意义(1)
由定积分的定义可得:
在闭区间 [a, b] 上,若函数 f ( x) 0 ,则 a f ( x ) d x 在几
第8次课反常积分及其审敛法

第五章定积分及其应用本节主要内容:1、无穷区间上的有界函数的反常积分的审敛法2、有限区间上的无界函数的反常积分的审敛法一、回顾定积分定义与计算()()011,1lim ()d ()d lim ()(()[,],,.,()[,].,,,,[,],,.)niii ba nbi i ai f x f x x f x x f x f x f x dx x y f x a b f x a b a b a b λλξξ→=→=∆=∆=∑⎰∑⎰设函数在上有界按照分割、求和、取极限的做法得若此极限存在则称此极限值为函数在上的定积分记为即为、定积分其中称为被积函数称积分表达式叫做积分变量为积分区间为积分下限为积分上限几何定义:曲线:由()[],,.[,][,][,]()d (1),,.d (2)0()d ()()()()d ()(),,()d ()d ,babbbaaab c aaf x x a x b x S f x x f x f x k f xg x x k f x x g x x k a c b f x x f x x a b a b a b λλλ>===+=+≤≤=⎰⎰⎰⎰⎰⎰及轴围成的曲边梯形面积为存在定理:若上连续,或者在上只有有限个第一类间断点,则上的定积分存在可积2、在性质线性性质 其中为任意常数可加性 在 若则[][][]()d ,()0()d 0,(),()(),()d ()2()d ()d (), ()().(3),,.1(4),bcbab baabbaaf x x a b f x f x x a b a b f xg x a M f x x g x dxf x x f x xf x b m b f m a x +≥≥<≤≤≤-≤⎰⎰⎰⎰⎰⎰保号性 在上如果则推上则推论在区间上的最大值论如果在区间估值定理与最小值, 设分别函数则是()[][][][]d ()(),, ()d ()()3)(5) ,, (),() (d (),()=().baba xa x Mb a f x a b a b f x x f b a f x a b F x f t t f x a b F x f x ξξ≤-=-='⎰⎰⎰定积分牛中值定理如果函数在上连续则在内至少有一个 使得、定积分与不定积分的关系原函数存在定理:若在上连续,则是在上的一个原函数.显然由此得[][]()(),(), ()d ()()()bba a F x f x ab f x a b f x x F x F b F a ==-⎰顿莱布尼茨公式:若是在上的一个原函数,在上连续,则()()()41()d ()()()2()[,](t)()[,](),(),()d ((t)(t))dt 2()d ()()()()du()bba a ba b b ba aaf x x F x F b F a f x a b x t a b f x x f u x v x u x v x v x x u βαϕϕαβϕαϕβϕϕ==-'='==='=⎰⎰⎰⎰⎰、定积分的计算牛顿莱布尼茨公式: 换元积分法:在上连续,单值,在上连续,又则分部积分法:- ,其中[]()()()0202(),(), ()[()()];0,() ().2(),()()()()();()aaa aa aT TA T T AA nT Ax v x a b f x dx f x f x dx f x f x dx f x dx f x f x T f x dx f x dx f x dx f x dx --+-+'=+-⎧⎪=⎨⎪⎩===⎰⎰⎰⎰⎰⎰⎰⎰在上连续5、常用的定积分公式:1是奇函数2是偶函数3如果是以为周期的周期函数,则()()02202200220()().4cos sin 1;1331,2422cos sin .13421,2535()(sin )(cos );(sin )(sin 2T n n n f x dx n N xdx xdx n n n n n xdx xdx n n n n n f x f x dx f x dx xf x dx f x πππππππππ∈==--⎧∙∙∙∙∙⎪⎪-==⎨--⎪∙∙∙∙∙⎪-⎩==⎰⎰⎰⎰⎰⎰⎰⎰在为正偶数为大于1的设函数[0,1]奇数上连续,正0).dx π⎰例1已知211,22()11,2x xe x f x x ⎧-≤≤⎪⎪=⎨⎪-≥⎪⎩,计算212(1)f x dx -⎰.例2证明以下结论:(1)2200()(sin )(cos );f x f x dx f x dx ππ=⎰⎰设函数在[0,1]上连续,(2)2201331,2422cos sin 13421,253n n n n n n n xdx xdx n n n n n πππ--⎧∙∙∙∙∙⎪⎪-==⎨--⎪∙∙∙∙∙⎪-⎩⎰⎰为正偶数为大于1的正奇数二、无穷区间上的有界函数的反常积分(无穷积分)1、定义1设函数f (x )在区间[a ,+∞)上连续,取b >a .如果极限dx x f ba b )(lim⎰+∞→存在,则称此极限为函数f (x )在无穷区间[a ,+∞)上的反常积分,记作dx x f a )(⎰+∞,即dx x f dx x f bab a)(lim)(⎰⎰+∞→+∞=.这时也称反常积分dx x f a )(⎰+∞收敛. 如果上述极限不存在,函数f (x )在无穷区间[a ,+∞)上的反常积分dx x f a )(⎰+∞就没有意义,此时称反常积分dx x f a )(⎰+∞发散.类似地,可定义反常积分dx x f b)(⎰∞-和dx x f )(⎰+∞∞-.2、计算:如果F (x )是f (x )的原函数,则ba b ba b ax F dx x f dx x f )]([lim )(lim)(+∞→+∞→+∞==⎰⎰)()(lim )()(lim a F x F a F b F x b -=-=+∞→+∞→.即简记形式:)()(lim )]([)(a F x F x F dx x f x a a -==+∞→∞++∞⎰.类似地)(lim )()]([)(x F b F x F dx x f x bb-∞→∞-∞--==⎰,)(lim )(lim )]([)(x F x F x F dx x f x x -∞→+∞→∞+∞-+∞∞--==⎰.例3(1)计算反常积分⎰+∞-0dt te pt(p 是常数,且p >0).(2)讨论反常积分dx x p a 1⎰+∞(a >0)的敛散性.3、无穷区间上的有界函数的反常积分的审敛法()[,)(0.)()0lim (),.1,0()1,0()p x a af x a a f x x f x l p l f x dx p l f x dx →+∞+∞+∞+∞>≥=>≤<+∞≤<≤+∞⎰⎰极设函数在区间上连续,且满足则有(1)当时,无穷限反常积分收敛; (限审敛法:2)当时,无穷限反常积分发散例4讨论下列反常积分的敛散性(1)1+∞⎰(2)32211xdx x+∞+⎰三、有限区间上的无界函数的反常积分(瑕积分)1、定义2设函数f (x )在区间(a ,b ]上连续,而在点a 的右邻域内无界.取ε>0,如果极限dx x f bt at )(lim ⎰+→存在,则称此极限为函数f (x )在(a ,b ]上的反常积分,仍然记作dx x f ba )(⎰,即dx x f dx x f bta tb a )(lim )(⎰⎰+→=.这时也称反常积分dx x f ba )(⎰收敛.如果上述极限不存在,就称反常积分dx x f ba )(⎰发散.瑕点:如果函数f (x )在点a 的任一邻域内都无界,那么点a 称为函数f (x )的瑕点,也称为无界定义2'设函数f (x )在区间(a ,b ]上连续,点a 为f (x )的瑕点.函数f (x )在(a ,b ]上的反常积分定义为dx x f dx x f bt at b a )(lim )(⎰⎰+→=.类似地,函数f (x )在[a ,b )(b 为瑕点)上的反常积分定义为dx x f dx x f ta bt b a )(lim )(⎰⎰-→=.在[a ,c )⋃(c ,b ](c 为瑕点)上的反常积分定义为dx x f dx x f dx x f btct ta ct ba )(lim )(lim )(⎰⎰⎰+-→→+=.2、反常积分的计算:如果F (x )为f (x )的原函数,则有bt at btat ba x F dx x f dx x f )]([lim )(lim )(++→→==⎰⎰)(lim )()(lim )(x Fb F t F b F ax at ++→→-=-=.简记形式:(1)当a 为瑕点时,)(lim )()]([)(x F b F x F dx x f ax ba ba +→-==⎰;(2)b 为瑕点时,)()(lim )]([)(a F x F x F dx x f b x ba ba -==-→⎰.(3)当c (a <c <b )为瑕点时,)](lim )([)]()(lim [)()()(x F b F a F x F dx x f dx x f dx x f cx cx bc c a b a +-→→-+-=+=⎰⎰⎰.例5(1)计算反常积分⎰-adx xa 0221.(2)讨论反常积分⎰-ba q a x dx)(的敛散性.3、有限区间上的无界函数的反常积分的审敛法1.()(,]()0.lim ()(),0,0()1,0()p x babaf x a b f x x a f x l p l f x dx p l f x dx →+∞≥-=<<≤<+∞≥<≤+∞⎰⎰设函数在区间上连续,且满足则有(1)当极时,瑕积分收敛;(2)瑕限审敛法:当时,积分发散例6讨论下列反常积分的敛散性(1)31ln dxx⎰(2)1201()k <⎰椭圆积分(3)101dx x ⎰。
第五章,定积分

②设f (x)在区间[a b]上有界 且只有有限个间断点 则f (x) 在[a b]上可积
③设f (x)在区间[a b]上只有有限个第一类间断点 则f (x) 在 [a b]上可积
④若f (x)在区间[a b]上单调,则f (x) 在[a b]上可积
4.定积分的性质
两点规定
(1)当ab时
b
a f (x)dx 0.
n i 1
f
i n
.
等式右端的极限可通过等式左端的积分来计算.
2.定积分的几何意义
(1)设
b
a
f
(x) dx存在,若在a,b上f
x
0,
则 b a
f
(x) d x
的值等
于曲线 y f x与直线 x a, x b以及 x 轴所围成的曲边
梯形的面积.
(2) 若在
a, b 上f
x
0,则 b a
(2)当a>b时
b
a
f (x)dx f (x)dx.
a
b
性质1 函数的和(差)的定积分等于定积分的和(差) ,即
b
a[
f
(x)
g(x)]dx
b
a
f
(x)dx
b
a g(x)dx
性质2 被积函数的常数因子可以提到积分号外面, 即
abk
f
(x)dx
k
b
a
f
(x)dx
性质3 如果将积分区间分成两部分,则在整个区间上的定
积分等于这两部分区间上定积分之和,即
b
a
f
(x)dx
c
a
f
(x)dx
b
c
f
—定积分的概念与性质-2022年学习资料

推广性质1知:有限个函数的代数和的定积分等于各-函数的定积分的代数和,即-[fx±f2x士工±fxdx-= d±f.xdr主r±f.xdr-性质2-被积函数的常数因子可以提到积分号外.-[kfxdx =k["fxd -k是常数-性质3如果积分区间[a,b]被分点c分成区间a,c]和[c,b],-则-心fxdr=ifxdr ifxdx-前页-后页-结束
根据定积分的定义,前面所讨论的两个引例就可-以用定积分概念来描述:-曲线fxfx≥0、x轴及两条直线x=a x=b所围-成的曲边梯形面积A等于函数fx在区间α,b]上的定积-分,即-A=广f-前贡-后页-结末
质点在变力Fs作用下作直线运动,由起始位置-a移动到b,变力对质点所做之功等于函数Fs在[α,b]-上的定 分,即-W ="Fsds-如果函数fx在区间[,b]上的定积分存在,则-称函数fx在区间a,b]上可积. 可以证明:若函数fx在区间[α,b]上连续,或只有有-限个第一类间断点,则fx在区间[α,b]上可积.-前 -后页-结束
定积分的几何意义:(P2ss-如果在a,b]上fx≥0,则fxdr在几何上表-示由曲线y=fx,直线x=a x=b及y-x轴所围成的曲边梯形的面积.-如果在a,b]上fx≤0,此时-由曲线y=x,直线x=,x=b及 x轴所围成的曲边梯形位于x轴的-下方,则定积分2fxdx在几何-上表示上述曲边梯形的面积4的相反数.-前贡 后页-结束
将闭区间[a,b]分成n个小区间:-[so,S1],[S1,S2]L,$-1S,],L,[Sm-1Sn]区间的长度-△s,=S:-S;-1i=1,2,L,n-2取近似-在每一个小区间s,-1s]上任取一点乡,把 5做为-质点在小区间上受力的近似值,于是,力F在小区间s,-1,s,]-上对质点所做的功的近似值为-△W: F5△s;i=1,2,L,n-前贡-后页-结末
@@@微积分基础(国家开放大学)---第5章---第1节---积分的几何应用
y f ( x)
y
x
y f ( x)
o
a
b
oa
(2)
c
(3)
b
x
(1)
(1) S f ( x)dx
a c a c
b
(2) S f ( x)dx
a b c b a c
b
(3) S | f ( x)dx | f ( x)dx f ( x)dx f ( x)dx
A
x
2
2 32 1 x 3 1 2 1 1 x |0 |0 . 3 3 3 3 3
【总结提升】
求两曲线围成的平面图形的面积的一般步骤: (1)作出示意图;(弄清相对位置关系)
(2)求交点坐标,确定图形范围(积分的上限,下限)
(3)写出平面图形的定积分表达式; (4)运用微积分基本定理计算定积分,求出面积.
1
x
x x ( x ) ( x) 3 3 1
3
2
3
8 . 3 1
1
5.如图,求曲线y=x2与直线y=2x所围图形的面积S.
y=2x, 由方程组 2 y = x ,
解
可得 x1=0,x2=2.
故所求图形的面积为
x dx=x S= 2xdx -
2 2 2 22 0
曲边形面积的求解思路
y
A 0 a bX a
1
A2 b a b
曲边形
曲边梯形(三条直边,一条曲边)
面积 A=A1-A2
类型2:由两条曲线y=f(x)和y=g(x),直线x=a,x=b
(a<b)所围成平面图形的面积S
y f ( x)
5.1定积分的概念和性质
x1 x1 x0 , x2 x2 x1 ,, xn xn xn1
用直线 x xi 将曲边梯形分成 n 个小曲边梯形; y 每个小曲边梯形的面积为 Ai 曲边梯形的面积
Ai
xi 1
o a x1
xi
2) 取近似. 在第i 个小曲边梯形上任取 i [ xi 1 , xi ] 作以 [ xi 1 , xi ] 为底 , f ( i ) 为高的小矩形, 并以此小 矩形面积近似代替相应 小曲边梯形面积 得
b
a
a
a
f ( x)dx 0
2.定积分的几何意义:
曲边梯形面积 y 0 a
y
a
0
b
b x
曲边梯形面积的负值
y
A1 a c
b
A3 A2
d
e
A4
A5 f b x
a f ( x) d x A1 A2 A3 A4 A5
A1 ( A2 ) A3 ( A4 ) A5
y
o a x1
xi 1
i
xi
Ai f ( i )xi
(xi xi xi 1 )
3) 求和.
将n个小矩形的面积之和作为所求曲 边梯形面积的近似值
A A i f ( i )xi
i 1 i 1
n
n
4) 取极限. 令
则曲边梯形面积
A Ai
i 1
( a b)
8. 积分中值定理 则至少存在一点
使
a f ( x) dx f ( )(b a)
b
5.2 微积分基本定理
一、牛顿 – 莱布尼兹公式 二、积分上限函数
高二数学-定积分概念-课件
0
( x f (t)dt)2
0
( x f (t)dt)2
0
0
依题意,在[0, x](x 0)上, f (t) 0, (x t) f (t) 0,
且(x t) f (t) 0,故
x
f (t)dt 0,
x
(x t) f (t)dt 0,
0
0
F(x) 0(x 0),从而F(x)在(0,)内单调增加。
(2) lim 4 sin n xdx 0. n 0
解: (利用积分中值定理)
(1)
1 2
xn
dx
n
(1 0)
(0 1)
0 1 x 1 2
2
原式 lim n 0.
n 2(1 )
(2)
4
sin
n
xdx
sin
n
(
0)
0
4
原式 lim sin n 0.
n 4
(0 )
n
n
(iii)求和: A Ai f (i )xi
i1
i1
o a xi1i xi
bx
(iv)取极限:令 max{ x1,xn},则曲边梯形面积
n
A lim 0 i1
f (i )xi
1.定积分定义 设函数f(x)在[a,b]上有界,
(i)分割: 在[a,b]内插入若干个分点a x0 xn1 xn b,
x
0
(1) (1) 2
例4 设f (x)在[0,)内连续,且f (x) 0.证明
x
tf (t)dt
F(x)
0 x
在(0,)内卫单调增加函数。
0 f (t)dt
证
x
x
高数考研基础班第五章 定积分
b−a 解 [ 理 为f ( x)在 a, b]上 平 值. 的 均
= f (ξ )
因 故它是有限个数的平均值概念的推广. 故它是有限个数的平均值概念的推广
1 n = lim ∑ f (ξi ) n→∞ n i =1
9
5.积分上限函数 积分上限函数
Φ( x) = ∫ f (t)dt
a
x a
x
认识它吗? 认识它吗?
x
f ( x )dx = ∫ f ( x )dx a a
x
+ lim
x →b
x →+∞
∫
x
x a
f ( t )dt
∫
b
a
f ( x )dx = lim− ∫ f ( t )dt
a
(b瑕点)
11
二、与概念有关的问题
定积分定义 ☆定积分定义
O
∫
b a
0 x
则下列结论正确的是( 则下列结论正确的是(C ) 5 3 B. F (3) = F (2) A. F (3) = − F ( − 2) 4 4 5 3 D. F (−3) = − F (−2) C. F ( − 3) = F (2) 4 4
3 F (3) = F ( − 3) = π 8
F (2) = F ( −2) =
λ → 0 i =1
n
∫
b
a
f ( x)dx.
T2
1
4
变速直线运动的路程
s = lim
∑ v (τ i ) ∆ t i = ∫T λ→0
i =1
n
v(t )dt.
2.存在定理 存在定理
定理的证明省略,只要求记住结论 定理的证明省略 只要求记住结论. 只要求记住结论
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章 定积分及其应用§5.1 定积分的概念习 题 5-11.填空题:(1)函数()f x 在区间[,]a b 上的定积分是积分和的极限,即()baf x dx ⎰=( ).(2)定积分的值只与( )及( )有关,而与( )的记法无关. (3)区间[,]a b 的长度的定积分的表示是( ). (4)被积函数()f x 在区间[,]a b 上连续是定积分()baf x dx ⎰存在的( ).(5)定积分的几何意义( ). 2.利用定积分的定义计算下列积分: (1)2baxdx ⎰; (2)1x e dx ⎰.3.利用定积分的定义计算由抛物线21y x =+,直线x a =、x b =(b a >)及x 轴所围成的图形的面积.4.利用定积分的几何意义,证明下列等式: (1)1310x -=⎰; (2)sin 0xdx ππ-=⎰;(3)4π=⎰; (4)11arctan 0xdx -=⎰;(5)11124x dx xdx -=⎰⎰ ; (6)2202cos 2cos xdx xdx πππ-=⎰⎰.5.利用定积分的几何意义求a⎰(0)b >的值.6. 将下列极限表示成定积分: (1)()201lim3nii i i x λξξ→=-∆∑,λ是[]7,5-上的分割;(2)01limni i x λ→=,λ是[]0,1上的分割.7.将下列和式的极限表示成定积分:(1)111lim 12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭; (2)112lim p p p p n n n +→∞+++(0p >);(3))221limn n n →∞+; (4)n .8.有一河,宽为200米,从一岸到正对岸每隔20米测量一次水深,测得数据如下(图5-1-8).试用梯形公式求此河横截面积的近似值.图5-1-8§5.2 定积分的性质习 题 5-21. 证明定积分的性质: (1)()()bb aakf x dx k f x dx =⎰⎰ (k 为常数); (2)1b baadx dx b a ⋅==-⎰⎰. 2. 估计下列积分值:(1)421(2)x dx +⎰; (2)3244(1sin )x dx ππ+⎰; (3)arctan x xdx ;(4)21x edx ⎰; (5)2211x dx x +⎰; (6)20sin x dx x π⎰. 3. 设()f x 及()g x 在[],a b 上连续,证明: (1) 若在[],a b 上,()0f x ≥,且()0baf x dx =⎰,则在[],a b 上,()0f x ≡;(2)若在[],a b 上,()0f x ≥,且()f x 不恒等于零,则()0baf x dx >⎰;(3)若在[],a b 上,()()f x g x ≤,且()()bbaaf x dxg x dx =⎰⎰,则在[],a b 上,()()f x g x ≡.4. 根据定积分性质及第3题的结论,比较下列每组积分的大小:(1)320sin xdx π⎰,220sin xdx π⎰; (2)221x dx ⎰,231x dx ⎰;(3)21ln xdx ⎰,221(ln )x dx ⎰; (4)10x e dx ⎰,21x e dx ⎰;(5)1xe dx ⎰,()101x dx +⎰; (6)20xdx π⎰,20sin xdx π⎰;(7)20sin xdx π⎰,02sin xdx π-⎰; (8)2cos xdx π-⎰,20cos xdx π⎰;(9)10xdx ⎰,()01ln 1x dx +⎰ (10)()01ln 1x dx +⎰,011xdx x+⎰;. 5. 利用积分中值定理求下列极限: (1)sin limn pnn x dx x+→∞⎰; (2)120lim 1nn x dx x →∞+⎰; (3)10lim 1n xx n x e dx e →∞+⎰.6. 设()f x 在[],a b 上连续,()0baf x dx =⎰.证明:()f x 在[],a b 上在[],a b 内至少存在一个零点.7. 设()f x 在[]0,1上连续,在()0,1内可导,且1233()(0)f x dx f =⎰.证明:在()0,1内至少存在一点ξ,使得()0f ξ'=.8. 设()f x 在[],a b 上连续,在(),a b 内可导,且存在(),c a b ∈,使得()()()caf x dx f b c a =-⎰.证明:在(),a b 内至少存在一点ξ,使得()0f ξ'=.§5.3 微积分基本公式习 题 5-31. 设0()cos xx t tdt ϕ=⎰,求(0)ϕ',4πϕ⎛⎫' ⎪⎝⎭. 2.求下列函数的一阶导数: (1)0()sin xtx e dt ϕ=⎰; (2)223()t xx e dt ϕ-=⎰;(3)2()x x ϕ=⎰; (4)2x y =;(5)32x xy =⎰; (6)()cos 2sin ()cos xxx t dt ϕπ=⎰;(7)22x txy t e dt -=⎰; (8)2()xe xy f t dt =⎰.3. 求下列函数的二阶导数:(1)()330sin xy t x tdt =-⎰; (2)258sin ()xy t f x dt dy t ⎛⎫= ⎪⎝⎭⎰⎰.4. 利用洛必达法则,求下列极限:(1)20cos limxx t dt x→⎰; (2)201lim arctan xx tdt x+→⎰;(3)202limsin 2x t x x e dt x x→-⎰; (4)()2202002sin limln 1x x xt dtt t dt→⎡⎤+⎣⎦⎰⎰;(5)121ln 1lim (1)xx tdtt x →-⎰+; (6)232lim(sin )x x x t dtt t t dt→-⎰⎰;(7)22201lim ()x t x x t t edt x -→+∞+⎰; (8)()222020lim xt xx t e dt te dt→⎰⎰.5. 设函数()y y x =由方程00cos 0y xte dt tdt +=⎰⎰所确定,求dydx. 6. 设函数()y y x =由方程20cos y x x y tdt -+=⎰所确定,求dy dx.7. 设0sin t x udu =⎰,0cos t y udu =⎰,求dydx.8.设20()(1)xt f x t t e dt -=-⎰,问x 为何值时,()f x 有极值?9. 求函数0()(4)xF x t t dt =-⎰在[1,5]-上的最大值与最小值.10. 计算下列各定积分: (1)24211()x dx x+⎰; (2)()13213x x dx --⎰; (3)332(21)x dx --⎰; (4)1(21)xe dx +⎰; (5)12111dx x -+⎰; (6)240tan xdx π⎰;(7)10⎰; (8)21201x dx x +⎰; (9)20cos 2x dx π⎛⎫ ⎪⎝⎭⎰; (10)41dx ⎰; (11)420213311x x dx x -+++⎰; (12)211e dx x ---+⎰; (13)20sin x dx π⎰; (14)设21,01()1,10x x f x x x ⎧+ ≤≤=⎨+ -≤<⎩,求11()f x dx -⎰. 11. 设()f x 连续,若()f x 满足1()()x f xt dt f x xe =+⎰,求()f x .12. 设13201()()1f x x f x dx x =++⎰,求()f x 与10()f x dx ⎰. 13. 设0ln(1)()(0)xt f x dt x t+=>⎰,求1()f x f x ⎛⎫+ ⎪⎝⎭. 14. 设1sin ,0()20,0x x f x x x ππ⎧ ≤≤⎪=⎨⎪ <>⎩或,求0()()x x f t dt ϕ=⎰在(,)-∞+∞内的表达式.§5.4 定积分的换元积分法与分部积分法习 题 5-41. 用换元积分法求下列定积分: (1)122(115)dxx --+⎰; (2)101xx e dx e +⎰; (3)220sin cos x xdx π⎰; (4)022122dx x x -⎰++; (5)1⎰; (6)2120t te dx -⎰; (7)1221xe dx x ⎰; (8)35201x dx x +⎰; (9)2502353x x dx x +-+⎰;(10)6e e⎰; (11)21e ⎰; (12)320sin cos d πθθθ⎰;(13)1(14);(15)ax ⎰;(16)3⎰(17)⎰;(18)0;(19) 0⎰; (20); (21)3122(1)xdx -+⎰;(22)1;(23)41⎰;(24)1⎰-;(25)⎰; (26)2⎰; (27)-⎰; (28)()223min 2,x dx -⎰(29)2sin sin cos xdx x xπ+⎰;(30)0π⎰. 2. 用分部积分法求下列定积分: (1)ln 2x xe dx ⎰; (2)1ln e x xdx ⎰;(3)41⎰; (4)1arctan x xdx ⎰; (5)220sin x xdx π⎰; (6)324sin xdx xππ⎰; (7)220cos x xdx π⎰; (8)1530ln x xdx ⎰ ;(9)230x e dx ;(10)22(1)x - ; (11)220cos x e xdx π⎰; (12)1sin(ln )ex dx ⎰ ;(13)22ln (1)e exdx x -⎰; (14)12(1)ln (1)e x x dx -++⎰;(15)221log x xdx ⎰;(16)20sin x x dx π⎰; (17)1ln eex dx ⎰ ; (18)()242sec 1tan x xdx x π+⎰;(19)161⎰; (20)122(1)m xdx -⎰(m 为自然数).3. 利用积分区间的对称性以及函数的奇偶性,计算下列定积分:(1)22sin cos 2x xdx ππ-⎰;(2)22ππ-⎰;(3)6sin x xdx ππ-⎰;(4)1⎰; (5)x dx ; (6)221cos xdx x ππ-+⎰;(7)522cos xdx ππ-⎰; (8)325425sin 21x xdx x x -+⎰+; (9))sin x x dx ππ-⎰+.(10)244cos 1x xdx e ππ--+⎰.4.已知()f x 是连续函数,证明 (1)1()()[()]baf x dx b a f a b a x dx =-+-⎰⎰;(2)200()[()(2)]aaf x dx f x f a x dx =+-⎰⎰;(3)()2321()2aa x f x dx xf x dx =⎰⎰(0a >).5. 设()f x 是连续函数,证明 (1) 当()f x 是偶函数时,则0()()xx f t dt ϕ=⎰为奇函数;(2)当()f x 是奇函数时,则0()()xx f t dt ϕ=⎰为偶函数.6. 证明:220()2()aaax dx x dx ϕϕ-=⎰⎰,其中()x ϕ为连续函数.7. 证明:110(1)(1)m n n m x x dx x x dx ϕϕ-=-⎰⎰.8. 证明:20sin 2sin nn xdx xdx ππ=⎰⎰.9. 证明:112211111xx dx dx x x =++⎰⎰(0x >). 10. 设31sin ()x t f x dt t =⎰,求120()x f x dx ⎰.若1sin ()n x t f x dt t=⎰,求110()n x f x dx -⎰.11. 若()f x ''在[0,]π连续,(0)2f =,()1f π=,证明:[()()]sin 3f x f x xdx π''+=⎰.12. 当0x >时,()f x 可导,且满足方程11()1()xf x f t dt x=+⎰, 求()f x .§5.5 广义积分习 题 5-51 计算下列瑕积分.(1)41dx x +∞⎰; (2)0e +∞⎰; (3)2122dx x x +∞-∞++⎰; (4)211(1)dx x x +∞+⎰; (5)1+∞⎰; (6) 0sin px e xdx ω+∞-⎰(0,0p ω>>);(7)21arctan xdx x+∞⎰;(8) 1⎰(9)1e⎰(10)10⎰;(11)21⎰;(12)()22011dx x -⎰.2. 求当k 为何值时,瑕积分()21ln kdx x x +∞⎰收敛?当k 为何值时,该瑕积分发散?又当k 为何值时,该瑕积分取得最小值?3. 计算瑕积分0n x n I x e dx +∞-=⎰(n 为自然数).4. 求c 为何值时,使2lim xc tx x c te dt x c -∞→+∞+⎛⎫= ⎪-⎝⎭⎰. 5.求2+∞⎰.6. 计算下列式子:(1)(7)2(4)(3)ΓΓΓ; (2)3(3)()29()2ΓΓΓ; (3)40x x e dx +∞-⎰; (4)2220x x e dx +∞-⎰. 7. 用Γ函数表示下列积分,并指出积分的收敛范围.(1)nxe dx +∞-⎰(0n >); (2)101ln pdx x ⎛⎫⎪⎝⎭⎰; (3)22x dx +∞--∞⎰;(4)mn x x edx +∞-⎰; (5)10⎰; (6)311dx x +∞+⎰. §5.6 定积分的几何应用习题5-61. 求由下列各组曲线所围成平面图形的面积:(1)1xy =,y x =,2x =; (2)x y e =,xy e -=,1x =; (3)2y x =,2x y +=; (4)3y x =,1y =,2y =,0x =;(5)0y =,1y =,ln y x =,0x =; (6)22x y =,228x y +=;(7) ln y x =,y 轴,ln y a =,ln y b =( 0b a >>);(8) 23y x =+,2y x =. 2. 直线x k =平分由2y x =,0y =,1x =所围之面积,求k 之值. 3. 求抛物线243y x x =-+-及在点(0,3)-和(3,0)处切线所围成图形的面积. 4. 求抛物线22y px =及其在点,2p p ⎛⎫⎪⎝⎭处的法线所围成的图形的面积. 5. 求曲线33cos ,sin x a t y a t ==,).0(>a 所围成图形的面积. 6. 求曲线2cos r a θ=).0(>a 所围成图形的面积.7. 求曲线2(2cos r a θ=+)).0(>a 所围成图形的面积. 8. 求对数螺线r ae θ=(0a >,πθπ-≤≤)及射线θπ=所围成图形的面积.9. 计算阿基米德螺线r a θ= (0a >)上相应于θ从0到2π的一段弧与极轴所围成的图形(如图5-6-22)的面积.图5-6-22 图5-6-2310.求由下列各曲线所围成图形的公共部分的面积. (1) 3cos r θ=及1cos r θ=+;(2) r θ=及2cos 2r θ=.11. 圆1r =被心形线1cos r θ=+分割成两部分,求这两部分的面积. 12.设sin y x =,02x π≤≤.问:为t 何值,图5-6-23中阴影部分的面积1s 与2s 之和最小?最大?13.求由下列已知曲线围成的平面图形绕指定的轴旋转而成的旋转体的体积.(1)2xy a =,0y =,x a =,2x a =(0a >),绕x 轴. (2)22(2)1x y +-=,绕x 轴.(3)ln y x =,0y =,x e =,绕x 轴和y 轴. (4)224x y +=,24(1)x y =--,0y >,绕x 轴. (5)5xy =,6x y +=,绕x 轴.(6)cos y x =,0x =,x π=,x 轴,绕y 轴.14. 求摆线(sin )(1cos )x a t t y a t =-⎧⎨=-⎩(02t π≤≤,0a >)的一拱与0y =所围成的图形绕直线2y a =旋转而成的旋转体的体积.15. 由心形线4(1cos )ρθ=+和直线0θ=及2πθ=所围成图形绕极轴旋转而成的旋转体的体积.16. 一个棱锥体的底面是长为2a 的正方形,高为h ,求此棱锥体的体积 (如图5-6-24).图5-6-24 图5-6-2517.设直线y ax b =+(0a >,0b >)与直线0x =,1x =及0y =所围成的梯形面积等于A ,试求a 、b ,使这个梯形绕x 轴旋转所得旋转体的体积最小.18.在由椭圆域2214y x +≤绕y 轴旋转而成的椭球体上,以y 轴为中心轴打一个圆孔,使剩下的部分的体积恰好等于椭球体体积的一半,求圆孔的直径.19.设有一锥体,其高为h ,上、下底都为椭圆,椭圆的轴长分别为2a 、2b 与2A 、2B ,求这锥体的体积.20.作半径为r 的球的外切正圆锥,问此圆锥的高h 为何值时,其体积V 最小?求出此最小值(如图5-6-25).21.把星形线232323x y a +=所围成的图形绕x 轴旋转(图5-6-26),计算所得旋转体的体积.图5-6-26 图5-6-27 22.用积分的方法证明图5-6-27所示球缺的体积为2()3H V H R π=-. 23.求圆盘222x y a +≤绕x b =-(0b a >>)旋转而成的旋转体的体积.24.证明:由平面图形x a =,x b =,0a b ≤<,0()y f x ≤≤绕y 轴旋转而成的旋转体的体积为2()baV xf x dx π=⎰.25.利用24题的结论,计算sin y x =(0x π≤≤)和x 轴所围成的图形绕y 轴旋转所成的旋转体的体积.习题5-71. 已知边际成本'2()25309C q q q =+-,固定成本为55,试求总成本()C q ,平均成本与变动成本.2. 已知边际收入为'()30.2R q q =-,q 为销售量,求总收入函数()R q ,并确定最高 收入的大小.3. 某产品生产q 个单位是总收入R 的变化率为'()200100qR q =-,求: (1)生产50个单位时的总收入;(2)在生产100个单位的基础上,再生产100个单位时总收入的增量.4. 已知某商品每周生产q 个单位时,总成本变化率为'()0.412C q q =-(元/单位),固 定成本500,求总成本()C q . 如果这种商品的销售单价是20元,求总利润()L q ,并问每周生产多少单位时才能获得最大利润?图5-7-56. 设某城市人口总数为F ,已知F 关于时间t (年)的变化率为dF dt =,假设在计算的初始时间(0)t =,城市人口数为100(万),试求t 年中该城市人口总数.7. 若边际消费倾向在收入为Y 时为1232Y -,且当收入为零时总消费支出070c =.(1)求消费函数()c Y ;(2)求收入由100增加到196时消费支出的增加数.8. 设储蓄边际倾向(即储蓄额S 的变化率)是收入y 的函数 '()0.3S y =, 求收入从100元增加到900元时储蓄的增加额.9. 如果需求曲线为2()500.025D q q =-,并已知需求量为20个单位,试求消费者剩余CS .10. 假设某国某年洛伦兹曲线近似地由3y x =(01x ≤≤)表示,试求该国的基尼系数.11. 某投资项目的成本为100万元,在10年中每年可收益25万元,投资率为5%,试 求这10年中该项投资的纯收入的贴现值.12. 一位居民准备购买一栋别墅,现价为300万元,如果以分期付款的方式,要求每年 付款21万元,且20年付清,而银行贷款的年利率为4%,按连续复利计息,请你帮这位购5. 某新产品的销售率由下式给出()10090x f x e -=-,式中x 是产品上市的天数,前四天的销售总数是曲线()y f x =与x 轴在之间的面积(如图5-7-5),求前四天总的销售量.房者作一决定:是采用一次付款合算还是分期付款合算?总习题五1.求下列极限:(1) limnn k →∞=. (2) 21lim inni n i nen ne→∞=+∑;(3)11lim n n i n →∞= (4)112lim p p p p n n n +→∞+++(0p >); (5)lim n →∞2.利用积分中值定理求下列极限: (1)sin lim0n pnn xdx x +→∞=⎰; (2)222lim n x n n x dx e+→∞⎰.3.求下列极限:(1)101lim (1sin 2)xtx t dt x →+⎰; (2)lim ()x a x a x f t dt x a →-⎰(其中()f x 连续);(3)()2arctan lim xx t dt→+ (4) ()2210limxt t x e dt→+∞⎰.4.(已知[]02()1()1xf t dt f x -=-⎰,求(0)f '.5. 已知()2021,0()0,x t e dtx f x x x ⎧-⎪≠=⎨⎪=0⎩⎰,求(0)f '. 6.设()f t 在0t ≤≤+∞上连续,若220()(1)x f t dt x x =+⎰,求(2)f .7. 求函数0()(3)xF x t t dt =-⎰在[1,5]-上的最大值与最小值.8. 证明:111ln(1)11ln 23n n n+=++++<+. 9. 设()f x 、()g x 在区间[,]a b 上均连续,证明:(1)()222()()()()bbbaaaf xg x dxf x dxg x dx ≤⋅⎰⎰⎰(柯西-施瓦茨不等式);(2)[]()()()111222222()()()()bbba aaf xg x dxf x dxg x dx +≤+⎰⎰⎰(闵可夫斯基不等式).10. 设函数()f x 在区间[,]a b 上连续,且()0f x >,证明:11ln ()ln ()b b a a f x dx f x dx b a b a ⎡⎤≥⎢⎥--⎣⎦⎰⎰. 11. 设()f x 在[0,]a (0a >)上有连续导数,且(0)0f =,证明:2()2aMa f x dx ≤⎰,其中0max ()x aM f x ≤≤'=.12. 设()f x 在[0,1]上连续且单调减少,试证:对任何(0,1)a ∈,有1()()af x dx a f x dx ≥⎰⎰.13. 设()x ϕ在[,]a b 上连续,()()()xaf x x b t dt ϕ=-⎰,证明:必存在(,)a b ξ∈,使得()f ξ'=0.14.设()f x 在区间[,]a b 上连续,()g x 在区间[,]a b 上连续且不变号.证明至少存在一点[,]a b ξ∈,使下式成立()()()()bbaaf xg x dx f g x dx ξ=⎰⎰(积分第一中值定理).15. 计算下列定积分:(1)3(1sin )x dx π-⎰; (2)e ;(3)⎰; (4)0ax ⎰ (0a >);(5)20sin 1cos x xdx xπ++⎰; (6)40ln(1tan )x dx π+⎰;(7)a⎰(0a >); (8);(9)121(21)x x dx -++⎰; (10)sin )x x dx ππ-⎰(11)42213||||1x x dx x -⎛⎫-+ ⎪+⎝⎭⎰; (12)设2,01()2,12x x f x x x ⎧ ≤≤=⎨-<<⎩,求20()f x dx ⎰.16.利用函数的奇偶性计算定积分121(x dx -+⎰. 17. 利用函数的周期性计算定积分2(sin 2)(tan 1)a ax x dx π++⎰.18. 设函数()f x 在(,)-∞+∞内连续,并满足条件()sin xu f x u e du x -=⎰,求()f x .19. 计算下列各题: (1)设(5)2f =,5()3f x dx =⎰,求5()xf x dx '⎰.(2)已知2()tan f x x =,求40()()f x f x dx π'''⎰.20. 证明()[()()]aaaf x dx f x f x dx -=+-⎰⎰,并求下列定积分:(1)441sin dx x ππ-+⎰; (2)244sin 1x x dx e ππ--+⎰; (3)244cos 1nxx dx e ππ--+⎰(n 为正整数). 21. 设()f x 在区间[,]a b 上连续,且()f x 关于2a bx +=对称的点处取相同的值.证明: 2()2()a b baaf x dx f x dx +=⎰⎰.22. 证明:112211111xx dt dt t t =++⎰⎰(0x >). 23. 判断下列瑕积分的敛散性:(1)1+∞⎰;(2)2+∞⎰;(3)2cos ln xdx x+∞⎰;(4) 0+∞⎰;(5)3(1)(2)dxx x x +∞--⎰;(6)1+∞⎰;(7)120ln 1xdx x -⎰; (8)1ln 11eex dx x --⎰.24. 已知sin 2x dx x π+∞=⎰,求220sin x dx x+∞⎰. 25. 求介于直线0x =,2x π=之间由曲线sin y x =和cos y x =所围成的平面图形的面积.26. 求椭圆22113x y +=和22113x y +=的公共部分的面积. 27. 求曲线x y e =及该曲线的过原点的切线和x 轴的负半轴所围成的平面图形的面积. 28. 设曲线21:1L y x =-(01)x ≤≤、及x 轴和y 轴所围成的区域被曲线21:L y ax =分为面积相等两部分,其中a 是大于零的常数,试确定a 的值.29. 求由柱体222x y a +≤与222x z a +≤(0a >)的公共部分所围成图形的体积.30.将曲线r =绕x 轴旋转而成的旋转体的体积. 31. 将抛物线2y x ax =-在横坐标0与c (0c a >>)之间的弧段绕x 轴旋转,问c 为 何值时,所得旋转体体积V 等于弦OP (P 为抛物线与x c =的交点)绕x 轴旋转所得锥体体积.32. 设抛物线2y ax bx c =++通过点(0,0),且当[0,1]x ∈时,0y ≥.试确定a b c 、、 的值,使得该抛物线与直线1x =,0y =所围成图形的面积为13,且使该图形绕x 轴旋转而成的旋转体的体积最小.33.一位居民准备购买一栋别墅价值为300万元,若首付为50万元,以后分期付款,每年付款数目相同,10年付清,而银行贷款的年利率为6%,按连续复利计息,每年应付款多少?(0.60.5448e-≈)34. 某公司投资2000万建成一条生产线,投产后,在t 时刻的追加成本和追加收益分别为23()52g t t =+ (百万/年)23()17t t ϕ=- (百万/年)试确定该生产线在何时停产可获得最大利润?最大利润是多少?.35.生产某种产品的固定成本为50万元,边际成本与边际收益分别为216100=-+(万元/单位产品)MC Q Q=-(万元/单位产品)MR Q894试确定工厂应将产量定为多少个单位时,才能获得最大利润?并求最大利润.。
