六年级奥数面积计算专题
六年级奥数——巧求面积(附习题及解答)

第五讲 巧求面积本讲主要介绍平面图形面积的一些巧妙算法,首先看一个例子.如图,BC=CE,AD=CD,求三角形ABC的面积是三角形CDE面积的几倍?解:连结BD,在△ABD与△BCD中,因为AD=DC,又因为这两个三角形的高是同一条高,所以S△ABD=S△BCD.在△BCD与△DCE中,因为BC=CE,又因为这两个三角形也具有同一条高,所以有S△BCD=S△CDE.因此,S△ABC=S△ABD+S△BCD=2S△CDE. 从以上的推导中看一看这两个三角形面积之比与这两个三角形的边有什么关系.CE于M,如右图,在△ACM与△DCN中,有AC∶CD=AM∶DN.因此,即,当两个三角形各有一个角,它们的和是180°时,这两个三角形的面积之比等于分别夹这两个角的两条边的长度乘积之比.类似可知,当两个三角形各有一个角,它们相等时,这个结论也成立.解:在△ABC与△CDE中,因为AD=DC,所以 AC=2CD,又因为BC=CE,所以S△ABC=2×1×S△CDE=2S△CDE.答:△ABC的面积是△CDE面积的2倍.下面我们就应用上面这个结论来看几个具体例子.例1 如图,三角形ABC的面积为1,并且AE=3AB,BD=2BC,那么△BDE的面积是多少?解:在△BDE与△ABC中,∠DBE+∠ABC=180°.因为AE=3AB,所以BE=2AB.又因为BD=2BC,所以S△BDE=2×2×S△ABC=4×1=4.答:△BDE的面积是4.例2 如图,在△ABC中,AB是AD的6倍,AC是AE的3倍.如果△ADE的面积等于1平方厘米,那么△ABC的面积是多少?解:在△ABC与△ADE中,∠BAC=∠DAE.因为AB=6AD,AC=3AE,所以S△ABC=6×3×S△ADE=18×1=18(平方厘米).答:△ABC的面积为 18平方厘米.例3 如图,将△ABC的各边都延长一倍至 A′、 B′、 C′,连接这些点,得到一个新的三角形A′B′C′.若△ABC的面积为1,求△A′B′C′的面积.解:在△A′B′B与△ABC中,∠A′BB′+∠ABC=180°.因为 AB=AA′,所以A′B=2AB,又因为B′B=BC,所以S△A′B′B=1×2×S△ABC=2S△ABC=2.同理S△B′C′C=2×1×S△ABC=2.S△A′C′A=2×1×S△ABC=2.所以S△A′B′C′=S△A′B′B+S△B′C′C+S△A′C′A+S△ABC=2+2+2+1=7答:△A′B′C′的面积为7.例4 如下图,将凸四边形ABCD的各边都延长一倍至 A′、B′、 C′、D′,连接这些点得到一个新的四边形A′B′C′D′,若四边形A′B′C′D′的面积为30平方厘米,那么四边形ABCD的面积是多少?分析 要求四边形ABCD的面积,必须求出四边形ABCD与四边形A′B′C′D′的关系,因而就要求出△A′B′B、△B′C′C、△C′D′D、△A′D′A与四边形ABCD的关系.解:连结AC、BD.在△A′B′B与△ABC中,∠A′BB′+∠ABC=180°.因为A′A=AB,所以A′B=2AB,又因为 B′B=BC,所以有S△A′B′B=2×1×S△ABC=2S△ABC.同理 有S△B′C′C=2×1×S△BCD=2S△BCDS△C′D′D=2×1×S△ADC=2S△ADCS△A′D′A=2×1×S△ABD=2S△ABD.所以 S四边形A′B′C′D′=S△A′B′B+S△B′C′C+S△C′D′D+S△A′D′A+S四边形ABCD =2S△ABC+2S△BCD+2S△ADC+2S△ABD+S四边形ABCD=2(S△ABC+S△ADC)+2(S△BCD+S△ABD)+S四边形ABCD=2S四边形ABCD+2S四边形ABCD+S四边形ABCD=5S四边形ABCD则S四边形ABCD=30÷5=6(平方厘米).答:四边形ABCD的面积为6平方厘米.B1C1=C1C,△A1B1C1的面积为1平方厘米,则△ABC的面积为多少平方厘米?解:连接A1C.如上图在△BB1C与△A1B1C1中,∠BB1C+∠A1B1C1=180°,因为A1B1=所以有S△BB1C=2×2×S△A1B1C1=4×1=4(平方厘米).在△A1C1C与△A1B1C1中,∠A1C1C+∠A1C1B1=180°,因为CC1=C1B1,A1C1=A1C1,所以有S△A1C1C=1×1×S△A1B1C1=1×1=1(平方厘米).在△ABD与△ADC中,∠ADB+∠ADC=180°.因为BD=DC,在△ABA1与△ABD中,∠BAA1=∠BAD.因为AB=AB,AA1=答:三角形ABC的面积为9平方厘米.习 题 五四边形DBCE的面积.(下图)2.下图中的三角形被分成了甲(阴影部分)、乙两部分,图中的数字是相应线段的长度,求两部分的面积之比.GA,求阴影部分面积占三角形ABC面积的几分之几?厘米,AE=11厘米,三角形DAE的面积是多少?的面积与三角形ABC 的面积之比.(下图)与三角形DEF的面积之比.7.如下图所示,把△ABC的BA边延长1倍到D点,AC边延长3倍到F点,CB边延长2倍到E点,连接DE、EF、FD,得到△DEF.已知三角形DEF的面积为54平方厘米,求△ABC的面积.的面积.9.在△ABC中,CD、AE、BF分别为BC、AC、AB长10.把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内按图示剪下两个内接正方形M、N.这两个正方形中面积较大的是哪一个?它比较小的正方形面积大多少平方厘米?习题五解答因为CD=1,DB=3,所以BC=1+3=4=4CD.所以S乙=S△ABC-S甲=6S甲-S甲=5S甲.所以S甲∶S乙=S甲∶5S甲=1∶5.答:甲乙两部分的面积之比为1∶5.3.解:利用正文中的结论容易求得:答:△ADE的面积为22平方厘米.所以S△DEF∶S△ABC=61∶120.答:△DEF与△ABC的面积之比为61∶120.S△ABE∶S△EDF=3∶4.答:三角形ABE与三角形EDF的面积之比为3∶4.7.解:S△ADF=4×1×S△ABC=4S△ABC,S△BED=2×2×S△ABC=4S△ABC,S△ECF=3×3×S△ABC=9S△ABC.所以S△DEF=S△ADF+S△EBD+S△ECF+S△ABC=4S△ABC+4S△ABC+9S△ABC+S△ABC=18S△ABC答:三角形ABC的面积为3平方厘米.8.解:连DF.因为AE=ED,所以有S△ABE=S△BED,S△AEF=S△DEF.所以S△BEA+S△AEF=S△BED+S△DEF=S△BDF=S阴影所以S△ABC=S△ABF+S△BDF+S△CDF9.解:记S1=S△AEN2,S2=S△BFN3,S3=S△CDN1,S=S△N1N2N3.由下图知S△ABE+S△BCF+S△CAD+S=S△ABC+S1+S2+S3但是S△ABE=S△BCF所以 S=S1+S2+S3.连结CN2,则即S△N1N2N3∶S△ABC=1∶7.答:S△N1N2N3与S△ABC之比为1∶7.10.解:为了方便,在下图中标上字母E、F、G、H、M1、N1、K,连结DK.页码,5/5习题五解答2011-10-28 ada99:11240_SR.HTM。
奥数圆面积计算六年级上册培优

奥数组合图形面积计算1:求出阴影部分的面积(单位:厘米)6×6×3.14×41 =9×3.14=28.26(平方厘米)2、求下面图形的阴影部分面积单位:厘米(1)6×6÷2=18(平方厘米)( 2)6×6=36(平方厘米)3、求出阴影部分的面积(单位:厘米)4×4×3.14×41-4×4÷2+4×2÷2 =12.56-8+4=8.56(平方厘米)4、求下列图形的阴影部分的面积(单位厘米)(1) 4×2=8(平方厘米) (2) 4×4÷2=8(平方厘米)5、两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO 1O 的面积。
3.14×12×41×2=1.57(平方厘米) 6、圆的周长为12.56厘米,AC 两点把圆周分成相等的两段弧,阴影部分(1)的面积与阴影部分(2)的面积相等,求平行四边形ABCD 的面积。
12.56÷3.14=4(厘米) 22×3.14=12.56(平方厘米)7、直径BC=8厘米,AB=AC ,D 为AC 的中点,求阴影部分的面积。
8×4÷2÷2=8(平方厘米)3.14×42×41-4×4÷2=12.56-8=4.56(平方厘米) 8+4.56=12.56(平方厘米)8、求阴影部分的面积。
(单位:厘米)。
CD:DF=FE:EBD F ×FE=CD ×EB=6×4=24(平方厘米)9、求四边形ABCD 的面积。
(单位:厘米)7×7÷2-3×3÷2=24.5-4.5=20(平方厘米)10、BE 长5厘米,长方形AEFD面积是38平方厘米。
(完整版)六年级奥数练习(阴影面积)1
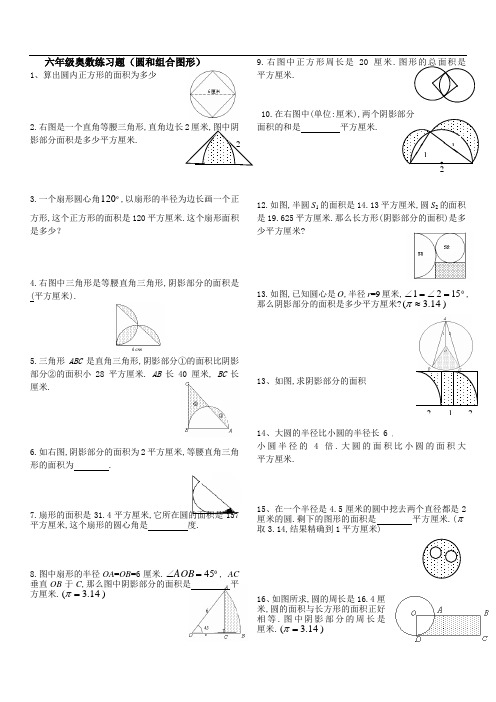
六年级奥数练习题(圆和组合图形)1、算出圆内正方形的面积为多少 2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米. 3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少? 4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB 长40厘米, BC 长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米. 10.在右图中(单位:厘米),两个阴影部分 面积的和是 平方厘米.12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面平方厘米.15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π2 1 2112217.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm ,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
六年级奥数练习(阴影面积)

六年级奥数练习(阴影面积)1、算出圆内正方形的面积为多少2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是多少平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是多少?4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. AB长40厘米, BC长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA=OB=6厘米.45=∠AOB, AC垂直OB于C,那么图中阴影部分的面积是平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.12.如图,半圆S1的面积是14.13平方厘米,圆S2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O,半径r=9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π13、如图,求阴影部分的面积 .14、大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大平方厘米.15、在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是平方厘米.(π取3.14,结果精确到1平方厘米)16、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π17.下图中正方形部分是一个水池,其余部分是草坪,已知正方形的面积是300平方米,草坪的面积是多少平方米?17、已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18、如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)19、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.20.如图{图在下面}两个连在一起的轮轴,已知小轮的半径是3分米,当这个小轮转3圈时,大轮正好转一圈,21.3只蜜蜂分别沿着阴影部分的边缘飞1次,那只蜜蜂飞过的路线最长?(3个正方形的边长都为4m )23.将半径分别是3厘米和2厘米的两个半圆如图放置,求阴影部分的周长24.求阴影部分的面积25.一个圆环外直径是内直径的二分之三倍,圆环面积150cm,求外圆的面积26.一个长方形的面积是20平方厘米,如果在这个长方形里画一个最大的半圆形,这个半圆形是多少平方厘米?因为这个半圆的直径是长方形的长,半径是宽,说明长方形的长是宽的2倍。
请计算六年级奥数阴影形状的面积。

请计算六年级奥数阴影形状的面积。
请计算六年级奥数阴影形状的面积介绍本文档将介绍如何计算六年级奥数题目中给定阴影形状的面积。
我们将使用简单的几何形状,并提供详细的步骤和计算公式。
计算步骤1. 确定阴影形状的几何形状类型。
常见的几何形状包括矩形、三角形和圆形。
2. 根据形状类型,选择相应的计算方法。
矩形的面积计算1. 矩形的面积计算公式为:面积 = 长 ×宽。
2. 如果题目已经给出了矩形的长度和宽度,则直接将两个数值相乘即可得到面积。
三角形的面积计算1. 三角形的面积计算公式为:面积 = 底 ×高 ÷ 2。
2. 如果题目已经给出了三角形的底和高,则将底和高相乘后再除以2即可得到面积。
圆形的面积计算1. 圆形的面积计算公式为:面积= π × 半径²,其中π 的近似值为3.14。
2. 如果题目已经给出了圆形的半径,则将半径的平方乘以π 即可得到面积。
示例题目题目一阴影部分是一个边长为5 cm的正方形,请计算该阴影形状的面积。
解答1. 根据题目描述,该阴影形状是一个正方形,边长为5 cm。
2. 使用矩形的面积计算公式,将边长相乘:面积 = 5 cm × 5 cm = 25 cm²。
3. 所以,该阴影形状的面积为25 cm²。
题目二阴影部分是一个底边长为10 cm、高为8 cm的三角形,请计算该阴影形状的面积。
解答1. 根据题目描述,该阴影形状是一个三角形,底边长为10 cm,高为8 cm。
2. 使用三角形的面积计算公式,将底和高相乘后再除以2:面积 = 10 cm × 8 cm ÷ 2 = 40 cm²。
3. 所以,该阴影形状的面积为40 cm²。
题目三阴影部分是一个半径为6 cm的圆形,请计算该阴影形状的面积。
解答1. 根据题目描述,该阴影形状是一个圆形,半径为6 cm。
2. 使用圆形的面积计算公式,将半径的平方乘以π:面积 =3.14 × 6 cm × 6 cm = 113.04 cm²。
专题10 面积计算(组合图形的面积)(原卷)

2022-2023学年小学六年级思维拓展举一反三精编讲义专题10 面积计算(组合图形的面积)对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
有些图形可以根据“容斥问题“的原理来解答。
在圆的半径r用小学知识无法求出时,可以把“r2”整体地代入面积公式求面积。
【典例分析01】如图20-1所示,求图中阴影部分的面积。
【思路导航】解法一:阴影部分的一半,可以看做是扇形中减去一个等腰直角三角形(如图20-2),等腰直角三角形的斜边等于圆的半径,斜边上的高等于斜边的一半,圆的半径为20÷2=10厘米【3.14×102×14-10×(10÷2)】×2=107(平方厘米)答:阴影部分的面积是107平方厘米。
解法二:以等腰三角形底的中点为中心点。
把图的右半部分向下旋转90度后,阴影部分的面积就变为从半径为10厘米的半圆面积中,减去两直角边为10厘米的等腰直角三角形的面积所得的差。
(20÷2)2×12-(20÷2)2×12=107(平方厘米)知识精讲典例分析【典例分析02】如图20-6所示,求图中阴影部分的面积(单位:厘米)。
【思路导航】解法一:先用长方形的面积减去小扇形的面积,得空白部分(a )的面积,再用大扇形的面积减去空白部分(a )的面积。
如图20-7所示。
3.14×62×14 -(6×4-3.14×42×14 )=16.82(平方厘米)解法二:把阴影部分看作(1)和(2)两部分如图20-8所示。
把大、小两个扇形面积相加,刚好多计算了空白部分和阴影(1)的面积,即长方形的面积。
3.14×42×14 +3.14×62×14 -4×6=16.28(平方厘米) 答:阴影部分的面积是16.82平方厘米。
六年级奥数专题圆的面积

六年级奥数专题圆的面积(总2页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除平面图形面积————圆的面积在正方形里的最大圆的面积占所在正方形的面积的3.144,而在圆内的最大正方形占所在圆的面积的2 3.14例题1。
求图中阴影部分的面积(单位:厘米)。
练习11.求下面各个图形中阴影部分的面积(单位:厘米)。
2.求下面各个图形中阴影部分的面积(单位:厘米)。
答练习21、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答2、计算下面图形中阴影部分的面积(单位:厘米,正方形边长4)。
答1 2练习41、如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米。
以AC、BC为直径画半圆,两个半圆的交点在AB边上。
求图中阴影部分的面积。
答例题5。
在图中,正方形的边长是10厘米,求图中阴影部分的23面积。
练习51、求下面各图形中阴影部分的面积(单位:厘米)。
答2、求右面各图形中阴影部分的面积(单位:厘米)。
答3、求右面各图形中阴影部分的面积(单位:厘米)。
答例题6。
在图的扇形中,正方形的面积是30平方厘米。
求阴影部分的面积。
练习61、 如图所示,平行四边形的面积是100平方厘米,求阴影部分的面积。
答圆的面积与组合圆积专题训练一、填空题1.算出下面圆内正方形的面积为 .2.右下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 .3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形120平方厘米.这个扇形面积是 .6厘米 244.如图所示,以B 、C 2厘米,则.(保留两位小数) 阴影部分的周长是 厘5.左下图三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B 长40厘米, BC 长 厘米6.如右下图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 .7.8.45=∠AOB , AC )14.3(=π9.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.64倍.大圆.剩下的图形的面积是 平方厘米)12.右上图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5 13.如左下图所示,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π14.如右下图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .15. 如左下图已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .16.右下图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.。
(完整word版)六年级奥数面积计算专题

面积计算〔一〕专题简析:在进行组合图形的面积计算时,要仔细观察,仔细思虑,看清组合图形是由几个根本单位组成的,还要找出图中的隐蔽条件与条件和要求的问题间的关系。
例题 1。
求图中阴影局部的面积〔单位:厘米〕。
66619- 1练习 1求下面各个图形中阴影局部的面积〔单位:厘米〕。
619- 219- 310例题 2。
求图 19- 5 中阴影局部的面积〔单位:厘米〕。
419- 5练习 2计算下面图形中阴影局部的面积〔单位:厘米〕。
19- 719- 819- 9例题 3。
如图 19-10 所示,两圆半径都是 1 厘米,且图中两个阴影局部的面积相等。
求长方形ABO 1O 的面积。
A BO O1练习 31、如图 19- 11 所示,圆的周长为 12.56 厘米, AC 两点把圆分成相等的两段弧,阴影部分〔 1〕的面积与阴影局部〔2〕的面积相等,求平行四边形ABCD 的面积。
CA 1BAD2C AOBDCB819- 1119-1219- 132、 如图 19- 12 所示,直径 BC =8 厘米,AB = AC ,D 为 AC 的重点,求阴影局部的面积。
3、 如图 19- 13 所示, AB = BC = 8 厘米,求阴影局部的面积。
例题 4。
如图 19- 14 所示,求阴影局部的面积〔单位:厘米〕。
C6 DBIAE 419- 14【思路导航 】我们可以把三角形ABC 看作是长方形的一局部,把它复原成长方形后〔如右图所示〕,因为原大三角形的面积与后加上的三角形面积相等, 并且空白局部的两组三角形面积分别相等,所以I 和 II 的面积相等。
练习 41、如图 19- 15 所示,求四边形ABCD 的面积。
2、如图 19- 16 所示, BE 长 5 厘米,长方形AEFD 面积是 38 平方厘米。
求CD 的长度。
3、图 19- 17是两个完满相同的直角三角形重叠在一起,依照图中的条件求阴影部分的面积〔单位:厘米〕。
CC3DFD○384030A45B BA E 5120719- 1519-1619-17例题 5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
面积计算(一)
专题简析:
在进行组合图形的面积计算时,要仔细观察,认真思考,看清组合图形是由几个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。
例题1。
求图中阴影部分的面积(单位:厘米)。
练习1
求下面各个图形中阴影部分的面积(单位:厘米)。
6 19-
1
19-2
19-
3
例题2。
求图19-5中阴影部分的面积(单位:厘米)。
练习2
计算下面图形中阴影部分的面积(单位:厘米)。
例题3。
如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等。
求长方形ABO 1O 的面积。
19-5 4 19-7
19-8 19-
9
练习3
1、如图19-11所示,圆的周长为12.56厘米,AC两点把圆分成相等的两段弧,阴影部
分(1)的面积与阴影部分(2)的面积相等,求平行四边形
2、如图19-12所示,直径BC=8厘米,AB=AC,D为AC的重点,求阴影部分的面积。
3、如图19-13所示,AB=BC=8厘米,求阴影部分的面积。
例题4。
如图19-14所示,求阴影部分的面积(单位:厘米)。
【思路导航】我们可以把三角形ABC看成是长方形的一部分,把它还原成长方形后(如右图所示),因为原大三角形的面积与后加上的三角形面积相等,并且空白部分
的两组三角形面积分别相等,所以I和II的面积相等。
19-11 19-12
C
B
C
19-13
19-14
B
4
6
I
1、 如图19-15所示,求四边形ABCD 的面积。
2、 如图19-16所示,BE 长5厘米,长方形AEFD 面积是38平方厘米。
求CD 的长度。
3、 图19-17是两个完全一样的直角三角形重叠在一起,按照图中的已知条件求阴影部
分的面积(单位:厘米)。
例题5。
如图19-18
所示,图中圆的直径AB 是4厘米,平行四边形ABCD 的面积是7平方厘米,
∠ABC =30度,求阴影部分的面积(得数保留两位小数)。
19-15
A
B 19-17 D
19-16 19-18 B B
1、如图19-19所示,∠1=15度,圆的周长位62.8厘米,平行四边形的面积为100
平方厘米。
求阴影部分的面积(得数保留两位小数)。
2、如图19-20所示,三角形ABC的面积是31.2平方厘米,圆的直径AC=6厘米,
BD:DC=3:1。
求阴影部分的面积。
3、如图19-21所示,求阴影部分的面积(单位:厘米。
得数保留两位小数)。
19-19
19-20
19-21
12
60
60
面积计算(二)
专题简析:
对于一些比较复杂的组合图形,有时直接分解有一定的困难,这时,可以通过把其中的部分图形进行平移、翻折或旋转,化难为易。
有些图形可以根据“容斥问题“的原理来解答。
在圆的半径r 用小学知识无法求出时,可以把“r 2”整体地代入面积公式求面积。
例题1。
如图20-1所示,求图中阴影部分的面积。
练习1
1、 如图20-4所示,求阴影部分的面积(单位:厘米)
2、 如图20-5所示,用一张斜边为29厘米的红色直角三角形纸片,一张斜边为49厘
米的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形。
求红蓝两张三角形纸片面积之和是多少?
例题2。
如图20-6所示,求图中阴影部分的面积(单位:厘米)。
20-
1 20-
4
10 6 B A D 20
-
5
49 29
29
49 20-6 6 4
20-7
【思路导航】
解法一:先用长方形的面积减去小扇形的面积,得空白部分(a )的面积,再用大扇形的面
积减去空白部分(a )的面积。
如图20-7所示。
3.14×62×14-(6×4-3.14×42×1
4
)=16.82(平方厘米)
解法二:把阴影部分看作(1)和(2)两部分如图20-8所示。
把大、小两个扇形面积相加,
刚好多计算了空白部分和阴影(1)的面积,即长方形的面积。
3.14×42×14+3.14×62×1
4
-4×6=16.28(平方厘米)
答:阴影部分的面积是16.82平方厘米。
1、如图20-9所示,△ABC 是等腰直角三角形,求阴影部分的面积(单位:厘米)。
2、如图20-10所示,三角形ABC 是直角三角形,
AC 长4厘米,BC 长2厘米。
以AC 、BC 为直径画半圆,两个半圆的交点在AB 边上。
求图中阴影部分的面积。
例题3。
在图20-12中,正方形的边长是10厘米,求图中阴影部分的面积。
、
20-8
加 减
20-12
练习3
求下面各图形中阴影部分的面积(单位:厘米)。
例题4。
在正方形ABCD 中,AC =6厘米。
求阴影部分的面积。
练习4
1、 如图20-19、20-20所示,图形中正方形的面积都是50平方厘米,分别求出每个图
形中阴影部分的面积。
2、 如图20-21所示,正方形中对角线长10厘米,过正方形两个相对的顶点以其边长为
半径分别做弧。
求图形中阴影部分的面积(试一试,你能想出几种办法)。
20-15
20-16 10 20-17
20-18 C
20-
19 20-20 20-21
例题5。
在图20-22的扇形中,正方形的面积是30平方厘米。
求阴影部分的面积。
练习5
1、如图20-24所示,平行四边形的面积是100平方厘米,求阴影部分的面积。
2、如图20-25所示,O是小圆的圆心,CO垂直于AB,三角形ABC的面积是45平方厘
米,求阴影部分的面积。
3、如图20-26
20-22
20-24 20-25
B
20-26
45。
