高一数学两角和与差的正弦、余弦和正切练习题

合集下载

两角和与差的正弦余弦正切公式练习题(含答案)

两角和与差的正弦余弦正切公式练习题(含答案)两角和差的正弦余弦正切公式练题一、选择题1.给出如下四个命题：①对于任意的实数α和β，等式cos(α+β)=cosαcosβ-sinαsinβ恒成立；②存在实数α，β，使等式cos(α+β)=cosαcosβ+sinαsinβ能成立；③公式tan(α+β)=tanα+tanβ成立的条件是α≠kπ+π(k∈Z)且β≠kπ+π(k∈Z)；1-tanαtanβ/2④不存在无穷多个α和β，使sin(α-β)=sinαcosβ-cosαsinβ。

其中假命题是（）A。

①②B。

②③C。

③④D。

②③④2.函数y=2sinx(sinx+cosx)的最大值是（）A。

1+2B。

2-1C。

2D。

2/33.当x∈[-π/2,π/2]时，函数f(x)=sinx+3cosx的（）A。

最大值为1，最小值为-1B。

最大值为1，最小值为-1/2C。

最大值为2，最小值为-2D。

最大值为2，最小值为-14.已知tan(α+β)=7，tanαtanβ=2/3，则cos(α-β)的值（）A。

1/2B。

2/2C。

-2D。

±25.已知π/2<β<α<3π/4，cos(α-β)=12/13，sin(α+β)=-3/5，则sin2α=（）A。

56/65B。

-56/65C。

6565/56D。

-5/66.sin15°sin30°sin75°的值等于（）A。

3/4B。

3/8C。

1/8D。

1/47.函数f(x)=tan(x+π/4)+1+tanx/4，g(x)=1-tanx，h(x)=cot(π/4-x)。

其中为相同函数的是（）A。

f(x)与g(x)B。

g(x)与h(x)C。

h(x)与f(x)D。

f(x)与g(x)及h(x)8.α、β、γ都是锐角，tanα=1/2，tanβ=1/5，tanγ=1/8，则α+β+γ等于（）A。

π/3B。

π/4C。

π/5D。

2022秋新教材高中数学第五章两角和与差的正弦余弦正切公式课后提能训练新人教A版必修第一册

第五章　5.5.1 第2课时A级——基础过关练1．sin 105°的值为( )A．B．C．D．【答案】D　【解析】sin 105°＝sin(45°＋60°)＝sin 45°·cos 60°＋cos 45°sin 60°＝×＋×＝.2．(多选)下列四个选项，化简正确的是( )A．cos(－15°)＝B．cos 15°cos 105°＋sin 15°sin 105°＝cos(15°－105°)＝0C．cos(α－35°)cos(25°＋α)＋sin(α－35°)sin(25°＋α)＝D．sin 14°cos 16°＋sin 76°cos 74°＝【答案】BCD　【解析】对于A，(方法一)原式＝cos(30°－45°)＝cos 30°cos 45°＋sin 30°sin 45°＝×＋×＝，(方法二)原式＝cos 15°＝cos(45°－30°)＝cos 45°cos 30°＋sin 45°sin 30°＝×＋×＝，A错误．对于B，原式＝cos(15°－105°)＝cos(－90°)＝cos 90°＝0，B正确．对于C，原式＝cos[(α－35°)－(25°＋α)]＝cos(－60°)＝cos 60°＝，C正确．对于D，原式＝cos 76°cos 16°＋sin 76°sin 16°＝cos(76°－16°)＝cos 60°＝，D正确．故选BCD．3．(2020年青岛高一期中)已知α，β为锐角，tan α＝，cos(α＋β)＝－，则tan β＝( )A．2B．C．D．【答案】A　【解析】因为α，β为锐角，所以0＜α＋β＜π，所以sin(α＋β)＝＝，tan(α＋β)＝＝－2，则tan β＝tan[(α＋β)－α]＝＝＝2.故选A．4．(2020年抚州高一期中)已知cos＝2cos(π＋α)，且tan(α＋β)＝，则tan β的值为( )A．－7B．7C．1D．－1【答案】B　【解析】因为cos＝2cos(π＋α)，所以sin α＝－2cos α，即 tan α＝－2.又因为tan(α＋β)＝＝＝，解得tan β＝7.故选B．5．已知cos(α－β)＝，sin β＝－，且α∈，β∈，则cos α＝( )A．B．C．－ D．－【答案】B　【解析】因为0＜α＜，－<β<0，所以0＜α－β＜π.又cos(α－β)＝，所以sin(α－β)＝.因为－<β<0，sin β＝－，所以cos β＝.所以cos α＝cos[(α－β)＋β]＝cos(α－β)cos β－sin(α－β)sin β＝×－×＝.6．(2020年上海黄浦区高一期中)已知sin x＝，x∈，则tan的值等于________．【答案】－　【解析】因为sin x＝，x∈，所以cos x＝－，tan x＝－.所以tan＝＝＝－.7．若sin α＋2cos α＝0(0＜α＜π)，则tan α＝________，tan＝________.【答案】－2　－　【解析】因为sin α＋2cos α＝0(0＜α＜π)，所以sin α＝－2cos α，即tan α＝－2.所以tan＝＝＝－.8．(2020年湘潭高一期中)已知tan α，tan β是方程2x2＋3x－5＝0的两个实数根，则tan(α＋β)＝________.【答案】－　【解析】因为tan α，tan β是方程2x2＋3x－5＝0的两个实数根，所以tan α＋tan β＝－，tan αtan β＝－.所以tan(α＋β)＝＝＝－.9．已知cos α＝(α为第一象限角)，求cos，sin的值．解：因为cos α＝，且α为第一象限角，所以sin α＝＝＝.所以cos＝cos cos α－sin sin α＝×－×＝，sin＝sincos α＋cossin α＝×＋×＝.B级——能力提升练10．sin(θ＋75°)＋cos(θ＋45°)－cos(θ＋15°)＝( )A．±1B．1C．－1D．0【答案】D　【解析】原式＝sin[60°＋(θ＋15°)]＋cos(θ＋45°)－cos(θ＋15°)＝－cos(θ＋15°)＋sin(θ＋15°)＋cos(θ＋45°)＝sin(θ－45°)＋cos(θ＋45°)＝0.故选D．11．已知tan(α＋β)＝3，tan(α－β)＝5，则tan 2α的值为( )A．－B．C．D．－【答案】A　【解析】tan 2α＝tan[(α＋β)＋(α－β)]＝＝＝＝－.12．在△ABC中，cos A＝，cos B＝，则△ABC的形状是( )A．锐角三角形B．钝角三角形C．直角三角形D．等边三角形【答案】B　【解析】由题意得sin A＝，sin B＝，所以cos C＝cos(π－A－B)＝－cos(A＋B)＝－cos A·cos B＋sin A sin B＝－×＋×＝－＝－＝－<0，所以C是钝角，故△ABC是钝角三角形．13．在△ABC中，tan A＋tan B＋＝tan A·tan B，则角C等于( )A．B．C．D．【答案】A　【解析】由已知，得tan A＋tan B＝·(tan A tan B－1)，即＝－.所以tan(A ＋B)＝－.所以tan C＝tan[π－(A＋B)]＝－tan(A＋B)＝，得C＝.14．已知cos α＝，sin(α－β)＝，且α，β∈.(1)求cos(2α－β)的值；(2)求β的值．解：(1)因为α，β∈，所以α－β∈.又因为sin(α－β)＝>0，所以0<α－β<.所以sin α＝＝，cos(α－β)＝＝.cos(2α－β)＝cos[α＋(α－β)]＝cos αcos(α－β)－sin αsin(α－β)＝×－×＝.(2)cos β＝cos[α－(α－β)]＝cos αcos(α－β)＋sin αsin(α－β)＝×＋×＝.又因为β∈，所以β＝.C级——探究创新练15．已知函数f(x)＝(sin x＋cos x)2－2cos2x(x∈R)．(1)求函数f(x)的周期和递增区间；(2)若函数g(x)＝f(x)－m在上有两个不同的零点x1，x2，求tan(x1＋x2)的值．解：(1)因为f(x)＝(sin x＋cos x)2－2cos2x＝1＋2sin x·cos x－2cos2x＝sin 2x－cos 2x＝sin(x∈R)，所以函数f(x)的周期T＝＝π.因为函数y＝sin x的单调递增区间为(k∈Z)，所以函数f(x)的单调递增区间由2kπ－≤2x－≤2kπ＋(k∈Z)，化简得kπ－≤x≤kπ＋(k∈Z)，即(k∈Z)．(2)因为方程g(x)＝f(x)－m＝0同解于f(x)＝m.在直角坐标系中画出函数f(x)＝sin在上的图象，如图，当且仅当m∈[1，)时，方程f(x)＝m在上的区间和有两个不同的解x1、x2，且x1与x2关于直线x＝对称，即＝，所以x1＋x2＝，故tan(x1＋x2)＝tan＝－1.。

完整版)两角和与差的正弦、余弦、正切经典练习题

完整版)两角和与差的正弦、余弦、正切经典练习题两角和与差的正弦、余弦、正切cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβ1、求值：1)cos15°2)cos80°cos20°+sin80°sin20°3)cos130°cos10°+sin130°sin10°5)sin75°7)cos(A+B)cosB+sin(A+B)sinB2.1)证明：cos(π/2-α)=sinα4)cos105°6)求cos75°cos105°+sin75°sin105°8)cos91°cos29°-sin91°sin29°2)已知sinθ=15π，且θ为第二象限角，求cos(θ-π)的值．3)已知sin(30°+α)=√3/2，60°<α<150°，求cosα．4)化简cos(36°+α)cos(α-54°)+sin(36°+α)sin(α-54°)．5)已知sinα=-4/5，求cosα的值。

6)已知cosα=-3π/32，α∈(π/2,π)，求sin(α+π/4)的值。

7)已知α，β都是锐角，cosα=32π/53，α∈(π/3,π/2)，cosβ=-3π/52，β∈(π/6,π/4)，求cos(α+β)的值。

8)已知cos(α+β)=-11/53，求cosβ的值。

9)在△ABC中，已知sinA=√3/5，cosB=1/4，求cosC的值.两角和与差的正弦sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβ利用和差角公式计算下列各式的值：1)sin72°cos42°-cos72°sin42°2)3sinx+cosx3)cos2x-sin2x证明：1)sinα+cosα=sin(α+π/2)2)cosθ+sinθ=2sin(θ+π/4)3)2(sin x+cos x)=2cos(x-π/4)1)已知sinα=-3/5，α是第四象限角，求sin(-α)的值。

高中数学必修5复习题及答案(A组)免费范文

篇一：高中数学必修5课后习题答案人教版高中数学必修5课后习题解答第一章解三角形1．1两角和与差的正弦、余弦和正切公式练习（P4） 1、（1）a?14，b?19，B?105?；（2）a?18cm，b?15cm，C?75?. 2、（1）A?65?，C?85?，c?22；或A?115?，C?35?，c?13；（2）B?41?，A?24?，a?24. 练习（P8） 1、（1）A?39.6?,B?58.2?,c?4.2 cm；（2）B?55.8?,C?81.9?,a?10.5 cm. 2、（1）A?43.5?,B?100.3?,C?36.2?；（2）A?24.7?,B?44.9?,C?110.4?. 习题1.1 A组（P10） 1、（1）a?38cm,b?39cm,B?80?；（2）a?38cm,b?56cm,C?90? 2、（1）A?114?,B?43?,a?35cm;A?20?,B?137?,a?13cm（2）B?35?,C?85?,c?17cm；（3）A?97?,B?58?,a?47cm;A?33?,B?122?,a?26cm； 3、（1）A?49?,B?24?,c?62cm；（2）A?59?,C?55?,b?62cm；（3）B?36?,C?38?,a?62cm；4、（1）A?36?,B?40?,C?104?；（2）A?48?,B?93?,C?39?；习题1.1 A组（P10）1、证明：如图1，设?ABC的外接圆的半径是R，①当?ABC时直角三角形时，?C?90?时，?ABC的外接圆的圆心O在Rt?ABC的斜边AB上.BCAC在Rt?ABC中，?sinA，?sinBABABab即?sinA，?sinB 2R2R所以a?2RsinA，b?2RsinB 又c?2R?2R?sin902RsinC （第1题图1）所以a?2RsinA, b?2RsinB, c?2RsinC②当?ABC时锐角三角形时，它的外接圆的圆心O在三角形内（图2），作过O、B的直径A1B，连接AC， 1?90?，?BACBAC则?A1BC直角三角形，?ACB. 11在Rt?A1BC中，即BC?sin?BAC1， A1Ba?sin?BAC?sinA， 12R所以a?2RsinA，同理：b?2RsinB，c?2RsinC③当?ABC时钝角三角形时，不妨假设?A为钝角，它的外接圆的圆心O 在?ABC外（图3）（第1题图2）作过O、B的直径A1B，连接AC.1则?A1BC直角三角形，且?ACB?90?，?BAC?180?11在Rt?A1BC中，BC?2Rsin?BAC， 1即a?2Rsin(180?BAC)即a?2RsinA同理：b?2RsinB，c?2RsinC综上，对任意三角形?ABC，如果它的外接圆半径等于则a?2RsinA,b?2RsinB, c?2RsinC2、因为acosA?bcosB，所以sinAcosA?sinBcosB，即sin2A?sin2B 因为0?2A,2B?2?，（第1题图3）所以2A?2B，或2A?2B，或2A?22B. 即A?B或A?B?所以，三角形是等腰三角形，或是直角三角形.在得到sin2A?sin2B后，也可以化为sin2A?sin2B?0 所以cos(A?B)sin(A?B)?0 A?B??2.?2，或A?B?0即A?B??2，或A?B，得到问题的结论.1．2应用举例练习（P13）1、在?ABS中，AB?32.2?0.5?16.1 n mile，?ABS?115?，根据正弦定理，得AS?ASAB?sin?ABSsin(6520?)?AB?sin?ABS16.1?sin115sin(6520?)∴S到直线AB的距离是d?AS?sin2016.1?sin115sin207.06（cm）. ∴这艘船可以继续沿正北方向航行. 2、顶杆约长1.89 m. 练习（P15）1、在?ABP中，?ABP?180?，?BPA?180(?)ABP?180(?)?(180?)在?ABP中，根据正弦定理，APAB?sin?ABPsin?APBAPa?sin(180?)sin(?)a?sin(?)AP?sin(?)asin?sin(?)所以，山高为h?APsinsin(?)2、在?ABC中，AC?65.3m，?BAC?25?2517?387?47??ABC?909025?2564?35?ACBC?sin?ABCsin?BAC?747AC?sin?BAC65.?3?sinBC?m 9.8?sin?ABCsin?6435井架的高约9.8m.200?sin38?sin29?3、山的高度为?382msin9?练习（P16） 1、约63.77?. 练习（P18） 1、（1）约168.52 cm2；（2）约121.75 cm2；（3）约425.39 cm2. 2、约4476.40 m2a2?b2?c2a2?c2?b2?c?3、右边?bcosC?ccosB?b?2ab2aca2?b2?c2a2?c2?b22a2?a左边? 【类似可以证明另外两个等式】 ?2a2a2a习题1.2 A组（P19）1、在?ABC中，BC?35?0.5?17.5 n mile，?ABC?14812622?根据正弦定理，14?8)?，1BAC?1801102248ACB?78(180ACBC?sin?ABCsin?BACBC?sin?ABC17.?5s?in22AC?8.8 2n milesin?BACsin?48货轮到达C点时与灯塔的距离是约8.82 n mile. 2、70 n mile.3、在?BCD中，?BCD?301040?，?BDC?180?ADB?1804510125?1CD?3010 n mile3CDBD根据正弦定理， ?sin?CBDsin?BCD10BD?sin?(18040125?)sin40?根据正弦定理，10?sin?40sin1?5在?ABD中，?ADB?451055?，?BAD?1806010110??ABD?1801105515?ADBDABADBDAB根据正弦定理，，即sin?ABDsin?BADsin?ADBsin15?sin110?sin55?10?sin?40?sin1?5BD?sin1?5?10s?in40?6.8 4n mile AD?sin1?10si?n110?sin70BD?sin5?5?10sin40?sin55n mile 21.6 5sin1?10sin15?sin70如果一切正常，此船从C开始到B所需要的时间为：AD?AB6.8?421.6520?min ?6?01?0?60 86.983030即约1小时26分59秒. 所以此船约在11时27分到达B岛. 4、约5821.71 m5、在?ABD中，AB?700 km，?ACB?1802135124?700ACBC根据正弦定理，sin124?sin35?sin21?700?sin?35700?sin21?AC?，BC?sin1?24sin124?700?sin?357?00s?in21AC?BC7?86.89 kmsin1?24si?n124所以路程比原来远了约86.89 km.6、飞机离A处探照灯的距离是4801.53 m，飞机离B处探照灯的距离是4704.21 m，飞机的高度是约4574.23 m.1507、飞机在150秒内飞行的距离是d?1000?1000? m3600dx? 根据正弦定理，sin(8118.5?)sin18.5?这里x是飞机看到山顶的俯角为81?时飞机与山顶的距离.d?sin18.5??tan8114721.64 m 飞机与山顶的海拔的差是：x?tan81sin(8118.5?)山顶的海拔是20250?14721.64?5528 m8、在?ABT中，?ATB?21.418.62.8?，?ABT?9018.6?，AB?15 mABAT15?cos18.6?根据正弦定理，，即AT? ?sin2.8?cos18.6?sin2.8?15?cos18.6?塔的高度为AT?sin21.4?sin21.4106.19 msin2.8?326?189、AE97.8 km 60在?ACD中，根据余弦定理：AB?AC??101.235 根据正弦定理，（第9题）?sin?ACDsin?ADCAD?sin?ADC5?7si?n66sin 44?ACD?0.51AC101.2356?ACD?30.9??ACB?13330.9?6?10 2?在?ABC中，根据余弦定理：AB?245.93222AB?AC?B2C245.9?3101?.22352204sBAC?0.58co? 472?AB?AC2?245.?93101.235?BAC?54.21?在?ACE中，根据余弦定理：CE?90.75222AE2?EC?A2C97.8?90.?751012.235sAEC?0.42co? 542?AE?EC2?97?.890.75?AEC?64.82?0AEC?(1?8?0?7?5?)?7564.8?2 18?所以，飞机应该以南偏西10.18?的方向飞行，飞行距离约90.75 km.10、如图，在?ABCAC??37515.44 km222AB?AC?B2C6400?37515?2.44422200?0.692 ?BAC? 42?AB?AC2?640?037515.448，2 ?BAC?9043.?8 ?BAC?133.? 2所以，仰角为43.82?1111、（1）S?acsinB28?33?sin45326.68 cm222aca36（2）根据正弦定理：，c?sinCsin66.5?sinAsinCsinAsin32.8?11sin66.5?S?acsinB362sin(32.866.5?)?1082.58 cm222sin32.8?2（3）约为1597.94 cm122?12、nRsin.2na2?c2?b213、根据余弦定理：cosB?2acaa2所以ma?()2?c2?2c?cosB22a2a2?c2?b22?()?c?a?c? B22ac12212?()2[a2?4c2?2(a?c?2b)]?()[2(b?c2)?a2]222（第13题）篇二：人教版高中数学必修5期末测试题及其详细答案数学必修5试题一．选择题（本大题共10小题，每小题5分，共50分）1.由a1?1，d?3确定的等差数列?an?，当an?298时，序号n等于（）Ａ．99Ｂ．100Ｃ．96Ｄ．1012.?ABC中，若a?1,c?2,B?60?，则?ABC的面积为（） A．12B．2 C.1 D.3.在数列{an}中，a1=1，an?1?an?2，则a51的值为（）A．99 B．49 C．102 D． 101 4.已知x?0，函数y?4x?x的最小值是（） A．5 B．4C．8 D．6 5.在等比数列中，a11?2，q?12，a1n?32，则项数n为（） A. 3B. 4C. 5D. 66.不等式ax2?bx?c?0(a?0)的解集为R，那么（）A. a?0,0B. a?0,0C. a?0,0D. a?0,0?x?y?17.设x,y满足约束条件??y?x,则z?3x?y的最大值为（）y2A． 5B. 3C. 7 D. -88.在?ABC中,a?80,b?100,A?45?,则此三角形解的情况是（）A.一解 B.两解 C.一解或两解 D.无解9.在△ABC中，如果sinA:sinB:sinC?2:3:4，那么cosC等于（）A.23 B.-2113 C.-3D.-410.一个等比数列{an}的前n项和为48，前2n项和为60，则前3n项和为（ A、63B、108 C、75 D、83）二、填空题（本题共4小题，每小题5分，共20分） 11.在?ABC中，B?450,c?b?A＝_____________; 12.已知等差数列?an?的前三项为a?1,a?1,2a?3，则此数列的通项公式为______三、解答题 (本大题共6个小题，共80分；解答应写出文字说明、证明过程或演算步骤) 15(12分) 已知等比数列?an?中，a1?a3?10,a4?a6?16(14分)(1) 求不等式的解集：?x(2)求函数的定义域：y?17 (14分)在△ABC中，BC＝a，AC＝b，a，b是方程x2?0的两个根，且2cos(A?B)?1。

5.4 两角和与差的余弦、正弦和正切

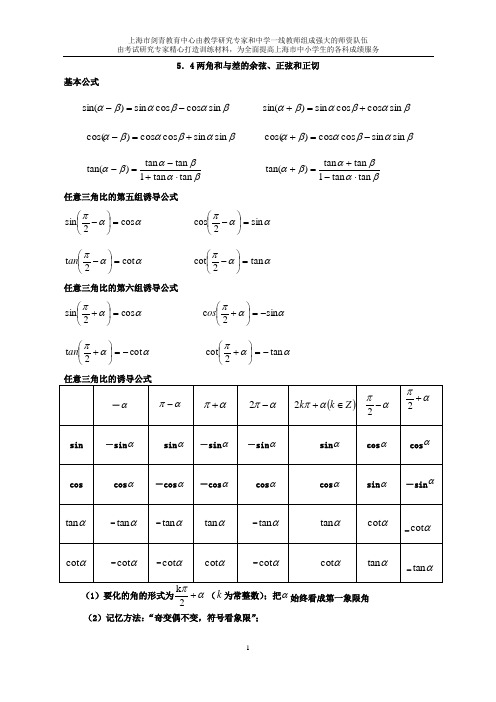
5．4两角和与差的余弦、正弦和正切基本公式βαβαβαsin cos cos sin )sin(-=- βαβαβαsin cos cos sin )sin(+=+βαβαβαsin sin cos cos )cos(+=- βαβαβαsin sin cos cos )cos(-=+βαβαβαtan tan 1tan tan )tan(⋅+-=- βαβαβαtan tan 1tan tan )tan(⋅-+=+ 任意三角比的第五组诱导公式ααπcos 2sin =⎪⎭⎫ ⎝⎛- ααπsin 2cos =⎪⎭⎫⎝⎛- ααπcot 2t =⎪⎭⎫ ⎝⎛-an ααπtan 2cot =⎪⎭⎫⎝⎛- 任意三角比的第六组诱导公式ααπcos 2sin =⎪⎭⎫ ⎝⎛+ ααπsin 2c -=⎪⎭⎫⎝⎛+os ααπcot 2t -=⎪⎭⎫ ⎝⎛+an ααπtan 2cot -=⎪⎭⎫⎝⎛+ 任意三角比的诱导公式（1）要化的角的形式为α+2（k 为常整数）；把α始终看成第一象限角（2）记忆方法：“奇变偶不变，符号看象限”；理解公式：a sin α＋b cos α＝22b a +sin （α＋ϕ） (其中，ϕ通常取πϕ20<≤，2222sin ,cos b a b b a a +=+=ϕϕ，ab=ϕtan α为任意角). 例1.求证：)4cos(2)cos (sin 2)3()4sin(2sin cos )2()6sin(cos 21sin 23)1(ππθθθπααα-=++=++=+x x x例2.利用和(差)角公式化简：)3cos(66)3sin(62)4(cos sin 3)3(cos 53sin 153)2(cos 21sin 23)1(x x x x x x x x -+---+ππ)6sin(cos 21sin 23πααα+=+例3.求证：)4tan(cos sin cos sin π-=+-x xx x x例4.若0＜α＜β＜4π，sin α＋cos α＝a ，sin β＋cos β＝b ，则（）A.ab ＜1B.a ＞bC.a ＜b Ｄ.ab ＞2 【当堂练习】1．化简)sin()sin()cos()cos(γββαγββα-----为（）A ．)2sin(γβα+-B ．)sin(γα- .cos()C αγ-D ．)2cos(γβα+- 2．已知3tan =α，则αααα22cos 9cos sin 4sin 2-+的值为（）A ．3B ．2110C ．13 D ．1303．已知4sin 25α=-，(,)44ππα∈-，sin 4α的值为（）A ．2425B ．2425-C ．45D ．7254．已知sin αcos α=38，且4π<α<2π,则cos α－sin α的值为（） A ．12 B ．—12 C ．14- D ．12±5．已知α+ β =3π, 则cos αcos β–sin αcos β–cos αsin β – sin αsin β 的值为（）A．B ．–1C ．1 D．6. 已知1tan 23α=，求tan α的值．7.已知4sin 5α=，(,)2παπ∈5cos 13β=-,β是第三象限角，求cos()αβ-的值.【家庭作业】一、选择题1．tan 70°＋tan 50°－3tan 70°·tan 50°＝ ( )A. 3B.33C ．－33D ．－ 32．若3sin x －3cos x ＝23sin(x －φ)，φ∈(－π，π)，则φ＝( )A ．－π6 B.π6 C.5π6 D ．－5π63．已知sin ⎝ ⎛⎭⎪⎫π4－x ＝35，则sin 2x 的值为( )A.725B.1625C.1425D.19254．已知cos ⎝ ⎛⎭⎪⎫π6－α＝33，则sin2⎝ ⎛⎭⎪⎫α－π6－cos ⎝ ⎛⎭⎪⎫5π6＋α的值是 ( )A.2＋33B ．－2＋33C.2－33D.－2＋33二、填空题5．函数y ＝2cos2x ＋sin 2x 的最小值是________．6．若0＜α＜π2＜β＜π，且cos β＝－13，sin(α＋β)＝13，则cos α＝________.7．已知α、β为锐角，且cos α＝17，cos(α＋β)＝－1114，则β的值为________．三、解答题8．已知tan ⎝ ⎛⎭⎪⎫π4＋α＝12.(1)求tan α的值； (2)求sin 2α－cos2α1＋cos 2α的值．【综合】一、选择题1．有四个关于三角函数的命题：p1：∃x ∈R ，sin2x 2＋cos2x 2＝12； p2：∃x 、y ∈R ，sin(x －y)＝sin x －sin y ；p3：∀x ∈[0，π],1－cos 2x 2＝sin x ； p4：sin x ＝cos y ⇒x ＋y ＝π2. 其中的假命题是 ( )A ．p1，p4B ．p2，p4C ．p1，p3D ．p2，p4 二、填空题2. 3－sin 70°2－cos210°＝________.3．若cos(α＋β)＝15，cos(α－β)＝35，则tan α·tan β＝________.三、解答题4．如图在平面直角坐标系xOy 中，以Ox 轴为始边作两个锐角α、β，它们的终边分别与单位圆相交于A 、B 两点．已知A 、B 两点的横坐标分别为210、255. (1)求tan(α＋β)的值； (2)求α＋2β的大小．5．已知函数f(x)＝4cos4x －2cos 2x －1cos 2x .(1)求f ⎝ ⎛⎭⎪⎫－1112π的值；(2)当x ∈⎣⎢⎡⎭⎪⎫0，π4时，求g(x)＝f(x)＋sin 2x 的最大值和最小值．6.sin14cos16cos14sin16︒︒+︒︒=7.比较大小：036cos 36sin + 038cos 38sin +；8．已知tan2α=2，求：（1）tan()4πα+的值；（2）6sin cos 3sin 2cos αααα+-的值．9.设α、β为锐角, sinα求α＋β.10.(1) 已知tan (α＋β)＝1, tan α＝3, 求tan β. (2) 设cos(α－2β)＝19-, sin(2α－β)＝23, 且2παπ<<, 0<β<2π,求cos(α＋β).11.求值：(1) 已知sinθ＝35, θ为锐角，求sin 2θ; (2) 已知sinθ＝35,sin2θ<0, 求tan 2θ.参考答案：例1（1）)6sin(cos 21sin 23πααα+=+ 证法一：左边＝sin αcos 6π＋cos αsin 6π＝sin （α＋6π）＝右边证法二：右边＝sin αcos 6π＋cos αsin 6π＝23sin α＋21cos α＝左边 (2)cos θ＋sin θ＝2sin （θ＋4π）证法一：左边＝2（22cos θ＋22sin θ）＝2（sin 4πcos θ＋cos 4πsin θ）＝2sin （θ＋4π）＝右边证法二：右边＝2（sin θcos 4π＋cos θsin 4π）＝2（22sin θ＋22cos θ）＝cos θ＋sin θ＝左边(3) 2（sinx+cosx ）=2cos (x-4π)证法一：左边＝2（sinx ＋cosx ）＝2（22sinx ＋22cosx ）＝2（cosxcos 4π＋sinxsin 4π）＝2cos （x －4π）＝右边证法二：右边＝2cos （x －4π）＝2（cosxcos 4π＋sinxsin 4π）＝2（22cosx ＋22sinx ）＝2（cosx ＋sinx ）＝左边例2.解：(1) 23sinx ＋21cosx ＝sinxcos 6π＋cosxsin 6π＝sin （x ＋6π）或：原式＝sinxsin 3π＋cosxcos 3π＝cos （x －3π）(2)315sinx －35cosx ＝65（23sinx －21cosx ）＝65（sinxcos 6π－cosxsin 6π）＝65sin （x －6π）或：原式＝65（sin 3πsinx －cos 3πcosx ）＝－65cos （x ＋3π）(3) 3sinx －cosx ＝2（23sinx －21cosx ）＝2sin （x －6π）＝－2cos （x ＋3π）(4) 26sin （3π－x ）＋66cos （3π－x ）＝32［21sin （3π－x ）＋23cos （3π－x ）］＝32［sin 6πsin （3π－x ）＋cos 6πcos （3π－x ）］＝32cos ［6π－（3π－x ）］＝32cos （x －6π）或：原式＝32［sin （3π－x ）cos 3π＋cos （3π－x ）sin 3π］＝32sin ［（3π－x ）＋3π］＝32sin（32π－x ）例3证明：左边＝)4tan()4cos(2)4sin(2πππ-=--x x x ＝右边或：右边＝tan （x －4π）＝xx xx x x x x x x cos sin cos sin 4sinsin 4cos cos 4sincos 4cos sin )4cos()4sin(+-=+-=--ππππππ＝左边例4：解：sin α＋cos α＝2sin （α＋4π）＝a sin β＋cos β＝2sin （β＋4π）＝b 又∵0＜α＜β＜4π∴0＜α＋4π＜β＋4π＜2π∴sin （α＋4π）＜sin （β＋4π） ∴a ＜b答案：C 当堂练习 1答案：C解析：利用两角差的余弦公式的逆用 2答案：B解析：二倍角的应用 3答案：B解析：三角函数基本关系式的平方关系的应用 4答案：B解析：平方关系、倍角公式的应用 5答案：B6解析：1tan 23α=，由此得2tan 6tan 10αα+-=解得tan 2α=-+tan 2α=-7答案：33cos()65αβ-=-解析：因为，(,)2παπ∈由此得4sin 5α=所以3cos 5α=-又因为5cos 13β=-,β是第三象限角，所以12sin 13β=-所以33cos()65αβ-=-家庭作业：1 解析：tan 70°＋tan 50°－3tan 70°·tan 50° ＝tan 120°(1－tan 70°·tan 50°)－3tan 70°·tan 50° ＝－ 3. 答案：D2 解析：23sin(x －φ)＝23(sin xcos φ－cos xsin φ) ＝3sin x －3cos x ，∴cos φ＝32，sin φ＝12. 又φ∈(－π，π)，∴φ＝π6. 答案：B3 解析：sin 2x ＝cos ⎝ ⎛⎭⎪⎫π2－2x ＝cos 2⎝ ⎛⎭⎪⎫π4－x ＝1－2sin2⎝ ⎛⎭⎪⎫π4－x ＝1－2×⎝ ⎛⎭⎪⎫35 2＝725. 答案：A 4 解析：sin2⎝ ⎛⎭⎪⎫α－π6－cos ⎝ ⎛⎭⎪⎫5π6＋α ＝1－cos2⎝ ⎛⎭⎪⎫π6－α＋cos ⎝ ⎛⎭⎪⎫π6－α＝2＋33.答案：A5 解析：y ＝(2cos2x －1)＋sin 2x ＋1＝cos 2x ＋sin 2x ＋1＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4＋1 ∴y 的最小值为1－ 2.答案：1－ 26 解析：∵0＜α＜π2＜β＜π，∴π2＜α＋β＜3π2， ∴sin β＝223，cos(α＋β)＝－223，∴cos α＝cos[(α＋β)－β] ＝cos(α＋β)cos β＋sin(α＋β)sin β ＝⎝ ⎛⎭⎪⎫－223×⎝ ⎛⎭⎪⎫－13＋13×223 ＝49 2.答案：4297 解析：cos β＝cos[(α＋β)－α] ＝cos(α＋β)cos α＋sin(α＋β)sin α ＝17×⎝ ⎛⎭⎪⎫－1114＋437×5314＝12. ∴β＝π3. 答案：π38 解：(1)由tan ⎝ ⎛⎭⎪⎫π4＋α＝1＋tan α1－tan α＝12.解得tan α＝－13. (2)sin 2α－cos2α1＋cos 2α＝2sin αcos α－cos2α2cos2α ＝tan α－12＝－56.综合训练1 解析：p1：∃x ∈R ，sin2x 2＋cos2x 2＝12是假命题；p2是真命题，如x ＝y ＝0时成立；p3是真命题， ∵∀x ∈[0，π]，sin x≥0， ∴1－cos 2x2＝sin2x ＝|sin x|＝sin x ；p4是假命题，如x ＝π2，y ＝2π时； sin x ＝cos y ，但x ＋y≠π2. 答案：A 2 解析：3－sin 70°2－cos210°＝3－sin 70°2－1＋cos 20°2＝23－sin 70°3－cos 20°＝23－cos 20°3－cos 20°＝2. 答案：23 解析：∵cos(α＋β)＝cos αcos β－sin αsin β＝15，cos(α－β)＝cos αcos β＋sin αsin β＝35， ∴cos αcos β＝25，sin αsin β＝15. ∴sin αsin βcos αcos β＝12，即tan α·tan β＝12. 答案：124 解：(1)由已知条件及三角函数的定义可知，cos α＝210，cos β ＝255.因为α为锐角，故sin α>0，从而sin α＝1－cos2α＝7210，同理可得sin β＝55，因此tan α＝7，tan β＝12. 所以tan(α＋β)＝tan α＋tan β1－tan αtan β＝7＋121－7×12＝－3. (2)tan(α＋2β)＝tan[(α＋β)＋β]＝－3＋121－－3×12＝－1. 又0<α<π2，0<β<π2，故0<α＋2β<3π2，从而由tan(α＋2β)＝－1得α＋2β＝3π4. 5 解：f(x)＝2cos2x －12cos2x ＋1－2cos2x cos 2x ＝cos 2x 2cos2x ＋1－2cos 2x cos 2x ＝2cos2x ＋1－2＝2cos2x －1＝cos 2x.(1)f ⎝ ⎛⎭⎪⎫－11π12＝cos 2⎝ ⎛⎭⎪⎫－11π12＝cos 11π6＝cos π6＝32. (2)g(x)＝cos 2x ＋sin 2x ＝2sin ⎝⎛⎭⎪⎫2x ＋π4. 由0≤x＜π4，故π4≤2x＋π4＜3π4， ∴22≤sin ⎝ ⎛⎭⎪⎫2x ＋π4≤1,1≤2sin ⎝⎛⎭⎪⎫2x ＋π4≤ 2.即g(x)的最小值是1，最大值是 2.6. 答案：12解析：sin14cos16cos14sin16︒︒+︒︒=sin 30︒=127. 答案：<8. 解析：（１）∵ tan 2α=2, ∴4tan 3α=-; 所以tan tan 4tan()41tan tan 4παπαπα++=-=17-；（２）由(１), 4tan 3α=-;6sin cos 6tan 173sin 2cos 3tan 26αααααα++==--. 9．答案：α＋β＝4π 解析：α、β为锐角, sinα∴ cosα, ∴cos(α＋β)＝cosαcosβ－sinαsinβ∴α＋β＝4π 10. 答案：tan β＝12- cos(α＋β) ＝239729- 解析：（1） ∵tan (α＋β)＝1, tan α＝3,∴tan β＝tan [(α＋β)－β]＝12-. (2) ∵cos(α－2β)＝19-, sin （2α-β）＝23, 且2παπ<<, 0<β<2π, ∴α－2β∈(4π, π), 2α－β∈(4π-, 2π), sin(α－2β)＝92α－β)＝3 ∴ cos 2αβ+＝cos[(α－2β)－(2α－β)]＋β)＝2cos 22αβ+－1＝239729- 11.答案：sin2θ==. t a n 32θ= 解析：(1) ∵sinθ＝35, θ为锐角, ∴ cosθ＝45, sin 2θ==. (2) ∵sinθ＝35,sin2θ<0, ∴cosθ<0, cosθ＝－45,tan 32θ=.。

高中数学必修四同步练习题库：两角和差的正弦、余弦和正切公式(简答题：容易)

两角和差的正弦、余弦和正切公式（简答题：容易）1、.已知,求的值2、已知为锐角，，，求的值.3、中，若，且为锐角，求角．4、求证：－2cos(α＋β)＝.5、已知在中，为中点，，（Ⅰ）求的值；（Ⅱ）求的值.6、在中，角所对边分别为的面积为6.(Ⅰ)求的值；(Ⅱ)求的值.7、函数的最大值为，它的最小正周期为. （1）求函数的解析式；（2）若，求在区间上的最大值和最小值.8、已知分别是的内角所对的边，.（1）证明：；（2）若,求.9、（2015秋•淮南期末）=（）A．1B．2C．3D．410、已知，求的值11、已知函数⑴求的最小正周期及对称中心；⑵若，求的最大值和最小值.12、阅读下面材料：根据两角和与差的正弦公式，有------①------②由①+②得------③令有代入③得.(Ⅰ) 类比上述推理方法，根据两角和与差的余弦公式，证明:;(Ⅱ)若的三个内角满足,试判断的形状. (提示:如果需要，也可以直接利用阅读材料及(Ⅰ)中的结论)13、如图，在平面直角坐标系中，以轴为始边，两个锐角,的终边分别与单位圆相交于A,B 两点．（Ⅰ）若，，求的值；（Ⅱ）若角的终边与单位圆交于点，设角的正弦线分别为，试问：以作为三边的长能否构成一个三角形？若能，请加以证明；若不能，请说明理由.14、已知15、已知（Ⅰ）求的值；（Ⅱ）求的值.16、阅读下面材料：根据两角和与差的正弦公式，有------①------②由①+②得------③令有代入③得.(1) 类比上述推理方法，根据两角和与差的余弦公式，证明:;(2)若的三个内角满足,直接利用阅读材料及(1)中的结论试判断的形状.17、已知为锐角，且求.18、（本小题满分12分）已知，写出用表示的关系等式，并证明这个关系等式．19、如图，有三个并排放在一起的正方形，.（1）求的度数；（2）求函数的最大值及取得最大值时候的x值。

20、（本小题12分）已知0<a<p，；(1)求的值；（2）求的值；21、求值： .22、（本题满分14分）在中，分别是所对的边，已知,，三角形的面积为，（1）求C的大小；（2）求的值．23、已知，（1）求的值；（2）求角.24、阅读下面材料：根据两角和与差的正弦公式，有------①------②由①+②得------③令有代入③得.(Ⅰ) 类比上述推理方法，根据两角和与差的余弦公式，证明:;(Ⅱ)若的三个内角满足,试判断的形状.(提示:如果需要，也可以直接利用阅读材料及(Ⅰ)中的结论)25、化简（1）（2）26、已知，求下列各式的值：（1）（2）27、已知均为锐角，求的值。

高一数学两角和与差的三角函数试题答案及解析

高一数学两角和与差的三角函数试题答案及解析1.的值为_____．【答案】【解析】【考点】1.两角和的余弦公式；2.特殊角的三角函数值.2.计算 = ．【答案】【解析】．【考点】两角差的正弦公式．3.；【答案】.【解析】把原式提取即，然后利用特殊角的三角函数值及两角和的正弦函数公式化简得原式．【考点】两角和与差的正弦函数．4.已知,,分别为三个内角,,的对边, =sin cos．(1)求；(2)若=,的面积为,求,．【答案】(1) ；(2)【解析】(1) 根据正弦定理可将变形为。

因为角三角形的内角，所以，可将上式变形为。

用化一公式即两角和差公式的逆用将上式左边化简可得，根据整体角的范围可得的值，即可得角的值。

(2)由三角形面积可得。

再结合余弦定理可得的值，解方程组可得的值。

解 (1)由=sin cos及正弦定理得sin sin+cos sin-sin=0,由sin≠0,所以sin（+）=,又0<<π,+故=．(2)△ABC的面积=sin=,故=4．由余弦定理知2=2+2-2cos,得代入=,=4解得,故【考点】1正弦定理；2三角形面积公式；3余弦定理。

5.设的值等于____________.【答案】【解析】由题可知.【考点】两角差的正切公式.6.已知，为第三象限角．（1）求的值；（2）求的值．【答案】（1）,; （2）,.【解析】（1）由同角间的基本关系式与的范围可得；（2）由两角和的正弦和倍角的正切公式展开可得.试题解析：解：（1），为第三象限角，； 3分； 6分由（1）得， 9分． 12分【考点】同角间的基本关系，两角和的正弦，倍角公式的正切公式.7.在中，内角A,B,C所对的边分别为a,b,c，且.（1）求A；（2）设，为的面积，求+的最大值，并指出此时B的值.【答案】（1）（2）当时，+取得最大值3.【解析】（1）由结合条件，易求得可求出A的值；（2）由，由正弦定理，得出代入+化简可知时取得最大值3.试题解析：（1）由余弦定理，得，又∵，∴A=. （5分）（2）由（1）得,又由正弦定理及，得，∴+=，∴当时，+取得最大值3. （13分）【考点】主要考查正弦定理，余弦定理，两角和的余弦公式.8.已知向量，，且（1）求及（2）若-的最小值是，求的值。