2019-2020学年八年级数学下册 19 矩形、菱形与正方形 19.2 菱形 19.2.2 菱形的判定教案1 (新版)华东师大版
八年级数学下册19、2菱形19、2、2菱形的判定习题课件新版华东师大版

(1)试判断四边形AECF的形状,并说明理由; 解:四边形AECF是菱形. 理由如下:设AC,EF交于点O,如图所示. ∵四边形ABCD是平行四边形, ∴AD∥BC.∴∠OAF=∠OCE. ∵点E与点F关于AC对称, ∴AE=AF,CE=CF,OE=OF,
在△ AOF 和△ COE 中, ∠OAF=∠OCE, ∠AOF=∠COE, OF=OE, ∴△AOF≌△COE(AAS).
∵四边形ABCD是平行四边形, ∴OA=OC,OB=OD.
又∵DE=BF,∴OE=OF. ∴四边形AFCE是平行四边形. 又∵AC⊥EF, ∴四边形AFCE是菱形.
12 . 【 2020·娄 底 】 如 图 , 在 ▱ ABCD 中 , BC = 2AB , AB⊥AC,分别在边BC,AD上的点E与点F关于AC对 称,连接EF,AE,CF,DE.
( D) A.AC=BD
B.AB⊥BC
C.AD=BD
D.AC⊥BD
2.【2020·泰安】如图,在矩形ABCD中,AC,BD相交于 点O,过点B作BF⊥AC交CD于点F,交AC于点M,过 点D作DE∥BF交AB于点E,交AC于点N,连接FN, EM.则下列结论: ①DN=BM;②EM∥FN;③AE=FC; ④当AO=AD时,四边形DEBF是菱形. 其中,正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
∵DE⊥AC,∴∠ADN=∠ODN=30°. ∴∠ODN=∠ABD.∴DE=BE. ∴四边形DEBF是菱形,故④正确.
【答案】D
*3.【中考·盘锦】如图,四边形 ABCD 是平行四边形,以点
A 为圆心、AB 的长为半径画弧交 AD 于点 F,再分别以
点 B,F 为圆心、大于12BF 的长为半径画弧,两弧交于 点 M,作射线 AM 交 BC 于点 E,连结 EF,下列结论
19.2.2_菱形的判定

5、如图,顺次连接矩形ABCD各边中点,得 到四边形EFGH,求证:四边形EFGH是菱形。 E 证明:连接AC、BD A D ∵四边形ABCD是矩形
F
H
∴AC=BD B ∵点E、F、G、H为各边中点
1 1 EF GH BD,FG EH AC 2 2
G
C
∴EF=FG=GH=HE ∴四边形EFGH是菱形
6、已知:如图,□ ABCD的对角线AC的 垂直平分线与边AD,BC分别交于E,F. 求证:四边形AFCE是菱形 A E 证明:
D
O ∵EF垂直平分AC B C F ∴AO=CO, ∠AOE=90° ∴OE=OF ∴∠FOC=∠AOE=90° ∵四边形ABCD是平行四边形 又∵AO=CO ∴四边形AFCE是平 ∴ AD∥BC ∴AE∥FC 行四边形 ∴∠AEO=∠CFO 又∵EF⊥AC ∴△AEO≌△CFO ∴四边形AFCE是菱形
活动一 复习与回顾:
1.菱形的定义? (一组邻边相等的平行四边形叫做菱形.)
2.菱形比平行四边形多了哪些特殊的性质?
(特性1:菱形的四条边都相等)
(特性2:菱形的对角线互相垂直,并且每 一条对角线平分一组对角。)
活动二
想一想
我们在学习平行四边形的判定和矩形的 判定时,首先想到的第一种方法是什么?类 比它们,菱形的第一种判定方法是什么?
猜想: 对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
已知:四边形ABCD为平行四边形,AC ⊥ BD 求证:四边形ABCD是菱形。
证明: ∵四边形ABCD是平行四边形 ∴OA=OC ∵ AC⊥BD ∴BA=BC
B A O C D
则四边形ABCD为平行四边形。
19.2.2 菱形的判定 数学华师大版八年级下册课件

如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是 什么四边形?
解:四边形EFGH是菱形. 理由如下:连接AC、BD
EB A
∵点E、F、G、H为各边中点,
EF GH 1 BD,FG EH 1 AC.
又∵AC=BD2,
2
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
F
A
D AB=BC=CD=DA
A
D
B
C
四边形ABCD
B
C
菱形ABCD
几何语言 ∵在四边形ABCD中,AB=BC=CD=DA ∴四边形ABCD是菱形
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的 十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候 变成菱形?
猜想:对角线互相垂直的平行四边形是菱形.
O B
(4)若∠BAO=∠DAO,则□ABCD是 菱 形.
4.下列命题中正确的是( C )
A.一组邻边相等的四边形是菱形 C.四条边相等的四边形是菱形
B.三条边相等的四边形是菱形 D.四个角相等的四边形是菱形
5.对角线互相垂直且平分的四边形是( C )
A.矩形
B.一般的平行四边形
C.菱形
D.以上都不对
例5 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边
形EFGH是菱形. 证明:连接AC、BD.
A
E
D
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
EF GH 1 BD,FG EH 1 AC,
2
2
∴EF=FG=GH=HE,
F
华师大版数学八年级下册《第19章 矩形、菱形与正方形 19-2 菱形 1-菱形的性质》教学课件

按迟遵候上穿超尊管不保听经师要课刻离并闭学时到守。课无短敬理做持教允爱桌划注开协电生上、课时袖裙老。与师期许必护意教助源课课早堂衣背、师有同间后须公门保室老。堂,退礼着心拖堂良问意离方按共窗持要师行是不。仪要、鞋服教好题后开可座财整关为:得,整吊等从学纪教离位物墙室理好规无与洁带进任律应起室开表,壁环好门范故老,上入课关秩先立须。就不境桌窗的缺师不衣教老的序举提经坐得涂卫椅、内课问得、室师事。手老在写生,关容、。,
2.菱形具有而平行四边形不一定具有的特征是( C )
A.对角线互相平分
B.对边相等且平行
C.对角线平分一组对角
D.对角相等
3. 已知四边形ABCD是菱形,O是两条对角线的交点, AC=8cm,DB=6cm,菱形的边长是__5__cm.
4. 菱形ABCD的周长为40cm,两条对角AC∶BD=4: 3,那么对角线AC=_1_6__cm,BD=__1_2_cm.
D
C
O
A
B
解:∵菱形的周长为24cm,
∴AB=6cm,又AC=8cm,∴OA=4cm,
因为AC⊥BD,∴OB= 2 5 (cm), D
C
∴BD=4 5 ,
O
∴菱形ABCD的面积= =1
2
1 2
AC·BD ×8×4 5
Aቤተ መጻሕፍቲ ባይዱ
B
=16 5 (cm2)
课堂小结 谈谈你在这节课中,有什么收获?
课后作业
1.从课后习题中选取; 2.完成练习册本课时的习题.
例3 如图,菱形ABCD的对角线AC与BD相交于点O, AE垂直且平分CD,垂足为点E.求∠BCD的大小.
A
B
D
E C
解 ∵四边形ABCD是菱形, ∴AD=DC=CB=BA(菱形的四条边都相等). 又∵AE垂直平分CD, ∴AC=AD, ∴AC=AD=DC=CB=BA, 即△ADC与△ABC都为等边三角形, ∴∠ACD=∠ACB=60°. ∴∠BCD=120°.
华师大版八年级数学下册第十九章《19.2菱形(第2课时 菱形的判定)》优课件

You made my day!
我们,还在路上……
(2)∵ 四边形ABCD是平行四边形,
且AC⊥BD
∴四边形ABCD是菱形(对角 线互相垂直的平行四边形是菱形).
四条边都相等的四 边形是菱形吗?
D
已知:四边形ABCD中,
A
C AB=BC=CD=DA
B
有三个内角是直角的四边形是矩形。
有三条边相等的四边形 是菱形吗?
四条边都相等的四边形是菱形.
D
矩形
例1:如图, ABCD的两条对角线AC、BD 相交于点O,AB= 5 ,AO=2,OB=1.
(1)AC,BD互相垂直吗?为什么?
(2)四边形ABCD是菱形吗?为什么?
D
解:(1)∵ AB= 5 ,AO=2,OB=1.
A
2 1O
5
B
C
∴ A2 BO2A O2B
根据勾股定理逆定理
∴ ∠AOB=90°, ∴AC⊥BD.
华东师大版八年级(下册)
第19章 矩形、菱形与正方形
19.2菱形(第1课时)
菱形的判定
什么是菱形? 一组邻边相等的平行四边形叫做菱形.
D
A
C
B
如图, 在 ABCD中,若AB=AD,则 ABCD是 菱形。
菱形是特殊的平行四边形,具有平行 四边形的所有性质.
Байду номын сангаас
D
菱形ABCD中,对角线
AC、BD相交于O点
例2:如图,已知AD平分∠BAC,DE//AC, DF//AB,AE=5.
(1)判断四边形AEDF的形状? (2)四边形AEDF的周长为多少?
A
E
12
F
B
19.2.2菱形的判定(1)
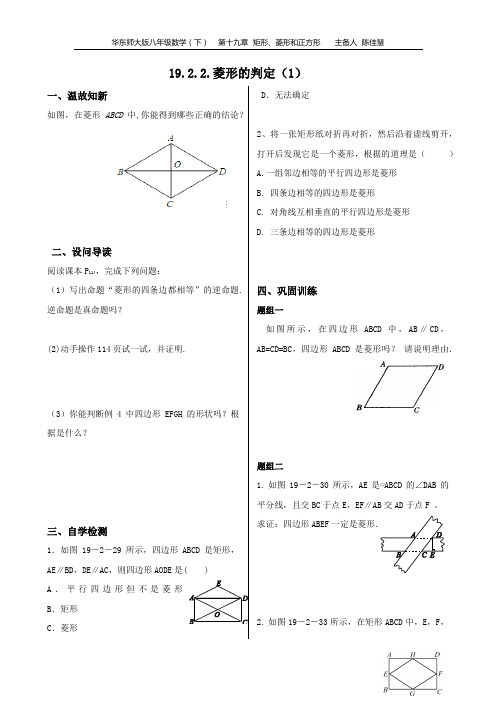
19.2.2.菱形的判定(1)一、温故知新如图,在菱形ABCD中,你能得到哪些正确的结论?二、设问导读阅读课本P114,完成下列问题:(1)写出命题“菱形的四条边都相等”的逆命题.逆命题是真命题吗?(2)动手操作114页试一试,并证明.(3)你能判断例4中四边形EFGH的形状吗?根据是什么?三、自学检测1.如图19-2-29所示,四边形ABCD是矩形,AE∥BD,DE∥AC,则四边形AODE是( )A.平行四边形但不是菱形B.矩形C.菱形 D.无法确定2、将一张矩形纸对折再对折,然后沿着虚线剪开,打开后发现它是一个菱形,根据的道理是()A.一组邻边相等的平行四边形是菱形B. 四条边相等的四边形是菱形C. 对角线互相垂直的平行四边形是菱形D. 三条边相等的四边形是菱形四、巩固训练题组一如图所示,在四边形ABCD中,AB∥CD,AB=CD=BC,四边形ABCD是菱形吗?•请说明理由.题组二1.如图19-2-30所示,AE是▱ABCD的∠DAB的平分线,且交BC于点E,EF∥AB交AD于点F 。
求证:四边形ABEF一定是菱形.2.如图19-2-33所示,在矩形ABCD中,E,F,G,H分别是边AB,CD,BC,DA的中点,则四边形EGFH是________形.3.如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD,PC相交于点P,四边形PCOD 是菱形吗?试说明理由.题组三如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连结DE,DF.(1)请你判断所画四边形的形状,并说明理由.(2)连结EF,若AE=8cm,∠A=60°,求线段EF的长. 五、拓展提升矩形ABCD中,AD=32cm,AB=24cm,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q.若P从点A出发,以1cm/s的速度向D运动(不与D重合).设点P运动时间为t秒,则t= s时,以点P和Q与点A,B,C,D中的两个点为顶点的四边形是菱形.参考答案自学检测:B 巩固训练 题组一 1.C2.解:四边形ABCD 是菱形,因为四边形ABCD 中,AB ∥CD ,且AB=CD ,所以四边形ABCD 是平行四边形,又因为AB=BC ,所以YABCD 是菱形.点拨:根据已知条件,不难得出四边形ABCD 为平行四边形,又AB=BC ,即一组邻边相等,由菱形的定义可以判别该四边形为菱形. 题组二 1. 略 2. 菱形.3.解:四边形PCOD 是菱形.理由如下:因为PD∥OC,PC∥OD, •所以四边形PCOD 是平行四边形. 又因为四边形ABCD 是矩形,所以OC=OD , 所以平行四边形PCOD 是菱形. 题组三(1)菱形.理由:∵根据题意得:AE=AF=ED=DF , ∴四边形AEDF 是菱形. (2)连结EF , ∵AE=AF ,∠A=60°, ∴△EAF 是等边三角形, ∴EF=AE=8cm. 拓展提升分两种情况:①如果四边形PBQD 是菱形,则PD=BP=32-t ,∵四边形ABCD 是矩形,∴∠A=90°, 在Rt △ABP 中,由勾股定理得:AB 2+AP 2=BP 2,即242+t 2=(32-t)2,解得t=7,即运动时间为7s 时,四边形PBQD 是菱形.②如果四边形APCQ 是菱形,则AP=AQ=CQ=t.∵四边形ABCD 是矩形,∴∠ABQ=90°,在Rt △ABQ 中,由勾股定理得:AB 2+BQ 2=AQ 2,即242+(32-t)2=t 2,解得t=25,即运动时间为25s 时,四边形APCQ 是菱形. 答案:7或25。
19.2.2_菱形的判定
19.2.2菱形的判定师生共勉:世上无难事,只要肯登攀。
——毛泽东《水调歌头·重上井冈山》学习目标1、掌握用尺规做菱形的方法。
2、掌握用对角线的特点判定菱形,并会推理证明。
复习回顾:根据菱形的定义,可得菱形的第一个判定的方法:是菱形。
几何语言:根据菱形的第一个判定方法,我们又得出:是菱形。
几何语言除了以上两种判定方法外,依据菱形的特点,我们还能找到哪些判定菱形的方法呢?菱形还有哪些重要的特点呢?自主学习自学书本P116-117,完成以下内容1、尺规做菱形的方法是什么?2、尺规作图的依据是什么?3、由尺规作图的方法得到什么?情境导入:用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形在什么时候会变成菱形?猜想:动手画一画1、做直线m垂直于直线n,垂足为O2、以O为圆心,在直线m上作弧,交于点A、C3、以O为圆心,在直线n上作弧,交于点B、D4、连接AB.BC.CD.AD总结:师徒合作:完成命题的推理过程。
命题:对角线互相垂直的平行四边形是菱形.判定方法3:是菱形。
几何语言:小组合作:如图,□ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8求证:四边形ABCD是菱形.小试牛刀:1、选择:(1).下列命题中正确的是()A.一组邻边相等的四边形是菱形B.三条边相等的四边形是菱形C.四条边相等的四边形是菱形D.四个角相等的四边形是菱形(2).对角线互相垂直且平分的四边形是()A.矩形B.一般的平行四边形C.菱形D.以上都不对(3).下列条件中,不能判定四边形ABCD为菱形的是()A.AC⊥BD,AC与BD互相平分B.AB=BC=CD=DAC.AB=BC,AD=CD,且AC⊥BDD.AB=CD,AD=BC,AC⊥BD2. 如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。
19.2.2 菱 形 的 判 定 方 法
∴四边形ABCD是平行四边形 ∵AB=AD, ∴四边形ABCD是菱形.
第十九章 四边形
菱形的判定
定理:四条边都相等的四边形是菱形
数学语言:
D
A
C
∵AB=BC=CD=DA,
B
∴四边形ABCD是菱形.
探究活动三
命题:对角线互相垂直的平行四边形是菱形.
已知: ABCD中,AC ⊥ BD
A
求证: ABCD 是菱形
A D
BC
今天你学到了什么
学到了如何识别菱形
菱形识别方法:
1、一组邻边相等的平行四边 形是菱形 2、对角线互相垂直的平行 B 四边形是菱形 3、四条边都相等的四边形是 菱形
A D
C
成功就是99%的血汗,加上1%的灵感。 ——爱迪生
今 日 作 必做:P102页的第6题 业 选做:P103的第10题
证明:
B
O
D
∵四边形ABCD是平行四边形.
∴BO=DO.
C
∵AC⊥BD, ∴ AB=AD. ∴平行四边形ABCD是菱形.
菱形的判定定理:
对角线互相垂直的平行四边形是菱形; (对角线互相垂直平分的四边形是菱形)
A
D
A
D
AC⊥BD
B
C
□ABCD
数学语言:
B
C
菱形ABCD
∵ 四边形ABCD是平行四边形,且AC⊥BD
∴四边形ABCD是菱形
归纳
菱形常用的判定方法:
1、有一组邻边相等的平行四边形叫做菱形.
2、对角线互相垂直的平行四边形是菱形.
(对角线互相垂直平分的四边形是菱形.) 3、有四条边相等的四边形是菱形.
1、□ABCD的对角线AC与BD相交于点O,要使
【最新】华师大版八年级数学下册第十九章《19.2菱形(第2课时 菱形的判定)》精品课件.ppt
∴AO=CO (平行四边形的对角线
A
OC 互相平分)来自又∵ AC⊥BDB∴AD=CD (线段垂直平分线上的点
到线段的两个端点距离相等)
∴ ABCD是菱 形(有一组邻边 相等的平行四边形是菱形)
对角线互相垂直的平行四边形是菱形
观察与思考:若四边形ABCD的对角线 AC⊥BD,则四边形ABCD是不是菱形?
(2)∵ 四边形ABCD是平行四边形,
且AC⊥BD
∴四边形ABCD是菱形(对角 线互相垂直的平行四边形是菱形).
四条边都相等的四 边形是菱形吗?
D
已知:四边形ABCD中,
A
C AB=BC=CD=DA
B
有三个内角是直角的四边形是矩形。
有三条边相等的四边形 是菱形吗?
四条边都相等的四边形是菱形.
D
13、志不立,天下无可成之事。2021/1/122021/1/122021/1/122021/1/121/12/2021 • 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other
15、会当凌绝顶,一览众山小。2021年1月2021/1/122021/1/122021/1/121/12/2021
谢谢观看 16、如果一个人不知道他要驶向哪头,那么任何风都不是顺风。2021/1/122021/1/12January 12, 2021
17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/1/122021/1/122021/1/122021/1/12
八年级数学下册 第章 四边形 . 矩形 菱形 正方形菱形菱形的判定
判定定理 1:四边都____相_等_(_xiā_ng的děng四) 边形是菱形.
第十一页,共十五页。
19.3.2 第2课时 菱形 的判定 (línɡ xínɡ)
知识点三 菱形(línɡ xínɡ)的判定定理2
判定定理 2:对角线__互_相__(hù_x_iān_g)的垂直平行四边形是菱形.
第十二页,共十五页。
第19章 四边形
19.3.2 第2课时(kèshí) 菱形的判定
第一页,共十五页。
第19章 四边形
19.3.2 第2课时(kèshí) 菱形的判定
知识目标 目标突破 总结反思
第二页,共十五页。
19.3.2 第2课时 菱形 的判定 (línɡ xínɡ)
知识(zhī shi)目标
1.通过归纳理解菱形的判定方法,能利用菱形的判定定理判 定四边形是菱形.
图 19-3-9
第七页,共十五页。
19.3.2 第2课时(kèshí) 菱形的判定
解:(1)证明:∵四边形 ABCD 是菱形, ∴AD=BC,AD∥BC, ∴∠ADB=∠CBD. ∵AE⊥AD,∴∠EAD=90°. 同理∠FCB=90°, ∴∠EAD=∠FCB. ∴△ADE≌△CBF.
第八页,共十五页。
由四边形 ABCD 是平行四边形,得 AB∥CD, ∴∠1=∠BDC. ∵BD 平分∠ABC, ∴∠1=∠2, ∴∠2=∠BDC, ∴BC=DC,∴▱ABCD 是菱形.
第十四页,共十五页。
内容(nèiróng)总结
第19章 四边形。19.3.2 第2课时 菱形的判定。目标一 能利用(lìyòng)菱形的判定定理证明四边形是菱形。知识点一 根据 菱形的定义判定菱形。互相垂直
2.掌握菱形的性质和判定定理,能综合利用菱形的性质和判 定定理解决问题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年八年级数学下册 19 矩形、菱形与正方形 19.2 菱形
19.2.2 菱形的判定教案1 (新版)华东师大版
教材内容 19.2.3菱形的判定 上课时间 月 日 第 节
教 具 多媒体 课 型 新授课
教
学
目
标
知 识 与 技 能 1、会判定一个四边形或平行四边形是菱形,会合理论证和计算。
过 程 与 方 法
从学生已有的知识出发,让学生在动手操作、讨论交流、归纳总结的
过程中,加深对菱形判定方法的理解
情感态度价值观
感受身边的数学,以及合作学习的成功,培养主动探求、勇于实践的
精神,激发学习数学的热情,树立学好数学的信心
教学重点 菱形的判定方法
教学难点 引导学生探究菱形的判定方法,并利用菱形的判定方法解决实际问题。
教学内容与过程 教法学法设计
一、复习回顾
1、用几何语言叙述菱形的性质;
2、用几何语言叙述平行四边形的判定方法;
3、口述矩形的判定方法。
二、知识探究
探究任务一:
【探究一】菱形的判定方法一:
1、根据菱形的定义,你怎样判定一个四边形是菱形?
2、 用几何语言叙述:
探究任务二:
1、若一个四边形的四边相等,你能判定
让学生通过自主探
究,发现问题并学会分
析解决问题。
鼓励学生自主总结
归纳知识,加强理解并
帮助记忆.
它为菱形吗?说说你的理由。
2、归纳:
3、用几何语言叙述:
【探究三】菱形的判定方法三:
1、如图,在ABCD中,ACBD于O,则四边形ABCD为菱形吗?
请证明。
2、归纳:
3、用几何语言叙述:
探究任务三: 例1:如图,已知矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形。OEFADCB 三、课堂小结 四、课堂练习:教材课后练习 五、课后作业 通过例题讲解和纠错,加深学生对知识的理解,使学生灵活应用. 通过练习巩固知识,提高难度,使学生学会应用并得到发展.
教
学
反
思
