电路-第2章习题-电阻电路的等效变换
《电路与电子技术》课件第2章

图2.9 电压源与电流源等效变换
由于
I US U US U
rS
rS rS
I
IS
U rS
若这两个电源等效,必有U=U′,I=I′,则等效条件为
US rS
IS 或 US
IS
rS
rS rS
(2.17) (2.18)
在处理电源等效时要注意: (1)恒压源与恒流源之间不能等效变换。 (2)凡和电压源串联的电阻、和电流源并联的电阻,无论是 不是电源内阻,均可当作内阻处理。 (3)电源等效是对外电路而言的,电源内部并不等效。例如 电压源开路时,内部不发出功率,而电流源开路时,内部仍有 电流流过,故有功率消耗。 (4)等效时要注意两种电源的正方向,电压源的正极为等效 电流源流出电流的端子,不能颠倒。 电源的等效变换是一种实用的网络简化法,利用它可以使 一些复杂网络的计算有一定程度的简化。
U
(2.2) (2.3) (2.4) (2.5)
2.并联电路的等效变换及分流关系
若干电阻并排连接,在电源作用下,各电阻两端电压相同,
则这些电阻的连接称为并联,如图2.2(a)所示。其等效电路如
图2.2(b)所示,等效电阻R为
1 1 1 1
或用电导表示为 R R1 R2
Rn
n
G G1 G2 Gn Gk
串联、并联时也可用一个等效电源替代,其方法是: (1)凡有多个恒压源串联,或多个恒流源并联,则等效电源
为多个电源的代数和,如图2.7所示。其中:US=US1+US2- US3,IS=IS1+IS2-IS3。
(2)凡是与恒压源并联的元件、与恒流源串联的元件均可除 去,即可将与恒压源并联的支路开路,与恒流源串联的支路短 路,如图2.8所示。
由KVL列出网孔电压方程
第2章简单电阻电路分析-2理想电压源电流源的串并联和等效变换

利用上述关系式,可测量电阻。
返回首页
习题讨论课1—
简单—电阻电路分析
(总第七、八讲)
重点和要求:
1. 参考方向的正确使用。
2. 分压、分流、功率的计算。
3. 欧姆定律、KCL、KVL的使用。
4. 等效的概念 电源的等效变换、电阻的Y-变换。
1. 求入端电阻。
(1) 求Rab、 Rac 。
c
4
4
2
2
4
a 3
a
(2) 求 Rab .
4 2
6
4
2 0.6
b
ab
2. 用电源等效变换化简电路。
(3) 求 Rab .
2 2 1 2 4
a
b 4
a
a
6A
10
等效 R
+ 2A
+
_ 6V
_ Us
b
b
3. 电路如图
g
2A
R=3
(1) 求I1, I2, I3, Uab, Ueg;
e
1 a
b 2 f
(2) 若R变为5 ,
U
I
+
US _
+
U
Ri
_
0
Ii
U=US – Ri I
R Ri: 电源内阻, 一般很小。
一个实际电压源,可用一个理想电压源uS与一个电阻Ri 串联的支路模型来表征其特性。
二、实际电流源
实际电流源,当它向外电路供给电流时,并不
是全部流出,其中一部分将在内部流动,随着端电 压的增加,输出电流减小。
I
u
GiU
is us Ri ,
Gi
1 Ri
电阻电路的等效变换习题ppt课件

100 10 60 50
a
20
b 100 100
a
b 100 60
5
20
40
例3
5
求: Rab
a b 7 6 20
Rab=10
20 5 a b
15 6
缩短无 电阻支路
6 6
15
7
4
a b
4
a b 7
6
15 10
15
3
例4
求: Rab c
25Ω
100V
12
例8: (1)
电阻网络的简化.
3
180
求图示电路的等效电阻.
6 12
6
72
60 80 60
4
3
180
72
72
6 12
24 18
(2)
4 72
6
24
13
3
72
180
30 30 30
3
(4)
180
72 90 90
(3 )
4
72
(5)
3
180
4
72 90
40 90 40
14
41.29
注意受控电压源与电阻的串联组合及受控电流源与电导的并联组合也可进行等效变换但注意在变换过程中保存控制量所在的支路不要把它消掉
i 6Ω 12Ω 3Ω +
i +
等效
u
R
u
-
1
i + 3Ω 6 Ω 6 Ω
i +
等效
u -
R
u -
2
3.电阻混联及等效变换
多个电阻部分串联、部分并联的连接方式
电阻电路的等效变换习题及答案
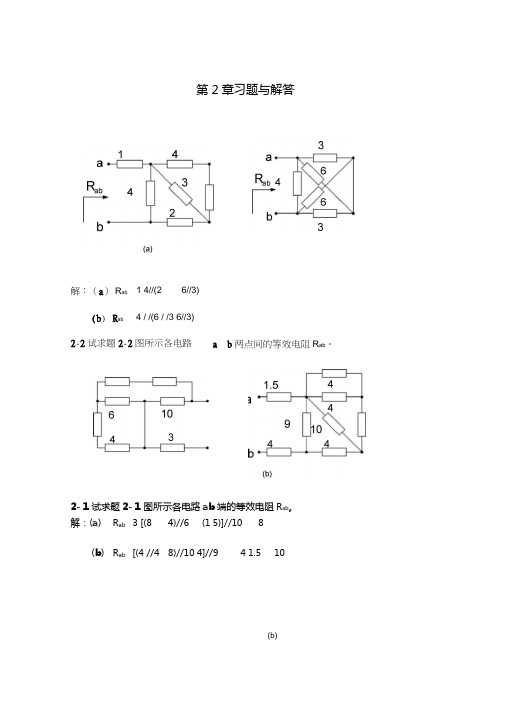
解:(a ) R ab 1 4//(26//3)(b ) R ab4 / /(6 / /3 6//3)2-2试求题2-2图所示各电路a 、b 两点间的等效电阻R ab 。
第2章习题与解答2- 1试求题2- 1图所示各电路ab 端的等效电阻R ab 。
解:(a ) R ab 3 [(84)//6(1 5)]//108(b ) R ab [(4 //4 8)//10 4]//94 1.510(b)2- 3试计算题2-3图所示电路在开关K打开和闭合两种状态时的等效电阻R ab⑻(b)解:(a)开关打开时(8 4)//4 3开关闭合时Rab4//4 2(b)开关打开时Rab(6 12)//(6 12) 9开关闭合时6//12 6//12 8题2-4图解:(a)从左往右流过1电阻的电流为l121/ (1 6//12 3//6) =21/ (1 4 2) 3A从上往下流过3电阻的电流为I3 63 2A3 6从上往下流过12电阻的电流为I 12所以I l3-l12=1A(b)从下往上流过6V电压源的电流为I(1+2) // ( 1+2) 1.5从上往下流过两条并联支路的电流分别为 2A 所以 U 2 2-1 2=2V2- 5试求题2-5图所示各电路ab 端的等效电阻 為,其中R R 211 11 )//(1 D 3 32(b )将图中的两个丫形变成△形,如图所示(b)题2-5图解:(a )如图,2.5I85即得40 21所以志 1.269 2-6计算题2-6图所示电路中a ]1I8888(a)解: 所以20 9题2- 6图(a )将图中的丫形变成△形,如图所示R ab 12//6 4(b )将图中的丫形变成△形,如图所示140 381、对-T~~110108A] I0Uab 532.5 { I—2612所以&b3//4 —2- 7对题2- 7图所示电路,应用Y—△等效变换求电路ab端的等效电阻角线电压U及总电压U ab。
第02章电阻电路的等效变换(丘关源)

(6)恒压源并联任何元件其两端电压不变;
恒流源串联任何元件其流出电流不变;
a a
+ us
-
+ +
-
对外等效
us
-
b
c
b c
对外等效
is
+
-
d
is
d
(1-30)
例1 用电源等效变换法求i R5
R1 u1 + R2 R3 i
+
i=?
解:
-u3
R4
is
R5 u3 — R3 i
应 用 举 例
一、理想电压源的串联和并联
1、串联 + uS1_ _ uS2 +
+ 注意参考方向
º uS=+uS1 …-uS2 i + uS _ º
等效
+
uS _
º +
_ º
2、并联
条件:uS=uS1=uS2 方向相同 º 恒压源中的电流由外电路决定。相同的恒压源才能并联 。
(1-21)
uS1_
u S2
+ _
i
º
3、恒压源与任意支路(非恒压源)并联的等效 i i + + + + 任意 uS 对外等效 uS _ u _ u 元件 _ _ 4、实际电压源的串联等效
+ i +
uS1 _
R1
_ uS2 + u
R2 _
等效
uS _ R + i +
u
_
uS=+uS1-uS2
R=R1 + R2
(1-22)
二、理想电流源的串联和并联
第2章 电阻电路的等效变换

_
+
实际 电流
uS_
源
RS
i+ 实际
u 电压 _源
端口特性 i =iS – GSu
iS=uS /RS GS=1/RS
u=uS – RS i i = uS/RS– u/RS
比较可得等效条件
小结 电压源变换为电流源:
+
i+
iS
uS_
u
i
+ GS u
_
RS
_
is us RS ,
GS
1 RS
电流源变换为电压源:
1.电阻2串.联3 电阻的串联和并联
①电路特点
R1
Rk
Rn
i + u1 _ + u k _ + un _
+
u
_
(a) 各电阻顺序连接,流过同一电流 (KCL);
(b) 总电压等于各串联电阻的电压之和 (KVL)。
u u1 uk un
②等效电阻
R1
Rk
Rn
i + u1 _ + u k _ + un _
R1
R2
i1
1
1 R1 R1 1
R2
i
R2i R1 R2
i2
1
1 R2 R1 1
R2
i
R1i R1 R2
(i i1)
④功率
p1=G1u2, p2=G2u2,, pn=Gnu2 p1: p2 : : pn= G1 : G2 : :Gn
总功率 p=Gequ2 = (G1+ G2+ …+Gn ) u2
2.1 引言
电阻电路 分析方法
(完整版)电阻电路的等效变换习题及答案
第 2 章习题与解答2-1试求题2-1图所示各电路ab端的等效电阻R ab题2-1 图解:(a) R ab 1 4//(2 6//3) 3b)R ab 4/ /(6/ /3 6/ /3) 22-2试求题2-2图所示各电路a、b两点间的等效电阻R ab解:(a) R ab 3 [(8 4)//6 (1 5)]/ /10 8(b) R ab [(4 / /4 8)/ /10 4]//9 4 1.5 102-3试计算题2-3图所示电路在开关K 打开和闭合两种状态时的等效电阻R ab(a)(b)1(a)题2-2 图解:(a)开关打开时R ab (8 4)/ /4 3开关闭合时R ab 4//4 2b)开关打开时R ab(6 12) / /(6 12) 9开关闭合时R ab6//12 6/ /12 8题2-4 图解:(a)从左往右流过1电阻的电流为I1 21/ (1 6/ /12 3 / /6)=21/ (1 42) 3A从上往下流过3电阻的电流为I3从上往下流过12 电阻的电流为I1263 2A366 3 1A12 6所以I I3-I12 =1Ab)从下往上流过6V 电压源的电流为I1+2) // (1+2) 1.56 4A2从上往下流过两条并联支路的电流分别为2A 所以 U 2 2-12=2V2-5试求题 2-5图所示各电路 ab 端的等效电阻 R ab ,其中 R 1 R 2 1b )将图中的两个 Y 形变成△形,如图所示2.58445即得2(b)题 2-5 图1 11所以 R ab ( 1 1)/(/ 1 1) 1ab3 3 2所以R ab 1.269解:(a)将图中的Y 形变成△形,如图所示所以R ab 12//6 4b)将图中的Y 形变成△形,如图所示209402140382-6计算题2-6图所示电路中a8888 8 8b(a)12所以R ab 3/ /4 122-7 对题2-7 图所示电路,应用Y—△等效变换求电路ab 端的等效电阻角线电压U 及总电压U ab 。
第二章 电路的等效变换
化部分)中的电压、电流和功率。
应用等效电路的概念,可以把由多个元件组 成的电路化简为只有少数几个元件甚至一个元 件组成的电路,从而使所分析的问题得到简化。
注意:
等效只是针对外电路而言,对 其内部电路是不等效的。
i
i
i
2Ω 2Ω u
(i
S+ iS'
)
i 1=i 2–i S
方法二: 将N2变换成电压源;
i 1=
uS – uS' R1+R'2
i 2=i 1+i S
电压源与电流源变换公式:
i R
1 变换条件
i 2
uS+
u
i=i iS u=u
G u
–
1
i=
uS – R
u
=
uS R
–
u R
电压源
电流源
令
2
i =i S–u G
1Ω u 5Ω
u
iS
i iS u
对外等效,但内 部电流不等效
对外等效,但内部电压不等效
应用电路等效变换的方法分析电路时,只可用变换后 的电路求解外部电路的电压、电流;求解内部电路的电压、 电流时要在原电路中求解。
§2—1 电阻的串联和并联
i R1
R2
iR
u1
u2
u
i
u
i
U1=
R1 U R1+R2
R=R1+R2
I
2I
2Ω 8Ω
2Ω
I 2Ω
+
8Ω
4I
–
电路B-第二章 电阻电路的等效变换
i12
R31i1 R23i2 R12 R23 R31
u1 R31i1 R31i12 R31 (i1 i12 ) u2 R23i12 R23i2 R23 (i2 i12 )
将i12表达式
代入上两式, 得到
u1 u2
R31 R12
R12
(R12 R23 ) R23 R31 R23 R31 R23 R31
i1 i1
R23 R31 R12 R23 R31 R23 (R12 R31) R12 R23 R31
i2 i2
式(2-ll)和(2-12)分别表示电阻星形联接和三角形联 接网络的 VCR方程。如果要求它们等效,则要 VCR 方程完全相同,也就是两式的对应系数分别相等,即:
R1
R3
电阻的三角形联接:将三个电阻首尾相连,形成一 个三角形,三角形的三个顶点分别与外电路的三个 结点相连,就构成三角形联接,又称为Δ形联接, 如图(b)所示。
电阻三端网络的端口特性,可用联系这些电压和电 流的两个代数方程来表征。
对于电阻星形联接的三端网络,外加两个电流源i1 和i2。用2b方程求出端口电压u1和u2的表达式为:
i1
R2 R1+R2
i
i2
R1 R1+R2
i
例l-12 图(a)所 示电路为双电源直 流分压电路。试求 电位器滑动端移动
时,a点电位Va的
变化范围。
解:将两个电位用两个电压源替代,得到图(b)所示 电路。当电位器滑动端移到最下端时,a点的电位为
1k
Va
Ucd
12V
24V 12V 1k 10k 1k
第二章 电阻电路的等效变换
关于等效的概念: 对于线性时不变电路元件,有时我们只对电
第2章电阻电路的等效变换.
概述重点1•等效变换的概念;2•电源的等效变换;3•输入电阻、等效电阻的概念与计算:■难点1•熟练地分析计算纯电阻电路的等效电阻一尤其是含有电桥或者具有对称性的复杂电路;2•熟练地计算含受控源的电阻电路的等效输入电阻;3•熟练地应用电源的等效变换计算分析电路;第一节普效及其爭赦变换—* >等效如果网络A和网络B对外端口的外特性完全相同,称网给A、B 对外电路等效.—Ib +C Ubl B等效概念的理解・上图所示,如果A. B等•效.将网络A和网络B都接到网络C (外屯路)上,则・网络A和网络B外柠性相同指(VCR)A= (VCR)B换句话说也就是在相同的外电路条件下满足:UxUbJzIb•网络A. B对外电路等效是指A、B相互替代后,C电路(未变化部分)的电流电压功率不变.•注意:相对于C电路(外电路),网络A. B内部不一定等效;等效变换原則:若用网络A替代网络B,应保证在任何时候网络A. B对外端U的外特性完全相同。
等效瓷换0的:对不关心的部分电路而言,力图用较简单的结构代督原來比较复杂的结构,即简化电路。
ES等效变换举例:I jy j "兀 u i 7 h R =R I +R2 g » iI-気『只关5、》第二节电阻网给等畝电阻的求样品如2.1等枚电阻对于一个复杂的电阻网络,可以等效成一个电阻元件.等效电阻在不同的场合下又可以称为:Ri ........ 输入电阻.Ro ……输出电阻等效电阻的求鮮方法串并联法・等电位点法-电阻的星形一三)a 形变换法IXI + !«sU 只关心U 、ii()Req2.2电阻的串并朕 2.2.1趣to 的串联1.串联等敢电阻的计算1-12.电阻相串联流过的电流相同•串联电阻为分压关系: 以两个电阻心和心串联为例:2.2.2电to 的幷朕1.井联等效电阻的计算I 07=i :丄或:R匕&2.电阻并联每个上而电压相同,并联各电阻存在分流关系. 以两个电阻&勺相并联为例:二 R\2 R"血汴意;熟絲址掌握事联1»斥关系与并联分说毘系的使用;/r4J G壬R.等效电阻2.23复杂网络串幷联关糸的判斯R1R3R4R5R5总结:将复杂网络简化为简单电路方法:1.明确计算哪个端口的等效电阻;2.将无电阻电路缩成一点(等电位),标明节点:3.进一步确定电阻的串并联关系・23等电住点法23J刎桥平街的持点常常用于屯阻电路等效电蛆计算ao boR:RiRfHlK.6•结构特点:支路数b”,节点数n=4任意两节点、间有一条也仅有一条支路相连按当RZR'R,时,电桥平衡, 此时有:• C点电位与广点、电位相等•屯阻彳上屯流为鸡I—►Rin因此,可做如下处理: •将电流为零的支路断开«•_*♦♦*♦**♦思考:两种处理*后计算结果相同否?23,2利用电堆对稀性求等败电阻利用电路在结构.元件参数上关于某一轴线或面对称的特性; 例:求下面的电路的输入电阻,其中所有的电阻均为4G.解:在计算中利用电路的对称性.由于电路的结构对称,电阻 值又全部相等.因此a,b,c 三个节点等电位,蓝色的电阻相当于 开路•—•ft♦♦=**♦*♦*•将电位相等的点短接Rin._I3沁例•求图示正方休结构电路的两个顶点b 间的等效电阻•各电阻值均 为仏7说明:这是一个关于某一轴面对称的例子•请学生分析电桥电路中电阻的连接特点:Y 形连接和△形连接・u23电阻的丫形和△形连按的爭效变换3沁ao引入:请大黍忠考如果电桥不平術, 如何计算等效电阻?说明无法采用等电位简化电路,同 吋电阻连接方式既非串联又非并联, 引出本方法•bo季C /hd解:R凤=& = /?厂扌凤23.1变换丸的推导為珞注总:此处倪要求拿41电阻相等的楕况.人三柏电珞^分析中应用 咅 &二& =心=心对. /e “ = g = «,3 ■3Ry电阻的Y ・Ai 换4S 无的椎导息堆:很据等效的帆念・有1・2・2- 3. l ・3i 可的电広对应相#.嵐流入各个*点rb 2. 3)的 电流对应相寻•根^«两种电路形式分别为出其伙安关*丸・ 各项分别相等©很家易得出丫也支拱a 式的结怡i&严竺座旦込詁+心十①?R\RiR 迫=R 占I + R'R 、十 RE = Ri_ & + RE隔L 空口加込十,讥+卒£然也很未易得出△•丫支换4S 戎的结论:R = ___________ R\\R\: ___ "R'R? + &R] 4 R 、R 、尺23&2R 、=•/?|/?2 + R 占、+ RERMu ■ R'R] - RE + RE3直|<1出R2R"第三节亀压源龟洗源的串系联 eg3.1 电压源 b各电压源数值代数相加(注意参考方向),等效成一个电压源;—=M 、| + W Q +.…-"山2.并联:一定要电压相等,方向一致的电压源才允许并联,否则违背KVL, ---------- 为平合理楼理■; -----------------------------------------------------------3.2电浇嫌 l.*JK一定要电流相等.方向一致的电流源才允许串联,否则违背KCL.为不 合理模型・2•幷咲&电流源代相加,等效成一个电流源;(注意:参考方向)n= X <«I-I'•■4r“字'几)rU3.3屯压源与支珞并联的等效电路' ------------- ■O注:N 为一个二端元件或二端电路问题:(1)如果N 也是一电压源,那么对它有何限制?(2)这样的变换对电压源Us 等效吗?3.4电浇源与元件的幷联N :二端元件或二端电路注:类似的变换对受挫电源也适用.不过矣注意受控电源的控制*•Is JLJ N-O+U+C)Us8V丄.丄—Qsv 5A亨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精选文档
2-1、求电路的入端电阻RAB 。
RAB = 2//2+4//6
答案 3.4Ω
2-2、求各电路的入端电阻RAB。
(6//6+9)//10
2-3、求各电路的入端电阻RAB。
→
解:(a)(3//6+1)//6=2Ω
(b) 等效电路如图所示:
即
2-
精选文档
4、 试求下图所示电路中的电流I。
答案
-1.1A
2-5、求图示电路中的电流i。
答案:- 0.1A
2-6、电路如图所示,求B点的电位VB。
解:该电路图可以改变成如下图所示的形式
2-
精选文档
7、电路如图所示,求电流I和电压UAB。
解:原电路可以等效变换为如下电路
2-8、电路如图所示,求AB端的等效电阻RAB。
解:在AB端外加电源,使u、i对二端电路来说是关联参考方向。由图可得:
得到
15
精选文档
2-9、求图 (a) 和 (b) 所示两电路的输入电阻。
2-10、
用电源等效变换法求图示电路中负载RL上的电压U。
12A
5
R
L
U
+
- 14V + -
4
14V
+
-
2 2
2
题2-8图
2-1
精选文档
1、化简为一个等效的电压源支路。
(a) (b) (c) (d)
其中111RUISS,222RUISS,21SSSIII,)(2121RRRRRS,SSSIRU。
恒流源与恒压源的串联和并联两种情况
(1) (2)
2-12、化简图示电路。
(a) (b) (c) (d)
2-13、在图(a)所示电路中,已知V12SU,31R,A5SI,62R,试求
2
R
支路中的电流2I。
(a) (b) (c)
解: 3)5312(633)(12112SSIRURRRIA
精选文档
2-14、在图示电路中,N为一个实际的直流电源。当开关S断开时,电压表读数为V10;
当开关S闭合时,电流表读数为A1。试求该直流电源N的电压源模型与电流源模型。
解:等效电路如图:
,
2-1
精选文档
5、电路如图所示。已知61R,1.02R,98.0,53R,VU9.4。求
?SU
解:因为电流控制的电流源3RI与串联,所以
3
R
U
I
,所以 ARUI1598.09.43
AIIII02.01)98.01()1(2
21221)1(IRIRRIIRU
S
VIRR002.611.0)98.01(6)1(21
(注:可编辑下载,若有不当之处,请指正,谢谢!)
I
U
US
I2 I R3 R2
R1
-
-
+
+
