三角函数五点法作图

合集下载

三角函数的图像和性质知识点及例题讲解

三角函数的图像和性质一、用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (,0) (23π,-1) (2,0)余弦函数y=cosx x [0,2]的图像中，五个关键点是：(0,1) (2π,0) (,-1) (23π,0) (2,1)二、正弦函数、余弦函数和正切函数的图象与性质：sin y x = cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+时，max 1y =；当22x k ππ=- 时，min 1y =-．当2x k π=时，max 1y =；当2x k ππ=+时，min1y =-．既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦上是增函数；在32,222k k ππππ⎡⎤++⎢⎥⎣⎦上是减函数．在[]2,2k k πππ-上是增函数；在[]2,2k k πππ+上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭上是增函数．对称性对称中心(),0k π 对称轴2x k ππ=+对称中心,02k ππ⎛⎫+ ⎪⎝⎭对称轴x k π=对称中心,02k π⎛⎫⎪⎝⎭无对称轴函数性质例作以下函数的简图(1)y=|sinx|，x ∈[0，2π]， (2)y=-cosx ，x ∈[0，2π]例利用正弦函数和余弦函数的图象，求知足以下条件的x 的集合：21sin )1(≥x 21cos )2(≤x3、周期函数概念：关于函数()y f x =，若是存在一个非零常数T ，使适当x 取概念域内的每一个值时，都有：()()f x T f x +=，那么函数()y f x =就叫做周期函数，非零常数T 叫做那个函数的周期。

注意：周期T 往往是多值的（如sin y x = 2π,4π,…,-2π,-4π,…都是周期）周期T 中最小的正数叫做()y f x =的最小正周期（有些周期函数没有最小正周期）sin y x =, cos y x =的最小正周期为2π （一样称为周期）正弦函数、余弦函数：ωπ=2T 。

三角函数的图像和性质(1)

y
− 6π
− 4π
y=sinx, x ∈ R
− 2π
1 0 -1
2π
4π
6π
x
正弦曲线 y
1
y=cosx, x ∈ R
− 6π
− 4π
− 2π
0 -1
2π
4π
x
余弦曲线
二、重难点讲解
y
1-
5. 五点作图法的五个关键点
图象的最高点 (π ,1) 图象的最高点 2 与x轴的交点轴的交点
( 0 , 0 ) (π , 0 ) (2π ,0)
，
_
，
y P A(1,0)
x
正弦线：正弦线： MP 余弦线：余弦线：OM 正切线：正切线： AT
M
O T
一、复习引入
1. 作出下列各角的正弦线、余弦线、正切线的正弦线、余弦线、正切线.
，
_
，
y
M 正弦线：正弦线： MP 余弦线：余弦线：OM 正切线：正切线： AT O P
A(1,0)
x
2π
-
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
图象的最低点图象的最低点
简图作法：五点作图法五点作图法) 简图作法：(五点作图法 (1) 列表列出对图象形状起关键作用的五点坐标) 列表( (2) 描点定出五个关键点) 描点( (3) 连线用光滑的曲线顺次连结五个点) 连线(
利用三角函数线作三角函数图象
作三角函数线得三角函数值，作三角函数线得三角函数值，描点 ( x, sin x ),连线连线如: x

4.4三角函数的图像性质及应用

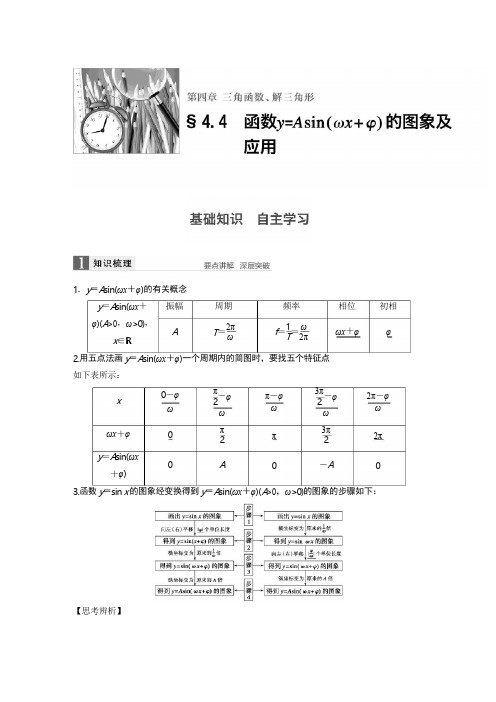
－φ－φ1．y＝A sin(ωx＋φ)的有关概念y＝A sin(ωx＋φ)(A>0，ω>0)，x∈R振幅A周期2πT＝ω频率1ωf＝T＝2π相位ωx＋φ初相φ2.用五点法画y＝A sin(ωx＋φ)一个周期内的简图时，要找五个特征点如下表所示：x0－φωπ2ωπ－φω3π2ω2π－φωωx＋φy＝A sin(ωx＋φ)π2Aπ3π2－A2π0 3.函数y＝sin x的图象经变换得到y＝A sin(ωx＋φ)(A>0，ω>0)的图象的步骤如下：【思考辨析】(2)y ＝sin ⎝x －4⎭的图象是由 y ＝sin ⎝x ＋4⎭的图象向右平移个单位得到的．(√ )1．y ＝2sin ⎝2x －4⎭的振幅、频率和初相分别为2．已知函数 f (x )＝sin ⎝2x ＋6⎭.若 y ＝f (x －φ) (0<φ< )是偶函数，则 φ＝解析因为 y ＝f (x －φ)＝sin ⎣2(x －φ)＋6⎦＝sin ⎝2x －2φ＋6⎭是偶函数，所以－2φ＋＝＋k π， k ∈Z ，得 φ＝－－，k ∈Z .又 0<φ< ，所以 φ＝ .3．(2015· 湖南改编)将函数 f (x )＝sin 2x 的图象向右平移 φ⎝0＜φ＜2⎭个单位后得到函数 g (x )的]判断下面结论是否正确(请在括号中打“√”或“×”)(1) 利用图象变换作图时“先平移，后伸缩”与“先伸缩，后平移”中平移的长度一致．( × )⎛ π⎫ ⎛ π⎫ π 2(3)由图象求解析式时，振幅 A 的大小是由一个周期内的图象中的最高点的值与最低点的值确定的．( √ )(4)函数 f (x )＝A sin(ωx ＋φ)的图象的两个相邻对称轴间的距离为一个周期．( × )(5)函数 y ＝A cos(ωx ＋φ)的最小正周期为 T ，那么函数图象的两个相邻对称中心之间的距离为T2.( √ )⎛ π⎫1 π答案 2，π，－4．⎛ π⎫ π 2.答案π3⎡ π⎤ ⎛ π⎫ π π 6 2π k π π π6 2 2 3⎛ π⎫π图象，若对满足|f (x 1)－g (x 2)|＝2 的 x 1，x 2，有|x 1－x 2|min ＝3，则 φ＝.答案π6解析因为 g (x )＝sin [2 x －φ ＝sin(2x －2φ)，所以|f (x 1)－g (x 2)|＝|sin 2x 1－sin(2x 2－2φ)|＝2.因为－1≤sin 2x 1≤1，－1≤sin(2x 2－2φ)≤1，所以 sin 2x 1 和 sin(2x 2－2φ)的值中，一个为 1，另一个为－1，不妨取 sin 2x 1＝1，sin(2x 2－2φ)π π＝－1，则 2x 1＝2k 1π＋2，k 1∈Z,2x 2－2φ＝2k 2π－2，k 2∈Z,2x 1－2x 2＋2φ＝2(k 1－k 2)π＋π，(k 1⎪⎪因为0<φ<，所以0<－φ<，则φ＝.答案y＝10sin⎝8x＋4⎭＋20，x∈[6,14]所以A＝×(30－10)＝10，b＝×(30＋10)＝20，所以ω＝.又×10＋φ＝2π，4所以y＝10sin⎝8x＋4⎭＋20，x∈[6,14]．5．(2014·安徽)若将函数f(x)＝sin(2x＋)的图象向右平移φ个单位，所得图象关于y轴对称，答案3π－k2)∈Z，π得|x1－x2|＝⎪(k1－k2)π＋2－φ⎪.πππ222ππ故当k1－k2＝0时，|x1－x2|min＝2－φ＝3，π64．(教材改编)如图，某地一天从6～14时的温度变化曲线近似满足函数y＝A sin(ωx＋φ)＋b，则这段曲线的函数解析式为．⎛π3π⎫解析从图中可以看出，从6～14时的是函数y＝A sin(ωx＋φ)＋b的半个周期，121212π又2×ω＝14－6，π8π83π解得φ＝，⎛π3π⎫π4则φ的最小正值是．8解析∵函数f(x)＝sin(2x＋)的图象向右平移φ个单位得到g(x)＝sin[2(x－φ)＋]＝sin(2x＋又∵g(x)是偶函数，∴－2φ＝kπ＋(k∈Z)．∴φ＝－－(k∈Z)．当k＝－1时，φ取得最小正值.例1已知函数y＝2sin⎝2x＋3⎭.(3)说明y＝2sin⎝2x＋3⎭的图象可由y＝sin x的图象经过怎样的变换而得到．解(1)y＝2sin⎝2x＋3⎭的振幅A＝2，周期T＝＝π，初相φ＝.(2)令X＝2x＋，则y＝2sin⎝2x＋3⎭＝2sin X.6y＝2sin⎝2x＋3⎭πππ444－2φ)，ππ42kππ283π8题型一函数y＝A sin(ωx＋φ)的图象及变换⎛π⎫(1)求它的振幅、周期、初相；(2)用“五点法”作出它在一个周期内的图象；⎛π⎫⎛π⎫2ππ23π⎛π⎫3列表如下：xXy＝sinX⎛π⎫π－π12π212π3π7π123π2－1－25π62π描点画出图象，如图所示：(3)方法一把 y ＝sin x 的图象上所有的点向左平移个单位长度，得到 y ＝sin ⎝x ＋3⎭的图象；再把 y ＝ sin ⎝x ＋3⎭ 的图象上所有点的横坐标缩短到原来的sin ⎝2x ＋3⎭的图象；最后把 y ＝sin ⎝2x ＋3⎭上所有点的纵坐标伸长到原来的 2 倍(横坐标不变 )，即可得到 y ＝2sin ⎝2x ＋3⎭的图象．方法二将 y ＝sin x 的图象上所有点的横坐标缩短为原来的倍(纵坐标不变)，得到 y ＝sin 2x再将 y ＝sin 2x 的图象向左平移个单位长度，得到 y ＝sin ⎣2⎝x ＋6⎭⎦＝sin ⎝2x ＋3⎭的图象；再将 y ＝sin ⎝2x ＋3⎭的图象上所有点的纵坐标伸长为原来的 2 倍(横坐标不变)，即得到 y ＝2sin ⎝2x ＋3⎭的图象．设 z ＝ωx ＋φ，由 z 取 0，，π， π，2π 来求出相应的 x ，通过列表，计算得出五点坐标，描(1)把函数 y ＝sin(x ＋ )图象上各点的横坐标缩短到原来的 (纵坐标不变)，再将图象向右平移个单位长度，那么所得图象的一条对称轴方程为(填正确的序号)．①x ＝－；②x ＝－；③x ＝；④x ＝ .(2)设函数 f (x )＝cos ωx ( ω>0)，将 y ＝f (x )的图象向右平移个单位长度后，所得的图象与原图π ⎛ π⎫ 3⎛ π⎫ 1 2倍 ( 纵坐标不变 ) ，得到 y ＝⎛ π⎫⎛ π⎫⎛ π⎫12的图象；π ⎡ ⎛ π⎫⎤ ⎛ π⎫ 6⎛ π⎫⎛ π⎫思维升华 (1)五点法作简图：用“五点法”作 y ＝A sin(ωx ＋φ)的简图，主要是通过变量代换，π 3 2 2点后得出图象．(2)图象变换：由函数 y ＝sin x 的图象通过变换得到 y ＝A sin(ωx ＋φ)的图象，有两种主要途径：“先平移后伸缩”与“先伸缩后平移”．π 162π3π π π π2 4 8 4π3象重合，则 ω 的最小值等于．答案 (1)① (2)6解析(1)将y＝sin(x＋)图象上各点的横坐标缩短到原来的(纵坐标不变)，得到函数y＝sin(2x＋)；再将图象向右平移个单位长度，得到函数y＝sin[2(x－)＋]＝sin(2x－)，故x 2(2)由题意可知，nT＝(n∈N*)，例2(1)已知函数y＝A sin(ωx＋φ)(A>0，ω>0，|φ|<)的图象上一个最高点的坐标为(2，2)，答案(1)y＝2sin⎝8x＋4⎭(2)f(x)＝2sin(2x＋)⎫解析(1)由题意得A＝2，＝6－2，所以T＝16，ω＝＝.又sin⎝8×2＋φ⎭＝1，所以＋φ＝＋2kπ(k∈Z)．又因为|φ|<，所以φ＝.41234π162πππππ63362π＝－是其图象的一条对称轴方程．π32ππ∴n·ω＝3(n∈N*)，∴ω＝6n(n∈N*)，∴当n＝1时，ω取得最小值6.题型二由图象确定y＝Asin(ωx＋φ)的解析式π2由这个最高点到其右侧相邻最低点间的图象与x轴交于点(6,0)，则此函数的解析式为．(2)函数f(x)＝A sin(ωx＋φ)(A＞0，ω＞0，|φ|＜π)的部分图象如图所示，则函数f(x)的解析式为．⎛ππ⎫π3T2ππ⎛ππ4T84πππ224(2)由题图可知A＝2，T7πππ＝－＝，所以T＝π，故ω＝2，因此f(x)＝2sin(2x＋φ)，又⎝12π，－ 2⎭为最小值点， ∴2× π＋φ＝2k π＋，k ∈Z ，∴φ＝2k π＋，k ∈Z ，∴φ＝ .故 f (x )＝ 2sin(2x ＋ )．则 A ＝，b ＝ .(2)求 ω，确定函数的最小正周期 T ，则可得 ω＝ . “最大值点”(即图象的“峰点”)时 ωx ＋φ＝；“最小值点”(即图象的“谷点”)时 ωx ＋φ＝ .函数 f (x )＝2sin(ωx ＋φ)⎝ω＞0，－2＜φ＜2⎭的部分图象如图所示，则 φ＝3解析 ∵ ＝ π－ π，⎛ 7 ⎫7 3π12 2π3又|φ|＜π，π3π3思维升华确定 y ＝A sin(ωx ＋φ)＋b (A ＞0，ω＞0)的步骤和方法：(1)求 A ，b ，确定函数的最大值 M 和最小值 m ，M －m M ＋m2 22πT(3)求 φ，常用的方法有：①代入法：把图象上的一个已知点代入(此时 A ，ω，b 已知)或代入图象与直线 y ＝b 的交点求解(此时要注意交点在上升区间上还是在下降区间上)．②特殊点法：确定 φ 值时，往往以寻找“最值点”为突破口．具体如下：π23π 2π答案－T 1152 12 12∴T ＝π.2π又 T ＝ ω (ω＞0)，2π∴ ω ＝π，⎛ ππ⎫.由五点作图法可知当x＝π时，2即2×π＋φ＝，∴φ＝－.y)．若初始位置为P0⎝2，⎭，当秒针从P(注：此时t＝0)正常开始走时，那么点P的纵坐答案y＝sin⎝－30t＋6⎭位是.又函数周期是60(秒)且秒针按顺时针旋转，即T＝⎪ω⎪＝60，所以|ω|＝π⎪2π⎪ππ63030所以y＝sin⎝－30t＋6⎭.例4已知关于x的方程2sin2x－3sin2x＋m－1＝0在⎝2，π⎭上有两个不同的实数根，则m ∴ω＝2.512πωx＋φ＝，5π122π3题型三三角函数图象性质的应用命题点1三角函数模型的应用例3如图，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置P(x，⎛31⎫2标y与时间t的函数关系式为．⎛ππ⎫解析设点P的纵坐标y与时间t的函数关系式为y＝sin(ωt＋φ)．由题意可得，函数的初相，即ω＝－，⎛ππ⎫命题点2方程根(函数零点问题)⎛π⎫的取值范围是．答案(－2，－1)解析方程2sin2x－3sin2x＋m－1＝0可转化为m＝1－2sin2x＋3sin2x＝cos2x＋3sin2x＝2sin⎝2x＋6⎭，x∈⎝2，π⎭.设2x＋＝t，则t∈⎝6π，6π⎭，6＝sin t，t∈⎝6π，6π⎭，有两个不同的实数根．∴y＝和y＝sin t，t∈⎝6π，6π⎭的图象有两个不同交点，如图：2由图象观察知，的范围为(－1，－)，解析由例4知，的范围是⎣－1，2⎭，∴－2≤m<1，图象的两相邻对称轴间的距离为.(1)求f⎝8⎭的值；(2)求函数y＝f(x)＋f⎝x＋4⎭的最大值及对应的x的值．＝2⎣2＝2sin⎝ωx＋φ－6⎭.⎛π⎫⎛π⎫π⎛713⎫∴题目条件可转化为m⎛713⎫2m⎛713⎫m122故m的取值范围是(－2，－1)．引申探究例4中，“有两个不同的实数根”改成“有实根”，则m的取值范围是．答案[－2,1)m⎡1⎫2∴m的取值范围是[－2,1)．命题点3图象性质综合应用例5已知函数f(x)＝3sin(ωx＋φ)－cos(ωx＋φ)(0＜φ＜π，ω＞0)为偶函数，且函数y＝f(x)π2⎛π⎫⎛π⎫解(1)f(x)＝3sin(ωx＋φ)－cos(ωx＋φ)⎡31⎤sin(ωx＋φ)－2cos(ωx＋φ)⎦⎛π⎫因为f(x)是偶函数，则 φ－＝＋k π(k ∈Z )，所以 φ＝＋k π(k ∈Z )，又因为 0＜φ＜π，所以 φ＝，ωx ＋＝2cos ωx .所以 f (x )＝2sin 2⎭⎝因此 f ＝2cos ＝ 2.⎝8⎭x ＋(2)y ＝2cos 2x ＋2cos 2⎣ ⎝ 4⎭⎦2x ＋＝2cos 2x ＋2cos 2⎭⎝－2x ＝2 2sin ⎝4 ⎭2x －＝－2 2sin4⎭⎝令 2x －＝2k π－ (k ∈Z )，y 有最大值 2 2，所以当 x ＝k π－ (k ∈Z )时，y 有最大值 2 2.设函数 f (x )＝3sin(ωx ＋φ)(ω>0，－ <φ< )的图象关于直线 x ＝对称，它的周期①f (x )的图象过点(0， )；π π6 22π32π3⎛ π⎫ 2π π由题意得 ω ＝2· 2，所以 ω＝2.故 f (x )＝2cos 2x .⎛π⎫ π4⎡ ⎛ π⎫⎤⎛ π⎫＝2cos 2x －2sin 2x⎛π ⎫⎛ π⎫ π π4 2π8思维升华 (1)三角函数模型的应用体现在两方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，建立数学模型再利用三角函数的有关知识解决问题．(2)方程根的个数可转化为两个函数图象的交点个数．(3)研究 y ＝A sin(ωx ＋φ)的性质时可将 ωx ＋φ 视为一个整体，利用换元法和数形结合思想进行解题．π π 2π2 2 3是 π，则下列说法正确的是．(填序号)32②f (x )在[ ， ]上是减函数；③f (x )的一个对称中心是( ，0)；∴f (x )＝3sin(2x ＋φ)，f ( )＝3sin( ＋φ)，则 sin( ＋φ)＝1 或－1.又 φ∈(－， )，＋φ∈( ， π)，∴ ＋φ＝ ⇒φ＝，∴f (x )＝3sin(2x ＋ )．①：令 x ＝0⇒f (x )＝，正确．②：令 2k π＋ <2x ＋ <2k π＋，k ∈Z⇒k π＋ <x <k π＋，k ∈Z .令 k ＝0⇒ <x < ，即 f (x )在( ， )上单调递减，而在( ， )上单调递增，错误．③：令 x ＝ ⇒f (x )＝3sin π＝0，正确．④：应平移个单位长度，错误．典例 (14 分)已知函数 f (x )＝2 3sin( ＋ )·cos( ＋ )－sin(x ＋π)．π 2π12 35π12④将 f (x )的图象向右平移|φ|个单位长度得到函数 y ＝3sin ωx 的图象．答案 ①③2π解析 ∵周期为 π，∴ ω ＝π⇒ω＝2，2π 4π3 34π3π π 4π 5π 112 23 6 64π 3π π3 2 6π 632π π 3π2 6 2π 2π6 3π 2π63π 2π π π6 3 12 65π12π124．三角函数图象与性质的综合问题x π x π2 4 2 4(1)求 f (x )的最小正周期；(2)若将f(x)的图象向右平移个单位长度，得到函数g(x)的图象，求函数g(x)在区间[0，π]上(2)将f(x)解析式中的x换成x－，得g(x)，然后利用整体思想求最值．解(1)f(x)＝23sin(＋)·cos(＋)－sin(x＋π)＝3cos x＋sin x[4分]＝2sin(x＋)，[6分]于是T＝＝2π.[7分](2)由已知得g(x)＝f(x－)＝2sin(x＋)，[9分]∵x∈[0，π]，∴x＋∈[，]，∴sin(x＋)∈[－，1]，[12分]∴g(x)＝2sin(x＋)∈[－1,2]．[13分]a sinα＋b cosα＝a2＋b2sin(α＋φ)(其中tanφ＝)，或a sinα＋b cosα＝a2＋b2cos(α－φ)(其中tanφ＝)，在历年高考中使用频率是相当高的，几乎年年使用到、考查到，应特别加以关注．(sin x·aπ6的最大值和最小值．思维点拨(1)先将f(x)化成y＝A sin(ωx＋φ)的形式再求周期；π6规范解答xπxπ2424π32π1ππ66ππ7π666π162π6故函数g(x)在区间[0，π]上的最大值为2，最小值为－1.[14分]解决三角函数图象与性质的综合问题的一般步骤：第一步：(化简)将f(x)化为a sin x＋b cos x的形式；第二步：(用辅助角公式)构造f(x)＝a2＋b2·b＋cos x·)；a2＋b2a2＋b2第三步：(求性质)利用f(x)＝a2＋b2sin(x＋φ)研究三角函数的性质；第四步：(反思)反思回顾，查看关键点、易错点和答题规范．温馨提醒(1)在第(1)问的解法中，使用辅助角公式baab(2)求g(x)的最值一定要重视定义域，可以结合三角函数图象进行求解．±1．函数y＝cos⎝2x－3⎭的部分图象可能是⎫[方法与技巧]1．五点法作图及图象变换问题(1)五点法作简图要取好五个关键点，注意曲线凸凹方向；(2)图象变换时的伸缩、平移总是针对自变量x而言，而不是看角ωx＋φ的变化．2．由图象确定函数解析式由图象确定y＝A sin(ωx＋φ)时，φ的确定是关键，尽量选择图象的最值点代入；若选零点代入，应根据图象升降找“五点法”作图中第一个零点．3．对称问题函数y＝A sin(ωx＋φ)的图象与x轴的每一个交点均为其对称中心，经过该图象上坐标为(x，A)的点与x轴垂直的每一条直线均为其图象的对称轴，这样的最近两点间横坐标的差的绝对值是半个周期(或两个相邻对称中心的距离)．[失误与防范]1．由函数y＝sin x的图象经过变换得到y＝A sin(ωx＋φ)的图象，如先伸缩，再平移时，要把x前面的系数提取出来．2．复合形式的三角函数的单调区间的求法．函数y＝A sin(ωx＋φ)(A>0，ω>0)的单调区间的确定，基本思想是把ωx＋φ看做一个整体．若ω<0，要先根据诱导公式进行转化．3．函数y＝A sin(ωx＋φ)在x∈[m，n]上的最值可先求t＝ωx＋φ的范围，再结合图象得出y ＝A sin t的值域．A组专项基础训练(时间：40分钟)⎛π．2x －，∴当2x －＝0，解析∵y ＝cos 3⎭⎝即 x ＝时，函数取得最大值 1，结合图象看，可使函数在 x ＝时取得最大值的只有④. 解析取 K ，L 中点 N ，则 MN ＝，因此 A ＝ .由 T ＝2 得 ω＝π.∵函数为偶函数，0<φ<π，∴φ＝，∴f (x )＝ cos πx ，3.已知函数 f (x )＝2sin(ωx ＋φ)(ω>0，且|φ|< )的部分图象如图所示，则函数解析由函数的图象可得 T ＝ π－ π，又图象过点( π，2)，∴2sin(2× π＋φ)＝2， ∴φ＝－＋2k π，k ∈Z ，∵|φ|< ，△KLM 为等腰直角三角形，∠KML ＝90°，KL ＝1，则 f ( )的值为．答案3 ∴f ( )＝ cos ＝ .答案 [k π－，k π＋ ]，k ∈Z答案 ④⎛ π⎫ π 3π π6 62．设偶函数 f (x )＝A sin(ωx ＋φ)(A >0，ω>0,0<φ<π)的部分图象如图所示，1641212π 2121 1 π 3 62 6 4π2f (x )的单调递增区间是．π 5π12 121 2 54 3 12∴T ＝π，则 ω＝2.5 512 12π3π2∴取 k ＝0，则 φ＝－，即得 f (x )＝2sin(2x － )，∴f (x )的单调增区间为 2k π－ ≤2x － ≤2k π＋，k ∈Z ，即单调递增区间为[k π－，k π＋ ]，k ∈Z .4．已知曲线 f (x )＝sin ωx ＋ 3cos ωx (ω＞0)相邻的两条对称轴之间的距离为，且曲线关于点 (x 0,0)中心对称，若 x 0∈⎣0，2⎦，则 x 0＝＝2⎝ sin ωx ＋＝2sin ⎝ωx ＋3⎭.∵曲线 f (x )＝2sin ⎝ωx＋3⎭相邻的两条对称轴之间的距离为，∴f (x )＝2sin ⎝2x ＋3⎭. 又 x 0∈⎣0，2⎦，∴x 0＝ . 5．函数 f (x )＝sin(2x ＋φ)⎝|φ|＜2⎭的图象向左平移个单位后所得函数图象的解析式是奇函数，则函数 f (x )在⎣0，2⎦上的最小值为答案－ 3解析由函数 f (x )的图象向左平移个单位得 g (x )＝sin ⎝2x ＋φ＋3⎭的图象，π π3 3π π π2 3 2π 5π12 12π2⎡ π⎤.答案π3解析 f (x )＝sin ωx ＋ 3cos ωx⎛1 2 3 ⎫ 2 cosωx ⎭⎛ π⎫⎛ π⎫ π 22π∴最小正周期 T ＝π＝ ω ，∴ω＝2，⎛ π⎫∵曲线关于点(x 0,0)中心对称；π∴2x 0＋3＝k π(k ∈Z )，k π π∴x 0＝ 2 －6(k ∈Z )，⎡ π⎤ π 3⎛ π⎫ π 6⎡ π⎤．2π ⎛ π⎫ 6因为是奇函数，所以 φ＋＝k π，k ∈Z ，又因为|φ|＜，所以 φ＝－，2x －.所以 f (x )＝sin 3⎭⎝0，，所以 2x － ∈ －，，又 x ∈⎣ 2⎦ ⎣ 33 ⎦ ∴ω＝＝100π.∴I ＝10sin(100πt ＋φ)．，10 ，∵图象过点⎝300⎭∴sin( ＋φ)＝1，＋φ＝2k π＋，k ∈Z ，∴φ＝2k π＋，k ∈Z ，又∵0<φ< ，∴φ＝ .100πt ＋，∴I ＝10sin6⎭⎝所以当 x ＝0 时，f (x )取得最小值为－ 3.ω>0,0<φ< ) 的图象如右图所示，则当 t ＝秒时，电流强度是解析由图象知 A ＝10，＝－＝， ∴10sin(100π× ＋φ)＝10，当 t ＝秒时，I ＝－5 安．7．若函数 f (x )＝sin(ωx ＋φ) (ω>0 且|φ|< )在区间⎣6， 3 ⎦上是单调递减函数，且函数从 1 减小2到－1，则 f ⎝4⎭＝ .答案3π3π π2 3⎛ π⎫⎡ π⎤ π ⎡ π 2π⎤ 326. 电流强度 I ( 安 ) 随时间 t ( 秒 ) 变化的函数I ＝ A sin(ωt ＋ φ)(A >0 ，π 12 100安．答案－5T4 1 12 300 300 1002πT⎛ 1 ⎫ 1300π π π3 3 2π6π π2 6⎛ π⎫1100π ⎡π 2π⎤⎛π⎫2解析由题意可得，函数的周期为2×⎝3－6⎭＝π，⎛⎫∴f(x)＝sin⎝2x＋6⎭，∴f⎝4⎭＝sin⎝2＋6⎭＝cos＝.8．已知函数f(x)＝A sin(ωx＋φ)(A＞0，ω＞0，|φ|＜)在一个周期内的图象如图所示．若方程可得φ＝答案或π解析由图象可知y＝m和y＝f(x)图象的两个交点关于直线x＝或x＝π对称，9．(2015·天津)已知函数f(x)＝sin2x－sin2⎝x－6⎭，x∈R.(2)求f(x)在区间⎣－3，4⎦上的最大值和最小值．1－cos⎝2x－3⎭解(1)由已知，有f(x)＝－⎛sin2x－所以f(x)的最小正周期T＝＝π.⎛2ππ⎫2π即ω＝π，∴ω＝2，∴f(x)＝sin(2x＋φ)．πππ由sin⎝2×6＋φ⎭＝1，|φ|<26，⎛π⎫⎛π⎫⎛ππ⎫π362π2f(x)＝m在区间[0，π]上有两个不同的实数x1，x2，则x1＋x2的值为．π433π263π4∴x1＋x2＝3或3π.⎛π⎫(1)求f(x)的最小正周期；⎡ππ⎤⎛π⎫1－cos2x221⎛13＝2⎝2cos2x＋2⎫1sin2x⎭－2cos2x＝311π⎫44cos2x＝2sin⎝2x－6⎭.2π2⎡ππ⎤⎡ππ⎤⎛π⎫1 (2)因为f(x)在区间⎣－3，－6⎦上是减函数，在区间⎣－6，4⎦上是增函数，且f⎝－3⎭＝－4，4 所以 f (x )在区间⎣－3，4⎦上的最大值为最小值为－ .10．设函数 f (x )＝ 3－ 3sin 2ωx －sin ωx cos ωx (ω>0)，且 y ＝f (x )图象的一个对称中心到最近的对称轴的距离为 .(2)求 f (x )在区间⎣π， 2 ⎦上的最大值和最小值．解 (1)f (x )＝ 3－ 3sin 2ωx －sin ωx cos ωx＝－ 3× － sin 2ωx ＝ 3 cos 2ωx － sin 2ωx＝－sin ⎝2ωx －3⎭.依题意知＝4× ，ω>0，所以 ω＝1.(2)由(1)知 f (x )＝－sin ⎝2x －3⎭.当 π≤x ≤ 时， ≤2x － ≤ .⎛2 故 f (x )在区间⎣π， 2 ⎦上的最大值和最小值分别为，－1.11．已知函数 f (x )＝A sin(ωx ＋φ) (A >0，|φ|< ，ω>0)的图象的一部分如图所⎛ π⎫1⎛π⎫3f ⎝－6⎭＝－2，f ⎝4⎭＝，⎡ π π⎤34 ，1 22π 4(1)求 ω 的值； ⎡ 3π⎤231－cos 2ωx 1 2 2 2 12 2⎛π⎫2π π 2ω 4⎛ π⎫3π 5π π 8π 2 3 3 3 所以－ 3 π⎫2 ≤sin ⎝2x －3⎭≤1.所以－1≤f (x )≤ 3.⎡ 3π⎤3 2B 组专项能力提升(时间：20 分钟)π 2示，则该函数的解析式为．答案 f (x )＝2sin ⎝2x ＋6⎭∴1＝2sin(ω·0＋φ)，即 sin φ＝ .∵|φ|< ，∴φ＝ .又∵ π 是函数的一个零点，且是图象递增穿过 x 轴形成的零点，∴ ω＋＝2π，∴ω＝2. ∴f (x )＝2sin ⎝2x ＋6⎭. 的交点中，若相邻交点距离的最小值为，则 f (x )的最小正周期为．解析 f (x )＝ 3sin ωx ＋cos ωx ＝2sin(ωx ＋ )(ω>0)．由 2sin(ωx ＋ )＝1 得 sin(ωx ＋ )＝，∴ωx ＋＝2k π＋或 ωx ＋＝2k π＋ π(k ∈Z )．故 f (x )的最小正周期 T ＝＝π.13．已知函数 f (x )＝cos ⎝3x ＋3⎭，其中 x ∈⎣6，m ⎦，若 f (x )的值域是⎣－1，－答案 ⎣ 9 ，18⎦⎛ π⎫解析观察图象可知：A ＝2 且点(0,1)在图象上，1 π π2 2 611 11π π12 12 6⎛ π⎫12．(2014· 天津改编)已知函数 f (x )＝ 3sin ωx ＋cos ωx (ω>0)，x ∈R .在曲线 y ＝f (x )与直线 y ＝1π3答案 ππ6π π 16 6 2π π π 56 6 6 6π π π 5令 k ＝0，得 ωx 1＋6＝6，ωx 2＋6＝6π，2π∴x 1＝0，x 2＝3ω.π 2π π由|x 1－x 2|＝3，得3ω＝3，∴ω＝2.2π2值范围是．⎡2π 5π⎤解析画出函数的图象．⎛ π⎫ ⎡π ⎤ ⎡ 3⎤ 2 ⎦ ，则 m 的取由 x ∈⎣6，m ⎦，可知 ≤3x ＋ ≤3m ＋，且 f ⎝ 9 ⎭＝cos π＝－1，＝－要使 f (x )的值域是⎣－1，－2 ⎦ 所以 π≤3m ＋ ≤ π，则 ≤m ≤ ，即 m ∈⎣ 9 ，18⎦.14．已知 f (x )＝sin ⎝ωx ＋3⎭ (ω>0)，f ⎝6⎭＝f ⎝3⎭，且 f (x )在区间⎝6，3⎭上有最小值，无最大值，答案 146 3 π解析依题意，x ＝＝时，y 有最小值，∴sin ⎝4ω＋3⎭＝－1，∴ ω＋＝2k π＋ (k ∈Z )，∴ω＝8k ＋ (k ∈Z )，∵f (x )在区间⎝6，3⎭上有最小值，无最大值， 15．已知函数 f (x )＝ 3sin ωx cos ωx ＋cos 2ωx － (ω>0)，其最小正周期为 . (2)将函数 f (x )的图象向右平移个单位长度，再将图象上各点的横坐标伸长到原来的 2 倍(纵坐标不变)，得到函数 y ＝g (x )的图象，若关于 x 的方程 g (x )＋k ＝0 在区间[0， ]上有且只有一解 (1)f (x )＝ 3sin ωx cos ωx ＋cos 2ωx －⎡π ⎤ 5π π π 6 3 3⎛π⎫ 5π 3 因为 f ⎝6⎭＝cos 6 2⎛2π⎫，⎡ 3⎤ ，π 7 2π 5π3 6 9 18⎡2π 5π⎤⎛ π⎫ ⎛π⎫ ⎛π⎫ ⎛π π⎫则 ω＝.3π π ＋ 2 4⎛π π⎫π π 3π4 3 2143⎛π π⎫π π π 14 ∴3－4<ω，即 ω<12，令 k ＝0，得 ω＝ 3 .1 π2 2(1)求 f (x )的表达式；π8π2个实数解，求实数 k 的取值范围．12＝sin2ωx＋－＝sin(2ωx＋)，所以ω＝2，所以f(x)＝sin(4x＋)．(2)将f(x)的图象向右平移个单位长度后，得到y＝sin(4x－)的图象；再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到y＝sin(2x－)的图象，所以g(x)＝sin(2x－)，因为0≤x≤，所以－≤2x－≤，cos2ωx＋11所以g(x)∈[－3又g(x)＋k＝0在区间[0，]上有且只有一个实数解，即函数y＝g(x)与y＝－k在区间[0，]上≤－k<或－k＝1，解得－3<k≤或k＝－1，，]∪{－1}.3π2226π2πππ由题意知f(x)的最小正周期T＝2，T＝2ω＝ω＝2，π6ππ83ππ33πππ2π23332，1]．ππ22有且只有一个交点，由正弦函数的图象可知－32233 22所以实数k的取值范围是(－33 22。

三角函数图象及应用

函数y ＝A sin(ωx ＋φ)的图象及应用1．y ＝A sin(ωx ＋φ)的有关概念y＝A sin(ωx ＋φ)(A >0，ω>0)，x ∈[0，＋∞)振幅周期频率相位初相A T ＝2πωf ＝1T ＝ω2πωx ＋φ φ2.如下表所示.x0－φωπ2－φωπ－φω3π2－φω2π－φωωx ＋φ 0 π2π 3π2 2π y ＝A sin(ωx ＋φ)A－A3.函数【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)作函数y ＝sin(x －π6)在一个周期内的图象时，确定的五点是(0,0)，(π2，1)，(π，0)，(3π2，－1)，(2π，0)这五个点．(×)(2)将函数y ＝3sin2x 的图象左移π4个单位长度后所得图象的解析式是y ＝3sin(2x ＋π4)．(×)(3)函数y ＝sin(x －π4)的图象是由y ＝sin(x ＋π4)的图象向右移π2个单位长度得到的．(√)(4)函数y ＝sin(－2x )的递减区间是(－3π4－k π，－π4－k π)，k ∈Z .(×)(5)函数f (x )＝sin 2x 的最小正周期和最小值分别为π，0.(√)(6)函数y ＝A cos(ωx ＋φ)的最小正周期为T ，那么函数图象的两个相邻对称中心之间的距离为T2.(√)1．(2014·XX)为了得到函数y ＝sin(2x ＋1)的图象，只需把函数y ＝sin2x 的图象上所有的点() A ．向左平行移动12个单位长度B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度答案A解析y ＝sin2x 的图象向左平移12个单位长度得到函数y ＝sin2(x ＋12)的图象，即函数y ＝sin(2x＋1)的图象．2．(2013·XX)函数f (x )＝2sin(ωx ＋φ)(ω>0，－π2<φ<π2)的部分图象如图所示，则ω，φ的值分别是() A ．2，－π3B ．2，－π6C ．4，－π6D ．4，π3答案A解析∵34T ＝5π12－⎝ ⎛⎭⎪⎫－π3，∴T ＝π，∴ω＝2，∴2×5π12＋φ＝2k π＋π2，k ∈Z ，∴φ＝2k π－π3，k ∈Z ，又φ∈⎝ ⎛⎭⎪⎫－π2，π2，∴φ＝－π3，故选A. 3．设函数f (x )＝cos ωx (ω>0)，将y ＝f (x )的图象向右平移π3个单位长度后，所得的图象与原图象重合，则ω的最小值等于() A.13B ．3 C ．6D ．9 答案C解析由题意可知，nT ＝π3 (n ∈N *)，∴n ·2πω＝π3(n ∈N *)，∴ω＝6n (n ∈N *)，∴当n ＝1时，ω取得最小值6.4．设函数f (x )＝3sin(ωx ＋φ)(ω>0，－π2<φ<π2)的图象关于直线x ＝2π3对称，它的周期是π，则下列说法正确的是________．(填序号) ①f (x )的图象过点(0，32)；②f (x )在[π12，2π3]上是减函数；③f (x )的一个对称中心是(5π12，0)；④将f (x )的图象向右平移|φ|个单位长度得到函数y ＝3sin ωx 的图象．答案①③解析∵周期为π，∴2πω＝π⇒ω＝2，∴f (x )＝3sin(2x ＋φ)，f (23π)＝3sin(4π3＋φ)，则sin(4π3＋φ)＝1或－1.又φ∈(－π2，π2)，4π3＋φ∈(5π6，116π)，∴4π3＋φ＝3π2⇒φ＝π6， ∴f (x )＝3sin(2x ＋π6)．①：令x ＝0⇒f (x )＝32，正确．②：令2k π＋π2<2x ＋π6<2k π＋3π2，k ∈Z⇒k π＋π6<x <k π＋2π3，k ∈Z .令k ＝0⇒π6<x <2π3，即f (x )在(π6，23π)上单调递减，而在(π12，π6)上单调递增，错误．③：令x ＝5π12⇒f (x )＝3sinπ＝0，正确．④：应平移π12个单位长度，错误.题型一函数y ＝A sin(ωx ＋φ)的图象及变换例1设函数f (x )＝sin ωx ＋3cos ωx (ω>0)的周期为π. (1)求它的振幅、初相；(2)用五点法作出它在长度为一个周期的闭区间上的图象；(3)说明函数f (x )的图象可由y ＝sin x 的图象经过怎样的变换而得到的．解(1)f (x )＝sin ωx ＋3cos ωx＝2(12sin ωx ＋32cos ωx )＝2sin(ωx ＋π3)，又∵T ＝π，∴2πω＝π，即ω＝2.∴f (x )＝2sin(2x ＋π3)．∴函数f (x )＝sin ωx ＋3cos ωx 的振幅为2，初相为π3.(2)令X ＝2x ＋π3，则y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3＝2sin X . 列表，并描点画出图象：x－π6 π12 π3 7π12 5π6X 0 π2 π 3π2 2π y ＝sin X 01 0 －1 0 y ＝2sin ⎝⎛⎭⎪⎫2x ＋π32－2(3)方法一把y ＝sin x 的图象上所有的点向左平移π3个单位长度，得到y ＝sin ⎝ ⎛⎭⎪⎫x ＋π3的图象，再把y ＝sin ⎝ ⎛⎭⎪⎫x ＋π3的图象上的点的横坐标缩短到原来的12倍(纵坐标不变)，得到y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象，最后把y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3上所有点的纵坐标伸长到原来的2倍(横坐标不变)，即可得到y＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象．方法二将y ＝sin x 的图象上每一点的横坐标x 缩短为原来的12倍，纵坐标不变，得到y ＝sin2x的图象；再将y ＝sin2x 的图象向左平移π6个单位长度，得到y ＝sin2⎝ ⎛⎭⎪⎫x ＋π6＝sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象；再将y ＝sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象上每一点的横坐标保持不变，纵坐标伸长为原来的2倍，得到y ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π3的图象．思维升华(1)五点法作简图：用“五点法”作y ＝A sin(ωx ＋φ)的简图，主要是通过变量代换，设z ＝ωx ＋φ，由z 取0，π2，π，32π，2π来求出相应的x ，通过列表，计算得出五点坐标，描点后得出图象．(2)图象变换：由函数y ＝sin x 的图象通过变换得到y ＝A sin(ωx ＋φ)的图象，有两种主要途径：“先平移后伸缩”与“先伸缩后平移”．(1)把函数y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)，再将图象向右平移π3个单位长度，那么所得图象的一条对称轴方程为()A ．x ＝－π2B ．x ＝－π4C ．x ＝π8D ．x ＝π4(2)(2014·XX)将函数y ＝3sin(2x ＋π3)的图象向右平移π2个单位长度，所得图象对应的函数()A ．在区间[π12，7π12]上单调递减B ．在区间[π12，7π12]上单调递增C ．在区间[－π6，π3]上单调递减D ．在区间[－π6，π3]上单调递增答案(1)A(2)B解析(1)将y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)，得到函数y ＝sin(2x＋π6)；再将图象向右平移π3个单位长度，得到函数y ＝sin[2(x －π3)＋π6]＝sin(2x －π2)，故x ＝－π2是其图象的一条对称轴方程．(2)y ＝3sin(2x ＋π3)的图象向右平移π2个单位长度得到y ＝3sin[2(x －π2)＋π3]＝3sin(2x －23π)．令2k π－π2≤2x －23π≤2k π＋π2得k π＋π12≤x ≤k π＋712π，k ∈Z ，则y ＝3sin(2x －23π)的增区间为[k π＋π12，k π＋712π]，k ∈Z . 令k ＝0得其中一个增区间为[π12，712π]，故B 正确．画出y ＝3sin(2x －23π)在[－π6，π3]上的简图，如图，可知y ＝3sin(2x－23π)在[－π6，π3]上不具有单调性，故C ，D 错误．题型二由图象求函数y ＝A sin(ωx ＋φ)的解析式例2(1)已知函数f (x )＝2sin(ωx ＋φ)(其中ω>0，|φ|<π2)的最小正周期是π，且f (0)＝3，则()A ．ω＝12，φ＝π6B ．ω＝12，φ＝π3C ．ω＝2，φ＝π6D ．ω＝2，φ＝π3(2)已知函数f (x )＝A sin(ωx ＋φ) (A >0，|φ|<π2，ω>0)的图象的一部分如图所示，则该函数的解析式为____________．答案(1)D(2)f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π6解析(1)∵f (x )(ω>0，|φ|<π2)的最小正周期为π，∴T ＝2πω＝π，ω＝2.∵f (0)＝2sin φ＝3，即sin φ＝32(|φ|<π2)，∴φ＝π3. (2)观察图象可知：A ＝2且点(0,1)在图象上， ∴1＝2sin(ω·0＋φ)，即sin φ＝12.∵|φ|<π2，∴φ＝π6.又∵1112π是函数的一个零点，且是图象递增穿过x 轴形成的零点，∴11π12ω＋π6＝2π，∴ω＝2.∴f (x )＝2sin ⎝⎛⎭⎪⎫2x ＋π6.思维升华根据y ＝A sin(ωx ＋φ)＋k 的图象求其解析式的问题，主要从以下四个方面来考虑： ①A 的确定：根据图象的最高点和最低点，即A ＝最大值－最小值2；②k 的确定：根据图象的最高点和最低点，即k ＝最大值＋最小值2；③ω的确定：结合图象，先求出周期T ，然后由T ＝2πω(ω>0)来确定ω；④φ的确定：由函数y ＝A sin(ωx ＋φ)＋k 最开始与x 轴的交点(最靠近原点)的横坐标为－φω(即令ωx ＋φ＝0，x ＝－φω)确定φ.如图为y ＝A sin(ωx ＋φ)的图象的一段．(1)求其解析式；(2)若将y ＝A sin(ωx ＋φ)的图象向左平移π6个单位长度后得y ＝f (x )，求f (x )的对称轴方程．解(1)由图象知A ＝3，以M ⎝ ⎛⎭⎪⎫π3，0为第一个零点，N ⎝ ⎛⎭⎪⎫5π6，0为第二个零点．列方程组⎩⎪⎨⎪⎧ω·π3＋φ＝0，ω·5π6＋φ＝π，解得⎩⎪⎨⎪⎧ω＝2，φ＝－2π3.∴所求解析式为y ＝3sin ⎝ ⎛⎭⎪⎫2x －2π3.(2)f (x )＝3sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x ＋π6－2π3＝3sin ⎝⎛⎭⎪⎫2x －π3，令2x －π3＝π2＋k π(k ∈Z )，则x ＝512π＋k π2 (k ∈Z )，∴f (x )的对称轴方程为x ＝512π＋k π2 (k ∈Z )．题型三函数y ＝A sin(ωx ＋φ)的性质例3(2014·XX 改编)已知函数f (x )＝3sin(ωx ＋φ)(ω>0，－π2≤φ<π2)的图象关于直线x ＝π3对称，且图象上相邻两个最高点的距离为π. (1)求ω和φ的值；(2)当x ∈[0，π2]时，求函数y ＝f (x )的最大值和最小值．解(1)因为f (x )的图象上相邻两个最高点的距离为π，所以f (x )的最小正周期T ＝π，从而ω＝2πT＝2.又因f (x )的图象关于直线x ＝π3对称，所以2·π3＋φ＝k π＋π2，k ∈Z ，由－π2≤φ<π2得k ＝0所以φ＝π2－2π3＝－π6.综上，ω＝2，φ＝－π6.(2)由(1)知f (x )＝3sin(2x －π6)，当x ∈[0，π2]时，－π6≤2x －π6≤56π，∴当2x －π6＝π2，即x ＝π3时，f (x )最大＝3；当2x －π6＝－π6，即x ＝0时，f (x )最小＝－32.思维升华函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的性质(1)奇偶性：φ＝k π(k ∈Z )时，函数y ＝A sin(ωx ＋φ)为奇函数；φ＝k π＋π2(k ∈Z )时，函数y ＝A sin(ωx ＋φ)为偶函数．(2)周期性：y ＝A sin(ωx ＋φ)存在周期性，其最小正周期为T ＝2πω.(3)单调性：根据y ＝sin t 和t ＝ωx ＋φ(ω>0)的单调性来研究，由－π2＋2k π≤ωx ＋φ≤π2＋2k π(k∈Z )得单调增区间；由π2＋2k π≤ωx ＋φ≤3π2＋2k π(k ∈Z )得单调减区间．(4)对称性：利用y ＝sin x 的对称中心为(k π，0)(k ∈Z )来解，令ωx ＋φ＝k π(k ∈Z )，求得其对称中心．利用y ＝sin x 的对称轴为x ＝k π＋π2(k ∈Z )来解，令ωx ＋φ＝k π＋π2(k ∈Z )得其对称轴．已知函数f (x )＝A sin(ωx ＋φ)(x ∈R ，ω，A >0,0<φ<π2)的最大值为2，最小正周期为π，直线x ＝π6是其图象的一条对称轴．(1)求函数f (x )的解析式；(2)求函数g (x )＝f (x －π12)－f (x ＋π12)的单调递增区间．解(1)∵最小正周期为π. ∴2πω＝π.即ω＝2.又∵直线x ＝π6是函数图象的一条对称轴，∴2×π6＋φ＝k π＋π2，k ∈Z ，即φ＝k π＋π6，k ∈Z .又∵φ∈(0，π2)，∴φ＝π6.又∵A ＝2，∴函数f (x )的解析式为f (x )＝2sin(2x ＋π6)．(2)g (x )＝f (x －π12)－f (x ＋π12)＝2sin[2(x －π12)＋π6]－2sin[2(x ＋π12)＋π6]＝2sin2x －2sin(2x ＋π3)＝2sin(2x －π3)．由2k π－π2≤2x －π3≤2k π＋π2，k ∈Z 可得k π－π12≤x ≤k π＋512π，k ∈Z .即函数g (x )的单调递增区间是 [k π－π12，k π＋512π]，k ∈Z .三角函数图象与性质的综合问题典例：(12分)已知函数f (x )＝23sin(x 2＋π4)·cos(x 2＋π4)－sin(x ＋π)．(1)求f (x )的最小正周期．(2)若将f (x )的图象向右平移π6个单位长度，得到函数g (x )的图象，求函数g (x )在区间[0，π]上的最大值和最小值．思维点拨(1)先将f (x )化成y ＝A sin(ωx ＋φ)的形式再求周期；(2)将f (x )解析式中的x 换成x －π6，得g (x )，然后利用整体思想求最值．规X 解答解(1)f (x )＝23sin(x 2＋π4)·cos(x 2＋π4)－sin(x ＋π)＝3cos x ＋sin x [3分]＝2sin(x ＋π3)，[5分]于是T ＝2π1＝2π.[6分](2)由已知得g (x )＝f (x －π6)＝2sin(x ＋π6)，[8分]∵x ∈[0，π]，∴x ＋π6∈[π6，7π6]，∴sin(x ＋π6)∈[－12，1]，[10分]∴g (x )＝2sin(x ＋π6)∈[－1,2][11分]故函数g (x )在区间[0，π]上的最大值为2，最小值为－1.[12分] 答题模板解决三角函数图象与性质的综合问题的一般步骤第一步：(化简)将f (x )化为a sin x ＋b cos x 的形式．第二步：(用辅助角公式)构造f (x )＝a 2＋b 2·(sin x ·aa 2＋b2＋cos x ·ba 2＋b 2)．第三步：(求性质)利用f (x )＝a 2＋b 2sin(x ＋φ)研究三角函数的性质．第四步：(反思)反思回顾，查看关键点、易错点和答题规X ．温馨提醒(1)在第(1)问的解法中，使用辅助角公式a sin α＋b cos α＝a 2＋b 2sin(α＋φ)(其中tan φ＝ba)，或a sin α＋b cos α＝a 2＋b 2cos(α－φ)(其中tan φ＝ab)，在历年高考中使用频率是相当高的，几乎年年使用到、考查到，应特别加以关注． (2)求g (x )的最值一定要重视定义域，可以结合三角函数图象进行求解.方法与技巧1．五点法作图及图象变换问题(1)五点法作简图要取好五个关键点，注意曲线凸凹方向；(2)图象变换时的伸缩、平移总是针对自变量x 而言，而不是看角ωx ＋φ的变化．2．由图象确定函数解析式由函数y ＝A sin(ωx ＋φ)的图象确定A 、ω、φ的题型，常常以“五点法”中的第一个零点⎝ ⎛⎭⎪⎫－φω，0作为突破口，要从图象的升降情况找准第一个零点的位置．要善于抓住特殊量和特殊点． 3．对称问题函数y ＝A sin(ωx ＋φ)的图象与x 轴的每一个交点均为其对称中心，经过该图象上坐标为(x ，±A )的点与x 轴垂直的每一条直线均为其图象的对称轴，这样的最近两点间横坐标的差的绝对值是半个周期(或两个相邻对称中心的距离)．失误与防X1．由函数y ＝sin x 的图象经过变换得到y ＝A sin(ωx ＋φ)的图象，如：先伸缩，再平移时，要把x 前面的系数提取出来．2．复合形式的三角函数的单调区间的求法．函数y ＝A sin(ωx ＋φ)(A >0，ω>0)的单调区间的确定，基本思想是把ωx ＋φ看做一个整体．若ω<0，要先根据诱导公式进行转化． 3．函数y ＝A sin(ωx ＋φ)在x ∈[m ，n ]上的最值可先求t ＝ωx ＋φ的X 围，再结合图象得出y ＝A sin t 的值域.A 组专项基础训练 (时间：45分钟)1．(2013·XX)将函数y ＝sin(2x ＋φ)的图象沿x 轴向左平移π8个单位后，得到一个偶函数的图象，则φ的一个可能取值为() A.3π4B.π4C ．0D ．－π4 答案B解析把函数y ＝sin(2x ＋φ)沿x 轴向左平移π8个单位后得到函数y ＝sin2⎝ ⎛⎭⎪⎫x ＋φ2＋π8＝sin ⎝ ⎛⎭⎪⎫2x ＋φ＋π4为偶函数，则φ的一个可能取值是π4.2．(2013·XX)函数f (x )＝sin x cos x ＋32cos2x 的最小正周期和振幅分别是() A ．π，1B ．π，2C ．2π，1D ．2π，2 答案A解析f (x )＝sin x cos x ＋32cos2x ＝12sin2x ＋32cos2x ＝sin ⎝⎛⎭⎪⎫2x ＋π3.所以最小正周期为π，振幅为1. 故选A.3.已知函数f (x )＝2sin(ωx ＋φ)(ω>0，且|φ|<π2)的部分图象如图所示，则函数f (x )的一个单调递增区间是() A ．[－7π12，5π12]B ．[－7π12，－π12]C ．[－π12，7π12]D ．[－π12，5π12]答案D解析由函数的图象可得14T ＝23π－512π，∴T ＝π，则ω＝2.又图象过点(512π，2)，∴2sin(2×512π＋φ)＝2，∴φ＝－π3＋2k π，k ∈Z ，∵|φ|<π2.∴取k ＝0，即得f (x )＝2sin(2x －π3)，其单调递增区间为[k π－π12，k π＋5π12]，k ∈Z ，取k ＝0，即得选项D.4.电流强度I (安)随时间t (秒)变化的函数I ＝A sin(ωt ＋φ)(A >0，ω>0,0<φ<π2)的图象如右图所示，则当t ＝1100秒时，电流强度是()A ．－5安B ．5安C ．53安D ．10安答案A解析由图象知A ＝10，T 2＝4300－1300＝1100，∴ω＝2πT＝100π.∴I ＝10sin(100πt ＋φ)．⎝ ⎛⎭⎪⎫1300，10为五点中的第二个点， ∴100π×1300＋φ＝π2.∴φ＝π6.∴I ＝10sin ⎝ ⎛⎭⎪⎫100πt ＋π6，当t ＝1100秒时，I ＝－5安．5．已知函数f (x )＝2sin ωx 在区间[－π3，π4]上的最小值为－2，则ω的取值X 围是()A ．(－∞，－92]∪[6，＋∞)B ．(－∞，－92]∪[32，＋∞)C ．(－∞，－2]∪[6，＋∞)D ．(－∞，－2]∪[32，＋∞)答案D解析当ω>0时，－π3ω≤ωx ≤π4ω，由题意知－π3ω≤－π2，即ω≥32；当ω<0时，π4ω≤ωx ≤－π3ω，由题意知π4ω≤－π2，∴ω≤－2.综上可知，ω的取值X 围是(－∞，－2]∪[32，＋∞)．6.设偶函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0,0<φ<π)的部分图象如图所示，△KLM 为等腰直角三角形，∠KML ＝90°，KL ＝1，则f (16)的值为________．答案34解析取K ，L 中点N ，则MN ＝12，因此A ＝12.由T ＝2得ω＝π.∵函数为偶函数，0<φ<π，∴φ＝π2，∴f (x )＝12cosπx ，∴f (16)＝12cos π6＝34.7．某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y ＝a ＋A cos ⎣⎢⎡⎦⎥⎤π6(x －6)(x ＝1,2,3，…，12，A >0)来表示，已知6月份的月平均气温最高，为28℃，12月份的月平均气温最低，为18℃，则10月份的平均气温值为________℃. 答案20.5 解析由题意得⎩⎨⎧ a ＋A ＝28，a －A ＝18，∴⎩⎨⎧a ＝23，A ＝5，∴y ＝23＋5cos ⎣⎢⎡⎦⎥⎤π6(x －6)，当x ＝10时，y ＝23＋5×⎝ ⎛⎭⎪⎫－12＝20.5.8．已知函数f (x )＝cos x sin x (x ∈R )，给出下列四个命题： ①若f (x 1)＝－f (x 2)，则x 1＝－x 2； ②f (x )的最小正周期是2π； ③f (x )在区间[－π4，π4]上是增函数；④f (x )的图象关于直线x ＝3π4对称．其中真命题是________．答案③④解析f (x )＝12sin2x ，当x 1＝0，x 2＝π2时，f (x 1)＝－f (x 2)，但x 1≠－x 2，故①是假命题； f (x )的最小正周期为π，故②是假命题；当x ∈[－π4，π4]时，2x ∈[－π2，π2]，故③是真命题；因为f (3π4)＝12sin 32π＝－12，故f (x )的图象关于直线x ＝34π对称，故④是真命题．9．已知函数f (x )＝cos x ·cos(x －π3)．(1)求f (2π3)的值；(2)求使f (x )<14成立的x 的取值集合．解(1)f (2π3)＝cos 2π3·cos π3＝－cos π3·cos π3＝－(12)2＝－14.(2)f (x )＝cos x cos(x －π3)＝cos x ·(12cos x ＋32sin x )＝12cos 2x ＋32sin x cos x ＝14(1＋cos2x )＋34sin2x ＝12cos(2x －π3)＋14. f (x )<14等价于12cos(2x －π3)＋14<14，即cos(2x －π3)<0，于是2k π＋π2<2x －π3<2k π＋3π2，k ∈Z .解得k π＋5π12<x <k π＋11π12，k ∈Z .故使f (x )<14成立的x 的取值集合为{x |k π＋5π12<x <k π＋11π12，k ∈Z }．10．(2014·XX)已知函数f (x )＝cos x (sin x ＋cos x )－12.(1)若0<α<π2，且sin α＝22，求f (α)的值；(2)求函数f (x )的最小正周期及单调递增区间．解方法一(1)因为0<α<π2，sin α＝22，所以cos α＝22. 所以f (α)＝22×(22＋22)－12＝12. (2)因为f (x )＝sin x cos x ＋cos 2x －12＝12sin2x ＋1＋cos2x 2－12 ＝12sin2x ＋12cos2x ＝22sin(2x ＋π4)，所以T ＝2π2＝π.由2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，得k π－3π8≤x ≤k π＋π8，k ∈Z . 所以f (x )的单调递增区间为[k π－3π8，k π＋π8]，k ∈Z .方法二f (x )＝sin x cos x ＋cos 2x －12＝12sin2x ＋1＋cos2x 2－12 ＝12sin2x ＋12cos2x ＝22sin(2x ＋π4)． (1)因为0<α<π2，sin α＝22，所以α＝π4，从而f (α)＝22sin(2α＋π4)＝22sin 3π4＝12.(2)T ＝2π2＝π.由2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ，得k π－3π8≤x ≤k π＋π8，k ∈Z . 所以f (x )的单调递增区间为[k π－3π8，k π＋π8]，k ∈Z .B 组专项能力提升 (时间：20分钟)11．将函数y ＝sin(x ＋φ)的图象F 向左平移π6个单位长度后得到图象F ′，若F ′的一个对称中心为⎝ ⎛⎭⎪⎫π4，0，则φ的一个可能取值是() A.π12B.π6C.5π6D.7π12 答案D解析图像F ′对应的函数y ＝sin ⎝ ⎛⎭⎪⎫x ＋π6＋φ，则π4＋π6＋φ＝k π，k ∈Z ，即φ＝k π－5π12，k ∈Z ，当k ＝1时，φ＝7π12，故选D.12．已知A ，B ，C ，D 是函数y ＝sin(ωx ＋φ)(ω>0,0<φ<π2)一个周期内的图象上的四个点，如图所示，A (－π6，0)，B 为y 轴上的点，C 为图象上的最低点，E 为该函数图象的一个对称中心，B 与D 关于点E 对称，CD →在x 轴上的投影为π12，则ω，φ的值为()A ．ω＝2，φ＝π3B ．ω＝2，φ＝π6C ．ω＝12，φ＝π3D ．ω＝12，φ＝π6答案A解析因为CD →在x 轴上的投影为π12，又点A (－π6，0)，所以函数的四分之一个最小正周期为π6＋π12＝π4.即函数的最小正周期为π，故ω＝2ππ＝2. 又点A (－π6，0)是处于递增区间上的零点，所以2×(－π6)＋φ＝2k π(k ∈Z )，则φ＝2k π＋π3(k ∈Z )．又因为0<φ<π2，所以φ＝π3.故选A.13．(2014·XX)已知函数f (x )＝sin(ωx ＋φ) (ω>0，－π2≤φ≤π2)的图象上的两个相邻的最高点和最低点的距离为22，且过点⎝ ⎛⎭⎪⎫2，－12，则函数的解析式为_________________________．答案f (x )＝sin ⎝⎛⎭⎪⎫πx 2＋π6解析据已知两个相邻最高点和最低点距离为22，可得⎝ ⎛⎭⎪⎫T 22＋(1＋1)2＝22，解得T ＝4，故ω＝2πT ＝π2，即f (x )＝sin ⎝ ⎛⎭⎪⎫πx 2＋φ，又函数图象过点⎝ ⎛⎭⎪⎫2，－12，故f (2)＝sin(π＋φ)＝－sin φ＝－12，又－π2≤φ≤π2，解得φ＝π6，故f (x )＝sin ⎝ ⎛⎭⎪⎫πx 2＋π6.14．(2014·XX)某实验室一天的温度(单位：℃)随时间t (单位：h)的变化近似满足函数关系：f (t )＝10－3cos π12t －sin π12t ，t ∈[0,24)．(1)XX 验室这一天的最大温差；(2)若要XX 验室温度不高于11℃，则在哪段时间实验室需要降温？解(1)因为f (t )＝10－2(32cos π12t ＋12sin π12t ) ＝10－2sin(π12t ＋π3)，又0≤t <24，所以π3≤π12t ＋π3<7π3，－1≤sin(π12t ＋π3)≤1.当t ＝2时，sin(π12t ＋π3)＝1；当t ＝14时，sin(π12t ＋π3)＝－1.于是f (t )在[0,24)上的最大值为12，最小值为8.故实验室这一天最高温度为12℃，最低温度为8℃，最大温差为4℃.(2)依题意，当f (t )>11时实验室需要降温．由(1)得f (t )＝10－2sin(π12t ＋π3)，故有10－2sin(π12t ＋π3)>11，即sin(π12t ＋π3)<－12.又0≤t <24，因此7π6<π12t ＋π3<11π6，即10<t <18.故在10时至18时实验室需要降温．15．已知函数f (x )＝3sin ωx ·cos ωx ＋cos 2ωx －12(ω>0)，其最小正周期为π2.(1)求f (x )的表达式；(2)将函数f (x )的图象向右平移π8个单位长度，再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y ＝g (x )的图象，若关于x 的方程g (x )＋k ＝0在区间[0，π2]上有且只有一个实数解，XX 数k 的取值X 围．解(1)f (x )＝3sin ωx ·cos ωx ＋cos 2ωx －12＝32sin2ωx ＋cos2ωx ＋12－12＝sin(2ωx ＋π6)，由题意知f (x )的最小正周期T ＝π2，T ＝2π2ω＝πω＝π2，所以ω＝2，所以f (x )＝sin(4x ＋π6)．(2)将f (x )的图象向右平移π8个单位长度后，得到y ＝sin(4x －π3)的图象；再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到y ＝sin(2x －π3)的图象，所以g (x )＝sin(2x －π3)，因为0≤x ≤π2，所以－π3≤2x －π3≤2π3，所以g (x )∈[－32，1] 又g (x )＋k ＝0在区间[0，π2]上有且只有一个实数解，即函数y ＝g (x )与y ＝－k 在区间[0，π2]上有且只有一个交点，由正弦函数的图象可知－32≤－k<32或－k＝1，解得－32<k≤32或k＝－1，所以实数k的取值X围是(－32，32]∪{－1}．。

三角函数的图象、性质及应用(高中数学知识点讲解)

(5)不能认为y=tan
x在定义域上为增函数,应在区间
kπ-
π 2
,kπ
+
π 2
(k∈Z)内
为增函数.
知能拓展
考法一关于三角函数图象的问题
例1 (1)(2018广东茂名化州二模,9)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<
φ<π)的部分图象如图所示,且f(α)=1,α∈
求φ及ω,从而
得到f(x)的解析式,由f(α)=1求α,进而得cos
2α
+
5π 6
.
A = 5,
(2)①根据已知表格中的数据可得方程组
π 3
ω
+
φ
=
π 2
,
解之可得函数f(x)的
5π 6
ω
+
φ
=
3π 2
,
解析式,进而可补全表格.
②由①并结合函数图象平移可得,g(x)=5sin
2
x
+
2θ -
π 3
-2x
实质上是y=tan
x与y=
π 3
-2x的复合,应
按复合函数单调性求解.
方法总结三角函数的单调性问题的常见类型及解题策略
1.已知三角函数解析式求单调区间
(1)求函数的单调区间应遵循简单化原则,将解析式进行化简,并注意复合
函数单调性规律“同增异减”.
(2)求形如y=Asin(ωx+φ)或y=Acos(ωx+φ)(其中ω>0)的单调区间时,要视“ωx
2π ω
=4×
7π 12
-
π 3
=π,得ω=2,故f(x)=3sin(2x+φ),将

高考数学一轮复习讲义第33课时三角函数的图像理

229课题：三角函数的图象考纲要求：1.掌握正弦、余弦、正切、余切函数的图象2.会用“五点法”画正弦、余弦函数和函数sin()y A x ωϕ=+的简图.3.了解sin()y A x ωϕ=+的物理意义，了解参数,,A ωϕ对函数变化的影响.自主学习1.用五点法画y即五点的横坐标总由ϕω+x ＝ππ2220、、、、来确定. 2.函数sin y x =的图象变换得到sin()y A x ωϕ=+的图象的步骤：由于x y sin =的图象得到)sin(ϕω+=x A y 的图象主要有下列两种方法:①x y sin =（相位变换）→ (周期变换) → (振幅变换)→ ； ②x y sin =(周期变换)→ （相位变换）→ (振幅变换)→ .3.当函数sin()y A x ωϕ=+(0,0A ω>>，x ∈[)0,+∞表示一个振动时，A 叫做振幅，2T πω=叫做周期，1f T=叫做频率，x ωϕ+叫做相位，ϕ叫做初相．基本知识方法1.“五点法”画正弦、余弦函数和函数sin()y A x ωϕ=+的简图，五个特殊点通常都是取三个平衡点，一个最高、一个最低点；2.给出图象求sin()y A x B ωϕ=++的解析式的难点在于,ωϕ的确定，本质为待定系数230法，基本方法是：①寻找特殊点（平衡点、最值点）代入解析式；②图象变换法，即考察已知图象可由哪个函数的图象经过变换得到的，通常可由平衡点或最值点确定周期T ，进而确定ω；③“对应点法”．3.对称性:()1函数sin()y A x ωϕ=+对称轴可由2x k πωϕπ+=+()k Z ∈解出；对称中心的横坐标是方程x k ωϕπ+=()k Z ∈的解，对称中心的纵坐标为0.( 即整体代换法)()2函数()cos y A x ωϕ=+对称轴可由x k ωϕπ+=()k Z ∈解出；对称中心的纵坐标是方程2x k πωϕπ+=+()k Z ∈的解，对称中心的横坐标为0.( 即整体代换法)正、余弦函数在对称轴处（最值处）的导数值为零.()3函数()tan y A x ωϕ=+对称中心的横坐标可由2k x ωϕπ+=()k Z ∈解出，对称中心的纵坐标为0，函数()tan y x ωϕ=+不具有轴对称性.4.0A >时，()sin y A x ωϕ=+，当22x k πωϕπ+=+()k Z ∈时，有最大值A ，当22x k πωϕπ+=-()k Z ∈时,有最小值A -；0A >时，与上述情况相反.典例分析：考点一：利用“五点法”作图问题1．已知函数cos 22x xy =+()x R ∈. ()1用“五点法”画出它的图象；()2求它的振幅、周期和初相；()3说明该函数的图象可由sin y x =的图象经过怎样的变换而得到.考点二：利用图像求三角函数解析式问题2．()1（2013四川）函数()2sin()f x x ωϕ=+231(0,)22ππωϕ>-<<的部分图象如图所示，则,ωϕ的值分别是 .A 2,3π- .B 2,6π-.C 4,6π-.D 4,3π()2(05天津文)函数sin()y A x ωϕ=+(20,,x πωϕ><的部分图象如图所示，则函数表达式为 .A )48sin(4ππ+-=x y .B )48sin(4ππ-=x y .C )48sin(4ππ--=x y .D )48sin(4ππ+=x y考点三：三角函数的图像变换问题3．()1将函数5sin(3)y x =-的周期扩大到原来的2倍，再将函数图象左移3π，得到图象对应解析式是 .A 335sin()22x y π=- .B 735sin()102x y π=- .C 5sin(6)6y x π=- .D 35cos 2xy =()2（07山东文）要得到函数sin y x =的图象，只需将函数cos y x π⎛⎫=-⎪3⎝⎭的图象 .A 向右平移π6个单位；.B 向右平移π3个单位；232.C 向左平移π3个单位；.D 向左平移π6个单位 ()3（04山东）为了得到函数6sin(2)y x π=-的图象，可以将函数x y 2cos =的图象.A 向右平移6π个单位长度 .B 向右平移3π个单位长度 .C 向左平移6π个单位长度 .D 向左平移3π个单位长度考点三：三角函数的图像对称性的考查问题4．()1(07福建)已知函数()sin (0)f x x ωωπ⎛⎫=+> ⎪3⎝⎭的最小正周期为π，则该函数的图象 .A 关于点0π⎛⎫ ⎪3⎝⎭，对称 .B 关于直线x π=4对称 .C 关于点0π⎛⎫⎪4⎝⎭，对称 .D .关于直线x π=3对称()2（05山东）已知函数)12cos()12sin(π-π-=x x y ，则下列判断正确的是 .A 此函数的最小正周期为π2，其图象的一个对称中心是,012π⎛⎫⎪⎝⎭.B 此函数的最小正周期为π，其图象的一个对称中心是,012π⎛⎫⎪⎝⎭ .C 此函数的最小正周期为π2，其图象的一个对称中心是,06π⎛⎫⎪⎝⎭.D 此函数的最小正周期为π，其图象的一个对称中心是,06π⎛⎫⎪⎝⎭考点四：三角函数的图像的综合应用问题5．（07陕西）设函数()f x a b =⋅，其中向量(cos2)a m x =，，(1sin21)b x =+，，x R ∈，且()y f x =的图象经过点π24⎛⎫ ⎪⎝⎭，．（Ⅰ）求实数m 的值；（Ⅱ）求函数()f x 的最小值及此233时x 值的集合．课外作业：1.要得到x x y 2cos 2sin +=的图象，只需将x x y 2cos 2sin -=的图象.A 向左平移8π .B 向右平移8π .C 向左平移4π .D 向右平移4π2.如果函数sin 2cos 2y x a x =+的图象关于直线8x π=-对称，则a =3.函数tan cos y x x = 的部分图象是4.（2013昆明调研）已知a R ∈，则函数()cos f x a ax =的图象可能是.A .B .C .D.A .B .C.D2345.（2013浙江六校联考）函数()()sin 04f x x πωω⎛⎫=+> ⎪⎝⎭与函数()()cos 2g x x ϕ=+，（ϕ≤2π的对称轴完全相同，则ϕ的值为.A 4π .B 4π- .C 2π .D 2π-走向高考：6.（05天津）要得到函数x y cos 2=的图象，只需将函数)42sin(2π+=x y 的图象上所有的点的.A 横坐标缩短到原来的21倍（纵坐标不变）,再向左平行移动8π个单位长度 .B 横坐标缩短到原来的21倍（纵坐标不变），再向右平行移动4π个单位长度.C 横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动4π个单位长度 .D 横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动8π个单位长度7.（06江苏）为了得到函数R x x y ∈+=),63sin(2π的图像，只需把函数R x x y ∈=,sin 2的图像上所有的点.A 向左平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变） .B 向右平移6π个单位长度，再把所得各点的横坐标缩短到原来的31倍（纵坐标不变） .C 向左平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） .D 向右平移6π个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）8. (07安徽)函数()3sin 2f x x π⎛⎫=- ⎪3⎝⎭的图象为C ，①图象C 关于直线1112x =π对称；②函数()f x 在区间5ππ⎛⎫- ⎪1212⎝⎭，内是增函数；235③由3sin 2y x =的图象向右平移π3个单位长度可以得到图象C ．以上三个论断中，正确论断的个数是 .A 0 .B 1 .C 2 .D 39.（06安徽）将函数sin (0)y x ωω=>,06a π⎛⎫=- ⎪⎝⎭平移，平移后的图象如图所示，则平移后的图象所对应函数的解析式是.A sin()6y x π=+.B sin()6y x π=- .C sin(2)3y x π=+.D sin(2)3y x π=-10.（05福建）函数sin()y x ωϕ=+(,x R ∈02ϕπ≤<)的部分图象如图，则.A 4,2πϕπω==.B 6,3πϕπω==.C 4,4πϕπω== .D 45,4πϕπω==11.（07广东文）已知简谐运动ππ()2sin 32f x x ϕϕ⎛⎫⎛⎫=+< ⎪⎪⎝⎭⎝⎭的图象经过点(01)，，则该简谐运动的最小正周期T 和初相ϕ分别为.A 6T =，π6ϕ=；.B 6T =，π3ϕ=；.C 6πT =，π6ϕ=；.D 6πT =，π3ϕ= 12.（2011辽宁）已知函数()()tan f x A x ωϕ=+0,2πωϕ⎛⎫>< ⎪⎝⎭，()y f x =的部分图像如下图，236则24f π⎛⎫=⎪⎝⎭________. 13.(07海南)函数πsin 23y x ⎛⎫=- ⎪⎝⎭在区ππ2⎡⎤-⎢⎥⎣，的简图是13.（2013湖北）将函数()sin y x x x R =+∈的图像向左平移()0m m >个长度单位后，所得到的图像关于y 轴对称，则m 的最小值是 .A 12π.B 6π.C 3π.D 56πx-.B .C.D。

5点法画三角函数

5点法画三角函数 “5点法画三角函数”是一种用于绘制正弦函数、余弦函数和正切函数图像的简单方法。这个方法的核心是通过选择合适的函数值来确定函数图像的特征点，进而连线得到函数图像。下面我们就来详细地介绍一下“5点法画三角函数”的实现步骤。第一步：确定函数定义域在绘制三角函数图像之前，我们需要确定三角函数的定义域和值域。对于正弦函数和余弦函数来说，它们的定义域是实数集R，值域是[-1,1]。而正切函数的定义域是实数集R-{(2n+1)*Pi/2 | n属于整数}，值域是全体实数R。第二步：选择特征点在“5点法画三角函数”中，我们选择5个特征点来确定函数图像的形状。对于正弦函数和余弦函数来说，我们选择0度、30度、45度、60度和90度这五个特征点。对于正切函数来说，我们选择-45度、-30度、0度、30度和45度这五个特征点。第三步：确定特征点的函数值根据三角函数在特定角度上的函数值，我们可以得到上一步中选择的五个特征点的函数值。对于正弦函数和余弦函数来说，我们可以使用科学计算器来计算特征点的函数值。对于正切函数来说，我们需要使用tan函数计算特征点的函数值。第四步：连线得到函数图像有了五个特征点的函数值之后，我们就可以通过连线来得到函数图像。对于正弦函数和余弦函数来说，我们用曲线来连接这五个点，得到一个波浪形的图像。对于正切函数来说，我们在特征点之间画直线，得到一条波动的直线。第五步：根据周期性复制图像我们知道，三角函数图像具有周期性。因此，我们可以通过复制图像来得到整个函数的图像。对于正弦函数和余弦函数来说，它们的周期是360度（也就是2Pi弧度）。因此，我们可以将图像复制4次，即在[0,360]、[360,720]、[720,1080]和[1080,1440]上绘制波浪形的图像。对于正切函数来说，它的周期是180度（也就是Pi弧度）。因此，我们可以将图像复制2次，即在[-90,90]和[90,270]上绘制波动的直线。总结起来，“5点法画三角函数”的步骤如下： 1. 确定函数定义域和值域； 2. 选择特征点； 3. 确定特征点的函数值； 4. 根据特征点连线得到函数图像； 5. 根据周期性复制图像。这个方法简单易懂，适用于初学者学习三角函数。需要注意的是，为了绘制出更加精确的图像，我们可以增加特征点的数量，使得连线更加平滑。不过，这也会增加计算和绘图的时间和难度。

三角函数图象的变换

4．4三角函数图象的变换1．用五点法画y＝A sin(ωx＋φ)在一个周期内的简图用五点法画y＝A sin(ωx＋φ)在一个周期内的简图时，要找五个特征点，如下表所示．2.图象变换(ω＞0)路径①：先向左(φ>0)或向右(φ<0)平移________个单位长度，得到函数y＝sin(x＋φ)的图象；然后使曲线上各点的横坐标变为原来的________倍(纵坐标不变)，得到函数y＝sin(ωx＋φ)的图象；最后把曲线上各点的纵坐标变为原来的________倍(横坐标不变)，这时的曲线就是y＝A sin(ωx＋φ)的图象．路径②：先将曲线上各点的横坐标变为原来的________倍(纵坐标不变)，得到函数y＝sinωx的图象；然后把曲线向左(φ>0)或向右(φ<0)平移________个单位长度，得到函数y＝sin(ωx＋φ)的图象；最后把曲线上各点的纵坐标变为原来的________倍(横坐标不变)，这时的曲线就是y＝A sin(ωx＋φ)的图象．3．函数y＝A sin(ωx＋φ)(A>0，ω>0)的物理意义简谐运动的图象所对应的函数解析式y＝A sin(ωx＋φ)，x∈[0，＋∞)，其中A>0，ω>0.在物理中，描述简谐运动的物理量，如振幅、周期和频率等都与这个解析式中的常数有关：A就是这个简谐运动的振幅，它是做简谐运动的物体离开平衡位置的最大距离；这个简谐运动的周期是T＝________，这是做简谐运动的物体往复运动一次所需要的时间；这个简谐运动的频率由公式f＝1T＝________给出，它是做简谐运动的物体在单位时间内往复运动的次数；ωx＋φ称为相位；x＝________时的相位φ称为初相．自查自纠1.2.||φ1ωA1ω⎪⎪⎪⎪φωA3. 2πωω2π0(2016·四川)为了得到函数y ＝sin ⎝⎛⎭⎫x ＋π3的图象，只需把函数y ＝sin x 的图象上所有的点( ) A ．向左平行移动π3个单位长度B ．向右平行移动π3个单位长度C ．向上平行移动π3个单位长度D ．向下平行移动π3个单位长度解：把函数y ＝sin x 的图象上所有的点向左平行移动π3个单位长度就得到函数y ＝sin ⎝⎛⎭⎫x ＋π3的图象．故选A .(2016·全国卷Ⅰ)将函数y ＝2sin ⎝⎛⎭⎫2x ＋π6的图象向右平移14个周期后，所得图象对应的函数为( ) A ．y ＝2sin ⎝⎛⎭⎫2x ＋π4 B ．y ＝2sin ⎝⎛⎭⎫2x ＋π3 C ．y ＝2sin ⎝⎛⎫2x －π4 D ．y ＝2sin ⎝⎛⎫2x －π3 解：函数y ＝2sin ⎝⎛⎭⎫2x ＋π6的周期为π，将函数y ＝2sin ⎝⎛⎭⎫2x ＋π6的图象向右平移14个周期即π4个单位，所得函数为y ＝2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4＋π6＝2sin ⎝⎛⎭⎫2x －π3.故选D .(2017·全国卷Ⅰ)已知曲线C 1：y ＝cos x ，C 2：y ＝sin ⎝⎛⎭⎫2x ＋2π3，则下面结论正确的是( ) A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2解：y ＝cos x ＝sin ⎝⎛⎭⎫x ＋π2，把曲线C 1上的各点的横坐标缩短到原来的12倍，纵坐标不变，得到函数y ＝sin ⎝⎛⎭⎫2x ＋π2的图象，再把所得的图象向左平移π12个单位长度，可得函数y ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π12＋π2＝sin ⎝⎛⎭⎫2x ＋2π3的图象，即曲线C 2.故选D .(南京市、盐城市2017届高三一模)将函数y ＝3sin ⎝⎛⎭⎫2x ＋π3的图象向右平移φ⎝⎛⎭⎫0<φ<π2个单位后，所得函数为偶函数，则φ＝________.解：因为y ＝3sin ⎝⎛⎭⎫2x ＋π3的图象向右平移φ⎝⎛⎭⎫0<φ<π2个单位后，所得函数为y ＝3sin ⎝⎛⎭⎫2（x －φ）＋π3，即y ＝3sin ⎝⎛⎭⎫2x ＋π3－2φ是偶函数，则2×0＋π3－2φ＝k π＋π2，φ＝－k 2π－π12，k ∈Z ，又因为0<φ<π2，所以k ＝－1，φ＝5π12.故填5π12.(2016·全国卷Ⅲ)函数y ＝sin x －3cos x 的图象可由函数y ＝sin x ＋3cos x 的图象至少向右平移________个单位长度得到．解：因为y ＝sin x ＋3cos x ＝2sin ⎝⎛⎭⎫x ＋π3，y ＝sin x －3cos x ＝2sin ⎝⎛⎭⎫x －π3＝2sin ⎣⎡⎦⎤⎝⎛⎫x ＋π3－2π3，所以函数y ＝sin x －3cos x 的图象可由函数y ＝sin x ＋3cos x 的图象至少向右平移2π3个单位长度得到．故填2π3.类型一五点法作图与求解析式(1)作出函数y ＝2sin ⎝⎛⎭⎫x 2＋π3的图象．解：周期T ＝2π12＝4π，振幅A ＝2.描点作图：【点拨】用“五点法”作y ＝A sin(ωx ＋φ)的简图，主要是通过变量代换，设X ＝ωx ＋φ，由X ＝0，π2，π，32π，2π来求出相应的x 值，通过列表，计算得出五点坐标，描点后得出图象．(2)(2016·全国卷Ⅱ)函数y ＝A sin(ωx ＋φ)的部分图象如图所示，则( )A ．y ＝2sin ⎝⎛⎭⎫2x －π6B ．y ＝2sin ⎝⎛⎭⎫2x －π3C ．y ＝2sin ⎝⎛⎭⎫x ＋π6D ．y ＝2sin ⎝⎛⎭⎫x ＋π3 解：由图可知，T ＝2⎣⎡⎦⎤π3－⎝⎛⎭⎫－π6＝π，所以ω＝2，由五点作图法结合各选项可知2×π3＋φ＝π2，所以φ＝－π6，所以函数的解析式为y ＝2sin ⎝⎛⎭⎫2x －π6.故选A . 【点拨】已知f (x )＝A sin(ωx ＋φ)(A ＞0，ω＞0)的部分图象求其解析式，常用如下两种方法：(1)升降零点法，由ω＝2πT ，即可求出ω；求φ时，若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0，则令ωx 0＋φ＝0(或ωx 0＋φ＝π)，即可求出φ；(2)代入最值法，将最值点(最高点、最低点)坐标代入解析式，再结合图形解出ω和φ.(2016·安徽安庆二模)已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0，|φ|<π2)的图象如图所示，则f (x )的递增区间为( )A.⎝⎛⎭⎫－π12＋k π2，5π12＋k π2，k ∈Z B.⎝⎛⎭⎫－π12＋k π，5π12＋k π，k ∈Z C.⎝⎛⎭⎫－π6＋2k π，5π6＋2k π，k ∈Z D.⎝⎛⎭⎫－π6＋k π，5π6＋k π，k ∈Z 解法一：由图象可知A ＝2，34T ＝11π12－π6＝3π4，所以T ＝π，故ω＝2.由f ⎝⎛⎭⎫1112π＝－2，得φ＝2k π－π3(k ∈Z )．因为|φ|<π2，所以φ＝－π3.所以f (x )＝2sin ⎝⎛⎭⎫2x －π3. 由2x －π3∈⎝⎛⎭⎫2k π－π2，2k π＋π2(k ∈Z )，得x ∈⎝⎛⎭⎫－π12＋k π，5π12＋k π(k ∈Z )．解法二：34T ＝11π12－π6＝3π4，所以T ＝π，π6－T 4＝π6－π4＝－π12，π6＋T 4＝π6＋π4＝5π12，所以f (x )的递增区间是⎝⎛⎭⎫k π－π12，k π＋5π12(k ∈Z )．故选B . 类型二三角函数的图象变换说明由函数y ＝sin x 的图象经过怎样的变换就能得到下列函数的图象．(1)y ＝sin ⎝⎛⎭⎫x ＋π3；(2)y ＝sin ⎝⎛⎭⎫2x －23π； (3)y ＝||sin x ；(4)y ＝sin ||x .解：(1)将y ＝sin x 的图象向左平移π3个单位长度，得到y ＝sin ⎝⎛⎭⎫x ＋π3的图象． (2)解法一：将y ＝sin x 的图象向右平移23π个单位长度，得到y ＝sin ⎝⎛⎭⎫x －23π的图象，再把y ＝sin ⎝⎛⎭⎫x －23π图象上所有点的横坐标缩短到原来的12(纵坐标不变)，就得到y ＝sin ⎝⎛⎭⎫2x －23π的图象．解法二：先把y ＝sin x 的图象上所有点的横坐标缩短到原来的12(纵坐标不变)，得到y ＝sin2x 的图象，再将y ＝sin2x 的图象向右平移π3个单位长度，就得到y ＝sin ⎝⎛⎭⎫2x －23π的图象．(3)将y ＝sin x 的图象的x 轴下方部分翻折到x 轴上方，去掉x 轴下方图象，即可得到y ＝||sin x 的图象． (4)先去掉y 轴左边的y ＝sin x 的图象，再将y 轴右边的图象翻折到y 轴左边，保留y 轴右边的图象，即可得到y ＝sin ||x 的图象．【点拨】(1)本题主要考查图象的平移、伸缩、对称变换．三角函数的图象变换，有两种选择：一是先伸缩再平移，二是先平移再伸缩．特别注意平移变换时，当自变量x 的系数不为1时，要将系数先提出．对称变换要注意翻折的方向．(2)三角函数名不同的图象变换问题，应先将三角函数名统一，再进行变换．(荆门市2017届调考)若将函数y ＝12sin(2x ＋π3)图象上的每一个点都向左平移π3个单位，得到g (x )的图象，则函数g (x )的单调递增区间为( )A.⎣⎡⎦⎤k π－π4，k π＋π4(k ∈Z ) B.⎣⎡⎦⎤k π＋π4，k π＋3π4(k ∈Z ) C.⎣⎡⎦⎤k π－2π3，k π－π6(k ∈Z ) D.⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z ) 解：因为y ＝12sin ⎝⎛⎭⎫2x ＋π3的图象上的每一个点都向左平移π3个单位，得到g (x )的图象，所以g (x )＝12sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π3＋π3，即g (x )＝12sin(2x ＋π)＝－12sin2x ，令2k π＋π2≤2x ≤2k π＋3π2，即k π＋π4≤x ≤k π＋3π4，函数g (x )的单调递增区间为⎣⎡⎦⎤k π＋π4，k π＋3π4(k ∈Z )．故选B .类型三函数y ＝Asin (ωx ＋φ)＋k 的图象及其变换(2017·山东)设函数f(x)＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2，其中0＜ω＜3.已知f ⎝⎛⎭⎫π6＝0. (1)求ω；(2)将函数y ＝f(x)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，再将得到的图象向左平移π4个单位，得到函数y ＝g(x)的图象，求g(x)在⎣⎡⎦⎤－π4，3π4上的最小值．解：(1)因为f(x)＝sin ⎝⎛⎭⎫ωx －π6＋sin ⎝⎛⎭⎫ωx －π2，所以f(x)＝32sin ωx －12cos ωx －cos ωx＝32sin ωx －32cos ωx ＝3·⎝⎛⎭⎫12sin ωx －32cos ωx＝3sin ⎝⎛⎭⎫ωx －π3. 由题设知f ⎝⎛⎭⎫π6＝0，所以ωπ6－π3＝k π，k ∈Z . 故ω＝6k ＋2，k ∈Z ，又0＜ω＜3，所以ω＝2.(2)由(1)得f (x )＝3sin ⎝⎛⎭⎫2x －π3，所以g (x )＝3sin ⎝⎛⎭⎫x ＋π4－π3＝3sin ⎝⎛⎭⎫x －π12. 因为x ∈⎣⎡⎦⎤－π4，3π4，所以x －π12∈⎣⎡⎦⎤－π3，2π3，当x －π12＝－π3，即x ＝－π4时，g (x )取得最小值－32.【点拨】(1)用辅助角法，将较复杂的三角式转化成y ＝A sin(ωx ＋φ)的形式．(2)要看清由谁平移到谁，若自变量的系数不为1时，要将系数先提出来，再平移．(2015·湖北)某同学用“五点法”画函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎫ω>0，|φ|<π2在某一个周期内的图象时，列(1)请将上表数据补充完整，并直接写出函数f (x )的解析式；(2)将y ＝f (x )图象上所有点向左平行移动θ(θ>0)个单位长度，得到y ＝g (x )的图象．若y ＝g (x )图象的一个对称中心为⎝⎛⎭⎫5π12，0，求θ的最小值．解：(1)根据表中已知数据，解得A ＝5，ω＝2，φ＝－π.数据补全如下表：且函数表达式为f (x )＝5sin ⎝⎭⎫2x －π6. (2)由(1)知f (x )＝5sin ⎝⎛⎭⎫2x －π6，将y ＝f (x )图象上所有点向左平行移动θ(θ>0)个单位长度，得g (x )＝5sin ⎝⎛⎭⎫2x ＋2θ－π6. 令2x ＋2θ－π6＝k π，k ∈Z ，解得x ＝k π2＋π12－θ，k ∈Z .由于函数y ＝g (x )的图象关于点⎝⎛⎭⎫5π12，0成中心对称，令k π2＋π12－θ＝5π12，解得θ＝k π2－π3，k ∈Z .由θ>0可知，当k ＝1时，θ取得最小值π6.1．五点法作函数图象及函数图象变换问题(1)当明确了函数图象基本特征后，“描点法”是作函数图象的快捷方式．“五点法”作图的优点是用简单的计算、列表、描点替代图形变换，不易出错，且图形简洁．(2)在进行三角函数图象变换时，提倡“先平移，后伸缩”，而“先伸缩，后平移”也经常出现在题目中，所以也必须熟练掌握，但要注意：先伸缩后平移时要把x 前面的系数提取出来． 2．根据y ＝A sin(ωx ＋φ)，x ∈R 的图象求解析式的步骤： (1)首先确定振幅和周期，从而得到A 与ω.(Ⅰ)A 为离开平衡位置的最大距离，即最大值与最小值的差的一半．(Ⅱ)ω由周期得到：①函数图象在其对称轴处取得最大值或最小值，且相邻的两条对称轴之间的距离为函数的半个周期；②函数图象与x 轴的交点是其对称中心，相邻两个对称中心间的距离也是函数的半个周期；③一条对称轴与其相邻的一个对称中心间的距离为函数的14个周期(借助图象很好理解记忆)．(2)求φ的值时最好选用最值点求．峰点：ωx ＋φ＝π2＋2k π；谷点：ωx ＋φ＝－π2＋2k π.也可用零点求，但要区分该零点是升零点，还是降零点．升零点(图象上升时与x 轴的交点)：ωx ＋φ＝2k π；降零点(图象下降时与x 轴的交点)：ωx ＋φ＝π＋2k π(以上k ∈Z )．3．辅助角公式a sin α＋b cos α＝a 2＋b 2sin(α＋φ)(φ由tan α＝ba 确定)的应用是高考的热点，应予以重视．1．为了得到函数y ＝sin(2x ＋1)的图象，只需把函数y ＝sin2x 的图象上所有的点( )A ．向左平行移动12个单位长度B ．向右平行移动12个单位长度C ．向左平行移动1个单位长度D ．向右平行移动1个单位长度解：因为y ＝sin(2x ＋1)＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋12，所以只需把函数y ＝sin2x 的图象上所有的点向左平移12个单位长度即可．故选A .2．将函数y ＝sin x 的图象上所有的点向右平行移动π10个单位长度，再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象的函数解析式是( )A ．y ＝sin ⎝⎛⎭⎫2x －π10B ．y ＝sin ⎝⎛⎭⎫2x －π5C ．y ＝sin ⎝⎛⎭⎫12x －π10D ．y ＝sin ⎝⎛⎭⎫12x －π20 解：将函数y ＝sin x 的图象上所有的点向右平行移动π10个单位长度可得y ＝sin ⎝⎛⎭⎫x －π10，再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)，可得y ＝sin ⎝⎛⎭⎫12x －π10.故选C . 3．(北京昌平区2017届期末)已知函数f (x )＝2sin(ωx ＋φ)(ω>0，|φ|<π2)的图象如图所示，则函数f (x )的解析式为( )A ．f (x )＝2sin ⎝⎛⎭⎫2x ＋π6B ．f (x )＝2sin ⎝⎛⎭⎫2x ＋π3C ．f (x )＝2sin ⎝⎛⎭⎫x ＋π6D ．f (x )＝2sin ⎝⎛⎭⎫x ＋π3 解：由图可知周期为T ＝2⎝⎛⎭⎫x 0＋π2－x 0＝π，所以ω＝2，f (x )＝2sin(2x ＋φ)，又函数图象经过点(0，3)，故f (x )＝2sin(2×0＋φ)＝3，sin φ＝32，又|φ|<π2，所以φ＝π3，则f (x )＝2sin ⎝⎛⎭⎫2x ＋π3.故选B . 4．函数f (x )＝2sin(ωx ＋φ)⎝⎛⎭⎫ω＞0，－π2＜φ＜π2的部分图象如图所示，则ω，φ的值分别是( )A ．2，－π3B ．2，－π6C ．4，－π6D ．4，π3解：由图可知，34T ＝5π12＋π3＝3π4，T ＝π，ω＝2πT ＝2.因为点⎝⎛⎭⎫5π12，2在图象上，所以2·5π12＋φ＝π2＋2k π，φ＝－π3＋2k π，k ∈Z .又－π2＜φ＜π2，所以φ＝－π3.故选A .5．(2017·辽宁抚顺模拟)将函数f (x )＝2sin ⎝⎛⎭⎫2x ＋π6的图象向左平移π12个单位，再向上平移1个单位，得到g (x )的图象．若g (x 1)g (x 2)＝9，且x 1，x 2∈[－2π，2π]，则2x 1－x 2的最大值为( )A.25π16B.35π6C.49π12D.17π4解：由题意可得g (x )＝f ⎝⎛⎭⎫x ＋π12＋1＝2sin ⎝⎛⎭⎫2x ＋π3＋1，所以g (x )max ＝3，又g (x 1)g (x 2)＝9，所以g (x 1)＝g (x 2)＝3，由g (x )＝2sin ⎝⎛⎭⎫2x ＋π3＋1＝3，得2x ＋π3＝π2＋2k π(k ∈Z )，所以x ＝π12＋k π，因为x 1，x 2∈[－2π，2π]，所以(2x 1－x 2)max ＝2×⎝⎛⎭⎫π12＋π－⎝⎛⎭⎫π12－2π＝49π12.故选C . 6. (2016·北京)将函数y ＝sin ⎝⎛⎭⎫2x －π3图象上的点P ⎝⎛⎭⎫π4，t 向左平移s (s ＞0)个单位长度得到点P ′.若P ′位于函数y ＝sin2x 的图象上，则( )A ．t ＝12，s 的最小值为π6B ．t ＝32，s 的最小值为π6C ．t ＝12，s 的最小值为π3D ．t ＝32，s 的最小值为π3解：因为点P ⎝⎛⎭⎫π4，t 在函数y ＝sin ⎝⎛⎭⎫2x －π3的图象上，所以t ＝sin ⎝⎛⎭⎫2×π4－π3＝sin π6＝12.又P ′⎝⎛⎭⎫π4－s ，12在函数y ＝sin2x 的图象上，所以12＝sin2⎝⎛⎭⎫π4－s ，则2⎝⎛⎭⎫π4－s ＝2k π＋π6或2⎝⎛⎭⎫π4－s ＝2k π＋56π，k ∈Z ，得s ＝－k π＋π6或s ＝－k π－π6，k ∈Z ，又s ＞0，故s 的最小值为π6.故选A .7．函数y ＝A sin(ωx ＋φ)(A ，ω，φ为常数，A >0，ω>0)在闭区间[－π，0]上的图象如图所示，则ω＝________．解：由图象知T ＝2π3，则ω＝2πT ＝2π2π3＝3.故填3.8．(2015·昆明模拟)把函数y ＝sin2x 的图象沿x 轴向左平移π6个单位，纵坐标伸长到原来的2倍(横坐标不变)后得到函数y ＝f (x )的图象，对于函数y ＝f (x )有以下四个判断：①该函数的解析式为y ＝2sin ⎝⎛⎫2x ＋π6； ②该函数图象关于点⎝⎛⎭⎫π3，0对称；③该函数在⎣⎡⎦⎤0，π6上是增函数； ④若函数y ＝f (x )＋a 在⎣⎡⎦⎤0，π2上的最小值为3，则a ＝2 3. 其中正确判断的序号是________．解：将函数y ＝sin2x 的图象向左平移π6得到y ＝sin2⎝⎛⎭⎫x ＋π6＝sin ⎝⎛⎭⎫2x ＋π3的图象，然后纵坐标伸长到原来的2倍得到y ＝2sin ⎝⎛⎭⎫2x ＋π3的图象，①不正确；y ＝f ⎝⎛⎭⎫π3＝2sin ⎝⎛⎭⎫2×π3＋π3＝2sin π＝0，函数图象关于点⎝⎛⎭⎫π3，0对称，②正确；由－π2＋2k π≤2x ＋π3≤π2＋2k π，k ∈Z ，得－5π12＋k π≤x ≤π12＋k π，k ∈Z ，即函数的单调增区间为[－5π12＋k π，π12＋k π]，k ∈Z ，当k ＝0时，增区间为⎣⎡⎦⎤－5π12，π12，③不正确；y ＝f (x )＋a ＝2sin ⎝⎛⎭⎫2x ＋π3＋a ，当0≤x ≤π2时，π3≤2x ＋π3≤4π3，当2x ＋π3＝4π3，即x ＝π2时，函数取得最小值，有y min ＝2sin 4π3＋a ＝－3＋a ＝3，得a ＝23，④正确．故填②④.9．已知函数f (x )＝3sin(ωx ＋φ)(ω＞0，－π2≤φ＜π2)的图象关于直线x ＝π3对称，且图象上相邻两个最高点的距离为π，求ω和φ的值．解：由题意，函数f (x )的最小正周期T ＝π，ω＝2πT ＝2ππ＝2.因为f (x )的图象关于直线x ＝π3对称，所以2·π3＋φ＝k π＋π2，φ＝k π－π6，k ∈Z .又－π2≤φ＜π2，所以φ＝－π6.10．(2016·山东)设f (x )＝23sin (π－x )sin x －(sin x －cos x )2. (1)求f (x )的单调递增区间；(2)把y ＝f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，再把得到的图象向左平移π3个单位，得到函数y ＝g (x )的图象，求g ⎝⎛⎭⎫π6的值．解：(1)由f (x )＝23sin (π－x )sin x －(sin x －cos x )2 ＝23sin 2x －(1－2sin x cos x )＝3(1－cos2x )＋sin2x －1＝sin2x －3cos2x ＋3－1＝2sin ⎝⎛⎭⎫2x －π3＋3－1，由2k π－π2≤2x －π3≤2k π＋π2(k ∈Z )，得k π－π12≤x ≤k π＋5π12(k ∈Z )，所以f (x )的单调递增区间是⎣⎡⎦⎤k π－π12，k π＋5π12(k ∈Z )．(2)由(1)知f (x )＝2sin ⎝⎛⎭⎫2x －π3＋3－1，把y ＝f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到y ＝2sin ⎝⎛⎭⎫x －π3＋3－1的图象，再把得到的图象向左平移π3个单位，得到y ＝2sin x ＋3－1的图象，即g (x )＝2sin x ＋3－1.所以g ⎝⎛⎭⎫π6＝2sin π6＋3－1＝ 3. 11．(2017·福建福州模拟)已知函数f (x )＝3sin2ωx ＋cos 4ωx －sin 4ωx ＋1(其中0<ω<1)，若点⎝⎛⎭⎫－π6，1是函数f (x )图象的一个对称中心．(1)求f (x )的解析式，并求距y 轴最近的一条对称轴的方程； (2)先列表，再作出函数f (x )在区间[－π，π]上的图象．解：(1)f (x )＝3sin2ωx ＋(cos 2ωx －sin 2ωx )(cos 2ωx ＋sin 2ωx )＋1 ＝3sin2ωx ＋cos2ωx ＋1＝2sin ⎝⎛⎭⎫2ωx ＋π6＋1. 因为点⎝⎛⎭⎫－π6，1是函数f (x )图象的一个对称中心，所以－ωπ3＋π6＝k π，k ∈Z ，所以ω＝－3k ＋12，k ∈Z .因为0<ω<1，所以k ＝0，ω＝12，所以f (x )＝2sin ⎝⎛⎭⎫x ＋π6＋1. 由x ＋π6＝k π＋π2，k ∈Z ，得x ＝k π＋π3，k ∈Z .令k ＝0，得距y 轴最近的一条对称轴方程为x ＝π3.(2)由(1)知，f (x )＝2sin ⎛⎭⎫x ＋π＋1，当x ∈[－π，π]时，列表如下：则函数f (x )在区间[－π，π]上的图象如图所示．(2016·厦门模拟)已知向量a ＝(2cos x ，3sin x )，b ＝(cos x ，2cos x )，函数f (x )＝a ·b ＋m ，m ∈R ，且当x ∈⎣⎡⎦⎤0，π2时，f (x )的最小值为2. (1)求f (x )的单调递增区间；专业文档珍贵文档 (2)先将函数y ＝f (x )的图象上点的纵坐标不变，横坐标缩短到原来的12，再把所得的图象向右平移π12个单位，得到函数y ＝g (x )的图象，求方程g (x )＝4在区间⎣⎡⎦⎤0，π2上的所有根之和．解：(1)f (x )＝2cos 2x ＋23sin x cos x ＋m＝cos2x ＋3sin2x ＋m ＋1＝2sin ⎝⎛⎭⎫2x ＋π6＋m ＋1. 因为x ∈⎣⎡⎦⎤0，π2，所以2x ＋π6∈⎣⎡⎦⎤π6，7π6，当2x ＋π6＝76π，即x ＝π2时，f (x )min ＝2×⎝⎛⎭⎫－12＋m ＋1＝2，解得m ＝2，所以f (x )＝2sin ⎝⎛⎭⎫2x ＋π6＋3，令2k π－π2≤2x ＋π6≤2k π＋π2得f (x )的增区间为⎣⎡⎦⎤k π－π3，k π＋π6(k ∈Z )． (2)将函数y ＝f (x )的图象上点的纵坐标不变，横坐标缩短到原来的12，得到f (x )＝2sin ⎝⎛⎭⎫4x ＋π6＋3，再把所得的图象向右平移π12个单位，得到函数y ＝g (x )的图象，所以g (x )＝2sin ⎣⎡⎦⎤4⎝⎛⎭⎫x －π12＋π6＋3＝2sin ⎝⎛⎭⎫4x －π6＋3，又g (x )＝4，得sin ⎝⎛⎭⎫4x －π6＝12，解得4x －π6＝2k π＋π6或4x －π6＝2k π＋5π6，k ∈Z . 即x ＝k π2＋π12或x ＝k π2＋π4(k ∈Z )，因为x ∈⎣⎡⎦⎤0，π2，所以x ＝π12或π4，故所有根之和为π12＋π4＝π3.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

振幅 A 2 ，周期 T 2
，初相
.
2
3
（ 2）解法一
y 2sin(2x ) 的简图． 3
①把函数 y 象；②把函数 y
sin x 的图象上所有点向右平移
个单位，得到函数 y sin( x ) 的图
3
3
sin( x ) 图象上所有点的根坐标缩短到原来的 3
1 （纵坐标不变），得到 2
函数 y sin( 2x ) 的图象； ③把函数 y sin( 2x ) 图象上所有的点的纵坐标伸长到原
五点法作图
例 1、（ l）利用“五点法”作函数周期和初相．
y sin( 2x ) 的图象，并指出这个函数的振幅、 3
（ 2）怎样由 y sin x 的图象得到 y sin( 2x ) 的图象？ 3
分析：令 t 2x
解：（ 1）列表：
，找出 y 3
sin t 图象的五个关键点对应的
x 值．
x
5
2
11
7
6
12
3
12
6
2x
0
3
2
3
2
2
y
0
2
0
－2
0
描点：（， 0），（ 5 ， 2），（ 2 ，0），（ 11 ，－ 2），（ 7 ， 0）。
6
12
3
12
6
用光滑的曲线将它们连结起来，就得到函数
y sin( 2x ) 在一个周期内的简图（图 3
1）．把这个简图利用函数的周期性向左、右扩展，就得到函数
3
3
来的 2 倍（横坐标不变），就得到函数 y
图 1．解法二
2sin( 2x
) 的图象见 3
①把函数 y sin x 的图象上所有的点的横坐标缩短到原来的
1 （纵坐标不变），得到函数 y sin 2x 的的点向右平移
个单位，得到函数
6
图1
y sin( 2x ) 的图象； ③把函数 y sin( 2x ) 的图象上所有的点的纵坐标伸长到原来
3
3
的 2 倍（根坐标不变），就得到函数 y 2sin( 2x ) 的图象见图 1． 3
小结：函数图象变换中，横向变换是对 x 变化的反映，纵向变换是对
y 变化的反映．