弹塑性时程分析法
动力弹塑性时程分析技术抗震应用阐述
动力弹塑性时程分析技术抗震应用阐述高层建筑是当前建筑的主要形式，新材料、新技术的应用使得建筑质量提高，功能越来越齐全。
但其结构设计也更复杂，施工难度加大，因此对其抗震施工技术提出了更高的要求。
高层建筑的投资数额较大，周期也相对较长，而动力弹性时程分析技术是一项综合性较强的技术工作，涉及每一个环节，一旦出现问题，必将影响到施工质量。
从而延误工期，甚至引发安全事故，带来严重的损失。
所以，在施工过程中，必须加强建筑结构抗震设计中对动力弹塑性时程分析技术的应用，进而保证及时解决潜在的隐患。
1.动力弹塑性时程分析技术概述弹塑性时程分析方法可以有效的将结构作为弹塑性振动体系进行相应的分析，并通过对地震波数据在地面运动中的输入应用，可以有效的进行下一步的积分运算，进而可以得出地面加速度随着时间的变化而发生的变化，同时，还可以得出结构的内力与变形随着时间的变化而变化的整个过程。
动力弹塑性时程分析技术的应用通常有以下几个步骤：第一，通过对几何模型的建立，进而实现网格的划分工作；第二，对材料的本构关系进行确定，并根据各个构件自身的单元类型及材料类型的确定，进而对结构的质量、刚度及阻尼矩阵进行确定；第三，根据本场地的地震波，并对模型的边界条件进行定义，进而得出相应的计算结果；第四，根据计算所得出的结果进行进一步的处理工作，并根据处理的结果进行结构整体性可靠度的评估。
2 高层建筑动力弹塑性时程分析技术管理现状2.1材料设备管理中的问题材料是建筑的基础，现代化高层建筑用途不同，所用的材料也千差万别，加上各种新型材料日新月异，种类繁多，管理十分复杂。
如果购置时质检把关不严、储存方式不合理，很容易出现材料不能及时供应等情况，或导致材料性能下降，或与工程技术要求不相符。
各项机械设备、电气设备也是施工中不可或缺的元素，由于制度不健全、监督不严，存在着违规操作等不规范行为，这就导致动力弹塑性时程分析技术在实际的工程施工过程中不能得到有效的反应。
YJK动力弹塑性时程分析详解
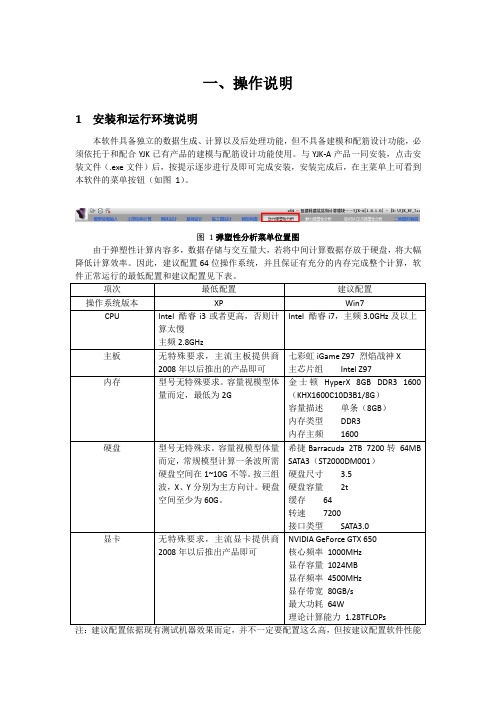
目标最佳。
2 弹塑性时程分析流程
完整的弹塑性时程分析过程如下图所示，程序提供下图所有功能模块，计算完成后以图 形和表格的方式输出超限结构弹塑性分析报告所用数据。
线弹性分析 与设计
分析与设计 施工图
选择地震波
3组或7组
弹塑性时程 分析
生成数据
含钢筋数据
动力方程求解
NewMark数 00200 -0.00200 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 0.00000 -0.00100 0.00000 -0.00000 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 -0.00100 0.00000 -0.00200 0.00200 0.00100 -0.00000 -0.00100 … 对话框中参数应按如下方式设置： 步长设置：0.02； 故数据起始行号：5，因前 5 行数据为说明行； 一行数据个数：5。
4.1.2 地震波选择
弹塑性动力时程分析结果，对地震波的依赖程度比较高。同一结构，采用不同的地震波， 计算结果可能有非常明显的差异。依据《高规》[4]5.5.1 条第 6 款：进行动力弹塑性计算时， 地面运动的加速度时程的选取、预估罕遇地震作用时的峰值加速度取值以及计算结果的选用 应符合该规程第 4.3.5 的规定。
弹塑性时程分析
弹塑性时程分析方法将结构作为弹塑性振动体系加以分析，直接按照地震波数据输入地面运动，通过积分运算，求得在地面加速度随时间变化期间内，结构的内力和变形随时间变化的全过程，也称为弹塑性直接动力法。
基本原理多自由度体系在地面运动作用下的振动方程为：式中、、分别为体系的水平位移、速度、加速度向量；为地面运动水平加速度，、、分别为体系的刚度矩阵、阻尼矩阵和质量矩阵。
将强震记录下来的某水平分量加速度－时间曲线划分为很小的时段，然后依次对各个时段通过振动方程进行直接积分，从而求出体系在各时刻的位移、速度和加速度，进而计算结构的内力。
式中结构整体的刚度矩阵、阻尼矩阵和质量矩阵通过每个构件所赋予的单元和材料类型组装形成。
动力弹塑性分析中对于材料需要考虑包括：在往复循环加载下，混凝土及钢材的滞回性能、混凝土从出现开裂直至完全压碎退出工作全过程中的刚度退化、混凝土拉压循环中强度恢复等大量非线性问题。
基本步骤弹塑性动力分析包括以下几个步骤：(1) 建立结构的几何模型并划分网格；(2) 定义材料的本构关系，通过对各个构件指定相应的单元类型和材料类型确定结构的质量、刚度和阻尼矩阵；(3) 输入适合本场地的地震波并定义模型的边界条件，开始计算；(4) 计算完成后，对结果数据进行处理，对结构整体的可靠度做出评估。
计算模型在常用的商业有限元软件中，ABAQUS、ADINA、ANSYS、MSC.MARC都内置了混凝土的本构模型，并提供了丰富的单元类型及相应的前后处理功能。
在这些程序中一般都有专用的钢筋模型，可以建立组合式或整体式钢筋。
以ABAQUS为例，它提供了混凝土弹塑性断裂和混凝土损伤模型以及钢筋单元。
其中弹塑性断裂和损伤的混凝土模型非常适合于钢筋混凝土结构的动力弹塑性分析。
它的主要优点有：(1) 应用范围广泛，可以使用在梁单元、壳单元和实体单元等各种单元类型中，并与钢筋单元共同工作；(2) 可以准确模拟混凝土结构在单调加载、循环加载和动力荷载下的响应，并且可以考虑应变速率的影响；(3) 引入了损伤指标的概念，可以对混凝土的弹性刚度矩阵进行折减，可以模拟混凝土的刚度随着损伤增加而降低的特点；(4) 将非关联硬化引入到了混凝土弹塑性本构模型中，可以更好的模拟混凝土的受压弹塑性行为，可以人为指定混凝土的拉伸强化曲线，从而更好的模拟开裂截面之间混凝土和钢筋共同作用的情况；(5) 可以人为的控制裂缝闭合前后的行为，更好的模拟反复荷载作用下混凝土的反应。
1王亚勇-弹塑性分析输出结果解读(贵阳2015)
30000
US052 US169 AS735-1 规范谱
X向
Y向
检验-底部剪力对比(满足规范要求)
规范谱 X向 Y向 US052 US169 S735-1 最大值/ 规范谱 87% 94% 最小值/ 规范谱 105% 72% 平均值/ 规范谱 98% 86%
30684.3 31527.5 32489.4 26742.6 28526.1 26916.6 26380.7 20581.3
40 US031 30 20
加速度（gal）
10 0
加速度（gal）
20 40 t (sec) 60
-10 -20 -30 40 -40 30 0
20
10 0 -10 -20 US032
80 -30
-40 0
100
20 40 t (sec) 60 80
加速度（gal）
10 0 -10 -20 -30 -40 0 20 40 60 80
L033-地震波输入外框架柱型钢M桁架Mises应力
XI’AN IFC ARCHITECTURAL DESIGN
L033-地震波输入外框架梁Mises应力
“超限汇报” XI’AN IFC ARCHITECTURAL DESIGN
错误的选波方法 - Tg
• • • • 挑选”小“的 不分场地类别 不分地震分组（近、远震） 由一条地震加速度记录的反应谱计算Tc： SA=ώPSV=（2π/TC）PSV TC= 2π（PSV/SA），是确定性的。 而规范反应谱是由统计平均得到，所以
Tg ≠ TC
小震弹性
输入地震波: 二组实际地震记录和一组人工模拟加速度时程（AS735、US052和 US169)
时间 （s）
MATLAB弹塑性时程分析法编程(参照类别)
MATLAB编程：format short g;F(21,14)=0;xg=[0 600 1100 1500 2100 2500 2900 350 2050 1500 1000 600 200 -700 -1300 -1700 -2000 -1800 -1500 -700 -250 200 -100 0 0 0];xg1=xg*2200/max(xg);xg2=diff(xg1);f(14)=0;f(4)=9000;t=0.05;m=250;c=240;for i =1:21f(3)=xg2(i);f(1)=0.05*i-0.05;f(2)=xg1(i);f(6)=-m*(f(3)-6*f(12)/t-3*f(11))+c*(3*f(12)+f(11)/2*t); f(5)=f(4)+6*m/t^2+3*c/t;f(7)=f(6)/f(5);f(9)=3/t*f(7)-3*f(12)-0.5*f(11)*t;f(8)=6/0.05^2*f(7)-6/0.05*f(12)-3*f(11);f(13)=f(2)+f(11);f(14)=f(13)*m;F(i,:)=f(1,:);f(10)=f(10)+f(7);f(12)=f(12)+f(9);f(11)=f(11)+f(8);if abs(f(10))>2&F(1,7)*f(7)>0f(4)=0;else f(4)=9000;endenda=max(abs(F(:,13)));b=max(abs(F(:,14)));Fabxlswrite('表格2.xls',F)计算书：课程设计计算书（题二）根据加速度调幅公式：m i a t a a a /)(max ,00*=)/(29002902s mm Gal a m ==得：29/)(222900/)(22000i i t a t a a =*= )(i t a =[0 600 1100 1500 2100 2500 2900 350 2050 1500 1000 600 200 -700 -1300 -1700 -2000 -1800 -1500 -700 -250 200 -100 0 0 0];所以经调幅后为0a =[0 455.2 834.9 1138.5 1593.9 1897.5 2201.1 265.7 1556.0 1138.5 759 455.4 151.8 -531.3 -986.7 -1290.3 -1518 -1366.2 -1138.5 -531.3 -189.8 151.8 -75.9 0 0 0 ]2.45502.455''1''2=-=-U U7.3792.4559.834''2''3=-=-U U依次类推可以求出地面运动加速度的差值。
sap2000弹塑性分析方法
SAP2000弹塑性分析方法运用总结结构的抗震设计一般可通过三个方面来实现，一种是增加结构的截面和刚度来“抗震”，此时如果要使结构在大震作用下保持弹性状态，结构需要具有如右图所示的承载能力，此时结构的设计截面会变得非常不经济；第二种方法是容许结构发生一定的塑性变形，并保证结构不发生倒塌的"耐"震设计（或叫延性设计）；第三种方法是通过一些装置地震响应比较（如阻尼器、隔振装置等）来吸收能量的"减"震或"隔"震设计。
当结构和结构构件具有一定的延性时，大震作用下部分构件会发生屈服，此时结构的周期会变长，结构周期的变长反过来减小了地震引起的惯性力，即塑性铰的出现吸收了部分地震能量，从而避免了结构的倒塌。
对结构抗震性能的评价以往多从强度入手，但结构在发生屈服后仍具有一定的耗能和变形能力，因此用能够反映结构延性和耗能能力的变形评价结构的抗震性能应更为合适。
通过动力弹塑性分析我们不仅要了解结构发生屈服和倒塌时的地震作用的大小，同时也要了解结构的变形能力（弹塑性层间位移角、延性系数等）、构件的变形能力、铰出现顺序等，从而实现“小震不坏、中震可修、大震不倒”的三水准设防目标。
目的：1) 评价建筑在罕遇地震下的抗震性，根据主要构件的塑性破坏情况和整体变形情况，确认结构是否满足性能目标的要求。
2) 研究超限对结构抗震性能的影响，包括罕遇地震下的最大层间位移；3)根据以上分析结果，针对结构薄弱部位和薄弱构件提高相应的加强措施。
弹塑性分析两种方法：1、静力弹塑性方法push-over2、动力弹塑性时程分析《建筑抗震设计规范》GB50011-2010（以下简称《抗规》)第1.0.1条中规定了三水准设防目标为“小震不坏、中震可修、大震不倒”。
《抗规》5.5.2条中分别规定了"应"进行弹塑性变形验算和"宜"进行弹塑性变形验算的结构。
精编弹塑性时程分析法资料
服点，后续反向加载时直线指向所经历过的最大位移点。 ④ 中途卸载时，卸载刚度取 k1。
《工程结构抗震与防灾》电子教案 东南大学 源自幼亮§4 弹塑性时程分析法
9
2. 双线型模型力学描述：
设 P(Ui ) 、U i 表示ti 时刻结构的恢复力与变形，则在ti1时刻刚度退化双线
P(Ui ) P(U7 )
刚度降低系数为
4
k4 k1
Py U yk1
故
P(U i1 )
P(U3)
P(U
7
)
Py Uy
(U i1
Py Uy
(U i1
U3) U7
)
（4.1.11）
《工程结构抗震与防灾》电子教案
东南大学
丁幼亮
§4 弹塑性时程分析法
U 0 ，U U6
初始条件为
U i U 6 ， P(U i ) P(U 6 ) 0
刚度降低系数为
P(U 2 )
(U 2 U 6 )k1
故
P(U i1 )
P(U 2 ) U2 U6
(U i1
U6 )
（4.1.7）
需要指出，式（4.1.2）～式（4.1.7）中，U 2 、 P(U 2 ) 、U 3 、U5 、 P(U5)
(1) 在弹性阶段,K 是定值,不随变形而变化. (2) 在弹塑性阶段,K 值随结构变形状态不同而改变。 (3) 由于地震下结构变形为一个循环往复的过程，因此 K 值随着变形也是
个循环往复的过程。
因此，弹塑性时程分析法必须首先确定刚度与变形之间的关系，
高层建筑动力弹塑性时程分析方法研究
高层建筑动力弹塑性时程分析方法研究
张 小 方 ’
（ 甘肃省建筑设计研究院 ，甘肃 兰 州 ７ ３ ０ ０ ０ ０）
【 摘 要】 近些年我 国高层建筑发展较快 ，怎样分析 高层 建筑
的抗震 性能成为 了重要 问题 ，时程分析可 以进一步判 断一栋建 筑物 的抗震 能力。本文介 绍 了动力弹塑性时程分析法 的作 用，指 出 了采
差。
（ ４ ） 对工程技术人 员素质要求较高 从结构模型建立 ， 地震波 选取 、材料 本构选 取、到参数 控制及庞 大计 算结果的整理及甄别都 要求技术人 员具有扎实 的专业素质 以及丰富的工程经验。 ５ 动力弹塑性时程分析方法计算 结果的处理 首先 要判断所 选多条地震波的计算结果是否基本一致 ，从而确 定所选地震 波的合理性。第二要查看各条地震波计算 的最大层间位 移角 能否满 足规 范的要求，这也是做弹塑性时程分析 的主要 目的 第三 ， 在最大有害层间位移角 曲线中找到结构的薄弱层 ，出现开裂 、 塑性铰 的部位，帮助设计人员对这些部位采取加强措旌 ，提高其抗 拉和抗压承 载力，从而改善结构的抗震性能 。 ‘ 最后 ，结构最大层 问 位 移角出现 位置 并不一定表示该层就是薄弱层 ，结构薄弱层 的判断 宜以结构 最大有害位移 角出现 的位置为准 。
６ 结 论
（ ２ ） 选择使 用于本场地的地 震波 不同的 地震 波会对弹性 动力 对程分析的计算结果产生一定的影响，有时影响较大 嗣此合理的 选波 ，往往成为采用这计算方法的关键 本文 建议 ，首先通过 弹性 时程分析得到基底剪力，然后与振型分解反应谱法进行对比，筛选
出合适的地震波进行弹塑性动力时程 分析 ‘ （ ３ ） 确 定混凝土、钢材两种材料的滞回； 构关系 ， 其中钢材的 本构关系常采用双线性本构关系。棍凝 土常采用三线性本梅关系０ （ ４ ） 定义计算过程各参数 。 （ ５ ） 计算完成后查看计算结果， 找 出结构 的最大层 间及有害层 间位移角 的数值 ，结构破坏情况 ，从而可 以评估结构的抗震能力 。
建筑结构爆破地震反应弹塑性精细时程分析
建筑结构爆破地震反应弹塑性精细时程分析[摘要]根据爆破的地震影响下的建筑的结构安全方面评价的分析，提出使用时程的分析方式进行整体的评价爆破方面的地震波安全程度，成立比较精确的结构弹塑性方面的动力研究结构的方式，制定了建筑结构中的爆破地震的反应中弹塑性的时程研究过程。
本文就建筑机构爆破地震反应弹塑性精细时程进行分析。
[关键词]建筑结构爆破地震弹塑性精细时程中图分类号：tu973.2 文献标识码：a 文章编号：1009-914x （2013）10-0129-01建筑的结构在爆破的地震波的影响中作出的安全评价长久以来都是人们非常重视的问题。
一些爆破的安全制度中也有很的明确规定，要将爆破的地震波动频率的峰值进行安全地振动的速度要求，但是地震波动的速度与主要频率的选择和采用都有着很大的困难。
现在所设计的结构都是根据抗震的规则来进行预防的设置的，但爆破的地震和自然的地震还是有着非常明显的不同。
必须采用时程的分析研究，才可以精准地断定爆破地震的状况下，结构产生动力的反应，从而进行全方位爆破震波的安全性的评估。
爆破的振动产生的破坏其实就是动态的随机的破坏情况。
从动力学的角度研究结构振动的动力反应，这个已经是分析振动对结构造成破坏的有效途径。
使用成熟一点的响应谱的理论方式来研究结构体处在不一样的动力环境中的爆破振动的反应，并且得到了一些成果。
但是，响应谱的理论是根据单个的自由程度系统的弹性的动力进行研究，不可以完全地表现出爆破时地震波对多个自由度的系统弹塑性的动力特点。
将实际测量的爆破的地震记录与爆破的震波模仿当作基础，通过时程的研究方式与有限元的原理研究结构将进行爆破震波与自然震波的环境中所出现的动力反应的不同。
但这样的方式都差分近似，并且对时间都特别地敏锐，并且精确度也不够高，在计算的时候会遇到一些问题。
1、结构的爆破地震响应中弹塑性的动力研究（一）结构中爆破地震响应中弹塑性的动力研究通过爆破的地震波的影响，结构体通常会从弹性的形态步入到弹塑性的形态，分析弹塑性的结构系统在爆破的地震环境里面的动力影响是非常有价值的，使用机制的质量方式或者是有限元的方式，获得n个自由方面结构体的动力计算方式。
SAUSAGE软件动力弹塑性时程分析方法及其应用
（ 3） 施加地震波激励，进行动力时程分析。
第 42 卷 增刊
王 欣，等． SAUSAGE 软件动力弹塑性时程分析方法及其应用
9
3 工程应用 本文选取某带加强层的框筒结构作为进行工程
案例分析。 3． 1 工程概况
渤海银行业务综合楼位于天津市六经路和六纬 路交界处，地面以上 51 层，底部 4 层设有裙房。标准 层层高 4． 5m，塔楼屋面高度为 240m，屋面造型飘架 的最高点高度为 270m，裙房屋面高度为 22． 2m。塔 楼平面尺寸为 57． 9m × 37． 9m，塔楼高宽比为 6． 3。
Elastic-plastic time-history analysis method and application of SAUSAGE Wang Xin1，2 ，Z． lee1，2
（ 1 ＲBS Architecture Engineer Design Associate，Guangzhou 510170，China； 2 Guangzhou Scientific Computing Consultants Co．，Ltd．，Guangzhou 510170，China） Abstract： The parallel processing of“GPU + CPU”adopted by SAUSAGE is introduced，the elastic-plastic time-history analysis method of SAUSAGE is specified，include the explicit method，steel and concrete constitutive model，fibre beam element and layered shell element，the build process of structural model and analysis steps． Then a framed-tube structure with outriggers was selected as a study case，the elastic-plastic time-history analysis under the rare earthquakes is carried out by SAUSAGE and ABAQUS，in order to study the seismic performance of this structural system，and showed the correctness and efficiency of SAUSAGE． Keywords： GPU； elastic-plastic time-history analysis； explicit method； fibre beam element； SAUSAGE； ABAQUS
静力弹塑性分析方法(Pushover方法)与动力弹塑性分析方法的优缺点比较
静力弹塑性分析方法（Pushover方法）与动力弹塑性分析方法的优缺点比较一、Pushover分析法1、Pushover分析法优点：（1）作为一种简化的非线性分析方法，Pushover方法能够从整体上把握结构的抗侧力性能，可以对结构关键机构及单元进行评估，找到结构的薄弱环节，从而为设计改进提供参考。
（2）非线性静力分析可以获得较为稳定的分析结果，减小分析结果的偶然性，同时花费较少的时间和劳力，较之时程分析方法有较强的实际应用价值。
2、Pushover分析法缺点：（1）它假定所有的多自由度体系均可简化为等效单自由度体系，这一理论假定没有十分严密的理论基础。
（2）对建筑物进行Pushover分析时首先要确定一个合理的目标位移和水平加载方式，其分析结果的精确度很大程度上依赖于这两者的选择。
（3）只能从整体上考察结构的性能，得到的结果较为粗糙。
且在过程中未考虑结构在反复加载过程中损伤的累积及刚度的变化。
不能完全真实反应结构在地震作用下性状。
二、弹塑性时程分析法1、时程分析法优点：（1）采用地震动加速度时程曲线作为输入，进行结构地震反应分析，从而全面考虑了强震三要素，也自然地考虑了地震动丰富的长周期分量对高层建筑的不利影响。
（2）采用结构弹塑性全过程恢复力特性曲线来表征结构的力学性质，从而比较确切地、具体地和细致地给出结构的弹塑性地震反应。
（3）能给出结构中各构件和杆件出现塑性铰的时刻和顺序，从而可以判明结构的屈服机制。
（4）对于非等强结构，能找出结构的薄弱环节，并能计算出柔弱楼层的塑性变形集中效应。
2、时程分析法缺点：（1）时程分析的最大缺点在于时程分析的结果与所选取的地震动输入有关，地震动时称所含频频成分对结构的模态n向应有选择放大作用，所以不同时称输入结果差异很大。
（2）时程分析法采用逐步积分的方法对动力方程进行直接积分，从而求得结构在地震过程中每一瞬时的位移、速度和加速度反应。
所以此法的计算工作十分繁重，必须借助于计算机才能完成。
103 天津某超高层项目ABAQUS软件大震弹塑性时程分析报告
[] = [] + []
α = 4ξπ/T
上式中，[]为结构阻尼矩阵，[]和[]分别为结构质量矩阵和刚度矩阵。实际工程计算时，
常忽略 β 阻尼，α 由阻尼比 ξ与周期 T 反算而得。
1.4.6
分析步骤
第一步：施工模拟加载。利用 ABAQUS 隐式计算模块 ABAQUS/STANDARD，通过单元的“生”
1.5.1
结构总体变形控制
（1）能够完成整个弹塑性时程分析过程而不发散；
（2）结构的最终状态仍然竖立不倒；
（3）结构主体的最大层间位移角小于规范限值，框架-核心筒结构为 1/100。
1.5.2
构件性能目标
《高层建筑混凝土结构技术规程》 （JCJ3-2010）第 3.11 节 结构抗震性能设计，将结
构的抗震性能分为 1～5 五个水准，对应的构件损坏程度则分为“无损坏、轻微损坏、轻度
损坏、中度损坏、比较严重损坏”五个级别。
《建筑抗震设计规范》
（GB5001-2010）附录 M
提供了实现构件性能水准评价的具体方法。
在 Abaqus 软件中构件的损坏主要以混凝土的受压损伤因子及钢材（钢筋）的塑性应变
程度作为评定标准，参照前述规范条文采用如下损伤程度与构件性能水准的对应关系：
1）钢材在屈服后其强度并不会下降，衡量其损坏程度的主要指标是塑性应变值。设钢
条相同。但对整个剪力墙构件而言，由于墙肢一般不满足平截面假定，在边缘混凝土单元出
现受压损伤后，构件承载力不会立即下降，其损坏判断标准应有所放宽。考虑到剪力墙的初
始轴压比通常为 0.5～0.6，当 50%的横截面受压损伤达到 0.5 时，构件整体抗压和抗剪承
载力剩余约 75%，仍可承担重力荷载，因此以剪力墙受压损伤横截面面积作为其严重损坏
浅谈弹塑性动力时程分析方法
浅谈弹塑性动力时程分析方法对于结构地震响应分析方法，发展到目前为止，可以归纳为以下三个发展阶段：静力法、拟静力法（即反应谱法）、动力法（主要为时程分析法）。
在结构进入弹塑性阶段后，结构的一些构件进入屈服状态、结构刚度发生变化、产生塑性区域。
而弹性静力法忽略了结构的动力特性和结构的非刚性等重要特性，此时已经不再适用，因此使用弹性静力法已经不能满足现代建筑结构的设计要求。
反应谱法能考虑结构的动力特性及其与地震作用之间的相互关系，但它不能给出结构地震反应的全过程，更无法给出各构件进入弹塑性变形阶段的内力和变形状态。
为了研究和计算高层建筑结构的弹塑性变形，有必要进行结构的弹塑性分析。
目前，结构的弹塑性分析主要分为弹塑性动力分析和弹塑性静力分析两大类[1] [2]。
1 现有弹塑性分析方法综述1.1 静力弹塑性分析方法静力弹塑性分析方法，即我们常说的Push-over法，主要用于进行变形验算，尤其是在大震下的抗倒塌验算。
它是结构地震相应分析的简化方法[3] [4] [5]。
Push-over法基本步骤大致如下[1]：（1）建立结构的计算模型、确定构件的相关参数以及要采用的恢复力模型。
（2）求出作用在结构上的竖向荷载并求出结构在竖向荷载作用下的内力，以便和水平荷载作用下的内力进行组合。
（3）根据结构的具体情况，确定对结构施加的水平荷载分布形式：倒三角或与第一振型等小的水平荷载模式。
水平荷载施加于各楼层的质心处，逐渐单调增加侧向力，以产生的那里跟善意不计算所得的内力叠加后，刚好使一个或者一批构件开列进入屈服状态为宜。
（4）对于上一步进入屈服的构件进行修改，形成一个“新”的结构，修改结构的刚度矩阵并求出“新”结构的自振周期，不断重复第3步直到结构的侧向位移达到预定的目标位移、或是结构变成为机构为止。
记录每一步的结构自振周期并累计每一步施加的荷载。
（5）将每一个不同的结构自振周期及其对应的水平力总量与结构自重（重力荷載代表值）的比值（地震影响系数）绘成曲线，也把相应场地的各条反应谱曲线绘在一起，以此来评估结构的抗震性能。
SAP2k第6章弹性及弹塑性时程分析
f r k d 1 r yield z
式中：k为弹性弹簧常数；yield为屈服力；r为指定的屈
服后刚度对弹性刚度的比值；z为一个内部的滞后变量，
此变量范围为|z|≤ 1，其屈服面由|z|= 1代表。。
其中exp 为等于或大于1 的指数。
此指数越大，屈服比率越陡。实际指
数限值大约是20。公式z‘ 等价于
Wen 模型A＝1 及α＝β＝0.5。
2.3 单元类型介绍——滞回（橡胶）隔震属性
双轴的滞后隔振器，对于两个剪切变形有耦合的塑性属性
，且对余下的4个变形有线性的有效刚度属性。 对 每 一 个
剪切变形自由度，用户可独立的指定线性或非线性的行为。
2.3 单元类型介绍——滞回（橡胶）隔震属性
●在每一曲线终点的斜率不能为负
2.3 单元类型介绍——多段线性塑性连接单元
用户定义多段线性曲线上的点时，对称的成对点将被
连接，即使是非对称的曲线。这样能够对滞回曲线的形状
进行一些控制。
2.3 单元类型介绍——多段线性塑性连接单元
Takeda模型
Takeda模型在卸载过程中，当通过水平轴时，卸载曲线
沿反向加载路径（Backbone Force Deformat ion ）
的切线方向。
2.3 单元类型介绍——多段线性塑性连接单元
枢纽点（Pivot）模型
这个模型与Takeda 塑性模型相似，但是具有一个附加
参数来控制退化滞回曲线。适用于钢筋混凝土单元，是基
于趋向于在力－变形（或弯矩－转动）平面内指定点、也
筏板基础等。
体单元
主要用于细部分析。
点单元
也称连接单元，可在两节点之间绘制，也可在一个节
MATLAB弹塑性时程分析法编程
MATLAB弹塑性时程分析法编程弹塑性时程分析是工程结构力学中的一种重要分析方法，用于评估结构在地震等动力荷载下的变形和应力分布。
MATLAB是一种非常强大的科学计算软件，具有丰富的工具箱和函数，可以方便地编写弹塑性时程分析的程序。
本文将介绍如何用MATLAB编程实现弹塑性时程分析。
1.弹塑性分析概述弹塑性分析是一种结构稳定性的计算方法，它考虑了结构的非线性行为，如塑性变形和残余应力。
弹塑性分析的基本思想是将结构划分为弹性和塑性两个部分，根据结构的实际受力情况，逐步计算结构的位移、应力和变形等参数。
2.弹塑性时程分析原理弹塑性时程分析是指以地震动作为输入，计算结构的时程响应。
其基本步骤是：首先，根据结构参数和地震动波特性，建立结构的动力模型。
然后，采用数值积分方法，按照时间步进逐步计算结构的位移、速度和加速度等参数，直到达到要求的计算时间。
在计算过程中，根据结构的非线性本构关系和塑性溃效准则，判断应力状态是否进入塑性阶段，并更新剩余强度等参数。
3.弹塑性时程分析MATLAB编程步骤(1)建立结构的动力模型首先，根据结构的几何形状和材料性质，使用MATLAB建立结构的节点和单元模型。
可以利用网格划分法或几何变换法进行离散化，以获得结构的节点和单元信息。
(2)定义地震动输入根据地震动加速度时程图，使用MATLAB定义地震动输入信号。
可以通过读取实测地震数据，或者使用地震动模拟软件产生地震动波进行模拟。
(3)定义结构的本构关系根据结构的材料性质和截面参数，使用MATLAB定义结构的本构关系。
可以根据结构的线性弹性或非线性塑性材料模型，采用协调变形法或增量处理法进行计算。
(4)制定计算控制策略根据结构的强度要求和计算时间，制定合理的计算控制策略。
这包括选择合适的时间步长和计算时程，以及考虑计算结果的误差控制和稳定性分析。
(5)编写弹塑性时程分析算法根据以上步骤，编写MATLAB程序来实现弹塑性时程分析。
弹塑性时程分析法
形关系式简述如下。
（1）正向或反向弹性阶段（01 段或 04 段）
此阶阶段有 U 0 ，U U y ；或U 0 ， U U y
初始条件为 U 0 0 ， P(U 0 ) 0 刚度降低系数为 1
故
P(Ui 1 )
k1Ui1 ，
k1
Py Uy
（4.1.2）
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
（4）正向硬化阶段卸载至零且第一次反向加载（34 段）
此阶段有U 0 ，U U 3
初始条件为U i U 3 ， P(U i ) P(U 3 ) 0
刚度降低系数为
(U 3
Py U
y
)k1
故P (U i 1 ) Nhomakorabea
U3
Py U
y
(U i 1
U3)
（4.1.5）
（5）反向硬化阶段加载（56 段）
p(x)
2
Qx
arctan
(2
x
)Qx
（3）正向硬化阶段卸载（23 段）
此阶段有U 0 ，U U 2
初始条件为U i U 2 ， P(U i ) P(U 2 ) 刚度降低系数为 1
故 P(U i1 ) P(U 2 ) k1 (U i1 U 2 )
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
11
§4 弹塑性时程分析法
刚度降低系数为
1
k2 k1
1
故 P(Ui1) Pc 1k1(Ui1 Uc )
（4.1.9）
《工程结构抗震与防灾》电子教案 东南大学 丁幼亮
16 （3）正向或反向硬化段（23 段或 67 段）
佳构STRAT软件大震弹塑性时程分析操作要点与技巧
佳构STRAT软件大震弹塑性时程分析操作要点与技巧(上海佳构软科技有限公司，2015/12)1、计算发散是计算不成功吗？大震模拟结构在强荷载下屈服、破坏。
当结构整体不足，或存在薄弱环节时，结构出现过大变形，是正常现象。
由于大震分析是数值模拟，与一般试验得到的想象毕竟有所不同。
数值分析的中的结构实效、破坏，往往表现为过大的变形。
薄弱环节导致的大震破坏，是数值分析的特点所致。
当局部构件出现大范围屈服，构件刚度趋于极小值。
在动力响应中，刚度极小的构件变形会放大、动力效应集中(类似高层中的辫梢效应、减震结构中的悬挂钟摆)。
这种局部的放大会导致相邻构件的破坏，并逐步扩散到整个结构，导致结构破坏，计算发散。
2、怎样根据分析结果，找到导致发散的“病灶”一旦计算发散，最终变形会是一个极大值(例如10e6)，图形已经混乱，无法找到破坏点。
这是可以将变形缩小(例如10e-6)。
然后，分步察看变形图。
找到开始发散的几步。
缩小图形的变形比例，会发现最初变形特别大的构件。
这些构件即是导致发散的病灶。
3、怎样增强薄弱构件1) 混凝土构件：增加配筋。
混凝土的抗震性能，主要来自于钢筋。
梁柱纵筋直接影响屈服承载力和屈服后的性能。
梁柱的箍筋，在考虑“约束混凝土”增强的时，能提高混凝土的屈服强度、和弹性模量。
2) 钢支撑：设二力杆，或不算自重。
高层中的钢支撑对抗震往往起关键作用(例如加强层)，支撑的应力比都很高，往往达到全截面屈服。
但如果存在弯矩，即便弯矩很小的情况下，都会导致截面应力分布不均匀，承载能力下降。
在反复荷载作用下，这种全截面屈服基础的上不均匀分布应力，各部分加卸载状态不同，刚度差异极大，往往导致破坏发散。
设二力杆是弯矩为0，全截面应力相同、状态相同，极大提高屈服后性能。
此外，STRA T软件中，二力杆仍包含自重的弯矩(实际情况就这样)，必要时支撑不算自重。
3) 剪力墙：a)避免狭长墙单元，适当合并节点。
b)增加配筋，不仅需要增加主要受力的暗柱钢筋，在有较大水平受力的部位还需要增加水平分布钢筋。
ABAQUS弹塑性时程分析报告
目录1 工程概况 (1)1.1工程与模型概况 (1)1.2进行罕遇地震弹塑性时程分析的目的 (1)2分析方法及采用的计算软件 (2)2.1分析方法 (2)2.2分析软件 (2)2.3分析步骤 (2)2.4结构阻尼选取 (3)3 结构抗震性能评价指标 (4)3.1结构的总体变形 (4)3.2构件性能评估指标 (4)5 罕遇地震弹塑性动力时程分析结果 (5)5.1地震波选取 (5)5.2各地震波组分析结果汇总 (6)5.2.1基底剪力 (6)5.2.2层间位移角 (7)5.2.3 结构顶点水平位移 (9)5.2.5 结构弹塑性整体计算指标评价 (10)6构件性能分析 (11)6.1钢管混凝土柱 (11)6.2主要剪力墙 (12)6.2.1 底部剪力墙 (13)6.2.2加强层 (13)6.2.3其他楼层 (14)6.3连梁 (15)6.4斜撑 (16)6.5钢梁的塑性应变 (17)7 罕遇地震作用下结构性能评价 (19)1 工程概况1.1 工程与模型概况（a ）三位模型 （b ）加强层结构布置图1.1 ABAQUS 计算模型1.2 进行罕遇地震弹塑性时程分析的目的对此工程进行罕遇地震作用下的弹塑性时程分析，以期达到以下目的： （1）评价结构在罕遇地震作用下的弹塑性行为，根据主要构件的塑性损伤和整体变形情况，确定结构是否满足“大震不倒”的设防水准要求；（2）研究结构在大震作用下的基底剪力、剪重比、顶点位移、层间位移角等综合指标，评价结构在大震作用下的力学性能；（3）检验混凝土墙肢在大震下的损伤情况，钢筋是否屈服； （4）检验钢管混凝土及钢结构构件在大震下的塑性情况； （5）研究防屈曲支撑的塑性变形情况；（6）根据以上分析结果，针对结构薄弱部位和薄弱构件提出相应的加强措施，以指导结构设计。
2分析方法及采用的计算软件2.1 分析方法目前常用的弹塑性分析方法从分析理论上分有静力弹塑性（pushover ）和动力弹塑性两类，从数值积分方法上分有隐式积分和显式积分两类。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 弹塑性时程分析法概述
高层建筑结构采用时程分析法可以达到以下目的： 能够比较好地描述出结构物在地震时实际的受力和变形状态，能够比 较真实的揭露出结构中的薄弱环节，以便有效地改进结构的抗震设计 其计算结果是对振型分解反应谱法的补充，即根据差异的大小和实际 可能，对反应谱法计算结果，按照总剪力判断、位移判断，以结构层 间剪力和层间变形为主要控制指标，加以比较、分析，适当调整反应 谱的计算结果，从而取得较为合理的抗震安全度和经济效果； 能够对已有的重要建筑物做出正确的抗震能力效评，从而从理论上指 导现有结构的抗震加固工作； 可以用空间的弹塑性时程分析作为平面的弹塑性时程分析以及弹性时 程分析等各种简化计算方法的比较标准。
g jS 1 g j
4 f j 1 3 g i S D 4 g j 1 3 f i S D
4 g i 1 3 g j S D
4 pi p j pi p j 3 其中, 当i、j端屈服时, p j f j ;当i、j端极限时, pi gi , p j g j
结构抗震分析与设计
主讲：李彬
1
主要内容
1 弹塑性时程分析法概述 2 结构的振动计算模型 3 结构的弹塑性本构模型 4 结构振动模型的刚度矩阵、质量矩阵和阻尼矩阵
5 对选用地震波的要求
6 结构动力平衡方程的求解方法
1 弹塑性时程分析法概述
时程分析法：从建筑结构的基本运动方程出发，直接输入
2 结构的振动计算模型
状态 两端弹性 i端屈服，j端弹性 i端弹性，j端屈服 两端屈服 i端极限，j端弹性 i端弹性，j端极限 i端极限，j端屈服 i端屈服，j端极限 两端极限
D 1
ka
kb
1 S 2
kc
S
3 4 f i S 41 f i
4 f i 1 3 f j S D gi S 1 gi
量的表示，杆非线性刚度方程为
M i k a M j kb kb kc
e
i j
2 结构的振动计算模型
单分量模型
吉伯森单分量模型
杆元在弹性范围内服从线弹性规律，仍用一根弹性杆表示 原杆件特性；杆件超出弹性范围后，在杆两端各设置一个
2 gi g j S D 3
4 g j 1 3 gi S D
2 结构的振动计算模型
双分量模型
克拉夫双分量模型用两根平行的杆代表双分量模型的工作 状态，其中一根分杆是弹性杆，另外一根分杆是“塑性” 杆。
弹性杆表示杆件的弹性变形性质，在任何情况下都保持刚 度ps。ps是原整体杆的端截面双线型恢复力模型的第二 刚度斜率，P以百分数表示，s为原整体杆件弹性阶段的刚 度斜率。
变形阶段）这一类模型时，杆可有以下4种状态：i端和j 端均线性；i端非线性，j端线性；i端线性，j端非线性；i 端和j端均非线性。每种状态都可求出相应的杆的单元刚 度系数。
2 结构的振动计算模型
四种状态
i端和j端均线性
ka
S
fi S 1 fi
kb
1 S 2
kc
S
i端非线性，j端线性
1 fi S 2 1 fi
2 结构的振动计算模型
简化为计算简图的原则：
要反映实际结构的主要力学性能；
要便于计算。 目前主要采用四种振动计算模型：总体模型、层模型、杆
系模型以及杆系-层模型。
2 结构的振动计算模型
总体模型
总体模型直接将整个结构等效化为具有很少几个自由度的 力学体系，而且通常简化为只有一个侧移自由度的体系。
3 4 f i S 41 f i
f jS 1 f j
4 f j 1 3 f i S D
i端线性，j端非线性
3 4 f i S 41 f i
4 f i 1 3 f j S D
2 结构的振动计算模型
1 弹性杆，其端弯矩增量 与转角增量的关系为： mie ps i j 2
塑性杆，其端弯矩增量 与转角增量的关系为： 1 m ip qs i' 'j q 1 p 2 i' i ai
2 结构的振动计算模型
杆系模型
该模型是以梁柱等杆件作为基本单元模型，杆系模型又称 为杆系计算简图。将高层建筑结构视为杆件体系，结构的 质量集中于各节点，动力自由度数等于结构节点位移自由 度数。而杆系模型按照弹塑性杆件采用的本构关系不同方 式分为集中塑性模型和杆件分段变刚度模型。
2 结构的振动计算模型
s
1 1 q1 s 4
ps ps
3 1 g s 4 4
ps
gs
3 1 g s 4 4
gs
1 弹塑性时程分析法概述
弹塑性时程分析法因考虑材料的非线性，是非线性振动问
题，叠加原理已不能适用，故不能采用振型分析法。常用 的方法是将地面运动时间分割成许多微小的时段，相隔∆t ，然后在每个时间间隔∆t内把结构体系当作线性体系来计 算，逐步求出体系在各时刻的反应。
M x C x K x M 1 x g K t t K t C t t C t
层模型
该模型以一个楼层为基本单元，用每层的刚度表示结构的 刚度，也称为层间模型。
串联多质点体系：将整个结构合并为一根竖杆，并将全部
建筑质量就近分别集中于各层楼盖处作为一个质点，考虑 两个方向的水平振动。
串联多刚片体系：对质量与刚度明显不对称、不均匀的结 构，应考虑双向水平振动和露面扭转的影响。此时，楼面 除了有质量mi外，还有转动惯量Ii对振动产生的影响。
原整体梁端弯矩增量为 ：Mi mie mip
2 结构的振动计算模型
四种状态 i端和j端均线性
ka
kb
1 s 2
1 ps 2
kc
s
ps
q 1 s 4
s
q 1 s 4
i端非线性，j端线性
i端线性，j端非线性
1 ps 2
ps ps
i端和j端均非线性
对应于建筑物场地的若干条实际地震及速度记录或人工模 拟的加速度时程曲线，通过积分运算求得在地面加速度随 时间变化期间内结构的各种反应值，这种计算方法称为结 构的时程分析法，亦称直接动力法、数值积分法。
M x C x K x M 1 x g
1 f jS 2 1 f j
2 f f S i j D 3
i端和j端均非线性
其中： D 1
4 fi f j fi f j 3
2 结构的振动计算模型
扩展的吉伯森单分量模型
扩展的吉伯森单分量模型是在杆件恢复力模型中考虑了材 料的极限状态及极限状态之后的下降段。因此杆端弯矩M 与转角θ 关系如下图所示。
xn
Sn
T
T
2 结构的振动计算模型
剪弯型层模型
高层建筑结构中的剪力墙结构、框架-剪力墙结构和“强 柱弱梁”的框架结构，即横梁与柱的线刚度比较小的框架 结构，它们的变形都包含有弯曲和剪切两种成分。这时楼 层的转角变形将是变形的主要成分，不可忽略，因此各层 的层间位移不仅与本层的刚度有关，而且与相邻的刚度都 有关系。
集中塑性模型
集中塑性模型将一个杆件的非线性变形集中于杆件的若干 特殊部位，而弹性变形则分布于整个构件。这种广义本构 关系为杆件的杆端力与杆件集中塑性变形的关系。该模型 又有单分量、双分量、三分量及多弹簧模型四类。
假设非弹性变形集中在杆两端出现，即所谓杆端塑性铰， 塑性铰的几何长度为零。杆端弯矩与杆端转角关系若以增
等效弹簧用以反映杆端的弹塑性变形特性。
2 结构的振动计算模型
在杆本身转动刚度为常数的情况下，端弯矩与转角的关系 可以用增量表示为：
' 1 ' M i Sij i j 2 i' i ai
2 结构的振动计算模型
当杆端截面恢复力模型采用双线型（具有线性和屈服两个
耦合对结构反应的显著影响，而目前尚缺乏一个简单、实 用的多维恢复力模型。
1 弹塑性时程分析法概述
对结构进行弹塑性时程分析时，需要解决以下几个问题：
确定结构的振动模型；
结构和构件的恢复力模型； 关于质量矩阵和阻尼矩阵；
结构振动方程的建立；
输入地震波的选择； 振动方程的积分方法； 编制电子计算机计算程序。
1 弹塑性时程分析法概述
弹性时程分析法：在第一阶段抗震计算中，建筑抗震设计
规范规定了用时程分析法进行补充计算，这时的计算所采 用的刚度矩阵[K]和阻尼矩阵[C]保持不变。 弹塑性时程分析法：在第二阶段抗震计算中，建筑抗震规 范规定采用时程分析法进行弹塑性变形计算，这时结构的 刚度矩阵[K]及阻尼矩阵[C]随结构及其构件所处的变形状 态，在不同时刻可能取不同的数值，称为弹塑性时程分析 。弹塑性时程分析法是第二阶段抗震计算时估算结构薄弱 层弹塑性层间变形的最基本的方法。
fi S 1 fi
1 fi S 2 1 fi
1 fi S 2 1 fi
3 4 f i S 41 f i
4 f j 1 3 f i S D
S
4 g i 1 3 f j S D 4 f i 1 3 g j S D
2 结构的振动计算模型
2 结构的振动计算模型
剪切型层模型
高层建筑结构中，特别是其横梁与柱的线刚度比比较大时 ，即“强梁弱柱”型的框架结构，结构的振动变形是剪切 型的，即横梁只产生平移而没有转动，并且各层层间位移 只与各层的刚度有关。