高二数学教案9.9棱柱和棱锥(二)
北师大版必修2《棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积》教案及教学反思

北师大版必修2《棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积》教案及教学反思一、教学目标1.理解棱柱、棱锥、棱台和圆柱、圆锥、圆台的概念。
2.学会利用公式计算棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积。
3.通过解题,巩固和灵活运用所学的知识。
4.培养学生的观察能力和解决问题的能力。
二、教学重难点(一) 教学重点1.理解棱柱、棱锥、棱台和圆柱、圆锥、圆台的概念。
2.学会利用公式计算棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积。
(二) 教学难点1.针对不同形状的物体,计算的公式和方法不同,学生需要通过实例练习掌握。
2.学生容易混淆“棱”和“边”这两个概念,需要严格区分并反复讲解。
三、教学过程(一) 导入环节老师可以通过举实际生活中的例子,帮助学生理解体积的概念。
例如蓝牙音箱、水杯、书、盒子等都是物体,都有一定的体积。
然后,引入本节课的主题——棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积。
(二) 讲解和练习1.棱柱的体积棱柱的体积公式为 V = Bh,其中B为底面积,h为高。
老师可以通过教材上的实例和板书,讲解棱柱的定义和计算公式。
然后,让学生在课堂上通过实例进行练习,巩固所学内容。
2.棱锥的体积棱锥的体积公式为 V = 1/3Bh,其中B为底面积,h为高。
同样,老师可以通过实例和板书讲解棱锥的定义和计算公式,并让学生进行练习。
3.棱台的体积棱台的体积公式为 V = 1/3h(R2+r2+Rr),其中h为高,R和r分别为上底和下底的半径。
老师同样可以通过实例和板书讲解棱台的定义和计算公式,并让学生进行练习。
4.圆柱的体积圆柱的体积公式为V = πr^2h,其中r为半径,h为高。
老师可以通过实例和板书讲解圆柱的定义和计算公式,并让学生进行练习。
5.圆锥的体积圆锥的体积公式为V = 1/3πr^2h,其中r为半径,h为高。
老师同样可以通过实例和板书讲解圆锥的定义和计算公式,并让学生进行练习。
6.圆台的体积圆台的体积公式为 V =1/3πh(R2+r2+Rr),其中h为高,R和r分别为上底和下底的半径。
《棱柱、棱锥和棱台》示范课教案【高中数学】
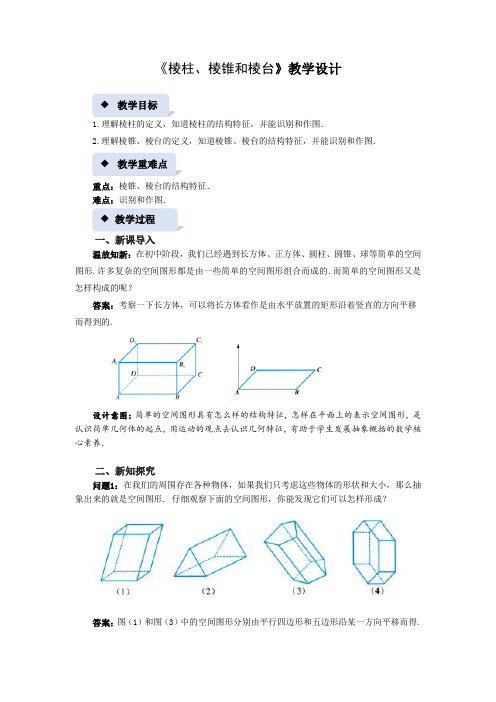
《棱柱、棱锥和棱台》教学设计1.理解棱柱的定义,知道棱柱的结构特征,并能识别和作图.2.理解棱锥、棱台的定义,知道棱锥、棱台的结构特征,并能识别和作图.重点:棱锥、棱台的结构特征.难点:识别和作图.一、新课导入温故知新:在初中阶段,我们已经遇到长方体、正方体、圆柱、圆锥、球等简单的空间图形.许多复杂的空间图形都是由一些简单的空间图形组合而成的.而简单的空间图形又是怎样构成的呢?答案:考察一下长方体,可以将长方体看作是由水平放置的矩形沿着竖直的方向平移而得到的.设计意图:简单的空间图形具有怎么样的结构特征,怎样在平面上的表示空间图形,是认识简单几何体的起点,用运动的观点去认识几何特征,有助于学生发展抽象概括的数学核心素养.二、新知探究问题1:在我们的周围存在各种物体,如果我们只考虑这些物体的形状和大小,那么抽象出来的就是空间图形.仔细观察下面的空间图形,你能发现它们可以怎样形成?答案:图(1)和图(3)中的空间图形分别由平行四边形和五边形沿某一方向平移而得.◆教学目标◆教学重难点◆教学过程◆追问1:图(2)和图(4)中的空间图形分别由怎么样的图形沿什么方向平移而得?答案:图(2)和图(4)中的空间图形分别由三角形和六边形平移而得.总结:一般地,由一个平面多边形沿某一方向平移形成的空间图形叫作棱柱(prism).平移起止位置的两个面叫作棱柱的底面,多边形的边平移所形成的面叫作棱柱的侧面.(1)(2)追问2:该怎么命名棱柱呢?答:底面为三角形、四边形、五边形……的棱柱分别称为三棱柱、四棱柱、五棱柱……例如,图(1)为三棱柱,图(2)为六棱柱,并分别记作棱柱ABC−A′B′C′、棱柱ABCDEF−A′B′C′D′E′F′.追问3:根据棱柱形成的过程,我们可以看出棱柱具有什么特点?答:(1)两个底面是全等的多边形,且对应边互相平行;(2)侧面都是平行四边形.设计意图:将一个图形上所有的点按某一确定的方向及相同距离移动就是平移,用运动的观点看静态的几何,发展学生的抽象概括的学科核心素养.问题2:与图对比,下面的空间图形是由上图发生什么样变化得到的?答:通过观察对比发现,当上图中各棱柱的一个底面收缩为一个点时,就可得到下图.当棱柱的一个底面收缩为一个点时,得到的空间图形叫作棱锥注意:棱锥中常见名称的含义追问1:该怎么命名棱锥呢?答:底面为三角形、四边形、五边形……的棱锥分别称为三棱锥、四棱柱、五棱锥……上图中的四棱柱可记作棱锥S−ABCD.追问2:根据棱锥形成的过程,我们可以看出棱锥具有什么特点?答:(1)底面是多边形;(2)侧面是有公共点的三角形.追问3:用一个平行于棱锥底面的平面去截棱锥,会形成什么空间图形呢?答:如图,用一个平行于棱锥底面的平面去截棱锥,截面和底面间形成的部分叫做棱台.设计意图:面动成体,用运动的观点看几何体,发展学生的空间想象能力.三、应用举例例1:画一个四棱柱.解:如图,画四棱柱可分三步完成:第一步画上底面——画一个四边形;第二步画侧棱——从四边形的每一个顶点画平行且相等的线段;第三步画下底面——顺次连接这些线段的另一个端点.例2:画一个三棱台.解:首先画一个三棱锥,在它的一条侧棱上取一点,然后从这点开始,顺次在各个侧面内画出与底面对应边平行的线段,最后将多余的线段擦去.四、课堂练习1.下面的几何体中是棱柱的有________.(填序号)2.下列说法正确的有________.(填序号)①棱锥的侧面为三角形,且所有侧面都有一个公共点;②棱台的侧面有的是平行四边形,有的是梯形;③棱台的侧棱所在直线均相交于同一点.参考答案:1.棱柱有三个特征:(1)有两个面相互平行.(2)其余各面是平行四边形.(3)侧棱相互平行.本题所给几何体中⑥⑦不符合棱柱的三个特征,而①②③④⑤都符合.2.棱锥是由棱柱的一个底面收缩为一个点而得到的几何体,因而其侧面均是三角形,且所有侧面都有一个公共点,故①对.棱台是棱锥被平行于底面的平面所截后,截面与底面之间的部分,因而其侧面均是梯形,且所有的侧棱延长后均相交于一点(即原棱锥的顶点),故②错,③对.因而正确的有①③.五、课堂小结在运动变化的观点下,棱柱、棱锥、棱台之间的关系可以用下图表示出来六、布置作业教材第144页练习第1、3、4题.。
新教材2023版高中数学北师大版必修第二册:棱柱棱锥和棱台课件

上底面:原棱锥的___截__面___; 下底面:原棱锥的_底__面_____.
侧面:其余各面 侧棱:相邻两个侧面的公共 边. 高:上底面、下底面之间的距 离. 斜高:正棱台各侧面都是
__全__等____的等腰梯形,这些等
腰梯形的高都相等.
状元随笔 对于多面体概念的理解,注意以下两个方面
(1)多面体是由平面多边形围成的.围成一个多面体至少要四个 面.一个多A、B 均为真命题;对于 C,一个图形要成为空间几何体,则 它至少需有 4 个顶点,3 个顶点只能构成平面图形,当有 4 个顶点时,可 围成 4 个面,所以一个多面体至少应有 4 个面,而且这样的面必是三角形, 故 C 也是真命题;对于 D,只有当截面与底面平行时才对.
答案:ABC
2.下列命题中正确的是________(填序号). ①有两个面平行,其余各面都是四边形的几何体叫棱柱; ②棱柱的一对互相平行的平面均可看作底面; ③三棱锥的任何一个面都可看作底面; ④棱台各侧棱的延长线交于一点.
高:过上底面上一点 O1 作下
底面的垂线,这点和垂足 O
间的距离__O__O_1___.
棱锥
有一个面是多__边__形___, 其余各面都是有一个 公共顶点的 __三__角__形__,由这些面 所围成的几何体叫作 棱锥. 正棱锥:底面是 _正_多__边__形__,且它的顶 点过底面___中__心___且 与底面垂直的直线 上.
解析:对于①,还可能是棱台;对于②,只要看一个正六棱柱模型即 知是错的;对于③,显然是正确的;④显然符合定义.故填③④.
把平行四边形的锐角画成__4_5_°____,横边长画成邻边长的 ___两__倍___.为了增强立体感,把被遮挡部分画成__虚__线____ 或__不__画____. (1)一个希腊字母:如 α,β,γ 等; (2)两个大写英文字母:表示平面的平行四边形的相对的两 个顶点; (3)四个大写英文字母:表示平面的平行四边形的四个顶点
【新教材精创】8.3.1 棱柱、棱锥、棱台的表面积和体积 教学设计(2)-人教A版高中数学必修第二册

【新教材】8.3.1棱柱、棱锥、棱台的表面积和体积教学设计(人教A版)本节是在学生已从棱柱、棱锥、棱台的结构特征和直观图两个方面认识了多面体的基础上,进一步从度量的角度认识棱柱、棱锥、棱台,主要包括表面积和体积.课程目标1.通过对棱柱、棱锥、棱台的研究,掌握棱柱、棱锥、棱台的表面积和体积计算公式.2.能运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.数学学科素养1.数学抽象:棱柱、棱锥、棱台的体积公式;2.数学运算:求多面体或多面体组合体的表面积和体积;3.数学建模:数形结合,运用棱柱、棱锥、棱台的表面积和体积公式进行计算和解决有关实际问题.重点:掌握棱柱、棱锥、棱台的表面积和体积计算公式和应用;难点:棱台的体积公式的理解.教学方法:以学生为主体,小组为单位,采用诱思探究式教学,精讲多练。
教学工具:多媒体。
一、情景导入在过去的学习中,我们已经接触过一些几何体的面积和体积的求法及公式,哪些几何体可以求出表面积和体积?要求:让学生自由发言,教师不做判断。
而是引导学生进一步观察.研探.二、预习课本,引入新课阅读课本114-115页,思考并完成以下问题1.怎么求柱体、锥体、棱台的表面积?2.柱体、锥体、棱台体的体积公式是什么?要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
三、新知探究(一)棱柱、棱锥、棱台的表面积1.棱柱、棱锥、棱台的表面积棱柱、棱锥、棱台都是由多个平面图形围成的多面体,因此它们的表面积等于各个面的面积之和,也就是展开图的面积.(二) 棱柱、棱锥、棱台的表面积1.棱柱:柱体的底面面积为S ,高为h ,则V =Sh .2.棱锥:锥体的底面面积为S ,高为h ,则V =13Sh . 3.棱台:台体的上、下底面面积分别为S′、S ,高为h ,则V =13(S ′+S ′S +S )h . 四、典例分析、举一反三题型一 棱柱、棱锥、棱台的表面积例1 已知如图,四面体S ABC -的棱长均为a ,求它的表面积.2【解析】因为四面体S -ABC 的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面面积的4倍.不妨求△SBC 的面积,过点S 作SD ⊥BC ,交BC 于点D ,如图所示.因为BC =SB =a ,SD 2a ==,所以S △SBC =12BC ·SD =12a 2.故四面体S -ABC 的表面积S =22. 解题技巧(求多面体表面积注意事项)1.多面体的表面积转化为各面面积之和.2.解决有关棱台的问题时,常用两种解题思路:一是把基本量转化到梯形中去解决;二是把棱台还原成棱锥,利用棱锥的有关知识来解决.跟踪训练一1、如图所示,有一滚筒是正六棱柱形(底面是正六边形,每个侧面都是矩形),两端是封闭的,筒高1.6 m ,底面外接圆的半径是0.46 m ,问:制造这个滚筒需要________m 2铁板(精确到0.1 m 2).【答案】5.6【解析】因为此正六棱柱底面外接圆的半径为0.46 m ,所以底面正六边形的边长是0.46 m.所以S 侧=ch =6×0.46×1.6=4.416 (m 2).所以S 表=S 侧+S 上底+S 下底=4.416+2×34×0.462×6≈5.6 (m 2). 故制造这个滚筒约需要5.6 m 2铁板.题型二 棱柱、棱锥、棱台的体积例2如图所示,正方体ABCD -A 1B 1C 1D 1的棱长为1,E 为线段B 1C 上的一点,则三棱锥A -DED 1的体积为________.【答案】16. 【解析】 V 三棱锥A -DED 1=V 三棱锥E -DD 1A =13×12×1×1×1=16. 例3 如图,一个漏斗的上面部分是一个长方体,下面部分是一个四棱锥,两部分的高都是0.5m ,公共面ABCD 是边长为1m 的正方形,那么这个漏斗的容积是多少立方米(精确到30.01m )?【答案】30.67m【解析】由题意知长方体''''ABCD A B C D -的体积110.5V =⨯⨯()30.5m=, 棱锥''''P A B C D -的体积1110.53V =⨯⨯⨯()316m =, 所以这个漏斗的容积112263V =+=()30.67m ≈. 解题技巧(求棱柱、棱锥、棱台体积的注意事项) 1.常见的求几何体体积的方法①公式法:直接代入公式求解.②等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.③分割法:将几何体分割成易求解的几部分,分别求体积.2.求几何体体积时需注意的问题柱、锥、台的体积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.跟踪训练二1、在正三棱柱ABC -A 1B 1C 1中,D 为棱AA 1的中点,若△BC 1D 是面积为6的直角三角形,则此三棱柱的体积为________;【答案】8 3.【解析】由题意,设AC =a (a >0),CC 1=b (b >0),则BD =C 1D =a 2+b 24,BC 1=a 2+b 2,由△BC 1D 是面积为6的直角三角形,得⎝⎛⎭⎫a 2+14b 2×2=a 2+b 2,得b 2=2a 2,又12×32a 2=6,∴a 2=8,∴b 2=16,即b =4.∵S △ABC =34a 2,∴V =34×8×4=8 3. 2、 如图,在多面体ABCDEF 中,已知面ABCD 是边长为4的正方形,EF ∥AB ,EF =2,EF 上任意一点到平面ABCD 的距离均为3,求该多面体的体积.【答案】见解析【解析】如图,连接EB ,EC .四棱锥E-ABCD的体积V四棱锥E-ABCD=13×42×3=16.∵AB=2EF,EF∥AB,∴S△EAB=2S△BEF.∴V三棱锥F-EBC=V三棱锥C-EFB=12V三棱锥C-ABE=12V三棱锥E-ABC=12×12V四棱锥E-ABCD=4.∴多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=16+4=20.五、课堂小结让学生总结本节课所学主要知识及解题技巧六、板书设计七、作业课本116页练习,119页习题8.3的1、6题.本节课的重点是掌握棱柱、棱锥、棱台的表面积和体积计算公式和应用,通过本节课的例题及练习,学生基本掌握.而本节课的难点可以通过三组体积公式对比,寻找其联系(棱台上底面和下底面面积一样时,图形变成棱柱,对应的公式,经推导也就变成棱柱的体积公式了; 棱台上底面无限缩小至点时,图形变成棱锥,对应的公式,经推导也就变成棱锥的体积公式了.)使学生对其更加理解.再有解决实际问题时可先抽象出几何图形,再利用相关公式解决.。
高中数学讲义(人教A版必修二):第21讲 棱柱、棱锥、棱台(教师版)

第21课棱柱、棱锥、棱台课程标准课标解读1.通过对实物模型的观察,归纳认知棱柱、棱锥、棱台的结构特征.2.理解棱柱、棱锥、棱台之间的关系.3.能运用棱柱、棱锥、棱台的结构特征描述现实生活中简单几何体的结构并进行有关计算.1.通过对实物模型的观察,归纳认知棱柱、棱锥、棱台的结构特征.2.理解棱柱、棱锥、棱台之间的关系.学会用连续变化的观点,或者函数的思想找到他们之间的区别与联系.3.在熟悉基本知识的基础上,能运用棱柱、棱锥、棱台的结构特征描述现实生活中简单几何体的结构并进行有关计算,提升数学抽象和数学运算能力.知识精讲知识点01空间几何体、多面体、旋转体的定义1.空间几何体:如果我们只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.2.多面体、旋转体类别多面体旋转体定义由若干个平面多边形围成的几何体一条平面曲线(包括直线)绕它所在平面内的一条定直线旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何体叫做旋转体图形相关概念面:围成多面体的各个多边形;棱:相邻两个面的公共边顶点:棱与棱的公共点轴:形成旋转体所绕的定直线【即学即练1】有两个面平行的多面体不可能是()A .棱柱B .棱锥C .棱台D .以上都错答案B解析由棱锥的结构特征可得.知识点02棱柱的结构特征1.棱柱的结构特征棱柱图形及表示定义:有两个面互相平行,其余各面都是四边形,并且相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱如图可记作:棱柱ABCDEF —A ′B ′C ′D ′E ′F ′相关概念:底面(底):两个互相平行的面;侧面:其余各面;侧棱:相邻侧面的公共边;顶点:侧面与底面的公共顶点分类:按底面多边形的边数分:三棱柱、四棱柱、五棱柱……2.几个特殊的棱柱(1)直棱柱:侧棱垂直于底面的棱柱叫做直棱柱(如图①③);(2)斜棱柱:侧棱不垂直于底面的棱柱叫做斜棱柱(如图②④);(3)正棱柱:底面是正多边形的直棱柱叫做正棱柱(如图③);(4)平行六面体:底面是平行四边形的四棱柱也叫做平行六面体(如图④).反思感悟棱柱结构的辨析方法(1)扣定义:判定一个几何体是不是棱柱的关键是棱柱的定义.①看“面”,即观察这个多面体是否有两个互相平行的面,其余各面都是四边形;②看“线”,即观察每相邻两个四边形的公共边是否平行.(2)举反例:通过举反例,如与常见几何体或实物模型、图片等不吻合,给予排除.【即学即练2】下列关于棱柱的说法:①所有的面都是平行四边形;②每一个面都不会是三角形;③两底面平行,并且各侧棱也平行;④被平面截成的两部分可以都是棱柱.其中正确的说法的序号是________.答案③④解析①错误,棱柱的底面不一定是平行四边形.②错误,棱柱的底面可以是三角形.③正确,由棱柱的定义易知.④正确,棱柱可以被平行于底面的平面截成两个棱柱.所以说法正确的序号是③④.知识点03棱锥的结构特征棱锥图形及表示定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥如图可记作:棱锥S —ABCD相关概念:底面(底):多边形面;侧面:有公共顶点的各个三角形面;侧棱:相邻侧面的公共边;顶点:各侧面的公共顶点分类:(1)按底面多边形的边数分:三棱锥、四棱锥……,其中三棱锥又叫四面体;(2)底面是正多边形,并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥【即学即练3】(多选)下列说法中,正确的是()A .棱锥的各个侧面都是三角形B .四面体的任何一个面都可以作为棱锥的底面C .棱锥的侧棱平行D .有一个面是多边形,其余各面是三角形的几何体是棱锥答案AB解析由棱锥的定义,知棱锥的各个侧面都是三角形,故A 正确;四面体就是由四个三角形所围成的几何体,因此四面体的任何一个面都可以作为三棱锥的底面,故B 正确;棱锥的侧棱交于一点,不平行,故C 错.棱锥的侧面是有一个公共顶点的三角形,故D 错.知识点04棱台的结构特征棱台图形及表示定义:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台如图可记作:棱台ABCD —A ′B ′C ′D ′相关概念:上底面:平行于棱锥底面的截面;下底面:原棱锥的底面;侧面:其余各面;侧棱:相邻侧面的公共边;顶点:侧面与上(下)底面的公共顶点分类:由三棱锥、四棱锥、五棱锥……截得的棱台分别叫做三棱台、四棱台、五棱台……【即学即练4】(多选)下列说法错误的是()A .有一个面是多边形,其余各面都是三角形,由这些面围成的多面体是棱锥B .有两个面平行且相似,其余各面都是梯形的多面体是棱台C .如果一个棱锥的各个侧面都是等边三角形,那么这个棱锥可能为六棱锥D .如果一个棱柱的所有面都是长方形,那么这个棱柱是长方体答案ABC解析有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥,即其余各面的三角形必须有公共的顶点,故A 错误;棱台是由棱锥被平行于棱锥底面的平面所截而得的,而有两个面平行且相似,其余各面都是梯形的多面体有可能不是棱台,因为它的侧棱长延长后不一定交于一点,故B 错误;当棱锥的各个侧面的共顶点的角之和是360°时,各侧面构成平面图形,故这个棱锥不可能为六棱锥,故C错误;若每个侧面都是长方形,则说明侧棱与底面垂直,又底面也是长方形,符合长方体的定义,故D正确.能力拓展考法01棱柱的结构特征【典例1】如图所示,长方体ABCD-A1B1C1D1,M,N分别为棱A1B1,C1D1的中点.①这个长方体是棱柱吗?如果是,是几棱柱?为什么?②用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.解①是棱柱,并且是四棱柱,因为以长方体相对的两个面作底面,是互相平行的,其余各面都是矩形,且四条侧棱互相平行,符合棱柱的定义.②截面BCNM右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱柱ABMA1-DCND1.【变式训练】下列命题中正确的是()A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.棱柱中互相平行的两个面叫棱柱的底面C.棱柱的侧面都是平行四边形,而底面不是平行四边形D.棱柱的侧棱都相等,侧面是平行四边形答案D考法02棱锥、棱台的结构特征【典例2】有下列四种叙述:①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②两个面平行且相似,其余各面都是梯形的多面体是棱台;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台;④棱台的侧棱延长后必交于一点.其中正确的有()A.0个B.1个C.2个D.3个答案B解析①中的平面不一定平行于底面,故①错;由棱台的定义知,④正确;②③可用反例去检验,如图所示,侧棱延长线不能相交于一点,故②③错.反思感悟判断棱锥、棱台的方法(1)举反例法结合棱锥、棱台的定义举反例直接排除关于棱锥、棱台结构特征的某些不正确说法.(2)直接法棱锥棱台定底面只有一个面是多边形,此面即为底面两个互相平行的面,即为底面看侧棱相交于一点延长后相交于一点【变式训练】下列关于棱锥、棱台的说法:①棱台的侧面一定不会是平行四边形;②由四个平面围成的封闭图形只能是三棱锥;③棱锥被平面截成的两部分不可能都是棱锥.其中正确说法的序号是________.答案①②解析①正确,棱台的侧面一定是梯形,而不是平行四边形;②正确,由四个平面围成的封闭图形是四面体也就是三棱锥;③错误,如图所示的四棱锥被平面截成的两部分都是棱锥.分层提分题组A基础过关练一、单选题1.下列命题:①有两个面平行,其他各面都是平行四边形的几何体叫做棱柱;②有两侧面与底面垂直的棱柱是直棱柱;③过斜棱柱的侧棱作棱柱的截面,所得图形不可能是矩形;④所有侧面都是全等的矩形的四棱柱一定是正四棱柱.其中正确命题的个数为()A.0B.1C.2D.3【答案】A【详解】①如图1,满足有两个面平行,其他各面都是平行四边形,显然不是棱柱,故①错误;ABB A与底面垂直,但不是直棱柱,②错误;②如图2,满足两侧面11③如图3,四边形11即过斜棱柱的侧棱作棱柱的截面,所得图形可能是矩形,③错误;④所有侧面都是全等的矩形的四棱柱不一定是正四棱柱,因为两底面不一定是正方形,④错误.故选:A2.一个棱锥所有的棱长都相等,则该棱锥一定不是()A.正三棱锥B.正四棱锥C.正五棱锥D.正六棱锥【答案】D【详解】因为正六变形的中心到底面顶点的距离等于边长,所以正六棱锥的侧棱必大于底面棱长,故选:D.3.如图是一个正方体的表面展开图,则图中“0”在正方体中所在的面的对面上的是()A.2B.1C.高D.考【答案】C【详解】解:将展开图还原成正方体可知,“0”在正方体中所在的面的对面上的是“高”,故选:C.4.某四棱锥的三视图如图所示,该四棱锥的最长棱的长度为()A.2B.C D.45.如图所示的几何体的结构特征是()A.一个棱柱中截去一个棱柱B.一个棱柱中截去一个圆柱C.一个棱柱中截去一个棱锥D.一个棱柱中截去一个棱台【答案】C【详解】图中的几何体为一个棱柱截去一个角,截去的角是一个棱锥.故选C.6.棱台不具备的特点是()A.两底面相似B.侧面都是梯形C.侧棱长都相等D.侧棱延长后都交于一点【答案】C【详解】根据棱台的定义知,棱台底面相似,侧面都是梯形,侧棱延长后都交于一点,但是侧棱长不一定相等,故选:C7.下列判断正确的是()A.正三棱锥一定是正四面体B.底面是正方形的四棱锥是正四棱锥C.底面是正方形的直四棱柱是正四棱柱D.底面是正方形的棱台是正四棱台【答案】C【详解】正三棱锥不一定是正四面体,侧棱长与底面边长可能不相等,故A错误;底面是正方形的四棱锥不一定是正四棱锥,顶点在底面的射影不一定是底面的中心,故B错误;由正四棱住的概念可知,底面是正方形的直四棱柱是正四棱柱,故C正确;底面是正方形的棱台不一定是正四棱台,原因是棱台的侧棱延长后的交点在两底面的射影不一定为正方形的中心,故D错误.故选:C8.过棱锥的高的两个三等分点,分别作与底面平行的两个平行截面,则自上向下的两个截面与底面的面积之比是().A .1:2:3B .C .1:4:9D .1:3:5【答案】C【详解】如图所示:当棱锥为三棱锥时,易知PDL PEI PFC △△△,相似比为1:2:3,则::1:2:3PL PI PC ,易知PKL PHI PBC △△△,::1:2:3KL HI BC ,同理::1:2:3JL GI AC ,::1:2:3JK GH AB ,故JKL GHI BC △△△A ,相似比为1:2:3,故面积比为1:4:9,当棱锥为n 棱锥,4n 时,可以看成是多个三棱锥的组合体,面积比不改变.综上所述:两个截面与底面的面积之比是1:4:9.故选:C.9.三棱锥P ABC 中,PA PB AB PC a AC b BC c ,,,若三角形PAC 和PBC 都是等腰直角三角形,则a b c ,,可能的不同取值有()A .1种B .2种C .3种D .至少4种【答案】C【详解】根据题意可画简图如下,PAB 为等边三角形,且,PAC PBC 都是等腰直角三角形,分类讨论如下:,2PA PC PA PC ①时,PC 所以,22,AC PC 2BC PB 此时,2,2,2;a b c ,2PA AC PA AC ②时,PC 90PBC ,此时2BC PB ,此时,AC PC AC PC ③时,AC PC 90BCP ,此时1BC PC ,此时二、多选题10.下列说法中正确的是()A .长方体是直四棱柱B .两个面平行,其余各面是梯形的多面体是棱台C .正棱锥的侧面是全等的等腰三角形D .平行六面体不是棱柱【答案】AC【详解】长方体是直四棱柱,A 正确;两个平面平行,其余各面是梯形的多面体,当侧棱延长后不交于同一点时,就不是棱台,B 错;正棱锥的侧面是全等的等腰三角形,C正确;平行六面体一定是棱柱,D错.故选:AC.11.一个正方体内接于一个球,过球心作一个截面,则截面的图形可能是()A.B.C.D.【答案】ABC【分析】根据正方体截面过外接球球心,讨论截面是否过顶点及所过顶点个数、是否与侧面平行,即可判断截面图形的元素.【详解】当过球心的截面不平行于侧面且不过顶点时,截面图形为A;当过球心的截面平行于一对侧面时,截面图形为C;当过球心的截面过其中4个顶点,则截面图形为圆中含一个长方形,B正确,D错误.故选:ABC三、填空题12.关于棱柱,下列说法正确的是______.(选填序号)①所有的棱长都相等;②相邻两个面的交线叫做侧棱;③棱柱中任意两个侧面都不可能互相平行;④棱柱中至少有两个面的形状完全相同;⑤在斜棱柱的所有侧面中,矩形最多有2个.【答案】④⑤【分析】依据棱柱的定义和分类去判断即可解决.【详解】①棱柱的所有的侧棱长都相等,所有的棱长不一定相等.判断错误;②相邻两个侧面的交线叫做侧棱,相邻两个面的交线可能是底面的边.判断错误;③正四棱柱中相对的两个侧面互相平行.判断错误;④棱柱的两个底面全等,则棱柱中至少有两个面的形状完全相同.判断正确;⑤在斜棱柱的所有侧面中,最多互相平行的两个侧面可以是矩形,则矩形最多有2个.判断正确;故答案为:④⑤13.下列说法中,正确的个数为________.(1)有一个面是多边形,其余各面都是三角形的几何体是棱锥;(2)有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台;(3)底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;(4)棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是正六棱锥.【答案】0【分析】根据棱锥的概念可判断(1);根据棱台的概念可判断(2);根据正三棱锥的概念可判断(3);根据正六棱锥的侧棱长一定大于底面边长可判断(4).【详解】对于(1),棱锥的定义是:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥,故错误;对于(2),有两个面互相平行,其余四个面都是等腰梯形的六面体不一定是棱台,只有当四个等腰梯形的腰延长后交于一点时,这个六面体才是棱台,如图1,侧棱延长线可能不交于一点,故错误;对于(3),底面是等边三角形,侧面都是等腰三角形的三棱锥不一定是正三棱锥,只有当三棱锥的顶点在底面的射影是底面中心时,才是正三棱锥,不一定是正三棱锥,故错误;对于(4),因为正六棱锥的底面是正六边形,侧棱在底面内的射影与底面边长相等,所以正六棱锥的侧棱长一定大于底面边长,故错误.故答案为:0.14.面数最少的棱柱为________棱柱,共有________个面围成.【答案】三5【详解】棱柱有相互平行的两个底面,其侧面至少有3个,故面数最少的棱柱为三棱柱,共有5个面围成.故答案为:三,5四、解答题15.已知一个直四棱柱的底面边长为5cm 的正方形,侧棱长都是8cm ,回答下列问题:(1)这个直四棱柱一共有几个面?几个顶点?几条棱?(2)将这个直四棱柱的侧面展开成一个平面图形,这个图形是什么形状?面积是多少?【答案】(1)6个面,8个顶点,12条棱(2)是长方形,2160cm 【分析】(1)由直四棱柱的特征即可得出答案.(2)由直四棱柱的特征可知侧面展开图为长方形,求出长方形面积即可.【详解】(1)由直四棱柱的特征可知直四棱柱一共有6个面,8个顶点,12条棱.(2)将直四棱柱的侧面展开是一个长方形.长方形的宽为直四棱柱的侧棱长,所以宽为8cm ,长为直四棱柱的底边边长的四倍,即5420(cm) ,所以长为20cm ,所以侧面展开图面积为2820160(cm )题组B 能力提升练一、单选题1.下列说法错误的是()A .一个棱柱至少有5个面B .长方体、正方体都是棱柱C .三棱柱的侧面是三角形D .六棱柱有6条侧棱、6个侧面,侧面为平行四边形【答案】C【详解】选项A:一个棱柱至少有5个面.判断正确;选项B:长方体、正方体都是棱柱.判断正确;选项C:三棱柱的侧面是平行四边形.判断错误;选项D:六棱柱有6条侧棱、6个侧面,侧面为平行四边形判断正确.故选:C2.下面图形中,为棱锥的是()A.①③B.①③④C.①②④D.①②【答案】C【详解】一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥,显然①②④满足棱锥定义,③不满足棱锥定义,所以①②④是棱锥,③不是棱锥.故选:C3.下列命题正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱D.棱柱的侧面都是全等的平行四边形【答案】C【详解】有两个面平行,其余各面都是四边形的几何体,A错;有两个面平行,其余各面都是平行四边形的几何体如图所示,B错;棱柱的侧面不一定是全等的平行四边形,D错;由棱柱的定义,C正确.故选:C.4.如图所示的几何体的结构特征是()A .一个棱柱中截去一个棱柱B .一个棱柱中截去一个圆柱C .一个棱柱中截去一个棱锥D .一个棱柱中截去一个棱台【答案】C【详解】图中的几何体为一个棱柱截去一个角,截去的角是一个棱锥.故选C.【点睛】本题考查空间几何体的组成,难度较易.5.如图,位于西安大慈恩寺的大雁塔,是唐代玄奘法师为保存经卷佛像而主持修建的,是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥,其侧棱与底面所成的角为45 ,则该正四棱锥的一个侧面与底面的面积之比为()A .2B .2C .3D .4【答案】D6.下列判断正确的是()A.正三棱锥一定是正四面体B.底面是正方形的四棱锥是正四棱锥C.底面是正方形的直四棱柱是正四棱柱D.底面是正方形的棱台是正四棱台【答案】C【详解】正三棱锥不一定是正四面体,侧棱长与底面边长可能不相等,故A错误;底面是正方形的四棱锥不一定是正四棱锥,顶点在底面的射影不一定是底面的中心,故B错误;由正四棱住的概念可知,底面是正方形的直四棱柱是正四棱柱,故C正确;底面是正方形的棱台不一定是正四棱台,原因是棱台的侧棱延长后的交点在两底面的射影不一定为正方形的中心,故D错误.故选:C7.下列说法正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.过空间内不同的三点,有且只有一个平面C.棱锥的所有侧面都是三角形D.用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台【答案】C【详解】如下图,两个三棱柱合在一起,仍然满足有两个面平行,其余各面都是四边形,但它不是棱柱,A错;当空间三点共线时,过这三点有无数个平面,B 错;根据棱锥的定义,C 正确;用一个与底面平行的平面去截棱锥,底面与截面之间的部分组成的几何体才叫棱台,不是任意平面都能截出棱台的,D 错.故选:C .8.已知正四棱柱1111ABCD A B C D 中,12312AA AB ,点M 是线段1BB 的中点,点N 是线段1DD 上靠近D 的三等分点,若正四棱柱1111ABCD A B C D 被过点1A ,M ,N 的平面所截,则所得截面的周长为()A .10 B .10 C .9 D .9 延长1C C 至Q ,使得CQ 记MQ 与BC 交于点R ,则142A N ,15A M ,9.如图,在正方体1111ABCD A B C D 中,E 是棱1CC 的中点,则过三点A 、D 1、E 的截面过()A .AB 中点B .BC 中点C .CD 中点D .BB 1中点【答案】B 【详解】取BC 的中点F ,连接EF ,AF ,如图,则1EF AD ∥,所以F 在截面上,故选:B二、多选题10.如图所示,观察四个几何体,其中判断正确的是()(多选)A.①是棱台B.②是圆台C.③是棱锥D.④是棱柱【答案】CD【详解】题图①中的几何体不是由棱锥被一个平面所截得到的,且上、下底面不是相似的图形,所以不是棱台;题图②中的几何体上、下两个面不平行,所以②不是圆台;图③中的几何体是三棱锥;题图④中的几何体前、后两个面平行,其他面都是平行四边形,且每相邻两个平行四边形的公共边都互相平行,所以④是棱柱.故选:CD.11.下列命题错误的是()A.棱柱的侧棱都相等,侧面都是全等的平行四边形B.用一个平面去截棱锥,棱锥底面与截面之间的部分是棱台C.四面体的任何一个面都可以作为棱锥的底面D.棱台的侧棱延长后交于一点,侧面是等腰梯形【答案】ABD【详解】棱柱的侧棱都相等,但侧面不一定是全等的平行四边形,A错误;用一个平行于底面的平面去截棱锥,棱锥底面与截面之间的部分才是棱台,B错误;四面体的任何一个面都可以作为棱锥的底面,C正确;棱台的侧棱延长后交于一点,但侧面不一定是等腰梯形,D错误.故选:ABD.三、填空题12.①直四棱柱一定是长方体;②正方体一定是正四棱柱;③底面是正多边形的棱柱是正棱柱;④有相邻两个侧面是矩形的棱柱是直棱柱;⑤平行六面体的六个面均为平行四边形;⑥直棱柱的侧棱长与高相等.以上说法中正确的命题有_________.【答案】②④⑤⑥【详解】①侧棱垂直于底面的四棱柱叫做直四棱柱,底面是长方形的直四棱柱才是长方体.底面如果不是长方形,则该直四棱柱不是长方体,故①错误;②上、下底面都是正方形,且侧棱垂直于底面的棱柱叫做正四棱柱,所以正方体是正四棱柱,但正四棱柱不一定是正方体,故②正确;③底面是正多边形的直棱柱是正棱柱,底面是正多边形且侧棱与底面不垂直的棱柱不是正棱柱,故③错误;④有两个相邻的侧面是矩形,说明侧棱与底面两条相交直线垂直,则侧棱与底面垂直,所以,有相邻两个侧面是矩形的棱柱是直棱柱,故④正确;⑤底面是平行四边形的四棱柱叫做平行六面体,而棱柱的各个侧面都是平行四边形,故⑤正确;⑥直棱柱的侧棱垂直于底面,因此侧棱长与高相等,故⑥正确.故答案为:②④⑤⑥四、解答题13.已知正六棱柱111111ABCDEF A B C D E F 1,则动点从A 沿侧面移到点1D 时的最短的路程是多长?则 22221133128AD AD DD ,所以127AD .即动点从A 沿侧面移到点1D 时的最短路程为27题组C 培优拔尖练一、单选题1.下列关于棱台的说法中错误的是()A .所有的侧棱所在直线交于一点B .只有两个面互相平行C .上下两个底面全等D .所有的侧面不存在两个面互相平行【答案】C【详解】由棱台的定义可知:A.所有的侧棱所在直线交于一点,正确;B.只有两个面互相平行,就是上、下底面平行,正确;C.棱台的上下两个底面不全等,故C 不正确;D.所有的侧面不存在两个面互相平行,正确.故选:C.2.侧面都是矩形的棱柱一定是()A .长方体B .三棱柱C .直平行六面体D .直棱柱【答案】D 【详解】侧面都是矩形的棱柱,只需侧棱和底面垂直,即侧面都是矩形的棱柱一定是直棱柱.故选:D 3.在四棱锥P ABCD 中,底面ABCD且2PA PB PC PD .若点E 、F 、G 分别为棱PB 、PC 、PD 上的动点(不包含端点P ),则AE EF FG GA 的最小值为()A .2B .C .D .4【答案】C【详解】把四棱锥P ABCD 沿PA 展开,得到如图所示图形:AE EF FG GA 的最小时,点,,E F G 与,A A 共线时,所以求AE EF FG GA 的最小值即求AA 的长。
高考数学总复习 9.6棱柱、棱锥的概念和性质课件 人教

考点
考纲要求
考查角度
棱柱、棱 棱柱、棱 理解棱柱、棱锥的 棱柱、棱锥的截面
锥的概念 锥的概念 概念和性质;能正 特征;线面位置关
及性质 及性质; 确画出直棱柱、正 系的计算与证明;
直棱柱、 棱柱的直观图;会 有关棱柱、棱锥的
正棱柱的 解决棱柱的直截面 概念的判断及性质
积是S直棱柱侧=ch. ②斜棱柱的侧面积等于它的直截面(垂直于侧棱并与每条侧
棱都相交的的体积等于它的底面积S乘以高h,即V棱柱=Sh. ①一般地,V柱体=Sh,其中S是底面积,h是高. ②V长方体=abc,其中a、b、c是长方体的长、宽、高; V正方体=a3,其中a为棱长.
体; ④对角线相等的平行六面体是直平行六面体; ⑤底面是正方形的长方体是正四棱柱. 其中真命题的个数是( )
A.1
B.2
C.3
D.4
解析:命题①不正确,因为侧棱不一定垂直于底面;②不正 确,因为底面有可能是菱形;③不正确,因为有两条侧棱 垂直于底面一边,可以得到相对的两侧面是矩形,不能得 出侧棱与底面垂直;④正确,由对角线相等,可得出平行 六面体的对角面是矩形,从而推得侧棱与底面垂直,所以 是直平行六面体;⑤正确,长方体是直四棱柱,再加上底 面是正方形,所以是正四棱柱.
②若体对角线与相交于一点的三个面所成的角分别为α、β、 γ,则cos2α+cos2β+cos2γ=2;sin2α+sin2β+sin2γ=1.
(5)由于长方体本身的特点,较容易建立空间直角坐标系,因 此,利用空间向量求解与长方体有关的问题较为简单.
二、棱锥
1.棱锥
有一个面是
,其余各面是有一个公共顶点的 ,
这些面围成的几多何边体形叫做棱锥.
人教高中数学必修二A版《基本立体图形》立体几何初步说课复习(棱柱、棱锥、棱台的结构特征)
课件
课件 课件
课件 课件
课件 课件
课件 课件
栏目 导引
第八章 立体几何初步
在三棱锥
课件
课件
课件
课件
课件
课件
课件
个人简历:课件/j ia nli/
课件
课件
手抄报:课件/shouchaobao/
课件
课件 课件
课件 课件
课件 课件
课件 课件
课件
课件
A-BCD
中,可以当作棱锥底面的三角形的个数为
()
A.1
B.2
C.3
D.4
解析:选 D.每个面都可作为底面,有 4 个.
展开成平面图形
第八章 立体几何初步
课件
课件
课件
课件
课件
课件
课件
个人简历:课件/j ia nli/
课件
课件
手抄报:课件/shouchaobao/
课件
课件 课件
课件 课件
课件 课件
课件 课件
课件
课件
问题导学
预习教材 P97-P100 的内容,思考以下问题: 1.空间几何体的定义是什么? 2.空间几何体分为哪几类? 3.常见的多面体有哪些? 4.棱柱、棱锥、棱台有哪些结构特征?
课件 课件
课件
课件
③棱台的侧棱所在直线均相交于同一点.
解析:棱锥是由棱柱的一个底面收缩为一个点而得到的几何体,因
而其侧面均是三角形,且所有侧面都有一个公共点,故①对.棱台
是棱锥被平行于底面的平面所截后,截面与底面之间的部分,因而
其侧面均是梯形,且所有的侧棱延长后均相交于一点(即原棱锥的顶
点),故②错,③对.因而正确的有①③. 答案:①③
高中数学人教A版必修二课件:棱柱、棱锥、棱台的结构特征 课件(37张)
[答案] (2)(3)(4)
[类题通法]
判断棱锥、棱台形状的两个方法 (1)举反例法: 结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台 结构特征的某些说法不正确.
(2)直接法:
棱锥 定底面 棱台
只有一个面是多边形, 两个互相平行的面,
此面即为底面 即为底面
看侧棱
相交于一点
延长后相交于一点
[活学活用] 2.试判断下列说法正确与否: ①由六个面围成的封闭图形只能是五棱锥;
形绕某定直线旋转而成?
提示:可以.
[导入新知] 1.空间几何体
概念
空间 几何 体
定义
在我们周围存在着各种各样的物体,它们都占据着空 形状 和_____ 大小 , 间的一部分.如果我们只考虑物体的_____ 而不考虑其他因素,那么由这些物体抽象出来的空间 图形就叫做空间几何体
概念
定义 平面多边形 围成的几何体叫做多面 由若干个_____________
答案:A
棱锥、棱台的结构特征 [例2] 下列关于棱锥、棱台的说法:
(1)用一个平面去截棱锥,底面和截面之间的部分组成的
几何体叫棱台; (2)棱台的侧面一定不会是平行四边形; (3)棱锥的侧面只能是三角形; (4)由四个面围成的封闭图形只能是三棱锥;
(5)棱锥被平面截成的两部分不可能都是棱锥,其中正确
面 ;相 多面 体.围成多面体的各个多边形叫做多面体的___ 体 公共边 叫做多面体的棱;棱与棱的 邻两个面的________ 公共点 叫做多面体的顶点 ________ 旋转 直线 旋转 由一个平面图形绕它所在平面内的一条定_____ 封闭几何体 叫做旋转体,这条定直线叫做 所形成的____________ 轴 旋转体的____
棱柱棱锥教案
棱柱棱锥教案【学习目标】:1、棱锥和棱台的定义、性质及它们之间的关系2、空间与平面问题的相互转化;【研习教材】:研习点一:棱锥及相关概念1.定义:叫做棱锥,画出一个三棱锥和四棱锥2.相关概念:(在棱锥中标出相关概念所在图像的位置)(1)棱锥的侧面(2)棱锥的顶点(3)棱锥的侧棱(4)棱锥的底面(5)棱锥的高联想·质疑如何理解棱锥?1.棱锥是多面体中的重要一种,它有两个本质的特征:①②2.棱锥有一个面是多边形,其余各面都是三角形,但是也要注意“有一个面是多边形,其余各面都是三角形的几何体是棱锥吗?。
如右图所示,此多面体有一个面是四边形,其余各面是三角形,但它不是棱锥!3.棱锥的分类:(1)按底面多边形的边数分为三棱锥、四棱锥、五棱锥等,其中三棱锥又叫(2)正棱锥:4.正棱锥的性质:(1)(2)5.棱锥的表示:(1)用顶点和底面各顶点的字母表示棱锥:如三棱锥P-ABC,四棱锥P-ABCD.(2)用对角面表示:如右图中的四棱锥可以用P-AC表示!研习点2.棱台及第一文库网相关概念1.定义:2.相关概念:(画一个三棱台和四棱台并且标出下面相关概念的位置)(1)棱台的下底面、上底面:(2)棱台的侧面:(3)棱台的侧棱:(4)棱台的高:3.棱台的`分类:(1)按底面多边形的边数分为三棱台、四棱台、五棱台等;(2)正棱台:4.正棱台的性质:(1)(2)(3)5.棱台的表示:棱台可用表示上、下底面的字母来命名,如右图中的棱台,可以记作棱台ABCD-A’B’C’D’,或记作棱台AC’,下底面为ABCD,上底面为A’B’C’D’,棱台的高为OO’. 探究解题新思路基础拓展型题型1:概念判断题例1.设有四个命题:①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体。
以上四个命题中,真命题的个数是( )(A)1 (B)2 (C)3 (D)4拓展·变式:棱台不具有的性质是( )(A)两底面相似(B)侧面都是梯形(C)侧棱长都相等(D)侧棱延长后交于一点题型2.考查棱柱间的关系1、已知集合A={正方体},B={长方体},C={正四棱柱},D={平行六面体},E={四棱柱},F={直平行六面体},则( )【研析】几种常见棱柱间的关系如下图所示:2.、有四个命题:①各侧面是全等的等腰三角形的四棱锥是正四棱锥,②底面是正多边形的棱锥是正棱锥;③棱锥的所有侧面可能都是直角三角形;④四棱锥中侧面最多有四个直角三角形。
高中数学必修二 (教案)简单几何体的表面积与体积
简单几何体的表面积与体积【第一课时】【教学目标】1.了解柱体、锥体、台体的侧面展开图,掌握柱体、柱、锥、台的体积2.能利用柱体、锥体、台体的体积公式求体积,理解柱体、锥体、台体的体积之间的关系【教学重难点】1.柱、锥、台的表面积2.锥体、台体的表面积的求法【教学过程】一、问题导入预习教材内容,思考以下问题:1.棱柱、棱锥、棱台的表面积如何计算?2.圆柱、圆锥、圆台的侧面展开图分别是什么?3.圆柱、圆锥、圆台的侧面积公式是什么?4.柱体、锥体、台体的体积公式分别是什么?5.圆柱、圆锥、圆台的侧面积公式、体积公式之间分别有怎样的关系?二、新知探究柱、锥、台的表面积例1:(1)若圆锥的正视图是正三角形,则它的侧面积是底面积的()A.2倍B.3 倍C.2 倍D.5 倍(2)已知正方体的8 个顶点中,有 4 个为侧面是等边三角形的三棱锥的顶点,则这个三棱锥与正方体的表面积之比为()A.1∶ 2B.1∶3C.2∶ 2D.3∶6(3)已知某圆台的一个底面周长是另一个底面周长的 3 倍,母线长为 3 ,圆台的侧面积为84π,则该圆台较小底面的半径为()A.7B.6C.5D.3【解析】(1)设圆锥的底面半径为r,母线长为l,则由题意可知,l=2r,于是S侧=πr·2r=2πr2,S底=πr2,可知选 C.(2)棱锥B′ACD′为适合条件的棱锥,四个面为全等的等边三角形,设正方体的棱长为1,则B′C=2,S△B′AC=3 2.三棱锥的表面积S锥=4×32=23,又正方体的表面积S正=6.因此S锥∶S正=23∶6=1∶ 3.(3)设圆台较小底面的半径为r,则另一底面的半径为3r.由S侧=3π(r+3r)=84π,解得r=7.【答案】(1)C(2)B(3)A[规律方法]空间几何体表面积的求法技巧(1)多面体的表面积是各个面的面积之和.(2)组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开为平面图形计算,而表面积是侧面积与底面圆的面积之和.柱、锥、台的体积例2:如图所示,正方体ABCDA1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥.(1)求剩余部分的体积;(2)求三棱锥AA1BD的体积及高.【解】(1)V三棱锥A1ABD=13S△ABD·A1A=13×1 2·AB·AD·A1A=16a3.故剩余部分的体积V=V正方体-V三棱锥A1ABD=a3-16a3=56a3.(2)V三棱锥AA1BD=V三棱锥A1ABD=1 6a 3.设三棱锥AA1BD的高为h,则V三棱锥AA1BD=13·S△A1BD·h=13×12×32(2a)2h=36a2h,故36a2h=16a3,解得h=3 3a.[规律方法]求几何体体积的常用方法(1)公式法:直接代入公式求解.(2)等积法:例如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.(3)补体法:将几何体补成易求解的几何体,如棱锥补成棱柱,棱台补成棱锥等.(4)分割法:将几何体分割成易求解的几部分,分别求体积.[提醒]求几何体的体积时,要注意利用好几何体的轴截面(尤其为圆柱、圆锥时),准确求出几何体的高和底面积.组合体的表面积和体积例3:如图在底面半径为2,母线长为 4 的圆锥中内接一个高为3的圆柱,求圆柱的表面积.【解】设圆锥的底面半径为 R ,圆柱的底面半径为 r ,表面积为 S . 则 R =OC =2,AC =4, AO =42-22=2 3. 如图所示,易知△AEB ∽△AOC ,所以AE AO =EB OC ,即323=r 2,所以 r =1,S 底=2πr 2=2π,S 侧=2πr ·h =23π. 所以 S =S 底+S 侧=2π+23π =(2+23)π.1.[变问法]本例中的条件不变,求圆柱的体积与圆锥的体积之比. 解:由例题解析可知:圆柱的底面半径为 r =1,高 h =3,所以圆柱的体积 V 1=πr 2h =π×12×3=3π.圆锥的体积 V 2=13π×22×23=833π.所以圆柱与圆锥的体积比为 3∶8.2.[变问法]本例中的条件不变,求图中圆台的表面积与体积.解:由例题解析可知:圆台的上底面半径 r =1,下底面半径 R =2,高 h =3,母线 l =2,所以圆台的表面积 S =π(r 2+R 2+r ·l +Rl )=π(12+22+1×2+2×2)=11π.圆台的体积 V =13π(r 2+rR +R 2)h =13π(12+2+22)×3=733π. 3.[变条件、变问法]本例中的“高为3”改为“高为 h ”,试求圆柱侧面积的最大值.解:设圆锥的底面半径为 R ,圆柱的底面半径为 r ,则R=OC=2,AC=4,AO=42-22=2 3.如图所示易知△AEB∽△AOC,所以AEAO =EBOC,即23-h23=r2,所以h=23-3r,S圆柱侧=2πrh=2πr(23-3r)=-23πr2+43πr,所以当r=1,h=3时,圆柱的侧面积最大,其最大值为23π.[规律方法]求组合体的表面积与体积的步骤(1)分析结构特征:弄清组合体的组成形式,找准有关简单几何体的关键量.(2)设计计算方法:根据组成形式,设计计算方法,特别要注意“拼接面”面积的处理,利用“切割”“补形”的方法求体积.(3)计算求值:根据设计的计算方法求值.【课堂总结】1.棱柱、棱锥、棱台的表面积多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.2.棱柱、棱锥、棱台的体积(1)V棱柱=Sh;(2)V棱锥=13Sh;V棱台=13h(S′+SS′+S),其中S′,S分别是棱台的上、下底面面积,h为棱台的高.3.圆柱、圆锥、圆台的表面积和体积名称图形公式圆柱底面积:S底=πr2侧面积:S侧=2πrl表面积:S=2πrl+2πr2体积:V=πr2l[名师点拨]1.柱体、锥体、台体的体积(1)柱体:柱体的底面面积为S ,高为h ,则V =Sh .(2)锥体:锥体的底面面积为S ,高为h ,则V =13Sh . (3)台体:台体的上、下底面面积分别为S ′、S ,高为h ,则V =13()S ′+SS ′+S h .2.圆柱、圆锥、圆台的侧面积公式之间的关系S 圆柱侧=2πrl ――→r ′=r S 圆台侧=π(r ′+r )l ――→r ′=0S 圆锥侧=πrl . 3.柱体、锥体、台体的体积公式之间的关系V 柱体=Sh ――→S ′=S V 台体=13(S ′+S ′S +S )h ――→S ′=0V 锥体=13Sh .【课堂检测】1.已知某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为( )A .22B .20C .10D .11解析:选A.所求长方体的表面积S =2×(1×2)+2×(1×3)+2×(2×3)=22.2.正三棱锥的高为3,侧棱长为23,则这个正三棱锥的体积为( )A.274B.94C.2734D.934解析:选D.由题意可得底面正三角形的边长为3,所以V =13×34×32×3=934.故选D.3.已知圆台的上、下底面的面积之比为9∶25,那么它的中截面截得的上、下两台体的侧面积之比是________.解析:圆台的上、下底面半径之比为3∶5,设上、下底面半径为3x ,5x ,则中截面半径为4x ,设上台体的母线长为l ,则下台体的母线长也为l ,上台体侧面积S 1=π(3x +4x )l =7πxl ,下台体侧面积S 2=π(4x +5x )l =9πxl ,所以S 1∶S 2=7∶9.答案:7∶9 4.如图,三棱台ABC A 1B 1C 1中,AB ∶A 1B 1=1∶2,求三棱锥A 1ABC ,三棱锥B A 1B 1C ,三棱锥CA 1B 1C 1的体积之比.解:设棱台的高为h ,S △ABC =S ,则S △A 1B 1C 1=4S .所以VA 1ABC =13S △ABC ·h =13Sh ,VC A 1B 1C 1=13S △A 1B 1C 1·h =43Sh .又V 台=13h (S +4S +2S )=73Sh , 所以VB A 1B 1C =V 台-VA 1ABC -VCA 1B 1C 1=73Sh -Sh 3-4Sh 3=23Sh , 所以体积比为1∶2∶4.【第二课时】 【教学目标】1.记准球的表面积和体积公式,会计算球的表面积和体积 2.能解决与球有关的组合体的计算问题【教学重难点】1.球的表面积与体积 2.与球有关的组合体【教学过程】一、问题导入预习教材内容,思考以下问题:1.球的表面积公式是什么?2.球的体积公式什么?二、新知探究球的表面积与体积例1:(1)已知球的体积是32π3,则此球的表面积是()A.12πB.16πC.16π3 D.64π3(2)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,若该几何体的体积是28π3,则它的表面积是()A.17π B.18πC.20π D.28π【解析】(1)设球的半径为R,则由已知得V=43πR3=32π3,解得R=2.所以球的表面积S=4πR2=16π.(2)由三视图可得此几何体为一个球切割掉18后剩下的几何体,设球的半径为r,故78×43πr3=283π,所以r=2,表面积S=78×4πr2+34πr2=17π,选A.【答案】(1)B(2)A[归纳反思]球的体积与表面积的求法及注意事项(1)要求球的体积或表面积,必须知道半径R或者通过条件能求出半径R,然后代入体积或表面积公式求解.(2)半径和球心是球的最关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就易如反掌了.球的截面问题例2:如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器厚度,则球的体积为()A.500π3cm3 B.866π3cm3C.1 372π3cm3 D.2 048π3cm3【解析】如图,作出球的一个截面,则MC=8-6=2(cm),BM=12AB=12×8=4(cm).设球的半径为R cm,则R2=OM2+MB2=(R-2)2+42,所以R=5,所以V球=43π×53=5003π (cm3).【答案】A[规律方法]球的截面问题的解题技巧(1)有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题.(2)解题时要注意借助球半径R,截面圆半径r,球心到截面的距离d构成的直角三角形,即R2=d2+r2.与球有关的切、接问题角度一球的外切正方体问题例3:将棱长为 2 的正方体木块削成一个体积最大的球,则该球的体积为()A.4π3B.2π3C.3π2D.π6【解析】由题意知,此球是正方体的内切球,根据其几何特征知,此球的直径与正方体的棱长是相等的,故可得球的直径为 2,故半径为 1,其体积是43×π×13=4π3.【答案】A角度二球的内接长方体问题例4:一个长方体的各个顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为 1,2,3,则此球的表面积为________.【解析】长方体外接球直径长等于长方体体对角线长,即 2R =12+22+32=14,所以球的表面积 S =4πR 2=14π. 【答案】14π角度三球的内接正四面体问题例5:若棱长为 a 的正四面体的各个顶点都在半径为 R 的球面上,求球的表面积.【解】把正四面体放在正方体中,设正方体棱长为 x ,则 a =2x ,由题意2R =3x =3×2a 2=62a ,所以 S 球=4πR 2=32πa 2.角度四球的内接圆锥问题例6:球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为________.【解析】①当圆锥顶点与底面在球心两侧时,如图所示,设球半径为 r ,则球心到该圆锥底面的距离是r 2,于是圆锥的底面半径为 r 2-⎝ ⎛⎭⎪⎫r 22=3r 2,高为3r 2.该圆锥的体积为 13 ×π×⎝ ⎛⎭⎪⎫3r 22 ×3r 2=38πr 3,球体积为43 πr 3,所以11 / 13该圆锥的体积和此球体积的比值为38πr 343πr 3=932. ②同理,当圆锥顶点与底面在球心同侧时,该圆锥的体积和此球体积的比值为332.【答案】932或332角度五球的内接直棱柱问题例7:设三棱柱的侧棱垂直于底面,所有棱的长都为 a ,顶点都在一个球面上,则该球的表面积为( )A .πa 2B.73πa 2C.113πa 2 D .5πa 2【解析】由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为 a .如图,P 为三棱柱上底面的中心,O 为球心,易知 AP=23×32a =33a ,OP =12a ,所以球的半径 R = OA 满足R 2=⎝ ⎛⎭⎪⎫33a 2+⎝ ⎛⎭⎪⎫12a 2=712a 2,故 S 球=4πR 2=73πa 2. 【答案】B[规律方法](1)正方体的内切球球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为 r 1=a 2,过在一个平面上的四个切点作截面如图(1). (2)长方体的外接球长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径,若长方体过同一顶点的三条棱长为 a ,b ,c ,过球心作长方体的对角线,则球的半径为 r 2=12 a 2+b 2+c 2,如图(2).12 / 13(3)正四面体的外接球正四面体的棱长 a 与外接球半径 R 的关系为:2R =62a .【课堂总结】1.球的表面积设球的半径为R ,则球的表面积S =4πR 2.2.球的体积设球的半径为R ,则球的体积V =43πR 3.[名师点拨]对球的体积和表面积的几点认识(1)从公式看,球的表面积和体积的大小,只与球的半径相关,给定R 都有唯一确定的S 和V 与之对应,故表面积和体积是关于R 的函数.(2)由于球的表面不能展开成平面,所以,球的表面积公式的推导与前面所学的多面体与旋转体的表面积公式的推导方法是不一样的.(3)球的表面积恰好是球的大圆(过球心的平面截球面所得的圆)面积的4倍.【课堂检测】1.直径为 6 的球的表面积和体积分别是( )A .36π,144πB .36π,36πC .144π,36πD .144π,144π解析:选 B .球的半径为 3,表面积 S =4π·32=36π,体积 V =43π·33=36π.2.一个正方体的表面积与一个球的表面积相等,那么它们的体积比是( ) A.6π6 B.π2C.2π2D.3π2π解析:选 A .设正方体棱长为 a ,球半径为 R ,由 6a 2=4πR 2 得a R =2π3,所以V 1V 2=a 343πR 3=34π⎝ ⎛⎭⎪⎫2π33=6π6. 3.若两球的体积之和是 12π,经过两球球心的截面圆周长之和为 6π,则两球的半径之差为( )A .1B .213 / 13C .3D .4解析:选 A .设两球的半径分别为 R ,r (R >r ),则由题意得⎩⎪⎨⎪⎧4π3R 3+4π3r 3=12π,2πR +2πr =6π,解得⎩⎨⎧R =2,r =1.故 R -r =1. 4.已知棱长为 2 的正方体的体积与球 O 的体积相等,则球 O 的半径为________.解析:设球 O 的半径为 r ,则43πr 3=23,解得 r =36π. 答案:36π5.已知过球面上 A ,B ,C 三点的截面和球心的距离为球半径的一半,且 AB =BC =CA =2,求球的表面积.解:设截面圆心为O ′,球心为 O ,连接 O ′A ,OA ,OO ′,设球的半径为 R .因为O ′A =23×32×2=233.在 Rt △O ′OA 中,OA 2=O ′A 2+O ′O 2,所以 R 2=⎝ ⎛⎭⎪⎫2332+14R 2, 所以 R =43,所以 S 球=4πR 2=649π.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课 题:9.9棱柱和棱锥(二)教学目的:1. 理解平行六面体的概念掌握平行六面体、长方体、正方体的概念及性质;,弄清直平行六面体、长方体、正方体的关系.2.掌握长方体对角线的性质,能利用其计算有关长度与角度的问题. 教学重点:平行六面体、长方体的概念及性质 教学难点:平行六面体、长方体的概念及性质 授课类型:新授课 课时安排:1课时教 具:多媒体、实物投影仪 教学过程:一、复习引入:1多面体的概念:由若干个多边形围成的空间图形叫多面体;每个多边形叫多面体的面,两个面的公共边叫多面体的棱,棱和棱的公共点叫多面体的顶点,连结不在同一面上的两个顶点的线段叫多面体的对角线.2.凸多面体:把多面体的任一个面展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫凸多面体.如 图的多面体则不是凸多面体.3.凸多面体的分类:多面体至少有四个面,按照它的面数分别叫四面体、五面体、六面体等说明:我们今后学习的多面体都是..凸多面体 4.棱柱的概念:有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫棱柱两个互相平行的面叫棱柱的底面(简称底);其余各面叫棱柱的侧面;两侧面的公共边叫棱柱的侧棱;两底面所在平面的公垂线段叫棱柱的高(公垂线段长也简称高)5.棱柱的分类:侧棱不垂直于底面的棱柱叫斜棱柱侧棱垂直于底面的棱柱叫直棱柱底面的是正多边形的直棱柱叫正棱柱棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱……设集合{}A =棱柱,{}B =斜棱柱,{}C =直棱柱,{}D =正棱柱, 则,BC AD C =⊂.6.棱柱的性质(1)棱柱的侧棱相等,侧面都是平行四边形;直棱柱侧面都是矩形;正棱柱侧面都是全等的矩形;(2)棱柱的两个底面与平行于底面的截面是对应边互相平行的全等的多边形 (3)过棱柱不相邻的两条侧棱的截面都是平行四边形. 7.直棱柱的直观图的画法画棱柱的直观图共分四个步骤: ①画轴; ②画底面; ③画侧棱;④成图.底面一定要画成水平放置位置的平面图形的直观图 二、讲解新课:1平行六面体、长方体、正方体底面是平行四边形的四棱柱是平行六面体.侧棱与底面垂直的平行六面体叫直平行六面体,底面是矩形的直平行六面体长方体,棱长都相等的长方体叫正方体.2.平行六面体、长方体的性质定理1:平行六面体的对角线交于一点,求证:对角线,,,AC BD CA DB ''''相交于一点,且在点O 处互相平分.证明:设O 是AC '的中点,则11()22AO AC AB AD AA ''==++, 设,,P M N 分别是,,BD CA DB '''的中点, 同理:1()2AP AB AD AA '=++, 1()2AM AB AD AA '=++, 1()2AN AB AD AA '=++,所以,,,,O P M N 四点重合,定理得证定理2:长方体的一条对角线长的平方等于一个顶点上的三条棱长的平方和. 已知:长方体AC '中,AC '是一条对角线, 求证:2222AC AB AD AA ''=++.证明:∵AC AB AD AA ''=++,∴2||()()AC AB AD AA AB AD AA '''=++⋅++, ∵AB AD ⊥,AB AA '⊥,AA AD '⊥,∴2||AC AB AB AD AD AA AA '''=⋅+⋅+⋅222||||||AB AD AA '=++, 即2222AC AB AD AA ''=++. 三、讲解范例:D'C'B'A'DC BAH OA'D'C'B'DCBA例1如图平行六面体ABCD A B C D ''''-中,,3A AB A AD BAD π''∠=∠∠=,,AB AD a AA b '===,求对角面BB D D ''的面积解:∵BD AD AB =-, ∴()AA BD AA AD AB ''⋅=⋅-,∵A AB A AD ''∠=∠,,AB AD a AA b '===,∴()(cos cos )0AA BD AA AD AB ab A AB A AD ''''⋅=⋅-=∠-∠=, ∴AA BD '⊥,∵//AA DD '',∴DD BD '⊥,所以,对角面BB D D ''是矩形,它的面积是BD BB ab '⨯=.例2.已知:正四棱柱ABCD A B C D ''''-的底面边长为2 (1)求二面角B AC B '--的大小;(2)求点B 到平面AB C '的距离 解:(1)连结BD ,设,AC BD 交于O ,连结B O',∵ABCD 是正方形,∴BO AC ⊥, 又∵BB '⊥底面ABCD , ∴B O AC '⊥,∴B OB '∠是二面角B AC B '--的平面角, 在Rt B OB '∆中,12OB AC ==BB '=, ∴45B OB '∠=,∴二面角B AC B '--为45.(2)作BH B O '⊥于H ,∵AC ⊥平面B OB ',∴BH AC ⊥, ∴BH ⊥平面AB C ',即BH 为点B 到平面AB C '的距离, 在等腰直角三角形B OB '中,∵BB BO '==∴1BH =,所以,点B 到平面AB C '的距离为1.例3.棱长为a 的正方体OABC O A B C ''''-中,,E F 分别为棱,AB BC 上的动点,且(0)AE BF x x a ==≤≤,(1)求证:A F C E ''⊥;(2)当BEF ∆的面积取得最大值时,求二面角B EF B '--的大小.证:(1)以O 为原点,直线,,OA OC OO '分别为,,x y z 轴建立空间直角坐标系, ∴AE BF x ==,则(,0,)A a a ',(0,,)C a a ',(,,0)E a x ,(,,0)F a x a -,∴(,,),(,,)A F x a a C E a x a a ''=--=--,2)(a a x a ax E C F A +-+-='⋅'220ax ax a a =-+-+=,∴A F C E ''⊥.(2)由,BF x EB a x ==-,则2211()()2228BEFx a x a S x a x ∆+-=-≤=, 当且仅当x a x =-,即2ax =时等号成立,此时,E F 分别为,AB BC 的中点, 取EF 的中点M ,连BM ,则BM EF ⊥,根据三垂线定理知EF B M '⊥,∴B MB '∠即为二面角B EF B '--的平面角,在RtBMF ∆中,,BM BF BB a '===, 在Rt B BM '∆中,tan B BB MB BM''∠=== 所以,二面角B EF B '--的大小是22arctan .例4 如图,M 、N 分别是棱长为1的正方体''''D C B A ABCD -的棱'BB 、''C B 的中点.求异面直线MN 与'CD 所成的角. 解:∵MN =)(21BC CC +,'CD =CC +, ∴·CD MN =)'(21BC CC +·)(CC +=21(2||CC +CC ·+·CC +·). ∵CD CC ⊥',BC CC ⊥',CD BC ⊥,∴0·'=CD CC ,0'·=CC BC ,0·=CD BC , ∴·CD MN =212||CC =21. 又∵22||=MN ,2||=CD ,∴ cos <,CD MN212·2221=, ∴<,CD MN >=60,即异面直线MN 与'CD 所成的角为60.评述 由以上例题,可以看到利用向量解几何题的一般方法:把线段或角度转化为向量表示式,并用已知向量表示未知向量,然后通过向量的运算去计算或证明. 四、课堂练习: 1正方体1111ABCD A B C D -中,11AA =,M 为AD 中点,N 为1BD 上一点,1:1:2D N NB =,MCBD P =,(1)求证:NP ⊥平面ABCD ;(2)求平面PNC 与平面11CC D D 所成的角; (3)求点C 到平面1D MB 的距离2.直平行六面体的两条对角线分别为9cm,底面周长为18cm ,侧棱长为4cm ,求它的表面积五、小结 :平行六面体的概念.直平行六面体、长方体、正方体的关系.长方体对角线的性质.能利用长方体对角线的性质计算有关长度与角度的问题. 解决棱柱中有关线线、线面、面面问题时,常用的方法是推理法、向量法,推理及运算时要灵活的结合运用棱柱的性质 六、课后作业:七、板书设计(略) 八、课后记:A C 1。
