2机械波答案(三学时) 大学物理下 西南交大峨眉校区
第2节 机械波(答案详解)

第2节机械波课时作业基础巩固(限时:20分钟满分:50分)一、选择题(有7题,每题6分,共42分)1.下列关于机械波的说法中,正确的是( A )A.发生干涉现象时,介质中振动加强的质点,振动的振幅最大,减弱点振幅可能为零B.产生多普勒效应的原因是波源频率发生了变化C.在一个周期内,介质的质点所走过的路程等于波长D.某一频率的声波,从空气进入水中时,波长和频率均增大解析:发生干涉现象时,介质中振动加强的质点振幅最大,减弱的点振幅最小,若两列波的振幅相等,减弱点的振幅可能为零,故A正确;产生多普勒效应的原因是振源与观察者之间距离变化,使观察者接收到的频率发生了变化,但波源频率并不改变,故B错误;质点简谐振动时,一个周期内通过的路程是四个振幅,与波长无关,故C错误;波速由介质决定,频率由波源决定,当声波从空气进入水中时,频率不变,波速变大,则波长变大,故D错误。
2. (2021·湖北新高考适应性考试)一列简谐横波沿x轴正方向传播,其波速为10 m/s,t=0时刻的波形如图所示。
下列说法正确的是( A )A.0~0.6 s时间内,质点P运动的路程为18 cmB.t=0.6 s时刻,质点P相对平衡位置的位移是6 cmC.t=1.2 s时刻,质点Q加速度最大D.t=1.4 s时刻,质点M沿y轴负方向运动解析:由题图可知,该波的波长为λ=8 m,波的周期T=λ=0.8 s,0~0.6vs时间内,质点P的路程s=3A=18 cm,故A正确;t=0.6 s时刻,质点P 处于平衡位置,相对平衡位置的位移为0,故B错误;t=1.2 s时刻,质点Q处于平衡位置,加速度为零,故C错误;t=1.4 s时刻,质点M处于波谷和平衡位置之间,沿y轴正方向运动,故D错误。
3.简谐横波在同一均匀介质中沿x轴正方向传播,波速为v。
若某时刻在波的传播方向上,位于平衡位置的两质点a、b相距为s,a、b之间只存在一个波谷,则从该时刻起,下列四幅波形图中质点a最早到达波谷的是( D )解析:根据机械波传播方向与质点振动方向之间的关系可知,A、C选个项中的质点a此时刻沿y轴正方向振动,a点要到达波谷至少还需34周期,B 、D 选项中的质点a 此时刻沿y 轴负方向振动,只需再经过14个周期即可第一次到达波谷。
大学物理2,12第十二章思考题

1、机械波的波函数为y = 0.03cos6π(t + 0.01x )上式中的各个物理量均采用国际单位。
该波的振幅、周期和波速分别为多少?该波沿着什么方向传播?【答案:0.03m ;1/3s ;100m/s ,x 轴负方向】详解:该波的振幅、周期和波速分别为m 03.0=Aπ6π2π2==ωT )s (31= (m/s)10001.01==u 由于变量x 前的符号为+,因此该波沿着x 轴负方向传播。
2、已知一列平面简谐波的波函数为y = A cos[ (at -bx ) +α](a 、b 和α均为正常量)则该波的频率、波长、周期和波速分别为多少? 【答案:π2a ;b 2π;a π2;ba 】 详解:将题目所给的平面简谐波的波函数与标准平面简谐波的波函数](cos[ϕω+-=uxt A y比较,即得该平面简谐波的频率、周期和波速分别为π2π2a ==ων a T π21==ν ba bu ==ω该波的波长为buT 2π==λ 3、一列平面简谐波沿x 正方向传播,波函数为]2π)42(π2cos[10.0--=x t y上式中的各个物理量均采用国际单位。
试画出该波在0.5s 时刻的波形图。
【答案:见题解图】详解:在0.5s 时刻的波形方程为]2π)425.0(π2cos[10.0--=x y )2πcos(10.0x -=x 2πcos 10.0= 因此,该时刻的波形图为4、在简谐波传播的过程中,沿传播方向相距为半个波长的两点的振动速度之比等于多少?(设这两点都不在最大位移处) 【答案:-1】详解:根据波长的定义,在简谐波传播的过程中,沿传播方向相距为一个波长的两点振动的相位相同,那么相距为半个波长的两点振动必然相位相同,即它们的速度大小相等、方向相反,如果这两点不处于最大位移处,它们振动速度之比必然等于-1。
5、一列声波在空气中的波长是0.25m ,传播速度是340m/s ,当它进入另一种介质时,波长变成了0.35m ,则它在该介质中的传播速度为多少? 【答案:503m/s 】详解:一列波从一种介质进入另一种介质时,其频率保持不变。
《大学物理》习题库试题及答案___05_机械波习题

一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是 [ b ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动 (D) D 点振动速度小于零[ d ]3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B[ c ]u=λ/T C=ϖ/u4.3413:下列函数f (x 。
t)可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播-的行波?(A) )A(bt),tf-=cos(xaxax(bt),Atf+xcos(=(B) )(C) bttAaxxf sin(⋅),sin==(D) btt(⋅axxA),cosf cos[a]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反(B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反[ a ]6.3483:一简谐横波沿Ox轴传播。
若Ox轴上P1和P2两点相距λ /8(其中λ为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同(B) 方向总是相反(C) 方向有时相同,有时相反(D) 大小总是不相等[ c ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则(A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大(D) 振动频率越低,波速越大[ B ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
大学物理波动篇机械波复习题及答案课件

种不同的媒质中传播, 在分界面上的 P 点
相遇, 频率n = 200Hz, 振幅A1=A2=2.00 10-
2m, S2 的位相比 S1 落后 /2。在媒质1中
波速 u1= 800 m s-1, 在媒质2中波速 u2=
1000 m s-1 , S1P=r1=4.00m,
静止的点。求两波的波长和两波源间最 小位相差。
o
S1
S2
x
d
29
解: 设S1 和 S2的振动初位相分别为 1 和 2在 x1点两波引起的振动位相差
2 2 d x1/ 1 2 x1 / 2k 1
2 1 2 d 2 x1/ 2k 1 (1)
在x2点两波引起的振动位相差
2 2 d x2/ 1 2 x2 / 2k 3
波分别通过图中的 o1和 o2 点,通过 o1 点 的简谐波在 M1M2 平面反射后,与通过 o2 点的简谐波在 P 点相遇,假定波在M1M2平 面反射时有半波损失,o1 和 o2 两点的振动
方程为,y10=Acos(2t) 和 y20=Acos(2t) , 且 o1m+mp=16,o2P = 6 (为波长) 求:
(A)波速为C/B; (B)周期为 1/B;
(C)波长为C/2 ; (D)圆频率为 B。
[]
5
5.一平面简谐波沿正方相传播, t=0 时刻的
波形如图所示, 则 P 处质点的振动在 t=0 时
刻的旋转矢量图是
y
u
A
x
o
P
( A)
o
x
A
(B)
o
x
A
(C ) A o
x
A
(D)
大学物理机械波习题附问题详解
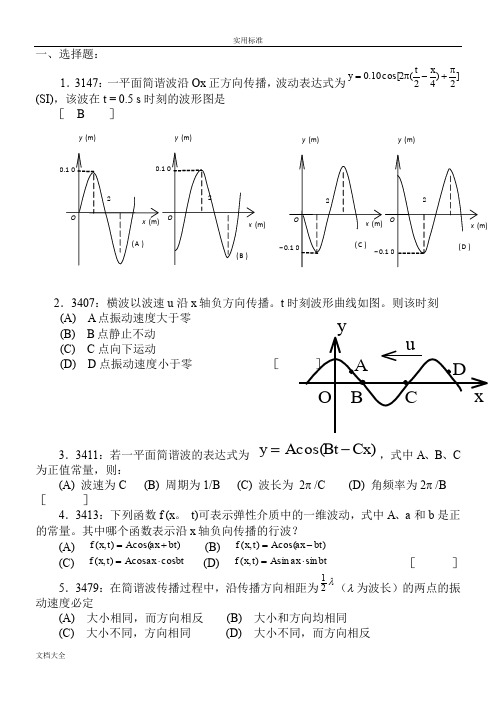
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反y (m) y (m) - y (m) y (m)[ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长 (B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
《大学物理》习题训练与详细解答四(机械波)

2 2 u Tu
x 2 的 振 动 方 程 为 : y A c o s ( t ) A c o s ( t . ) 8 u 2 8 2 y A c o s ( t ) 4 3 x 2 3 x 的 振 动 方 程 为 : y A c o s ( t ) A c o s ( t . ) 8 u 2 8 2 y A c o s ( t ) 4
答案为:(A)
4
4.图2所示,一平面简谐波沿OX轴正向传播,波长为 A c o s ( 2 v t ) ,则P2点 若P1点处质点的振动方程为 y 1 处质点的振动方程为
与P1点处质点振动状态相同的那些点的位置是
L L y c o s [2 ( t 1 2) ] 2 A x L k (k 1 , 2 ......) 1
( 2 )试以 A 点 距 5 cm 处的 B 点 (A 在 的左边)为坐标 出 原 波 点写
A c o s ( t ) 解:(1)对照振动方程的标准形式 y 0 可得 A 0 . 0 3 m ,, 0 = 4 0
c20 m /s ,沿x轴正向传播的波的波 以A为坐标原点、 动方程 y Acos[ (t x) ] 0 u x y 0.03cos4 (t ) (m ) 注意单位转换 20
t x y Acos[2 ( ) 0 ] T x y 0.1cos[4 (t ) 0 ] 20
15
又t 0 , y A c o s A , 0 0 0
x y 0 . 1 cos 4 ( t ) ( m ) ( x 0 ) 20 (2)由波动方程求t0时刻的波形方程,只须令波动方程 的t为常数t0. 则所求t=T/4时刻的波形方程为
《大学物理》习题册题目及答案第16单元 机械波
第16单元 机械波(一)学号 姓名 专业、班级 课程班序号一 选择题[ C ]1.在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的 (B) 波源振动的速度与波速相同 (C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后 (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前[ A ]2. 一横波沿绳子传播时的波动方程为)104cos(05.0t x y ππ-= (SI),则(A) 其波长为0.5 m (B) 波速为5 m ⋅s -1(C) 波速为25 m ⋅s -1 (D)频率为2 Hz[ C ]3. 一简谐波沿x 轴负方向传播,圆频率为ω,波速为u 。
设t = T /4时刻的波形如图所示,则该波的表达式为: (A) )/(cos u x t A y -=ω (B) ]2/)/([cos πω+-=u x t A y (C) )/(cos u x t A y +=ω (D) ])/([cos πω++=u x t A y[ D ]4. 一平面简谐波沿x 轴正向传播,t = T/4时的波形曲线如图所示。
若振动以余弦函数表示,且此题各点振动的初相取π-到π之间的值,则 (A) 0点的初位相为00=ϕ(B) 1点的初位相为 21πϕ-=(C) 2点的初位相为 πϕ=2(D) 3点的初位相为 23πϕ-=[ D ]5. 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中: (A) 它的动能转换成势能。
(B) 它的势能转换成动能。
(C) 它从相邻的一段质元获得能量其能量逐渐增大。
(D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小。
二 填空题1.频率为100Hz 的波,其波速为250m/s ,在同一条波线上,相距为0.5m 的两点的相位差为52π. 2. 一简谐波沿x 轴正向传播。
1x 和2x 两点处的振动曲线分别如图(a)和(b)所示。
4.西邮大物答案-机械波
一、选择题:1.B 2.C 3.B 4.A 5.C 6.D二、填空题:1. 3π 2.),3,2,1( , ; 2 =±+-k k L L λφλπ 3.Hz m m 125 , 2.0 , 8.04.] 2) 2 (2 cos[ ; ] 2) 2 (2 cos[πλππλπ--=+--=t u A y u x t uA y P 5.] ) (2 cos[1πλνπ++=x t A y ; ) 2 2 c o s () 22 c o s (2ππνπλπ+⋅+⋅=t x A y 6.] ) 2 ( cos[ 0πω+-+=ux x t A y 三、计算题: 1 解: (1)已知波动方程 )cos(Cx Bt A y -= (0≥x )和标准形式)22cos(λππυx t A y -= 比较得:波振幅为A ,频率πυ2B =,波长C πλ2=,波速C B u ==λυ,周期B T πυ21==. (2)将l x =代入波动方程得 )cos(Cl Bt A y -=(3)因任一时刻t 同一波线上两点之间的位相差为 )(212x x -=∆λπφ 将d x x =-12,及Cπλ2=代入上式,即得 Cd =∆φ 2 解: (1)图知,1.0=A m ,且0=t 时,0,000>=v y ,∴230πφ=, 又5.225===λυu Hz ,则ππυω52== 则波动方程为)]235(5cos[1.0ππ+-=x t y m (2) 0=t 时的波形为(b)图图(b) 图(c)将5.0=x m 代入波动方程,得该点处的振动方程为)5cos(1.0)235.05.055cos(1.0πππππ+=+⨯-=t t y m 振动曲线(c)图所示. 3解: (1) u w I = 53106300100.18--⨯=⨯==u I w 3m J -⋅ 4max 102.12-⨯==w w 3m J -⋅ (2) νπλπωu d w d w V W 224141===7251024.9300300)14.0(41106--⨯=⨯⨯⨯⨯=πJ .4.解::设 , 21S S 连线及延长线为 x 方向,以 1S 为坐标原点,则:m 4=λ ,令:m S S l 1121==P O P ’ Q1S 2S(1) 2S 右侧 m x 11>(取Q 点),则从 21,S S 分别传播来的两波在Q 点的相位差为:πλπφλπφφφ5)](2[2201021-=----=-l x x 11m x >∴处各点均因干涉而静止。
大学物理同步训练第版机械波详解
同步训练答案第五章 机械波许照锦第五章 机械波一、选择题1. 已知一平面简谐波的波动表达式为y =6cos (πt −3πx +π/2)(SI ),则 (A )其波速为3 m/s (B )其波速为1/3 m/s (C )其频率为πHz(D )其频率为1.5Hz答案:B分析:由波动方程可知ω=π,k =3π,故频率f =ω2π⁄=0.5Hz ,波速u =ωk ⁄=1/3m/s 。
2. 一平面简谐波的波形曲线如图1所示,则 (A )其周期为8s (B )其波长为10m(C )x =6m 的质点向右运动(D )x =6m 的质点向下运动答案:D分析:如图分析可得该简谐波的波长为λ=8m ,B 选项错误;将波沿着波传播方向做一微小平移(如图中红色虚线所示),可得x =6m 的质点向下运动,故D 选项正确。
该图信息不全,无法得到波的周期,A 选项错误;质点仅在其平衡位置来回振动,不会随波一起运动,故C 选项错误。
3. 如果上题中的波速u =10 m/s ,则其频率为 (A )1.25 Hz (B )1 Hz(C )0.8 Hz(D )条件不够,无法求解答案:A分析:由波速的计算公式u =ωk ⁄=λT ⁄=fλ可得其频率为f =u λ⁄=1.25 Hz ,故A 正确。
4. 有一平面简谐波沿Ox 轴的正方向传播,已知其周期为0.5 s ,振幅为1 m ,波长为2 m ,且在t =0时坐标原点处的质点位于负的最大位移处,则该简谐波的波动方程为 (A )y =cos(πt −4πx +π) (B )y =cos(4πt +πx +π)(C )y =cos(4πt −πx −π)(D )y =cos(4πt −πx ) 答案:C分析:由已知条件可得振幅A =1 m ,角频率ω=2πT ⁄=4π rad/s ,角波数k =2πλ⁄=π 1/m ,由波沿正向传播可得角波数前符号为负,由初始条件及旋转矢量图可得原点处质点振动初相为φ=π或−π,代入波动表达式y =cos(ωt −kx +φ)可得y =cos(4πt −πx −π)。
机械波习题答案
第十一章 机械波一. 选择题[ C ]1. 一沿x 轴负方向传播的平面简谐波在t = 2 s 时的波形曲线如图所示,则原点O 的振动方程为 (A) )21(cos 50.0ππ+=t y , (SI). (B) )2121(cos 50.0ππ-=t y , (SI).(C) )2121(cos 50.0ππ+=t y , (SI).(D) )2141(cos 50.0ππ+=t y ,(SI).提示:设O 点的振动方程为O 0()cos()y t A t ωϕ=+。
由图知,当t=2s 时,O 点的振动状态为:O 0(2)cos(2)=0 0y A v ωϕ=+>,且,∴0322πωϕ+=,0322πϕω=-,将0ϕ代入振动方程得:O 3()cos(2)2y t A t πωω=+-。
由题中所给的四种选择,ω取值有三种:,,24πππ,将ω的三种取值分别代入O 3()cos(2)2y t A t πωω=+-中,发现只有答案(C )是正确的。
[ B ]2. 图中画出一向右传播的简谐波在t 时刻的波形图,BC 为波密介质的反射面,波由P 点反射,则反射波在t 时刻的波形图为提示:由题中所给波形图可知,入射波在P 点的振动方向向下;而BC 为波密介质反射面,故在P 点反射波存在“半波损失”,即反射波与入射波反相,所以,反射波在P 点的振动方向向上,又P 点为波节,因而得答案B 。
[ A ]3. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是提示:由图可知,P 点的振动在t=0[ B ]4. 一平面简谐波在弹性媒质中传播时,某一时刻媒质中某质元在负的最大位移处,则它的能量是(A) 动能为零,势能最大. (B) 动能为零,势能为零. (C) 动能最大,势能最大. (D) 动能最大,势能为零.提示:动能=势能,在负的最大位移处时,速度=0,所以动能为零,势能也为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《大学物理(下)》作业 No.2 机械波
班级 学号 姓名 成绩
一 选择题
1.一横波沿弹性绳传播时的波动方程为y=0.05cos(4πx-10πt)(SI),则
(A)其波长为0.5m (B)波速为5m/s
(C)波速为25m/s (D)频率为2HZ
[ A ]
提示: y=0.05cos(4πx-10πt)=0.05cos(10πt-4πx),
ω=10πrad/s,υ=5Hz,λ=0.5m,v=2.5m/s
2.一平面简谐波,沿x轴负方向传播,圆频率为ω,波速为u,设t=T/4时刻的波形如图,则该波的波动
方程为
(A)y=Acosω(t-x/u)
(B)y=Acos[ω(t-x/u)+π/2]
(C)y=Acosω(t+x/u)
(D)y=Acos[ω(t+x/u)+π]
[ D ]
提示: 以O点为参考点,初始时刻的波形图应是T/4时刻的波形向波传播的反方向平移λ/4,依此可求
出O点振动的初相位为π
或:O点T/4时的旋转矢量沿顺时针方向转π/2。
3.一简谐波沿x轴正方向传播,t=T/4时的波形曲线如图所示,若振动以余弦函数表示,同时各点振动的
初相位取-π到π之间的值,则
(A)0点的初相位为φ0=0
(B)1点的初相位为φ1=-π/2
(C)2点的初相位为φ2=π
(D)3点的初相位为φ3=-π/2
[ D ]
提示:同上题可得:0、1、2、3点的初相位分别为π、π/2、0、-π/2。
或:T/4时后一个点的相位是前一个点初始时刻的相位经过T/4传过来的。
或:各点T/4时的旋转矢量沿顺时针方向转π/2。
4.如图所示,S1和S2为两相干波源,它们的振动方向垂直于图面,均产生波长λ的简谐波,并且波在P
点相遇后发生干涉相消,已知S1P=2 λ ,S2P=2.2 λ 。若S1的振动方程为y1= Acos(2πt+π/2),则S2的
振动方程为
(A)y2= Acos(2πt-π/2)
(B)y2= Acos(2πt-π)
(C)y2= Acos(2πt+π/2)
(D)y2= Acos(2πt-0.1π)
[ D ]
提示:由相干波源条件知ω=2πrad/s,振幅为A,
由于r1与r2的存在而产生的相位差为0.4π,设S2的初相位为φ2,则:
φ2-π/2-0.4π应为π的整数倍,只有答案D满足。
5. 一平面简谐波在弹性媒质中传播,在媒质质元从最大位移处回到平衡位置的过程中
(A) 它的势能转换成动能. (B) 它的动能转换成势能.
A
-A
O
y
u
x
A
-A
O
y
u
x
1
2
3
4
S
1
S2
r1
r2
P
(C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加.
(D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小.
[ C ]
二 填空题
1. 沿弦线传播的一入射波在x = L处(B点)发生反射,反射点为自由端(如
图).设波在传播和反射过程中振幅不变,且反射波的表达式为
)(2cos2xtAy, 则入射波的表达式为y1 =2cos2()xLAt
.
提示:因为是自由端无半波损失,则入射波和反射波在B点引起振动相同:
)(2cosLtAyB,由此入射波波函数为:1cos[2()2]LLxyAt
2. S1,S2为振动频率、振动方向均相同的两个点波源,振动方向垂直纸面,两者
相距23(为波长)如图.已知S1的初相为21.
(1)若使射线S2C上各点由两列波引起的振动均干涉相消,则S2的初相应为
2,1,0
2
2kk
.
(2)若使S1 S2连线的中垂线MN上各点由两列波引起的振动均干涉相消,则S2的初位相应为
2,1,0
2
2kk
.
3. 一声源的振动频率为S,相对于空气以vS的速率运动,在其运动方向上有一相对于空气为静止的接收
器R.设声波在空气中的传播速度为u,则接收器R接收到的声波频率R = ssvuu .
4.有两列波动方程分别为y1= Acos2π(νt-x/λ)和y2= Acos2π(νt+x/λ)且沿相反方向传播的相干波
叠加后形成驻波,其波腹位置的坐标为 2,1,02kkx 。
提示:驻波波函数为txAyyy2cos2cos221,
波腹满足12cosx,即,2,1,02kkx
解得:2,1,02kkx
三 计算题
1. 在弹性媒质中有一沿x轴正向传播的平面波,其表达式为)214cos(01.0xty (SI).若在x =
S1 S2
M
N
C
B x
y
O
L
y
2
5.00 m处有一媒质分界面,且在分界面处反射波相位突变,设反射波的强度不变,试写出反射波的表达
式.
参考解答:反射波在x=5m处引起的振动为:
)2154cos(01.00ππty
(SI)
以x=5m处为参考点得到波函数为:
150.01cos(452)2210.01cos(4)()2xyttxSI
ππ
ππ
2. 如图所示,S1,S2为两平面简谐波相干波源.S2的相位比S1的相位超前/4 ,波长 = 8.00 m,r1 = 12.0
m,r2 = 14.0 m,S1、S2在P点引起的振动振幅分别为0.30 m、 0.20 m,求P点的合振幅.
参考解答:
4
)(24)(2121212rr
rr
)(464.0cos2212221mAAAAA
3. 一列平面简谐波在媒质中以波速u = 5 m/s沿x轴正向传播,原点O处质元的振动曲线如图所示.
(1) 求解并画出x = 25 m处质元的振动曲线.
(2) 求解并画出t = 3 s时的波形曲线.
参考解答:
对原点,radsradmA2,/2,10202,其振动方程为:
20210cos()()22ytm
π
波函数为:2210cos[()]()252xytmπ
(1)x=25m处振动为:225210cos(1)()2tym
(2)t=3s时波函数:
23210cos(1)()10sxym
t (s)
4
2
O
y (cm)
2
P
S1
S2
r1
r2
