2.3.3-4直线与平面垂直、平面与平面垂直的性质导学案
2.3.3-2.3.4直线与平面垂直的性质

2 a,E 为 PA 的中点.
求证:平面 EDB⊥平面 ABCD.
名师导引:证明平面 EDB⊥平面 ABCD 的思路是 什么?(在平面 EDB 内寻找一条直线与平面 ABCD 垂直) 证明:设 AC EO∥PC. BD=O,连接 EO,E 为 PA 的中点,则
∵PC=CD=a,PD=
2 2 2
2 a,
跟踪训练 1 1:如图所示,在正方体 ABCD A1B1C1D1 中, M 是 AB 上一点,N 是 A1C 的中点,MN⊥平面 A1DC.
求证:(1)MN∥AD1; (2)M 是 AB 的中点.
证明:(1)∵四边形 ADD1A1 为正方形, ∴AD1⊥A1D. 又 CD⊥平面 ADD1A1, ∴CD⊥AD1. ∵A1D CD=D, ∴AD1⊥平面 A1DC. 又 MN⊥平面 A1DC, ∴MN∥AD1. (2)连接 ON,在△A1DC 中, A1O=OD,A1N=NC,
l⊥β)
1:地面上有两根相距 a 米的与地面 垂直的立柱,它们的高分别是 b 米和 c 米(b>c), 则它们上端的距离为 米.
解析:如图所示,根据题意可 知 AD=b,BC=c,AB=a,由线面垂 直的性质可得这两根立柱平 行,过点 C 向 AD 作垂线,设垂 足为 E,则可得 CD= 答案:
2.3.3 直线与平面垂直的性质 2.3.4 平面与平面垂直的性质
课前预习
栏 目 导 航
课堂探究
【课标要求】
1.通过直观感知、操作确认,归纳出直线与 平面、平面与平面垂直的性质定理. 2.掌握直线与平面垂直,平面与平面垂直 的性质,并能运用性质定理解决一些简单 问题. 3.掌握平行与垂直之间的转化.
【实例】 在日常生活中常见到一排排和地面垂 直的电线杆.一排电线杆中的每根杆都与地面 垂直,那平面垂直的性质定理
《直线与平面平面与平面垂直的性质》导学案

第7课时直线与平面、平面与平面垂直的性质1.理解直线与平面垂直、平面与平面垂直的性质定理,能用图形语言和符号语言表述这些定理,并能加以证明.2.能运用直线与平面垂直、平面与平面垂直的性质定理证明一些空间位置关系的简单问题.装修工人在安装门窗时,经常使用铅垂线对比门窗,测量门窗是否安装得竖直,这是应用了什么原理?装修工人判断的依据是什么?问题1:(1)上述情境中,装修工人应用了直线与平面垂直的性质定理,因为铅垂线受重力影响始终是与地面的,当装修工人把铅垂线与门的边线靠近时,观察上下铅垂线与门线间的间隔是否一致,当线上间隔不同时,说明门线与铅垂线,也就说明门安装得.(2)直线与平面垂直的性质定理及表示:垂直于同一个平面的两条直线平行.符号表示:.问题2:叙述平面与平面垂直的性质定理,并根据图形用符号语言写出这个定理.性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线与另一个平面垂直.符号表示:.问题3:空间中垂直关系是如何转化的?由线面垂直和面面垂直的判定定理和性质定理可知,线线垂直、线面垂直及面面垂直的转化关系可用下图表示:由上图可以看出,几种垂直关系的转化就是线面和面面垂直的判定定理和性质定理的反复交替运用的结果.在线线垂直和线面垂直的转化中,平面在其中起到了至关重要的作用,应考虑线和线所在平面的特征,以找出需要证明的转化.如证线线垂直,可先证线面垂直,进而由性质定理得到线线垂直.因此,关系是线线垂直、面面垂直关系的枢纽.问题4:关于线面垂直、面面垂直,还有其他重要结论吗?直线和平面垂直的两个重要结论:①过一点有且平面和已知直线垂直.②过一点有且直线和已知平面垂直.平面和平面垂直的两个重要结论:①若两个平面垂直,则过第一个平面内的点作第二个平面的垂线必在平面内.②两个相交平面同时垂直第三个平面,则它们的交线于第三个平面.1.已知a、b为异面直线,b与c垂直,则().A.a⊥cB.b∥cC.b与c相交D.不确定2.下列说法中正确的个数为().①如果一条直线垂直于一个平面内的无数条直线,那么这条直线和这个平面垂直;②过空间一点有且只有一条直线与已知平面垂直;③一条直线和一个平面不垂直,那么这条直线和平面内的所有直线都不垂直;④垂直于同一平面的两条直线平行.A.1B.2C.3D.43.已知l,m是直线,α,β,γ是平面,给出下列说法:①若α⊥β,且β⊥γ,则α∥γ;②若α∩β=l,且l⊥γ,则α⊥γ且β⊥γ;③若l⊥α,α⊥β,则l∥β.其中正确的是.4.如图,四边形ABCD是平行四边形,直线SC⊥平面ABCD,E是SA的中点,求证:平面EDB⊥平面ABCD.线面垂直的性质定理的应用如图,已知正方体ABCD—A1B1C1D1中,EF与异面直线AC、A1D都垂直相交,求证:EF∥BD1.线面垂线的判定与性质的综合应用如图,已知α∩β=AB,EC⊥平面α,C为垂足,ED⊥平面β,D为垂足.求证:CD⊥AB.面面垂直的性质定理的应用如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD=4,M是AE的中点.求证:平面BDM⊥平面ECA.已知a、b为异面直线,AB与a、b都垂直相交,若a⊥α,b⊥β,且α∩β=c.求证:AB∥c.已知底面为正方形的四棱锥P—ABCD的侧棱PA⊥底面ABCD,过点A在侧面PAB内作AE⊥PB于E,过E作EF⊥PC于F.那么图中AF与PC的位置关系如何?如图,在△ABC中,∠BAC=60°,线段AD⊥平面ABC,E为CD上一点,且平面ABE⊥平面DBC.求证:点A在平面DBC内的射影不可能是△BCD的垂心.1.设a,b是两条异面直线,下列说法中正确的是().A.有一平面与a,b都垂直B.有且仅有一条直线与a,b都垂直C.过直线a有且仅有一平面与b平行D.过空间中任一点必可以作一直线与a,b都相交2.已知直线l⊥平面α:①若直线m⊥l,则m∥α;②若m⊥α,则m∥l;③若m∥α,则m⊥l;④若m∥l,则m⊥α,上述判断正确的是().A.①②③B.②③④C.①③④D.②④3.把Rt△ABC斜边上的高CD折成直二面角A-CD-B后,互相垂直的面有对.4.三棱锥P—ABC中,PB=PC,AB=AC,点D为BC中点,AH⊥PD于点H,连接BH,求证:平面ABH⊥平面PBC.(2013年·天津卷改编)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.证明:B1C1⊥CE.考题变式(我来改编):答案第7课时直线与平面、平面与平面垂直的性质知识体系梳理问题1:(1)垂直不平行不竖直(2) a⊥α,b⊥α⇒a∥b问题2:α⊥β,α∩β=l, AB⊂β,且AB⊥l于B⇒AB⊥α问题3:线面垂直问题4:只有一个只有一条第一个垂直基础学习交流1.D因为b与c垂直,故b与c可能相交,也可能异面,于是,a与c的关系不确定.2.B①错误,无数条直线可能是平行直线,不能判断直线和平面垂直;②正确;③错误,与该直线在平面内的正投影垂直的所有直线,都与该直线垂直;④正确.3.②①错误,反例是墙角处三个平面两两垂直.②正确,因为如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.③错误,还可能l⊂β.4.解:连接AC交BD于点O,连接EO,因为四边形ABCD是平行四边形,所以O是AC的中点,且E是SA的中点,所以EO∥SC.因为SC⊥平面ABCD,所以EO⊥平面ABCD,且EO⊂平面EDB,所以平面EDB⊥平面ABCD.重点难点探究探究一:【解析】连接AB1,B1C,BD,∵DD1⊥平面ABCD,AC⊂平面ABCD,∴DD1⊥AC.又∵AC⊥BD,∴AC⊥平面BDD1B1,∴AC⊥BD1.同理BD1⊥B1C,∴BD1⊥平面AB1C.∵EF⊥A1D,且A1D∥B1C,∴EF⊥B1C.又∵EF⊥AC,∴EF⊥平面AB1C,∴EF∥BD1.【小结】当题目所给的条件垂直关系较多,但又需要证明平行关系时,往往要考虑垂直的性质定理,从而完成由垂直关系向平行关系的转化.探究二:【解析】∵EC⊥α,AB⊂α,∴EC⊥AB,同理ED⊥AB,即AB⊥EC,AB⊥ED,又EC∩ED=E,∴AB⊥面ECD,而CD⊂面ECD,∴AB⊥CD.【小结】本题是线线垂直、线面垂直的循环.证明线线垂直、则要先证明线面垂直,关键就是面的选择,选择过哪条直线的平面与另一条直线垂直.探究三:【解析】(1)取AC的中点F,连接MF、BF,则MF∥CE且MF=CE.又∵BD∥CE,BD=CE,∴MF∥BD,MF=BD,∴四边形MFBD是平行四边形,∴DM∥BF.∵EC⊥平面ABC,EC⊂平面ACE,∴平面ACE⊥平面ABC.又∵BF⊥AC,∴BF⊥平面ACE.又∵DM∥BF,∴DM⊥平面ACE.又∵DM⊂平面BDM,∴平面BDM⊥平面ECA.【小结】证明面面垂直的关键点和难点,就是在一个平面内确定另一个平面的垂线,一旦找错垂线,将给问题的解决带来很大麻烦,也是不可证明的.确定这条垂线的基本方法就是根据平面与平面垂直的性质,要着眼于平面内交线的垂线,若图形中没有现成的垂线,需要根据条件作出交线的垂线,再证明此直线垂直于另一个平面.思维拓展应用应用一:如图,过点B作BB1⊥α,则BB1∥a,∴AB⊥BB1.又∵AB⊥b,∴AB垂直于由b和BB1确定的平面.∵b⊥β,∴b⊥c,同理,BB1⊥c,∴c也垂直于由b和BB1确定的平面,∴AB∥c.应用二:∵F∈PC,∴AF与PC相交,只要进一步考察是否垂直.如果有AF⊥PC,由已知EF⊥PC,EF∩AF=F,得PC⊥面AEF,∴PC⊥AE.又已知AE⊥PB,PC∩PB=P,得AE⊥面PBC,∴AE⊥BC.而由PA⊥BC,AB⊥BC,知BC⊥面PAB,可知BC⊥AE成立.∴AF⊥PC成立.于是,图中AF与PC垂直相交.应用三:过点A作AH⊥BE,H为垂足.∵平面ABE⊥平面DBC,AH⊂平面ABE,平面ABE∩平面DBC=BE,∴AH⊥平面DBC,∴点H即为点A在平面DBC内的射影.假设H是△BCD的垂心,则BE⊥CD.∵AH⊥平面BCD,DC⊂平面DBC,∴AH⊥DC.又∵AH∩BE=H,∴CD⊥平面ABE.又∵AB⊂平面ABE,∴CD⊥AB.∵AD⊥平面ABC,AB⊂平面ABC,∴AD⊥AB,又∵AD∩CD=D,∴AB⊥平面ACD,∴AB⊥AC,这与已知中∠BAC=60°相矛盾,∴假设不成立,∴点A在平面DBC内的射影不可能是△BCD的垂心.基础智能检测1.C A中若有一平面与a,b都垂直,则a∥b,矛盾;B中将a,b平移到一个平面内,则与该平面垂直的直线与a,b 都垂直;C正确;D中设过直线a且与b平行的平面为α,则在平面α内过直线a之外的点,不可能作一直线与a,b都相交.2.B①错,还有可能m⊂α;②正确;③正确;④正确.3.3平面BCD⊥平面ACD,平面ADB⊥平面BCD,平面ABD⊥平面ADC.4.解:∵PB=PC,AB=AC,BD=DC,∴BC⊥PD且BC⊥AD,∴BC⊥面PAD,∴面PAD⊥面PBC.∵AH⊥PD,面PAD∩面PBC=PD,∴AH⊥面PBC.又AH⊂面ABH,于是面AHB⊥面PBC.全新视角拓展因为侧棱CC1⊥底面A1B1C1D1,B1C1⊂平面A1B1C1D1,所以CC1⊥B1C1.经计算可得B1E=,B1C1=,EC1=,从而B1E2=B1+E,所以在△B1EC1中,B1C1⊥C1E,又CC1,C1E⊂平面CC1E,CC1∩C1E=C1,所以B1C1⊥平面CC1E,又CE⊂平面CC1E,故B1C1⊥CE.思维导图构建α∥βb⊥αl⊥β。
“直线与平面,平面与平面垂直导学案

拨
提
升
例3如图,四棱锥P—ABCD的底面矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.求证:侧面PAB⊥侧面PBC;
例4如图,已知 于点A, 于点B, , ,且
求证: ∥
B
A
C
达
标
检
测
1判断下列命题的真假
①两个平面垂直,过其中一个平面内一点作与它们交线垂直的直线,必垂直于另一个平面.( )
②两个平面垂直,分别在这两个平面内且互相垂直的两直线,一定分别与另一平面垂直.( )
③两个平面垂直,分别在这两个平面内的两直线互相垂直.( )
④两个平面垂直,一个平面内的任一条直线必垂直于另.
一个平面( )
⑤两个平面垂直,一个平面内的已知直线必垂直于另一个平面内的无数条直线.( )
2如图,在四棱锥 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
符号表示:
二、新知探究
1.直线和平面垂直的性质
已知 ,求证
2平面与平面垂直的性质
如图,若α⊥β,α∩β=CD,AB α,AB CD于B,求证
文字语言表示:
符号表示:
互
动
交
流
例1判断下列命题是否正确
1.垂直于同一条直线的两个平面互相平行()
2.垂直于同一个平面的两条直线互相平行()
3.一条直线在平面内,另外一条直线与这个平面垂直,则这两条直线平面与平面垂直的性质
课型
流程
学习内容
个性笔记
明确
目标
1.掌握并会应用直线与平面垂直的性质.
2.掌握并会应用面面垂直的性质.
3.理解线线垂直、线面垂直、面面垂直的内在联系.
直线与平面、平面与平面垂直的性质教案
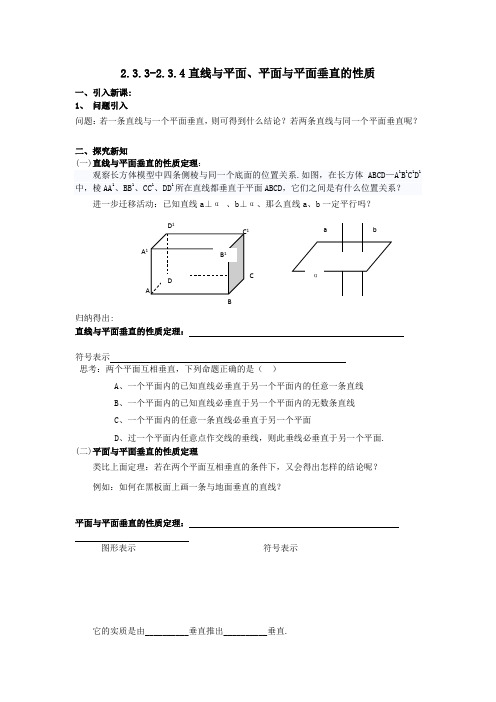
2.3.3-2.3.4直线与平面、平面与平面垂直的性质一、引入新课:1、 问题引入问题:若一条直线与一个平面垂直,则可得到什么结论?若两条直线与同一个平面垂直呢?二、探究新知 (一)直线与平面垂直的性质定理:观察长方体模型中四条侧棱与同一个底面的位置关系.如图,在长方体ABCD —A 1B 1C 1D1中,棱AA 1、BB 1、CC 1、DD 1所在直线都垂直于平面ABCD ,它们之间是有什么位置关系? 进一步迁移活动:已知直线a ⊥α 、b ⊥α、那么直线a 、b 一定平行吗?归纳得出:直线与平面垂直的性质定理:符号表示思考:两个平面互相垂直,下列命题正确的是( )A 、一个平面内的已知直线必垂直于另一个平面内的任意一条直线B 、一个平面内的已知直线必垂直于另一个平面内的无数条直线C 、一个平面内的任意一条直线必垂直于另一个平面D 、过一个平面内任意点作交线的垂线,则此垂线必垂直于另一个平面.(二)平面与平面垂直的性质定理类比上面定理:若在两个平面互相垂直的条件下,又会得出怎样的结论呢? 例如:如何在黑板面上画一条与地面垂直的直线?平面与平面垂直的性质定理:图形表示 符号表示它的实质是由__________垂直推出__________垂直.a bα A 1 B D 1 A C C 1 B 1 D三、运用新知例1:如图,已知 =CA αβα⊥, 于点A ,CB β⊥于点B,,a a AB α⊂⊥, 求证://a .注意:空间内,垂直于同一条直线的两直线平行的结论不成立.思考1: 如图,正方体ABCD-A 1B 1C 1D 1,EF 与异面直线AC ,A 1D 都垂直相交. 求证:EF//BD 1.例2:如图所示,P 是四边形ABCD 所在平面外的一点,ABCD 是∠DAB =60°且边长为a 的菱形.侧面PAD 为正三角形,其所在平面垂直于底面ABCD .(1)若G 为AD 边的中点,求证:BG ⊥平面PAD ;(2)求证:AD ⊥PB .思考2;如图,在三棱锥P -ABC 中,PA ⊥平面ABC ,平面PAB ⊥平面PBC求证:BC ⊥AB .A BC α β l a A BC D A B1 C1 D1 E F。
必修2第二章直线与平面垂直的性质导学案

2.3.3 直线与平面垂直的性质【学习目标】①.掌握直线与平面垂直,平面与平面垂直的性质定理.②.能运用性质定理解决一些简单问题【重点难点】重点:直线与平面垂直性质的简单应用难点: 直线与平面垂直性质的简单应用【使用说明及学法指导】阅读课本P70~P71,完成下列题目预习案一、知识梳理1、 直线与平面垂直的性质定理 :_____________________________________________符号语言: ;直线与平面垂直的性质告诉我们:__________________________________________二、问题导学1、过平面外一点可以作几条直线垂直于这个平面?2、垂直于同一条直线的两条直线是否平行?三、预习自测1、 判断题①.平行于同一条直线的两条直线互相平行; ( )②.垂直于同一条直线的两条直线互相平行; ( )③.平行于同一个平面的两条直线互相平行; ( )④.垂直于同一个平面的两条直线互相平行. ( )⑤.一条直线在平面内,另一条直线与这个平面垂 直,则这两条直线互相垂( ) ⑥ ( )2、已知直线a 、b 和平面α,且a ⊥b ,a ⊥α,则b 与α的位置关系:____________3、如图,AB ∥α,AD ⊥α,BC ⊥α,垂足为D 、C ,PA ⊥AB ,求证:CD ⊥平面PAD.探究案 【例1】:如图 ,四棱锥 P -ABCD 中, P A ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,P A =AB =BC ,点 E 是 PC 的中点.证明:(1)CD ⊥AE ;(2)PD ⊥平面 ABE .//,,a a b b αα⊥⊥则α P D CB A【例2】.如图,已知PA ⊥矩形ABCD 所在平面,M 、N 分别是AB 、PC 的中点 求证:(1);MN CD ⊥(2)若45PDA ∠=,求证:MN ⊥面PCD课堂检测1、已知 b ⊥平面α,a ⊂α, 则直线a 与直线b 的位置关系是( )A .a ∥bB .a ⊥bC .直线 a 与直线 b 垂直相交D .直线 a 与直线 b 垂直且异面2.已知直线a 、b 和平面βα,,下列命题中错误的是( )A .若αα⊥⊥b a b a 则,,//B .若b a b a //,//,,则βαβα⊥⊥C .若b a b a //,//,//,//则βαβαD .若b a b a ⊥⊥⊥⊥则,,,βαβα3. 在正方体ABCD —A 1B 1C 1D 1中,M 为CC 1的中点,AC 交BD 于点O ,求证:A 1O ⊥平面MBD.4.已知H 是锐角三角形ABC 的垂心,过H 作平面ABC 的垂线,在垂线上取一点P ,使∠APB =90º,求证:PB ⊥平面P ACPAB C M N。
直线与平面垂直的性质导学案

直线与平面垂直的性质导学案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN2.3.3直线与平面垂直的性质课前预习学案一、预习目标:通过对图形的观察,知道直线于平面垂直的性质二、预习内容:1、直线与平面垂直的判定方法有哪些?2、在空间,过一点,有几条直线与已知平面垂直?过一点,有几个平面与已知直线垂直3、判断题(判断下列命题是否正确)(1)、在平面中,垂直于同一直线的两条直线互相平行。
(2)、在空间中,垂直于同一直线的两条直线互相平行。
(3)、垂直于同一平面的两直线互相平行。
(4)、垂直于同一直线的两平面互相平行。
4、若直线和平面如果垂直,则其应具备的性质是什么?三、提出疑惑同学们,通过你的自主学习,你还有那些疑惑,请填在下面的表格中疑惑点疑惑内容课内探究学案一、学习目标:(1)明确直线与平面垂直的性质定理。
(2)利用直线与平面垂直的性质定理解决问题。
学习重点:直线和平面垂直的性质定理和推论的内容和简单应用。
学习难点:直线和平面垂直的性质定理和推论的证明,等价转化思想的渗透。
二、学习过程探究一、直线与平面垂直的性质1、如图,长方体ABCD—A′B′C′D′中,棱 A A′、B B′、CC′、D D′所在直线都垂直于平面ABCD,它们之间具有什么位置关系?2、 已知:a α⊥,b α⊥。
求证:b ∥a (由1让学生自行证明) 得直线与平面垂直的性质定理 三种语言刻画 探究二、定理的应用例1已知βαβα//,,求证⊥⊥l l 变式1:下列命题中错误的是()A 、若一直线垂直于一平面,则此直线必垂直于这个平面上的所有直线。
B 、若一个平面通过另一个平面的一条垂线,则这两个平面互相垂直。
C 、若一直线垂直于一个平面的一条垂线,则此直线必平行于这个平面D 、若平面内的一条直线和这个平面的一条斜线的射影垂直,则也和这条直线垂直。
(四)课堂检测 1、课本71P 页:1、2.2、设直线a,b 分别在正方体ABCD —A ′B ′C ′D ′中两个不同的平面内, 欲使b ∥a,a 、b 应满足什么条件?课后巩固练习与提高1.若,,a b c 表示直线,α表示平面,下列条件中,能使a α⊥的是 ( ) ()A ,,,a b a c b c αα⊥⊥⊂⊂ ()B ,//a b b α⊥()C ,,a b A b a b α=⊂⊥ ()D //,a b b α⊥2.已知l 与m 是两条不同的直线,若直线l ⊥平面α,①若直线m l ⊥,则//m α;②若m α⊥,则//m l ;③若m α⊂,则m l ⊥;④//m l ,则m α⊥。
高一数学必修二2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质导学案(解析版)
2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质一、课标解读1.掌握直线和平面垂直的性质定理和推论的内容、推导和简单应用。
2.掌握等价转化思想在解决问题中的运用.3.使学生掌握直线与平面垂直,平面与平面垂直的性质定理.4.能运用性质定理解决一些简单问题.了解直线与平面、平面与平面垂直的判定定理和性质定理间的相互联系.二、自学导引问题1:如图,长方体ABCD —A ′B ′C ′D ′中,棱A A ′、B B ′、C C ′、D D ′所在直线都垂直于平面ABCD ,它们之间具有什么位置关系?问题2:已知:a α⊥,b α⊥。
求证:b ∥a直线和平面垂直的性质定理: 垂直于同一个平面的两条直线平行。
符号语言作用:a b问题3:黑板所在平面与地面所在平面垂直,你们能否在黑板上画一条直线与地面垂直呢?问题4:如图,长方体ABCD-A'B'C'D中,平面A'ADD’与平面ABCD垂直,直线A'A垂直于其交线AD,平面A'ADD’内的直线A'A与平面ABCD垂直吗?问题5:设α⊥β,α∩β=CD,A B α,AB⊥CD,AB∩CD=B,研究直线AB与平面β的位置关系。
归纳得到平面与平面垂直的性质定理:定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
想一想:用符号语言如何表述这个定理?三、典例精析例1 如图所示,正方体1111ABCD A B C D -中,D A AC EF 1及与异面直线都垂直相交. 求证:EF ∥1BD变式训练1 如图所示,已知SA 垂直于ABCD 所在平面,过A 且垂直于SC 的平面分别交 .,,,,G F E SD SC SB 于求证:SB AE ⊥例2 如图所示,平面⊥⊥PAC ABC PAB 平面平面,平面ABC ,⊥AE 平面PBC ,E 为垂足.(1) 求证:ABC PA 平面⊥(2) 当E 为PBC ∆的垂心时,求证:ABC ∆是直角三角形变式训练2 如图所示,是所在平面外一点,是四边形ABCD ABCD P60=∠DAB 且 边长ABCD PAD a 面垂直于底面为正三角形,其所在平的菱形,侧面. (1) 若PAD BG AD G 平面边的中点,求证:为⊥ (2) 求证:PB AD ⊥四、自主反馈 1.两异面直线在平面α内的射影( )A .相交直线B .平行直线C .一条直线—个点D .以上三种情况均有可能2.若两直线a 与b 异面,则过a 且与b 垂直的平面( )A .有且只有—个B .可能存在也可能不存在C .有无数多个D .—定不存在3.在空间,下列哪些命题是正确的( )①平行于同一条直线的两条直线互相平行;②垂直于同一条直线的两条直线互相平行;③平行于同一个平面的两条直线互相平行;④垂直于同—个平面的两条直线互相平行.A .仅②不正确B .仅①、④正确C .仅①正确D .四个命题都正确4.若平面α的斜线l 在α上的射影为l ′,直线b ∥α,且b ⊥l ′,则b 与l ( )A .必相交B .必为异面直线C .垂直D .无法确定5.下列命题①平面的每条斜线都垂直于这个平面内的无数条直线;②若一条直线垂直于平面的斜线,则此直线必垂直于斜线在此平面内的射影; ③若平面的两条斜线段相等,则它们在同一平面内的射影也相等;④若一条线段在平面外并且不垂直于这个平面,则它的射影长一定小于线段的长. 其中,正确的命题有( )A .1个B .2个C .3个 n 4个6.在下列四个命题中,假命题为( )A .如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直B .垂直于三角形两边的直线必垂直于第三边C .过点A 垂直于直线a 的所有直线都在过点A 垂直于a 的平面内D .如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面7.已知P 是四边形ABCD 所在平面外一点且P 在平面ABCD 内的射影在四边形ABCD 内,若P 到这四边形各边的距离相等,那么这个四边形是( )A .圆内接四边形B .矩形C .圆外切四边形D .平行四边形8.在△ABC 中,AB =AC =5,BC =6,P A ⊥平面ABC ,P A =8,则P 到BC 的距离等于( )A .5B .52C .35D .45答案2.3.3 直线与平面垂直的性质2.3.4 平面与平面垂直的性质例1 证明:连接BD C B AB ,,11ABCD AC ABCD DD 平面平面⊂⊥,1D DD BD BD AC AC DD =⊥⊥∴11,, 又111,BD AC B BDD AC ⊥∴⊥∴平面C AB BD C B BD 1111,平面同理可证⊥∴⊥C BD A AD EF AC EF 11//,,又⊥⊥C AB EF C B EF 11,平面⊥∴⊥∴1//BD EF ∴例2 证明(1)在平面F AC DF D ABC 于作内取一点⊥,AC ABC PAC 且交线为平面平面,⊥AP DF PAC PA PAC DF ⊥∴⊂⊥∴,,平面平面AP DG G AB DG ⊥⊥同理可证于作,D DF DG ABC DF DG = 内,且都在平面,ABC PA 平面⊥∴(2)连接H PC BE 于并延长交BE PC PBC E ⊥∴∆的垂心,是又已知AE PC PBC AE ⊥∴的垂线,是平面AB PC ABE PC ⊥∴⊥∴,平面PAC AB AB PA ABC PA 平面平面又⊥∴⊥∴⊥,, 是直角三角形即ABC AC AB ∆⊥∴,变式训练1.SA BC ABCD BC ABCD SA ⊥∴⊂⊥,平面,平面证明:SAB SA SAB AB A SA AB AB BC 平面平面⊂⊂=⊥,,, BC AE SAB AE SAB BC ⊥∴⊂⊥∴,,平面平面 SC AE AEFG AE AEFG SC ⊥∴⊂⊥,,平面平面 SBC BC SBC SC C BC SC 平面平面又⊂⊂=,, SB AE SBC SB SBC AE ⊥∴⊂⊥∴,,平面平面2.略自主反馈1.D 2.B 3.B 4.C 5.A 6.A 7.C 8.D。
第二章 2.3.3~2.3.4 直线、平面与平面垂直的性质
2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质学习目标 1.掌握空间中线面、面面垂直的性质定理.2.能够运用线面、面面垂直的性质定理证明一些简单的问题.3.理解线面垂直、面面垂直的判定定理和性质定理之间的相互联系.知识点一直线与平面垂直的性质定理知识点二平面与平面垂直的性质定理1.如果两条平行直线中的一条垂直于一个平面,则另一条也垂直于这个平面.(√)2.若平面α⊥平面β,任取直线l⊂α,则必有l⊥β.(×)3.若一条直线垂直于两个平行平面中的一个,则该直线也垂直于另一个平面.(√)4.已知两个平面垂直,过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.(×)题型一线面垂直性质定理的应用例1如图,已知正方体A1C.(1)求证:A1C⊥B1D1;(2)M,N分别为B1D1与C1D上的点,且MN⊥B1D1,MN⊥C1D,求证:MN∥A1C. 考点直线与平面垂直的性质题点应用线面垂直的性质定理判定线线平行证明(1)如图,连接A1C1.∵CC1⊥平面A1B1C1D1,B1D1⊂平面A1B1C1D1,∴CC1⊥B1D1.∵四边形A1B1C1D1是正方形,∴A1C1⊥B1D1.又∵CC1∩A1C1=C1,A1C1,CC1⊂平面A1C1C,∴B1D1⊥平面A1C1C.又∵A1C⊂平面A1C1C,∴B1D1⊥A1C.(2)连接B1A,AD1.∵B1C1∥AD,且B1C1=AD∴四边形ADC1B1为平行四边形,∴C1D∥AB1.∵MN⊥C1D,∴MN⊥AB1.又∵MN⊥B1D1,AB1∩B1D1=B1,AB1,B1D1⊂平面AB1D1,∴MN⊥平面AB1D1.由(1)知A1C⊥B1D1.同理可得A1C⊥AB1.又∵AB1∩B1D1=B1,AB1,B1D1⊂平面AB1D1,∴A1C⊥平面AB1D1.∴A1C∥MN.反思感悟证明线线平行的常用方法(1)利用线线平行定义:证共面且无公共点.(2)利用三线平行公理:证两线同时平行于第三条直线.(3)利用线面平行的性质定理:把证线线平行转化为证线面平行.(4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直.(5)利用面面平行的性质定理:把证线线平行转化为证面面平行.跟踪训练1如图,α∩β=l,P A⊥α,PB⊥β,垂足分别为A,B,a⊂α,a⊥AB.求证:a∥l.考点直线与平面垂直的性质题点应用线面垂直的性质定理判定线线平行证明∵P A⊥α,l⊂α,∴P A⊥l.同理PB⊥l.∵P A∩PB=P,P A,PB⊂平面P AB,∴l⊥平面P AB.又∵P A⊥α,a⊂α,∴P A⊥a.∵a⊥AB,P A∩AB=A,P A,AB⊂平面P AB,∴a⊥平面P AB.∴a∥l.题型二面面垂直性质定理的应用例2如图,在三棱锥P-ABC中,P A⊥平面ABC,平面P AB⊥平面PBC.求证:BC⊥AB.考点平面与平面垂直的性质题点应用面面垂直的性质判定线线垂直证明如图,在平面P AB内,作AD⊥PB于点D.∵平面P AB⊥平面PBC,且平面P AB∩平面PBC=PB,AD⊂平面P AB,∴AD⊥平面PBC.又BC⊂平面PBC,∴AD⊥BC.又∵P A⊥平面ABC,BC⊂平面ABC,∴P A⊥BC,又∵P A∩AD=A,∴BC⊥平面P AB.又AB⊂平面P AB,∴BC⊥AB.反思感悟证明线面垂直,一种方法是利用线面垂直的判定定理,另一种方法是利用面面垂直的性质定理.本题已知面面垂直,故可考虑面面垂直的性质定理.利用面面垂直的性质定理证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.跟踪训练2如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M,AC⊥BC,且AC=BC.(1)求证:AM⊥平面EBC;(2)求直线EC与平面ABE所成角的正切值.(1)证明∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,BC⊥AC,∴BC⊥平面ACDE.又AM⊂平面ACDE,∴BC⊥AM.∵四边形ACDE是正方形,∴AM⊥CE.又BC∩CE=C,∴AM⊥平面EBC.(2)解取AB的中点F,连接CF,EF.∵EA⊥AC,平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,∴EA⊥平面ABC,∵CF⊂平面ABC,∴EA⊥CF.又AC=BC,∴CF⊥AB.∵EA∩AB=A,∴CF⊥平面AEB,∴∠CEF即为直线EC与平面ABE所成的角.在Rt△CFE中,CF=2,FE=6,tan∠CEF=26=33.垂直关系的综合应用典例在四棱锥P-ABCD中,底面ABCD是边长为a的菱形,∠DAB=60°,侧面P AD为等边三角形,其所在平面垂直于底面ABCD.(1)求证:AD⊥PB;(2)若E为BC边上的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD?并证明你的结论.(1)证明设G为AD的中点,连接PG,BG,如图.因为△P AD为等边三角形,所以PG⊥AD.在菱形ABCD中,∠DAB=60°,因为G为AD的中点,所以BG⊥AD.又因为BG∩PG=G,所以AD⊥平面PGB.因为PB⊂平面PGB,所以AD⊥PB.(2)解当F为PC的中点时,满足平面DEF⊥平面ABCD.设F为PC的中点,则在△PBC中,EF∥PB.在菱形ABCD中,GB∥DE,而PB∩GB=B,EF∩DE=E,所以平面DEF∥平面PGB.由(1)得,PG⊥平面ABCD,而PG⊂平面PGB,所以平面PGB⊥平面ABCD,所以平面DEF⊥平面ABCD.[素养评析]以四棱锥为载体,通过对线线、线面、面面垂直关系的论述,使学生掌握推理的基本形式和规则,发现表述论证过程,学会有逻辑地思考问题,提升逻辑推理的数学核心素养.1.在空间中,下列哪些命题是正确的()①平行于同一条直线的两条直线互相平行;②垂直于同一条直线的两条直线互相平行;③平行于同一个平面的两条直线互相平行;④垂直于同一个平面的两条直线互相平行.A.①③④B.①④C.①D.①②③④答案 B2.下列命题正确的是()①⎭⎪⎬⎪⎫a ∥b ,a ⊥α⇒b ⊥α; ② ⎭⎪⎬⎪⎫a ⊥α,a ⊥b ⇒b ∥α; ③⎭⎪⎬⎪⎫a ∥α,a ⊥b ⇒b ⊥α. A.①② B.①③ C.②③ D.① 答案 D3.已知平面α⊥平面β,则下列命题中真命题的个数是( ) ①α内的任意直线必垂直于β内的无数条直线;②在β内垂直于α与β的交线的直线必垂直于α内的任意一条直线; ③α内的任意一条直线必垂直于β;④过β内的任意一点作α与β交线的垂线,则这条直线必垂直于α. A.4 B.3 C.2 D.1考点 平面与平面垂直的性质题点 应用面面垂直的性质判定线面垂直 答案 C解析 ①设α∩β=l ,a ⊂α,b ⊂β,b ⊥l ,则a ⊥b ,故β内与b 平行的无数条直线均垂直于α内的任意直线,为真命题;②β内垂直于α与β交线的直线垂直于平面α,则它垂直于α内的任意直线,为真命题;③α内不与交线垂直的直线不垂直于β,为假命题;④垂直于交线的直线必须在平面β内才与平面α垂直,否则不垂直,为假命题.4.如图所示,已知AF ⊥平面ABCD ,DE ⊥平面ABCD ,且AF =DE ,AD =6,则EF =________.考点 平面与平面垂直的性质 题点 有关面面垂直性质的计算 答案 6解析 ∵AF ⊥平面ABCD ,DE ⊥平面ABCD , ∴AF ∥DE .又AF =DE ,∴四边形AFED 为平行四边形, 故EF =AD =6.5.如图所示,在四棱锥S -ABCD 中,底面ABCD 是矩形,侧面SDC ⊥底面ABCD ,求证:平面SDC⊥平面SBC.考点平面与平面垂直的性质题点面面垂直性质的综合应用证明因为底面ABCD是矩形,所以BC⊥CD.又平面SDC⊥平面ABCD,平面SDC∩平面ABCD=CD,BC⊂平面ABCD,所以BC⊥平面SDC.又因为BC⊂平面SBC,所以平面SDC⊥平面SBC.1.线面垂直的性质定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了“垂直”与“平行”关系相互转化的依据.2.面面垂直的性质定理揭示了“面面垂直、线面垂直及线线垂直”间的内在联系,体现了数学中的转化与化归思想,其转化关系如下:一、选择题1.对于任意的直线l与平面α,在平面α内必有直线m,使m与l()A.平行B.相交C.垂直D.互为异面直线答案 C2.已知m ,n 为两条不同直线,α,β为两个不同平面,给出下列命题:①⎩⎪⎨⎪⎧ m ⊥α,m ⊥n ⇒n ∥α; ②⎩⎪⎨⎪⎧m ⊥β,n ⊥β⇒m ∥n ; ③⎩⎪⎨⎪⎧m ⊥α,m ⊥β⇒α∥β; ④⎩⎪⎨⎪⎧m ⊂α,n ⊂β,α∥β⇒m ∥n .其中正确命题的序号是( ) A.②③ B.③④ C.①②D.①②③④考点 直线与平面垂直的性质题点 应用线面垂直的性质定理判定线线平行 答案 A解析 ①中n ,α可能平行或n 在平面α内;②③正确;④两直线m ,n 平行或异面,故选A.3.设平面α⊥平面β,若平面α内的一条直线a 垂直于平面β内的一条直线b ,则( ) A.直线a 必垂直于平面β B.直线b 必垂直于平面α C.直线a 不一定垂直于平面β D.过a 的平面与过b 的平面垂直 答案 C解析 当两个平面垂直时,在一个平面内只有垂直于交线的直线才垂直于另一个平面. 4.已知l ⊥平面α,直线m ⊂平面β.有下面四个命题:①α∥β⇒l ⊥m ;②α⊥β⇒l ∥m ;③l ∥m ⇒α⊥β;④l ⊥m ⇒α∥β. 其中正确的两个命题是( ) A.①② B.③④ C.②④D.①③考点 线、面平行、垂直的综合应用 题点 平行与垂直的判定 答案 D解析 ∵l ⊥α,α∥β,∴l ⊥β,∵m ⊂β,∴l ⊥m ,故①正确;∵l ∥m ,l ⊥α,∴m ⊥α,又∵m⊂β,∴α⊥β,故③正确.5.如图,设平面α∩平面β=PQ,EG⊥平面α,FH⊥平面α,垂足分别为G,H.为使PQ⊥GH,则需增加的一个条件是()A.EF⊥平面αB.EF⊥平面βC.PQ⊥GED.PQ⊥FH考点平面与平面垂直的性质题点应用面面垂直的性质判定线线垂直答案 B解析因为EG⊥平面α,PQ⊂平面α,所以EG⊥PQ.若EF⊥平面β,则由PQ⊂平面β,得EF⊥PQ.又EG与EF为相交直线,所以PQ⊥平面EFHG,所以PQ⊥GH,故选B.6.如图,在四面体ABCD中,已知AB⊥AC,BD⊥AC,那么D在平面ABC内的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部考点平面与平面垂直的性质题点应用面面垂直的性质判定线线垂直答案 A解析在四面体ABCD中,已知AB⊥AC,BD⊥AC,AB∩BD=B,∴AC⊥平面ABD.又∵AC⊂平面ABC,∴平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,D在平面ABC内的射影H必在直线AB上.故选A.7.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出如下命题:①若α⊥β,α∩β=m,n⊂α,n⊥m,则n⊥β;②若α⊥γ,β⊥γ,则α∥β;③若α⊥β,m⊥β,m⊄α,则m∥α;④若α⊥β,m∥α,则m⊥β.其中正确命题的个数为()A.1B.2C.3D.4答案 B解析①正确;③正确.8.在三棱锥P-ABC中,平面P AC⊥平面ABC,∠PCA=90°,△ABC是边长为4的正三角形,PC=4,M是AB边上的一动点,则PM的最小值为()A.2 3B.27C.4 3D.47答案 B解析连接CM,则由题意PC⊥平面ABC,可得PC⊥CM,所以PM=PC2+CM2,要求PM的最小值只需求出CM的最小值即可,在△ABC中,当CM⊥AB时CM有最小值,此时有CM=4×32=23,所以PM的最小值为27.二、填空题9.a,b是异面直线,直线l⊥a,l⊥b,直线m⊥a,m⊥b,则l与m的位置关系是________. 考点直线与平面垂直的性质题点应用线面垂直的性质定理判定线线平行答案平行解析由线面垂直的性质定理可得.10.如图,平面ABC⊥平面ABD,∠ACB=90°,CA=CB,△ABD是正三角形,O为AB中点,则图中直角三角形的个数为________.考点平面与平面垂直的性质题点应用面面垂直的性质判定线线垂直答案 6解析∵CA=CB,O为AB的中点,∴CO⊥AB.又平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,CO⊂平面ABC,∴CO⊥平面ABD. ∵OD⊂平面ABD,∴CO⊥OD,∴△COD为直角三角形.∴图中的直角三角形有△AOC,△COB,△ABC,△AOD,△BOD,△COD共6个.11.已知m,n是空间两条不同的直线,α,β是两个不同的平面,下面有四个命题:①m⊥α,n∥β,α∥β⇒m⊥n;②m⊥n,α∥β,m⊥α⇒n∥β;③m⊥n,α∥β,m∥α⇒n⊥β;④m⊥α,m∥n,α∥β⇒n⊥β.其中所有真命题的序号是________.答案①④三、解答题12.如图,三棱锥P-ABC中,已知△ABC是等腰直角三角形,∠ABC=90°,△P AC是直角三角形,∠P AC=90°,平面P AC⊥平面ABC,求证:平面P AB⊥平面PBC.考点平面与平面垂直的性质题点面面垂直性质的综合应用证明∵平面P AC⊥平面ABC,平面P AC∩平面ABC=AC,P A⊥AC,P A⊂平面P AC,∴P A⊥平面ABC.又BC⊂平面ABC,∴P A⊥BC.又∵AB⊥BC,AB∩P A=A,AB⊂平面P AB,P A⊂平面P AB,∴BC⊥平面P AB.又BC⊂平面PBC,∴平面P AB⊥平面PBC.13.如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.考点线、面平行、垂直的综合应用题点平行与垂直的判定证明(1)在平面ABD内,因为AB⊥AD,EF⊥AD,则AB∥EF.又因为EF⊄平面ABC,AB⊂平面ABC,所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,BC⊂平面BCD,BC⊥BD,所以BC⊥平面ABD.因为AD⊂平面ABD,所以BC⊥AD.又AB⊥AD,BC∩AB=B,AB⊂平面ABC,BC⊂平面ABC,所以AD⊥平面ABC.又因为AC⊂平面ABC,所以AD⊥AC.14.如图,若边长为4和3与边长为4和2的两个矩形所在的平面互相垂直,则cos α∶cos β=________.答案5∶2解析由题意,两个矩形的对角线长分别为5,25,所以cos α=525+4=529,cos β=2529,所以cos α∶cos β=5∶2.15.如图,四棱锥P-ABCD的底面是边长为a的菱形,∠BCD=120°,平面PCD⊥平面ABCD,PC=a,PD=2a,E为P A的中点,求证:平面EDB⊥平面ABCD.证明设AC∩BD=O,连接EO,则EO∥PC.∵PC=CD=a,PD=2a,∴PC2+CD2=PD2,∴PC⊥CD.∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,∴PC⊥平面ABCD,∴EO⊥平面ABCD.又EO⊂平面EDB,故有平面EDB⊥平面ABCD.。
21-22版:2.3.3 直线与平面垂直的性质~2.3.4 平面与平面垂直的性质(创新设计)
@《创新设计》
10
课前预习
课堂互动
课堂反馈
规律方法 证明线线平行常用的方法 (1)利用线线平行定义:证共面且无公共点. (2)利用三线平行公理:证两线同时平行于第三条直线. (3)利用线面平行的性质定理:把证线线平行转化为证线面平行. (4)利用线面垂直的性质定理:把证线线平行转化为证线面垂直. (5)利用面面平行的性质定理:把证线线平行转化为证面面平行.
@《创新设计》
14
课前预习
课堂互动
课堂反馈
@《创新设计》
(1)证明 ∵O,M分别为AB,VA的中点,∴OM∥VB. ∵VB⊄平面MOC,OM⊂平面MOC, ∴VB∥平面MOC. (2)证明 ∵AC=BC,O为AB的中点,∴OC⊥AB. 又∵平面VAB⊥平面ABC,且平面VAB∩平面ABC=AB,OC⊂平面ABC,∴OC⊥平面 VAB. ∵OC⊂平面MOC,∴平面MOC⊥平面VAB.
∴DD1⊥AC. 又AC⊥BD,DD1∩BD=D,DD1,BD⊂平面BDD1B1, ∴AC⊥平面BDD1B1, 又BD1⊂平面BDD1B1,
@《创新设计》
9
课前预习
课堂互动
课堂反馈
∴AC⊥BD1. 同理可证BD1⊥B1C, 又AC∩B1C=C,AC,B1C⊂平面AB1C, ∴BD1⊥平面AB1C. ∵EF⊥A1D,A1D∥B1C,∴EF⊥B1C. 又∵EF⊥AC,AC∩B1C=C,AC,B1C⊂平面AB1C, ∴EF⊥平面AB1C,∴EF∥BD1.
【训练3】 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,E为 CD的中点. (1)求证:BD⊥平面PAC; (2)若∠ABC=60°,求证:平面PAB⊥平面PAE. (1)证明 因为PA⊥平面ABCD,BD⊂平面ABCD, 所以PA⊥BD. 因为底面ABCD为菱形,所以BD⊥AC. 又PA∩AC=A,所以BD⊥平面PAC.
《2.3.3 直线与平面垂直的性质》和《2.3.4 平面与平面垂直的性质》教学设计
《空间中直线、平面的垂直关系》教学设计一、教材内容解析本节课的内容是探究空间直线与平面、平面与平面垂直的性质,选自人教A 版教材《2.3.3 直线与平面垂直的性质》和《2.3.4 平面与平面垂直的性质》。
空间中直线、平面的垂直关系是一种非常重要的的位置关系,它不仅应用广泛,而且是空间问题平面化的典范。
这类问题求解的关键是根据线面、面面之间的互化关系,借助创设辅助线和面,找出符号语言和图形语言之间的关系。
通过对有关概念和定理的概括、证明和应用,使学生体会“转化”的观点,提高学生的空间想象力和逻辑推理能力。
本节内容是学习了线面垂直和面面垂直判定之后的进一步探究,进一步巩固“观察模型——直观感知——操作确认——推理证明——拓展应用”定理学习模式,培养学生空间概念,空间想象能力以及逻辑推理能力。
二、教学目标设置根据本课教材的特点,新大纲对本节课的教学要求,结合学生身心发展的合理需要,确定以下教学目标:(1)知识与技能目标:①让学生在观察物体模型的基础上,进行操作确认,获得对性质定理的正确认识;②会证明性质定理,并能运用性质定理解决一些简单问题。
(2)过程与方法目标:①通过“直观感知、操作确认,推理证明”,培养学生逻辑推理能力;②了解直线与平面、平面与平面垂直的判定定理和性质定理间的相互联系,掌握转化思想在解决问题中的运用;③通过类比空间中直线与平面的平行关系、平面与平面的平行关系的学习方法来探究本节课中的垂直关系。
(3)情感态度与价值观目标:①让学生亲身经历数学研究的过程,体验探索的乐趣,增强学习数学的兴趣;②提高学生的合情推理能力和空间想象力,培养学生的质疑思辨、创新精神;③进一步体会几何中的公理化体系,提升学生的科学素养。
教学重点:学生经历“观察模型——直观感知——操作确认——推理证明——拓展应用”定理学习过程,培养空间想象能力和逻辑推理能力,感悟数学中的“转化”的思想,并能类比此方法用于其它数学命题的学习,解决更多的生活中的实际问题,所以性质定理的发现及证明是本节课的重点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
罗田一中高一数学必修2导学案
编者:刘秀丹 审核:杨德兵 学生____________
一.学习目标
1.掌握直线与平面垂直的性质定理及平面与平面垂直的性质定理的应用。
2.进一步理解线线垂直、线面垂直、面面垂直的相互转化及转化的数学思想。
3.通过探索发现线面垂直和面面垂直的性质规律,培养空间想象能力、逻辑思
维能力和类比思维能力。
二.自学导引
1.直线与平面垂直的性质定理:_________________________________________. (线面垂直→线线平行).符号表示:_______________________________.
拓展:直线与平面垂直的其它性质:
⑴ 直线与平面垂直,则直线垂直于平面内的所有直线;
⑵ 垂直于同一条直线的两个平面互相平行
2.平面与平面垂直的性质定理: _________________________________________ __________________________________________.(面面垂直→线面垂直)
符号表示:
拓展:两个平面垂直的其它性质:
⑴ 如果两个平面互相垂直,那么经过一个平面内一点且垂直于另外一个平面的直线,必在
这个平面内;
⑵ 如果两个相交平面都垂直于另一个平面,那么这两个平面的交线垂直于这个平面;
⑶ 三个两两垂直的平面,它们的交线也两两垂直.
三.典型例题:
题型一 直线与平面垂直的性质的应用
例一.已知,l CA αβα⋂=⊥与A ,B ,CB a a AB βα⊥⊂⊥于点,,求证//a l
[规律方法]利用线面垂直的性质证明线线平行,关键是找(构造)出平面,
使所证直线都与该平面垂直。
[变式1]已知一条直线l 和一个平面α平行,求证:直线l 上各点到平面α的距离相等
题型二 平面与平面垂直的性质的应用
例二.在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面V AD 是等边三角形,平面VAD
⊥底面ABCD.
(1) 求证:AB ⊥平面VAD.
(2) 求平面VAD 与平面VDB 所成的二面角的正切值。
[变式2]如图,平面α⊥平面β,AB αβ=,a ∥α,a AB ⊥,求证:a β⊥.
[规律方法]若已知有面面垂直的条件,可设法找出一个平面上的一条直线垂
直于它们的交线,这样就能得到线面垂直的结论。
注意:1.两个平面垂直的性
质定理及应用,可证明线面垂直、线线垂直、线在面内及求直二面角;2.判定定
理和性质定理的交替运用,三种垂直关系的相互转化.
题型三 线面、面面垂直的探究问题
例三.如图,已知△BCD 中,∠BCD=90°,BC=CD=1,AB ⊥平面BCD ,∠ADB=60°,E 、F 分别是
AC 、AD 上的动点,且 )(10<<==λλAD
AF AC AE (Ⅰ)求证:不论λ为何值,总有平面BEF ⊥平面ABC ;
(Ⅱ)当λ为何值时,平面BEF ⊥平面ACD ?
四.跟踪训练
1.下列命题中,正确的是( )
A.过平面外一点,可作无数条直线和这个平面垂直
B.过一点有且仅有一个平面和一条定直线垂直
C.若,a b 异面,过a 一定可作一个平面与b 垂直
D .,a b 异面,过不在,a b 上的点M ,一定可以作一个平面和,a b 都垂直.
2.两条平行直线在平面内的射影可能是:①两条平行线;②两条相交直线;③一条直线; ④两个点. 上述四个结论中,可能成立的个数是( )
A 、1个
B 、2个
C 、3个
D 、4个
3.对于直线,m n 和平面,αβ,能得出αβ⊥的一个条件是 ( )
A.,//m n m α⊥,//n β
B.,,m n m n αβα⊥⋂=⊂
C.//,,m n n m βα⊥⊂
D.//,,m n m n αβ⊥⊥
4. 下列命题错误的是( ).
A.αβ⊥⇒α内所有直线都垂直于β
B.αβ⊥⇒α内一定存在直线平行于β
C.α不垂直β⇒α内不存在直线垂直β
D.α不垂直β⇒α内一定存在直线平行于β
5. 已知αβ⊥,下列命题正确个数有( ).
①αβ内的已知直线必垂直于内的任意直线
②αβ内的已知直线必垂直于内的无数条直线
③α内的任一直线必垂直于β
A.3
B.2
C.1
D.0
6. 已知αβ⊥,,a b αβ⊂⊂,b 是α的斜线,a ⊥b ,则a 与β的位置关系是( ).
A.a ∥β
B. a 与β相交不垂直
C. a β⊥
D.不能确定
7.从平面外一点P 引与平面相交的直线,使P 点与交点的距离等于1,则满足条件的直线条数不可能是 ( )
A.0条
B.1条
C.2条
D.无数条
8.已知平面α的斜线a 与α内一直线b 相交成θ角,且a 与α相交成1ϕ角,a 在α上的射影c 与b 相交成2ϕ角,则有 ( )
9.与空间四边形四个顶点距离相等的平面共有( )
A 、4个
B 、5个
C 、6个
D 、7个
10. 若平面αβ⊥平面,直线a α⊂,则a 与β的位置关系为_____________________.
11. 直线m 、n 和平面α、β满足m n ⊥,m α⊥,αβ⊥,则n 和β的位置关系为__________.
12.如图,,,CD CD AB αββ⊥⊂⊥,CE ,EF ⊂α,90FEC ∠=°,
求证:面EFD ⊥面DCE .
13.如图,三棱锥P —ABC 中,PA ⊥底面ABC ,侧面PAB ⊥侧面PBC ,求证:AB ⊥BC
P 中,平面PAD⊥平面ABCD,
14、如图,在四棱锥ABCD
AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF∥平面PCD;(2)平面BEF⊥平面PAD
15. R t△ABC中,AB=AC= 2 ,AD是斜边BC上的高,以AD为折痕将△ABD折起,使∠BDC=90°.
(1)求证:平面ABD⊥平面BDC;
(2)求证:∠BAC=60°;
(3)求点A到平面BDC的距离;
(4)求点D到平面ABC的距离.。
