温度场和温度应力计算
超长结构温度应力计算探讨

超长结构温度应⼒计算探讨超长结构温度应⼒计算探讨⼀、温度作⽤的特点:温度作⽤是在规定时期内结构或结构构件由于温度场变化所引起的作⽤,具有以下特点:1)温度作⽤是由结构材料“热胀冷缩”效应被结构内、外约束阻碍⽽在结构内产⽣的内⼒作⽤,属于间接作⽤;2)温度作⽤随外界环境的变化⽽变化,有明显的时间性,属于可变作⽤;3)建筑结构从开始建造到拆除都会受到所处温度场影响,因⽽温度作⽤伴随着结构的⽣命全周期过程;4)引起结构温度变化因素很多,有⽓候季节变化、太阳暴晒辐射和其它⼈为因素(如⽕灾)等,诱因多样性使温度作⽤有别于其它(荷载)作⽤。
⼆、温度作⽤的规范规定:2.1什么时候需要进⾏温度作⽤计算根据温度作⽤的特点可知,结构中产⽣的温度作⽤⼤⼩主要与结构材料线膨胀系数和结构长度有关。
表1为常⽤材料线膨胀系数αT,可见结构钢和混凝⼟的线膨胀系数⾮常接近。
正因为如此,在计算钢筋混凝⼟结构的温度作⽤时才可以只按混凝⼟⼀种材料近似考虑。
材料确定的情况下,长度越长,温度作⽤越⼤。
在完全没有约束的情况下,总长为100m、截⾯为600x600的普通混凝⼟梁温度每升⾼或降低20℃,梁长度将增加或减少20mm;如果端部的变形完全受到约束,将在梁内部产⽣约2160KN(按强度等级为C30计算)的轴向压⼒或拉⼒,该⼒约为混凝⼟轴向抗拉强度标准值的3倍。
T实际结构不可能没有约束,总会在结构中产⽣温度应⼒,当结构长度较⼩时,可忽略温度应⼒和温度变形对结构的影响。
现⾏规范根据不同的结构形式给出该长度(温度区段长度)经验值,详见表2,当结构超出该长度时才有必要进⾏温度作⽤计算。
表2: 钢筋混凝⼟结构伸缩缝最⼤间距(m)建筑结构设计时,应⾸先采取有效构造措施来减少或消除温度作⽤效应,如设置结构的活动⽀座或节点、设置温度缝、采⽤隔热保温措施等。
当结构或构件在温度作⽤和其他可能组合的荷载共同作⽤下产⽣的效应(应⼒或变形)可能超过承载能⼒极限状态或正常使⽤极限状态时,⽐如结构某⼀⽅向平⾯尺⼨超过伸缩缝最⼤间距或温度区段长度、结构约束较⼤、房屋⾼度较⾼等,结构设计中⼀般应考虑温度作⽤。
温度应力计算
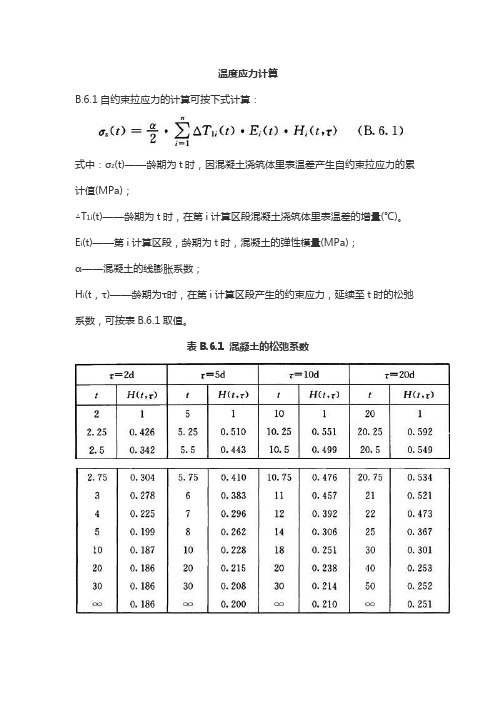
温度应力计算B.6.1自约束拉应力的计算可按下式计算:式中:σz(t)——龄期为t时,因混凝土浇筑体里表温差产生自约束拉应力的累计值(MPa);△T1i(t)——龄期为t时,在第i计算区段混凝土浇筑体里表温差的增量(℃)。
E i(t)——第i计算区段,龄期为t时,混凝土的弹性模量(MPa);α——混凝土的线膨胀系数;H i(t,τ)——龄期为τ时,在第i计算区段产生的约束应力,延续至t时的松弛系数,可按表B.6.1取值。
表B.6.1 混凝土的松弛系数注:τ为龄期,H(t,τ)为在龄期为τ时产生的约束应力,延续至t时的松弛系数。
B.6.2混凝土浇筑体里表温差的增量可按下式计算:式中:j——为第i计算区段步长(d)。
B.6.3在施工准备阶段,最大自约束应力可按下式计算:式中:σzmax——最大自约束应力(MPa);△T1max——混凝土浇筑后可能出现的最大里表温差(℃);E(t)——与最大里表温差△T1max相对应龄期t时,混凝土的弹性模量(MPa);H(t,τ)——在龄期为τ时产生的约束应力,延续至t时(d)的松弛系数。
B.6.4外约束拉应力可按下式计算:式中:σx(t)——龄期为t时,因综合降温差,在外约束条件下产生的拉应力(M Pa);△T2i(t)——龄期为t时,在第i计算区段内,混凝土浇筑体综合降温差的增量(℃)。
μ——混凝土的泊松比,取0.15;R i(t)——龄期为t时,在第i计算区段,外约束的约束系数。
L——混凝土浇筑体的长度(mm);H——混凝土浇筑体的厚度,该厚度为块体实际厚度与保温层换算混凝土虚拟厚度之和(mm);C x——外约束介质的水平变形刚度(N/mm3),可按表B.6.4取值。
表B.6.4 不同外约束介质的水平变形刚度取值(10-2N/mm3)。
第九章 热应力问题

满足微分方程,而不一定要满足边界条件。(2)不计变温T,
求出微分方程的一组补充解,使它和特解叠加以后,能满足
边界条件。
25
引用一个函数(x,y) ,将位移特解取为:
u ' , v'
x
y
函数 称为位移势函数。以 u 和 v 分别作为u和v代入微分
( v" x
u") y
28
这样总的位移分量是:u u'u",v v'v" 需满足位移边界条件
总的应力分量是: x x ' x", y y ' y", z z ' z"
需满足应力边界条件。在应力边界问题中(没有位移边界条
件),可以把相应于位移补充解的应力分量直接用应力函数
力问题的
E换
成
1
E
2
换成 1
换成(1 )
则得到在平面应变条件下的相应方程。 23
热应力问题
温度场和热传导的基本概念 热传导微分方程 温度场的边界条件 按位移求解温度应力的平面问题 位移势函数的引用 轴对称温度场平面热应力问题
24
位移势函数的引用
由上一节知:在平面应力的情况下按位移求解温度应力问
17
x
1 E
[
x
( y
z )] T
y
1 E
[
y
( z
x )] T
z
1 E
yz
[ z
( x y )] T
机械温度场分析及热应力的评估

机械温度场分析及热应力的评估概述机械温度场分析及热应力的评估是工程领域中重要的一项研究内容。
随着现代科技的快速发展,工程结构的尺寸越来越小,工作温度也越来越高,机械温度场分析和热应力的评估成为保证结构安全和可靠性的重要环节。
本文将从理论模型、数值模拟以及实验测试等角度,探讨机械温度场分析及热应力的评估方法和应用。
一、理论模型的建立机械温度场分析通常需要建立一定的理论模型。
理论模型依据热传导理论,考虑材料的热导率、热扩散系数等参数,利用热传导方程求解结构在不同温度加载下的温度场。
根据材料的热应力-应变关系,可以进一步计算出结构在温度变化过程中的热应力分布。
在建立理论模型时需要考虑多种因素,例如材料参数的准确性、结构尺寸的影响、温度场的非线性效应等。
理论模型的准确性决定了后续数值模拟和实验测试的可靠性,因此在建立模型时需要进行充分的论证和验证。
二、数值模拟的应用数值模拟是机械温度场分析中常用的方法之一。
通过建立结构的有限元模型,利用有限元软件对结构进行热分析,可以得到结构在不同温度场下的应力分布和变形情况。
数值模拟方法可以处理复杂的结构和边界条件,为结构设计和改进提供了有力的支持。
在进行数值模拟时,需要对模型进行网格划分、边界条件的设定、材料参数的输入等。
同时,还需进行数值模拟结果的验证。
与实验测试相比,虽然数值模拟能够快速得到结果,但存在一定的误差。
因此,在使用数值模拟进行机械温度场分析时,需要进行误差分析和结果验证,以提高模拟结果的准确性。
三、实验测试的实施实验测试是机械温度场分析的重要手段之一。
通过实验测试可以直接获得结构的温度场、应力分布、变形情况等数据。
实验测试方法多种多样,例如红外测温、应变片测试等。
不同的实验方法适用于不同的材料和结构,需要根据具体情况选择合适的测试方法。
实验测试的优势在于提供准确的数据,可以直接对结构进行观测和测量。
然而,实验测试也存在一些局限性,例如测试时间和成本较高、难以处理复杂边界条件等。
超长结构温度应力计算探讨精

超长结构温度应力计算探讨一、温度作用的特点:温度作用是在规定时期内结构或结构构件由于温度场变化所引起的作用,具有以下特点:1温度作用是由结构材料“热胀冷缩”效应被结构内、外约束阻碍而在结构内产生的内力作用,属于间接作用;2温度作用随外界环境的变化而变化,有明显的时间性,属于可变作用;3建筑结构从开始建造到拆除都会受到所处温度场影响,因而温度作用伴随着结构的生命全周期过程;4引起结构温度变化因素很多,有气候季节变化、太阳暴晒辐射和其它人为因素(如火灾等,诱因多样性使温度作用有别于其它(荷载作用。
二、温度作用的规范规定:2.1什么时候需要进行温度作用计算根据温度作用的特点可知,结构中产生的温度作用大小主要与结构材料线膨胀系数和结构长度有关。
表1为常用材料线膨胀系数αT,可见结构钢和混凝土的线膨胀系数非常接近。
正因为如此,在计算钢筋混凝土结构的温度作用时才可以只按混凝土一种材料近似考虑。
材料确定的情况下,长度越长,温度作用越大。
在完全没有约束的情况下,总长为100m、截面为600x600的普通混凝土梁温度每升高或降低20℃,梁长度将增加或减少20mm;如果端部的变形完全受到约束,将在梁内部产生约2160KN(按强度等级为C30计算的轴向压力或拉力,该力约为混凝土轴向抗拉强度标准值的3倍。
表1: 常用材料的线膨胀系数αT材料线膨胀系数αT(×10-6/℃轻骨料混凝土7普通混凝土10砌体6~10钢,锻铁,铸铁12不锈钢16铝,铝合金24实际结构不可能没有约束,总会在结构中产生温度应力,当结构长度较小时,可忽略温度应力和温度变形对结构的影响。
现行规范根据不同的结构形式给出该长度(温度区段长度经验值,详见表2,当结构超出该长度时才有必要进行温度作用计算。
表2: 钢筋混凝土结构伸缩缝最大间距(m结构类型室内或土中露天排架结构装配式100 70框架结构装配式75 50 现浇式55 35剪力墙结构装配式65 40 现浇式45 30挡土墙、地下室墙壁等类结构装配式40 30 现浇式30 20建筑结构设计时,应首先采取有效构造措施来减少或消除温度作用效应,如设置结构的活动支座或节点、设置温度缝、采用隔热保温措施等。
温度应力计算·
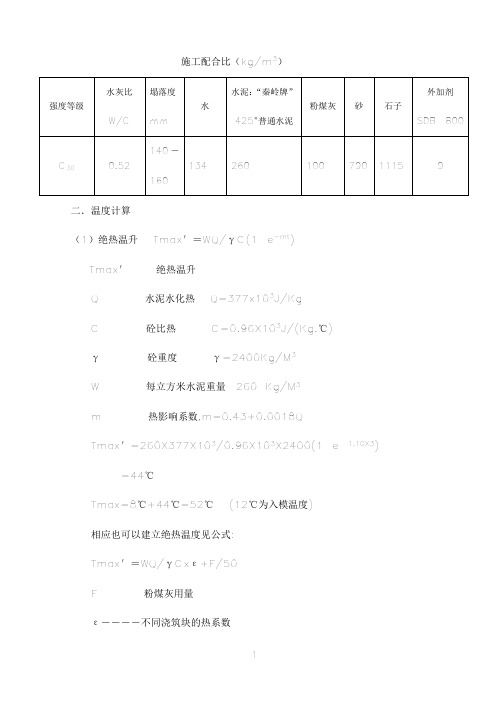
施工配合比(kg/m3)二.温度计算(1)绝热温升Tmax′=WQ/γC(1-e-mt) Tmax′---绝热温升Q-----水泥水化热Q=377x103J/KgC-----砼比热C=0.96X103J/(Kg.℃)γ-----砼重度γ=2400Kg/M3W-----每立方米水泥重量260 Kg/M3m-----热影响系数,m=0.43+0.0018QTmax′=260X377X103/0.96X103X2400(1-e-1.10X3) =44℃Tmax=8℃+44℃=52℃(12℃为入模温度)相应也可以建立绝热温度见公式:Tmax′=WQ/γCxε+F/50F-----粉煤灰用量ε――――不同浇筑块的热系数Tmax′=260X377X103/Tmax=8+55=63℃取Tmax=63℃三. 温应力计算1.将砼的收缩随时间的进程换算成当量温度计算:Ty(t)= εy(t)/αα=1x10-5砼线膨胀系数εy(t)=ε0M1M2M3······M10(1-e0.01t)Ty(t)------当量温度εy(t)----任意时间的收缩(mm/mm)M1-----水泥品种为普通水泥,取1.0M2-----水泥细度为4000孔,取1.35M3-----骨料为石灰石,取1.00M4-----水灰比为0.52,取1.64M5-----水泥浆量为0.2,取1.00M6------自然养护30天,取0.93M7------环境相对湿度为50%,取0.54M8------水里半径倒数为0.4,取1.2M9------机械振捣,取1.00M10------含筋率为8%,取0.9ε0--ε∞---最终收缩,在标准状态下ε0=3.24X10-4εy(30)=1.01x10-4Ty(30)=10.1℃εy(27)=0.92 x10-4Ty(27)=9.2℃εy(24)=0.83 x10-4Ty(24)=8.3℃εy(21)=0.73 x10-4 Ty(21)=7.3℃εy(18)=0.64 x10-4Ty(18)=6.4℃εy(15)=0.54 x10-4Ty(15)=5.4℃εy(12)=0.439 x10-4 Ty(12)=4.39℃εy(9)=0.335 x10-4 Ty(9)=3.35℃εy(6)=0.226 x10-4 Ty(6)=2.26℃εy(3)=0.114 x10-4 Ty(3)=1.14℃计算中心温度当量温差:△T6=2.26-1.14=1.12℃△T9=3.35-2.26=1.09℃△T12=4.39-3.35=1.04℃△T15=5.4-4.39=1.01℃△T18=6.4-5.4=1.0℃△T21=7.3-6.4=0.9℃△T24=8.3-7.3=1.0℃△T27=9.2-8.3=0.9℃△T30=10.1-9.2=0.9℃2.计算中心温度砼基础施工时处于散热条件,考虑上下表面及侧面的散热条件,当体积厚达3m时,,散热影响系数取0.97;当中心浇筑完第四天后,水化热达峰值。
温度应力问题的基本解法
) s
m(1
)T
(2)
这是按位移求解温度应力平面应力问题的应力边界条件。
位移边界条件仍然为:
us u,vs v
将式(1)、(2)与第二章§2-8中式(1)、(2)对比,可见
第十九页
E T 及 E T 1 x 1 y
代替了体力分量 X 及 Y ,而:
l ET 及m ET
1
1
代替了面力分量X 及 Y 。
r r
第二十九页
几何方程简化为
r
dur dr
,
ur r
x
1 E
[
x
(
y
z )] T
y
1 E
[
y
( z
x )] T
z
1 E
[ z
( x
y )] T
第十四页
yz
2(1 E
)
yz
zx
2(1 E
) zx
xy
2(1 E
)
xy
对于平面应力的变温问题,上式简化为
x
1 E
[ x
y ] T
y
1 E
[
y
x ] T
xy
2(1 E
y2 ) b2
b
o
b
x
其中的T0 是常量。若 a》b ,试求其温
度应力。
y
解:位移势函数 所应满足的微分方程为
2
(1
)T(0 1
y2 b2
)
取
Ay2 By2
代入上式,得
2A 12By 2
(1
)T(0 1
y2 b2
)
比较两边系数,得 A (1 )T0 ,B (1 )T0
日照下混凝土箱梁温度场和温度应力研究
日照下混凝土箱梁温度场和温度应力研究1. 本文概述本文主要研究了日照作用下混凝土箱梁的温度场分布和温度应力。
随着土木工程技术的发展,钢筋混凝土箱梁结构被广泛应用于建筑领域。
在实践中发现,日照会对钢筋混凝土箱梁产生明显的温度效应,影响结构的受力性能和安全性。
研究混凝土箱梁的日照温度效应具有重要意义。
本文首先通过实验和数值模拟方法,对不同条件下的箱梁日照温度效应进行了研究。
研究结果表明,日照时间、强度、角度等因素都会影响箱梁的温度分布。
箱梁表面的温度变化幅度较大,而内部温度变化幅度较小。
太阳辐射强度对箱梁的温度分布和应力分布也有较大影响,高辐射强度会导致箱梁表面温度升高,从而引发更大的应力。
箱梁的传热性能与其结构尺寸、材料参数等因素有关,这些因素会影响日照温度效应的表现。
为了更好地理解和预测日照温度效应,本文还分析了钢筋混凝土箱梁日照温度应力的形成机理和计算方法。
同时,以现行的桥梁规范为依据,计算了试验模型的温度应力,并提出了钢筋混凝土箱梁日照温度裂缝控制的建议。
这些研究成果对于工程设计人员和规范编制具有重要的参考价值。
本文的研究旨在提高对混凝土箱梁日照温度效应的认识,为实际工程中箱梁的结构设计和安全评估提供科学依据,从而提高结构的安全性和耐久性。
2. 混凝土箱梁温度场的影响因素分析混凝土的热物理性质,如比热容、导热系数和热膨胀系数,对其温度响应至关重要。
比热容影响材料吸收和释放热量的能力,导热系数决定热量在材料内部的传导速度,而热膨胀系数则关系到材料在温度变化时的体积变化。
日照条件下,环境温度、相对湿度、风速和太阳辐射强度是主要的环境影响因素。
太阳辐射直接加热箱梁表面,而环境温度和风速影响热量的对流和辐射损失。
相对湿度则通过影响水分的蒸发和混凝土的干燥速率来间接影响温度场。
混凝土箱梁的几何尺寸、形状和方向对其温度分布有显著影响。
较大的表面积和较薄的截面会导致更快的温度变化。
箱梁的朝向也会影响其接收到的太阳辐射量,从而影响温度分布。
温度应力计算
混凝土施工裂缝控制混凝土温度的计算①混凝土浇筑温度:T j=T c+(T q-T c)×(A1+A2+A3+……+A n)式中:T c—混凝土拌合温度(℃),按多次测量资料,在没有冷却措施的条件下,有日照时混凝土拌合温度比当时温度高5-7 ℃,无日照时混凝土拌合温度比当时温度高2-3 ℃,我们按3 ℃计;、T q—混凝土浇筑时的室外温度(考虑最夏季最不利情况以30 ℃计);A1、A2、A3……A n—温度损失系数,A1—混凝土装、卸,每次A=(装车、出料二次);A2—混凝土运输时,A=θt查文献[5]P33表3-4得6 m3滚动式搅拌车运输θ=,运输时间t约30分钟,A=×30=;A3—浇捣过程中A=, 浇捣时间t约240min, A=×240=;T j=33+(T q-T c)×(A1+A2+A3)=33+(30-33)××2++=33+(-3)×= ℃②混凝土的绝热温升:T(t)=W×Q×(1-e-mt)/(C×r)式中:T(t)—在t龄期时混凝土的绝热温升(℃);W—每m3混凝土的水泥用量(kg/m3),取350kg/m3;Q—每公斤水泥28天的累计水化热(KJ/kg), 采用425号矿渣水泥Q =335kJ/kg(文献[5] P14表2-1);C—混凝土比热KJ/(kg·K) ;r—混凝土容重2400 kg/m3;e—常数,;m—与水泥品种、浇筑时温度有关,可查文献[5]P35表3-5;t—混凝土龄期(d)。
混凝土最高绝热温升T h =W×Q/(C×r)=350×335/×2400)=(℃)③混凝土内部中心温度:T max(t)=T j+ T1(t)式中:T max(t)—t龄期混凝土内部中心温度;T j—混凝土浇筑温度(℃);ξ—不同浇筑块厚度的温降系数,查文献[5]P44表3-8得,对3 m厚混凝土3天时ξ=;T 1(t)—混凝土内部水泥水化热的平均温升,T 1(t)=T(t)×ξ。
大体积混凝土温度应力计算
计算结果分析
温度应力分布情况 应力与应变关系 裂缝产生原因及分布规律 计算结果与实际监测数据的对比分析
结论与建议
结论:大体积混凝土温度应力计算案例 分析表明,温度应力对混凝土结构的影 响较大,需要采取有效的措施进行控制。
建议:在设计和施工过程中,应充分考 虑温度应力的影响,采取适当的构造措 施和施工方法,以减少温度应力对混凝 土结构的影响。
求解温度场:通过有限元法或有限差分法等数值计算方法,求解大体积混凝土的温度场。
计算应力应变:根据温度场计算结果,结合弹性力学理论,计算大体积混凝土的应力应 变。
建立数学模型
确定温度场和应力场的基本方程
建立温度应力和收缩应力的计算公 式
添加标题
添加标题
确定边界条件和初始条件
添加标题
添加标题
考虑混凝土的弹塑性本构关系
Part Five
大体积混凝土温度 应力计算案例分析
工程概况
工程名称:大体积混凝土温度应力计算案例分析 建设地点:某市 建设规模:建筑面积约为XX平方米 建设单位:某建筑公司
计算模型建立
确定计算模型:根据实际情况选择合适的计算模型,如有限元法、有限差分法等。 建立温度场:根据混凝土的物理性质和边界条件,建立温度场方程。 确定初始条件和边界条件:根据实际情况确定初始温度和边界温度。 求解温度场:采用合适的数值方法求解温度场方程,得到各点的温度分布。
确定材料参数
混凝土的弹性模量 混凝土的热膨胀系数 混凝土的导热系数 混凝土的密度
求解方程
建立数学模型
求解温度场方 程
确定边界条件 和初始条件
计算温度应力
结果分析
计算结果:根据计算公式和参数,得出大体积混凝土温度应力计算结果 结果分析:分析计算结果,确定大体积混凝土的温度应力分布和变化规律 影响因素:分析各因素对大体积混凝土温度应力的影响程度和作用机制 优化建议:根据计算结果和分析,提出优化大体积混凝土温度应力的建议和措施
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附计算书3:温度场和温度应力计算一、温度场计算计算以本工程厚底板为例,用差分法计算底板28d 水化热温升曲线。
计算中各参数的取值如下:W ——每m 3胶凝材料用量,440kg/ m 3;Q ——胶凝材料水化热总量(kJ/kg );,本例采纳实测值260kJ/kg ;c ——混凝土的比热,取 (kg •C );ρ——混凝土的质量密度,取2400kg/ m 3;α——导温系数,取0.0035m 2/h ;m ,取。
混凝土的入模温度取10C ,地基温度为18C ,大气温度为18C 。
温度场计算差分公式如下:1,1,,1,,222(21)2n k n kn k n k n k T T t t T aT a T x x-+++∆∆=•--+∆∆∆ ()⑴试算t ∆、x ∆,确信2xt∆∆α。
取t ∆ = 天 = 12小时,x ∆ = ,即分3层则412625.04.0120035.022≈=⨯=∆∆x t α,可行。
代入该值得出相应的差分法公式为k k n kn k n k n T T T T T ∆+⋅++⋅=+-+,,1,11,475.02525.0⑵画出相应的计算示用意,并进行计算。
底板厚,分3层,每层0.4m ,相应的计算示意如以下图。
从上至下各层混凝土的温度别离用1T 、2T 、3T 表示,相应k 时刻各层的温度即为k T ,1、k T ,2、k T ,3。
混凝土与大气接触的上表面边界温度用0T 表示,与地基接触的下表面边界温度用0'T 表示。
k = 0,即第05.00=⋅=∆⋅t k 天,上表面边界0T ,取大气温度,0T = 18C 各层混凝土温度取入模温度,即0,1T =0,2T = 0,3T = 10C下表面边界0'T ,取地基温度,0'T = 18C ;k = 1,即第5.05.01=⋅=∆⋅t k 天,温升=-⋅⋅⋅=-=∆⋅⋅-⋅-⋅-∆⋅⋅-∆⋅-⋅-)(24000.1260440)(5.015.05.0)11(5.0)1(max 1e e eeT T tk m tk m C上表面边界温度0T ,散热温升为0,始终维持不变,0T = 18C第一层混凝土温度1,1T ,见计算图示中方框1,1,1T 的边界为0T 和0,2T ,在0,1T 的基础上考虑温升1T ∆,即C T T T T T 644.22475.02525.010,10,201,1=∆+⋅++⋅=第二层混凝土温度1,2T ,见计算图示中方框2,1,2T 的边界为0,1T 和0,3T ,在0,2T 的基础上考虑温升1T ∆,即C T T T T T 544.20475.02525.010,20,30,11,2=∆+⋅++⋅=第三层混凝土温度1,3T ,见计算图示中方框3,1,3T 的边界为0,2T 和0'T ,在0,3T 的基础上考虑温升1T ∆,即2,003,13,010.5250.47522.6442T T T T T C'+=+⋅+∆=︒下表面边界温度0'T ,需要考虑散热温升2/1T ∆,因此需每一步都需进行修正。
见计算图示中方框6,0'T 的边界为0,3T 和地基温度18C ,在0'T 的基础上考虑温升2/1T ∆,即3,0100180.5250.47526.44422T T T T C +∆''=+⋅+=︒以上即完成了一遍k = 1时,各温度计算。
同理k = 2,即第15.02=⋅=∆⋅t k 天,温升2T ∆ = C , 上表面0T = 18C ,02,11,21,120.5250.47529.0852T T T T T C +=+⋅+∆=︒ 1,13,12,22,120.5250.47529.8582T T T T T C+=+⋅+∆=︒ 2,103,23,120.5250.47531.3022T T T T T C '+=+⋅+∆=︒3,1200180.5250.47531.44122T T T T C +∆''=+⋅+=︒同理可计算k = 3~56,即第~28天的各层温度值,本算例中再也不进行详细计算,最终计算结果如表1。
表1 不同混凝土龄期下各层混凝土温度值(单位:℃)二、温度应力计算例如以下计算例如依照步长为1天进行。
一、里表温差ΔT 1计算 公式如下)()()(1t T t T t T b m -=∆ () 计算结果见表2⑴各龄期混凝土收缩当量温差计算依照公式1132101.00M M M M )1()(⋅⋅⋅⋅⋅⋅-=-t yy e t εε () αε/)()(t t T y y = ()其中 取×10-4石家庄市内年平均气温值取℃ 计算结果见表3 ⑵综合降温差ΔT 2计算公式如下[]21()4()()()()()6m bm dm y w T t T t T t T t T t T t ∆=+++-()计算结果见表2表2 综合温差计算结果y ε注:表中*ΔT 1和*ΔT 2列中括号内数值为依照以下公式计算结果,其值在计算自约束应力和外约束应力时利用。
)()()(111j t T t T t T i -∆-∆=∆ ())()()(222t T j t T t T i ∆--∆=∆ ()表3各龄期混凝土收缩当量温差计算结果1、各龄期的混凝土弹性模量基础混凝土浇灌初期,处于升温时期,呈塑性状态,混凝土的弹性模量很小,由变形转变引发的应力也很小,温度应力一样可忽略不计。
通过数日,弹性模量随时刻迅速上升,现在由变形转变引发的应力状态(即混凝土降温引发拉应力)随着弹性模量的上升显著增加,因此必需考虑弹性模量的转变规律,一样按以下公式计算:)1(09.0)0()(t t e E E --=式中 )(t E ——任意龄期的弹性模量;0E ——最终的弹性模量,一样取成龄的弹性模量,取24/1015.3mm N ⨯; t ——混凝土浇灌后到计算时的天数。
各时期弹性模量:24)1(/10271.0mm N E ⨯= 24)2(/10519.0mm N E ⨯= 24)3(/10745.0mm N E ⨯= 24)6(/10314.1mm N E ⨯= 24)9(/10749.1mm N E ⨯=24)12(/10080.2mm N E ⨯= 24)15(/10333.2mm N E ⨯= 24)18(/10527.2mm N E ⨯= 24)21(/10674.2mm N E ⨯= 24)24(/10787.2mm N E ⨯= 24)27(/10873.2mm N E ⨯=24)30(/10938.2mm N E ⨯=2、 自约束应力计算依照公式),()()(2)(11τασt H t E t T t i i ni i z ••∆•=∑= ()41.010(1) 4.581271010.622Mpaσ-⨯=⨯⨯⨯=41.010(2)(4.58127101 3.15151901) 1.442Mpaσ-⨯=⨯⨯⨯+⨯⨯=41.010(3)(4.58127100.278 3.15151900.278 1.16674501)0.832Mpaσ-⨯=⨯⨯⨯+⨯⨯+⨯⨯=依照表2中计算结果,天后ΔT 1i (t )变成负值,同时由于徐变效应,自约束应力计算值将减小,本算例中再也不计算。
3、 外约束应力的计算公式如下 )()()()(1)(112t R t H t E t T t i i i ni ix ⨯••∆-=∑=μασ ()式中 L ——底板长度,考虑单组底板最长为27000mm ;HEC x=β 其中 H ——基础底板厚度,本例为1200mm ;x C ——总阻力系数(地基水平剪切刚度),N/mm 3,本工程采纳钢制模版加支撑钢结构,考虑成型混凝土结构要知足验收标准,近似将混凝土外侧结构看做高强度混凝土,阻力系数取 N/mm 3。
前期升温外约束应力为压应力,由于初期弹性模量较小且徐变时刻较长,其值不大,实际应用中可将这部份压应力作为平安储蓄。
外约束应力计算时从降温时期开始。
1)9天(第1台阶降温)自第9天至第30天的徐变应力:52.18310β-==⨯5270002.183100.294722L β-=⨯⨯= 查表得1.0452Lch β=45(9)1.74910 1.0107.561(1)0.2140.01510.15 1.045Mpaσ-⨯⨯⨯⨯=⨯-⨯=-2)12天(第2台阶降温)自第12天至第28天的徐变应力:52.00210β-==⨯5270002.002100.270322L β-=⨯⨯=查表得 1.0372L ch β= 45(12)1.74910 1.010 5.881(1)0.2150.00910.15 1.037Mpa σ-⨯⨯⨯⨯=⨯-⨯=-3)15天 (第3台阶降温)自第15天至第30天的徐变应力:51.89010β-==⨯ 5270001.89100.255222L β-=⨯⨯= 查表得1.0332L ch β= 45(15)1.74910 1.010 4.321(1)0.2150.00710.15 1.033Mpa σ-⨯⨯⨯⨯=⨯-⨯=-4)18天 (第4台阶降温)自第18天至第30天的徐变应力:51.81610β-==⨯ 5270001.816100.245222L β-=⨯⨯= 查表得 1.032L ch β=45(12)1.74910 1.010 3.951(1)0.2150.00610.15 1.03Mpa σ-⨯⨯⨯⨯=⨯-⨯=- 5)21天 (第5台阶降温)自第21天至第30天的徐变应力:51.76510β-==⨯ 5270001.765100.237622L β-=⨯⨯= 查表得1.0282L ch β=45(21) 1.74910 1.0100.81(1)0.3010.00110.15 1.028Mpa σ-⨯⨯⨯⨯=⨯-⨯=-由计算可知从第21天起温度收缩应力较小为,因此至30天内大体能够忽略不计。
6)总降温产生的最大拉应力max 0.0150.0090.0070.0060.0010.038Mpa σ*=++++=混凝土C35,取MPa R f 2.2=由计算得:混凝土浇筑完成后第二天自约束应力值最大,为1. 44Mpa总降温产生的最大拉应力为:max ()0.97 2.20 1.482 1.151.44tk f t K λσ*⨯===>知足抗裂条件因此混凝土浇筑完成前三天内,混凝土自约束应力较大,相对混凝土外收缩应力相对混凝土阻碍较小,因此混凝土浇筑完成后的前三天为混凝土养护的关键时刻段。
