2010年全国初中数学竞赛(海南赛区)初赛试卷参考答案
全国初中数学竞赛(海南赛区)初赛试题(含答案)

11、(3x-2y)212、 13、2 14、3 15、2<x<7
16、13.5 17、1或7 18、5
答案提示:
12、
13、由 得 所以有 所以x的值为2.
因为关于x的方程x2-4x+a=0的两个实数根为x1、x2,由根与系数的关系得x1+x2=4,所以 ,解得 ,所以a=3.
全国初中数学竞赛(海南赛区)
数学试卷
(本试卷共4页,满分120分,考试时间:3月10日8:30——10:30)
题号
一
二
三
总分
(1—10)
(11—18)
19
20
得分
一、选择题(本大题满分50分,每小题5分)
在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母
代号填写在下表相应题号下的方格内
8、由矩形AOBC的面积为8,可求矩形PEOF的面积为2,
又点P在第一象限,所以K=2,故选择B.
9、如图,分别以大的正方形中间”十”字所在的直线为对称轴可画出2、3两图,分别以正方形对角线所在直线为对称轴可画出4、5两图,再加上第1幅图,总共有5个符合条件的三角形,故选择A.
10、若点M在圆上,点M与圆心A的距离等于圆的半径 ,容易判断点(2,0)是圆A与X轴正半轴的交点、点(0,-2)是圆A与y轴负半轴的交点,另外,可以通过构造直角三角形判断点(2,-2)与圆心A的距离等于 ,也可以用两点公式求出点(2,-2)与圆心A的距离等于 ,因此A、B、C三个选项中的点均在圆上,而点(1,-2)与圆心A的距离等于1,小于圆A的半径,点(1,-2)不在圆上,故选择D.
19、海南省某种植园收获香蕉20000千克,其中香牙蕉12000千克、黄帝蕉8000千克,准备运往海口与文昌销售;根据市场供需,海口需要香蕉15000千克,文昌需要香蕉5000千克,海口与文昌两地的香蕉售价如下表所示:
全国初中数学竞赛海南赛区初赛试题及参考 答案

2008年全国初中数学竞赛(海南赛区)初 赛 试 卷(本试卷共6页,满分120分,考试时间:3月20日8:30——10:30)一、选择题(本大题满分50分,每小题5分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母 代号填写在下表相应题号下的方格内1. 若a 为实数,则化简2a 的结果是A . -aB . aC . ±aD . |a | 2.如果1)1(2++-x m x 是完全平方式,则m 的值为 A .-1 B .1 C .1或-1 D . 1或-33. 如图1,点A 、B 、C 顺次在直线l 上,点M 是线段AC 的中点,点N 是线段BC 的中点.若想求出MN 的长度,那么只需条件A .AB =12 B .BC =4 C .AM =5D . CN =24.在平面直角坐标系y o x 内,已知A (3,-3),点P 是y 轴上一点,则使△AOP 为等腰三角形的点P 共有A .2个B .3个C .4个D . 5个图1N MCB Al5.已知关于x 的方程01)2(=-+x b a 无解,那么b a 的值是 A .负数 B .正数 C .非负数 D .非正数6.一次函数)1(-=x k y 的图像经过点M (-1,-2),则其图像与y 轴的交点是 A .(0,-1) B .(1,0) C .(0,0) D .(0,1)7.如图2,在线段AE 同侧作两个等边三角形△ABC 和△CDE (∠ACE <120°),点P 与点M 分别是线段BE 和AD 的中点,则△CPM 是A .钝角三角形B .直角三角形C .等边三角形D .非等腰三角形8.某校初一运动队为了备战校运动会需要购置一批运动鞋.已知该队伍有20名同学,统计表如下表.由于不小心弄脏了表格,有两个数据看不到.鞋码 38 39 40 41 42 人数532下列说法中正确的是A .这组数据的中位数是40,众数是39B .这组数据的中位数与众数一定相等C .这组数据的平均数P 满足39<P <40D .以上说法都不对 9.如图3,A 、B 是函数xky =图像上两点, 点C 、D 、E 、F 分别在坐标轴上,且与点A 、B 、O 构成正方形和长方形. 若正方形OCAD 的面积为6, 则长方形OEBF 的面积是A . 3B . 6C . 9D . 1210. 某商店有5袋面粉,各袋重量在25~30公斤之间,店里有一磅秤,但只有能称50~70公斤重量的秤砣,现要确定各袋面粉的重量,至少要称A .4次B .5次C .6次D . 7次图3图2 ABCDPM二、填空题(本大题共7小题,每小题5分,满分35分)11.如果不等式组⎩⎨⎧<->-01a x x 无解,则a 的取值范围是____________.12.已知1=-b a ,122-=-b a ,则=-20082008b a_________.13.如图4,在菱形ABCD 中,AE ⊥BC ,E 为垂足, 若cosB 54=,EC =2,P 是AB 边上的一个动点,则线段PE 的长度的最小值是__________.14.小丁、小明、小倩在一起做游戏时,需要确定做游戏的先后顺序.他们约定用“剪子、布、锤子”的方式确定.那么在一个回合中三个人都出“布”的概率是_________.15.已知a 、b 为实数,且1=b a ,1≠a ,设11+++=b b a a M ,1111+++=b a N ,则N M -的值等于________.16. 如图5,在△ABC 中,AB =AC =5,BC =2,以AB 为直径的⊙O 分别交AC 、BC 两边于点D 、E ,则△CDE 的面积为_________.17. 一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图6所示,要摆成这样的图形,至少需用______块小正方体18. 若直线b y =(b 为实数)与函数342+-=x x y 的图象至少有三个公共点,则实数b 的取值范围是_________.图5 AB CD EO ·图4ABCDE P ·图6主视图左视图三、解答题(本大题满分30分,每小题15分)19. 某大型超市元旦假期举行促销活动,规定一次购物不超过100元的不给优惠;超过100元而不超过300时,按该次购物全额9折优惠;超过300元的其中300元仍按9折优惠,超过部分按8折优惠.小美两次购物分别用了94.5元和282.8元,现小丽决定一次购买小美分两次购买的同样的物品,则小丽应该付款多少元?20. 如图7,正方形ABCD 的边长为1,点F 在线段CD 上运动,AE 平分∠BAF 交BC 边于点E .(1)求证: AF =DF +BE .(2)设DF =x (0≤x ≤1),△ADF 与△ABE 的面积和S 是否存在最大值?若存在,求出此时x 的值及S . 若不存在,请说明理由.图7ABC DE F2008年全国初中数学竞赛(海南赛区) 初赛试卷参考答案一、1. D 2. D 3. A 4. C 5. D 6. A 7. C 8. C 9. B 10. B 二、11. a ≤1 12. -1 13. 4.8 14. 271 15. 0 16. -1 17. 52 18. 0<b ≤1 解答提示:1.∵ 当a <0时,2a =|a |=-a . 故选D . 2.21±=+m ,解得1=m 或3-=m . 故选D . 3.()AB BC AC BC AC NC MC MN 21212121=-=-=-=,∴只要已知AB 即可.故选A .4. 分别以点A 、O 、P 三点为等腰三角形的顶点三种情况考虑.5. 关于x 的方程01)2(=-+x b a 无解,则02=+b a . ∴有0==b a 或者a 、b 异号,故选D .6. ∵一次函数)1(-=x k y 的图像经过点M (-1,-2),则有()211-=--k ,解得1=k .所以函数解析式为1-=x y .令0=x 代入得1-=y .故其图像与y 轴的交点是(0,-1).故选A .7.易得△ACD ≌△BCE .所以△BCE 可以看成是△ACD 绕着点C 顺时针旋转60°而得到的.又M 为线段AD 中点,P 为线段BE 中点,故CP 就是CM 绕着点C 顺时针旋转60°而得.所以CP =CM 且,∠PCM =60°,故△CPM 是等边三角形,选C .8.(1)由中位数及众数的意义以及表格可知当这组数据的中位数是40时,众数必然是40,所以A 错误.(2)当39码与40码的人数都是5时,中位数与众数不等,所以B 错误.(3)假设剩余10人全部穿39码鞋,可得平均数为39.35;假设剩余10人全部穿40码鞋,可得平均数为39.85.可以判断C 正确.(或者设穿39码鞋的有x 人,且由0≤x ≤10也可得解) 故选C .9. ∵ 62121OC OD 21OCAD ==⋅=⋅=k y x S A A 正方形, ∴ 62121OF OE 21B B OCAD ==⋅=⋅=k y x S 长方形 ,故选B .10.拿出任意三袋,假设它们的重量分别为x 千克、y 千克、z 千克,两两一称,记录下相应的重量,若分别等于a 千克、b 千克、c 千克,则有方程组⎪⎩⎪⎨⎧=+=+=+c x z b z y ay x 容易求出x 、y 、z ;另外两袋分别与已知重量的其中一袋一起称,即可求出其重量.所以需要称5次,故选B .11.解不等式组⎩⎨⎧<->-001a x x 得⎩⎨⎧<>ax x 1,因为原不等式组无解,所以必有a ≤1.12.∵ ()()122-=-+=-b a b a b a ,又1=-b a ,则1-=+b a∴ ⎩⎨⎧=--=+11b a b a ,解得⎩⎨⎧-==1b a . 故()1102008200820082008-=--=-b a . 13. 设菱形ABCD 的边长为x ,则AB =BC =x ,又EC =2,所以BE =x -2,因为AE ⊥BC 于E ,所以在Rt △ABE 中, cosB x x 2-=,又cosB 54=,于是542=-x x ,解得x =10,即AB =10. 所以易求BE =8,AE =6,当EP ⊥AB 时,PE 取得最小值. 故由三角形面积公式有:21AB ·PE =21BE ·AE ,求得PE 的最小值为4.8 .14.用树状图列出一个回合中三个人所出手势的各种结果.上面只画出树状图的一部分(列出9种结果),把图中小丁的“剪”改为“布”重复上述画法,可再列出9种结果,最后改为“锤”同样也列出9种结果,所以共有27种结果,故求得P (布,布,布)=27115.∵1=b a ,1≠a ,∴ =+++=+++=+++=)1()1(11a b b b a a b a b b b a a a b b a a M N b a =+++1111. ∴ N M -=0.16. 如图,连结AE 、BD ,作DF ⊥EC 于点F . ∵ AB 是⊙O 的直径 ,∴ ∠ADB =∠AEB =90°又∵ AB =AC ,∴CE =21BC =1,∴ AE =222=-CE AC ∵ BD AC AE BC ⋅=⋅2121,∴ BD =554,∴ 在△ABD 中,AD =553,∴ CD =552 剪 剪 剪 布 锤布 剪 布 锤 锤 剪 布 锤 小丁 小明 小倩 A BCD E F O · AB CDE P又∵△CDF ∽△CAE ,∴AEDFCA CD =,可求得DF =54. ∴ △CDE 的面积为5221=⋅DF CE . 解法2:如图,连结AE 、BD ,DE .∵ AB 是⊙O 的直径 ,∴ ∠ADB =∠AEB =90°又∵ AB =AC ,∴ BE =CE =1,∴ AE =222=-CE AC .∵ BD AC AE BC ⋅=⋅2121,∴ BD =554,∴ 在△ABD 中,AD =553,∴ CD =552. ∴ S △CDE =21S △BDC =⨯2152552554212121=⨯⨯⨯=⨯⨯CD BD . 17.小正方体个数最少情况如图所示(图中数字表示该位置小正方体的个数)所以最少为5块.18. y =x 2-4x +3=(x -2)22-4x +3|y =b 线,结合①②,易知b三、19.因为100×0.9=90<94.5<100,300×0.9=270<282.8设小美第二次购物的原价为x 元,则(x -300)×0.8+300316情况1: 小美第一次购物没有优惠,第二次购物原价超过300元 则小丽应付(316+94.5-300)×0.8+300×0.9=358.4(元)情况2: 小美第一次购物原价超过100元,第二次购物原价超过300元; 则第一次购物原价为:94.5÷0.9=105(元)所以小丽应付(316+105-300)×0.8+300×0.9=362.8(元).20.(1)证明: 如图,延长CB 至点G ,使得BG =DF ,连结AG . 因为ABCD 是正方形,所以在Rt △ADF 和Rt △ABG 中,AD =AB ,∠ADF =∠ABG =90°,DF =BG . ∴ Rt △ADF ≌Rt △ABG (SAS ),∴AF =AG ,∠DAF =∠BAG . 又 ∵ AE 是∠BAF 的平分线∴∠EAF =∠BAE , ∴ ∠DAF +∠EAF =∠BAG +∠BAE 即∠EAD =∠GAE .∵ AD ∥BC ,∴∠GEA =∠EAD ,∴∠GEA =∠GAE ,∴ AG =GE . 即AG =BG +BE .∴俯视图 2 12 图① 1AB C DE O ·AF =DF +BE ,得证.(2)AB BE AD DF S S S ABE ADF ⋅+⋅=+=∆∆2121 ∵ AD =AB =1, ∴ )(21BE DF S +=由(1)知,AF =DF +BE , 所以AF S 21=.在Rt △ADF 中,AD =1,DF =x , ∴12+=x AF ,∴1212+=x S . 由上式可知,当x 2达到最大值时,S 最大.而0≤x ≤1,所以,当x =1时,S 最大值为2211212=+x .ABCDEF G。
海南省2010年初中毕业生学业考试数学科试题及答案
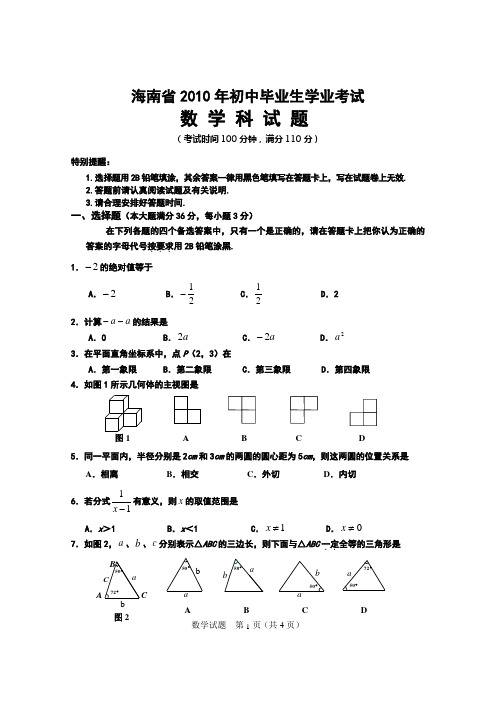
1 数学试题 第 页(共4页) 海南省2010年初中毕业生学业考试数 学 科 试 题(考试时间100分钟,满分110分)特别提醒:1.选择题用2B 铅笔填涂,其余答案一律用黑色笔填写在答题卡上,写在试题卷上无效.2.答题前请认真阅读试题及有关说明.3.请合理安排好答题时间.一、选择题(本大题满分36分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的,请在答题卡上把你认为正确的答案的字母代号按要求...用2B 铅笔涂黑. 1.2-的绝对值等于A .2-B .21- C .21D .22.计算a a --的结果是A .0B .a 2C .a 2-D .2a 3.在平面直角坐标系中,点P (2,3)在A .第一象限B .第二象限C .第三象限D .第四象限 4.如图1所示几何体的主视图是图1ABCD5.同一平面内,半径分别是2cm 和3cm 的两圆的圆心距为5cm ,则这两圆的位置关系是A .相离B .相交C .外切D .内切 6.若分式11-x 有意义,则x 的取值范围是 A .x >1 B .x <1 C .1≠x D .0≠x 7.如图2,a 、b 、c 分别表示△ABC 的三边长,则下面与△ABC 一定..全等的三角形是A B C D50°图2CA acba72°50°58°baabba50°72°B50°2 数学试题 第 页(共4页)8.方程3 x - 1 = 0的根是A .3B .31 C .31- D .3- 9.在正方形网格中,α ∠的位置如图3所示,则 tan α的值是A .33 B .35C .21D .210.如图4, 在梯形ABCD 中,AD//BC ,AC 与BD 相交于点O ,则下列三角形中,与△BOC 一定..相似的是 A .△ABD B .△DOA C .△ACD D .△ABO11.如图5, 在△ABC 中,AB=AC ,AD ⊥BC 于点D ,则下列结论不一定...成立的是 A .AD = BD B .BD = CD C .∠1 =∠2 D .∠B =∠C12.在反比例函数 的图象的任一支上,y 都随x 的增大而增大,则k 的值可以..是 A .-1 B .0 C .1 D .2二、填空题(本大题满分18分,每小题3分)13.计算:=⋅32a a __________.14.某工厂计划a 天生产60件产品,则平均每天生产该产品__________件.15.海南省农村公路通畅工程建设,截止2009年9月30日,累计完成投资约4 620 000 000元,数据4 620 000 000用科学记数法表示应为____________.16.一道选择题共有四个备选答案,其中只有一个是正确的,若有一位同学随意选了其中一个答案,那么他选中正确答案的概率是_________.17.如图6,在平行四边形ABCD 中,AB = 6cm ,∠BCD 的平分线交AD 于点E ,则线段DE 的长度是__________ cm .18.如图7,将半径为4cm 的圆形纸片折叠后,圆弧恰好经过圆心O ,则折痕AB 的长度为_________cm .D ABC图4O 图3α图5ADBC21 ABCED图6图71ky x-=3 数学试题 第 页(共4页)三、解答题(本大题满分56分)19.(满分8分,每小题4分)(1)计算:23)31(10⨯-- (2)解方程:0111=--x 20.(满分8分)从相关部门获悉,2010年海南省高考报名人数共54741人,图8是报名考生分类统计图根据以上信息,解答下列问题:(1)2010年海南省高考报名人数中,理工类考生___________人;(2)请补充完整图8中的条形统计图和扇形统计图(百分率精确到0.1%);(3)假如你自己绘制图8中扇形统计图,你认为文史类考生对应的扇形圆心角应为 °(精确到1°).21.(满分8分)如图9,在正方形网格中,△ABC都在格点上,结合所给的平面直角坐标系解答下列问题: (1)将△ABC 向右平移5个单位长度,画出平移后的△A 1B 1C 1 ;(2)画出△ABC 关于x 轴对称的△A 2B 2C 2 ; (3)将△ABC 绕原点O 旋转180°,画出旋转后的△A 3B 3C 3 ;(4)在△A 1B 1C 1 、△A 2B 2C 2 、△A 3B 3C 3 中 △________与△________成轴对称;△________与△________成中心对称.图9图82010年海南省高考报名考生分类条形统计图2010年海南省高考报名考生分类扇形统计图4 数学试题 第 页(共4页)22.(满分8分)2010年上海世博会入园门票有11种之多,其中“指定日普通票”价格为200元一张,“指定日优惠票”价格为120元一张,某门票销售点在5月1日开幕式这一天共售出这两种门票1200张,收入216000元,该销售点这天分别售出这两种门票多少张? 23.(满分11分)如图10,四边形ABCD 和四边形AEFG 均为正方形,连接BG 与DE 相交于点H .(1)证明:△ABG ≌△ADE ;(2)试猜想∠BHD 的度数,并说明理由;(3)将图中正方形ABCD 绕点A 逆时针旋转(0°<∠BAE <180°),设△ABE 的面积为1S ,△ADG 的面积为2S ,判断1S 与2S 的大小关系,并给予证明.24.(满分13分)如图11,在平面直角坐标系中,直线3+-=x y 与x 轴、y 轴分别交于点B 、C ;抛物线c bx x y ++-=2经过B 、C 两点,并与x 轴交于另一点A . (1)求该抛物线所对应的函数关系式;(2)设)(y x P ,是(1)所得抛物线上的一个动点,过点P 作直线x l ⊥轴于点M ,交直线BC 于点N .① 若点P 在第一象限内.试问:线段PN 的长度是否存在最大值 ?若存在,求出它的最大值及此时x 的值;若不存在,请说明理由; ② 求以BC 为底边的等腰△BPC 的面积.CF GEDBA图10H5页(共4页)一、选择题(每小题3分,共36分)1. D 2.C 3.A 4.A 5.C 6.C 7.B 8.B 9.D 10.B 11.A 12.D 二、填空题(每小题3分,共18分) 13、 14、 15、 16、 17、6 18、34三、解答题(共56分)19.(1)原式=10-(- )×9 ……分=10-(-3) ……分 =10+3 ……分 =13 ……分 (2)两边都乘以)1(-x 得: 1-)1(-x =0 ……分1-1+x =0 ……分x =2 ……分检验:当x =2时入1-x ≠0,所以原方程的根是x =2. ……分 20.海南省2010年初中毕业生学业考试数学课时题参考答案2010年海南省高考报名考生分类条形统计图2010年海南省高考报名考生分类扇形统计图31a605a 91062.4⨯416 数学试题 第 页(共4页)解: (1) 33510 ……分(2)如图所示 ……分 (3) 123 ……分21.(1)△111C B A 如图所示……分(2)△222C B A 如图所示……分(3)△333C B A 如图所示 ……分(4)△222C B A 、△333C B A △111C B A 、△333C B A……分22.解法一:设该销售点这天售出“指定日普通票x 张” ,“指定日优惠票”y 张,依题意得 ……分⎩⎨⎧=+=+2160001202001200y x y x ……分 解得 ⎩⎨⎧==300900y x ……分 答:这天售出“指定日普通票900张” ,“指定日优惠票”300张.……分解法二:设该销售点这天售出“指定日普通票x 张”,则“指定日优惠票”销售了(1200-x )张,依题意得 ……分200x +120(1200-x )=216000 ……分 解得x =900 ∴1200-x =300 ……分 答:这天售出“指定日普通票”900张 ,“指定日优惠票”300张 .7数学试题 第 页(共4页) ……分23.(1)证法一:证明:在正方形ABCD 和正方形AEFG 中∠GAE =∠BAD =90° ……分 ∠GAE+∠EAB =∠BAD+EAB即∠GAB =∠EAD ……分 又AG =A E AB =AD∴△ABG ≌△ADE ……分证法二:证明:因为四边形ABCD 与四边形AEFG 都是正方形,所以∠GAE=∠BAD=90°,AG=AE ,AB=AD ,所以△EAD 可以看成是△GAB 逆时针旋转90°得到,所以△ABG ≌△ADE (2)证法一:我猜想∠BHD =90°理由如下:∵△ABG ≌△ADE ∴∠1=∠2 ……分 而∠3=∠4 ∴∠1+∠3=∠2+∠4∵∠2+∠4=90 ∠1+∠3=90° ……分 ∴∠BHD =90° ……分 证法二:我猜想∠BHD =90°理由如下:由(1)证法(二)可知△EAD 可以看成是△GAB 逆时针旋转90°得到,BG 与DE 是一组对应边,所以BG ⊥DE ,即∠BHD =90° (3)证法一:当正方形ABCD 绕点A 逆时针旋转0°<∠BAE <180°时,S 1和S 2总保持相等. ……分 证明如下:由于0°<∠BAE <180°因此分三种情况: ①当0°<∠BAE <90°时 (如图10) 过点B 作BM ⊥直线AE 于点M , 过点D 作DN ⊥直线AG 于点N . ∵∠MAN =∠BAD =90° ∴∠MAB =∠NAD又∠AMB =∠AND =90° AB =AD∴△AMB ≌△AND ∴BM =DN 又AE =AGCA B D E G F M N图10H 13248 数学试题 第 页(共4页)∴DN AG 21BM AE 21⋅=⋅ ∴21S S = ……分 ②当∠BAE =90°时 如图10(a )∵AE =AG ∠BAE =∠DAG =90°AB =AD ∴△ABE ≌△ADG∴21S S = ……分③当90°<∠BAE <180°时 如图10(b ) 和①一样;同理可证21S S =综上所述,在(3)的条件下,总有21S S =.……分证法二:①当0°<∠BAE <90°时,如图10(c) 作EM ⊥AB 于点M ,作GN ⊥AD 交DA 延长线于点N , 则∠GNA =∠EMA =90° 又∵四边形ABCD 与 四边形AEFG 都是正方形, ∴AG =AE ,AB =AD ∴∠GAN+∠EAN =90°,∠EAM+∠EAN =90° ∴∠G AN =∠EAM∴△GAN ≌△EAM (AAS )∴G N =EM ∵ABCDE F G 图10(a ) ABCDE F G图10(b ) ABDEG F 图10(c )HM N C12ADG S AD GN ∆=⋅12ABES AB EM ∆=⋅9 数学试题 第 页(共4页)∴21S S = ②③同证法一类似证法三:当正方形ABCD 绕点A 逆时针旋转0°<∠BAE <180°时,S 1和S 2总保持相等. ……分 证明如下:由于0°<∠BAE <180°因此分三种情况: ①当0°<∠BAE <90°时 如图10(d ) 延长GA 至M 使AM=AG ,连接DM ,则有AD M AD G S S ∆∆=∵AE=AG=AM ,又∠1+∠2=90° ∠3+∠2=90° ∴∠1=∠3∴△ABE ≌△ADM (SAS ) ∴AD G AD M ABE S S S ∆∆∆==∴21S S = ……分 ②当∠BAE =90°时 (同证法一) ……分③当90°<∠BAE <180°时 如图10(e ) 和①一样; 同理可证21S S =综上所述,在(3)的条件下, 总有21S S =……分证法四:①当0°<∠BAE <90°时如图10(f ) 延长DA 至M 使AM=AD ,连接GM ,则有AMG ADG S S ∆∆=再通过证明△ABE 与△AMG 全等从而证出21S S =ADG ABE S S ∆∆= CBM HADGF图10(f)EBC图10(d )ABCDEF G图10(e )M10数学试题 第 页(共4页) ②③同证法一类似证法五:(这种证法用三角函数知识证明,无须分类证明) 如图10(g)四边形ABCD 与四边形AEFG 都是正方形,∴AG=AE ,AB=AD当∠BAE=α时,∠G AD=180°-α则 sin(180°-α)=sin α即 ∴21S S =24.(1)由于直线3+-=x y 经过B 、C 两点,令y =0得x =3;令x =0,得y =3∴B (3,0),C (0,3) ……分∵点B 、C 在抛物线c bx x y ++-=2上,于是得93b+c=0c=3-+⎧⎨⎩ ……分 解得b=2,c=3 ……分∴所求函数关系式为322++-=x x y ……分 (2)①∵点P (x ,y )在抛物线322++-=x x y 上, 且PN ⊥x 轴,∴设点P 的坐标为(x , 322++-x x ) ……分1sin 2AEB S AE AB α∆=⋅1sin(180)2AGD S AG AD α︒∆=⋅-1sin 2AG AD α=⋅AEB AGDS S ∆∆= CABEGF 图10(g )HD11 数学试题 第 页(共4页)同理可设点N 的坐标为(x ,3+-x ) ……分又点P 在第一象限,∴PN=PM-NM=(322++-x x )-(3+-x )=-x x 32+ =49)23(2+--x ……分 ∴当23=x 时, 线段PN 的长度的最大值为4. ……分 ②解法一:由题意知,点P 在线段BC 的垂直平分线上,又由①知,OB =OC∴BC 的中垂线同时也是∠BOC 的平分线,∴设点P 的坐标为),(a a 又点P 在抛物线322++-=x x y 上,于是有322++-=a a a ∴032=--a a ……分 解得2131,213121-=+=a a ……分 ∴点P 的坐标为: ()2131,2131++ 或 ()2131,2131-- …分 若点P 的坐标为 ()2131,2131++ ,此时点P 在第一象限,在Rt △OMP 和Rt △BOC 中, 12M P O M ==,OB=OC=3 BO C BO CP S ∆∆-=四边形S S BPC12 数学试题 第 页(共4页) B O P B O C =2S S ∆∆- 11=2BO PM-BO22⨯⋅⋅⋅ 19=2322⨯⨯若点P 的坐标为 , 此时点P 在第三象限,则BO C CO P BO P BPC S S S S ∆∆∆∆++=11323322=⨯+⨯⨯193222=⨯+392+=62= ……分解法二:由题意知,点P 在线段BC 的垂直平分线上,又由①知,OB =OC∴BC 的中垂线同时也是∠BOC 的平分线,∴设点P 的坐标为(),a a又点P 在抛物线322++-=x x y 上,于是有322++-=a a a ∴032=--a a …分解得2131,213121-=+=a a ……分∴点P 的坐标为:()2131,2131++ 或 ()2131,2131--…分 ()2131,2131--13 数学试题 第 页(共4页) 若点P 的坐标为(),此时点P 在第一象限,在Rt △OMP 和Rt △BOC 中,MP OM ==,OB=OC=3BO C BMP CO MP S S ∆∆∆-+=梯形S S BPC()111222OC MP MO BM PM BO CO =+⋅+⋅-⋅= = = = 若点P 的坐标为 ()2131,2131-- , 此时点P 在第三象限,(与解法一相同)……分 当点P 在第一象限时,△BPC 面积其它解法有:①OP =2⋅,BC=23BO C BO CP S ∆∆-=四边形S S BPC2613333212322131212121-=⨯⨯-⋅⋅+⋅=⋅-⋅=OCOB BC OP②BPC PNC PNB S S S ∆∆∆=+11PN OM+PN MB 22=⋅⋅⋅⋅1PN OB 2=⋅⋅ (本答案仅供参考33212131213132121312131321⨯⨯-+⋅⎪⎪⎭⎫⎝⎛+-++⋅⎪⎪⎭⎫ ⎝⎛++292131321313213121-⎪⎪⎭⎫ ⎝⎛+-++++⋅291333-+26133-……分 1PN OM+MB 2=⋅()。
2010年全国初中数学联赛3(整理好)

二、已知等腰三角形△ABC中,AB=AC,∠C的平分线与AB边交于点P,M为△ABC的内
切圆⊙I与BC边的切点,作MD∥AC,交⊙I于点D.证明:PD是⊙I切线.
三、已知二次函数y=x2+bx-c的图象经过两点P(1,a),Q(2,10a).
(1)如果a,b,c都是整数,且c<b<8a,求a,b,c的值.
(2)设二次函数y=x2+bx-c的图象与x轴的交点为A,B,与y轴的交点为C.如果关
于x的方程x2+bx-c=0的两个根都是整数,求△ABC的面积.
第二试(B)
一、设正整数a,b,c为三角形的三边长,满足a2+b2+c2-ab-ac-bc=13,求符合条件且
周长不超过30的三角形的个数(全等的三角形只计算1次).
二、同A卷第二题.
三、同A卷第三题.
第二试(C)
一、同B卷第一题.
二、同A卷第二题.
三、设p是大于2的质数,k为正整数.若函数y=x2+px+(k+1)p-4的图象与x轴的两个
交点的横坐标至少有一个为整数,求k的值.。
2010年海南省数学科中考模拟试题(四)以及答案

新世纪教育网精选资料版权全部@新世纪教育网2010 年海南省中考数学模拟试题(一)答案一、(本大分36 分,每小 3 分)CACB ACBD DBAC二、填空(本大分18 分,每小 3 分)13.—314. 015.x1 0, x2216. 2 17. 10m18. 3三、解答(本大分 56 分)19.解:x< 4(1)a(a 2 b 2 )( 2)解不等式①得⋯⋯⋯ (5分 )a 2ab解不等式②得x2⋯⋯⋯ (6分) a=(a b)(a b)⋯⋯⋯ (2 分)a(a b)∴ 个不等式的解集1x< 4 ⋯⋯⋯(8分) =a b⋯⋯⋯ (3分)当 a2,b22原式 =2( 2 2 )2⋯⋯⋯ (4 分)20.解:八年有x 名学生,九年有(x+100 )名学生,依意得:⋯⋯⋯(1 分)100011800⋯⋯⋯ (4分)x x100∴ x2700x100000 0⋯⋯⋯ (5分 )解得 x1200, x2 500x1200, x2500均是原方程的解⋯⋯⋯ (6分 )又当x2500, 1000÷<500=2 5不切合条件舍去,∴ x200,x100300⋯⋯⋯ (7 分)答:八年有 200 名学生,九年有 300 名学生。
⋯⋯⋯ (8 分)21.(1)抽, 200(2)众数(3)20 人、 36 人⋯⋯⋯ (5 分)“家下”政策知度条形160140新世纪教育网精选资料版权全部 @新世纪教育网22.(1)所作 A 1 B 1 C 1 如 10 所示C 1点B 的坐 (3,0) ,1点 C 1 的坐 (4,3) ;B 1⋯⋯⋯(4 分)(2)所作 A 2 B 2C 2 如 10 B 2所示⋯⋯⋯ (6 分) 10(3)因A 2B 2C 2 由 △ ABC 旋 获得,C 2因此 A 2 B 2C 2 与 △ ABC 全等, 因此SA 2B 2C2S ABC⋯⋯⋯ (8 分) 23. (1)明:∵ADE 和 BCE 都是等 三角形∴ AE=DE , CD=BE ∠AED=∠ BEC∴ ∠ AED+∠DEC=∠BEC+∠DEC124 36DMC即∠ AEC=∠DEB∴ ACE ≌ DBE ( SAS )⋯⋯⋯ (3 分 ) (2)①在 11 上画出四 形 ⋯⋯⋯ (5 分 ) ②四 形 PQMN 菱形⋯⋯⋯ (6 分)∵P 、Q 分 是 AB 与 BC 的中点1 ∴PQ//AC2同理 MN//1 ACPN//1BD22∴ PQ/ /MN∴四 形 PQMN 是平行四 形 ⋯⋯⋯ (7 分)由( 1) ACE ≌ DBE 得 AC=BD∴PQ=PN∴四 形 PQMN 是菱形。
奥数-2011年全国初中数学竞赛海南赛区初赛试题及参考答案

2011年全国初中数学竞赛(海南赛区)初赛试卷参考答案一、选择题(本大题满分50分,每小题5分) 题 号 1 2 3 4 5 6 7 8 9 10 答 案 CADABBDCAB提示:2. ∵3n=-15,∴n=-5,m=3+(-5)=-2. 故选A.3. ∵a +|a |=0, ∴|a |=-a , ∴a ≤0,进而a -1≤0∴22)1(a a +-=|a -1|+|a |=-(a -1)-a =1-2a . 故选D.4. ∵直线y =-x -4不经过第一象限,∴无论m 为何实数,直线y =x +m 与y =-x -4的交点不可能在第一象限,故选A.8. 如图2,由题意可知,∠ACB =90°,∠ABC =60°,则AB =2BC =8米,所以选择C. 9. 如图3,由已知可知△ABC 与△BOC 相似,可得OC BC BC AC =,即BC 2=AC ·OC .设OA=BC=x ,可得方程x 2=x +1,解这个方程得2511+=x ,2512-=x (不合题意,舍去).故选A.10.如图4以点A 为圆心,250km 为半径画圆,交OM 于点B 、C ,作AN ⊥BC 于点N ,则可求出AN=150km ,又AC=250km ,利用勾股定理可求出CN=200km ,则BC=400km ,当台风中心在线段BC 上时,A 市都会受到台风的影响,所以A 市受台风影响持续的时间为400÷20=20小时,所以选择B. 二、填空题(本大题满分40分,每小题5分)11. 因为n 是关于x 的方程022=++n mx x 的根,所以022=++n mn n ,所以0)2(=++m n n ,又0≠n则02=++n m ,所以则n m +的值为-2.A O BC北东 图4 M NABCA B C D O 图3光 线A BC 图2 水平线 30° 60°12. 222222(2)(2)2(1)242()b a ab b a b a b a b a ba b a b a b a b a b++++---÷=⋅=+-+++, 又03=+b a 所以b a 3-= 所以原式=25323=+---b b b b .13. 由频率分布直方图可知,“25~45”的学生人数有21人,所以仰卧起坐次数在25~45次的频率是0.7.14. 如图6,连接AC 可知△ABC 是等腰直角三角形,所以∠ABC =45°.15. 与原点的距离为1的交点有(1,0)或(-1,0),由此可求得该二次函数的 解析式有两个,分别为:x x y +=2或x x y 31312+-=. 16. 如图7,由222222251520=+=+=OB AO AB ,可知连杆AB 的长度等于25cm ,当滑块A 向下滑到O 点时,滑块B 距O 点的距离是25 cm ,故滑块B 滑动了25-15 =10 cm . 17. △COD 是△AOB 绕点O 顺时针旋转40°后得到的图形,点C 恰好在AB 上,所以可知OA=OC ,∠AOC =∠BOD =40°, ∴∠ACO=70°,又∠AOD= 90°,∴∠BOC= 10°, ∴∠B= 60°. 18. 如图9,连接BM EM BE ,,.由题意得四边形ABNM 和四边形FENM 关于直线MN 对称. ∴MN 垂直平分BE .∴EM BM = ∵点E 是CD 的中点,DE=1∴ 在Rt ABM △和在Rt DEM △中,222AM AB BM +=,222DM DE EM +=, ∴2222AM AB DM DE +=+.设x AM =,则x DM -=4,∴22221)4(2+-=+x x . 解得813=x ,即813=AM .三、解答题(本大题满分30分,每小题15分)19.(1)证明:过点O 作OM//AB 交PC 于点M , 则∠COM=∠CAB .∵ 四边形ABCD 是正方形,∴ OA=OC ,∠CAB=∠CBD=∠COM=45°, ∴ AP=2OM . 又∵ ∠1=∠2,∴ ∠1+∠COM=∠2+∠CBD, 即 ∠OMQ=∠OQM.∴ OM=OQ ∴ AP =2OQ .(本小题也可以过点A 作直线平行于OQ 证明) (2)根据题意作出图形,如图10所示①ⅰ、当PC 绕点P 逆时针旋转90°时,作EF ⊥AB 交BA 延长线于点F,则∠EFP=∠PBC=90°,∠3+∠CPB=90°. 又∠2+∠CPB=90°,∴∠3=∠2. 又PE 由PC 绕点P 旋转形成 ∴PE=PC ∴△EPF ≌△CPB.NABCD EFM图9AB CD PE EO Q M1 2 G F 3 图10∴EF=BP=x , ∴AP=1-x ∴x x EF AP S APE )1(2121-=⋅=∆. ∴△APE 的面积S 与x 的函数关系式为x x S 21212+-= (10<x<).ⅱ、当PC 绕点P 顺时针旋转90°时,作EG ⊥AB 交AB 延长线于点G,则同理可得△EPG ≌△CPB ,EG=BP=x .∴△APE 的面积S 与x 的函数关系式为x x S 21212+-= 由ⅰ、ⅱ可得△APE 的面积S 与x 的函数关系式为x x S 21212+-=,(10<x<)②由①知S 与x 的函数关系式为x x S 21212+-=,(10<x<)即81)21(212+--=x S ,(10<x<)∴当21=x 时S 的值最大,最大值为81.此时点P 所在的位置是边AB 的中点处.20.(1)设参加社会实践的老师有m 人,学生有n 人,则学生家长有m 2人,若都买二等座单程火车票且花钱最少.....,则全体学生都需买二等座学生票,依题意得: ⎩⎨⎧=+⨯=+112205136817010)3(81n m n m 解得⎩⎨⎧==18010n m 则202=m 答:参加社会实践的老师、家长与学生各有10、20与180人. (2)由(1)知所有参与人员总共有210人,其中学生有180人, ①当210180x <≤时,最经济的购票方案为:学生都买学生票共180张,(180-x )名成年人买二等座火车票,)210(x -名成年人买一等座火车票.∴火车票的总费用(单程)y 与x 之间的函数关系式为:)210(81)180(6818051x x y -+-+⨯=即1395013+-=x y (210180x <≤)②当1800<x<时,最经济的购票方案为:一部分学生买学生票共x 张,其余的学生与家长老师一起购买一等座火车票共)210(x -张.∴火车票的总费用(单程)y 与x 之间的函数关系式为:)210(8151x x y -+=即1701030+-=x y (1800<x<) (3)由(2)小题知,当210180x <≤时,1395013+-=x y ,由此可见,当209=x 时,y 的值最小,最小值为11233元,当180=x 时,y 的值最大,最大值为11610元.当1800<x<时,1701030+-=x y ,由此可见,当179=x 时,y 的值最小,最小值为11640元,当1=x 时,y 的值最大,最大值为16980元.所以可以判断按(2)小题中的购票方案,购买一个单程火车票至少要花11233元,最多要花16980元..cn。
2010年全国初中数学竞赛题
2010年全国初中数学竞赛试题考试时间.2010年3月21日9.30~11.30满分150分一、选择题(共5题,每小题7分,计35分)1、 若10,20==c b b a ,则cb b a ++的值为( ) A 、2111 B 、1121 C 、21110 D 、11210 2、 若实数b a ,满足02212=++-b ab a ,则a 的取值范围是( ) A 、2-≤a B 、4≥a C 、42≥-≤a a 或 D 、42≤≤-a3、如图,在四边形ABCD 中,∠B=135°,∠C=120°AB=32, BC=24,224=-CD ,则AD 边长是( )A 、62B 、64C 、64+D 、622+4、在一列数k x x x x 321,,中,已知,11=x 且当2≥k 时, ,4241411⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡--+=-k k x x k k (取整符号[]a 表示不超过实数a 的最大整数, 如[][]02.0,26.2==),则2010x 等于( )A 、1B 、2C 、3D 、45、如图在平面直角坐标系xOy 中,等腰梯形ABCD 的顶点坐标分别为A (1,1),B (2,-1),C (-2,-1),D (-1,1)。
y 轴上一点P (0,2)绕点A 旋转180°得 点1P ,点1P 绕点B 旋转180°得点2P ,点2P 绕点C 旋转180°得点3P ,点3P 绕点D 旋转180°得点4P ,……,重复操作依次得到点1P ,2P ,……则点2010P 的坐标是( )A 、(2010,2)B (2010,-2)、C 、(2012,-2)D 、(0,2)二、填空题(每小题7分,计35分)6、已知15-=a ,则1227223--+a a a 的值等于 ;7、一辆客车、一辆货车、一辆小轿车在一条笔直的公路上朝同一方向匀速行驶,在某一时刻, 客车在前,小轿车在后,货车在客车与小轿车的正中间,过了10分钟,小轿车追上了货 DA B C 第3题车;又过了5分钟,小轿车追上客车;再过了 分钟货车追上客车; 8、如图在平面直角坐标系xOy 中,多边形OABCDE 的顶点坐标分别为O (0,0),A (0,6), B (4,6),C (4,4),D (6,4),E (6,0)。
全国初中数学竞赛海南赛区初赛试题及参考答案
20XX 年全国初中数学竞赛(海南赛区)初 赛 试 卷(本试卷共6页,满分120分,考试时间:3月20日8:30——10:30)一、选择题(本大题满分50分,每小题5分)在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母 代号填写在下表相应题号下的方格内1. 若a 为实数,则化简2a 的结果是A . -aB . aC . ±aD . |a | 2.如果1)1(2++-x m x 是完全平方式,则m 的值为A .-1B .1C .1或-1D . 1或-3 3. 如图1,点A 、B 、C 顺次在直线l 上,点M 是线段AC 的中点,点N 是线段BC 的中点.若想求出MN 的长度,那么只需条件A .AB =12 B .BC =4 C .AM =5D . CN =24.在平面直角坐标系y o x 内,已知A (3,-3),点P 是y 轴上一点,则使△AOP 为等腰三角形的点P 共有A .2个B .3个C .4个D . 5个图1N MCB l5.已知关于x 的方程01)2(=-+x b a 无解,那么b a 的值是A .负数B .正数C .非负数D .非正数 6.一次函数)1(-=x k y 的图像经过点M (-1,-2),则其图像与y 轴的交点是 A .(0,-1) B .(1,0) C .(0,0) D .(0,1) 7.如图2,在线段AE 同侧作两个等边三角形△ABC 和△CDE (∠ACE <120°),点P 与点M 分别是线段BE 和AD 的中点,则△CPM 是A .钝角三角形B .直角三角形C .等边三角形D .非等腰三角形8.某校初一运动队为了备战校运动会需要购置一批运动鞋.已知该队伍有20名同学,统计表如下表.由于不小心弄脏了表格,有两个数据看不到.鞋码 38 394041 42 人数532下列说法中正确的是A .这组数据的中位数是40,众数是39B .这组数据的中位数与众数一定相等C .这组数据的平均数P 满足39<P <40D .以上说法都不对 9.如图3,A 、B 是函数xky =图像上两点, 点C 、D 、E 、F 分别在坐标轴上,且与点A 、B 、O 构成正方形和长方形. 若正方形OCAD 的面积为6, 则长方形OEBF 的面积是A . 3B . 6C . 9D . 1210. 某商店有5袋面粉,各袋重量在25~30公斤之间,店里有一磅秤,但只有能称50~70公斤重量的秤砣,现要确定各袋面粉的重量,至少要称A .4次B .5次C .6次D . 7次图3图2 ABCDPM二、填空题(本大题共7小题,每小题5分,满分35分)11.如果不等式组⎩⎨⎧<->-001a x x 无解,则a 的取值范围是____________.12.已知1=-b a ,122-=-b a ,则=-20082008b a_________.13.如图4,在菱形ABCD 中,AE ⊥BC ,E 为垂足, 若cosB 54=,EC =2,P 是AB 边上的一个动点,则线段PE 的长度的最小值是__________.14.小丁、小明、小倩在一起做游戏时,需要确定做游戏的先后顺序.他们约定用“剪子、布、锤子”的方式确定.那么在一个回合中三个人都出“布”的概率是_________.15.已知a 、b 为实数,且1=b a ,1≠a ,设11+++=b b a a M ,1111+++=b a N ,则N M -的值等于________.16. 如图5,在△ABC 中,AB =AC =5,BC =2,以AB 为直径的⊙O 分别交AC 、BC 两边于点D 、E ,则△CDE 的面积为_________.17. 一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图6所示,要摆成这样的图形,至少需用______块小正方体18. 若直线b y =(b 为实数)与函数342+-=x x y 的图象至少有三个公共点,则实数b 的取值范围是_________.图5 AB CD EO ·图4ABCDE P ·图6主视图左视图三、解答题(本大题满分30分,每小题15分)19. 某大型超市元旦假期举行促销活动,规定一次购物不超过100元的不给优惠;超过100元而不超过300时,按该次购物全额9折优惠;超过300元的其中300元仍按9折优惠,超过部分按8折优惠.小美两次购物分别用了94.5元和282.8元,现小丽决定一次购买小美分两次购买的同样的物品,则小丽应该付款多少元?20. 如图7,正方形ABCD 的边长为1,点F 在线段CD 上运动,AE 平分∠BAF 交BC 边于点E .(1)求证: AF =DF +BE .(2)设DF =x (0≤x ≤1),△ADF 与△ABE 的面积和S 是否存在最大值?若存在,求出此时x 的值及S . 若不存在,请说明理由.图7ABC DE F20XX 年全国初中数学竞赛(海南赛区)初赛试卷参考答案一、1. D 2. D 3. A 4. C 5. D 6. A 7. C 8. C 9. B 10. B 二、11. a ≤1 12. -1 13. 4.8 14. 271 15. 0 16. -1 17. 5218. 0<b ≤1 解答提示:1.∵ 当a <0时,2a =|a |=-a . 故选D .2.21±=+m ,解得1=m 或3-=m . 故选D .3.()AB BC AC BC AC NC MC MN 21212121=-=-=-=,∴只要已知AB 即可.故选A .4. 分别以点A 、O 、P 三点为等腰三角形的顶点三种情况考虑.5. 关于x 的方程01)2(=-+x b a 无解,则02=+b a . ∴有0==b a 或者a 、b 异号,故选D .6. ∵一次函数)1(-=x k y 的图像经过点M (-1,-2),则有()211-=--k ,解得1=k .所以函数解析式为1-=x y .令0=x 代入得1-=y .故其图像与y 轴的交点是(0,-1).故选A .7.易得△ACD ≌△BCE .所以△BCE 可以看成是△ACD 绕着点C 顺时针旋转60°而得到的.又M 为线段AD 中点,P 为线段BE 中点,故CP 就是CM 绕着点C 顺时针旋转60°而得.所以CP =CM 且,∠PCM =60°,故△CPM 是等边三角形,选C .8.(1)由中位数及众数的意义以及表格可知当这组数据的中位数是40时,众数必然是40,所以A 错误.(2)当39码与40码的人数都是5时,中位数与众数不等,所以B 错误.(3)假设剩余10人全部穿39码鞋,可得平均数为39.35;假设剩余10人全部穿40码鞋,可得平均数为39.85.可以判断C 正确.(或者设穿39码鞋的有x 人,且由0≤x ≤10也可得解) 故选C .9. ∵ 62121OC OD 21OCAD ==⋅=⋅=k y x S A A 正方形,∴ 62121OF OE 21B B OCAD ==⋅=⋅=k y x S 长方形 ,故选B . 10.拿出任意三袋,假设它们的重量分别为x 千克、y 千克、z 千克,两两一称,记录下相应的重量,若分别等于a 千克、b 千克、c 千克,则有方程组⎪⎩⎪⎨⎧=+=+=+c x z b z y ay x 容易求出x 、y 、z ;另外两袋分别与已知重量的其中一袋一起称,即可求出其重量.所以需要称5次,故选B .11.解不等式组⎩⎨⎧<->-001a x x 得⎩⎨⎧<>ax x 1,因为原不等式组无解,所以必有a ≤1.12.∵ ()()122-=-+=-b a b a b a ,又1=-b a ,则1-=+b a∴ ⎩⎨⎧=--=+11b a b a ,解得⎩⎨⎧-==1b a . 故()1102008200820082008-=--=-b a .13. 设菱形ABCD 的边长为x ,则AB =BC =x ,又EC =2,所以BE =x -2,因为AE ⊥BC 于E ,所以在Rt △ABE 中, cosB x x 2-=,又cosB 54=,于是542=-x x ,解得x =10,即AB =10.所以易求BE =8,AE =6,当EP ⊥AB 时,PE 取得最小值. 故由三角形面积公式有:21AB ·PE =21BE ·AE ,求得PE 的最小值为4.8 .14.用树状图列出一个回合中三个人所出手势的各种结果.上面只画出树状图的一部分(列出9种结果),把图中小丁的“剪”改为“布”重复上述画法,可再列出9种结果,最后改为“锤”同样也列出9种结果,所以共有27种结果,故求得P (布,布,布)=27115.∵1=b a ,1≠a ,∴ =+++=+++=+++=)1()1(11a b b b a a b a b b b a a a b b a a M N b a =+++1111. ∴ N M -=0.16. 如图,连结AE 、BD ,作DF ⊥EC 于点F . ∵ AB 是⊙O 的直径 ,∴ ∠ADB =∠AEB =90°又∵ AB =AC ,∴CE =21BC =1,∴ AE =222=-CE AC∵ BD AC AE BC ⋅=⋅2121,∴ BD =554,∴ 在△ABD 中,AD =553,∴ CD =552 又∵△CDF ∽△CAE ,∴AEDFCA CD =,可求得DF =54. ∴ △CDE 的面积为剪 剪 剪 布 锤布 剪 布 锤 锤 剪 布 锤 小丁 小明 小倩 A BCD E F O · A B CDE P5221=⋅DF CE . 解法2:如图,连结AE 、BD ,DE .∵ AB 是⊙O 的直径 ,∴ ∠ADB =∠AEB =90°又∵ AB =AC ,∴ BE =CE =1,∴ AE =222=-CE AC .∵ BD AC AE BC ⋅=⋅2121,∴ BD =554,∴ 在△ABD 中,AD =553,∴ CD =552. ∴ S △CDE =21S △BDC =⨯2152552554212121=⨯⨯⨯=⨯⨯CD BD . 17.小正方体个数最少情况如图所示(图中数字表示该位置小正方体的个数)所以最少为5块.18. y =x 2-4x +3=(x -2)22-4x +3|的图象如图②所示,而当=b 结合①②,易知b 的取值范围为0三、19.因为100×0.9=90<94.5<100,300×0.9=270<282.8设小美第二次购物的原价为x 元,则(x -300)×0.8+300×情况1: 小美第一次购物没有优惠,第二次购物原价超过300元 则小丽应付(316+94.5-300)×0.8+300×0.9=358.4(元)情况2: 小美第一次购物原价超过100元,第二次购物原价超过300元; 则第一次购物原价为:94.5÷0.9=105(元)所以小丽应付(316+105-300)×0.8+300×0.9=362.8(元).20.(1)证明: 如图,延长CB 至点G ,使得BG =DF ,连结AG . 因为ABCD 是正方形,所以在Rt △ADF 和Rt △ABG 中,AD =AB ,∠ADF =∠ABG =90°,DF =BG . ∴ Rt △ADF ≌Rt △ABG (SAS ),∴AF =AG ,∠DAF =∠BAG . 又 ∵ AE 是∠BAF 的平分线∴∠EAF =∠BAE , ∴ ∠DAF +∠EAF =∠BAG +∠BAE 即∠EAD =∠GAE .∵ AD ∥BC ,∴∠GEA =∠EAD ,∴∠GEA =∠GAE ,∴ AG =GE . 即AG =BG +BE .∴ AF =DF +BE ,得证.(2)AB BE AD DF S S S ABE ADF ⋅+⋅=+=∆∆2121俯视图 2 12 图① 1ABC DE O ·∵ AD =AB =1, ∴ )(21BE DF S +=由(1)知,AF =DF +BE , 所以AF S 21=.在Rt △ADF 中,AD =1,DF =x , ∴12+=x AF ,∴1212+=x S . 由上式可知,当x 2达到最大值时,S 最大.而0≤x ≤1,所以,当x =1时,S 最大值为2211212=+x .ABCDEF G。
2010年全国初中数学竞赛天津赛区初赛考试试题.答案
2010年全国初中数学竞赛天津赛区初赛试题参考答案及评分标准一、选择题(本大题共5小题,每小题7分,满分35分) (1)计算2222010200920102009201122009--⨯+⨯的值为( ). (A )1 (B )1- (C )2 009 (D )2 010【解】选A .原式22222222010200920102009120102009(20112)20102009--===---.[例11] (2005-4)设22211148()34441004A =⨯++---,则与A 最接近的正整数是( ).(A)18 (B)20 (C)24 (D)25[解答]当n ≥3时,有()()211111422422n n n n n ⎛⎫==- ⎪--+-+⎝⎭,所以22211148()34441004A =⨯++---111111481452698102⎡⎤⎛⎫⎛⎫⎛⎫=⨯-+-+- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦111111112123499100101102⎛⎫=⨯+++---- ⎪⎝⎭1111251299100101102⎛⎫=-⨯+++ ⎪⎝⎭,因为11111111411212129910010110299999999992⎛⎫⎛⎫⨯+++<⨯+++=⨯< ⎪ ⎪⎝⎭⎝⎭, 所以与A 最接近的正整数是25,选D.[点评]数列求和问题是一类基本问题,裂项相消法则是其中一个基本方法,要特别注意裂项后哪些项没有抵消.当然,只有符合一定的特点的式子(数列)才能裂项,常见的裂项有:()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭=.(3)如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,E 是AD 的中点,6AB BC CD ++=, BE =,则梯形ABCD 的面积等于( ).(A )13 (B )8ABCD E 第(3)题(C )132(D )4 【解】选D .如图,过点E 作//EF AB 交BC 于点F ,则12BF BC =,11()(6)22EF AB CD BC =+=-,又∵BC AB ⊥,∴EF BC ⊥∴在Rt △BFE 中,222EF BF BE +=.∴22211[(6)]()22BC BC -+=,即2680BC BC -+=,解得 2BC =或4BC =,则2EF =或1EF =, ∴ 4ABCD S EF BC =⋅=梯形. (4)某个一次函数的图象与直线132y x =+平行,与x 轴,y 轴的交点分别为A ,B ,并且过点(2-,4-),则在线段AB 上(包括点A ,B ),横、纵坐标都是整数的点有( ).(A )3个 (B )4个 (C )5个 (D )6个 【解】选B .根据题意,设一次函数的解析式为12y x b =+,由点(2-,4-)在该函数图象上,得14(2)2b -=⨯-+,解得3b =-.所以,132y x =-.可得点A (6,0),B (0,3-). 由06x ≤≤,且x 为整数,取0,2,4,6x =时,对应的y 是整数. 因此,在线段AB 上(包括点A 、B ),横、纵坐标都是整数的点有4个.(5)如图,一个半径为r 的圆形纸片在边长为a(a ≥)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ).(A )2π3r(B2(C)2π)r (D )2πr 【解】选C .如图,当圆形纸片运动到与A ∠的两边相切的位置时,过圆形纸片的圆心1O 作两边的垂线,垂足分别为D ,E ,连1AO ,则Rt △1ADO 中,130O AD ∠=︒,1O D r =,AD =.∴12112ADO S O D AD ∆=⋅=.有1122ADO ADO E S S ∆=四形形.∵由题意,1120DO E ∠=,得12π3O DE S r =扇形,∴圆形纸片不能接触到的部分的面积为22π3)3r -2π)r =第(5)题ABC D EFCNCABDM第(8)题二、填空题(本大题共5小题,每小题7分,满分35分)(6)如图,有五张点数分别为2,3,7,8,9的扑克牌,从中任意抽取两张,则其点数之积是偶数的概率为 .【解】710. 根据题意,当不考虑抽牌顺序时,可以画出如下的树形图从上图可以看出,从五张牌中任意抽取两张,共有10种抽法,其中抽取的点数之积是偶数的有7种,所以点数之积是偶数的概率710P =.(7)如图,是一个树形图的生长过程,自上而下,一个空心圆生成一个实心圆,一个实心圆生成一个实心圆和一个空心圆,依此生长规律,第9行的实心圆的个数【解】21个.观察图形规律,可得,从第3行起,每行中的实心圆的个数都是上两行实心圆个数的和.于是,第7行实心圆的个数为3+5=8(个); 第8行实心圆的个数为5+8=13(个); 第9行实心圆的个数为8+13=21(个). (8)如图,在△ABC 中,中线CM 与高线 CD 三等分ACB ∠,则B ∠等于 (度).【解】30︒.根据题意,可得CD AB ⊥,AM MB =,ACD MCD BCM ∠=∠=∠. ∵ACD MCD ∠=∠,CD CD =,90CDA CDM ∠=∠=︒,点数之积 3 7 8 96 2 14 16 183 78921 24 27 56 78963 8 972 第(6)题1行 2行 3行 4行 5行 6行……第(7)题∴△ACD ≅△MCD ∠. ∴12AD DM AM ==. 过点M 作MN BC ⊥于点N ,∵DCM NCM ∠=∠,CM CM =,90CDM CNM ∠=∠=︒, ∴△DCM ≅△NCM ∠. ∴DM NM =.于是12NM MB =,∴在Rt △MNB 中,30B ∠=︒.(9)有n 个连续的自然数1,2,3,…,n ,若去掉其中的一个数x 后,剩下的数的平均数是16,则满足条件的n 和x 的值分别是 .(参考公式:2)1(321+=++++=n n n S n ) 【解】30n =,1x =;31n =,16x =;32n =,32x =.由已知,n 个连续的自然数的和为(1)2n n n S +=.若x n =,剩下的数的平均数是12n S n nn -=-; 若1x =,剩下的数的平均数是 1112n S nn -=+-,故16122n n+≤≤,解得 3032n ≤≤. 当30n =时,30(301)29162x ⨯+⨯=-,解得1x =; 当31n =时,31(311)30162x ⨯+⨯=-,解得16x =; 当32n =时,32(321)31162x ⨯+⨯=-,解得32x =. (10)母亲节到了,小红,小莉,小莹到花店买花送给自己的母亲.小红买了3枝玫瑰,7枝康乃馨,1枝百合花,付了14元;小莉买了4枝玫瑰,10枝康乃馨,1枝百合花,付了16元;小莹买上面三种花各2枝,则她应付 元.【解】20.方法一:设玫瑰、康乃馨、百合花的单价分别为x 元,y 元,z 元, 根据已知条件,列出方程组3714,41016.x y z x y z ++=⎧⎨++=⎩消去z ,得23x y =-. ③ 将③代入①,得82z y =+.④由③,④得 10x y z ++=.有 2()20x y z ++=. 所以,小莹应付20元. 方法二:(37)(410)2()m x y z n x y z x y z +++++=++,(34)(710)()222m n x m n y m n z x y z +++++=++.①②∴342,7102,2.m n m n m n +=⎧⎪+=⎨⎪+=⎩解得4,6.n m =-⎧⎨=⎩∴2()6(37)4(410)61441620x y z x y z x y z ++=⨯++-++=⨯-⨯=. 三、解答题(本大题共4小题,每小题满分20分,共80分) (11)(本小题满分20分)已知,抛物线2y ax bx c =++(0≠a )经过A 、B图中的曲线是它的一部分.根据图中提供的信息,(Ⅰ)确定a ,b ,c 的符号; (Ⅱ)当b 变化时,求a b c ++的取值范围.【解】(Ⅰ)如图,由抛物线开口向上,得0a >.……3由抛物线过点(0,1)-,得10c =-<. ……6分 由抛物线对称轴在y 轴的右侧,得02ba->,又 0a >,得0b <. ∴0a >,0b <,0c <. ……………………………………10分 (Ⅱ)由抛物线过点(1,0)-,得0a b c -+=.即1a b =+,由0a >,得1b >-. ……………………………………16分 ∴10b -<<,∴(1)12a b c b b b ++=++-=.∴20a b c -<++<. ……………………………………20分 (12)(本小题满分20分)设直角三角形的两条直角边长分别为,a b ,斜边长为c .若,,a b c 均为整数,且1()3c ab a b =-+,求满足条件的直角三角形的个数.【解】由勾股定理,得222c a b =+. ……………………………………3分又1()3c ab a b =-+,得2222112[()]()()()393c ab a b ab ab a b a b =-+=-+++.即2222212()()293a b ab ab a b a ab b +=-++++.整理,得6()180ab a b -++=.即(6)(6)18a b --=. ………………………8分 因为,a b 均为正整数,不妨设a b <, 可得61,618,a b -=⎧⎨-=⎩或62,69,a b -=⎧⎨-=⎩或63,6 6.a b -=⎧⎨-=⎩可解出7,24,25,a b c =⎧⎪=⎨⎪=⎩或8,15,17,a b c =⎧⎪=⎨⎪=⎩或9,12,15.a b c =⎧⎪=⎨⎪=⎩所以,满足条件的直角三角形有3个. ……………………………………20分 (13)(本小题满分20分)AC如图,在△ABC 中,45ABC ∠=,点D 在边BC 上,60ADC ∠=,且12BD CD =.将△ACD 以直线AD 为轴做轴对称变换,得到△AC D ',连接BC ',(Ⅰ)求证BC BC '⊥; (Ⅱ)求C ∠的大小.(Ⅰ)【证明】∵△AC D '是△ACD 沿AD 做轴对称变换得到的,∴△AC D '≌△ACD .有C D CD '=,ADCADC '∠=∠.………………3分∵12BD CD =,60ADC ∠=,∴12BD C D '=,18060BDC ADC ADC ''∠=-∠-∠=.……5分取C D '中点P ,连接BP ,则△BDP 为等边三角形,△BC P '为等腰三角形,…8分有113022BC D BPD BDC ''∠=∠=∠=︒.∴90C BD '∠=,即BC BC '⊥. ……10分(Ⅱ)【解】如图,过点A 分别作,,BC C D BC ''的垂线,垂足分别为,,E F G .∵ADC ADC '∠=∠,即点A 在C DC '∠的平分线上, ∴AE AF =.……13分 ∵90C BD '∠=,45ABC ∠=, ∴45GBA C BC ABC '∠=∠-∠=,即点A 在GBC ∠的平分线上,∴AG AE =.……16分 于是,AG AF =,则点A 在GC D '∠的平分线上.…………………………18分 又∵30BC D '∠=︒,有150GC D '∠=. ∴12AC D '∠=75GC D '∠=.∴C ∠75AC D '=∠=.………………………20分 (14)(本小题满分20分)(Ⅰ)如图(a ),在正方形ABCD 内,已知两个动圆1O 与2O 互相外切,且1O 与边AB 、AD 相切,2O 与边BC 、CD 相切.若正方形ABCD 的边长为1,1O 与2O 的半径分别为1r ,2r .①求1r 与2r 的关系式;②求1O 与2O 面积之和的最小值.(Ⅱ)如图(b ),若将(Ⅰ)中的正方形ABCD 改为一个ABCDC 'PA 图(a )BDC 'FGAC宽为1,长为32的矩形,其他条件不变,则1O 与2O 面积的 和是否存在最小值,若不存在,请说明理由;若存在,请求出 这个最小值.【解】(Ⅰ)如图(a ),在正方形ABCD 中,连接AC ,显然1O 与2O 在AC 上,且1AO =,1212O O r r =+,22CO =,由1122AC AO O O CO =++=,122r r +++=∴122r r += ………………………5分②根据题意,1r 12≤,2r 12≤,可得21122r r =-≤,即321r 12≤.∵1O 与2O 的面积之和2212π()S r r =+,∴2211(2)πSr r =+21122(26r r =-+-2122(32r =-+-32-2212≤,…………8分∴当1r =时,1O 与2O是等圆,其面积和的最小值为(3π-. ……………………………………10分(Ⅱ)如图(b ),作辅助线,得到Rt △12O O P , 则1212O O r r =+,1121232O P AB r r r r =--=--, 212121O P BC r r r r =--=--.∵在Rt △12O O P 中,2221212O O O P O P =+,∴2221212123()()(1)2r r r r r r +=--+--.即2121213()5()04r r r r +-++=.解得1252r r +=+1252r r +=图(a )B图(b )由于1235122r r +<+=,故1252r r +=∴1252r r +=……………………………………15分 ∵1O 与2O 的面积之和2212π()S r r =+,而2221212()2r r r r ++≥,当且仅当12r r =时,等号成立,∴当12r r =时,1O 与2O 面积和存在最小值,最小值为25(2π2-,即37(π8-. ……………………………………20分。
2010年“数学周报杯”全国初中数学竞赛试卷(解析版)
2010年“数学周报杯”全国初中数学竞赛试卷一、选择题(共5小题,每小题7分,满分35分)1.(7分)若,则的值为()A.B.C. D.2.(7分)若实数a,b满足,则a的取值范围是()A.a≤﹣2 B.a≥4 C.a≤﹣2或a≥4 D.﹣2≤a≤43.(7分)如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=,BC=,CD=,则AD边的长为()A.B.C.D.4.(7分)在一列数x1,x2,x3,…中,已知x1=1,且当k≥2时,(取整符号[a]表示不超过实数a的最大整数,例如[2.6]=2,[0.2]=0),则x2010等于()A.1 B.2 C.3 D.45.(7分)如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P (0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是()A.(2010,2)B.(2010,﹣2)C.(2012,﹣2)D.(0,2)二、填空题(共5小题,每小题7分,满分35分)6.(7分)已知a=﹣1,则2a3+7a2﹣2a﹣12的值等于.7.(7分)一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问过分钟,货车追上了客车.8.(7分)如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l 经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是.9.(7分)如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A 作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D,若CD=CF,则=.10.(7分)对于i=2,3,…,k,正整数n除以i所得的余数为i﹣1.若n的最小值n0满足2000<n0<3000,则正整数k的最小值为.三、解答题(共4小题,满分80分)11.(20分)如图,△ABC为等腰三角形,AP是底边BC上的高,点D是线段PC 上的一点,BE和CF分别是△ABD和△ACD的外接圆直径,连接EF.求证:.12.(20分)如图1,抛物线y=ax2+bx(a>0)与双曲线相交于点A,B.已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).(1)求实数a,b,k的值;(2)如图2,过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△COE∽△BOA的点E的坐标(提示:C点的对应点为B).13.(20分)求满足2p2+p+8=m2﹣2m的所有素数p和正整数m.14.(20分)从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?2010年“数学周报杯”全国初中数学竞赛试卷参考答案与试题解析一、选择题(共5小题,每小题7分,满分35分)1.(7分)若,则的值为()A.B.C. D.【解答】解:∵,∴得.故选:D.2.(7分)若实数a,b满足,则a的取值范围是()A.a≤﹣2 B.a≥4 C.a≤﹣2或a≥4 D.﹣2≤a≤4【解答】解:把看作是关于b的一元二次方程,因为b是实数,所以关于b的一元二次方程的判别式△≥0,即a2﹣4(a+2)≥0,a2﹣2a﹣8≥0,(a﹣4)(a+2)≥0,解得a≤﹣2或a≥4.故选:C.3.(7分)如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=,BC=,CD=,则AD边的长为()A.B.C.D.【解答】解:如图,过点A,D分别作AE,DF垂直于直线BC,垂足分别为E,F.由已知可得BE=AE=,CF=,DF=2,于是EF=4+.过点A作AG⊥DF,垂足为G.在Rt△ADG中,根据勾股定理得AD=====.故选:D.4.(7分)在一列数x1,x2,x3,…中,已知x1=1,且当k≥2时,(取整符号[a]表示不超过实数a的最大整数,例如[2.6]=2,[0.2]=0),则x2010等于()A.1 B.2 C.3 D.4【解答】解:已知x1=1,当k=2时,x2=x1+1﹣4([]﹣[0])=2;当k=3时,x3=x2+1﹣4([]﹣[])=3;当k=4时,=4;当k=5时,=1;当k=6时,=2;…∵2010=502×4+2∴x2010=x2=2,故选:B.5.(7分)如图,在平面直角坐标系xOy中,等腰梯形ABCD的顶点坐标分别为A(1,1),B(2,﹣1),C(﹣2,﹣1),D(﹣1,1).以A为对称中心作点P (0,2)的对称点P1,以B为对称中心作点P1的对称点P2,以C为对称中心作点P2的对称点P3,以D为对称中心作点P3的对称点P4,…,重复操作依次得到点P1,P2,…,则点P2010的坐标是()A.(2010,2)B.(2010,﹣2)C.(2012,﹣2)D.(0,2)【解答】解:根据题意,以A为对称中心作点P(0,2)的对称点P1,即A是PP1的中点,又由A的坐标是(1,1),结合中点坐标公式可得P1的坐标是(2,0);同理P2的坐标是(2,﹣2),记P2(a2,b2),其中a2=2,b2=﹣2.根据对称关系,依次可以求得:P3(﹣4﹣a2,﹣2﹣b2),P4(2+a2,4+b2),P5(﹣a2,﹣2﹣b2),P6(4+a2,b2),令P6(a6,b2),同样可以求得,点P10的坐标为(4+a6,b2),即P10(4×2+a2,b2),由于2010=4×502+2,所以点P2010的坐标是(2010,﹣2),故选:B.二、填空题(共5小题,每小题7分,满分35分)6.(7分)已知a=﹣1,则2a3+7a2﹣2a﹣12的值等于0.【解答】解:由已知得(a+1)2=5,所以a2+2a=4则原式=2a3+4a2+2a+3a2﹣4a﹣12=2a(a2+2a+1)+3a2﹣4a﹣12=2a(a+1)2+3a2﹣4a﹣12=2a×5+3a2﹣4a﹣12=3a2+6a﹣12=3(a2+2a)﹣12=3×4﹣12=0故答案07.(7分)一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问过15分钟,货车追上了客车.【解答】解:设小轿车速度为a,货车为b,客车为c,某一刻的相等间距为m,则=10①,=10+5②,化简可得:2(10c﹣10a)=15c﹣15b,所以:a=4b﹣3c假设再过t分钟,货车追上客车,则10a﹣10b=(15+t)(b﹣c)15+t=10(a﹣b)/(b﹣c)将a代入15+t=10×3=30,解得:t=15.所以再过15分钟,货车追上了客车.8.(7分)如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l 经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线l的函数表达式是.【解答】解:如图,延长BC交x轴于点F;连接OB,AF;连接CE,DF,且相交于点N.由已知得点M(2,3)是OB,AF的中点,即点M为矩形ABFO的中心,所以直线l把矩形ABFO分成面积相等的两部分.又因为点N(5,2)是矩形CDEF的中心,所以,过点N(5,2)的直线把矩形CDEF分成面积相等的两部分.于是,直线MN即为所求的直线l.设直线l的函数表达式为y=kx+b,则解得,故所求直线l的函数表达式为.故答案为.9.(7分)如图,射线AM,BN都垂直于线段AB,点E为AM上一点,过点A 作BE的垂线AC分别交BE,BN于点F,C,过点C作AM的垂线CD,垂足为D,若CD=CF,则=.【解答】解:设AF=a,FC=b;∵AM⊥AB,BN⊥AB,∴AM∥BN;∴△AEF∽△CBF;∴AE:BC=AF:FC=a:b;Rt△ABC中,BF⊥AC,由射影定理,得:AB2=AF•AC=a(a+b);∵AM⊥AB,BN⊥AB,CD⊥AM,∴四边形ABCD是矩形,∴CD=AB=CF=b;∴b2=a(a+b),即a2+ab﹣b2=0,()2+()﹣1=0解得=(负值舍去);∴==.10.(7分)对于i=2,3,…,k,正整数n除以i所得的余数为i﹣1.若n的最小值n0满足2000<n0<3000,则正整数k的最小值为9.【解答】解:因为n+1为2,3,…,k的倍数,所以n的最小值n0满足n0+1=[2,3,…,k],其中[2,3,…,k]表示2,3,…,k的最小公倍数.由于[2,3,…,8]=840,[2,3,…,9]=2520,[2,3,…,10]=2520,[2,3,…,11]=27720,因此满足2000<n0<3000的正整数k的最小值为9.故答案为9.三、解答题(共4小题,满分80分)11.(20分)如图,△ABC为等腰三角形,AP是底边BC上的高,点D是线段PC 上的一点,BE和CF分别是△ABD和△ACD的外接圆直径,连接EF.求证:.【解答】证明:如图,连接ED,FD.∵BE和CF都是直径,∴ED⊥BC,FD⊥BC,∴D,E,F三点共线,连接AE,AF,∵∠AFE与∠ACB是同弧所对的圆周角,∴∠AFE=∠ACB,∴∠AEF=∠ABC=∠ACB=∠AFD,∴△ABC∽△AEF,作AH⊥EF,垂足为H,又∵AP⊥BC,DF⊥BC,∴四边形APDH是矩形,∴AH=PD,∵△ABC∽△AEF,∴,∴,∴.12.(20分)如图1,抛物线y=ax2+bx(a>0)与双曲线相交于点A,B.已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).(1)求实数a,b,k的值;(2)如图2,过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△COE∽△BOA的点E的坐标(提示:C点的对应点为B).【解答】解:(1)∵反比例函数经过A(1,4),∵k=1×4=4,即y=;设B(m,),已知A(1,4),可求得直线AB:y=﹣x+4+;∵S=×(4+)×(1﹣m)=3,△BOA∴2m2+3m﹣2=0,即m=﹣2(正值舍去);∴B(﹣2,﹣2).由于抛物线经过A、B两点,则有:,解得;∴y=x2+3x.故a=1,b=3,k=4.(2)设抛物线与x轴负半轴的交点为D;∵直线AC∥x轴,且A(1,4),∴C(﹣4,4);已求得B(﹣2,﹣2),则有:∠COD=∠BOD=45°,即∠BOC=90°;①将△BOA绕点O顺时针旋转90°得到△B1OA1,作AM⊥x轴于M,作A1N⊥x 轴于N.∵A的坐标是(1,4),即AM=4,OM=1,∵∠AOM+∠NOA1=90°,∠OAM+∠AOM=90°∴∠OAM=∠NOA1,又∵OA=OA1,∠AMO=∠A1NO∴△AOM≌△OA1N,∴A1N=OM=1,ON=AM=4∴A1的坐标是(4,﹣1),此时B1是OC的中点,延长OA1至E1,使得OE=2OA1,则△COE1∽△B1OA1∽△BOA;则E1(8,﹣2);②以OC所在直线为对称轴,作△B1OA1的对称图形△B1OA2,延长OA2至E2,使得OE2=2OA2,则△COE2≌△COE1∽△BOA;易知A2(1,﹣4),则E2(2,﹣8);故存在两个符合条件的E点,且坐标为E1(8,﹣2),E2(2,﹣8).13.(20分)求满足2p2+p+8=m2﹣2m的所有素数p和正整数m.【解答】解:由题设得p(2p+1)=(m﹣4)(m+2),由于p是素数,故p是(m﹣4)的因数,或p是(m+2)的因数.(5分)(1)若p整除(m﹣4),令m﹣4=kp,k是正整数,于是m+2>kp,3p2>p(2p+1)=(m﹣4)(m+2)>k2p2,故k2<3,从而k=1,所以解得(10分)(2)若p整除(m+2),令m+2=kp,k是正整数.当p>5时,有m﹣4=kp﹣6>kp﹣p=p(k﹣1),3p2>p(2p+1)=(m﹣4)(m+2)>k(k﹣1)p2,故k(k﹣1)<3,从而k=1,或2,由于p(2p+1)=(m﹣4)(m+2)是奇数,所以k≠2,从而k=1,于是,这不可能.当p=5时,m2﹣2m=63,m=9;当p=3,m2﹣2m=29,无正整数解;当p=2时,m2﹣2m=18,无正整数解.综上所述,所求素数p=5,正整数m=9.14.(20分)从1,2,…,2010这2010个正整数中,最多可以取出多少个数,使得所取出的数中任意三个数之和都能被33整除?【解答】解:首先,如下61个数:11,11+33,11+2×33,11+60×33(即1991)满足题设条件,另一方面,设a1<a2<a n是从1,2,2010中取出的满足题设条件的数,对于这n个数中的任意4个数a i,a j,a k,a m,因为33|(a i+a k+a m),33|(a j+a k+a m),所以33|(a j﹣a i),∴所取的数中任意两数之差都是33的倍数,设a i=a1+33d i,i=1,2,3,n,由33|(a1+a2+a3),得33|(3a1+33d2+33d3),所以33|3a1,11|a1,即a1≥11,≤,故d n≤60,所以n≤61,综上所述,n的最大值为61.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年全国初中数学竞赛(海南赛区)
初赛试卷参考答案
一、选择题
1. 若x ≥0,则|x |-x =x -x =0;若x <0,则|x |-x =-x -x =-2x >0,故选C.
2.由题意有a 2+2ab +b 2=8,a 2-2ab +b 2=12,两式相减得4ab =-4,得ab =-1,故选B . 3.由bk <0,知b >0,k <0或b <0,k >0,前者直线经过第一、二、四象限,后者直线经过第一、三、四象限,因而必经过第一、四象限,选D .
4.由已知条件知乙胜的概率为20%,又和棋概率为50%,故乙不输的概率为70%,选C . 5.由20102018-20102009=2010x ×2009×2019, 20102009(2010-1)(2010+1)= 2010x ×2009×2019,
则有20102009×2009×2019= 2010x ×2009×2019,则有x =2009,选B . 6. 两队联合承包每天完成工程的b a 11+,完成这项工程需要的时间为1÷(b
a 1
1+)=
b a ab + 天. 选C .
7.根据题意可知符合条件的点A 和点B 分别在以点C 为圆心的两个同心圆上. 故选D. 8.由图象可知,直角梯形的高BC =2,上底CD =3,所以3322
1
=⨯⨯=
∆BCD S ,选A . 9.分别连结OA 、OB ,则OA ⊥CA ,OB ⊥CB ,即可求得,选B .
10.由已知条件知∠EDF =45°,由三角形外角性质得∠CDF +45°=∠BED +45°,∴∠BED =
∠CDF ,设CD =1,CF =x ,则CA =CB =2,所以DF =FA =2-x ,在Rt △CDF 中,有x 2+1=(2-x )2,解得x =43
,所以sin ∠BED =sin ∠CDF =5
3=DF CF ,选A . 二、填空题
11.(1,1+3)或(-1,1+3);在直角坐标系中,以P (0,1)为顶点,作出∠QPO =150°可求得. 12.由
45
32
2=-+x x 解得511=x .
13.英语、日语至少会一门的人数为50-8=42人,设既会英语又会日语的为x 人,则只会英语
的为(36-x )人;只会日语的为(20-x )人,于是得(36-x )+x +(20-x )=42,解得x =14.
14.由312
2=+
x
x ,得5122
=++x x ,所以5)1(2=+x x ,又x <0,所以51-=+x x . 15.由a +b +c =1可得a a c b 11=++,则M =11-=+a a c b ,同理11
-=+=b
b c a N ,
P =11-=+c c b a ,由c <b <0<a ,得b c a 111>>,111111->->-b
c a ,∴M >P >N .
16.过D 作DG ⊥AM ,则有2×3=22
21⨯⋅+⋅BM
AB DG AM ,DG =2.4;
17.3;当P 在对角线AC 与MN 的交点处时PC +PD 最小. 18.1;∵
BQ AQ BP AD BP BC ==,∴ 1==-=-=-BQ
BQ
BQ AB AQ BQ AB BQ AQ BQ AB BP BC .
三、解答题
19.(1)四边形ABCD 是梯形或菱形,证明如下:
① 当点P 不与点A 重合时, ∵ △ABC 与△CPD 都是等边三角形, ∴ ∠ACB =∠DCP =60°,∴ ∠1=∠2,
又AC =BC ,DC =PC ,∴△ADC ≌△BPC ,∴∠DAC =∠B =∠BCA =60°,∴ AD ∥BC . 又∠1=∠2<60°,∴ ∠DCB <120°,即 ∠B +∠DCB <180°,∴ DC 与AB 不平行, ∴ 四边形ABCD 是梯形.
② 当点P 与点A 重合时,PC 与AC 重合,此时AB =BC =CA =AD =DC ,四边形ABCD 是菱形,综上所述,四边形ABCD 是梯形或菱形.
(2)由(1)知∠BAD =120°,AD =BP =x ,过P 作DA 延长线的垂线PM ,M 为垂足,
则∠PAM =60°,∠APM =30°,
又BP =x ,AB =1,∴ AP =1-x ,∴ AM =
)1(2
1
x -,PM =)1(23x - C
B
D
A
P
1 2
M
∴16
3
)21(43)(43)1(23212122+
--=--=-⋅=⋅=
x x x x x PM AD y (0<x <1). 当21=x 时,y 取最大值为163
,即当2
1=x 时△PAD 面积取得最大面积为163.
20.(1)设购买一件A 种电器和一件B 种电器所需的资金分别为a 元和b 元.
依题意得: ⎩⎨
⎧=+=+2050
22300
2b a b a 解之得⎩⎨⎧==850600b a (答略)
(2)设该单位购买A 、B 两种电器分别为m 件和n 件.则
600m +850n =15750 , 15
315
1217+
-=n m . ∵ A 种电器不超过5件, ∴ 15
315
1217+
-
n ≤5. ∴ n ≥15,即可购买B 种电器至少有15件. (3)设购买A 种电器x 件,则购买B 种电器为(6-x )件,依题意得:
⎩⎨
⎧≥-+≤-+700
)6(1501004000
)6(700500x x x x , 解之得1≤x ≤4 . ∵ x 取整数,∴ x =1,2,3,4. 即共有4种购买方案.。
