计量经济学:课程实验方法与案例汇编(新)
计量经济学计量经济学教学案例

计量经济学教学案例案例一 简单线性回归模型一、主题与背景用真实数据进行简单线性回归分析,应用Eviews6.0分析软件进行操作,与课本内容相对应,分析模型的截距、斜率以及可决系数,引导学生熟悉Eviews6.0的基本操作,能够解读分析报告,并尝试进行被解释变量的预测,体会变量测度单位的改变和函数形式变化给OLS 估计结果和统计特征的影响。
二、情景描述对于由CEO 构成的总体,令y 代表年薪(salary),单位为千美元。
令x 表示某个CEO 所在公司在过去三年的平均股本回报率(roe ,股本回报率定义为净收入占普通股价的百分比)。
为研究该公司业绩指标和CEO 薪水之间的关系,可以定义以下模型:Salary=0β+1βroe + u . 斜率参数1β衡量当股本回报率增长一个单位(一个百分点)时CEO 年薪的变化量,由于更高的股本回报率预示更高的CEO 年薪,所以,1β>0。
三、教学过程设计(一)数据说明数据集CEOSAL1.RAW 包含1990年209位CEO 的相关信息,该数据来自《商业周刊》(5/6/91),该样本中CEO 年薪的平均值为$1,281,120,最低值和最高值分别为$223,000和$14,822,000,1988、1989和1990年的平均股本回报率是17.18%。
(二)操作建议1:在 eviews6.0命令输入窗口定义变量:data salary roe2、用 edit+/- 编辑数据3、描述统计分析过程:view---descriptive stats---common sample4、画散点图:Scat roe salary5、在eviews6.0命令输入窗口运行简单线性回归 Ls salary c roe6、用resids 观测残差7、产生新序列:S eries lsalary =log(salary)8、改变函数形式:Ls lsalary c lsales9、改变变量测度单位:Ls salary*1000 c roe四、教学研究(一)案例结论1、回归结果估计出的回归线为:salˆary = 963.191 + 18.501 roe(1)截距和斜率保留了3位小数,回归结果显示,如果股本回报率为0,年薪的预测值为截距963.191千美元,可以把年薪的预测变化看做股本回报率变化的函数:∆salˆary = 18.501 (∆roe),这意味着当股本回报率增加1个百分点,即∆roe =1,则年薪的预测变化就是18.5千美元,在线性方程中,估计的变化与初始年薪无关。
计量经济学:课程实验方法与案例汇编

《计量经济学》试验方法与案例实验一 一元线性回归模型分析某市城市居民年人均鲜蛋需求量(Y :公斤),年人均可支配收入(X :元)的例子。
通过抽样调查,得到1988—1998年的样本观测值。
其数值结果如下:解:ΣX 2=15325548.8 ΣY 2=3055.25 ΣXY=213349.96 n=11 ΣX=12601.67 ΣY=182.30,离差形式:8.888903118.153255481167.126012222=⨯-=-=⎪⎭⎫⎝⎛∑∑X X xn04.351125.3055113.1822222=⨯-=-=⎪⎭⎫⎝⎛∑∑Y Yy n63.4539113.1821167.126011196.213349=⨯⨯-=-=∑∑y x n XY xy 解:(1)计算一元线性回归模型参数估计量及建立模型0051.08.153********.18267.1260196.2133491167.12601)(222=-⨯⨯-⨯=∑--=∑∑∑∑x x n y x xy n b 72.101167.126010051.0113.182=⨯-=-=-=∑∑nx b ny x b y a 则直线回归方程为:X bX a Y 0051.072.10+=+=∧(请注意:如果样本数据较大,也可以采用离差形式的公式计算出参数估计量)即:0051.08.88890363.45392===∑∑∧xxy b72.101167.126010051.0113.182=⨯-=-=∧x b Y a 结果与用基本公式完全相等。
(2)样本决定系数(或可决系数) r 2=(Σy 2-Σe 2)/Σy 2=1-(Σe 2/Σy 2)=1-(11.89/35.04)=1-0.3393=0.6607 其中,残差平方和:Σe 2=Σy 2- b Σxy=35.04-0.0051*4539.63=11.89 (3)参数估计量的方差、标准差 S 2(a)= (Σe 2ΣX 2)/[n(n-2) Σx 2]=(11.89*15325548.8/11*9*888903.8)=2.0736 S 2(b)=(Σe 2)/[ (n-2)Σx 2]=11.89/9*888903.8=0.00000148 则S (a)=1.44,S (b)=0.0012 (4) 参数估计量的显著性检验T (a)=a/S (a)=10.72/1.44=7.44,T (b)=b/S (b)=0.0051/0.0012=4.25 得知T (a)>T α/2(n-2)=2.26, T (b)>T α/2(n-2)=2.26即a 、b 均显著不为零,说明解释变量X 对Y 有显著影响。
计量经济学实验报告

计量经济学实验报告实验报告实验课程名称:计量经济学实验案例1:近年来,中国旅游业⼀直保持⾼速发展,旅游业作为国民经济新的增长点,在整个社会经济发展中的作⽤⽇益显现。
中国的旅游业分为国内旅游和⼊境旅游两⼤市场,⼊境旅游外汇收⼊年均增长22.6%,与此同时国内旅游也迅速增长。
改⾰开放20多年来,特别是进⼊90年代后,中国的国内旅游收⼊年均增长14.4%,远⾼于同期GDP 9.76%的增长率。
为了规划中国未来旅游产业的发展,需要定量地分析影响中国旅游市场发展的主要因素。
解题过程:⾸先,通过Eviews,得出回归模型:Y=-274.377+0.013X2+5.438X3+3.272X4+12.986X5-563.108X6tc=-0.208 t2=1.031 t3=3.940 t4=3.465 t5=3.108 t6=-1.753R^2=0.995 F=173.354 DW=2.311从估计结果来看,模型可能存在多重共线性。
因为在OLS下,R^2^2与F值较⼤,⽽各参数估计量的t检验值较⼩,说明各解释变量对Y的联合线性作⽤显著,但各个解释变量存在共线性从⽽使得它们对Y的独⽴作⽤不能分辨,故t检验不显著。
应⽤Eviews,写下命令:cor X2 X3 X4 X5 X6。
得到相关系数矩阵。
可以从中看出五个经济变量之间两两简单相关系数⼤都在0.80以上,甚⾄有的在0.96以上。
表明模型存在着严重的多重共线性。
从⽽为了消除多重共线性,这⾥采⽤逐步回归法。
第⼀步,⽤每个解释变量分别对被解释变量做简单回归。
得:Y=-3462+0.0842X2 t=8.666 R^2=0.903 F=75Y=-2934+9.052X3 t=13 R^2=0.956 F=173Y=640+11.667X4 t=5.196 R^2=0.771 F=27Y=-2265+34.332X5 t=6.46 R^2=0.839 F=42Y=-10897+2014X6 t=8.749 R^2=0.905 F=77根据R^2统计量的⼤⼩排序,可见重要程度依次为X3, X6, X2, X5, X4。
《计量经济学》课程实验报告
《计量经济学》课程实验报告年级专业:2012级金融学姓名:*** 学号:2012******一、实验目的1.学会Eviews工作文件的建立、数据输入、数据的编辑和描述;2.掌握用Eviews软件通过阿尔蒙多项式变换法估计分布滞后模型。
二、实验内容根据某地区1980-2001年固定资产投资Y与销售额X的资料,取阿尔蒙多项式的次数M=2,阿尔蒙多项式变换法估计分布滞后模型:错误!未找到引用源。
,将系数错误!未找到引用源。
(i=0,1,2,3,4)用二次多项式近似,则原模型可变为:错误!未找到引用源。
,由此用Eviews软件得出分布滞后模型的最终估计式。
三、实验数据教材第186页,表7.5:某地区1980-2001年固定资产投资Y与销售额X的资料四、实验步骤1.分析固定资产投资Y与销售额X的关系;2.模型设定:错误!未找到引用源。
;将系数错误!未找到引用源。
(i=0,1,2,3,4)用二次多项式近似,则原模型可变为:错误!未找到引用源。
;3.用Eviews计算错误!未找到引用源。
(i=0,1,2,3,4)。
步骤如下:(1)建立工作文件:双击Eviews图标,进入Eviews主页。
在菜单选项中依次点击New—Workfile,出现“Workfile Range”。
在““Workfile Frequency”中选择数据频率“Annual”,并在“Start Date”菜单中输入“1980”,在“End”菜单中输入“2001”,点击“OK”,出现未命名文件的“Workfile UNTITLED”工作框。
已有对象“c”为截距项,“resid”为剩余项。
(2)输入数据:在“Quick”菜单中点击“Empty Group”,出现数据编辑窗口。
将第一列命名为“Y”:方法是按上行键“↑”,对应“obs”格自动上跳,在对应的第二行有边框的“obs”空格中输入变量名为“Y”,再按下行键“↓”,变量名一下各格出现“NA”,依次输入Y的对应数据。
计量经济课程实验
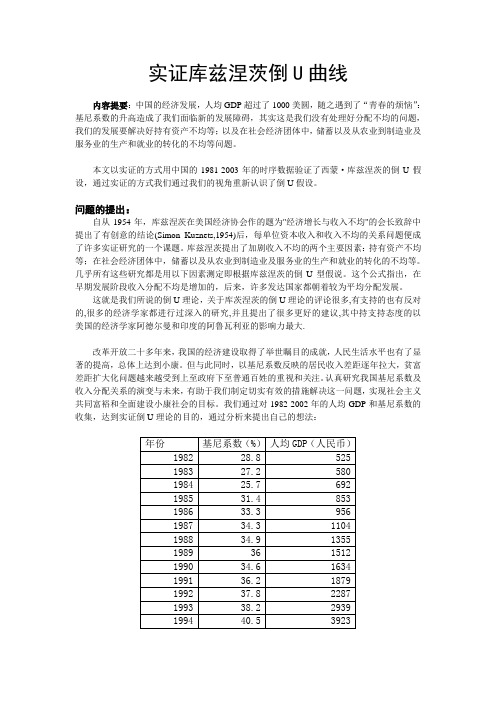
实证库兹涅茨倒U曲线内容提要:中国的经济发展,人均GDP超过了1000美圆,随之遇到了“青春的烦恼”:基尼系数的升高造成了我们面临新的发展障碍,其实这是我们没有处理好分配不均的问题,我们的发展要解决好持有资产不均等;以及在社会经济团体中,储蓄以及从农业到制造业及服务业的生产和就业的转化的不均等问题。
本文以实证的方式用中国的1981-2003年的时序数据验证了西蒙·库兹涅茨的倒U假设,通过实证的方式我们通过我们的视角重新认识了倒U假设。
问题的提出:自从1954年,库兹涅茨在美国经济协会作的题为"经济增长与收入不均"的会长致辞中提出了有创意的结论(Simon Kuznets,1954)后,每单位资本收入和收入不均的关系问题便成了许多实证研究的一个课题。
库兹涅茨提出了加剧收入不均的两个主要因素:持有资产不均等;在社会经济团体中,储蓄以及从农业到制造业及服务业的生产和就业的转化的不均等。
几乎所有这些研究都是用以下因素测定即根据库兹涅茨的倒U型假说。
这个公式指出,在早期发展阶段收入分配不均是增加的,后来,许多发达国家都朝着较为平均分配发展。
这就是我们所说的倒U理论,关于库茨涅茨的倒U理论的评论很多,有支持的也有反对的,很多的经济学家都进行过深入的研究,并且提出了很多更好的建议,其中持支持态度的以美国的经济学家阿德尔曼和印度的阿鲁瓦利亚的影响力最大.改革开放二十多年来,我国的经济建设取得了举世瞩目的成就,人民生活水平也有了显著的提高,总体上达到小康。
但与此同时,以基尼系数反映的居民收入差距逐年拉大,贫富差距扩大化问题越来越受到上至政府下至普通百姓的重视和关注。
认真研究我国基尼系数及收入分配关系的演变与未来,有助于我们制定切实有效的措施解决这一问题,实现社会主义共同富裕和全面建设小康社会的目标。
我们通过对1982-2002年的人均GDP和基尼系数的收集,达到实证倒U理论的目的,通过分析来提出自己的想法:数据来自<<中国统计摘要2004>>由于我们借用Simon Kuznets,的倒U 理论来反映这两个数据的关系。
计量经济学实际案例

二、均值分析1、分性别对身高进行的比较假设男女身高相等,否定假设可认为男生身高明显高于女生。
2、分南北地区进行比较(1)身高假设两者均值相等,检验结果不能否定原假设,因而不能认为南北方身高有显著差异。
(2)体重通过假设两者均值相等,检验结果无法否定原假设,因而认为南北方体重没有明显差异。
3、分出生年份月份进行比较年份性别身高体重84 男均值172.00 56.00N 1 1总计均值172.00 56.00N 1 185 男均值180.33 70.67N 3 3女均值161.00 51.00N 2 2总计均值172.60 62.80N 5 586 男均值174.20 65.40N 20 20女均值162.11 52.28N 18 18总计均值168.47 59.1887 男均值178.50 66.58N 6 6女均值164.83 52.83N 18 18总计均值168.25 56.27N 24 2488 男均值170.50 65.00N 2 2女均值167.00 53.50N 2 2总计均值168.75 59.25N 4 489 女均值165.00 50.00N 1 1总计均值165.00 50.00N 1 1总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表可看出,各年份出生的人身高体重无显著性差异。
总计均值171.00 64.00N 6 6 3 男均值174.50 69.50N 4 4 女均值160.25 50.75N 4 4 总计均值167.38 60.13N 8 8 4 男均值181.25 68.50N 4 4 女均值162.25 52.00N 4 4 总计均值171.75 60.25N 8 8 5 男均值169.50 65.25N 2 2 女均值156.00 43.00N 1 1 总计均值165.00 57.83N 3 3 6 男均值175.00 63.00N 1 1 女均值171.50 57.50N 4 4 总计均值172.20 58.60N 5 5 7 男均值171.00 64.33N 3 3 女均值167.00 50.50N 2 2 总计均值169.40 58.80N 5 5 8 男均值179.20 64.90N 5 5 女均值161.50 52.50N 2 2 总计均值174.14 61.36N 7 7 9 男均值171.67 58.00N 3 3 女均值163.33 54.33N 3 3 总计均值167.50 56.1710 男均值174.67 61.83N 3 3总计均值174.67 61.83N 3 311 女均值162.50 51.67N 12 12总计均值162.50 51.67N 12 1212 男均值171.00 66.50N 2 2女均值167.00 57.00N 1 1总计均值169.67 63.33N 3 3总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表同样可得出,各月出生的人身高体重无显著性差异。
计量经济学案例分析汇总
计量经济学案例分析1一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。
但是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也有明显差异。
例如,2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元,最高的上海市达人均10464元,上海是黑龙江的2.35倍。
为了研究全国居民消费水平及其变动的原因,需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费,由于各地区的城市与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。
而且,由于各地区人口和经济总量不同,只能用“城市居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异,并不是城市居民消费在不同时间的变动,所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入,其他因素虽然对居民消费也有影响,但有的不易取得数据,如“居民财产”和“购物环境”;有的与居民收入可能高度相关,如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大,如“零售物价指数”、“利率”。
计量经济学实验教学案例实验七_虚拟变量
实验七虚拟变量【实验目的】掌握虚拟变量的设置方法。
【实验内容】一、试根据表7-1的1998年我国城镇居民人均收入与彩电每百户拥有量的统计资料建立我国城镇居民彩电需求函数;资料来源:据《中国统计年鉴1999》整理计算得到二、试建立我国税收预测模型(数据见实验一);三、试根据表7-2的资料用混合样本数据建立我国城镇居民消费函数。
表7-2 我国城镇居民人均消费支出和可支配收入统计资料资料来源:据《中国统计年鉴》1999-2000整理计算得到【实验步骤】一、我国城镇居民彩电需求函数⒈相关图分析;键入命令:SCAT X Y,则人均收入与彩电拥有量的相关图如7-1所示。
从相关图可以看出,前3个样本点(即低收入家庭)与后5个样本点(中、高收入)的拥有量存在较大差异,因此,为了反映“收入层次”这一定性因素的影响,设置虚拟变量如下:⎩⎨⎧=低收入家庭中、高收入家庭01D图7-1 我国城镇居民人均收入与彩电拥有量相关图⒉构造虚拟变量;方式1:使用DATA 命令直接输入; 方式2:使用SMPL 和GENR 命令直接定义。
DATA D1 GENR XD=X*D1 ⒊估计虚拟变量模型: LS Y C X D1 XD再由t 检验值判断虚拟变量的引入方式,并写出各类家庭的需求函数。
按照以上步骤,虚拟变量模型的估计结果如图7-2所示。
图7-2 我国城镇居民彩电需求的估计我国城镇居民彩电需求函数的估计结果为:i i i i XD D x y0088.08731.310119.061.57ˆ-++= =t (16.249)(9.028) (8.320) (-6.593)2R =0.9964 2R =0.9937 F =366.374 S.E =1.066虚拟变量的回归系数的t 检验都是显著的,且模型的拟合优度很高,说明我国城镇居民低收入家庭与中高收入家庭对彩电的消费需求,在截距和斜率上都存在着明显差异,所以以加法和乘法方式引入虚拟变量是合理的。
计量经济学操作实验及案例分析
计量经济学课程实验实验一 EViews软件的基本操作【实验目的】了解EViews软件的基本操作对象,掌握软件的基本操作。
【实验内容】一、EViews软件的安装;二、数据的输入、编辑与序列生成;三、图形分析与描述统计分析;四、数据文件的存贮、调用与转换。
实验内容中后三步以表1-1所列出的税收收入和国内生产总值的统计资料为例进行操作。
单位:亿元资料来源:《中国统计年鉴1999》【实验步骤】一、安装EViews软件㈠EViews对系统环境的要求⒈一台386、486奔腾或其他芯片的计算机,运行Windows3.1、Windows9X、Windows2000、WindowsNT或WindowsXP操作系统;⒉至少4MB内存;⒊VGA、Super VGA显示器;⒋鼠标、轨迹球或写字板;⒌至少10MB以上的硬盘空间。
㈡安装步骤⒈点击“网上邻居”,进入服务器;⒉在服务器上查找“计量经济软件”文件夹,双击其中的setup.exe,会出现如图1-1所示的安装界面,直接点击next按钮即可继续安装;⒊指定安装EViews软件的目录(默认为C:\EViews3,如图1-2所示),点击OK按钮后,一直点击next按钮即可;⒋安装完毕之后,将EViews的启动设置成桌面快捷方式。
图1-1 安装界面1图1-2 安装界面2二、数据的输入、编辑与序列生成 ㈠创建工作文件 ⒈菜单方式启动EViews 软件之后,进入EViews 主窗口(如图1-3所示)。
图1-3 EViews 主窗口在主菜单上依次点击File/New/Workfile ,即选择新建对象的类型为工作文件,将弹出一个对话框(如图1-4所示),由用户选择数据的时间频率(frequency )、起始期和终止期。
图1-4 工作文件对话框其中, Annual ——年度 Monthly ——月度Semi-annual ——半年 Weekly ——周 Quarterly ——季度 Daily ——日 Undated or irregular ——非时序数据工作区域状态栏选择时间频率为Annual(年度),再分别点击起始期栏(Start date)和终止期栏(End date),输入相应的日前1985和1998。
计量经济学实验2
实验2-3实验目的:ARMA模型识别及估计与应用(ADF检验、Q统计量、ACF、PACF)、ECM模型建模、V AR模型建模检验与应用、离散选择模型建模估计与检验案例分析案例1 中国支出法GDP的ARMA(p,q)模型估计中国支出法GDP是非平稳的,但它的一阶差分是平稳的,即支出法GDP是I(1)时间序列。
可以对经过一阶差分后的GDP建立适当的ARMA(p,q)模型。
(1)GDP单整性检验首先检验1978~2000年间中国支出法GDP时间序列的平稳性,即原序列的平稳性。
用Eviews同时估计出上述3个模型的适当形式。
只要其中有一个模型的检验结果拒绝了零假设,就可以认为时间序列是平稳的,当3个模型的检验结果都不能拒绝零假设时,则认为时间序列是非平稳的。
Eviews中,GDP平稳性的ADF检验模型3、2、1的检验结果如下:根据3个模型检验结果τ统计量都大于临界值(左侧单尾),因此在α=0.05的显著性水平下,接受原假设,即GDP序列存在单位根,是非平稳序列。
进一步对一阶差分后的序列检验判断GDP是否是一阶单整序列,即I(1)。
对GDP一阶差分后序列进行ADF检验,首先采用模型3进行检验,检验结果为:由于τ=-5.183232<-4.498307(显著性水平α=0.01的临界值),因此在α=0.01的显著性水平下,拒绝原假设,即一阶差分后的GDP序列不存在单位根,是平稳序列,因此GDP序列是一阶单整的,即I(1)。
(2)ARMA(p,q)模型识别令GDPD1 =ΔGDP,观察GDPD1该平稳序列的样本自相关和偏自相关函数图:图中,ACF 呈现拖尾,而PACF 呈现截尾特征,进一步结合样本偏自相关函数r k *,当k >p 时,r k *渐近服从如下正态分布:r k *~N (0,1/n ),因此,如果计算的r k,则有95.5%的把握判断时间序列在p 之后截尾。
观察上表发现,偏自相关函数值在k >2以后,*0.426k r <≈,可以认为:偏自相关函数是截尾的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《计量经济学》:试验方法与案例汇编(2011年03)实验一 一元线性回归模型分析某市城市居民年人均鲜蛋需求量(Y :公斤),年人均可支配收入(X :元)的例子。
通过抽样调查,得到1988—1998年的样本观测值。
其数值结果如下:解:ΣX 2=15325548.8 ΣY 2=3055.25 ΣXY=213349.96 n=11 ΣX=12601.67 ΣY=182.30,离差形式:8.888903118.153255481167.126012222=⨯-=-=⎪⎭⎫⎝⎛∑∑X X xn04.351125.3055113.1822222=⨯-=-=⎪⎭⎫⎝⎛∑∑Y Yy n63.4539113.1821167.126011196.213349=⨯⨯-=-=∑∑y x n XY xy 解:(1)计算一元线性回归模型参数估计量及建立模型0051.08.153********.18267.1260196.2133491167.12601)(222=-⨯⨯-⨯=∑--=∑∑∑∑x x n y x xy n b 72.101167.126010051.0113.182=⨯-=-=-=∑∑nx b ny x b y a 则直线回归方程为:X bX a Y 0051.072.10+=+=∧(请注意:如果样本数据较大,也可以采用离差形式的公式计算出参数估计量)即:0051.08.88890363.45392===∑∑∧xxy b72.101167.126010051.0113.182=⨯-=-=∧x b Y a 结果与用基本公式完全相等。
(2)样本决定系数(或可决系数) r 2=(Σy 2-Σe 2)/Σy 2=1-(Σe 2/Σy 2)=1-(11.89/35.04)=1-0.3393=0.6607 其中,残差平方和:Σe 2=Σy 2- b Σxy=35.04-0.0051*4539.63=11.89 (3)参数估计量的方差、标准差 S 2(a)= (Σe 2ΣX 2)/[n(n-2) Σx 2]=(11.89*15325548.8/11*9*888903.8)=2.0736 S 2(b)=(Σe 2)/[ (n-2)Σx 2]=11.89/9*888903.8=0.00000148 则S (a)=1.44,S (b)=0.0012 (4) 参数估计量的显著性检验T (a)=a/S (a)=10.72/1.44=7.44,T (b)=b/S (b)=0.0051/0.0012=4.25 得知T (a)>T α/2(n-2)=2.26, T (b)>T α/2(n-2)=2.26即a 、b 均显著不为零,说明解释变量X 对Y 有显著影响。
(5)方程显著性检验F 检验:F=(Σy 2-Σe 2)/( Σe 2/n-2)=(35.04-11.89)/(11.89/11-2)=17.523查表得F 临界值:F α(1,n-2)= F 0.05(1,9)=5.12,故F>F α,通过F 检验,说明Y 与X 线性显著。
实验二 多元线性回归模型(为了便于同学们理解,现以二元线性回归模型为例)模型形式:μii iiX b Xb b Y +++=22111、参数估计量公式:∑∑∑∑∑∑∑--=∧)(21222212122211X X X X X X X X X bY Y ∑∑∑∑∑∑∑--=∧)(21222212112122X X X X X X X X X b Y YXb X bbY 2211∧-∧-=∧2、随机误差项方差估计量122--=∧∑k n etσ3、残差平方和))())((22211122()(Y Y Y Y XXb X X bY Y et--∧---∧-=∑∑∑-∑练习题:1、若回归模型为Y=a+b X+ε,并且已经根据X 和Y 的16组样本数据,计算出下列各值:ΣX 2=5089.84 ΣY 2=1111.01 ΣXY=2367.19 n=11 ΣX=240.78 ΣY=114.22 求:(1)模型参数的估计量;(2)总离差平方和、残差平方和;(3)样本决定系数; (4)参数估计量的标准差。
2、 已知Y 和X 之间存在线性因果关系,并已经获得如下数据请利用一元线性回归模型进行分析(参数估计、显著性检验、);预测当X=90时,Y的预测值。
3、自己动手查找某个国家、地区或地方的收入和消费数据,模仿本章的例题,进行线性回归分析(参数估计、模型检验及解释参数经济意义),并对结果进行讨论。
4、令Y表示一名妇女生育孩子的生育率,X表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为:Y= b0+b1X+μ问:(1)随机误差项μ包含哪些未引入模型中的因素,它们可能与教育水平相关吗?(2)上述简单回归模型能够准确揭示教育对生育率在其他条件不变下的影响吗?请说明。
5、对于人均存款(S)与人均收入(I)之间的关系S=b0+b1I+μ,使用美国32年的年度数据,得到如下估计模型(括号内为标准差)S=384.105+0.067I(151.105)(0.011) R2=0.538 试回答:(1)b1的经济意义是什么?(2)b0和b1的符号应该怎样的?为什么?实际的符号与你的直觉是一样吗?如果有冲突的话,你可以说明原因吗?(3)你对拟合良度有什么看法?(4)对回归得到的两个参数估计量进行检验。
(显著性水平为0.01)教材P98(6)6、某地区家庭人均鸡肉年消费量(Y),家庭月平均收入X(元),肌肉价格P1(元/kg),检验)。
实验三 异方差性检验与处理一、异方差的处理方法如果预测模型通过检验证实随机项存在异方差,则可以采用两种方法对模型参数进行校正,也就是重新对其进行估计。
而处理异方差,其关键问题是找出异方差的具体形式,为了简单起见,我们仅以一元线性回归模型为例,对于异方差形式提出两种假定。
一元线性回归模型为μiiiX b b Y ++=1假定1:随机误差项的方差与解释变量X i 的平方成正比。
即:XE ii22)(2σμ=,式中,σ2为常数对一元线性回归模型进行转换:用解释变量X i 分别去除一元模型两端各项得:υμi iii iii Xb b Xb X b XY +⋅+=++=1011式中,υi=Xii μXE E iX ii i2)(1)(22==μυE i )(2μ=σ2证明转换后的新模型具有等方差性。
需要强调的是原模型中的常数项b 0成了转换后模型中Xi1的系数,原模型中X i 的系数b 1成了转换后模型的常数项。
对经过转换后的新模型应用普通最小二乘法(即OLS 法),即可得到XYii 对Xi1的回归方程:Xb b XY iii 11∧+∧=∧参数估计值∧∧bb 01和得到,则可以建立预测模型Xb b Y ii∧+∧=∧1假定2:随机误差项的方差与解释变量X i 成正比, 即XE iiσμ2)(2=,式中,σ2为常数在此,克服异方差的方法类似于假定1,但原模型两端不是用x i 去除了,而改为用Xi去除两端各项。
则经过转换后的模型:V X b Xb XX Xb Xb XY iiiii iiiii++=+⋅+=110μ式中,=V i Xii μσσμμ22)()(11)(222=⋅===X XE XE E i iiiiX iiV同样,转换以后的新模型也克服了异方差,具有等方差性。
对模型V X b Xb XY iiiii++=1采用OLS 法回归,得到因变量为XYii,自变量为Xi1和Xi的二元回归方程:X b Xb XY iiii∧+∧=∧10,则原模型回归参数∧∧bb 01和得到,即可写出预测模型方程:Xb b Y ii∧+∧=∧1二、举例:异方差判断、处理在研究某地区居民储蓄倾向时,得到了如下数据资料。
判断用线性回归模型研究居民储蓄倾向时,误差项是否存在异方差,并给出处理方法。
第一步,进入软件操作系统,并创建工作文件即:FILE (文件)/NEW (新文件)/workfile(工作文件),然后根据对话框提示的数据类型和样本范围进行选择,再加以确定(OK );第二步,输入数据。
可以通过菜单或命令“data+变量名”,输入上述表中数据; 第三步,作散点图。
点中两组数据名称,并用graph 命令或菜单操作(quick/qraph/scatter/with regression line )根据两个变量间数据分布情况,可以认为两者之间存在明显的线性关系,但从数据的分布也可以看出异方差存在的可能性。
(可通过回归残差e 序列分布情况来判断模型随机项存在递增异方差) 回归可以得到直线回归模型:LS C Y X 下面,进一步采用G-Q 检验法进行确认异方差。
因为X 已经按照大小顺序存在,可以删除中间c=n/4=31/4=7个数据,将前后各12组数据分别构成两个子样本并进行回归,得到两个回归直线模型5.144771088.0184.73821=+-=∑∧eXY2.769899029.007.114122=+=∑∧eXY根据两个回归模型的残差平方和计算F 统计量为: F=769899.2/144711.5=5.32给定显著性水平为0.05,查两个自由度均为12-1-1=10的F 分布表的临界值F 0.05(10,10)=2.98。
因为F> F 0.05(10,10),说明原模型存在明显的异方差。
由于根据残差序列图可以看出,回归残差的绝对值有随着X 线性增长的趋势,因此考虑对一元线性回归模型进行转换:用解释变量X i 分别去除一元模型两端各项得:υμi iii iii Xb b Xb X b XY +⋅+=++=1011然后再用最小二乘法,以Y/X 为被解释变量,以1/X 为解释变量进行参数估计,可得回归直线模型: 生成两个新序列: genr y1=Y/X genr x1=1/XXY 0847.012.648+-=∧经进一步检验,模型结果得到了明显改善。
第四章 异方差性:软件实现(重要归纳内容)本章的重点内容总结:异方差检验及修正一、异方差的检验方法一:图示法 步骤:首先,对被解释变量和解释变量进行回归:LS Y C X其次,在主菜单中,点击Quick/Graph 得到对话框“Series List ”,在对话框中现列出横坐标X,同时列出纵坐标Y,点击“OK”,出现“Graph”对话框,再点击“Show Options”出现对话框“Graph Options”,在左上角图形类型Graph Type 下拉列表里选择“Scatter Diagram,在右下角散点图项目下选择“Regression Line,再点击“OK”,即可得到X 、Y之间的散点图。
这是随机误差项存在异方差的初步经验证据。
