一阶RL电路全响应公式推导
电路原理课件-一阶电路的全响应

t 0
t
暂态分量
i R (t ) i Rf [i R (0 ) i Rf ]e
t 0
电容中的电流响应为
U0 iC ( t ) I s i R ( t ) e R
U0 iC ( 0 ) I s R iCf 0
t RC
I se
2 10 0 V 4V 5
2. 求稳态值
uC1 f uC 2 f 0
3. 求时间常数
RC RC1 C2 25 s
4. 写出响应表达式
uC 1 (t ) 4e
t 25 V
uC1(0-)=10
uC(t)/V
t 0
4 uC2(0-)=0 0 τ 电容电压曲线
3) 求τ
Req 14 2 1 s 14 7
4) 写出i (t)
iL (t ) 4 (1 4)e
7 t
4 5e
7 t
A
t 0
例4 在图示电路中,电感电流iL(0)=0。t=0时,开关S1闭合后,经 过0.1s,再闭合开关S2。试求电感电流iL(t)。 解: 1、0+≤ t ≤0.1-s时
U0 Is R iC(0-)=0 0
零状态分量
i R( t ) iC (t) t
零输入分量
t
U0 - Is R
-U0/R
一阶电路对阶跃激励的全响应的一般表达式
r (t ) rf (t ) r (0 ) rf (0 ) eFra bibliotek
t
t 0
全响应的初始值、稳态解和电路的时间常数,称为 一阶线性电路全响应的三要素。这种方法就叫做三要素 法。
4-4一阶电路的全响应 三要素法
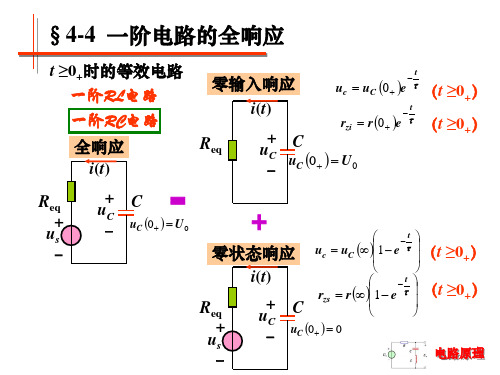
t
t r 1 e
t r r 0 r e
(t ≥0+)
电路原理
§4-4 一阶电路的全响应
r (t ) r () r (0 ) r () e
t
t 0
全响应的初始值、稳态解和电路的时间常数,称为一阶线性 电路全响应的三要素。求出初始值、稳态值和时间常数即可按上 式直接写出全响应的函数式。这种方法就叫做三要素法。
注意:
1)零输入响应、零状态响应和全响应都可采用三要 素法进行求解; 2)三要素法只能用于求解一阶电路的响应。
电路原理
§4-4 一阶电路的全响应∙ 求解步骤
作出t=0-时的等效电路,求出uC(0-)或iL(0-);
根据换路定则,求出uC(0+)或iL(0+); 根据t>0时的电路,求出L或C两端看进去的有源二端电
阻网络的戴维宁等效电路(一阶RC电路)或诺顿等效电 路(一阶RL电路);
根据一阶电路零状态响应的一般形式求出uC(t)或iL(t) ;
电容电压的稳态值uc(∞)即为得到的戴维宁等效电路中的 电压源电压,电感电流的稳态值iL(∞)即为诺顿等效中的 电流源的电流。根据Req可求出时间常数τ ;
根据t>0时的电路,将电容用电压为uC(t)的电压源代替,
i f 0.5 A
3) 求τ
uo 10 × io 10i0 40i0 3
Req
uo 40W io L 1 s Req 40
电路原理
§4-4 一阶电路的全响应∙ 例题
4) 写出i (t)
i ( t ) i f [i (0 ) i f ]e 0.5 0.7e
一阶电路的全响应
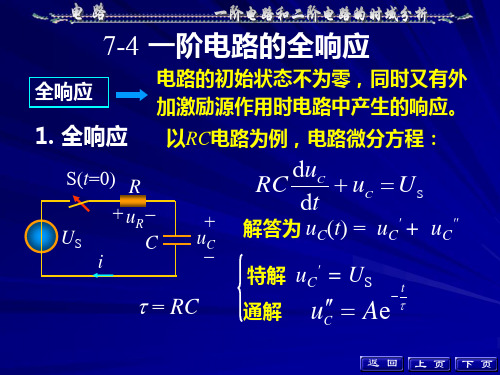
+ 10V
-
3
i(t) (2 2e5t ) A
S2(t=0.2s)
返回 上页 下页
t > 0.2s
i(0.2 ) (2 2e50.2 )A 1.26A
i(0.2 ) 1.26A
2 L / R 1/2s 0.5s
i(∞) 10/2A 5A
i(t) (5 3.74e2(t0.2) ) A
+ 10V
uC (∞) (10 1)V 11V –
+ uC
-
1A +
u
-
返回 上页 下页
RC (11) 1s 2s
全响应: uC (t) (11 Ae0.5t )V
1
1 1
uC (t) (11 10e0.5t )V
iC
(t
)
duC dt
5e0.5t A
+ 10V –
+ -uC
1A +
返回 上页 下页
或求出稳态分量 全响应
代入初值有
iL (∞) 24 /12A 2A
iL (t) (2 Ae20t )A
6=2+A
A=4
例4-2 t=0时 ,开关S闭合,求t >0后的iC、uC及电流 源两端的电压(uC(0-)=1V,C=1F)。
解 这是RC电路全响
应问题,有
1
1 1
稳态分量:
iL (t) [6 (2 6)e5t ]A (6 4e5t )A t 0
i1(t) [2 (0 2)e5t ]A (2 2e5t )A
i2 (t) [4 (2 4)e5t ]A (4 2e5t )A
返回 上页 下页
一阶电路零输入响应零状态响应全响应

t
uc (t) uc () [uc (0 ) uc ()] e
1t
R0 I se RC V
t0
第四章 动态电路的时域分析
电路的放电电流根据三要素公式:
RC
y() ic () 0
y(0 )
iC (0 )
R0 I S Rt
ic (t) ic () [ic (0 ) ic ()] e
+ U-
+
uR -
L
+-ui LL
iL (0 ) 0
iL (0 ) iL (0 ) 0
t=0 ( U 0 iL(0 ) 0 )
iL
()
t
U R
L
R
iL (t) iL () [iL (0 ) iL ()]e
U
Rt
eL
A
t0
R
第四章 动态电路的时域分析
第四章 动态电路的时域分析
3.3 一阶电路的零输入响应、
零输入响应:
零状态响应和全响应
外加激励为零,仅由动态元件初始储能所产生的u和i。
零状态响应: 电路初始储能为零,换路后仅由外加激励所产生的响应。
全响应: 假若电路的初始状态不为零,同时又有外加激励电源的 作用,这时电路的响应称为完全响应。
第四章 动态电路的时域分析
s
t
C
C
C
C
0 3e1066 t 3e1.7105t V(t 0)
第四章 动态电路的时域分析
1
iC
(
t
)
C duC
dt
2.55
5.5一阶电路的全响应及三要素法

d ()
d
2.4×10−12
−
5
0.251
1
2
4
3
+
+
1
−
0.251
−
图 5-17′′ 求
4
3
eq
+
oc
−
(V)
( ≥ 0+)
1μF
4
图 5-18 戴维南等效电路
= 3 e− (A)( = 2.4 × 10−12 )
( ≥ 0+)
求1 ()。
如图 5-17′所示,两个节点②和①的 KCL 为
由分量的待定常数。
2.一阶电路全响应的解
全响应问题的解分解为后一稳态值
强制分量1 ()以及从前
一稳态到达后一稳态需要经过的过渡过程
自由分量2 ()。分量
−/
1 () = (∞),分量2 () = e
= [(0+ ) − (∞)]e−/ (2 ()推导
见右侧)。那么全响应()=强制分量1 ()+自由分量2 (),即
一阶电路全响应为
0 = (0− )
() = 0 e−/ + s (1 − e−/ ) ( ≥ 0+ )
3.求全响应的方法——三要素法
从全响应的表达式可以看出,线性电路的三个重要因素:前一稳
态值(0+ )、后一稳态值(∞)以及一个时间常数参数决定了全响应。
因此,针对一个具体的线性电路,只需得到这三个要素值就可得到全
时间常数为 = = × 3 = 0.5(s)。
1
2
+
⑵ ≥ 0+ 时间开关打开,等效电路如图 5-15′′所示,电路零
一阶电路的全响应——三要素公式【PPT课件】

6A
2
Is
US 3H
(a)
u
大 学 电 路 与 系 统
(2)求解零状态响应iLf(t)和uf(t) 。
零状态响应是初始状态为零,仅由独立源所引起的 R2
响应;故 iLf(0+)=0,电感相当于开路。画出其0+等效 12V
电路,如图 (b)所示,所以
R3 US
iLf(0+) uf(0+) R4
RLiL
L1uS
(a)
(b)
制 作
若用y(t)表示响应,用f (t)表示外加激励,上述方程统一表示为
ddy(tt)1y(t)bf(t)
τ为时常数,对RC电路, τ= RC; 对RL电路, τ= L/R。
第 5-2 页
前一页
下一页 返回本章目录
y(t) = yh(t) + yp(t)
特征根 s = - 1/τ, yh(t) = Ke- t/τ ,
学 电 路 与
1316uL(0)13863
系 统
得uL(0+) = 6V, i(0+) = uL(0+) /6=1A
(a) 3Ω
i(0+) 3A
18V uL(0+)
6Ω
6A
(b) 0+图
3Ω
多 媒
(3)画∞等效电路,如图(c)。
i(∞) 3A
体 室
显然有 uL(∞) = 0, i(∞) = 0,
18V uL(∞) iL(∞) 6Ω
路 与
iL(0+) =iL(0-)=12/(2+1)=12/3=4(A)
系 统
uC (0+)= uC(0-)=1×iL(0-)=4(V)
电路学:6.5 一阶电路的全响应

t t0 t t0
(t-t0) 1
0 t0
t
阶跃信号用途: 1) 描述开关动作
t=0
+
电
2V
-
路
2)表示各种信号
+电 2 (t) V 路
-
f1 (t)
A
f1 (t ) A[ (t) (t t0 )]
0 t0 t
f2 (t) 2 1
0 12
f2 (t) (t) (t 1) 2 (t 2)
uC (0 ) uC (0 ) 0
画0+图如右, 用节点法
a + u (0+) -
2A 4
4
uab
(0
)(
1 4
1 4
)
2
2i(0 4
)
4i(0 ) uab (0 )
i(0+)+ 2i (0+) -
b
解得: i(0 ) 0.8A uab (0 ) 3.2V
则:
u(0 ) 4.8 V
2,计算稳态值u()、i()
后迭加。 u(t) uC (t) uL (t)
RC部分: t=0
1A
+ 1A 1
2
uC
0.5F -
0.5F +u- C +
1H uL -
+
2
u(t)
2 _
uC (0 ) uC (0 ) 1V
uC () 2 V
C RC 1s
所以 uC (t) 2 et V t 0
RL部分: t=0
iS
iL
GL
diL (t dt
)
iL
(t
)
一阶电路全响应
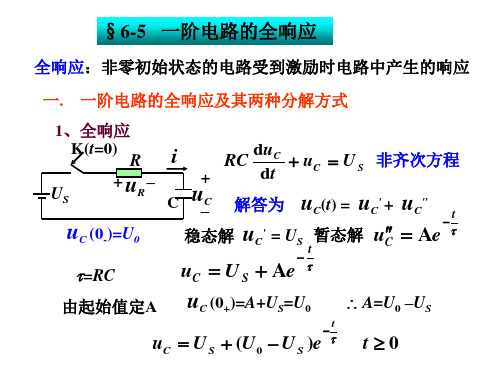
零状态响应
零输入响应
便于叠加计算
二. 三要素法分析一阶电路
以一阶RC电路全响应说明:
t
uc U s (U0 U S )e
时间常数
稳态分量t→∞
电容电压uc(∞)
电容电压
初值uc(0)
上式可以写成:Uc(t) Uc() [Uc(0) Uc()]et/
推广
在直流激励下,电路的任意一个全响应可用f(t)表示,则:
0
t
零输入响应
(3).两种分解方式的比较 全响应 = 强制分量(稳态解)+自由分量(暂态解)
稳态解
暂态解
t
uc U s (U0 U S )e (t ≥ 0)
物理概念清楚
全响应= 零状态响应 + 零输入响应
t
t
uC U S (1 e ) U0e
(t 0)
强制分量(稳态解)
uc
US
U0
uc
0
u" C
U0 -US
自由分量(暂态解)
u' C t
稳态解 全解 暂态解
(2). 全响应= 零状态响应 + 零输入响应
t
t
uC U S (1 e ) U0e
(t 0)
零状态响应
零输入响应
K(t=0) R
i
= US
+uR–
C
+
uC
–
uC (0-)=U0
t
f (t) f () [ f (0 ) f ()]e
其解答一般形式为:
令 t = 0+
f (0 ) f () A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一阶RL电路全响应公式推导
一、实验目的
(1)通过实验,学会计算含RL电路的一阶响应。
(2)学会利用multisim仿真、测量一阶电路。
(3)观察RL电路响应的变化过程。
二、实验原理
当电路已经处于稳定状态的情况时,讨论激励和响应的关系,为稳态分析。
当电路中含有储能元件,即含有电感和电容元件,这类元件的电压和电流关系式微分、积分关系而不是代数关系,因此根据基尔霍夫定理和元件特性方程所列写的电路方程,是以电路或电压为变量的微分方程。
故称这类元件为动态元件,含有动态元件的电路称为动态电路。
如果只含有一个动态元件,描述电路的特性方程是一阶微分方程,这种电路称为一阶电路。
在动态电路中,当电路的结构或元件的参数发生改变时(例如,电路中电源或无源元件的断开或接入,信号的突然注入等),可能使电路改变原来的工作状态,而转变到另一个工作状态,这种转变往往需要经历一个过程,工程上称为过渡过程。
过渡过程又称为过渡状态或暂态。
在描述电路过渡过程的微分方程中,电路的任何电压和电流及其n-1阶导数在t=0+时的值称为初始值。
其中电感电流和电容电压的初始值,即和称为独立的初始值,其余的称为非独立的初
始值。
独立的初始值决定了电路的初始能量。
在电路前后电容电流和电感电压为有限值的条件下,换路前后瞬间电容电压和电感电流不能跃变。
即
上述两个式子,称为换路定理。
一阶电路可以分为零状态响应、零输入响应和全响应三种情况,其中零状态响应和零输入响应为全响应的特殊情况。
实际计算过程,可以运用一阶电路的等效化简和三要素法,讨论电路中的电压电流情况。
但三要素法只适用于在直流或正弦信号激励时的一阶电路。
三要素法运用步骤和方法包括一下4步:
1)计算电压或电流的初始值。
对于电容电压和电感电流可以通过换路定理求的。
而除此之外的初始值,可根据等效电路求的。
在等效电路中,电感相当于的电流源,电容相当于的电压源。
2)计算电压或电流的稳态值。
把换路后电路中的所有电容看成开路,所有电感当作短路处理。
3)计算电路的时间常数τ。
对于τ中的电阻应该理解为是从L或C元件两端向电路的其余部分看进去的入端电阻。
4)将以上求得的三要素代入下式,即得所求响应的全响应表达式。
三、实验内容
如图所示电路中,已知,求。
解:
方法一:三要素法
因电源为阶跃信号,故时,电源保持1V。
由题目得,,由换路定律可得
当时,利用回路电流法得
得
接下来用简化电路求τ
去除1V独立源,并将电容替换为1V电压源,求出等效电阻可得此时电流为,故等效电阻为
化简后等效电路为
故
故
方法二:微分方程法
用回路电流法可得
将两式整合并将代入得
解微分方程得
结果与三要素法一致。
四、仿真验证
根据题目所给电路,在multisim中连接电路,如图所示
仿真时闭合开关S1
示波器中所得波形为
因τ过小,所以无法再示波器中看到全部波形,当波形稳定时,所得波形为
虽无法显示全部波形,但能根据示波器中数据验证计算所得结果正确。
五、实验结论
对例题的计算和仿真验证了三要素法在解决RL一阶电路的正确性,同时也说明三要素法是一阶电路计算时适用最广的方法。
在对例题进行计算时,也发现常规的微分方程也可用来解决一阶电路,在一些复杂电路时,甚至更为高效也发现常规的微分方程也可用来解决一阶电路,在一些复杂电路时,甚至更为高效。
在仿真时,由于τ过小,导致示波器无法显示整个波形,所以在验证表达式时遇到难题,但通过代入值特定值计算,也可验证结果正确。
通过该实验的设计,我熟悉了模拟仿真的步骤与整体设计方法,知识点得到了复习,对学习有所帮助。
