相交线与平行线培优卷

合集下载

（完整版）初一下学期相交线与平行线数学试题培优试卷

一、选择题1．如图，//,AB CD ABK ∠的平分线BE 的反向延长线和DCK ∠的平分线CF 的反向延长线相交于点 24H K H ∠-∠=︒，，则K ∠=（）A ．76︒B ．78︒C ．80︒D ．82︒2．如图a 是长方形纸带，∠DEF=26°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（）A ．102°B ．108°C ．124°D ．128° 3．已知∠A 的两边与∠B 的两边互相平行，且∠A=20°，则∠B 的度数为（）. A ．20° B ．80° C ．160° D ．20°或160° 4．下列几个命题中，真命题有（）①两条直线被第三条直线所截，内错角相等；②如果1∠和2∠是对顶角，那么12∠=∠；③一个角的余角一定小于这个角的补角；④三角形的一个外角大于它的任一个内角．A ．1个B ．2个C ．3个D ．45．如图，直线//a b ，三角板的直角顶点在直线b 上，已知125∠=︒，则2∠等于（）．A ．25°B ．55°C ．65°D ．75°6．下列命题是真命题的有（）（1）相等的角是对顶角；（2）两条直线被第三条直线所截，同位角相等；（3）在同一平面内，过两点有且只有一条直线与已知直线垂直；（4）经过直线外一点，有且只有一条直线与已知直线平行；（5）一个角的余角一定大于这个角．A ．0个B ．1个C ．2个D ．3个7．如图，//CD AB ，BC 平分ACD ∠，CF 平分ACG ∠，50BAC ∠=︒，12∠=∠，则下列结论：①CB CF ⊥，②165∠=︒，③24ACE ∠=∠，④324∠=∠．其中正确的是（）A ．①②③B ．①②④C ．②③④D ．①②③④ 8．如果，直线//AB CD ，65A ∠=︒，则EFC ∠等于（）A ．105︒B ．115︒C ．125︒D ．135︒9．如图，长方形ABCD 中，7AB =，第一次平移长方形ABCD 沿AB 的方向向右平移5个单位，得到长方形1111D C B A ，第3次平移将长方形1111D C B A 沿11A B 的方向向右平移5个单位，得到长方形2222A B C D ，…第n 次平移将长方形1111n n n n A B C D ----的方向平移5个单位，得到长方形(2)n n n n A B C D n >，若n AB 的长度为2022，则n 的值为（）A ．403B ．404C ．405D ．40610．如图，△OAB 为等腰直角三角形（∠A ＝∠B ＝45°，∠AOB ＝90°），△OCD 为等边三角形（∠C ＝∠D ＝∠COD ＝60°），满足OC ＞OA ，△OCD 绕点O 从射线OC 与射线OA 重合的位置开始，逆时针旋转，旋转的角度为α（0°＜α＜360°），下列说法正确的是（）A ．当α＝15°时，DC ∥ABB ．当OC ⊥AB 时，α＝45°C ．当边OB 与边OD 在同一直线上时，直线DC 与直线AB 相交形成的锐角为15° D ．整个旋转过程，共有10个位置使得△OAB 与△OCD 有一条边平行二、填空题11．如图，已知AB CD ∥，CE 、BE 的交点为E ，现作如下操作：第一次操作，分别作ABE ∠和DCE ∠的平分线，交点为1E ，第二次操作，分别作1ABE ∠和1DCE ∠的平分线，交点为2E ，第三次操作，分别作2ABE ∠和2DCE ∠的平分线，交点为3E ，…第n 次操作，分别作1n ABE -∠和1n DCE -∠的平分线，交点为n E ．若1n E ∠=度，那BEC ∠等于__________度．12．小明将一副三角板中的两块直角三角尺的直角顶点C 按如图所示的方式叠放在一起，当∠ACE ＜180°且点E 在直线AC 的上方时，他发现若∠ACE ＝_____，则三角板BCE 有一条边与斜边AD 平行．13．如图，直线MN ∥PQ ，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连结AB ．∠ABM 的平分线BC 交PQ 于点C ，连结AC ，过点A 作AD ⊥PQ 交PQ 于点D ，作AF ⊥AB 交PQ 于点F ，AE 平分∠DAF 交PQ 于点E ，若∠CAE=45°，∠ACB=52∠DAE ，则∠ACD 的度数是_____．14．如图，AB ∥CD ，点P 为CD 上一点，∠EBA 、∠EPC 的角平分线于点F ，已知∠F ＝40°，则∠E ＝_____度．15．如图，a ∥b ，∠2＝∠3，∠1＝40°，则∠4的度数是______度．16．如图，直线，将含有角的三角板的直角顶点放在直线上，若，则的度数为________17．如图，AB ∥CD ，EM 是∠AMF 的平分线，NF 是∠CNE 的平分线，EN ，MF 交于点O ．若∠E +60°＝2∠F ，则∠AMF 的大小是___．18．如图，//AB DE ，AD AB ⊥，AE 平分BAC ∠交BC 于点F ．如果24CAD ∠=︒，则=E ∠__︒．19．如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB ，CD ．若CD ∥BE ，∠1＝28°，则∠2的度数是______．20．如图，将一副三角板按如图放置，90,45,60BAC DAE B E ∠=∠=︒∠=︒∠=︒，则①13∠=∠；②2180CAD ∠+∠=︒；③如果230∠=︒，则有//AC DE ；④如果245∠=︒，BC AD．上述结论中正确的是________________（填写序号）．则有//三、解答题21．如图，直线HD//GE，点A在直线HD上，点C在直线GE上，点B在直线HD、GE之间，∠DAB＝120°．（1）如图1，若∠BCG＝40°，求∠ABC的度数；（2）如图2，AF平分∠HAB，BC平分∠FCG，∠BCG＝20°，比较∠B，∠F的大小；（3）如图3，点P是线段AB上一点，PN平分∠APC，CN平分∠PCE，探究∠HAP和∠N 的数量关系，并说明理由．22．已知：AB//CD．点E在CD上，点F，H在AB上，点G在AB，CD之间，连接FG，EH，GE，∠GFB＝∠CEH．（1）如图1，求证：GF//EH；（2）如图2，若∠GEH＝α，FM平分∠AFG，EM平分∠GEC，试问∠M与α之间有怎样的数量关系（用含α的式子表示∠M）？请写出你的猜想，并加以证明．23．（1）如图①，若∠B+∠D=∠E，则直线AB与CD有什么位置关系？请证明（不需要注明理由）．（2）如图②中，AB//CD，又能得出什么结论？请直接写出结论．（3）如图③，已知AB//CD，则∠1+∠2+…+∠n-1+∠n的度数为．24．已知，如图1，射线PE 分别与直线AB ，CD 相交于E 、F 两点，∠PFD 的平分线与直线AB 相交于点M ，射线PM 交CD 于点N ，设∠PFM ＝α°，∠EMF ＝β°，且（40﹣2α）2＋|β﹣20|＝0（1）α＝，β＝；直线AB 与CD 的位置关系是；（2）如图2，若点G 、H 分别在射线MA 和线段MF 上，且∠MGH ＝∠PNF ，试找出∠FMN 与∠GHF 之间存在的数量关系，并证明你的结论；（3）若将图中的射线PM 绕着端点P 逆时针方向旋转（如图3），分别与AB 、CD 相交于点M 1和点N 1时，作∠PM 1B 的角平分线M 1Q 与射线FM 相交于点Q ，问在旋转的过程中1FPN Q∠∠的值是否改变？若不变，请求出其值；若变化，请说明理由． 25．已知：如图，直线AB //CD ，直线EF 交AB ，CD 于P ，Q 两点，点M ，点N 分别是直线CD ，EF 上一点（不与P ，Q 重合），连接PM ，MN ．（1）点M ，N 分别在射线QC ，QF 上（不与点Q 重合），当∠APM +∠QMN =90°时， ①试判断PM 与MN 的位置关系，并说明理由；②若PA 平分∠EPM ，∠MNQ =20°，求∠EPB 的度数．（提示：过N 点作AB 的平行线）（2）点M ，N 分别在直线CD ，EF 上时，请你在备用图中画出满足PM ⊥MN 条件的图形，并直接写出此时∠APM 与∠QMN 的关系．（注：此题说理时不能使用没有学过的定理）【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】分别过K 、H 作AB 的平行线MN 和RS ，根据平行线的性质和角平分线的性质可用ABK ∠和DCK ∠分别表示出H ∠和K ∠，从而可找到H ∠和K ∠的关系，结合条件可求得K ∠．【详解】解：如图，分别过K 、H 作AB 的平行线MN 和RS ，//AB CD ，//////AB CD RS MN ∴， 12RHB ABE ABK ∴∠=∠=∠，12SHC DCF DCK ∠=∠=∠， 180NKB ABK MKC DCK ∠+∠=∠+∠=︒，1180180()2BHC RHB SHC ABK DCK ∴∠=︒-∠-∠=︒-∠+∠， 180BKC NKB MKC ∠=︒-∠-∠180ABK DCK =∠+∠-︒，36021801802BKC BHC BHC ∴∠=︒-∠-︒=︒-∠，又24BKC BHC ∠-∠=︒，24BHC BKC ∴∠=∠-︒，1802(24)BKC BKC ∴∠=︒-∠-︒，76BKC ∴∠=︒，故选：A ．【点睛】本题主要考查平行线的性质，掌握平行线的判定和性质是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④//a b ，////⇒b c a c ．2．A解析：A【分析】先由矩形的性质得出∠BFE=∠DEF=26°，再根据折叠的性质得出∠CFG=180°-2∠BFE ，∠CFE=∠CFG-∠EFG 即可．【详解】∵四边形ABCD 是矩形，∴∠BFE=∠DEF=26°，∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°，故选A．【点睛】本题考查了翻折变换（折叠问题）、矩形的性质、平行线的性质；熟练掌握翻折变换和矩形的性质，弄清各个角之间的关系是解决问题的关键．3．D解析：D【详解】试题分析：如图，∵∠A=20°，∠A的两边分别和∠B的两边平行，∴∠B和∠A可能相等也可能互补，即∠B的度数是20°或160°，故选D.4．B解析：B【分析】根据平行线的性质对①进行判断；根据对顶角的性质对②进行判断；根据余角与补角的定义对③进行判断；根据三角形外角性质对④进行判断．【详解】解：两条平行直线被第三条直线所截，内错角相等，所以①错误；如果∠1和∠2是对顶角，那么∠1=∠2，所以②正确；一个角的余角一定小于这个角的补角，所以③正确；三角形的外角大于任何一个与之不相邻的一个内角，所以④错误．故选：B．【点睛】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．5．C解析：C【分析】利用平行线的性质，可证得∠2=∠3，利用已知可证得∠1+∠3=90°，求出∠3的度数，进而求出∠2的度数．【详解】∵a//b∴∠2=∠3，∵∠1+∠3=180°-90°=90°∴∠3=90°-∠1=90°-25°=65°∴∠2=65°．故选C．【点睛】本题主要考查了平行线的性质，灵活运用“两直线平行、同位角相等”是解答本题的关键．6．B解析：B【分析】根据对顶角与同位角的定义、垂线的性质、平行公理、余角的定义逐个判断即可得．【详解】解：（1）相等的角不一定是对顶角，则原命题是假命题；（2）两条平行线被第三条直线所截，同位角相等，则原命题是假命题；（3）在同一平面内，过一点有且只有一条直线与已知直线垂直，则原命题是假命题；（4）经过直线外一点，有且只有一条直线与已知直线平行，则原命题是真命题；（5）一个角的余角不一定大于这个角，如70︒角的余角等于20︒，则原命题是假命题；综上，是真命题的有1个，故选：B．【点睛】本题考查了对顶角与同位角的定义、垂线的性质、平行公理、余角，熟练掌握各定理与性质是解题关键．7．B解析：B【分析】根据角平分线的性质可得12ACB ACD∠=∠，12ACF ACG∠=∠，，再利用平角定义可得∠BCF=90°，进而可得①正确；首先计算出∠ACB的度数，再利用平行线的性质可得∠2的度数，从而可得∠1的度数；利用三角形内角和计算出∠3的度数，然后计算出∠ACE的度数，可分析出③错误；根据∠3和∠4的度数可得④正确．【详解】解：如图，∵BC 平分∠ACD ，CF 平分∠ACG ， ∴1122ACB ACD ACF ACG ∠=∠∠=∠，， ∵∠ACG +∠ACD =180°，∴∠ACF +∠ACB =90°，∴CB ⊥CF ，故①正确，∵CD ∥AB ，∠BAC =50°，∴∠ACG =50°，∴∠ACF =∠4=25°，∴∠ACB =90°-25°=65°，∴∠BCD =65°，∵CD ∥AB ，∴∠2=∠BCD =65°，∵∠1=∠2，∴∠1=65°，故②正确；∵∠BCD =65°，∴∠ACB =65°，∵∠1=∠2=65°，∴∠3=50°，∴∠ACE =15°，∴③∠ACE =2∠4错误；∵∠4=25°，∠3=50°，∴∠3=2∠4，故④正确，故选：B ．【点睛】此题主要考查了平行线的性质，以及角平分线的性质，关键是理清图中角之间的和差关系．8．B解析：B【分析】先求∠DFE 的度数，再利用平角的定义计算求解即可．【详解】∵AB ∥CD ，∴∠DFE =∠A =65°，∴∠EFC =180°-∠DFE =115°，故选B．【点睛】本题考查了平行线的性质，平角的定义，熟练掌握平行线的性质是解题的关键．9．A解析：A【分析】根据平移的性质得出AA1=5，A1A2=5，A2B1=A1B1-A1A2=7-5=2，进而求出AB1和AB2的长，然后根据所求得出数字变化规律，进而得出AB n=（n+1）×5+2求出n即可．【详解】解：∵AB=7，第1次平移将长方形ABCD沿AB的方向向右平移5个单位，得到长方形A1B1C1D1，第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位，得到长方形A2B2C2D2…，∴AA1=5，A1A2=5，A2B1=A1B1-A1A2=7-5=2，∴AB1=AA1+A1A2+A2B1=5+5+2=12，∴AB2的长为：5+5+7=17；∵AB1=2×5+2=12，AB2=3×5+2=17，∴AB n=（n+1）×5+2=2022，解得：n=403．故选：A．【点睛】此题主要考查了平移的性质以及一元一次方程的应用，根据平移的性质得出AA1=5，A1A2=5是解题关键．10．A解析：A【分析】设OC与AB交点为M，OD与AB交点为N，当α＝15°时，可得∠OMN＝α+∠A＝60°，可证DC∥AB；当OC⊥AB时，α+∠A＝90°，可得α＝30°；当边OB与边OD在同一直线上时，应分两种情况，则直线DC与直线AB相交形成的锐角也有两种情况；整个旋转过程，因OC、OB、OD、OA都有交点，只有AB和CD存在平行，根据图形的对称性可判断有两个位置使得△OAB与△OCD有一条边平行．【详解】解：设OC与AB交点为M，OD与AB交点为N，当α＝15°时，∠OMN＝α+∠A＝60°，∴∠OMN＝∠C，∴DC∥AB，故A正确；当OC⊥AB时，α+∠A＝90°或α﹣180°＝90°﹣∠A，∴α＝45°或225°，故B错误；当边OB 与边OD 在同一直线上时，应分两种情况，则直线DC 与直线AB 相交形成的锐角也有两种情况，故C 错误；整个旋转过程，因OC 、OB 、OD 、OA 都有交点，只有AB 和CD 存在平行，根据图形的对称性可判断有两个位置使得△OAB 与△OCD 有一条边平行，故D 错误；故选A ．【点睛】本题主要考查了平行线的性质与判定，垂直的定义，解题的关键在于能够熟练掌握相关知识进行求解.二、填空题11．【分析】先过E 作EF ∥AB ，根据AB ∥CD ，得出AB ∥EF ∥CD ，再根据平行线的性质，得出∠B=∠1，∠C=∠2，进而得到∠BEC=∠ABE+∠DCE ；根据∠ABE 和∠DCE 的平分线交点为E1，解析：2n【分析】先过E 作EF ∥AB ，根据AB ∥CD ，得出AB ∥EF ∥CD ，再根据平行线的性质，得出∠B =∠1，∠C =∠2，进而得到∠BEC =∠ABE +∠DCE ；根据∠ABE 和∠DCE 的平分线交点为E 1，则可得出∠CE 1B =∠ABE 1+∠DCE 112=∠ABE 12+∠DCE 12=∠BEC ；同理可得∠BE 2C =∠ABE 2+∠DCE 212=∠ABE 112+∠DCE 112=∠CE 1B 14=∠BEC ；根据∠ABE 2和∠DCE 2的平分线，交点为E 3，得出∠BE 3C 18=∠BEC ；…据此得到规律∠E n 12n =∠BEC ，最后求得∠BEC 的度数．【详解】如图1，过E 作EF ∥AB ．∵AB ∥CD ，∴AB ∥EF ∥CD ，∴∠B =∠1，∠C =∠2．∵∠BEC =∠1+∠2，∴∠BEC =∠ABE +∠DCE ；如图2．∵∠ABE 和∠DCE 的平分线交点为E 1，∴∠CE 1B =∠ABE 1+∠DCE 112=∠ABE 12+∠DCE 12=∠BEC ． ∵∠ABE 1和∠DCE 1的平分线交点为E 2， ∴∠BE 2C =∠ABE 2+∠DCE 212=∠ABE 112+∠DCE 112=∠CE 1B 14=∠BEC ； ∵∠ABE 2和∠DCE 2的平分线，交点为E 3， ∴∠BE 3C =∠ABE 3+∠DCE 312=∠ABE 212+∠DCE 212=∠CE 2B 18=∠BEC ； …以此类推，∠E n 12n=∠BEC ， ∴当∠E n =1度时，∠BEC 等于2n 度．故答案为：2n ．【点睛】本题考查了角平分线的定义以及平行线性质：两直线平行，内错角相等的运用．解决问题的关键是作平行线构造内错角，解题时注意：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．12．或或【分析】分三种情形画出图形分别建立好几何模型求解，即可解决问题．【详解】解：有三种情形： ①如图1中，当AD ∥BC 时．∵AD ∥BC ， ∴∠D ＝∠BCD ＝30°，∵∠ACE+∠E解析：30或120︒或165︒【分析】分三种情形画出图形分别建立好几何模型求解，即可解决问题．【详解】解：有三种情形： ①如图1中，当AD ∥BC 时．∵AD ∥BC ， ∴∠D ＝∠BCD ＝30°，∵∠ACE+∠ECD ＝∠ECD+∠DCB ＝90°，∴∠ACE ＝∠DCB ＝30°．②如图2中，当AD∥CE时，∠DCE＝∠D＝30°，可得∠ACE＝90°+30°＝120°．③如图2中，当AD∥BE时，延长BC交AD于M．∵AD∥BE，∴∠AMC=∠B=45°，∴∠ACM＝180°-60°-45°＝75°，∴∠ACE＝75°+90＝165°，综上所述，满足条件的∠ACE的度数为30°或120°或165°．故答案为30°或120°或165°．【点睛】本题考查旋转变换、平行线的判定和性质、三角形内角和定理等知识，解题的关键是学会用分类讨论的首先思考问题，属于中考常考题型．13．27°．【分析】延长FA与直线MN交于点K，通过角度的不断转换解得∠BCA=45°. 【详解】解：延长FA与直线MN交于点K，由图可知∠ACD=90°-∠CAD=90°-(45°+∠EAD解析：27°．【分析】延长FA与直线MN交于点K，通过角度的不断转换解得∠BCA=45°.【详解】解：延长FA与直线MN交于点K，由图可知∠ACD=90°-∠CAD=90°-(45°+∠EAD)=45°-12∠FAD=45°-12(90°-∠AFD)=12∠AFD，因为MN∥PQ，所以∠AFD=∠BKA=90°-∠KBA=90°-(180°-∠ABM)=∠ABM-90°，所以∠ACD=12∠AFD=12(∠ABM-90°)=∠BCD-45°，即∠BCD-∠ACD=∠BCA=45°，所以∠ACD=90°-(45°+∠EAD)=45°-∠EAD=45°-25∠BCA=45°-18°=27°.故∠ACD的度数是：27°.【点睛】本题利用平行线、垂直、角平分线综合考查了角度的求解.14．80【详解】如图，根据角平分线的性质和平行线的性质，可知∠FMA=∠CPE=∠F+∠1，∠ANE=∠E+2∠1=∠CPE=2∠FMA，即∠E=2∠F=2×40°=80°.故答案为80.解析：80【详解】如图，根据角平分线的性质和平行线的性质，可知∠FMA=12∠CPE=∠F+∠1，∠ANE=∠E+2∠1=∠CPE=2∠FMA，即∠E=2∠F=2×40°=80°.故答案为80.15．40【解析】试题分析：如图，分别作a、b的平行线，然后根据a∥b，可得∠1=∠5，∠6=∠7，∠8=∠4，然后根据∠2=∠3，即∠5+∠6=∠7+∠8，然后由∠1=40°，可求得∠4=40°.解析：40【解析】试题分析：如图，分别作a、b的平行线，然后根据a∥b，可得∠1=∠5，∠6=∠7，∠8=∠4，然后根据∠2=∠3，即∠5+∠6=∠7+∠8，然后由∠1=40°，可求得∠4=40°.故答案为：40.16．【解析】试题分析：过B作BE∥m，则根据平行公理及推论可知l∥BE，然后可证明得到∠1+∠2=∠ABC=45°，因此可求得∠2=20°.故答案为：20.解析：【解析】试题分析：过B作BE∥m，则根据平行公理及推论可知l∥BE，然后可证明得到∠1+∠2=∠ABC=45°，因此可求得∠2=20°.故答案为：20.17．【分析】作，则，，而，所以，同理可得，变形得到，利用等式的性质得，加上已给条件，于是得到，易得的度数．【详解】解：作，如图，，，，，是的平分线，，，，同理可得，，，，解析：40︒【分析】作//EH AB ，则1AME ∠=∠，2CNE ∠=∠，而12AME AMF ∠=∠，所以12MEN AMF CNE ∠=∠+∠，同理可得12F AMF CNE ∠=∠+∠，变形得到22F AMF CNE ∠=∠+∠，利用等式的性质得322F E AMF ∠-∠=∠，加上已给条件602MEN F ∠+︒=∠，于是得到3602AMF ∠=︒，易得AMF ∠的度数．【详解】解：作//EH AB ，如图，//AB CD ，//EH CD ，1AME ∴∠=∠，2CNE ∠=∠， EM 是AMF ∠的平分线，12AME AMF ∴∠=∠， 12MEN ∠=∠+∠，12MEN AMF CNE ∴∠=∠+∠，同理可得，12F AMF CNE ∠=∠+∠， 22F AMF CNE ∴∠=∠+∠，322F MEN AMF ∴∠-∠=∠， 602MEN F ∠+︒=∠，即260F MEN ∠-∠=︒， ∴3602AMF ∠=︒， 40AMF ∴∠=︒，故答案为：40︒．【点睛】本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补，合理作辅助线和把一般结论推广是解决问题的关键．18．33【分析】根据求出∠C=90°，再求出∠BAD=66°，根据角平分线性质得∠DAE=33°，由三角形的外角性质得∠ADE=114°，最后由三角形内角和定理可得结论．【详解】解：∵，，∴∠解析：33【分析】根据//AB DE 求出∠C=90°，再求出∠BAD=66°，根据角平分线性质得∠DAE=33°，由三角形的外角性质得∠ADE=114°，最后由三角形内角和定理可得结论．【详解】解：∵//AB DE ，AD AB ⊥，∴∠180BAD D ∠+∠=︒，且90BAD ∠=︒∴90D ∠=︒∵∠CAD =24°∴∠BAC =90°-∠CAD =90°-24°=66°，∵AE 是∠BAC 的平分线∴∠EAB =11663322BAC ∠=⨯︒=︒ ∵//AB DE ，∴33E EAB ∠=∠=︒故答案为：33【点睛】此题主要考查了平行线的性质，角平分线的定义，准确识图，灵活运用相关知识是解题的关键．19．56°【分析】由折叠的性质可得∠3＝∠1＝28°，从而求得∠4＝56°，再根据平行线的性质定理求出∠EBD ＝180°﹣∠4＝124°，最后再根据平行线性质定理求出∠2＝56°．解：如解析：56°【分析】由折叠的性质可得∠3＝∠1＝28°，从而求得∠4＝56°，再根据平行线的性质定理求出∠EBD＝180°﹣∠4＝124°，最后再根据平行线性质定理求出∠2＝56°．【详解】解：如图，由折叠的性质，可得∠3＝∠1＝28°，∴∠4＝∠1+∠3＝56°，∵CD∥BE，AC∥BD，∴∠EBD＝180°﹣∠4＝124°，又∵CD∥BE，∴∠2＝180°﹣∠CBD＝180°﹣124°＝56°．故答案为：56°．【点睛】本题考查了平行线的性质，解题的关键是根据平行线的性质找出图中角度之间的关系．20．①②③④【分析】根据余角的概念和同角的余角相等判断①；根据①的结论判断②；根据平行线的判定定理判断③和④，即可得出结论．【详解】解：∵∠1+∠2=90°，∠3+∠2=90°，∴∠1=∠3，解析：①②③④【分析】根据余角的概念和同角的余角相等判断①；根据①的结论判断②；根据平行线的判定定理判断③和④，即可得出结论．【详解】解：∵∠1+∠2=90°，∠3+∠2=90°，∴∠1=∠3，∵∠CAD+∠2=∠1+∠2+∠3+∠2=90°+90°=180°，故②正确；∵∠2=30°，∴∠1=60°=∠E，∴AC∥DE，故③正确；∵∠2=45°，∴∠3=45°=∠B，∴BC∥AD，故④正确；故答案为：①②③④．【点睛】本题考查的是平行线的性质和余角、补角的概念，掌握平行线的性质定理和判定定理是解题的关键．三、解答题∠HAP；理由见解析．21．（1）∠ABC＝100°；（2）∠ABC＞∠AFC；（3）∠N＝90°﹣12【分析】（1）过点B作BM//HD，则HD//GE//BM，根据平行线的性质求得∠ABM与∠CBM，便可求得最后结果；（2）过B作BP//HD//GE，过F作FQ//HD//GE，由平行线的性质得，∠ABC＝∠HAB+∠BCG，∠AFC＝∠HAF+∠FCG，由角平分线的性质和已知角的度数分别求得∠HAF，∠FCG，最后便可求得结果；（3）过P作PK//HD//GE，先由平行线的性质证明∠ABC＝∠HAB+∠BCG，∠AFC＝∠HAF+∠FCG，再根据角平分线求得∠NPC与∠PCN，由后由三角形内角和定理便可求得结果．【详解】解：（1）过点B作BM//HD，则HD//GE//BM，如图1，∴∠ABM＝180°﹣∠DAB，∠CBM＝∠BCG，∵∠DAB＝120°，∠BCG＝40°，∴∠ABM＝60°，∠CBM＝40°，∴∠ABC＝∠ABM+∠CBM＝100°；（2）过B 作BP //HD //GE ，过F 作FQ //HD //GE ，如图2，∴∠ABP ＝∠HAB ，∠CBP ＝∠BCG ，∠AFQ ＝∠HAF ，∠CFQ ＝∠FCG ，∴∠ABC ＝∠HAB +∠BCG ，∠AFC ＝∠HAF +∠FCG ，∵∠DAB ＝120°，∴∠HAB ＝180°﹣∠DAB ＝60°，∵AF 平分∠HAB ，BC 平分∠FCG ，∠BCG ＝20°，∴∠HAF ＝30°，∠FCG ＝40°，∴∠ABC ＝60°+20°＝80°，∠AFC ＝30°+40°＝70°，∴∠ABC ＞∠AFC ；（3）过P 作PK //HD //GE ，如图3，∴∠APK ＝∠HAP ，∠CPK ＝∠PCG ，∴∠APC ＝∠HAP +∠PCG ，∵PN 平分∠APC ，∴∠NPC ＝12∠HAP +12∠PCG ，∵∠PCE ＝180°﹣∠PCG ，CN 平分∠PCE ，∴∠PCN ＝90°﹣12∠PCG ，∵∠N +∠NPC +∠PCN ＝180°，∴∠N ＝180°﹣12∠HAP ﹣12∠PCG ﹣90°+12∠PCG ＝90°﹣12∠HAP ，即：∠N ＝90°﹣12∠HAP ．【点睛】本题考查了角平分线的定义，平行线性质和判定：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想与方程思想的应用，理清各角度之间的关系是解题的关键，也是本题的难点．22．（1）见解析；（2）902FME α∠=︒-，证明见解析．【分析】（1）由平行线的性质得到CEH EHB ∠=∠，等量代换得出GFB EHB ∠=∠，即可根据“同位角相等，两直线平行”得解；（2）过点M 作//MQ AB ，过点G 作//GP AB ，根据平行线的性质及角平分线的定义求解即可．【详解】（1）证明：//AB CD ，CEH EHB ∴∠=∠，GFB CEH ∠=∠，GFB EHB ∴∠=∠，//GF EH ∴；（2）解：902FME α∠=︒-，理由如下：如图2，过点M 作//MQ AB ，过点G 作//GP AB ，//AB CD ，//MQ CD ∴，AFM FMQ ∴∠=∠，QME MEC ∠=∠，FME FMQ QME AFM MEC ∴∠=∠+∠=∠+∠，同理，FGE FGP PGE AFG GEC ∠=∠+∠=∠+∠，FM 平分AFG ∠，EM 平分GEC ∠，2AFG AFM ∴∠=∠，2GEC MEC ∠=∠，2FGE FME ∴∠=∠，由（1）知，//GF EH ，180FGE GEH ∴∠+∠=︒，GEH α∠=，180FGE α∴∠=︒-，2180FME α∴∠=︒-，902FME α∴∠=︒-．【点睛】此题考查了平行线的判定与性质，熟记平行线的判定与性质及作出合理的辅助线是解题的关键．23．（1）AB //CD ，证明见解析；（2）∠E 1+∠E 2+…∠E n =∠B +∠F 1+∠F 2+…∠F n -1+∠D ；（3）(n -1)•180°【分析】（1）过点E作EF//AB，利用平行线的性质则可得出∠B=∠BEF，再由已知及平行线的判定即可得出AB∥CD；（2）如图，过点E作EM∥AB，过点F作FN∥AB，过点G作GH∥AB，根据探究（1）的证明过程及方法，可推出∠E+∠G=∠B+∠F+∠D，则可由此得出规律，并得出∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D；（3）如图，过点M作EF∥AB，过点N作GH∥AB，则可由平行线的性质得出∠1+∠2+∠MNG =180°×2，依此即可得出此题结论．【详解】解：（1）过点E作EF//AB，∴∠B=∠BEF．∵∠BEF+∠FED=∠BED，∴∠B+∠FED=∠BED．∵∠B+∠D=∠E（已知），∴∠FED=∠D．∴CD//EF（内错角相等，两直线平行）．∴AB//CD．（2）过点E作EM∥AB，过点F作FN∥AB，过点G作GH∥AB，∵AB∥CD，∴AB∥EM∥FN∥GH∥CD，∴∠B=∠BEM，∠MEF=∠EFN，∠NFG=∠FGH，∠HGD=∠D，∴∠BEF+∠FGD=∠BEM+∠MEF+∠FGH+∠HGD=∠B+∠EFN+∠NFG+∠D=∠B+∠EFG+∠D，即∠E+∠G=∠B+∠F+∠D．由此可得：开口朝左的所有角度之和与开口朝右的所有角度之和相等，∴∠E1+∠E2+…∠En=∠B+∠F1+∠F2+…∠F n-1+∠D．故答案为：∠E1+∠E2+…∠E n=∠B+∠F1+∠F2+…∠F n-1+∠D．（3）如图，过点M作EF∥AB，过点N作GH∥AB，∴∠APM +∠PME =180°，∵EF ∥AB ，GH ∥AB ，∴EF ∥GH ，∴∠EMN +∠MNG =180°，∴∠1+∠2+∠MNG =180°×2，依次类推：∠1+∠2+…+∠n -1+∠n =(n -1)•180°．故答案为：(n -1)•180°．【点睛】本题考查了平行线的性质与判定，属于基础题，关键是过E 点作AB （或CD ）的平行线，把复杂的图形化归为基本图形．24．（1）20，20，//AB CD ；（2）180FMN GHF ∠+∠=︒；（3）1FPN Q∠∠的值不变，12FPN Q=∠∠ 【分析】（1）根据2(402)|20|0αβ-+-=，即可计算α和β的值，再根据内错角相等可证//AB CD ；（2）先根据内错角相等证//GH PN ，再根据同旁内角互补和等量代换得出180FMN GHF ∠+∠=︒；（3）作1PEM ∠的平分线交1M Q 的延长线于R ，先根据同位角相等证//ER FQ ，得1FQM R =∠∠，设PER REB x ==∠∠，11PM R RM B y ==∠∠，得出12EPM R ∠=∠，即可得12FPN Q=∠∠．【详解】解：（1）2(402)|20|0αβ-+-=，4020α∴-=，200β-=，20αβ∴==，20PFM MFN ∴∠=∠=︒，20EMF ∠=︒，EMF MFN ∴∠=∠，//AB CD ∴；故答案为：20、20，//AB CD ；（2）180FMN GHF ∠+∠=︒；理由：由（1）得//AB CD ，MNF PME ∴∠=∠，MGH MNF ∠=∠，PME MGH ∴∠=∠，//GH PN ∴，GHM FMN ∴∠=∠，180GHF GHM ∠+∠=︒，180FMN GHF ∴∠+∠=︒；（3）1FPN Q ∠∠的值不变，12FPN Q=∠∠；理由：如图3中，作1PEM ∠的平分线交1M Q 的延长线于R ，//AB CD ，1PEM PFN ∴∠=∠，112PER PEM ∠=∠，12PFQ PFN =∠∠， PER PFQ ∴∠=∠，//ER FQ ∴，1FQM R ∴∠=∠，设PER REB x ==∠∠，11PM R RM B y ==∠∠，则有：122y x R y x EPM =+∠⎧⎨=+∠⎩，可得12EPM R ∠=∠，112EPM FQM ∴∠=∠，∴112EPM FQM ∠=∠．【点睛】本题主要考查平行线的判定与性质，熟练掌握内错角相等证平行，平行线同旁内角互补等知识是解题的关键．25．（1）①PM ⊥MN ，理由见解析；②∠EPB 的度数为125°；（2）∠APM +∠QMN =90°或∠APM -∠QMN =90°．【分析】（1）①利用平行线的性质得到∠APM =∠PMQ ，再根据已知条件可得到PM ⊥MN ； ②过点N 作NH ∥CD ，利用角平分线的定义以及平行线的性质求得∠MNH =35°，即可求解；（2）分三种情况讨论，利用平行线的性质即可解决．【详解】解：（1）①PM⊥MN，理由见解析：∵AB//CD，∴∠APM=∠PMQ，∵∠APM+∠QMN=90°，∴∠PMQ +∠QMN=90°，∴PM⊥MN；②过点N作NH∥CD，∵AB//CD，∴AB// NH∥CD，∴∠QMN=∠MNH，∠EPA=∠ENH，∵PA平分∠EPM，∴∠EPA=∠MPA，∵∠APM+∠QMN=90°，∴∠EPA +∠MNH=90°，即∠ENH +∠MNH=90°，∴∠MNQ +∠MNH +∠MNH=90°，∵∠MNQ=20°，∴∠MNH=35°，∴∠EPA=∠ENH=∠MNQ +∠MNH=55°，∴∠EPB=180°-55°=125°，∴∠EPB的度数为125°；（2）当点M，N分别在射线QC，QF上时，如图：∵PM⊥MN，AB//CD，∴∠PMQ +∠QMN=90°，∠APM=∠PMQ，∴∠APM +∠QMN=90°；当点M，N分别在射线QC，线段PQ上时，如图：∵PM⊥MN，AB//CD，∴∠PMN=90°，∠APM=∠PMQ，∴∠PMQ -∠QMN=90°，∴∠APM -∠QMN=90°；当点M，N分别在射线QD，QF上时，如图：∵PM⊥MN，AB//CD，∴∠PMQ +∠QMN=90°，∠APM+∠PMQ=180°，∴∠APM+90°-∠QMN=180°，∴∠APM -∠QMN=90°；综上，∠APM +∠QMN=90°或∠APM -∠QMN=90°．【点睛】本题主要考查了平行线的判定与性质，熟练掌握两直线平行，内错角相等；两直线平行，同旁内角互补；两直线平行，同位角相等等知识是解题的关键．。

相交线与平行线培优练习附答案

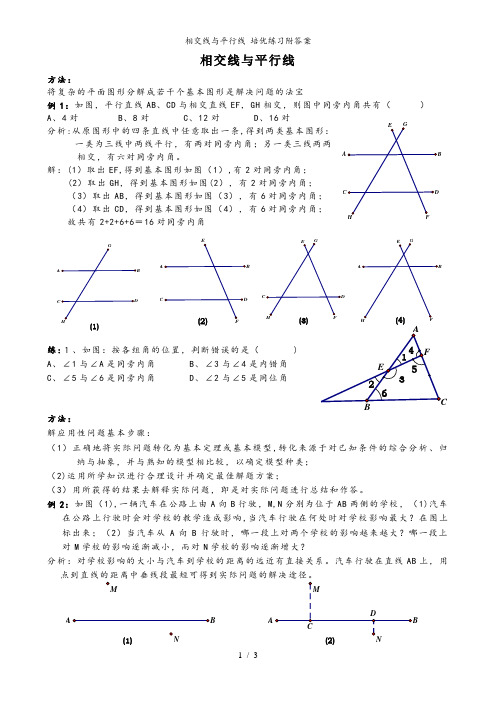
故共有 2+2+6+6＝16 对同旁内角
H
）
B D F
E G
EG
EG
A
B
A
B
A
B
C
D
C
D
C
D
H
(1)
(2)
F
H
(3)
F
H
(4)
F
A
练 :１、如图：按各组角的位置，判断错误的是（
)
A、∠1 与∠A 是同旁内角
B、∠3 与∠4 是内错角
C、∠5 与∠6 是同旁内角
D、∠2 与∠5 是同位角
EG
一类为三线中两线平行，有两对同旁内角；另一类三线两两
相交，有六对同旁内角。
A
解：(1）取出 EF,得到基本图形如图（1）,有 2 对同旁内角；

(2）取出 GH，得到基本图形如图(2），有 2 对同旁内角；（3）取出 AB，得到基本图形如图（3），有 6 对同旁内角； C
（4）取出 CD，得到基本图形如图（4），有 6 对同旁内角；
甲乙两同学从此题证明中发现，问题的实质在于 AA1 ∥ BA2 ，它与连接 A1 、 A2 两点之间
的折线段无关。因此，如图３ ,甲同学将 A1 、A3 之间的折线段增加到４条 A1B1 ，B1 A2 ，A2 B2 ，
例 2：如图（1),一辆汽车在公路上由 A 向 B 行驶，M,N 分别为位于 AB 两侧的学校，（1)汽车
在公路上行驶时会对学校的教学造成影响 ,当汽车行驶在何处时对学校影响最大？在图上标出来；（2）当汽车从 A 向 B 行驶时，哪一段上对两个学校的影响越来越大？哪一段上

(完整版)七年级下册数学相交线与平行线试卷及答案(人教版) (一)培优试题

一、选择题1．如图，//AB CD ，P 为平行线之间的一点，若AP CP ⊥，CP 平分∠ACD ，68ACD ∠=︒，则∠BAP 的度数为（）A ．56︒B ．58︒C ．66︒D ．68︒2．如图，直线//AB CD ，点E ，F 分别在直线．AB 和直线CD 上，点P 在两条平行线之间，AEP ∠和CFP ∠的角平分线交于点H ，已知78P ∠=︒，则H ∠的度数为（）A ．102︒B ．156︒C ．142︒D ．141︒3．如图所示，若AB ∥EF ，用含α、β、γ的式子表示x ，应为（）A ．αβγ++B ．βγα+-C ．180αγβ︒--+D ．180αβγ︒++- 4．如图，//,AD BC D ABC ∠=∠,点E 是边DC 上一点，连接AE 交BC 的延长线于点H ，点F 是边AB 上一点，使得FBE FEB ∠=∠，作FEH ∠的角平分线EG 交BH 于点G ，若100DEH ︒∠=，则BEG ∠的度数是（）A ．30︒B ．40︒C ．50︒D ．60︒5．如图，//AB CD ，PF CD ⊥于F ，40AEP ∠=︒，则EPF ∠的度数是（）A ．120︒B ．130︒C ．140︒D ．150︒6．如图，两个直角三角形重叠在一起，将ABC 沿AB 方向平移2cm 得到DEF ，CH ＝2cm ，EF ＝4cm ，下列结论：①BH //EF ；②AD ＝BE ；③DH ＝CH ；④∠C ＝∠BHD ；⑤阴影部分的面积为6cm 2．其中正确的是（）A ．①②③④⑤B ．②③④⑤C ．①②③⑤D ．①②④⑤ 7．如图，△ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，AB ＝5，P 为直线AB 上一动点，连接PC ，则线段PC 的最小值是（）A ．3B ．2.5C ．2.4D ．28．小明、小亮、小刚一起研究一道数学题，如图，已知EF AB ⊥，CD AB ⊥．小明说：“如果还知道CDG BFE ∠=∠，则能得到AGD ACB ∠=∠．”小亮说：“把小明的已知和结论倒过来，即由AGD ACB ∠=∠，可得到CDG BFE ∠=∠．” 小刚说：“连接FG ，如果//FG AB ，则能得到GFC ADG ∠=∠．”则说法正确的人数是（）A ．3人B ．2人C ．1人D ．0人9．如图，从①12∠=∠，②C D ∠=∠，③//DF AC 三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为（）A ．0B ．1C ．2D ．310．已知，如图，点D 是射线AB 上一动点，连接CD ，过点D 作//DE BC 交直线AC 于点E ，若84ABC ∠=︒，20CDE ∠=︒，则ADC ∠的度数为（）A ．104︒B ．76︒C ．104︒或76︒D ．104︒或64︒二、填空题11．如图，已知AB ∥CD ，点E ，F 分别在直线AB ，CD 上点P 在AB ，CD 之间且在EF 的左侧．若将射线EA 沿EP 折叠，射线FC 沿FP 折叠，折叠后的两条射线互相垂直，则∠EPF 的度数为 _____．12．如图，Rt △AOB 和Rt △COD 中，∠AOB ＝∠COD ＝90°，∠B ＝40°，∠C ＝60°，点D 在边OA 上，将图中的△COD 绕点O 按每秒10°的速度沿顺时针方向旋转一周，在旋转的过程中，在第________秒时，边CD 恰好与边AB 平行．13．如图①：MA 1∥NA 2，图②：MA11NA 3，图③：MA 1∥NA 4，图④：MA 1∥NA 5，……，则第n 个图中的∠A 1+∠A 2+∠A 3+…+∠A n+1______.（用含n 的代数式表示）14．如图，已知直线l 1∥l 2，∠A ＝125°，∠B ＝85°，且∠1比∠2大4°，那么∠1＝______．15．如图，将直角三角形ABC 沿AB 方向平移得到三角形4,1,4,3DEF AD EF CH ===，三角形ABC 周长为12．下列结论：①//BH EF ；②AD BE =；③ACB DFE ∠=∠；④四边形ACFE 的周长为14；⑤阴影部分的面积为203．其中正确的是_________．16．已知，//BC OA ，100B A ∠=∠=︒，点E ，F 在BC 上，OE 平分BOF ∠，且FOC AOC ∠=∠，下列结论正确得是：__________．①//OB AC ；②45EOC ∠=︒；③:1:3OCB OFB ∠∠=；④若OEB OCA ∠=∠，则60OCA ∠=︒.17．已知//AB CD ，ABE α∠=，FCD β∠=，CFE γ∠=，且BE EF ⊥，请直接写出α、β、γ的数量关系________．18．如图，已知40ABC ∠=︒，点D 为ABC ∠内部的一点，以D 为顶点，作EDF ∠，使得//DE BC ，//DF AB ，则EDF ∠的度数为___________．19．如图，直线//MN PQ ，MN 与直线AB ,AC 分别交于D ，E ，PQ 与直线AB ，AC 分别交于F ，G ，若75C ∠=︒，26BGF ∠=︒，则AEN ∠=_________度．20．把一张对边互相平行的纸条，折成如图所示，EF 是折痕，若32EFB ∠=︒，则下列结论：（1）'32C EF ∠=︒；（2）148AEC ∠=︒；（3）64BGE ∠=︒；（4）116BFD ∠=︒．正确的有________个．三、解答题21．已知，//AE BD ，A D ∠=∠．（1）如图1，求证：//AB CD ；（2）如图2，作BAE ∠的平分线交CD 于点F ，点G 为AB 上一点，连接FG ，若CFG ∠的平分线交线段AG 于点H ，连接AC ，若ACE BAC BGM ∠=∠+∠，过点H 作HM FH ⊥交FG 的延长线于点M ，且3518E AFH ∠-∠=︒，求EAF GMH ∠+∠的度数．22．已知直线AB//CD，点P、Q分别在AB、CD上，如图所示，射线PB按逆时针方向以每秒12°的速度旋转至PA便立即回转，并不断往返旋转；射线QC按逆时针方向每秒3°旋转至QD停止，此时射线PB也停止旋转．（1）若射线PB、QC同时开始旋转，当旋转时间10秒时，PB'与QC'的位置关系为；（2）若射线QC先转15秒，射线PB才开始转动，当射线PB旋转的时间为多少秒时，PB′//QC′．23．已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E＋∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．24．如图1，把一块含30°的直角三角板ABC 的BC 边放置于长方形直尺DEFG 的EF 边上．（1）根据图1填空：∠1＝ °，∠2＝ °；（2）现把三角板绕B 点逆时针旋转n °．①如图2，当n ＝25°，且点C 恰好落在DG 边上时，求∠1、∠2的度数；②当0°＜n ＜180°时，是否会存在三角板某一边所在的直线与直尺（有四条边）某一边所在的直线垂直？如果存在，请直接写出所有n 的值和对应的那两条垂线；如果不存在，请说明理由．25．如图，已知直线//AB 射线CD ，100CEB ∠=︒．P 是射线EB 上一动点，过点P 作PQ //EC 交射线CD 于点Q ，连接CP ．作PCF PCQ ∠=∠，交直线AB 于点F ，CG 平分ECF ∠．（1）若点P ，F ，G 都在点E 的右侧，求PCG ∠的度数；（2）若点P ，F ，G 都在点E 的右侧，30EGC ECG ∠-∠=︒，求CPQ ∠的度数；（3）在点P 的运动过程中，是否存在这样的情形，使:4:3EGC EFC ∠∠=？若存在，求出CPQ ∠的度数；若不存在，请说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】过P点作PM//AB交AC于点M，直接利用平行线的性质以及平行公理分别分析即可得出答案．【详解】解：如图，过P点作PM//AB交AC于点M．∵CP平分∠ACD，∠ACD＝68°，∠ACD＝34°．∴∠4＝12∵AB//CD，PM//AB，∴PM//CD，∴∠3＝∠4＝34°，∵AP⊥CP，∴∠APC＝90°，∴∠2＝∠APC－∠3＝56°，∵PM//AB，∴∠1＝∠2＝56°，即：∠BAP的度数为56°，故选：A．【点睛】此题主要考查了平行线的性质以及平行公理等知识，正确利用平行线的性质分析是解题关键．2．D解析：D【分析】过点P作PQ∥AB，过点H作HG∥AB，根据平行线的性质得到∠EPF=∠BEP+∠DFP=78°，结合角平分线的定义得到∠AEH+∠CFH，同理可得∠EHF=∠AEH+∠CFH．【详解】解：过点P作PQ∥AB，过点H作HG∥AB，AB CD，//则PQ∥CD，HG∥CD，∴∠BEP=∠QPE，∠DFP=∠QPF，∵∠EPF=∠QPE+∠QPF=78°，∴∠BEP+∠DFP=78°，∴∠AEP+∠CFP=360°-78°=282°，∵EH平分∠AEP，HF平分∠CFP，∴∠AEH+∠CFH=282°÷2=141°，同理可得：∠EHF=∠AEH+∠CFH=141°，故选D．【点睛】本题主要考查了平行线的性质，解决问题的关键是作平行线构造内错角，利用两直线平行，内错角相等得出结论．3．C解析：C【分析】过C作CD∥AB，过M作MN∥EF，推出AB∥CD∥MN∥EF，根据平行线的性质得出α+∠BCD=180°，∠DCM=∠CMN，∠NMF=γ，求出∠BCD=180°-α，∠DCM=∠CMN=β-γ，即可得出答案．【详解】过C作CD∥AB，过M作MN∥EF，∵AB∥EF，∴AB∥CD∥MN∥EF，∴α+∠BCD=180°，∠DCM=∠CMN，∠NMF=γ，∴∠BCD=180°-α，∠DCM=∠CMN=β-γ，∴x=∠BCD+∠DCM=180αγβ︒--+，故选：C．【点睛】本题考查了平行线的性质的应用，主要考查了学生的推理能力．4．B解析：B【分析】AD∥BC，∠D=∠ABC，则AB∥CD，则∠AEF=180°-∠AED-∠BEG=180°-2β，在△AEF中，100°+2α+180°-2β=180°，故β-α=40°，即可求解．【详解】解：设FBE=∠FEB=α，则∠AFE=2α，∠FEH的角平分线为EG，设∠GEH=∠GEF=β，AD∥BC，∴∠ABC+∠BAD=180°，而∠D=∠ABC，∴∠D+∠BAD=180°，∴AB∥CD，∠DEH=100°，则∠CEH=∠FAE=80°，∠AEF=180°-∠FEG-∠BEG=180°-2β，在△AEF中，在△AEF中，80°+2α+180-2β=180°故β-α=40°，而∠BEG=∠FEG-∠FEB=β-α=40°，故选：B．【点睛】此题考查平行线的性质，解题关键是落脚于△AEF内角和为180°，即100°+2α+180°-2β=180°，题目难度较大．5．B解析：B【分析】过点P 作MN ∥AB ，结合垂直的定义和平行线的性质求∠EPF 的度数．【详解】解：如图，过点P 作MN ∥AB ，∵∠AEP=40°，∴∠EPN=∠AEP=40°∵AB ∥CD,PF ⊥CD 于F ，∴PF ⊥MN ，∴∠NPF=90∴∠EPF=∠EPN+∠NPF=40°+90°=130°故答案为B【点睛】本题考查了平行线的判定定理和性质，作出辅助线构造平行线是解答本题的关键． 6．D解析：D【分析】根据平移的性质直接可判断①②；先根据线段的和差可得2cm BH =，再根据直角三角形的斜边大于直角边即可判断③；根据平行线的性质可判断④；根据阴影部分的面积等于直角梯形BEFH 的面积即可判断⑤．【详解】解：由题意得：90ABC ∠=︒，由平移的性质得：,4cm,2cm AB DE BC EF AD BE =====，//,//,90BH EF AC DF E ABC ∠=∠=︒，则结论①②正确；2cm CH =，2cm BH BC CH CH ∴=-==，在Rt BDH 中，斜边DH 大于直角边BH ，DH CH ∴>，即结论③错误；//AC DF ，C BHD ∴∠=∠，即结论④正确；由平移的性质得：ABC 的面积等于DEF 的面积，则阴影部分的面积为ABC BDH DEF BDH SS S S -=-，BEFH S =直角梯形，2BH EF BE +=⋅， 2422+=⨯， 26(cm )=，即结论⑤正确；综上，结论正确的是①②④⑤，故选：D ．【点睛】本题考查了平移的性质、平行线的性质等知识点，熟练掌握平移的性质是解题关键． 7．C解析：C【分析】当PC ⊥AB 时，PC 的值最小，利用面积法求解即可．【详解】解：在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，AB ＝5，∵当PC ⊥AB 时，PC 的值最小，此时：△ABC 的面积＝12•AB •PC ＝12•AC •BC ，∴5PC ＝3×4，∴PC ＝2.4，故选：C ．【点睛】本题主要考查了垂线段最短和三角形的面积公式，解题的关键是学会利用面积法求高． 8．B解析：B【分析】由EF ⊥AB ，CD ⊥AB ，知CD ∥EF ，然后根据平行线的性质与判定即可得出答案.【详解】解:∵EF ⊥AB ，CD ⊥AB ，∴CD ∥EF ，∴∠BCD =∠BFE ，若∠CDG =∠BFE ，∴∠BCD =∠CDG ，∴DG ∥BC ，∴∠AGD =∠ACB ，∴小明的说法正确；若∠AGD =∠ACB ，∴DG ∥BC ，∴∠BCD =∠CDG∴∠BCD=∠BFE∴小亮的说法正确；连接GF，如果FG//AB，∠GFC=∠ABC若∠GFC=∠ADG则∠ABC=∠ADG则DG∥BC但是DG∥BC不一定成立∴小刚的说法错误；综上知：正确的说法有两个．故选B.【点睛】本题主要考查的是平行线的判定与性质，熟知平行线的判定定理是解答此题的关键. 9．D解析：D【分析】分别任选其中两个条件作为已知，然后结合平行线的判定与性质，证明剩余一个条件是否成立即可．【详解】解：如图所示：（1）当①∠1=∠2，则∠3=∠2，故DB∥EC，则∠D=∠4；当②∠C=∠D，故∠4=∠C，则DF∥AC，可得：∠A=∠F，即①②可证得③；（2）当①∠1=∠2，则∠3=∠2，故DB∥EC，则∠D=∠4，当③∠A=∠F，故DF∥AC，则∠4=∠C，故可得：∠C=∠D，即①③可证得②；（3）当③∠A=∠F，故DF∥AC，则∠4=∠C，当②∠C=∠D，则∠4=∠D，故DB∥EC，则∠2=∠3，可得：∠1=∠2，即②③可证得①.故正确的有3个．故选：D．【点睛】本题主要考查了平行线的判定和性质，正确掌握并熟练运用平行线的判定与性质是解题关键．10．D解析：D【分析】分点D在线段AB上及点D在线段AB的延长线上两种情况考虑：当点D在线段AB上时，由DE∥BC可得出∠ADE的度数，结合∠ADC=∠ADE+∠CDE可求出∠ADC的度数；当点D 在线段AB的延长线上时，由DE∥BC可得出∠ADE的度数，结合∠ADC=∠ADE-∠CDE可求出∠ADC的度数．综上，此题得解．【详解】解：当点D在线段AB上时，如图1所示．∵DE∥BC，∴∠ADE=∠ABC=84°，∴∠ADC=∠ADE+∠CDE=84°+20°=104°；当点D在线段AB的延长线上时，如图2所示．∵DE∥BC，∴∠ADE=∠ABC=84°，∴∠ADC=∠ADE-∠CDE=84°-20°=64°．综上所述：∠ADC=104°或64°．故选：D．【点睛】本题考查了平行线的性质，分点D在线段AB上及点D在线段AB的延长线上两种情况，求出∠ADC的度数是解题的关键．二、填空题11．45°或135°【分析】根据题意画出图形，然后利用平行线的性质得出∠EMF与∠AEM和∠CFM的关系，然后可得答案．【详解】解：如图1，过作，，，，，，，同理可得，由折叠可解析：45°或135°【分析】根据题意画出图形，然后利用平行线的性质得出∠EMF与∠AEM和∠CFM的关系，然后可得答案．【详解】解：如图1，MN AB，过M作//AB CD，//，AB CD NM////AEM EMN ∴∠=∠，NMF MFC ∠=∠，90EMF ∠=︒，90AEM CFM ∴∠+∠=︒，同理可得P AEP CFP ∠=∠+∠，由折叠可得：12AEP PEM AEM ∠=∠=∠，12PFC PFM CFM ∠=∠=∠， 1()452P AEM CFM ∴∠=∠+∠=︒，如图2，过M 作//MN AB ，//AB CD ， ////AB CD NM ∴，180AEM EMN ∴∠+∠=︒，180NMF MFC ∠+∠=︒，360AEM EMF CFM ∴∠+∠+∠=︒，90EMF ∠=︒，36090270AEM CFM ∴∠+∠=︒-︒=︒，由折叠可得：12AEP PEM AEM ∠=∠=∠，12PFC PFM CFM ∠=∠=∠， 12701352P ∴∠=︒⨯=︒，综上所述：EPF ∠的度数为45︒或135︒，故答案为：45°或135°．【点睛】本题主要考查了平行线的性质，关键是正确画出图形，分两种情况分别计算出∠EPF 的度数．12．10或28【分析】作出图形，分①两三角形在点O 的同侧时，设CD 与OB 相交于点E ，根据两直线平行，同位角相等可得∠CEO=∠B ，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE ，然解析：10或28【分析】作出图形，分①两三角形在点O 的同侧时，设CD 与OB 相交于点E ，根据两直线平行，同位角相等可得∠CEO=∠B，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE，然后求出旋转角∠AOD，再根据每秒旋转10°列式计算即可得解；②两三角形在点O的异侧时，延长BO与CD相交于点E，根据两直线平行，内错角相等可得∠CEO=∠B，再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠DOE，然后求出旋转角度数，再根据每秒旋转10°列式计算即可得解．【详解】解：①两三角形在点O的同侧时，如图1，设CD与OB相交于点E，∵AB∥CD，∴∠CEO=∠B=40°，∵∠C=60°，∠COD=90°，∴∠D=90°-60°=30°，∴∠DOE=∠CEO-∠D=40°-30°=10°，∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°，∵每秒旋转10°，∴时间为100°÷10°=10秒；②两三角形在点O的异侧时，如图2，延长BO与CD相交于点E，∵AB∥CD，∴∠CEO=∠B=40°，∵∠C=60°，∠COD=90°，∴∠D=90°-60°=30°，∴∠DOE=∠CEO-∠D=40°-30°=10°，∴旋转角为270°+10°=280°，∵每秒旋转10°，∴时间为280°÷10°=28秒；综上所述，在第10或28秒时，边CD恰好与边AB平行．故答案为10或28．【点睛】本题考查了平行线的判定，平行线的性质，旋转变换的性质，难点在于分情况讨论，作出图形更形象直观．13．【解析】分析：分别求出图①、图②、图③中，这些角的和，探究规律后，理由规律解决问题即可．详解：如图①中,∠A1+∠A2=180∘=1×180∘，如图②中,∠A1+∠A2+∠A3=360∘=2解析：n180︒【解析】分析：分别求出图①、图②、图③中，这些角的和，探究规律后，理由规律解决问题即可．详解：如图①中,∠A1+∠A2=180∘=1×180∘，如图②中,∠A1+∠A2+∠A3=360∘=2×180∘，如图③中,∠A1+∠A2+∠A3+∠A4=540∘=3×180∘，…，第n个图, ∠A1+∠A2+∠A3+…+∠A n+1学会从=n180︒，故答案为180n︒.点睛：平行线的性质.14．【分析】延长AB，交两平行线与C、D，根据平行线的性质和领补角的性质计算即可；【详解】延长AB，交两平行线与C、D，∵直线l1∥l2，∠A＝125°，∠B＝85°，∴，，，∴，∴，解析：17︒【分析】延长AB，交两平行线与C、D，根据平行线的性质和领补角的性质计算即可；【详解】延长AB，交两平行线与C、D，∵直线l 1∥l 2，∠A ＝125°，∠B ＝85°，∴4285∠+∠=︒，13125∠+∠=︒，34180∠+∠=︒，∴852*******︒-∠+︒-∠=︒，∴1230∠+∠=︒，又∵∠1比∠2大4°，∴2=14∠∠-︒，∴2134∠=︒，∴117∠=︒；故答案是17︒．【点睛】本题主要考查了平行线的性质应用，准确计算是解题的关键．15．①②③④【分析】①由平移变换可知，因为点B 、H 、C 三点在同一条直线上可得出结论； ②由平移变换可知，可得到，，即可得出结论；③因为平移前后角的度数是不变的，即可得出结论；④由平移变换可知四边解析：①②③④【分析】①由平移变换可知//BC EF ，因为点B 、H 、C 三点在同一条直线上可得出结论； ②由平移变换可知DE AB =，可得到AB AD DB =+，DE BE DB =+，即可得出结论； ③因为平移前后角的度数是不变的，即可得出结论；④由平移变换可知四边形ADFC 是平行四边形，四边形ACFE 的周长为：AD CF DE EF AC ++++，求解即可；⑤S 阴影=ADFC HCF SS -，根据条件求解即可．【详解】①DEF 是由ABC 平移得来的，//,BC EF ∴ 又点B 、H 、C 三点在同一条直线上，∴//BH EF ，∴①正确；②DEF 是由ABC 平移得来的，,,,,DE AB AB AD DB DE BE DB AD BE ∴==+=+∴=∴②正确；③DEF 是由ABC 平移得来的，∴平移前后角的度数是不变的，∴ACB DFE ∠=∠，∴③正确； ④三角形ABC 周长为12，12AB BC AC ∴++=， DEF 是由ABC 平移得来的，∴边的长度不变且//AC DF ，12,12,DE EF DF DE EF AC ∴++=∴++=∴四边形ADFC 是平行四边形，1,AD CF ∴==四边形ACFE 的周长为：AD CF DE EF AC ++++，∴四边形ACFE 的周长为：2+12=14，∴④正确；⑤由④得四边形ADFC 是平行四边形，1CF AD ∴==， S 阴影=ADFC HCF S S -，,,,BC AE BC AD BC CF ⊥∴⊥∴⊥S ∴阴影=12AD EF HC CF -141412324310,3=⨯-⨯⨯=-= ∴⑤错误．故答案为：①②③④．【点睛】本题主要考查了图形的平移变换，平行线的公理，平行四边形的性质，有一定综合性，熟练掌握和运用这些性质是解题的关键．16．①④【分析】①由BC ∥OA ，∠B=∠A=100°，∠AOB=∠ACB=180°-100°=80°，得到∠A+∠AOB=180°，得出OB ∥AC ．②OE 平分∠BOF ，得出∠FOE=∠BOE=∠BO 解析：①④【分析】①由BC ∥OA ，∠B =∠A =100°，∠AOB =∠ACB =180°-100°=80°，得到∠A +∠AOB =180°，得出OB ∥AC ．②OE 平分∠BOF ，得出∠FOE =∠BOE =12∠BOF ，∠FOC =∠AOC =12∠AOF ，从而计算出∠EOC =∠FOE +∠FOC =40°．③由∠OCB =∠AOC ，∠OFB =∠AOF =2∠AOC ，得出∠OCB ：∠OFB =1：2．④由∠OEB =∠OCA =∠AOE =∠BOC ，得到∠AOE -∠COE =∠BOC -∠COE ，∠BOE =∠AOC ，再得到∠BOE =∠FOE =∠FOC =∠AOC =14∠AOB =20°，从而计算出∠OCA =∠BOC =3∠BOE =60°．【详解】解：∵BC ∥OA ，∠B =∠A =100°，∴∠AOB =∠ACB =180°-100°=80°，∴∠A +∠AOB =180°，∴OB ∥AC ．故①正确；∵OE 平分∠BOF ，∴∠FOE =∠BOE =12∠BOF ，∴∠FOC =∠AOC =12∠AOF ，∴∠EOC =∠FOE +∠FOC =12（∠BOF +∠AOF ）=12×80°=40°．故②错误；∵∠OCB =∠AOC ，∠OFB =∠AOF =2∠AOC ，∴∠OCB ：∠OFB =1：2．故③错误；∵∠OEB =∠OCA =∠AOE =∠BOC ，∴∠AOE -∠COE =∠BOC -∠COE ，∴∠BOE =∠AOC ，∴∠BOE =∠FOE =∠FOC =∠AOC =14∠AOB =20°， ∴∠OCA =∠BOC =3∠BOE =60°．故④正确．故答案为：①④．【点睛】本题考查了平行线的性质及判定，以及角的计算，熟练掌握平行线的判定与性质是解本题的关键．17．（上式变式都正确）【分析】过点E 作，过点F 作，可得出（根据平行于同一直线的两条直线互相平行），根据平行线的性质，可得出各个角之间的关系，利用等量代换、等式的性质即可得出答案．【详解】解：如图解析：90γαβ+=︒+（上式变式都正确）【分析】过点E 作//EM AB ，过点F 作//FN AB ，可得出//////AB EM FN CD （根据平行于同一直线的两条直线互相平行），根据平行线的性质，可得出各个角之间的关系，利用等量代换、等式的性质即可得出答案．【详解】解：如图所示，过点E 作//EM AB ，过点F 作//FN AB ，∵//AB CD ，∴//////AB EM FN CD ，∵//AB EM ，∴ABE BEM ∠=∠，∵//EM FN ，∴MEF EFN ∠=∠，∵//NF CD ，∴NFC FCD ∠=∠，∴ABE EFN NFC BEM MEF FCD ∠+∠+∠=∠+∠+∠，∴ABE EFC BEF FCD ∠+∠=∠+∠，∵ABE α∠=，FCD β∠=，CFE γ∠=，且BE EF ⊥，∴90αγβ+=︒+，故答案为：90αγβ+=︒+．【点睛】题目主要考察平行线的性质及等式的性质，作出相应的辅助线、找出相应的角的关系是解题关键．18．或【分析】由题意可分两种情况分别画出图形，然后根据平行线的性质进行求解即可．【详解】解：由题意得：①如图，∵，，∴，∵，∴；②如图，∵，，∴，∵，∴，∴；综上所述解析：40︒或140︒【分析】由题意可分两种情况分别画出图形，然后根据平行线的性质进行求解即可．【详解】解：由题意得：①如图，∵//DF AB ，40ABC ∠=︒，∴40DFC ABC ∠=∠=︒，∵//DE BC ，∴40DFC EDF ∠=∠=︒；②如图，∵//DF AB ，40ABC ∠=︒，∴40DFC ABC ∠=∠=︒，∵//DE BC ，∴180DFC EDF ∠+∠=︒，∴140EDF ∠=︒；综上所述：EDF ∠的度数为40︒或140︒；故答案为40︒或140︒．【点睛】本题主要考查平行线的性质，熟练掌握平行线的性质是解题的关键，注意分类讨论． 19．131【分析】过点C 作CH ∥MN ，根据平行线的性质求出∠NEC 即可．【详解】解：过点C 作CH ∥MN ，∵，∴CH ∥PQ ，∴，∵，∴，∵CH ∥MN ，∴,∴故答案为：131．解析：131【分析】过点C 作CH ∥MN ，根据平行线的性质求出∠NEC 即可．【详解】解：过点C 作CH ∥MN ，∵//MN PQ ，∴CH ∥PQ ，∴26HCB BGF ∠=∠=︒，∵75ACB ∠=︒，∴49ACH ∠=︒，∵CH ∥MN ，∴49CEN ACH ∠=∠=︒,∴131180CEN AEN ∠︒∠==︒-故答案为：131．【点睛】本题考查了平行线的性质与判定，解题关键是恰当作平行线，根据平行线的性质进行推理计算．20．3【分析】（1）根据平行线的性质即可得到答案；（2）根据平行线的性质得到：∠AEF=180°-∠EFB=180°-32°=148°，又因为∠AEF=∠AEC+∠GEF ，可得∠AEC ＜148°，解析：3【分析】（1）根据平行线的性质即可得到答案；（2）根据平行线的性质得到：∠AEF =180°-∠EFB =180°-32°=148°，又因为∠AEF =∠AEC +∠GEF ，可得∠AEC ＜148°，即可判断是否正确；（3）根据翻转的性质可得∠GEF =∠C ′EF ，又因为∠C′EG =64°，根据平行线性质即可得到∠BGE =∠C′EG =64°，即可判断是否正确；（4）根据对顶角的性质得：∠CGF =∠BGE =64°，根据平行线得性质即可得：∠BFD =180°-∠CGF 即可得到结果．【详解】解：（1）∵//AE BG ，∠EFB=32°，∴∠C ′EF =∠EFB =32°，故本小题正确；（2）∵AE ∥BG ，∠EFB =32°，∴∠AEF =180°-∠EFB =180°-32°=148°，∵∠AEF =∠AEC +∠GEF ，∴∠AEC ＜148°，故本小题错误；（3）∵∠C′EF =32°，∴∠GEF =∠C ′EF =32°，∴∠C′EG =∠C′EF +∠GEF =32°+32°=64°，∵AC′∥BD′，∴∠BGE =∠C′EG =64°，故本小题正确；（4）∵∠BGE =64°，∴∠CGF =∠BGE =64°，∵//DF CG ，∴∠BFD =180°-∠CGF =180°-64°=116°，故本小题正确．故正确的为：（1）（3）（4）共3个，故答案为：3．【点睛】本题考查的是平行线的性质及翻折变换的性质，熟知图形翻折不变性的性质是解答此题的关键．三、解答题21．（1）见解析；（2）72︒【分析】（1）根据平行线的性质得出180A B ∠+∠=︒，再根据等量代换可得180B D ∠+∠=︒，最后根据平行线的判定即可得证；（2）过点E 作//EP CD ，延长DC 至Q ，过点M 作//MN AB ，根据平行线的性质及等量代换可得出ECQ BGM DFG ∠=∠=∠，再根据平角的含义得出ECF CFG ∠=∠，然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB ∠=∠∠=∠；设,FAB CFH αβ∠=∠=，根据角的和差可得出2AEC AFH ∠=∠，结合已知条件35180AEC AFH ∠-∠=︒可求得18AFH ∠=︒，最后根据垂线的含义及平行线的性质，即可得出答案．【详解】（1）证明：//AE BD180A B ∴∠+∠=︒A D ∠=∠180B D ∴∠+∠=︒//AB CD ∴；（2）过点E 作//EP CD ，延长DC 至Q ，过点M 作//MN AB//AB CDQCA CAB ∴∠=∠，BGM DFG ∠=∠，CFH BHF ∠=∠，CFA FAG ∠=ACE BAC BGM ∠=∠+∠ECQ QCA BAC BGM ∴∠+∠=∠+∠ECQ BGM DFG ∴∠=∠=∠180,180ECQ ECD DFG CFG ∠+=︒∠+=︒ECF CFG ∴∠=∠//AB CD//AB EP ∴,PEA EAB PEC ECF ∴∠=∠∠=∠AEC PEC PEA ∠=∠-∠AEC ECF EAB ∴∠=∠-∠ECF AEC EAB ∴∠=∠+∠AF 平分BAE ∠12EAF FAB EAB ∴∠=∠=∠ FH 平分CFG ∠12CFH HFG CFG ∴∠=∠=∠ //CD AB,BHF CFH CFA FAB ∴∠=∠∠=∠设,FAB CFH αβ∠=∠=AFH CFH CFA CFH FAB ∠=∠-∠=∠-∠AFH βα∴∠=-，BHF CFH β∠=∠=222ECF AFH AEC EAB AFH AEC β∴∠+∠=∠+∠+∠=∠+22ECF AFH E BHF ∴∠+∠=∠+∠2AEC AFH ∴∠=∠35180AEC AFH ∠-∠=︒18AFH ∴∠=︒FH HM ⊥90FHM ∴∠=︒90GHM β∴∠=︒-180CFM NMF ∠+∠=︒90HMB HMN β∴∠=∠=︒-EAF FAB ∠=∠18EAF CFA CFH AFH β∴∠=∠=∠-∠=-︒189072EAF GMH ββ∴∠+∠=-︒+︒-=︒72EAF GMH ∴∠+∠=︒．【点睛】本题考查了平行线的判定及性质，角平分线的定义，能灵活根据平行线的性质和判定进行推理是解此题的关键．22．（1）PB ′⊥QC ′；（2）当射线PB 旋转的时间为5秒或25秒或45秒时，PB ′∥QC ′【分析】（1）求出旋转10秒时，∠BPB ′和∠CQC ′的度数，设PB ′与QC ′交于O ，过O 作OE ∥AB ，根据平行线的性质求得∠POE 和∠QOE 的度数，进而得结论；（2）分三种情况：①当0＜t ≤15时，②当15＜t ≤30时，③当30＜t ＜45时，根据平行线的性质，得出角的关系，列出t 的方程便可求得旋转时间．【详解】解：（1）如图1，当旋转时间30秒时，由已知得∠BPB ′＝10°×12＝120°，∠CQC ′＝3°×10=30°，过O 作OE ∥AB ，∵AB∥CD，∴AB∥OE∥CD，∴∠POE＝180°﹣∠BPB′＝60°，∠QOE＝∠CQC′＝30°，∴∠POQ＝90°，∴PB′⊥QC′，故答案为：PB′⊥QC′；（2）①当0＜t≤15时，如图，则∠BPB′＝12t°，∠CQC′＝45°+3t°，∵AB∥CD，PB′∥QC′，∴∠BPB′＝∠PEC＝∠CQC′，即12t＝45+3t，解得，t＝5；②当15＜t≤30时，如图，则∠APB′＝12t﹣180°，∠CQC'＝3t+45°，∵AB∥CD，PB′∥QC′，∴∠BPB′＝∠BEQ＝∠CQC′，即12t﹣180＝45+3t，解得，t＝25；③当30＜t≤45时，如图，则∠BPB′＝12t﹣360°，∠CQC′＝3t+45°，∵AB∥CD，PB′∥QC′，∴∠BPB′＝∠BEQ＝∠CQC′，即12t﹣360＝45+3t，解得，t＝45；综上，当射线PB旋转的时间为5秒或25秒或45秒时，PB′∥QC′．【点睛】本题主要考查了平行线的性质，第（1）题关键是作平行线，第（2）题关键是分情况讨论，运用方程思想解决几何问题．23．（1）∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND；（2）120°；（3）不变，30°【分析】（1）过E作EH∥AB，易得EH∥AB∥CD，根据平行线的性质可求解；过F作FH∥AB，易得FH∥AB∥CD，根据平行线的性质可求解；（2）根据（1）的结论及角平分线的定义可得2（∠BME+∠END）+∠BMF-∠FND=180°，可求解∠BMF=60°，进而可求解；∠BME，进而可求解．（3）根据平行线的性质及角平分线的定义可推知∠FEQ=12【详解】解：（1）过E作EH∥AB，如图1，∴∠BME＝∠MEH，∵AB∥CD，∴HE∥CD，∴∠END＝∠HEN，∴∠MEN＝∠MEH＋∠HEN＝∠BME＋∠END，即∠BME＝∠MEN﹣∠END．如图2，过F作FH∥AB，∴∠BMF＝∠MFK，∵AB∥CD，∴FH∥CD，∴∠FND＝∠KFN，∴∠MFN＝∠MFK﹣∠KFN＝∠BMF﹣∠FND，即：∠BMF＝∠MFN＋∠FND．故答案为∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND．（2）由（1）得∠BME＝∠MEN﹣∠END；∠BMF＝∠MFN＋∠FND．∵NE平分∠FND，MB平分∠FME，∴∠FME＝∠BME＋∠BMF，∠FND＝∠FNE＋∠END，∵2∠MEN＋∠MFN＝180°，∴2（∠BME＋∠END）＋∠BMF﹣∠FND＝180°，∴2∠BME＋2∠END＋∠BMF﹣∠FND＝180°，即2∠BMF＋∠FND＋∠BMF﹣∠FND＝180°，解得∠BMF＝60°，∴∠FME＝2∠BMF＝120°；（3）∠FEQ的大小没发生变化，∠FEQ＝30°．由（1）知：∠MEN＝∠BME＋∠END，∵EF平分∠MEN，NP平分∠END，∴∠FEN＝12∠MEN＝12（∠BME＋∠END），∠ENP＝12∠END，∵EQ∥NP，∴∠NEQ＝∠ENP，∴∠FEQ＝∠FEN﹣∠NEQ＝12（∠BME＋∠END）﹣12∠END＝12∠BME，∵∠BME＝60°，∴∠FEQ＝12×60°＝30°．【点睛】本题主要考查平行线的性质及角平分线的定义，作平行线的辅助线是解题的关键．24．（1）120，90；（2）①∠1=120°-n°，∠2=90°+n°；②见解析【分析】（1）根据邻补角的定义和平行线的性质解答；（2）①根据邻补角的定义求出∠ABE，再根据两直线平行，同位角相等可得∠1=∠ABE，根据两直线平行，同旁内角互补求出∠BCG，然后根据周角等于360°计算即可得到∠2；②结合图形，分A B、B C、AC三条边与直尺垂直讨论求解．【详解】解：（1）∠1=180°-60°=120°，∠2=90°；故答案为：120，90；（2）①如图2，∵∠ABC=60°，∴∠ABE=180°-60°-n°=120°-n°，∵DG∥EF，∴∠1=∠ABE=120°-n°，∠BCG=180°-∠CBF=180°-n°，∵∠ACB+∠BCG+∠2=360°，∴∠2=360°-∠ACB-∠BCG=360°-90°-（180°-n°）=90°+n°；②当n=30°时，∵∠ABC=60°，∴∠ABF=30°+60°=90°，AB⊥DG（EF）；当n=90°时，∠C=∠CBF=90°，∴BC⊥DG（EF），AC⊥DE（GF）；当n=120°时，∴AB⊥DE（GF）．【点睛】本题考查了平行线角的计算，垂线的定义，主要利用了平行线的性质，直角三角形的性质，读懂题目信息并准确识图是解题的关键．25．（1）40°；（2）65°；（3）存在，56°或20°【分析】（1）依据平行线的性质以及角平分线的定义，即可得到∠PCG的度数；（2）依据平行线的性质以及角平分线的定义，即可得到∠ECG=∠GCF=25°，再根据PQ∥CE，即可得出∠CPQ=∠ECP=65°；（3）设∠EGC=4x，∠EFC=3x，则∠GCF=4x-3x=x，分两种情况讨论：①当点G、F在点E 的右侧时，②当点G、F在点E的左侧时，依据等量关系列方程求解即可．【详解】解：（1）∵∠CEB=100°，AB∥CD，∴∠ECQ=80°，∵∠PCF=∠PCQ，CG平分∠ECF，∴∠PCG＝∠PCF+∠FCG＝12∠QCF+12∠FCE=12∠ECQ=40°；（2）∵AB∥CD∴∠QCG=∠EGC，∠QCG+∠ECG=∠ECQ=80°，∴∠EGC+∠ECG=80°，又∵∠EGC-∠ECG=30°，∴∠EGC=55°，∠ECG=25°，∴∠ECG=∠GCF=25°，∠PCF=∠PCQ=12（80°-50°）=15°，∵PQ∥CE，∴∠CPQ=∠ECP=65°；（3）设∠EGC=4x，∠EFC=3x，则∠GCF=∠FCD=4x-3x=x，①当点G、F在点E的右侧时，则∠ECG=x，∠PCF=∠PCD=32 x，∵∠ECD=80°，∴x+x+32x+32x=80°，解得x=16°，∴∠CPQ=∠ECP=x+x+32x=56°；②当点G、F在点E的左侧时，则∠ECG=∠GCF=x，∵∠CGF=180°-4x，∠GCQ=80°+x，∴180°-4x=80°+x，解得x=20°，∴∠FCQ=∠ECF+∠ECQ=40°+80°=120°，∴∠PCQ＝12∠FCQ＝60°，∴∠CPQ=∠ECP=80°-60°=20°．【点睛】本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补；两直线平行，内错角相等．。

初一数学培优卷-相交线与平行线

1O F E D C B A O D C B A 60︒30︒34l 3l 2l 112D C B A DC BA ODC BAG H K F ED C B Ad ecb a 3412E D C A FE D CB A 34D C B A 21初一数学培优卷－相交线与平行线重点、难点、疑点补充：1.如图1所示,三条直线AB,CD,EF 相交于一点O,则∠AOE+∠DOB+∠COF 等于( • )A.150°B.180°C.210°D.120°2.如图2所示,直线AB 和CD 相交于点O,若∠AOD 与∠BOC 的和为236°,则∠AOC•的度数为( )A.62°B.118°C.72°D.59°（1）（2）（3） 3.如图3所示,直线L 1,L 2,L 3相交于一点,则下列答案中,全对的一组是( ) A.∠1=90°,∠2=30°,∠3=∠4=60° B.∠1=∠3=90°,∠2=∠4=30C.∠1=∠3=90°,∠2=∠4=60°;D.∠1=∠3=90°,∠2=60°,∠4=30° 4.下列说法正确的有( ) ①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角; ④若两个角不是对顶角,则这两个角不相等. A.1个 B.2个 C.3个 D.4个5.若4条不同的直线相交于一点,则图中共有几对对顶角?若n 条不同的直线相交于一点呢?6.如图1所示,下列说法不正确的是( ) A.点B 到AC 的垂线段是线段AB; B.点C 到AB 的垂线段是线段AC C.线段AD 是点D 到BC 的垂线段; D.线段BD 是点B 到AD 的垂线段(1)7.如图1,能表示点到直线(线段)的距离的线段有( ) A.2条 B.3条 C.4条 D.5条 8.下列说法正确的有( )①平面内,过直线上一点有且只有一条直线垂直于已知直线; ②平面内，过直线外一点有且只有一条直线垂直于已知直线; ③平面内,过一点可以任意画一条直线垂直于已知直线; ④平面内,有且只有一条直线垂直于已知直线. A.1个 B.2个 C.3个 D.4个9.如右图所示,AD ⊥BD,BC ⊥CD,AB=acm,BC=bcm,则BD 的范围是( ) A.大于acm B.小于bcmC.大于acm 或小于bcmD.大于bcm 且小于acm 10.到直线L 的距离等于2cm 的点有( )A.0个B.1个;C.无数个D.无法确定11.点P 为直线m 外一点,点A,B,C 为直线m 上三点,PA=4cm,PB=5cm,PC=2cm,则点P 到直线m 的距离为( )A.4cmB.2cm;C.小于2cmD.不大于2cm 12.O 为直线AB 上一点,∠AOC=13∠BOC,OC 是∠AOD 的平分线. (1)求∠COD 的度数;(2)判断OD 与AB 的位置关系,说明理由.13.在同一平面内,两条不重合直线的位置关系可能是( ) A.平行或相交 B.垂直或相交; C.垂直或平行 D.平行、垂直或相交 14.下列说法正确的是( )A.经过一点有一条直线与已知直线平行B.经过一点有无数条直线与已知直线平行C.经过一点有且只有一条直线与已知直线平行D.经过直线外一点有且只有一条直线与已知直线平行15.在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的个数为( )A.0个B.1个C.2个D.3个 16.下列说法正确的有( )①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种; ③若线段AB 与CD 没有交点,则AB ∥CD; ④若a ∥b,b ∥c,则a 与c 不相交.A.1个B.2个C.3个D.4个 17.过一点画已知直线的平行线,则( ) A.有且只有一条 B.有两条;C.不存在D.不存在或只有一条18.同一平面内的三条直线,其交点的个数可能为________.19.直线L 同侧有A,B,C 三点,若过A,B 的直线L 1和过B,C 的直线L 2都与L 平行,则A,•B,C 三点________,理论根据是___________________________. 20.如图1所示,下列条件中,能判断AB ∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠4D.∠BAC=∠ACD(1) (2) (3)21.如图2所示,如果∠D=∠EFC,那么( )A.AD ∥BCB.EF ∥BCC.AB ∥DCD.AD ∥EF 22.如图3所示,能判断AB ∥CE 的条件是( )A.∠A=∠ACEB.∠A=∠ECDC.∠B=∠BCAD.∠B=∠ACE 23.下列说法错误的是( )A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行24.不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互( ) A.平行B.垂直C.平行或垂直 D.平行或垂直或相交25.如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=600,∠E=•30°,试说明AB ∥CD.26.如图所示,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗?•为什么?。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2016-2017学年七年级下册《相交线与平行线》测试题
数学(培优卷)
本试卷分选择题与非选择题两部分,共三大题25小题,共6页,满分150分.考试用时120分钟.
第一部分选择题(共30分)
一、选择题(本大题共10小题.每小题3分,满分30分.在每小题给出得四个选项中,只有一项就是符合题目要求得.)
1、如图,下列判断正确得就是( )
A 、∠2与∠5就是对顶角
B 、∠2与∠4就是同位角
C 、∠3与∠6就是同位角
D 、∠5与∠3就是内错角
2、如图
,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC ＝150°, ∠BCD A B .AB ∥DC C D .AB 与CD 相交 3、如图,下列说法错误得就是
( )
A.若a ∥b,b ∥c,则a ∥c
B.若∠1＝∠2,则a ∥c
C.若∠3＝∠2,则b ∥c
D.若∠3＋∠5＝180°,则a ∥c 4、在一个平面内,任意四条直线相交,交点得个数最多为( ) A 、7 B 、6 C 、5 D 、4 5、如图,AB ∥EF ,CD ⊥EF ,∠BAC ＝50°,则∠ACD ＝( )
A 、120°
B 、130°
C 、140°
D 、150°
A 、 20°
B 、16°
C 、 23°
D 、26°
9、如图,若OP ∥QR ∥ST,则下列等式中正确得就是( )
A 、∠1+∠2-∠3=90º
B 、∠1-∠2+∠3=90º
C 、∠1+∠2+∠3=180º
D 、∠2+∠3-∠1=180º
10、下列说法正确得个数为( )
(1)如果∠1+∠2+∠3=180°,那么∠1、∠2与∠3互为补角; (2)如果∠A+∠B=90°,那么∠A 就是余角;
第2题图
第3题图
第8题图第9题图
(3)互为补角得两个角得平分线互相垂直; (4)有公共顶点且又相等得角就是对顶角; (5)如果两个锐角相等,那么它们得余角也相等.
A 、1
B 、2
C 、3
D 、4
第二部分非选择题(共120分)
二、填空题(本大题共6小题.每小题3分,满分18分.)
11、把下列命题写成“如果…那么…”得形式:不能被2整除得数就是奇数
12、如图,已知AB ∥CD ,BC ∥DE 、若∠A ＝20°,∠C ＝120°,则∠AED 得度数就是、
13、如图,若AO ⊥OC,DO ⊥OB,∠AOB ∶∠BOC=32∶13,则∠COD=
14、将一副直角三角板ABC 与EDF 如图放置(其中∠A =60°,∠F =45°),使点E 落在AC 边上,且ED ∥BC ,则∠CEF 得
15、、EF 相交于同一点O,如果∠AOE=2∠AOC,∠COF=∠AOE,那么 \ ∠DOE=
、
16、一个人从点方向走到点B,再从点B 出发向南偏西15°方向走到点C,那么 ∠ABC 三、解答题(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤.)
17、如图所示,一块正方形地板,边长为60cm,上面横竖各有两道宽为5cm 得花纹(图中阴影部分),那么空白部分得面
积就是多少？(9分)
18、顶点在网格交点得多边形叫做格点多边形,如图,在一个9×9得正方形网格中有一个格点△ABC 、设网格中小正方形得边长为1个单位长度、(9分)
(1)在网格中画出△ABC 向上平移4个单位后得到得△A 1B 1C; (2)在(1)中△ABC 向上平移过程中,求边AC 所扫过区域得面积、
19、如图,∠AEF ＋∠CFE ＝180°,∠1＝∠2,EG 与HF 平行吗？为什么？(9分)
20、已知:如图,AB ∥CD,EF ∥AB,BE 、DE 分别平分∠ABD 、∠BDC 、求证:∠1与∠2互余、(10分)
21、如图,∠BAF ＝46°,∠ACE ＝136°,CE ⊥CD 、问CD ∥AB 吗？为什么？(10
第13题图第14题图
B
A 第16题图
第17题图
B
22、如图所示,在折线ABCDEFG中,已知∠1=∠2=∠3=∠4=∠5,延长AB,GF交于点M、试探索∠AMG与∠3得关系,并说明理由、 (12分)
23、我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气,同样会发生折射现象.如图所示就是光线从空气射入水中,再从水中射入空气得示意图.由于折射率相同,已知∠1＝∠4,∠2＝∠3,请您用所学知识来判断光线c与光线d就是否平行？并说明理由.(12分)
24、如图,把一张长方形得纸片按如图所示得方式折叠,EM、FM折痕,折叠后得C点落在B’M或B’M得延长线上,求∠EMF得度数。

(14分)
25、如图,已知直线a∥b,且直线d与a、b分别交于A、B两点,直线c与a、b分别交于M、N两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间得关系并说出理由;(14分)
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间得关系就是否发生变化？
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间得关系,并说明理由(点P与A、B不重合)、
参考答案
一、选择题
1 2 3 4 5 6 7 8 9 10
A B C B C C D A D A
二、填空题
11、如果一个数不能被2整除,那么这个数就是奇数12、80°
13、64°14、15°15、90°16、45°
三、解答题
17、解:通过平移,将上面横竖两道花纹移到正方形地板得边上,
则剩下得空白部分可以瞧成就是边长为50cm得正方形
则空白部分面积为(60－2×5)²＝2500cm²
故答案为:2500cm²
18、
19、解:平行.
理由:∵∠AEF＋∠CFE＝180°,
∴AB∥CD、
∴∠AEF＝∠EFD、
∵∠1＝∠2,
∴∠AEF－∠1＝∠EFD－∠2,
即∠GEF＝∠HFE、
∴GE∥FH、
20、证:∵AB∥CD,
∴∠ABD+∠BDC=180°,
∵BE、DE分别平分∠ABD、∠BDC,
∴∠EBD+∠EDB=90°,
∴∠BED=90°,
∴∠1+∠2=90°.
21、解:CD∥AB、
理由:∵CE⊥CD,
∴∠DCE＝90°、
又∵∠ACE＝136°,
∴∠ACD＝360°－∠ACE－∠DCE＝360°－136°－90°＝134°、
∵∠BAF＝46°,
∴∠BAC＝180°－∠BAF＝180°－46°＝134°、
∴∠ACD＝∠BAC、
∴CD∥AB、22、
23、解:c∥d、理由如下:
∵∠1＋∠5＝180°,∠4＋∠6＝180°,∠1＝∠4, ∴∠5＝∠6、
∵∠2＝∠3,
∴∠2＋∠5＝∠3＋∠6、
∴c∥d、
24、
25、
解:(1)∠1+∠2=∠3;
理由:过点P作a得平行线,
∵a∥b,
∴a∥b∥PQ,
∴∠1=∠4,∠2=∠5,
∵∠4+∠5=∠3,
∴∠1+∠2=∠3;
(2)同理可知:∠1+∠2=∠3;
(3)同理:∠1－∠2=∠3或∠2－∠1=∠3.
理由:当点P在下侧时,过点P作a得平行线PQ,
∵a∥b,
∴a∥b∥PQ,
∴∠2=∠4,∠1=∠3+∠4,
∴∠1－∠2=∠3;
当点P在上侧时,同理可得∠2－∠1=∠3、。