弧长法在边坡稳定非线性有限元分析中的应用
圆弧法在岩坡稳定分析中的应用

日 =圩 s () 6
沿着这个计算 滑动面是不稳定的 ; 如果 F s=l 则沿着 这个计算滑
动面 处 于 极 限 平衡 状 态 。
本文运用条分法对滑动弧 内岩体进行分析。把滑体分为 /条 , t ' 其 中第 i 条传给滑动 面上 的重量为 , 将 分解 为法向力 ⅣI 和
构面的渗水性 、 地下水位 的高低有关 。本文 通过实际工 程推导坡
高与坡角的关 系 , 在实际的采用 中取得 了良好的效果 。 并
() 3
将 式
1 力 学分析 方程
岩 坡 方 程 分析 见 图 1 。
0
H /
I l
∑c + 。 ∑Ⅳ l t
=
:
—
—
—
—
7o‘ (gf g ) cs t —t p
Z 而 C i
()
则:
I= i 。 厂 Nt g
从而可确定折减 系数 :
其作用方向与岩体滑动方 向相反 。
滑动面上 颗粒之 间的凝聚力也阻止滑动弧岩体下滑 , : 即
:
c=Cl。 i
掣
:。。 。 , + 4 一 。 9 詈
又 :i N =Wi s。T :Win 且 = c O, i s 0, o i —
() 7
l oO。代入得 : i ¥i e
由于分 向力 通过圆心 , 对岩体 滑动不起作 用 , 但其 可使岩 条滑动面上产生摩擦力,= , :t 是 滑动弧所在 岩体 的 g (
内摩 擦 角 ) 。
2 0 2 50 3
第3 6卷 第 3 2期 201 年 11月 0
文章 编 号 :0 96 2 (0 0 3 —13 0 10 —8 5 2 1 )2 00 — 3
abaqus在岩土工程中的应用边坡稳定分析

高等土力学边坡稳定分析专业:岩土工程姓名:xxx指导老师:xxx学号:xxx1.前言边坡稳定分析是边坡设计的前提,它决定着边坡是否失稳以及边坡失稳时存在多大推力,以便为支护结构设计提供科学依据。
然而这个问题至今仍未得到妥善解决,因为解决这一问题必须先要查清坡体的地质状况及其强度参数,同时又要有科学合理的分析方法[1]。
对于均质土坡,传统方法主要有:极限平衡法,极限分析法,滑移线场法等,就目前工程应用而言,主要还是极限平衡法,但需要事先知道滑动面位置和形状。
对于均质土坡,可以通过各种优化方法来搜索危险滑动面,但是对于岩质边坡,由于实际岩体中含有大量不同构造、产状和特性的不连续结构面,传统极限平衡方法尚不能搜索出危险滑动面以及相应的稳定安全系数。
边坡稳定分析涉及复杂的地质地形边界条件、材料的应力-应变的非线性行为、初始地应力、水压力、地震荷载的耦合分析等等,多数情况下不能获得解析解。
在计算机和计算方法不断发展的背景下,以有限元为代表的数值分析方法在 20 世纪 70年代已逐步在岩土工程中推广应用,并发展成为一种强有力的计算分析工具。
然而传统的数值分析方法一般只是得出边坡应力、位移、塑性区等,不能直接与边坡稳定建立定量关系。
随着计算机技术的发展,有限元强度折减法近来在国内外受到关注[2~12],对于均质土坡已经得到了较好的结论,但尚未在工程中实用,本文采用有限元强度折减法,对均质土坡进行了系统分析,证实了其实用于工程的可行性,得到了节理岩质边坡坡体的危险滑动面和相应的稳定安全系数。
该方法可以对贯通和非贯通的节理岩质边坡进行稳定分析,同时可以考虑地下水、施工过程对边坡稳定性的影响,可以考虑各种支挡结构与岩土材料的共同作用,为边坡稳定分析开辟了新的途径。
2.有限元强度折减法原理c' = c /ω,tanϕ' =tanϕ/ω这种方法早在 70 年代就提出来了。
1975 年Zienkiewize 就利用有限元进行边坡稳定分析,但是由于受计算条件的限制,此法一直没有流行起来。
瑞典圆弧法 边坡稳定性分析例题

(10)将每一段的重力Gi化为二个分力: a.在滑动曲线法线方向分力:Ni=Gicosαi b.在滑动曲线切线方向分力:Ti=Gisinαi 并分别求出此两者之和,ΣNi和ΣTi (11)算出滑动曲线圆弧长L (12)计算稳定系数
K2
n
f N i CL
i 1 n
T
i
i
= 1.54
(6)将圆弧范围土体分成8~10段,本例采用8段,先由坡脚起每 5m一段,最后一段可能略少。 (7)算出滑动曲线每一分段中点与圆心竖线之间的偏角αi Xi sinαi= R 式中:Xi——分段中心距圆心竖线的水平距离,圆心竖线左侧 为负,右侧为正; R——滑动曲线半径。 (8)每一分段的滑动弧曲线可近似取直线,将各分段图形简化为 梯形或三角形,计算其面积Ωi,其中包括荷载换算成土柱部分 的面积在内。 (9)以路堤纵向长度1m计算出各分段的重力Gi
解 (1)用方格纸以1∶50比例绘出路堤横断面。 (2)将挂车-80换算成土柱高(当量高度)。 (3)按4.5H法确定滑动圆心辅助线。在此取坡脚θ=25°
13 (θ=arctg 2518' ),由表得β1=25°,β2=35°。 27.5
据此两角分别自坡脚和左顶点作直线相交于O点,BO的延长 线即为滑动圆心辅助线。 (4)绘出三条不同位置的滑动曲线:①一条通过路基中线;② 一条通过路基的右边缘(如图中的圆弧所示);③一条通过距 右边缘1/4路基宽度处。 (5)滑动圆弧中心可用直线连接可能滑弧的两端点,并作此直 线的中垂线相交于滑动圆心辅助线BO于A点。A点即是该滑 动曲线的中心。
Ω m2 29.9 57.5 56 51 49.7 38.5 24 4.8
G=Ω kN 508 971 951 866 845 654 408 82
边坡稳定性分析的有限元法

第21卷 第5期 地 下 空 间 V ol.21 No.5 2001年12月 U N DERG RO U N D SPA CE Dec.2001 文章编号:1001-831X(2001)05-0450-05边坡稳定性分析的有限元法赵尚毅,时卫民,郑颖人(后勤工程学院军事土木工程系,重庆 400041)摘 要:本文把强度折减理论用于有限元法中,成功地解决了有限元在边坡稳定分析中的应用问题。
有限元法不但满足力的平衡条件,而且考虑了材料的应力应变关系,计算时不需做任何假定,使得计算结果更加精确合理,而且可以很直观的得到坡体的实际滑移面。
本文结合工程算例,对边坡加锚杆前后的稳定性进行了分析,并与传统的求稳定系数的方法进行了比较,表明有限元法解决边坡问题是可行的。
关键词:边坡;稳定性分析;有限元;共同作用中图分类号:T B115;TU457 文献标识码:A1 引言目前,研究边坡稳定性的传统方法主要有:极限平衡法,极限分析法,滑移线场法等,这些建立在极限平衡理论基础上的各种稳定性分析方法没有考虑土体内部的应力应变关系,无法分析边坡破坏的发生和发展过程,无法考虑变形对边坡稳定的影响,没有考虑土体与支挡结构的共同作用及其变形协调。
在求安全系数时通常需要假定滑裂面形状为折线、圆弧、对数螺旋线等。
有限单元法能考虑土的应力应变关系,本文试图对利用有限单元法来进行边坡稳定分析作进一步探讨。
2 有限元法进行边坡稳定分析的优点当我们对边坡进行支挡处理后,比如锚杆加固后,要对它的安全性作出评估,这就需要考虑土体与锚杆的共同作用及其变形协调问题。
传统的以极限平衡理论为基础的分析方法是不能解决此问题的。
而有限单元法能考虑土的应力应变关系,比极限平衡法更为精确合理,而且能够考虑土体与锚杆的共同作用及其变形协调,其优点如下:(1)考虑了土体的非线性弹塑性本构关系;(2)能够模拟土体与其支挡结构的共同作用,从而能对支挡前后的土坡进行稳定性分析;(3)能够动态模拟土坡的失稳过程及其滑移面形状。
midas gts 边坡稳定性分析

Basic Tutorials
第 6 部分
结果
分析后,在结果目录树上可以查看变形、应力等结果。所有结果可以按云图、表格、图 形等提供。在本例题中,需要查看的主要结果项目如下。
• 安全系数/破坏形状
• 通过‘剪切面(Clipping plane)’评估结果。
▶最大剪切应变(旱季) ▶▶最大剪切应变(雨季)
6.2 查看剪切面
在 GTS NX 上,可以使用‘剪切面’分割模型,确认各剪切面上的结果。 • 在工作目录树>结果>旱季>边坡稳定分析上,选择查看结果的阶段(输出最小安全系
数的阶段) > Solid Strains > E-MAX SHEAR。 • 在高级视图工具条上,选择剪切面( )。在定义剪切面时,平面方向输入‘X‘、距离
10
摩擦角
42
19
▶定义岩土材料-一般
▶▶定义岩土材料-渗 透性
▶▶▶定义岩土材料-非 线性
Chapter 8. 三维边坡稳定分析 | 3
Basic Tutorials
Chapter 8.三维边坡稳定分析
3.2 定义属性
属性体现网格的物理属性。在划分网格时,将属性Байду номын сангаас配给网格组。
名称
基岩
风化土
类型
三维
▶模型示意图
▶剖面图
通过本例题,可以学习如下主要功能及分析方法: • 利用栅格面功能生成地表面、地层面 • 划分网格 • 边坡稳定分析 • 分析结果–安全系数及最大剪应变 • 分析结果–使用剪切面功能检查某一指定断面的结果 本模型是由风化土和基岩组成的三维模型。通过分析旱季和雨季下的边坡稳定性,识别 可能出现破坏的部分,消除隐患。
边坡稳定性分析方法及其适用条件

边坡稳定性分析方法及其适用条件边坡稳定性是指边坡在外力作用下保持不倒塌或滑动的能力,边坡稳定性分析方法一般可以分为经验法、力学方法和数值模拟方法三类。
不同方法适用于不同类型的边坡,且各方法在分析准确性、工程实施条件、运算速度以及数据要求等方面有所不同。
1.经验法:经验法是基于大量实际工程经验和观测总结出的简化计算方法,适用于边坡规模较小、地质条件比较简单的情况。
根据边坡的高度、坡度、土质等因素,通过经验公式计算出边坡的稳定性系数,从而判断边坡的稳定性。
2.力学方法:力学方法是通过岩土力学原理和边坡土体的力学性质来分析边坡稳定性。
力学方法主要应用于边坡高度较大、复杂地质条件的情况。
常用的力学方法包括平衡法、极限平衡法、有限元法等。
-平衡法:平衡法是基于边坡的平衡条件进行分析的方法,通过计算剪力平衡方程来确定边坡的稳定性。
平衡法适用于坡度较小、土体不饱和、坡面无裂缝等条件下的边坡稳定性分析。
-极限平衡法:极限平衡法是在平衡法的基础上引入抗剪参数的概念,通过计算抗剪参数的极限值来判断边坡的稳定性。
极限平衡法适用于任意坡度、土体饱和或部分饱和的边坡稳定性分析。
-有限元法:有限元法是一种基于连续介质力学和离散化原理的数值分析方法,将边坡土体划分成网格,通过求解有限元方程来计算边坡的应力和变形,并进而判断边坡的稳定性。
有限元法适用于复杂地质条件和复杂边坡形状的稳定性分析。
3.数值模拟方法:数值模拟方法是通过数值计算和模拟来分析边坡稳定性,主要利用计算机和专业软件进行模拟计算。
数值模拟方法通常适用于复杂地质条件、复杂边坡形状、非线性、动力等问题的研究。
常用的数值模拟方法包括有限差分法、边界元法、粒子法等。
总体来说,经验法适用于边坡规模较小、较简单的情况;力学方法适用于边坡规模较大、地质条件复杂的情况;数值模拟方法适用于复杂的边坡形状和非线性、动力问题。
在实际工程中,边坡稳定性分析通常采用多种方法相结合的方式,综合考虑不同方法的分析结果,从而提高分析的准确性。
弧长法基本原理
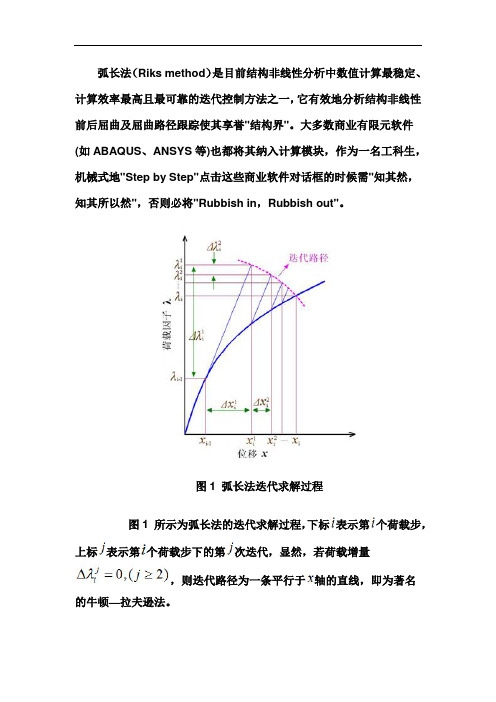
弧长法(Riks method)是目前结构非线性分析中数值计算最稳定、计算效率最高且最可靠的迭代控制方法之一,它有效地分析结构非线性前后屈曲及屈曲路径跟踪使其享誉"结构界"。
大多数商业有限元软件(如ABAQUS、ANSYS等)也都将其纳入计算模块,作为一名工科生,机械式地"Step by Step"点击这些商业软件对话框的时候需"知其然,知其所以然",否则必将"Rubbish in,Rubbish out"。
图1 弧长法迭代求解过程图1 所示为弧长法的迭代求解过程,下标表示第个荷载步,上标表示第个荷载步下的第次迭代,显然,若荷载增量,则迭代路径为一条平行于轴的直线,即为著名的牛顿—拉夫逊法。
设第个荷载步收敛于,那么对于第个荷载步来说,需要进行次迭代才能达到新的收敛点。
外部参照力,在ABAQUS需要用户以外荷载的形式输入,因此,作用在结构上的真实力大小为。
由于牛顿—拉夫逊法在迭代过程中,以荷载控制(或位移控制)时,荷载增量步(或位移增量步)为常数,它无法越过极值点得到完整的荷载—位移曲线,事实上,也只有变化的荷载增量步才能使求解过程越过极值点。
从图1中可以看出,弧长法的荷载增量步是变化的,可以自动控制荷载,但这又使原方程组增加了一个多余的未知量,因此需要额外补充一个控制方程,即:(1)该控制方程说明,其迭代路径是以上一个荷载步收敛点为圆心半径为的圆弧,所以称为弧长法。
通常用户需指定初始弧长半径或固定的弧长半径,当设定了初始弧长半径时,根据收敛速率,一般按式(2)计算,其中为荷载步期望收敛迭代次数,一般取6, 为上一荷载步的迭代次数,大于10时取10。
(2)1. 当时,根据上一个荷载步收敛结束时的构形,得到用于第个荷载步收敛计算的切线刚度矩阵,即图1中的蓝色平行线的斜率。
通过式(2)可得相应的切线位移。
(3)(4)(5)很容易由式(5)求得,但不能确定其符号,而的符号决定了跟踪分析是向前还是返回,因此非常重要。
弧长法算法

矩阵不是正定的,则节点荷载 ∆f i +1 = − ∆f i 。 2.1.2、 弧长法的具体实现方法 在实际计算中,先进行矩阵正定性判别,利用 Lancsoz 方法,进行两步 Lancsoz 过程, 得到相应的 Ritz 值 θ 1 ,θ n 。因为 θ 2 ≈ λ n , λ n 为刚度矩阵最小的特征值。如果 θ 2 < 0 ,则 认为刚度矩阵为非正定。 弧长法程序模块由三个子程序组成: 1:subroutine ArcLeng(TotalP,TotalU,F,ArcL),功能:弧长法迭代核心程序 2:subroutine Judge(PD,GK),功能:判断刚度矩阵的正定性 3:subroutine Solve(GK,Gload,Gdisp),功能:求解迭代方程组
《高等数值分析》课程研究
数值误差“吃掉” ,最后没有出现有些文献中声称的那样明显的效果,因此,在这个预处理 方法上, 还需要一些讨论。 以 Hilbert 矩阵为例, 在双精度下, 当矩阵 n>5 时, 预处理 Lanczos 的结果精度对普通高斯消去已经没有什么优势了。 因此,我认为基于 Lancsoz 方法求解的尝试没有取得预想效果,需要用新的方法代替。 2.2.2、A3 预处理技术 取预处理矩阵 M=A3,即取原矩阵的三条主对角线元素为预处理矩阵,对原矩阵进行预 处理。为了比较其效果,这里以 Hilbert 矩阵为例,比较其效果。 方程 Hx = b , H 为 Hilbert 矩阵,分别用普通高斯消去法和预处理后的消去法得到结 果~ x ,记误差为 b − A~ x
r (i ) ⋅ r (i ) = S 2
∆u ( i +1) (∆u ( i +1) + 2r ( i ) ) = 0
