统计学第2章课堂补充练习及答案
《统计学》课后习题答案

《统计学》课后习题答案《统计学》习题参考答案湖南商学院统计系第1章总论1.统计的三种涵义是:统计⼯作、统计资料和统计学.2.统计⼯作必须涉及:为谁统计、由谁统计、统计什么和如何统计等基本问题.3.统计⼯作具有:信息职能、咨询职能和监督职能,其中最基本的职能是信息职能.4.统计资料按计量⽅法不同,分为计点资料和计量资料;按资料是否直接取得,分为原始资料和次级资料;按统计资料的时间属性不同,分为静态资料和动态资料;按统计资料所涵盖的范围不同,分为全⾯资料和抽样资料. .统计资料具有时间、空间和数据三个要素。
5.统计学是研究现象总体的数量表现和规律性的⽅法论科学。
按照发展阶段和侧重点不同,可分为描述.统计学和推断统计学;按照理论与实践应⽤的关系,可分为理论统计学和应⽤统计学。
6.简述统计研究最基本的研究⽅法有哪些? 统计的研究过程主要包括哪些步骤?统计研究最基本的研究⽅法有⼤量观察法、统计分组法、综合指标法、归纳推断法,统计的研究过程主要包括统计设计、统计调查、统计整理、统计分析等步骤。
第2章统计计量1.四种具体的计量⽔准分别是列名⽔准、顺序⽔准、间隔⽔准、⽐例⽔准;其中属性⽔准包括列名⽔准和顺序⽔准,数量⽔准包括间隔⽔准和⽐例⽔准.2. 统计指标按反映的总体内容与性质不同,可分为数量指标与质量指标两⼤类.3.数量指标由于计量单位不同,可分为实物指标和价值指标, 按反映的计量时间特点不同,分为流量指标和存量指标(或时期指标和时点指标), 所反映的总体内容不同可分为总体单位总量和总体标志总量,总体标志总量/总体单位总量为平均指标。
4.质量指标按表现形式不同可分为平均指标和相对指标。
5..统计指标设计⼀般应遵循哪些准则?统计指标设计⼀般应遵循的原则主要有(1)统计指标的名称、涵义要有理论依据。
(2)统计指标必须有明确的计算⼝径。
(3)统计指标要有科学的计算⽅法。
(4)统计指标要有统⼀的计量单位。
6.建⽴统计指标体系应遵循哪些原则?建⽴统计指标体系应遵循的原则主要有1.必须明确建⽴统计指标体系的⽬的,2.必须明确基本统计指标和分类指标。
高等职业教育“十一五”规划教材《统计学》第二章课后习题及答案

高等职业教育“十一五”规划教材《统计学》第二章课后习题及答案高等职业教育“十一五”规划教材《统计学》第二章课后习题及答案一.判断题1.在统计调查方案中,调查期限是指调查资料所属的时间,调查时间是指调查工作的起止时间。
错,正好相反。
2.全面调查是对调查对象的各方面都进行调查。
错,全面调查是对被调查对象中的所有单位全部进行调查。
3.经常性调查是指随着调查对象的不断变化,而随时将变化情况进行连续不断的登记。
错,不是随时,而是连续不断地登记。
4.抽样调查是所有调查方式中最有科学依据的方式方法,因此它适用于任何调查任务错,它是可以排除主观因素的影响,对总体的数量做出科学的估计,抽样误差可以事先计算和控制,但是任何一种统计调查方法都有优势和局限性,具体情况具体分析。
5.每月月初登记职工人数属经常性调查对。
二.单选1.重点调查中重点单位是按(B)选择的A.这些单位数量占总体全部单位总量的很大比例B.这些单位的标志总量占总体标志总量的很大比例C.这些单位有典型意义,是工作的重点D.这些单位能用以推算总体标志总量。
2.有意识地选择三个家村点调查农民收入情况,这种调查方式属于(A)A.典型调查B.重点调查C.抽样调查D.普查3. 2000年11月1日零点的第五次全国人口普查是(C)A.典型调查B.重点调查C.一次性调查D.经常性调查4.通过调查大庆、胜利等几个主要油田来了解我国石油生产的基本情况,这种调查方式属于(B)A.普查B.重点调查C.典型调查D.抽样调查5.工人对生产的一批零件进行检查,一般采用(D)A.普查B.重点调查C.典型调查D.抽样调查三、多项选择题1.重点调查是( BCDE)。
A. 全面调查 B. 非全面调查 C. 专门调查D. 可用于经常性调查E. 可用于一次性调查2. 工业普查是(ACE)。
A. 全面调查B. 非全面调查C. 专门调查D. 经常性调查E. 一次性调查3.下列表述中不正确的是(ACE)。
统计学课后第二章习题答案

第2章练习题1、二手数据的特点是()A.采集数据的成本低,但搜集比较困难B. 采集数据的成本低,但搜集比较容易C.数据缺乏可靠性D.不适合自己研究的需要2、从含有N个元素的总体中,抽取n个元素作为样本,使得总体中的每一个元素都有相同的机会(概率)被抽中,这样的抽样方式称为()A.简单随机抽样B.分层抽样C.系统抽样D.整群抽样3、从总体中抽取一个元素后,把这个元素放回到总体中再抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A.重复抽样B.不重复抽样C.分层抽样D.整群抽样4、一个元素被抽中后不再放回总体,然后从所剩下的元素中抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A.不重复抽样B.重复抽样C.系统抽样D.多阶段抽样5、在抽样之前先将总体的元素划分为若干类,然后从各个类中抽取一定数量的元素组成一个样本,这样的抽样方式称为()A. 简单随机抽样B. 系统抽样C.分层抽样D.整群抽样6、先将总体各元素按某种顺序排列,并按某种规则确定一个随机起点,然后每隔一定的间隔抽取一个元素,直至抽取n个元素形成一个样本。
这样的抽样方式称为()A. 分层抽样B. 简单随机抽样C.系统抽样D.整群抽样7、先将总体划分为若干群,然后以群作为抽样单位从中抽取部分群,再对抽中的各个群中所包含的所有元素进行观察,这样的抽样方式称为()A. 系统抽样B. 多阶段抽样C.分层抽样D.整群抽样8、为了调查某校学生的购书费用支出,从男生中抽取60名学生调查,从女生中抽取40名学生调查,这种调查方是()A. 简单随机抽样B. 整群抽样C.系统抽样D.分层抽样9、为了调查某校学生的购书费用支出,从全校抽取4个班级的学生进行调查,这种调查方法是()A. 系统抽样B. 简单随机抽样C.分层抽样D.整群抽样10、为了调查某校学生的购书费用支出,将全校学生的名单按拼音顺序排列后,每隔50名学生抽取一名学生进行调查,这种调查方法是?()A.分层抽样B. 整群抽样C.系统抽样D.简单随机抽样11、为了了解女性对某种化妆品的购买意愿,调查者在街头随意拦截部分女性进行调查。
第二章统计学基础课后习题答案

第二章数据搜集
一、填空题
1.桌面 2.随机 3.统计报表 4.访问法、观察法、实验法5.结构式.无结构 6.观察法 7.调查 8.调查
二、单选题
1.B 2.B 3.C 4.A 5.D 6.B 7.B 8.C
三、多选题
1.ACE 2.CDE 3.ABC 4.BD 5.ABCD
四、简单题
1.调查方案包括的主要内容:(1)调查目的和调查任务;(2)调查对象和调查单位;(3)调查项目;(4)样本容量、调查方式、调查方法;(5)调查时间和调查工作期限;(6)调查经费预算;(7)调查的组织计划和管理措施。
2.抽样调查的特点:(1)按随机原则抽取调查单位;(2)按一定的置信度推断总体;(3)抽样调查的误差可以事先计算和控制。
判断抽样的特点:(1)深入细致的调查方式,强调调查单位的典型代表性;(2)灵活的调查方式,可注重量和质的分析;(3)调查单位根据调查目的和任务有意识的选择。
3.问卷设计中,问题的提问方式应注意:(1)避免笼统抽象问题;(2)避免含糊不清的概念;(3)问题要通俗易懂,尽量不使用专业术语;(4)避免引导性提问;(5)忌语言生硬、令人难堪;(6)避免断定性问题;(7)避免多重性问题;(8)避免敏感性、禁忌性问题。
4.问卷设计中,问题的排列顺序应遵循的原则:(1)最初的提问应该是被访者容易回答且较为关心的问题;(2)提问的内容应该从简单逐步转向复杂;(3)对相关的内容应进行系统整理,使被访者不断增加兴趣;(4)调查的核心问题应排在前面;(5)专业性强的问题放在后面;(6)敏感问题放在后面;(7)封闭式问题放在前面,开放式问题放在后面。
五、判断题
1.错 2.对 3.错 4.错 5.对。
统计学 第二章习题参考答案(书上习题)向蓉美
第二章习题参考答案1.可分情况讨论:若经费允许且调查范围较小,如一个村镇,或者一个贫困区县,或者要求的精度很高,那么可以进行普查,因为普查的结果准确,但费时费力。
一般情况下,应该选择抽样调查。
因为抽样调查具有以下优点:(1)可以减少调查的工作量,调查内容可以求多、求全或求专,可以保证调查对象的完整性。
(2)可以从数量上以部分推算总体,利用概率论和数理统计原理,以一定的概率保证推算结果的可靠程度,起到全面调查认识总体的功能,可以在一定程度上保证调查的精度。
(3)可以大大减少调查费用,提高调查效率。
(4)收集、整理数据、综合样本的速度快,能够保证调查的时效性。
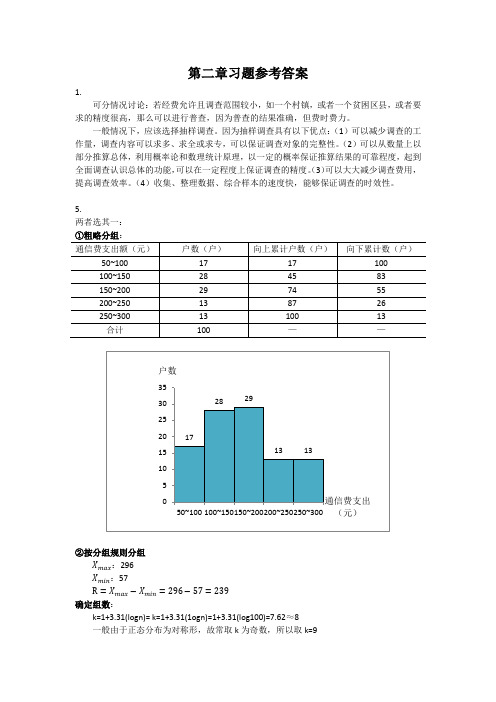
5.两者选其一:①粗略分组:②按分组规则分组X max:296X min:57R=X max−X min=296−57=239确定组数:k=1+3.31(logn)= k=1+3.31(1ogn)=1+3.31(log100)=7.62≈8一般由于正态分布为对称形,故常取k为奇数,所以取k=9确定组距:n=X max−X mink =2399≈27为了便于分析,组距宜取5或10的倍数(书P32),因此n取30确定组界:通常从最小值开始。
先把最小值放在第一组的中间位置上。
最小值为57,因此第一组的下界为57−302=42,上界为57+302=72,分组:6.画折线图和柱形图皆可。
柱形图既可以用来表示定性数据的分布,也可以用来进行同类现象在不同空间、不同时间的对比(书P39);折线图主要用于显示时间序列数据,反映现象随时间变化的特征(书P40)但折线图能够更加清晰地反映出事物变化的趋势,因为本题中可能更注重整体趋势而非单个点的比较,所以折线图更好。
2、3、4题大家都做的不错哈。
概率论与数理统计第二章课后习题及参考答案.

概率论与数理统计第二章课后习题及参考答案1.离散型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=≤=.4,1,42,7.0,21,2.0,1,0)()(x x x x x X P x F 求X 的分布律.解:)0()()(000--==x F x F x X P ,∴2.002.0)01()1()1(=-=----=-=F F X P ,5.02.07.0)02()2()2(=-=--==F F X P ,3.07.01)04()4()4(=-=--==F F X P ,∴X 的分布律为2.设k a k X P 32()(==, ,2,1=k ,问a 取何值时才能成为随机变量X 的分布律.解:由规范性,a a a n n k k 2321]32(1[32lim)32(11=--=⋅=+∞→∞+=∑,∴21=a ,此时,k k X P 32(21)(⋅==, ,2,1=k .3.设离散型随机变量X 的分布律为求:(1)X 的分布函数;(2)21(>X P ;(3))31(≤≤-X P .解:(1)1-<x 时,0)()(=≤=x X P x F ,11<≤-x 时,2.0)1()()(=-==≤=X P x X P x F ,21<≤x 时,7.0)1()1()()(==+-==≤=X P X P x X P x F ,2≥x 时,1)2()1()1()()(==+=+-==≤=X P X P X P x X P x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤<≤--<=.2,1,21,7.0,11,2.0,1,0)(x x x x x F .(2)方法1:8.0)2()1()21(==+==>X P X P X P .方法2:8.02.01)21(121(1)21(=-=-=≤-=>F X P X P .(3)方法1:1)2()1()1()31(==+=+-==≤≤-X P X P X P X P .方法2:101)01()3()31(=-=---=≤≤-F F X P .4.一制药厂分别独立地组织两组技术人员试制不同类型的新药.若每组成功的概率都是0.4,而当第一组成功时,每年的销售额可达40000元;当第二组成功时,每年的销售额可达60000元,若失败则分文全无.以X 记这两种新药的年销售额,求X 的分布律.解:设=i A {第i 组取得成功},2,1=i ,由题可知,1A ,2A 相互独立,且4.0)()(21==A P A P .两组技术人员试制不同类型的新药,共有四种可能的情况:21A A ,21A A ,21A A ,21A A ,相对应的X 的值为100000、40000、60000、0,则16.0)()()()100000(2121====A P A P A A P X P ,24.0)()()()40000(2121====A P A P A A P X P ,24.0)()()()60000(2121====A P A P A A P X P ,36.0)()()()0(2121====A P A P A A P X P ,∴X 的分布律为5.对某目标进行独立射击,每次射中的概率为p ,直到射中为止,求:(1)射击次数X 的分布律;(2)脱靶次数Y 的分布律.解:(1)由题设,X 所有可能的取值为1,2,…,k ,…,设=k A {射击时在第k 次命中目标},则k k A A A A k X 121}{-== ,于是1)1()(--==k p p k X P ,所以X 的分布律为1)1()(--==k p p k X P , ,2,1=k .(2)Y 的所有可能取值为0,1,2,…,k ,…,于是Y 的分布律为1)1()(--==k p p k Y P , ,2,1,0=k .6.抛掷一枚不均匀的硬币,正面出现的概率为p ,10<<p ,以X 表示直至两个面都出现时的试验次数,求X 的分布律.解:X 所有可能的取值为2,3,…,设=A {k 次试验中出现1-k 次正面,1次反面},=B {k 次试验中出现1-k 次反面,1次正面},由题知,B A k X ==}{,=AB ∅,则)1()(1p p A P k -=-,p p B P k 1)1()(--=,p p p p B P A P B A P k X P k k 11)1()1()()()()(---+-=+=== ,于是,X 的分布律为p p p p k X P k k 11)1()1()(---+-==, ,3,2=k .7.随机变量X 服从泊松分布,且)2()1(===X P X P ,求)4(=X P 及)1(>X P .X 100000060000400000P0.160.240.240.36解: )2()1(===X P X P ,∴2e e2λλλλ--=,∴2=λ或0=λ(舍去),∴224e 32e !42)4(--===X P .)1()0(1)1(1)1(=-=-=≤-=>X P X P X P X P 222e 31e 2e 1----=--=.8.设随机变量X 的分布函数为⎩⎨⎧<≥+-=-.0,0,0,e )1(1)(x x x x F x 求:(1)X 的概率密度;(2))2(≤X P .解:(1)⎩⎨⎧<≥='=-.0,0,0,e )()(x x x x F x f x ;(2)2e 31)2()2(--==≤F X P .9.设随机变量X 的概率密度为xx Ax f e e )(+=-,求:(1)常数A ;(2))3ln 210(<<X P ;(3)分布函数)(x F .解:(1)⎰⎰+∞∞--+∞∞-+==xAx x f xx d e e d )(1A A x A x x x 2|e arctan d e 21e 2π==+=∞+∞-∞+∞-⎰,∴π2=A .(2)61|e arctan 2d e e 12)3ln 210(3ln 2103ln 210==+=<<⎰-x xx x X P ππ.(3)x xx x xx t t f x F e arctan 2d e e 12d )()(ππ=+==⎰⎰∞--∞-.10.设连续型随机变量X 的分布函数为⎪⎪⎩⎪⎪⎨⎧>≤<-+-≤=.a x a x a a x B A a x x F ,1,,arctan ,,0)(其中0>a ,试求:(1)常数A ,B ;(2)概率密度)(x f .解:(1) 2arcsin (lim )0()(0)(π⋅-=+=+-=-=+-→B A a x B A a F a F a x ,1)(lim )0()(2==+==⋅++→x F a F a F B A a x π,∴21=A ,π1=B .(2)⎪⎩⎪⎨⎧≥<-='=.a x a x x a x F x f ,0,,1)()(22π.11.设随机变量X 的概率密度曲线如图所示,其中0>a .(1)写出密度函数的表达式,求出h ;(2)求分布函数)(x F ;(3)求)2(a X aP ≤<.解:(1)由题设知⎪⎩⎪⎨⎧≤≤-=其他.,0,0,)(a x x ah h x f 2d )(d )(10ahx x a h h x x f a=-==⎰⎰+∞∞-,∴ah 2=,从而⎪⎩⎪⎨⎧≤≤-=其他.,0,0,22)(2a x x a a x f .y hO a x(2)0<x 时,0d 0d )()(===⎰⎰∞-∞-xxt t t f x F ,a x <≤0时,220202d )22(d 0d )()(a x a x t t a a t t t f x F xx-=-+==⎰⎰⎰∞-∞-,a x ≥时,1)(=x F ,∴X 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.a x a x axa x x x F ,1,0,2,0,0)(22.(3)41411(1)2()()2(=--=-=≤<a F a F a X a P .12.设随机变量X 在]6,2[上服从均匀分布,现对X 进行三次独立观察,试求至少有两次观测值大于3的概率.解:由题意知⎪⎩⎪⎨⎧≤≤=其他.,0,62,41)(x x f ,记3}{>=X A ,则43d 41)3()(63==>=⎰x X P A P ,设Y 为对X 进行三次独立观测事件}3{>X 出现的次数,则Y ~43,3(B ,所求概率为)3()2()2(=+==≥Y P Y P Y P )(()(333223A P C A P A P C +=3227)43(41)43(333223=+⋅=C C .13.设随机变量X 的概率密度为⎩⎨⎧<<=其他.,0,10,3)(2x x x f 以Y 表示对X 的三次独立重复观察中事件}21{≤X 出现的次数,求:(1)}21{≤X 至少出现一次的概率;(2)}21{≤X 恰好出现两次的概率.解:由题意知Y ~),3(p B ,其中81d 321(2102==≤=⎰x x X P p ,(1)}21{≤X 至少出现一次的概率为512169)811(1)1(1)0(1)1(33=--=--==-=≥p Y P Y P .(2)}21{≤X 恰好出现两次的概率为51221811(81()1()2(223223=-=-==C p p C Y P .14.在区间],0[a 上任意投掷一个质点,以X 表示这个质点的坐标.设这个质点落在],0[a 中任意小区间内的概率与这个小区间的长度成正比例.试求X 的分布函数.解:0<x 时,事件}{x X ≤表示X 落在区间],0[a 之外,是不可能事件,此时0)()(=≤=x X P x F ;a x ≤≤0时,事件}{x X ≤发生的概率等于X 落在区间],0[x 内的概率,它与],0[x 的长度x 成正比,即x k x X P x F =≤=)()(,a x =时,1)(=≤x X P ,所以a k 1=,则此时axx F =)(;a x ≥时,事件}{x X ≤是必然事件,有1)(=x F ,综上,⎪⎪⎩⎪⎪⎨⎧≥<≤<=,a x a x a x x x F ,1,0,,0,0)(.15.设X ~),2(2σN ,又3.0)42(=<<X P ,求)0(>X P .解:)24222()42(σσσ-<-<-=<<X P X P 3.0)0(2(=Φ-Φ=σ,∴8.03.0)0()2(=+Φ=Φσ,∴8.0)2()2(1)0(1)0(=Φ=-Φ-=≤-=>σσX P X P .16.设X ~)4,10(N ,求a ,使得9.0)10(=<-a X P .解:)10()10(a X a P a X P <-<-=<-)22102(a X a P <-<-=)2()2(a a -Φ-Φ=9.01)2(2=-Φ=a,∴95.0)2(=Φa,查标准正态分布表知645.12=a,∴290.3=a .17.设X ~)9,60(N ,求分点1x ,2x ,使得X 分别落在),(1x -∞,),(21x x ,),(2∞x 的概率之比为3:4:5.解:由题知5:4:3)(:)(:)(2211=><<<x X P x X x P x X P ,又1)()()(2211=>+<<+<x X P x X x P x X P ,∴25.041)(1==<x X P ,33.031)(21==<<x X x P ,125)(2=>x X P ,则5833.0127)(1)(22==>-=≤x X P x X P .25.0)360()360360()(111=-Φ=-<-=<x x X P x X P ,查标准正态分布表知03601<-x ,∴03601>--x ,则75.0)360(1)360(11=-Φ-=--Φx x 查标准正态分布表,有7486.0)67.0(=Φ,7517.0)68.0(=Φ,75.02)68.0()67.0(=Φ+Φ,∴675.0268.067.03601=+=--x ,即975.571=x .5833.0360()360360()(222=-Φ=-≤-=≤x x X P x X P ,查标准正态分布表知5833.0)21.0(=Φ,∴21.03602=-x ,即63.602=x .18.某高校入学考试的数学成绩近似服从正态分布)100,65(N ,如果85分以上为“优秀”,问数学成绩为“优秀”的考生大致占总人数的百分之几?解:设X 为考生的数学成绩,则X ~)100,65(N ,于是)85(1)85(≤-=>X P X P )1065851065(1-≤--=X P 0228.09772.01)2(1=-=Φ-=,即数学成绩为“优秀”的考生大致占总人数的2.28%.19.设随机变量X 的分布律为求2X Y =的分布律.解:Y 所有可能的取值为0,1,4,9,则51)0()0(====X P Y P ,307)1()1()1(==+-===X P X P Y P ,51)2()4(=-===X P Y P ,3011)3()9(====X P Y P ,∴Y 的分布律为20.设随机变量X 在)1,0(上服从均匀分布,求:(1)X Y e =的概率密度;(2)X Y ln 2-=的概率密度.解:由题设可知⎩⎨⎧<<=其他.,0,10,1)(x x f ,(1)当0≤y 时,=≤}{y Y ∅,X 2-1-013P5161511513011X 0149P51307513011∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;e 0<<y 时,)e ()()(y P y Y P y F X Y ≤=≤=)(ln )ln (y F y X P X =≤=,此时,yy f y y y F y F y f X XY X 1)(ln 1)(ln )(ln )()(=='⋅'='=;e ≥y 时,1)()(=≤=y Y P y F Y ,0)(=y f Y ;∴⎪⎩⎪⎨⎧<<=其他.,0,e 0,1)(y y y f Y .(2)当0≤y 时,=≤}{y Y ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;当0>y 时,)e ()ln 2()()(2y Y X P y X P y Y P y F -≥=≤-=≤=)e (1)e (122y X y F X P ---=<-=,此时,222e 21)e ()e ()()(yy y X Y X F y F y f ---='⋅'-='=;∴⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY .21.设X ~)1,0(N ,求:(1)X Y e =的概率密度;(2)122+=X Y 的概率密度;(3)X Y =的概率密度.解:由题知22e 21)(x X xf -=π,+∞<<∞-x ,(1)0≤y 时,=≤=}e {y Y X ∅,∴0)()(=≤=y Y P y F Y ,0)(=y f Y ;0>y 时,)(ln )ln ()e ()()(y F y X P y P y Y P y F X X Y =≤=≤=≤=,此时,2)(ln 2e 21)(ln 1)(ln )(ln )()(y X XY X y f yy y F y F y f -=='⋅'='=π;综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2)(ln 2y y y f y Y π.(2)1<y 时,=≤+=}12{2y X Y ∅,∴0)()(=≤=y Y P y F Y ;1≥y 时,21()12()()(22-≤=≤+=≤=y X P y X P y Y P y F Y )2121(-≤≤--=y X y P 当1=y 时,0)(=y F Y ,故1≤y 时,0)(=y F Y ,0)(=y f Y ;当1>y 时⎰⎰------==210221212d e22d e21)(22y x y y x Y x x y F ππ,此时,41e)1(21)()(---='=y Y Y y y F y f π,综上,⎪⎩⎪⎨⎧≤>-=--.1,0,1,e )1(21)(41y y y y f y Y π.(3)0<y 时,=≤=}{y X Y ∅,∴0)()()(=≤=≤=y X P y Y P y F Y ,0≥y 时,)()()()(y X y P y X P y Y P y F Y ≤≤-=≤=≤=)()(y F y F X X --=,0=y 时,0)(=y F Y ,∴0≤y 时,有0)(=y F Y ,0)(=y f Y ;0>y 时,22e 22)()()()()(y X X Y Y Y yf y f y F y F y f -=-+=-'+'=π,综上,⎪⎩⎪⎨⎧≤>=-.0,0,0,e 22)(22y y y f yY π.22.(1)设随机变量X 的概率密度为)(x f ,+∞<<∞-x ,求3X Y =的概率密度.(2)设随机变量X 的概率密度为⎩⎨⎧>=-其他.,00,e )(x x f x 求2X Y =的概率密度.解:(1)0=y 时,0)()(=≤=y Y P y F Y ,0)(=y f Y ;0≠y 时,)()()()()(333y F y X P y X P y Y P y F X Y =≤=≤=≤=,3233331())(()()(-⋅=''='=y y f y y F y F y f XY Y ;∴⎪⎩⎪⎨⎧=≠=-.0,0,0),(31)(332y y y f y y f Y .(2)由于02≥=X Y ,故当0<y 时,}{y Y ≤是不可能事件,有0)()(=≤=y Y P y F Y ;当0≥y 时,有)()(()()()(2y F y F y X y P y X P y Y P y F X X Y --=≤≤-=≤=≤=;因为当0=y 时,0)0()0()(=--=X X Y F F y F ,所以当0≤y 时,0)(=y F Y .将)(y F Y 关于y 求导数,即得Y 的概率密度为⎪⎩⎪⎨⎧≤>-+=.,;,000)](([21)(y y y f y f y y f X X Y ,⎪⎩⎪⎨⎧≤>+=-.0,0,0),e e (21y y yyy .23.设随机变量X 的概率密度为⎪⎩⎪⎨⎧<<=其他.,0,0,2)(2ππx xx f 求X Y sin =的概率密度.解:由于X 在),0(π内取值,所以X Y sin =的可能取值区间为)1,0(,在Y 的可能取值区间之外,0)(=y f Y ;当10<<y 时,使}{y Y ≤的x 取值范围是),arcsin []arcsin ,0(ππy y - ,于是}arcsin {}arcsin 0{}{ππ<≤-≤<=≤X y y X y Y .故)arcsin ()arcsin 0()()(ππ<≤-+≤<=≤=X y P y X P y Y P y F Y ⎰⎰-+=ππyX y X x x f x x f arcsin arcsin 0d )(d )(⎰⎰-+=ππππyy x xx xarcsin 2arcsin 02d 2d 2,上式两边对y 求导,得22222121)arcsin (21arcsin 2)(yyy yyy f Y -=--+-=ππππ;综上,⎪⎩⎪⎨⎧<<-=其他.,0,10,12)(2y y y f Y π.。
统计学教程答案第二章
∑ X 7 + 9 + 10 + 14 + 15 = = 11.00 n 5
∑ (X − X ) =0.00
∑X = 666.40mg/ml n
2
X =
S=
∑ (X − X ) =551.99mg/ml n −1 S CV = × 100% =82.83% X
X = ∑X = 127.20 mg/ml n
(2)求中位数,均数和标准差。 ①求中位数
M = Lx +
②求均数
ix n 2. 0 (80・50%-38)=12.24g − ∑ f L =12.0+ fM 2 17
X =
③求标准差
∑ fX =12.78 ∑f
2
S=
3.答案:
2 ∑ (X − X ) ∑ fX − ((∑ fX ) ∑ f ) = =3.77g n −1 ∑ f −1 2
统计学教程
第二章 计量资料的统计描述
五、习题答案要点
(一)名词解释 1.答案:频数表(frequency table)用来表示一批数据各观察值或在不同取值区间的 出现的频繁程度(频数) 。对于离散数据,每一个观察值即对应一个频数,如某医院某年度一 日内死亡 0,1,2…20 个病人的天数。对于散布区间很大的离散数据和连续型数据,数据散 布区间由若干组段组成,每个组段对应一个频数。 2.答案:算术均数(arithmetic mean)描述一组数据在数量上的平均水平。总体均数 用μ表示,样本均数用 X 表示。 3.答案:几何均数(geometric mean)用以描述对数正态分布或数据呈倍数变化资料的 水平。记为 G。 4.答案:中位数(median)将一组观察值由小到大排列,n 为奇数时取位次居中的变量 值;为偶数时,取位次居中的两个变量的平均值。 5.答案:极差(range)亦称全距,即最大值与最小值之差,用于资料的粗略分析,其 计算简便但稳定性较差。 6.答案:百分位数(percentile)是将 n 个观察值从小到大依次排列,再把它们的位次 依次转化为百分位。百分位数的另一个重要用途是确定医学参考值范围。
数理统计第二章课后习题答案
第二章 参数估计2.2 对容量为n 的子样,对密度函数其22(),0(;)0,0x x f x x x ααααα⎧-⎪=⎨⎪≤≥⎩ 中参数α的矩法估计。
解:1202()()a E x x x dx ααα==-⎰22022()x x dx ααα=-⎰2321221333ααααααα=-=-= 所以 133a x α∧== 其中121,21(),,,n n x x x x x x x n =+++ 为n 个样本的观察值。
2.6 设总体X 的密度函数为12(;),,,,n f x X X X θ 为其样本,求下列情况下θ∧的MLE 。
(ii)1,01(;)0,x x f x αθθ-⎧=⎨⎩ 其它 0θ (v )1,0(;)0,x e x f x θθθ-⎧≥⎪=⎨⎪⎩其它 0θ 解:(ii)1111()n n n i i i i L x x θθθθθ--====∏∏1ln ()ln (1)ln n i i L n x θθθ==+-∑11111ln ()ln 01(ln )(ln )n i i n n i i i i d L n x d n x x n θθθθ=∧--===+==-=-∑∑∑ (v)111()n i i x n L e θθθ=-∑= 11ln ()ln()nii L n x θθθ==--∑211ln ()101,n i i n i i d L n X d x x X n θθθθθ=∧==-+===∑∑2.10 设总体123(,1),,,X N X X X μ 为一样本,试证明下述三个估计变量11232123312313151021153412111362X X X X X X X X X μμμ=++=++=++ 都是μ的无偏估计量,并求出每一估计量的方差,问哪一个最小? 证:1123131()()()()5102E E X E X E X μ=++131()5102μμ=++= 同理:2123115()()()()3412E E X E X E X μ=++ 115()3412μμ=++= 3123111()()()()362E E X E X E X μ=++ 111()362μμ=++= ∴12,,μμμ是μ的无偏估计量。
统计学习题答案 第2章 统计数据的描述
第2章统计数据的描述——练习题●1.为评价家电行业售后服务的质量,随机抽取了由100家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C.一般;D.差;E.较差。
调查结果如下:B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D CC B C ED B C C B CD A C B C DE C E BB EC C AD C B A EB ACDE A B D D CA DBC C A ED C BC B C ED B C C B C(1) 指出上面的数据属于什么类型;(2)用Excel制作一张频数分布表;(3) 绘制一张条形图,反映评价等级的分布。
解:(1)由于表2.21中的数据为服务质量的等级,可以进行优劣等级比较,但不能计算差异大小,属于顺序数据。
(2)频数分布表如下:服务质量等级评价的频数分布服务质量等级家庭数(频数)频率%A1414B2121C3232D1818E1515合计100100(3)条形图的制作:将上表(包含总标题,去掉合计栏)复制到Excel表中,点击:图表向导→条形图→选择子图表类型→完成(见Excel练习题2.1)。
即得到如下的条形图:●2.某行业管理局所属40个企业2002年的产品销售收入数据如下(单位:万元):152 124 129 116 100 103 92 95 127 104105 119 114 115 87 103 118 142 135 125117 108 105 110 107 137 120 136 117 10897 88 123 115 119 138 112 146 113 126(1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率;(2)如果按规定:销售收入在125万元以上为先进企业,115万~125万元为良好企业,105万~115万元为一般企业,105万元以下为落后企业,按先进企业、良好企业、一般企业、落后企业进行分组。
统计学课后第二章习题答案
第2章练习题1、二手数据的特点是()A。
采集数据的成本低,但搜集比较困难 B. 采集数据的成本低,但搜集比较容易C。
数据缺乏可靠性 D.不适合自己研究的需要2、从含有N个元素的总体中,抽取n个元素作为样本,使得总体中的每一个元素都有相同的机会(概率)被抽中,这样的抽样方式称为()A。
简单随机抽样 B.分层抽样 C.系统抽样 D。
整群抽样3、从总体中抽取一个元素后,把这个元素放回到总体中再抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A。
重复抽样 B.不重复抽样 C.分层抽样 D.整群抽样4、一个元素被抽中后不再放回总体,然后从所剩下的元素中抽取第二个元素,直至抽取n个元素为止,这样的抽样方法称为()A.不重复抽样B。
重复抽样C.系统抽样D。
多阶段抽样5、在抽样之前先将总体的元素划分为若干类,然后从各个类中抽取一定数量的元素组成一个样本,这样的抽样方式称为()A。
简单随机抽样B。
系统抽样C.分层抽样D.整群抽样6、先将总体各元素按某种顺序排列,并按某种规则确定一个随机起点,然后每隔一定的间隔抽取一个元素,直至抽取n个元素形成一个样本。
这样的抽样方式称为()A. 分层抽样B. 简单随机抽样C。
系统抽样D。
整群抽样7、先将总体划分为若干群,然后以群作为抽样单位从中抽取部分群,再对抽中的各个群中所包含的所有元素进行观察,这样的抽样方式称为()A. 系统抽样B。
多阶段抽样C。
分层抽样D。
整群抽样8、为了调查某校学生的购书费用支出,从男生中抽取60名学生调查,从女生中抽取40名学生调查,这种调查方是() A。
简单随机抽样B. 整群抽样C.系统抽样D。
分层抽样9、为了调查某校学生的购书费用支出,从全校抽取4个班级的学生进行调查,这种调查方法是()A. 系统抽样B. 简单随机抽样C.分层抽样D。
整群抽样10、为了调查某校学生的购书费用支出,将全校学生的名单按拼音顺序排列后,每隔50名学生抽取一名学生进行调查,这种调查方法是?()A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学第2章数据的描述课堂练习及答案
值?为什么?(文字回答即可)
(2)试通过计算,比较分析哪一组的身高差异大?
度值更好?试说明理由。
位数及均值的关系,并据此判断甲车间数据分布的形态。
(2)通过计算判断哪个车间工人平均奖金额的代表性强?
1[解]:(1)应采用“离散系数(标准差系数)”。
(2)有关计算如下表:
所以:成年组身高的均值:1.17210
===
n x 成(cm ) 幼儿组身高的均值:3.7110
713
==∑=n x x 幼(cm) 成年组的标准差:()20.41109.15812
=-=-∑-=n x x S 成(cm)
幼儿组的标准差:()50.21
101.5612
=-=-∑-=n x x S 幼(cm) 成年组的离散系数: 4.20
2.44%172.1S V x ==
=成成成
幼儿组的离散系数: 2.50
3.51%71.3
S V x
==
=幼幼幼
因为:V V 幼成< 所以幼儿组的身高差异大。
2[解]:(提示:用中位数。
因为收入分布为右偏,且频数较多的几个组的家庭百分比相差不大,众数不十分明显。
)
3[解]:有关计算表如下:
(1)因为:甲车间的最大频数为50,所以甲车间的众数组为30-40,于是:30=L
50=f 81=-f 161=+f 10=i
则:甲车间奖金的众数:
()()()()
3653.351016508508
50301111≈=⨯-+--+=∙-+--+
=+--i f f f f f f L M O (元)
因为:乙车间的最大频数为55,所以乙车间的众数组为40-50,于是:
40=L 55=f 301=-f 81=+f 10=i
则:乙车间奖金的众数:
()()()()
47.4310855305530
55401112=⨯-+--+=∙-+--+
=+--i f f f f f f L M O (元)
甲车间中位数的位置=
402
80
2
==
∑f
,因为甲车间的向上累计频数62>40,所以甲车间的中位数组为30-40。
于是30=L 121=-S m
50=f m 10=i
则:甲车间奖金的中位数为:
366.35105012403021
1≈=⨯-+=∙-∑+
=-i f S f
L M m
m e (元) 乙车间中位数的位置=
502
1002==∑f ,因为乙车间的向上累计频数92>50,所以乙车间的中位数组为:40-50。
于是40=L 371=-S m
55=f m 10=i
则:乙车间奖金的中位数为:
36.42105537504021
2
=⨯-+=∙-∑+=-i f S f
L M m
m e (元) 甲车间的均值365.358028401
11≈==∑∑=
f f x x (元) 乙车间的均值3.4110041302
22==∑∑=
f f x x (元) 对于甲车间而言:因为36111≈≈≈x M M e O ,所以甲车间奖金数据近似服从“对称分布”。
对于乙车间而言,因为47.4336.423.41222=<=<=M M x O e ,有“极小值”,表明乙车间奖金的数据分布呈“左篇(负偏)分布”。
(2)(注:这里是将甲、乙车间视为总体,若为样本资料,则标准差公式的分母必须是自由度11n f --∑或)
甲车间的奖金的标准差为:()73.78047802
1==∑∑-=f
f
x x σ
乙车间的奖金的标准差为:()57.710057312
2==∑
∑-=f f
x x σ
甲车间的离散系数:111
7.73
21.77%35.5
V x
σ
=
=
= 乙车间的离散系数:222
7.57
18.33%41.3
V x
σ==
= 因为:V V 21>表明甲车间奖金的差异程度大,反映出乙车间平均奖金的代表性要好于甲车间。
