高中教材变式题9:圆锥曲线与方程
高中生圆锥曲线练习题及讲解

高中生圆锥曲线练习题及讲解圆锥曲线是高中数学中的一个重要概念,通常包括椭圆、双曲线和抛物线。
下面是一些圆锥曲线的练习题以及相应的讲解。
### 练习题1:椭圆的标准方程给定一个椭圆的两个焦点距离为2c,且长轴长度为2a,求椭圆的标准方程。
解答步骤:1. 根据椭圆的性质,我们知道长轴和短轴的关系为 \( a^2 = b^2 +c^2 \)。
2. 题目给出 \( 2c \) 和 \( 2a \),可以求出 \( c \) 和 \( a \) 的值。
3. 将 \( c \) 和 \( a \) 的值代入上述公式,求出 \( b \) 的值。
4. 最终,椭圆的标准方程为 \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)。
### 练习题2:双曲线的渐近线已知双曲线的方程为 \( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \),求其渐近线方程。
解答步骤:1. 双曲线的渐近线方程可以通过 \( \frac{x^2}{a^2} -\frac{y^2}{b^2} = 0 \) 得到。
2. 将上述方程简化,得到 \( y = \pm \frac{b}{a}x \)。
3. 这就是双曲线的渐近线方程。
### 练习题3:抛物线的焦点和准线给定抛物线的方程 \( y^2 = 4ax \),求其焦点和准线。
解答步骤:1. 抛物线的焦点位于 \( (a, 0) \)。
2. 准线方程为 \( x = -a \)。
3. 焦点和准线是抛物线的重要特征,可以通过方程直接得出。
### 练习题4:圆锥曲线的参数方程已知椭圆的参数方程为 \( x = a \cos(\theta) \) 和 \( y = b\sin(\theta) \),求其标准方程。
解答步骤:1. 将参数方程中的 \( \cos(\theta) \) 和 \( \sin(\theta) \) 替换为 \( x/a \) 和 \( y/b \)。
高三理科数学秋季讲义 第9讲.圆锥曲线基本量与性质巩固、曲线与方程. 教师版
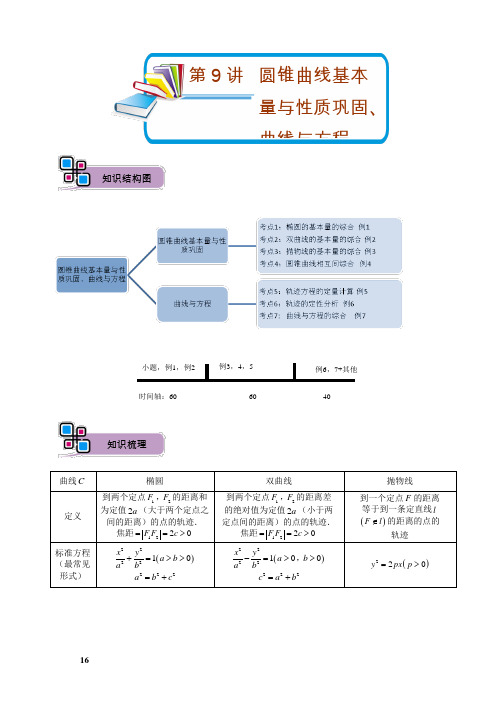
例6,7+其他例3,4,5小题,例1,例2时间轴:60 60 40知识梳理知识结构图第9讲 圆锥曲线基本量与性质巩固、曲线与方程若双曲线22221x y a b -=( ) A .2y x =± B .y = C .12y x =± D .y x =±【解析】B1.双曲线22+1mx y =的虚轴长是实轴长的2倍,则m 等于( )A .14-B .4-C .4D .14【解析】A ;2.设抛物线24x y =的焦点为F ,经过点()14P ,的直线l 与抛物线相交于A 、B 两点,且点P 恰为AB 的中点,则AF BF += . 【解析】10;3.若点O 和点F 分别为椭圆22143x y +=的中心和左焦点,点P 为椭圆上的任意一点,则OP FP ⋅的最大值为( )A .2B .3C .6D .8 【解析】C ;小题热身真题再现4.已知两定点(2,0)A -,()1,0B ,如果动点P 满足2PA PB =,则点P 的轨迹所包围的图形的面积等于( )A .πB .4πC .8πD .9π 【解析】B ;1.设点P 是椭圆22221x y a b +=(0a b >>)上的动点,1F ,2F 是椭圆的左右焦点,2PF x ⊥轴,P 点在第一象限,那么P 点坐标为 .【解析】2b c a ⎛⎫⎪⎝⎭,;可拓展到双曲线和抛物线,有类似结论.2.双曲线的渐近线有重要性质:双曲线22221(00)x y a b a b-=>>,的焦点到渐近线的距离为_____,顶点到渐近线的距离为 .【解析】b ;3.如图把椭圆2212516x y +=的长轴AB 分成8份,过每个分点作x 轴的垂线交椭圆的上半部分于127P P P ,,,七个点,F 是椭圆的一个焦点,则127PF P F P F +++=_____.暑期知识回顾9.1圆锥曲线基本量综合【解析】35;4.一动圆的圆心在抛物线28y x =上,且动圆恒与直线20x +=相切,则此动圆必过定点( ) A .()40, B .()20, C .()02, D .()02-, 【解析】B ;5.已知点()11A ,,1F 是椭圆22195x y +=的左焦点,P 是椭圆上的任意一点,则1PF PA +的最小值为 . 【解析】6考点1:椭圆的基本量综合【例1】⑴求适合下列条件的椭圆的标准方程: ①过点(32)-,且与椭圆224936x y +=有相同焦点;②长轴与短轴长之和为20,焦距为③以边长为4的正ABC △的顶点B 、C 为焦点,经过顶点A .⑵已知椭圆22+11510x y =的焦点为12F F ,,P 为椭圆上一动点,1260F PF ∠=︒,求12F PF S △.⑶如图所示,椭圆中心在原点,F 是左焦点,直线1AB 与BF 交于D ,且190BDB ∠=︒,则椭圆的离心率为( )AB C D【解析】⑴ ①+11510= ②22+13616x y =或者22+11636x y = ③22+11612x y =或者22+11216x y = ⑵ 12F PF S =△;⑶ B ;【设计意图】⑴复习椭圆的基本性质;⑵焦点三角形面积公式2tan 2S b θ=;⑶椭圆离心率的综合题目.经典精讲【拓展】设椭圆22221(0)x y a b a b+=>>的左、右焦点分别为12F F A ,,是椭圆上的一点,212AF F F ⊥,原点O 到直线1AF 的距离为113OF.证明:a =.【解析】由题设212AF F F ⊥及1(0)F c -,,2(0)F c ,,不妨设点()A c y ,,其中0y >.由于点A 在椭圆上, 有22221c y a b +=,即222221a b y a b-+=.解得2b y a =,从而得到2b Ac a ⎛⎫ ⎪⎝⎭,.212b AF a a=-在三角形12AF F 中由面积相等得1112223AF OF F F AF ⋅=⋅∴222223b b a c c a a ⎛⎫-⋅=⋅ ⎪⎝⎭,∴a =.该题也可求解直线1AF 的方程,利用点O 到该直线的距离求解,运算较繁.也可利用三角形相似求解,有关焦点三角形的问题,要增强解三角形的意识.【拓展】(2012年四川卷)椭圆22143x y +=的左焦点为F ,直线x m =与椭圆相交于点A B ,,当FAB △ 的周长最大时,FAB △的面积是 .【解析】3;【拓展】在直线:90l x y -+=上任意取一点M ,经过M 点且以椭圆221123x y +=的焦点为焦点作椭圆,所作椭圆的长轴最短为 .【分析】要使所作椭圆的长轴最短,当然想到椭圆的定义.基本的解题思路如下:长轴最短→三点一直线→寻求对称→对称变换.在一系列的变化过程中巧妙的运用对称,使我们找到一种简明的解题方法.通过此对称性主要利用1221||||||NF NF F F '+≥.【解析】考点2:双曲线的基本量综合【例2】⑴求适合下列条件的双曲线的标准方程.①虚轴长为12,离心率为54;②焦距为26,且经过点()012M ,; ③与双曲线221916x y -=有公共渐近线,且经过点(3A -,.⑵设1F ,2F 分别是双曲线2219y x -=的左、右焦点,若点P 在双曲线上,且120PF PF ⋅=,则12PF PF +=( )A B.CD .⑶如图,1F 和2F 分别是双曲线22221(0,0)x y a b a b-=>>的两个焦点,A 和B 是以O 为圆心,以1OF 为半径的圆与该双曲线左支的两个交点,且2F AB △是等边三角形,则双曲线的离心率为( )AB D .1【解析】⑴ ①2216436x y -=或2216436y x-=.②22114425y x -=. ③224194x y -=.⑵ B ⑶ D ;【评注】即使是解析法解题,也须不失时机地引入几何手段.注意选项,直接排除AB .【拓展】设P 是双曲线()2222100x y a b a b-=>>,左支上的一点,1F 、2F 分别是双曲线的左、右焦点,则以2PF 为直径的圆与以双曲线的实轴为直径的圆的位置关系是( ) A .内切 B .外切 C .内切或外切D .不相切【解析】A ;考点3:抛物线的基本量综合【例3】⑴根据下列条件求抛物线的标准方程.①抛物线的焦点是双曲线22169144x y -=的左顶点; ②经过点()23A -,;③焦点在直线240x y --=上;④抛物线焦点F 在x 轴上,直线3y =-与抛物线交于点A ,5AF =. ⑵已知动点M的坐标满足方程3412x y +-,则动点M 的轨迹是( ) A .椭圆 B .双曲线 C .抛物线 D .以上都不对⑶已知点(03)A ,-,()23B ,,设点P 为抛物线2x y =上一点,求PAB △面积的最小值及取到最小值时P 点的坐标.【解析】⑴ ①212y x =-.②292y x =或243x y =-.③28x y =-或216y x =.④为22y x =±或218y x =±. ⑵ C ;⑶当3924P ⎛⎫⎪⎝⎭,时,PAB △面积有最小值34S =.【拓展】已知抛物线2y x =,动弦x【分析1】要求AB 12观察到1y 、2y 是梯形ABCD 的两底,这样使得中点纵坐标y 成为中位线,可以利用几何图形的性质和抛物线定义求解.【分析2】要求AB 中点M 的纵坐标y 的最小值,可列出y 关于某一变量的函数,然后求此函数的最小值.【答案】点M 纵坐标的最小值为34.【拓展】设P 是抛物线24y x =上的一个动点.⑴ 求点P 到点()11A -,的距离与点P 到直线1x =-的距离之和的最小值; ⑵ 若()32B ,,求PB PF +的最小值.【解析】⑴⑵ PB PF +的最小值是4.【教师备案】(本内容中涉及过焦点的直线与抛物线相交所得焦点弦的问题)其它的性质:性质a.过抛物线22y px =上一点()00M x y ,的切线方程是:()00y y p x x =+ 【证明】对方程22y px =两边取导数:22y y p '⋅=,∴py y'=是切线的斜率.00|x x p k y y ='==.由点斜式方程:()()20000001p y y x x y y px px y y -=-⇒=-+∵202y px =,代入⑴即得:()00y y p x x =+.性质b .⑴若AB 是抛物线22(0)y px p =>的焦点弦,且直线AB 的倾斜角为α,则22si n p AB α=()0α≠.⑵ 焦点弦中通径(过焦点且垂直于抛物线对称轴的弦)最短.【证明】⑴ 设11(,)A x y ,22(,)B x y ,当直线AB 的斜率存在时,设直线:AB y 2p k x ⎛⎫=- ⎪⎝⎭,由2()22p y k x y px ⎧=-⎪⎨⎪=⎩得,2220ky py kp --= ∴122py y k+=,212y y p =-, ∴2222121212122222y y p AB y y x x p p p p p p p k ⎡⎤⎛⎫=-=++=++=++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦222222(1)2(1tan )2tan sin p k p pk ααα++===. 易验证,结论对斜率不存在时也成立.⑵ 由⑴:AB 为通径时,90α=︒,2sin α的值最大,AB 最小.性质c .设O 为抛物线的顶点,F 为抛物线的焦点且PQ 为过焦点的弦,若OF a =,PQ b =.则OPQ S =△【解析】如图2,不妨设抛物线方程为24y ax =,点()11P x y ,、点()22Q x y ,x图2则由抛物线定义知:12122PQ PF QF x a x a x x a =+=+++=++ 又PQ b =,则122x x b a +=-.由24y ax =得:2212244y y b a a a+=-,即()221242y y a b a +=-. 又PQ 为过焦点的弦,所以2124y y a =-,则21y y -==所以,2112OPQ S OF y y =⋅-=△ 【点评】将焦点弦分成两段,利用定义将焦点弦长用两端点横坐标表示,结合抛物线方程,利用韦达定理是常见的基本技能.由性质b 、c可推出焦点三角形的面积公式也可以为:222sin p p S α==△.考点4:圆锥曲线相互间综合【例4】⑴如下图,已知AB 10=,图中的一系列圆是圆心分别为A B ,的两组同心圆,每组同心圆的半径分别是123n ,,,,,利用这两组同心圆可以画出以A B ,为焦点的双曲线,若其中经过点M N P ,,的双曲线的离心率分别记为M e ,N e ,P e ,则它们的大小关系是________(用“<”连接).⑵若椭圆()222210x y a b a b+=>>的左、右焦点分别为12F F ,,线段12F F 被抛物线2y bx =的焦点分为3:1的两段,则此椭圆的离心率为( )A .1617B C .45D⑶已知1F 、2F 是两个定点,点P 是以1F 和2F 为公共焦点的椭圆和双曲线的一个交点,并且12PF PF ⊥,1e 和2e 分别是上述椭圆和双曲线的离心率,则( )A .2212114e e +=B .22124e e += C .2212112e e += D .22122e e +=⑷已知抛物线()220y px p =>与双曲线22221x y a b-=有相同的焦点F ,点A 是两曲线的交点,且AF x ⊥轴,则双曲线的离心率为( )AB1 C1 D.12【解析】⑴ M P N e e e <<⑵ B ⑶ C ; ⑷ C ;考点5:轨迹方程的定量计算【教师备案】求动点轨迹方程的一般步骤:⑴ 建立适当的坐标系 ⑵ 设出要求轨迹点的坐标 ⑶ 列出方程. ⑷ 化简⑸ 检验是否有不满足条件的点,或漏掉某些点【铺垫】⑴直接法动点M 到定点()10F ,的距离与到定直线l :3x =的距离的和为定值4.求点M 的轨迹.⑵定义法:圆的性质——直径所对的圆周角为直角.类似的,对于椭圆能得到什么呢?设AB 为椭圆22221x y a b+=的“直径”(过中心的弦),P 为椭圆上一点(异于A B ,),P A P B ,仍垂直吗?会有什么关系?x经典精讲9.2曲线与方程思想⑶代入法:若所求轨迹上的动点()P x y ,与另一个已知轨迹(曲线)():0C f x y =,上的动点()11Q x y ,存在着某种联系,则可以把点Q 的坐标用点P 的坐标表示出来,然后代入曲线C 的方程()0f x y =,中并化简,即得动点P 轨迹方程.这种求轨迹方程的方法叫做代入法(又称相关点法).如图所示,已知(40)P ,是圆2236x y +=内的一点,A B 、是圆上两动点,且满足90APB ∠=︒,求矩形APBQ 的顶点Q 的轨迹方程.x⑷参数法:根据题设条件,用一个参数分别表示出动点()x y ,的坐标x 和y ,或列出两个含同一个参数的动点()x y ,的坐标x 和y 之间的关系式,这样就间接地把x 和y 联系起来了,然后联立这两个等式并消去参数,即可得到动点的轨迹方程.这种求轨迹的方法称为参数法.过抛物线2y x =的顶点O 作两条互相垂直的弦OA 、OB ,以OA 、OB 为邻边作矩形AOBM ,如图,求点M 的轨迹方程.【解析】⑴()()()2240312434y x x y x x ⎧=⎪⎨=--<⎪⎩≤≤≤. ⑵设1100()()A x y P x y ,,,,则11()B x y --,,2201010122010101PA PBy y y y y y k k x x x x x x -+-⋅=⋅=-+-,又因为2200221x y a b +=,2211221x y a b +=,所以:22012201y y x x --22b a=-,即:,PA PB 的斜率之积为定值. 这种定义总结如下:PA PB k k λ⋅=,1.如果0λ>,动点轨迹为不完整的双曲线 2.如果=0λ,动点轨迹为不完整的两条直线 3.如果0λ<,1λ≠-动点轨迹为不完整的椭圆 4.如果=1λ-,动点轨迹为不完整的圆.轨迹上都没有与A B ,的横坐标一样的所有点. ⑶2256x y +=. ⑷22y x =-.【例5】⑴ 直接法动点()P x y ,到两定点(30)A -,和(30)B ,的距离的比等于2(即||2||PA PB =),求动点P 的轨迹方程.⑵ 定义法在平面直角坐标系xOy 中,点B 与点()11A -,关于原点O 对称,P 是动点,且直线AP 与BP 的斜率之积等于2.求动点P 的轨迹方程.⑶ 代入法点B 是椭圆2212516x y +=上的动点,()100A ,为定点,求线段AB 的中点M 的轨迹方程.⑷ 参数法过抛物线2:C y x =-上一点()11P -,作斜率为1k 、2k 的两条直线,分别交抛物线C 于异于点P 的两点()11A x y ,,()22B x y ,,且满足120k k +=.若点M 满足BM MA =,求点M 的轨迹方程.【解析】⑴ 22516x y +=(-),轨迹是以50(,)为圆心,4为半径的圆. ⑵ 2221(1)x y x -=≠±.⑶ 分析:题中涉及了三个点A B M ,,,其中A 为定点,而B 、M 为动点,且点B 的运动是有规律的,显然M 的运动是由B 的运动而引发的,可见M 、B 为相关点,故采用相关点法求动点M 的轨迹方程.()22451254x y -+=⑷ 1x =-(1y -≤且5y -≠).考点6:轨迹的定性分析【例6】有的习题只需要能够确定轨迹的基本形状,不需要准确求出轨迹的方程,或者有的题目根本就没有平面直角坐标系,解题时只需要判断形状即可. ⑴已知定点(11)A ,和直线20l x y :+-=,那么到定点A 的距离和到定直线l 的距离相等的点的轨迹为( )A .椭圆B .双曲线C .抛物线D .直线⑵已知椭圆的焦点是12F F P 、,是椭圆上的一个动点,如果M 是线段1F P 的中点,则动点M的轨迹是( )A .圆B .椭圆C .双曲线的一支D .抛物线⑶ABC △中,A 为动点,B C 、为定点,02a B ⎛⎫- ⎪⎝⎭,,02a C ⎛⎫⎪⎝⎭,,且满足条件1sin sin sin 2C B A -=,则动点A 的轨迹方程是__________.⑷若点P 到直线1x =-的距离比它到点(20),的距离小1,则点P 的轨迹为( ) A .圆 B .椭圆 C .双曲线 D .抛物线⑸曲线C 是平面内与两个定点1(10)F -,和2(10)F ,的距离的积等于常数2(1)a a >的点的轨迹,给出下列三个结论: ①曲线C 过坐标原点;②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则12F PF △的面积不大于212a .其中,所有正确结论的序号是____________.【解析】⑴ D ;⑵ B ;⑶ 2222161613x y a a -=(0x >且0y ≠).⑷D ; ⑸②③.【拓展】如图,AB 是平面α的斜线段,A 为斜足.若点P 在平面α内运动,使得ABP △的面积为定值,则动点P 的轨迹是( )αPB AA .圆B .椭圆C .一条直线D .两条平行直线【解析】B ;考点7:曲线与方程综合【例7】⑴曲线C 是平面内到定点(01)F ,和定直线:1l y =-的距离之和等于4的点的轨迹,给出下列三个结论:① 曲线C 关于y 轴对称;② 若点(,)P x y 在曲线C 上,则||2y ≤; ③ 若点P 在曲线C 上,则1||4PF ≤≤. 其中,所有正确结论的序号是_____.⑵已知以4T =为周期的函数(11]()12(13]x f x x x ⎧∈-⎪=⎨--∈⎪⎩,,,,其中0m >.若方程3()f x x=恰有5个实数解,则m 的取值范围为( )A.83⎫⎪⎪⎝⎭ B.⎝ C .4833⎛⎫ ⎪⎝⎭, D.43⎛ ⎝ 【解析】⑴ ①②③⑵ B ;【拓展】方程1169x xy y+=-的曲线即为函数()y f x =的图象,对于函数()y f x =,有如下结论:①()f x 在R 上单调递减;②函数()4()3F x f x x =+不存在零点; ③函数()y f x =的值域是R ;④若函数()g x 和()f x 的图象关于原点对称,则函数()y g x =的图象就是方程1169y y x x +=确定的曲线.其中所有正确的命题序号是( )A .①②B .②③C .①③④D .①②③【解析】D ;【拓展】曲线C 是平面内到定点(1,0)A 的距离与到定直线1x =-的距离之和为3的动点P 的轨迹. 则曲线C 与y 轴交点的坐标是 ;又已知点(1)B a ,(a 为常数),那么PB PA +的最小值()d a = .【解析】(0,; 1.41,4, 1.41,2, 1 1.a a a a a a -+-<-⎨⎪--<<⎪⎩≤或≥≤ 【教师备案】第二问比较困难,运算量比较大,会耽误时间较多,如无充分备课,可跳过.【专题补充】(如有时间可以补充,体现教师对高考的研究水平,学生版不出现)性质1 若椭圆()2222:10x y C a b a b+=>>,12F F ,分别为左、右焦点,点P 为椭圆上任意一点,则以1PF为直径的1O ⊙与以长轴为直径的O ⊙内切. 【解析】如图所示,在12F PF △中,O ,1O 分别为12F F ,1PF 的中点,所以1212OO PF =,又因为以1PF 为直径的1O ⊙的半径为1112r PF =,O ⊙的半径2r a =,所以21112r r a PF -=-.又因为122PF PF a +=,所以211211122r r a PF PF OO -=-==,所以两圆内切.性质2 若双曲线()2222:100x y C a b a b-=>>,,12FF ,分别为左、右焦点,则⑴ 当点P 为双曲线左支上任意一点时,以1PF 为直径的1O ⊙与以长轴为直径的O ⊙外切; ⑵ 当点P 为双曲线右支上任意一点时,以1PF 为直径的1O ⊙与以长轴为直径的O ⊙内切.【解析】证明同性质1类似,过程略.【演练1】双曲线221259x y -=的左右焦点分别为1F ,2F ,过焦点1F 的直线与双曲线左支交于A B ,两点,若弦AB 的长为4,则2ABF △的周长为 .【解析】28【演练2】已知点P 的抛物线24y x =-上的一个动点,则点P 到点()02M ,的距离与点P 到该抛物线准线的距离之和的最小值为 .【解析5【演练3】设12F F ,为双曲线2211620x y -=的两个焦点,点P 在双曲线上满足1290F PF ∠=︒,则P 的坐标为 .【解析】4101433⎛⎫± ⎪⎝⎭.课后习题。
圆锥曲线的方程与性质

第26练 圆锥曲线的方程与性质1.(2020·全国Ⅰ)已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p 等于( ) A .2 B .3 C .6 D .9 答案 C解析 设A (x ,y ),由抛物线的定义知,点A 到准线的距离为12,即x +p2=12.又因为点A 到y 轴的距离为9,即x =9, 所以9+p2=12,解得p =6.2.(2021·新高考全国Ⅰ)已知F 1,F 2是椭圆C :x 29+y 24=1的两个焦点,点M 在C 上,则|MF 1|·|MF 2|的最大值为( )A .13B .12C .9D .6 答案 C解析 由椭圆C :x 29+y 24=1,得|MF 1|+|MF 2|=2×3=6, 则|MF 1|·|MF 2|≤⎝⎛⎭⎪⎫|MF 1|+|MF 2|22=32=9, 当且仅当|MF 1|=|MF 2|=3时等号成立.3.(2022·全国甲卷)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为13,A 1,A 2分别为C 的左、右顶点,B 为C 的上顶点.若BA 1—→·BA 2—→=-1,则C 的方程为( ) A.x 218+y 216=1 B.x 29+y 28=1 C.x 23+y 22=1 D.x 22+y 2=1 答案 B解析 依题意得A 1(-a ,0),A 2(a ,0),B (0,b ), 所以BA 1—→=(-a ,-b ),BA 2—→=(a ,-b ),BA 1—→·BA 2—→=-a 2+b 2=-(a 2-b 2)=-c 2=-1,故c =1, 又C 的离心率e =c a =1a =13,所以a =3,a 2=9,b 2=a 2-c 2=8, 所以C 的方程为x 29+y 28=1.4.(2021·全国甲卷)已知F 1,F 2是双曲线C 的两个焦点,P 为C 上一点,且∠F 1PF 2=60°,|PF 1|=3|PF 2|,则C 的离心率为( ) A.72 B.132C.7D.13 答案 A解析 设|PF 2|=m ,则|PF 1|=3m ,则|F 1F 2|=m 2+9m 2-2×3m ×m ×cos 60°=7m ,所以C的离心率e =c a =2c 2a =|F 1F 2||PF 1|-|PF 2|=7m 2m =72.5.(2021·全国乙卷)设B 是椭圆C :x 2a 2+y 2b 2=1(a >b >0)的上顶点,若C 上的任意一点P 都满足|PB |≤2b ,则C 的离心率的取值范围是( ) A.⎣⎡⎭⎫22,1B.⎣⎡⎭⎫12,1C.⎝⎛⎦⎤0,22 D.⎝⎛⎦⎤0,12 答案 C解析 依题意,B (0,b ),设椭圆上一点P (x 0,y 0),则|y 0|≤b ,x 20a 2+y 20b 2=1,可得x 20=a 2-a 2b2y 20,则|PB |2=x 20+(y 0-b )2=x 20+y 20-2by 0+b 2=-c 2b2y 20-2by 0+a 2+b 2≤4b 2.因为当y 0=-b 时,|PB |2=4b 2,所以-b 3c 2≤-b ,得2c 2≤a 2,所以离心率e =c a ≤22. 6.(2022·全国甲卷)若双曲线y 2-x 2m2=1(m >0)的渐近线与圆x 2+y 2-4y +3=0相切,则m =________. 答案33解析 双曲线y 2-x 2m 2=1(m >0)的渐近线为y =±xm,即x ±my =0,不妨取x +my =0,圆x 2+y 2-4y +3=0, 即x 2+(y -2)2=1,所以圆心为(0,2),半径r =1,依题意知圆心(0,2)到渐近线x +my =0的距离d =|2m |1+m 2=1,解得m =33或m =-33(舍去). 7.(2022·新高考全国Ⅰ)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0),C 的上顶点为A ,两个焦点为F 1,F 2,离心率为12.过F 1且垂直于AF 2的直线与C 交于D ,E 两点,|DE |=6,则△ADE 的周长是________. 答案 13解析 ∵椭圆的离心率为e =c a =12,∴a =2c ,∴b 2=a 2-c 2=3c 2,∴椭圆的方程为x 24c 2+y 23c 2=1,即3x 2+4y 2-12c 2=0,不妨设左焦点为F 1,右焦点为F 2,如图所示,∵|AF 2|=a ,|OF 2|=c ,a =2c , ∴∠AF 2O =π3,∴△AF 1F 2为正三角形,∵过F 1且垂直于AF 2的直线与C 交于D ,E 两点,DE 为线段AF 2的垂直平分线,∴直线DE 的斜率为33,斜率的倒数为3, ∴直线DE 的方程为x =3y -c , 代入椭圆方程3x 2+4y 2-12c 2=0, 整理化简得13y 2-63cy -9c 2=0,判别式Δ=(63c )2+4×13×9c 2=62×16×c 2, 设D (x 1,y 1),E (x 2,y 2), ∴|DE |=1+(3)2|y 1-y 2|=2×Δ13=2×6×4×c13=6, ∴ c =138,则a =2c =134,∵DE 为线段AF 2的垂直平分线,根据对称性知, |AD |=|DF 2|,|AE |=|EF 2|,∴△ADE 的周长等于△F 2DE 的周长,利用椭圆的定义得到△F 2DE 的周长为|DF 2|+|EF 2|+|DE |=|DF 2|+|EF 2|+|DF 1|+|EF 1|=|DF 1|+|DF 2|+|EF 1|+|EF 2|=2a +2a =4a =13.8.(2022·浙江)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左焦点为F ,过F 且斜率为b 4a 的直线交双曲线于点A (x 1,y 1),交双曲线的渐近线于点B (x 2,y 2)且x 1<0<x 2.若|FB |=3|F A |,则双曲线的离心率是________. 答案364解析 如图,过F 且斜率为b 4a 的直线AB 的方程为y =b4a(x +c ),渐近线l 2的方程为y =bax ,联立⎩⎨⎧y =b4a(x +c ),y =ba x ,得B ⎝⎛⎭⎫c 3,bc 3a ,由|FB |=3|F A |,得A ⎝⎛⎭⎫-5c 9,bc 9a , 而点A 在双曲线上,于是25c 281a 2-b 2c 281a 2b 2=1,解得c 2a 2=8124,所以离心率e =364.9.(2022·衡水模拟)已知双曲线C :x 2m -y 22m +3=1与双曲线x 2-y 2=6有相同的焦点.则C 的渐近线方程为( ) A.2x ±y =0 B .x ±2y =0 C.3x ±y =0 D .x ±3y =0答案 C 解析 由x 2-y 2=6,得x 26-y 26=1, 由题意得m +2m +3=12,解得m =3, 所以C :x 23-y 29=1,所以C 的渐近线方程为y =±3x , 即3x ±y =0.10.(2022·宝鸡模拟)设抛物线C :x 2=4y 的焦点为F ,准线l 与y 轴的交点为M ,P 是C 上一点,若|PF |=5,则|PM |等于( ) A.21 B .5 C .27 D.41 答案 D解析 如图所示,过点P 作PQ 垂直于l ,交l 于点Q ,不妨设P (x ,y )(x >0),根据抛物线定义得|PF |=|PQ |=y +p2=y +1=5,所以y =4,所以x =4,即P (4,4), 所以|QM |=4, 所以|PM |=|PQ |2+|QM |2=52+42=41.11.(2022·梅州模拟)双曲线x 29-y 216=1的两个焦点为F 1,F 2,点P 在双曲线上,若PF 1⊥PF 2,则点P 到x 轴的距离为( ) A.85 B.165 C .4 D.163 答案 B解析 设点P (x ,y ), 由双曲线x 29-y 216=1,可知F 1(-5,0),F 2(5,0), ∵PF 1⊥PF 2, ∴y -0x +5·y -0x -5=-1, 即x 2+y 2=25,代入双曲线方程x 29-y 216=1,得25-y 29-y 216=1,∴y 2=25625,∴|y |=165,∴P 到x 轴的距离是165.12.(2022·淄博模拟)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的右焦点为F ,上顶点为B ,直线BF 与C 相交于另一点A ,点A 在x 轴上的射影为A 1,O 为坐标原点,若BO →=2A 1A —→,则C 的离心率为( ) A.33 B.12 C.22 D.32答案 A解析 由题意得F (c ,0),B (0,b ),设A (x ,y ), 因为BO →=2A 1A —→, 所以BF →=2F A →,所以(c ,-b )=2(x -c ,y ),得⎩⎨⎧x =3c 2,y =-b2,即A ⎝⎛⎭⎫3c 2,-b 2, 因为点A 在椭圆C :x 2a 2+y 2b 2=1(a >b >0)上,所以9c 24a 2+b 24b 2=1,化简得c 2a 2=13,所以离心率e =c a =33.13.(2022·临沂模拟)已知F 1,F 2分别为双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,点P在第二象限内,且满足|F 1P |=a ,(F 2P —→+F 2F 1—→)·F 1P —→=0,线段F 1P 与双曲线C 交于点Q ,若|F 1P |=3|F 1Q |,则C 的离心率为( ) A.213 B.305 C.516 D.10510答案 C解析 取F 1P 的中点M ,如图,(F 2P —→+F 2F 1—→)·F 1P —→=0⇒F 1P ⊥F 2M . 由题意可得,⎩⎪⎨⎪⎧|QF 2|-|QF 1|=2a ,|QF 1|=a 3⇒|QF 2|=7a 3, 又|F 1M |=a 2,|QM |=a 2-a 3=a 6.由|F 2M |2=|F 1F 2|2-|F 1M |2 =|QF 2|2-|QM |2, 得4c 2-a 24=49a 29-a 236, 整理得,c 2=1712a 2,则c a=1712=516. 14.(2022·厦门模拟)过抛物线C :y 2=4x 的焦点F 的直线l 与C 交于A ,B 两点,设A (x 1,y 1),B (x 2,y 2),已知M (3,-2),N (-1,1),则下列结论不正确的是( ) A .若直线l 垂直于x 轴,则|AB |=4 B .y 1y 2=-4C .若P 为C 上的动点,则|PM |+|PF |的最小值为5D .若点N 在以AB 为直径的圆上,则直线l 的斜率为2 答案 C解析 当直线l 垂直于x 轴时,其方程为x =1,联立⎩⎪⎨⎪⎧ y 2=4x ,x =1,可得⎩⎪⎨⎪⎧ x =1,y =2或⎩⎪⎨⎪⎧x =1,y =-2,所以A (1,2),B (1,-2),或A (1,-2),B (1,2), 所以|AB |=4,A 对;由已知可得直线l 的斜率不为0, 故可设其方程为x =my +1,联立⎩⎪⎨⎪⎧y 2=4x ,x =my +1,化简可得y 2-4my -4=0,Δ=(4m )2+16>0,则y 1+y 2=4m ,y 1y 2=-4,B 对;点N 在以AB 为直径的圆上,则NA →·NB →=0, 又N (-1,1),所以(x 1+1)(x 2+1)+(y 1-1)(y 2-1)=0, 又x 1=my 1+1,x 2=my 2+1,所以(my 1+2)(my 2+2)+(y 1-1)(y 2-1)=0, 所以(m 2+1)y 1y 2+(2m -1)(y 1+y 2)+5=0, 所以4m 2-4m +1=0,故m =12,此时直线l 的斜率为2,D 对;如图,过点P 作PP 1垂直于准线x =-1,垂足为P 1, 过点M 作MM 1垂直于准线x =-1,垂足为M 1,则|PP 1|=|PF |,所以|PM |+|PF |=|PM |+|PP 1|≥|MM 1|=4, 当且仅当点P 的坐标为(1,-2)时,等号成立, 所以|PM |+|PF |的最小值为4,C 错.15.(2022·宣城模拟)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线与直线l :x -2y -5=0平行,且双曲线的一个焦点在直线l 上,则双曲线的方程是________. 答案 x 24-y 2=1解析 由题意可知,b a =12,直线l :x -2y -5=0与x 轴的交点坐标为(5,0),由双曲线的一个焦点在直线l 上可知,(5,0)即为双曲线的一个焦点,故c =5,则a 2+b 2=5,解得a 2=4,b 2=1, 故双曲线方程为x 24-y 2=1.16.(2022·杭州模拟)已知F 是椭圆x 2a 2+y 2b 2=1(a >b >0)的一个焦点,若直线y =kx 与椭圆相交于A ,B 两点,且∠AFB =135°,记椭圆的离心率为e ,则e 2的取值范围是__________. 答案 ⎣⎢⎡⎭⎪⎫2-24,1解析 设F ′为椭圆的另一焦点,如图,连接AF ,BF ,BF ′,AF ′,根据椭圆和直线的对称性,可得四边形AFBF ′为平行四边形, 又因为∠AFB =135°,所以∠F AF ′=45°,在△AFF ′中,|FF ′|2=|AF |2+|AF ′|2-2|AF |·|AF ′|cos ∠F AF ′=(|AF |+|AF ′|)2-(2+2)×|AF |·|AF ′|,所以(|AF |+|AF ′|)2-(2+2)×⎝⎛⎭⎪⎫|AF |+|AF ′|22≤(|FF ′|)2, 当且仅当|AF |=|AF ′|时,等号成立, 即2-24≤⎝ ⎛⎭⎪⎫|FF ′||AF |+|AF ′|2, 又因为|FF ′|=2c ,|AF |+|AF ′|=2a , 所以e 2≥2-24, 又因为e 2<1,故2-24≤e 2<1.[考情分析] 圆锥曲线的方程与几何性质是高考的重点,多以选择题、填空题或解答题第一问的形式命题,题目常为中档难度. 一、圆锥曲线的定义与标准方程 核心提炼1.圆锥曲线的定义(1)椭圆:|MF 1|+|MF 2|=2a (2a >|F 1F 2|); (2)双曲线:||MF 1|-|MF 2||=2a (2a <|F 1F 2|); (3)抛物线:|MF |=d (d 为M 点到准线的距离).温馨提醒:应用圆锥曲线定义解题时,易忽视定义中隐含条件导致错误.2.圆锥曲线的标准方程(1)椭圆:x 2a 2+y 2b 2=1(a >b >0)(焦点在x 轴上)或y 2a 2+x 2b 2=1(a >b >0)(焦点在y 轴上);(2)双曲线:x 2a 2-y 2b 2=1(a >0,b >0)(焦点在x 轴上)或y 2a 2-x 2b 2=1(a >0,b >0)(焦点在y 轴上);(3)抛物线:y 2=2px ,y 2=-2px ,x 2=2py ,x 2=-2py (p >0). 练后反馈题目 1 2 3 7 11 15 正误错题整理:二、椭圆、双曲线的性质 核心提炼椭圆、双曲线的性质(1)椭圆、双曲线中a ,b ,c 之间的关系 ①在椭圆中:a 2=b 2+c 2;离心率为e =ca =1-b 2a 2. ②在双曲线中:c 2=a 2+b 2;离心率为e =c a=1+b 2a2.(2)双曲线的渐近线方程与焦点坐标①双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±ba x ;焦点坐标F 1(-c ,0),F 2(c ,0).②双曲线y 2a 2-x 2b 2=1(a >0,b >0)的渐近线方程为y =±ab x ,焦点坐标F 1(0,-c ),F 2(0,c ).练后反馈题目 4 5 6 8 9 12 13 16 正误错题整理:三、抛物线的性质 核心提炼抛物线的焦点坐标与准线方程(1)抛物线y 2=2px (p >0)的焦点F ⎝⎛⎭⎫p 2,0,准线方程x =-p 2. (2)抛物线x 2=2py (p >0)的焦点F ⎝⎛⎭⎫0,p 2,准线方程y =-p 2. 练后反馈题目 10 14 正误错题整理:1.[T13补偿](2022·东北师大附中模拟)过双曲线C :x 2a 2-y 24=1(a >0)的右顶点A 作一条渐近线的平行线,交另一条渐近线于点P ,△OAP 的面积为1(O 为坐标原点),则双曲线C 的离心率为( ) A. 2 B. 3 C.62 D.32答案 A解析 双曲线的右顶点为A (a ,0), 双曲线的渐近线方程为y =±2ax ,过A 与y =2a x 平行的直线方程为y =2a(x -a ),联立⎩⎨⎧y =2a (x -a ),y =-2a x ,解得⎩⎪⎨⎪⎧x =a 2,y =-1,即P ⎝⎛⎭⎫a2,-1, 则S △OAP =12|OA |·|y P |=12a =1,解得a =2.所以双曲线C :x 24-y 24=1,则c =a 2+b 2=22,所以离心率e =ca= 2.2.[T12补偿](2022·赤峰模拟)椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,过点F 1的直线l 交椭圆C 于A ,B 两点,若|F 1F 2|=|AF 2|,AF 1—→=2F 1B —→,则椭圆C 的离心率为( ) A.57 B.22 C.53 D.13 答案 D解析 因为|F 1F 2|=|AF 2|=2c , 由椭圆定义知|AF 1|=2a -2c , 又AF 1—→=2F 1B —→,所以|BF 1|=a -c ,再由椭圆定义知|BF 2|=2a -(a -c )=a +c , 因为∠AF 1F 2+∠BF 1F 2=π, 所以cos ∠AF 1F 2=-cos ∠BF 1F 2, 所以由余弦定理可得 |AF 1|2+|F 1F 2|2-|AF 2|22|AF 1|·|F 1F 2|=-|BF 1|2+|F 1F 2|2-|BF 2|22|BF 1|·|F 1F 2|,即(2a -2c )2+(2c )2-(2c )22(2a -2c )·2c=-(a -c )2+(2c )2-(a +c )22(a -c )·2c,化简可得a 2+3c 2-4ac =0,即3e 2-4e +1=0, 解得e =13或e =1(舍去).3.[T4补偿](2022·赣州模拟)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0),P 是椭圆C 上的点,F 1(-c ,0),F 2(c ,0)是椭圆C 的左、右焦点,若PF 1—→·PF 2—→≤ac 恒成立,则椭圆C 的离心率e 的取值范围是( )A.⎣⎢⎡⎭⎪⎫5-12,1B .(0,2-1] C.⎝⎛⎦⎥⎤0,5-12 D .[2-1,1)答案 A解析 设P (x 0,y 0),∴PF 2—→=(c -x 0,-y 0),PF 1—→=(-c -x 0,-y 0), ∴PF 1—→·PF 2—→=x 20-c 2+y 20≤ac , ∵点P 在椭圆上,∴x 20a 2+y 20b2=1,x 0∈[-a ,a ], ∴y 20=a 2b 2-b 2x 20a 2, ∴x 20-c 2+y 20=x 20-c 2+a 2b 2-b 2x 20a 2≤ac , 两边都乘以a 2化简后得c 2x 20-2a 2c 2+a 4≤a 3c ,∴x 20≤a 3c +2a 2-a 4c 2,x 20∈[0,a 2], ∴a 2≤a 3c +2a 2-a 4c2, ∴1≤1e +2-1e 2⇒⎝⎛⎭⎫1e -122≤54, ∴e ≥5-12, 又∵椭圆离心率e ∈(0,1), ∴e ∈⎣⎢⎡⎭⎪⎫5-12,1.4.[T14补偿]已知O 为坐标原点,抛物线E 的方程为y =14x 2,E 的焦点为F ,直线l 与E 交于A ,B 两点,且AB 的中点到x 轴的距离为2,则下列结论不正确的是( ) A .|AB |的最大值为6 B .E 的准线方程为y =-1C .若AF →=2FB →,则直线AB 的方程为y =24x +1D .若OA ⊥OB ,则△AOB 面积的最小值为16答案 C解析 由题意知E 的标准方程为x 2=4y , 故E 的准线方程为y =-1,故B 正确;设AB 的中点为M ,分别过点A ,B ,M 作准线的垂线,垂足分别为C ,D ,N ,如图所示,因为M 到x 轴的距离为2, 所以|MN |=2+1=3.由抛物线的定义知|AC |=|AF |,|BD |=|BF |, 所以2|MN |=|AC |+|BD |=|AF |+|BF |=6. 因为|AF |+|BF |≥|AB |, 所以|AB |≤6,故A 正确;由AF →=2FB →得直线AB 过点F (0,1),直线AB 的斜率存在, 设直线AB 的方程为y =kx +1,A (x 1,y 1),B (x 2,y 2),联立方程得⎩⎪⎨⎪⎧y =kx +1,x 2=4y ,化简得x 2-4kx -4=0, 则x 1x 2=-4. 由于AF →=2FB →,所以(-x 1,1-y 1)=2(x 2,y 2-1), 得x 1=-2x 2,得x 1=±22, 所以y 1=14x 21=2,所以k =±24, 直线AB 的方程为y =±24x +1,故C 错误;由OA ⊥OB ,得x 1x 2+y 1y 2=0,又⎩⎨⎧y 1=x 214,y 2=x224,所以x 1x 2+116(x 1x 2)2=0,由题意知x 1x 2≠0,所以x 1x 2=-16. 又k AB =y 2-y 1x 2-x 1=x 224-x 214x 2-x 1=x 1+x 24,故直线AB 的方程为y -y 1=x 1+x 24(x -x 1).由于y 1=x 214,所以y =x 1+x 24x -x 1x 24=x 1+x 24x +4,则直线AB 恒过点(0,4), 所以S △AOB =12×4|x 1-x 2|=2(x 1+x 2)2+64≥16,所以△AOB 面积的最小值为16,故D 正确.5.[T10补偿](2022·毕节模拟)设点A n (-n ,y n )(n ∈N *)在抛物线y 2=-6x 上,F 是焦点,则|A 1F |+|A 2F |+…+|A 40F |等于( ) A .880 B .878 C .876 D .882 答案 A解析 由题意知,抛物线开口向左, 焦半径公式|A n F |=p 2+n =32+n ,所以|A 1F |+|A 2F |+…+|A 40F | =32×40+(1+2+…+40) =60+40×(1+40)2=880.6.[T16补偿](2022·新余模拟)已知F 是椭圆E :x 2a 2+y 2b2=1(a >b >0)的左焦点,椭圆E 上一点P(2,1)关于原点的对称点为Q,若△PQF的周长为42+25,则离心率e=________.答案3 2解析如图,P与Q关于原点对称,则Q(-2,-1),∴|PQ|=212+22=25,又△PQF的周长为|PQ|+|PF|+|QF|=42+25,设椭圆的右焦点为M,则由椭圆的性质可得|PF|=|QM|,∴|QM|+|QF|=2a=42,得a=22,将点P代入椭圆方程可得48+1b2=1,解得b=2,∴c=a2-b2=6,则离心率e=ca =622=32.。
高中数学圆锥曲线与方程练习题汇编

圆锥曲线与方程一、选择题1.双曲线3x 2-y 2=9的实轴长是 ( )A .2 3B .22C .4 3D .4 2 2.以x 24-y 212=-1的焦点为顶点,顶点为焦点的椭圆方程为 ( ) A.x 216+y 212=1 B.x 212+y 216=1 C.x 216+y 24=1 D.x 24+y 216=1 3.对抛物线y =4x 2,下列描述正确的是 ( )A .开口向上,焦点为(0,1)B .开口向上,焦点为⎝⎛⎭⎫0,116 C .开口向右,焦点为(1,0)D .开口向右,焦点为⎝⎛⎭⎫0,116 4.若k ∈R ,则k >3是方程x 2k -3-y 2k +3=1表示双曲线的 ( ) A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分又不必要条件5.若双曲线x 23-16y 2p 2=1的左焦点在抛物线y 2=2px (p >0)的准线上,则p 的值为( ) A .2 B .3 C .4 D .4 26.设双曲线x 2a 2-y 29=1(a >0)的渐近线方程为3x ±2y =0,则a 的值为 ( ) A .4 B .3 C .2 D .17.已知F 1、F 2是椭圆的两个焦点,满足MF 1→·MF 2→=0的点M 总在椭圆内部,则椭圆离心率的取值范围是 ( )A .(0,1) B.⎝⎛⎦⎤0,12 C.⎝⎛⎭⎫0,22 D.⎣⎡⎭⎫22,1 8.已知点P 在抛物线y 2=4x 上,那么点P 到点Q (2,-1)的距离与点P 到抛物线焦点距离之和取得最小值时,点P 的坐标为 ( ) A.⎝⎛⎭⎫14,-1 B.⎝⎛⎭⎫14,1 C.⎝⎛⎭⎫12,-1 D.⎝⎛⎭⎫12,1 9.已知直线l 与抛物线y 2=8x 交于A 、B 两点,且l 经过抛物线的焦点F ,A 点的坐标为(8,8),则线段AB 的中点到准线的距离是 ( ) A.254 B.252 C.258D .25 10.设双曲线x 2a 2-y 2b2=1的一条渐近线与抛物线y =x 2+1只有一个公共点,则双曲线的离心率为 ( ) A.54 B .5 C.52D. 5 11.若双曲线x 29-y 24=1的渐近线上的点A 与双曲线的右焦点F 的距离最小,抛物线y 2=2px (p >0)通过点A ,则p 的值为 ( )A.92 B .2 C.21313 D.1313二、填空题13.已知长方形ABCD ,AB =4,BC =3,则以A 、B 为焦点,且过C 、D 两点的椭圆的离心率为______.14.椭圆x 24+y 2=1的两个焦点F 1,F 2,过点F 1作垂直于x 轴的直线与椭圆相交,其中一个交点为P ,则|PF 2|=______.15.已知抛物线y 2=4x ,过点P (4,0)的直线与抛物线相交于A (x 1,y 1),B (x 2,y 2)两点,则y 21+y 22的最小值是________.16.F 1,F 2分别是椭圆x 22+y 2=1的左,右两个焦点,过F 2作倾斜角为π4的弦AB ,则△F 1AB 的面积为________. 17.已知双曲线x 29-y 216=1的左、右焦点分别为F 1、F 2,若双曲线上一点P 使得∠F 1PF 2=90°,则△F 1PF 2的面积为________. 三.解答题18.设椭圆E 的方程为22221(0),x y a b a b+=>>点O 为坐标原点,点A 的坐标为(,0)a ,点B的坐标为(0,b ),点M 在线段AB 上,满足2,BM MA =直线OM (Ⅰ)求E 的离心率e ;(Ⅱ)设点C 的坐标为(0,-b ),N 为线段AC 的中点,证明:MN ⊥AB .19.(本小题满分14分)已知椭圆C:2233x y +=,过点()D 1,0且不过点()2,1E 的直线与椭圆C 交于A ,B 两点,直线AE 与直线3x =交于点M .(I )求椭圆C 的离心率;(II )若AB 垂直于x 轴,求直线BM 的斜率;(III )试判断直线BM 与直线D E 的位置关系,并说明理由.20.已知点F 为抛物线2:2(0)E y px p =>的焦点,点(2,)A m 在抛物线E 上,且3AF =. (Ⅰ)求抛物线E 的方程;(Ⅱ)已知点(1,0)G -,延长AF 交抛物线E 于点B ,证明:以点F 为圆心且与直线GA 相切的圆,必与直线GB 相切.圆锥曲线与方程测试题答案一.选择题1.A 2.D 3.B 4.A 5.C 6.C 7.C 8.A 9.A 10.D 11.C二.填空题13.12 14.72 15.32 16.4317.16 三.解答题18.【解析】 (Ⅰ)解:由题设条件知,点)31,32(b a M ,又105=OM k 从而1052=a b . 进而b b a c b a 2,522=-==,故552==a c e . (Ⅱ)证:由N 是AC 的中点知,点N 的坐标为⎪⎭⎫⎝⎛-2,2b a ,可得⎪⎭⎫ ⎝⎛=65,6b a . 又()b a ,-=,从而有()22225616561a b b a -=+-=⋅ 由(Ⅰ)得计算结果可知,522b a =所以0=⋅,故AB MN ⊥.19.解析:(Ⅰ)椭圆C 的标准方程为2213x y +=.所以a =1b =,c =所以椭圆C 的离心率3c e a ==. (Ⅱ)因为AB 过点(1,0)D 且垂直于x 轴,所以可设1(1,)A y ,1(1,)B y -. 直线AE 的方程为11(1)(2)y y x -=--.令3x =,得1(3,2)M y -.所以直线BM 的斜率112131BM y y k -+==-. (Ⅲ)直线BM 与直线D E 平行.证明如下:当直线AB 的斜率不存在时,由(Ⅱ)可知1BM k =.又因为直线D E 的斜率10121DE k -==-,所以//BM DE . 当直线AB 的斜率存在时,设其方程为(1)(1)y k x k =-≠.设11(,)A x y ,22(,)B x y ,则直线AE 的方程为1111(2)2y y x x --=--. 令3x =,得点1113(3,)2y x M x +--. 由2233(1)x y y k x ⎧+=⎨=-⎩,得2222(13)6330k x k x k +-+-=. 所以2122613k x x k +=+,21223313k x x k -=+. 直线BM 的斜率11212323BM y x y x k x +---=-. 因为11112121(1)3(1)(2)(3)(2)1(3)(2)BM k x x k x x x x k x x -+--------=-- 121221(1)[2()3)(3)(2)k x x x x x x --++-=-- 2222213312(1)[3)1313(3)(2)k k k k k x x -+-+-++=-- 0=,所以1BM DE k k ==.所以//BM DE .综上可知,直线BM 与直线D E 平行.20.(I )由抛物线的定义得F 22p A =+. 因为F 3A =,即232p +=,解得2p =,所以抛物线E 的方程为24y x =. (II )设以点F 为圆心且与直线G A 相切的圆的半径为r .因为点()2,m A 在抛物线:E 24y x =上,所以m =±(2,A .由(2,A ,()F 1,0可得直线F A的方程为)1y x =-.由)214y x y x⎧=-⎪⎨=⎪⎩,得22520x x -+=, 解得2x =或12x =,从而1,2⎛B ⎝. 又()G 1,0-,故直线G A的方程为30y -+=,从而r == 又直线G B的方程为30y ++=,所以点F 到直线G B的距离d r ===. 这表明以点F 为圆心且与直线G A 相切的圆必与直线G B 相切.。
高中数学第二章圆锥曲线与方程第9课时双曲线及其标准方程A版-1ppt课件全省公开课一等奖

代入点
A1,4
310,得
b2=9,
∴双曲线的标准方程为1y62 -x92=1.
(2)设所求双曲线方程为 mx2+ny2=1(mn<0).
∵点(3,-4 2),94,5在双曲线上,
9m+32n=1 ∴8116m+25n=1,
解得mn==1-16.19
∴双曲线标准方程为1y62 -x92=1.
点评 求解双曲线的方程主要是依据题目给出的条件确定 a2、b2 的 值,注意焦点在哪个轴上;求解过程中也可以用换元思想.
变式训练 2 当 0°≤α≤180°时,方程 x2cosα+y2sinα=1 表示 的曲线怎样变化?
解析:(1)当 α=0°时,方程为 x2=1,它表示两条平行直线 x
=±1.
(2)当 0°<α<90°时,方程为
x2 1
+y2 1=Fra bibliotek.cosα sinα
①当 0°<α<45°时,0<co1sα<si1nα,它表示焦点在 y 轴上的椭
解析:设动圆半径为 r,则由已知|PA|=r,|PC|=r+4, ∴|PC|=|PA|+4,即|PC|-|PA|=4. ∵C(-3,0),A(3,0),∴|AC|=6.∴4<|AC|. ∴P 的轨迹是以 A、C 为焦点的双曲线的右支. ∵a=2,c=3,∴b2=c2-a2=5. ∴点 P 的轨迹方程是x42-y52=1(x>0).
讲重点 深刻解读双曲线的定义 1.距离的差要加绝对值号,否则只有双曲线的一支.若 F1, F2 表示双曲线的左、右焦点,有两种情形: (1)若点 P 满足|PF2|-|PF1|=2a(a>0),则点 P 在左支上.如左 下图.
(2)若点 P 满足|PF1|-|PF2|=2a(a>0),则点 P 在右支上.如右 上图.
(完整word版)高中数学圆锥曲线与方程测试题

、选择题 圆锥曲线与方程双曲线3x 2— y 2= 9的实轴长是 A . 2 3 B . 2 2 C . 4 3 x 2 v 2 以一%=—1的焦点为顶点,顶点为焦点的椭圆方程为 2 2 2 2A£ 十V - = 1B —出=1 A. 16 十 1212 十 16对抛物线y = 4x 2,下列描述正确的是 A .开口向上, 焦点为 B .开口向上, C .开口向右, D .开口向右, 焦点为焦点为 焦点为(2 2D.x十 w=1(0,1) 0,£(1,0) 1,洛x 2 工若k € R ,则k>3是方程一 =1表示双曲线的 k — 3 k 十 3A .充分不必要条件B •必要不充分条件D •既不充分又不必要条件 C .充要条件号—追羊=1的左焦点在抛物线 y 2= 2px (p>0)的准线上,则3 P若双曲线 C . 4设双曲线 2 2<—乞= a 2 91(a>0)的渐近线方程为3xi2y = 0,D . 4.2则a 的值为C . 2p 的值为(已知F 1、 的取值范围是 A . (0,1)F 2是椭圆的两个焦点,满足 MF 1 MF 2= 0 的点 M 总在椭圆内部, 则椭圆离心率C. 0, y 2= 4x 上,那么点 之和取得最小值时,点 P 的坐标为1 1彳 A _,— 1 B. 一, 1 4 4已知直线l 与抛物线y 2= 8x 交于A 、 则线段AB 的中点到准线的距离是25 A 一A. 4 已知点P 在抛物线 P 到点 25 Q(2,-D •子,1 1)的距离与点P 到抛物线焦点距离 10 .设双曲线 a 2 - b 2率为 代5 11.若双曲线 y2= 14(p>0)通过点A ,则D.|,1 B 两点,且I 经过抛物线的焦点 F , A 点的坐标为 (8,8),25C.8D . 25 的一条渐近线与抛物线 y = x 2+ 1只有一个公共点,则双曲线的离心 C^5C. 2D. .5的渐近线上的点 A 与双曲线的右焦点 F 的距离最小,抛物线 y 2 = 2pxp 的值为132 A .9一点P ,使得|PF i |= 3|PF 2|,则双曲线的离心率 e 的取值范围为 ( )A . [2 ,+^ )B . [ .'2+8 )C . (1,2]D . (1, .'2]、填空题13. 已知长方形 ABCD , AB = 4, BC = 3,则以A 、B 为焦点,且过 C 、D 两点的椭圆的离心 率为 ______ .x 214. 椭圆4 + y 2= 1的两个焦点F 1, F 2,过点F 1作垂直于x 轴的直线与椭圆相交,其中一个交点为P ,则|PF 2|= ________ .15. ____________________ 已知抛物线y 2= 4x ,过点P(4,0)的直线与抛物线相交于 A(X 1, y” , B(x 2, y 2)两点,则y 2 + y 2的最小值是 .16.F 1, F 2分别是椭圆x2 + y 2 = 1的左,右两个焦点,过F 2作倾斜角为n 的弦AB ,则厶F 1AB的面积为 _________ . 三、解答题17. 已知双曲线 曽—話=1的左、右焦点分别为F 1、F 2,若双曲线上一点 P 使得/ F 1PF 2 = 90 ° 求厶F 1PF 2的面积.18. 如图,直线I : y = x + b 与抛物线C : x 2= 4y 相切于点A.(1) 求实数b 的值;(2) 求以点A 为圆心,且与抛物线 C 的准线相切的圆的方程. 19. 已知双曲线的方程为x 2—= 1,试问:是否存在被点B (1,1)平分的弦?如果存在,求出弦所在的直线方程;如果不存在,请说明理由. 20. 设圆C 与两圆(x + 5)2 + y 2= 4, (x — 5)2 + y 2= 4中的一个内切,另一个外切.(1) 求圆C 的圆心轨迹L 的方程;(2) 已知点M(3^5, 埒),F( .'5 ,0),且P 为L 上的动点,求||MP|—|FP||的最大值及此时 点P 的坐标.21. 过抛物线y 2 = 4x 的焦点F 作直线I 与抛物线交于 A 、B 两点.求证:△ AOB 不是直角三 角形. 22 .已知椭圆 G : x 2+当=1 (a>b>0)的离心率为严,右焦点为(2 2, 0),斜率为1的直线I a b 3与椭圆G 交于A 、B 两点,以AB 为底边作等腰三角形,顶点为 P(— 3,2).(1)求椭圆G 的方程;(2)求厶PAB 的面积.2x 12.已知双曲线二 a ^2= 1 (a>0, b>0)的左,右焦点分别为 bF i , F 2,若在双曲线的右支上存在D.4圆锥曲线与方程测试题答案3.B4.A5.C6.C7. C8.A9.A13- 14.7 15.32 16.4 17.162 23 18. (1) - 1 (2)(x — 2)2+ (y — 1严=419•解 如图所示,设被B(1,1)平分的弦所在的直线方程为 代入双曲线方程x 2—y2=1,得(k 2— 2)x 2— 2k(k — 1)x + k 2 — 2k + 3= 0,•••△= [ — 2k(k — 1)]2— 4(k 2— 2)(k 2— 2k + 3)>0.3解得 k<2,且 k #±;2, 2k k — 1•X 1 + x 2 =k 2 — 2k k — 1••B(1,1)是弦的中点,• = 1.k 2 — 23••k = 2>2・故不存在被点B(1,1)所平分的弦.20.解(1)设圆C 的圆心坐标为(x , y),半径为r. 圆(x + ;'5)2+ y 2= 4 的圆心为 F 1( — ,:5, 0),半径为 2, 圆(x —.⑸2+ y 2= 4的圆心为F(.;5, 0),半径为2.|CF 1 = r + 2,由题意得|CF| = r — 2|CF 1= r — 2, 或|CF = r + 2, •■|CF 1|— |CF|= 4. '•|F 1F|= 2 . 5>4.•••圆C 的圆心轨迹是以 F 1(—•. 5, 0), F( .'5, 0)为焦点的双曲 线,其方程为x— y 2= 1.4 ⑵由图知,|FP||W |MF|,「.当M , P , F 三点共线,且 点P 在MF 延长线上时,|MP —|FP |取得最大值|MF |, 且 |MF|=^¥ —V 52+ 誓—02 = 2.直线MF 的方程为y =— 2x + 2/5,与双曲线方程联立得 y =— 2x + 2 .'5,整理得 15x 2— 32 .'5x + 84 = 0. 解得X 1 =舍去),x 2= 晋.此时y =— 晋.10.D 11.C 12.Cx 2 —y 2= 1,•••当||MP|—|FP||取得最大值2时,点P 的坐标为(655,- 芈).21.证明•••焦点F 为(1,0),过点F 且与抛物线交于点 A 、B 的直线可设为ky = x — 1,代入 抛物线y 2=4x ,得 y 2 — 4ky — 4= 0,则有 y A y B =— 4, 则 X A X B =y A y B =i.4 4又|OA| |OB|cos/AOB = = X A X B + y A y B = 1 — 4=— 3<0, 得ZAOB 为钝角,故△ AOB 不是直角三角形. 22. 解 ⑴由已知得c = 2 2, C =严.a 3 解得 a = 2』3,又b 2= a 2—c 2= 4. x 2 y 2所以椭圆G 的方程为12 + 丁 = 1. (2)设直线l 的方程为y = x + m.y = x + m得 4x 2 + 6mx + 3m 2—12 = 0.①设 A 、B 的坐标分别为(X 1, y 1), (X 2, y 2)(X 1<X 2), AB 中点为 E (X 0, y 0),x1 +X 23mm则 X 0= ~2~ ~, y 0= X 0+ m =—;AB 是等腰△ PAB 的底边,所以PE 1AB.m 2—;PE 的斜率k ==— 1.3m-3 +丁此时方程①为4x 2 + 12x = 0.解得 X 1 = — 3, X 2 = 0.所以 y 1=— 1 , y 2= 2.所以|AB|= 3 2.此时,点P ( — 3,2)到直线AB : 1 9所以A PAB 的面积S = ?|AB| d = ^.解得 m = 2.x 2 12+ y 2 飞=1因为 所以x — y + 2= 0的距离d = | — 3— 2 +2|.2。
高中数学中的圆锥曲线方程
高中数学中的圆锥曲线方程圆锥曲线是高中数学中一个重要的概念,它是平面上由一个动点和一个定点到动点的距离之比保持不变的点的轨迹。
圆、椭圆、抛物线和双曲线都是圆锥曲线的特例。
在高中数学中,学生需要学习如何根据给定的条件确定圆锥曲线的方程。
本文将探讨高中数学中的圆锥曲线方程。
首先,让我们来看看圆的方程。
圆是最简单的圆锥曲线,它的方程可以表示为(x-a)²+(y-b)²=r²,其中(a,b)是圆心的坐标,r是半径的长度。
这个方程告诉我们,圆上的每一个点到圆心的距离都等于半径的长度。
通过给定圆心和半径的信息,我们可以轻松地确定圆的方程。
接下来,我们来讨论椭圆的方程。
椭圆是一个拉伸的圆,它的方程可以表示为(x-h)²/a²+(y-k)²/b²=1,其中(h,k)是椭圆的中心坐标,a和b是椭圆在x轴和y轴上的半长轴长度。
这个方程告诉我们,椭圆上的每一个点到椭圆中心的距离之比等于a 和b的比值。
通过给定椭圆的中心坐标和半长轴长度的信息,我们可以确定椭圆的方程。
抛物线是一个开口向上或向下的曲线,它的方程可以表示为y=ax²+bx+c,其中a、b和c是常数。
这个方程告诉我们,抛物线上的每一个点的y坐标都等于x的平方乘以一个常数,并加上另外两个常数。
通过给定抛物线上的三个点的坐标,我们可以确定抛物线的方程。
最后,我们来讨论双曲线的方程。
双曲线是一个开口向左和向右的曲线,它的方程可以表示为(x-h)²/a²-(y-k)²/b²=1,其中(h,k)是双曲线的中心坐标,a和b是双曲线在x轴和y轴上的半长轴长度。
这个方程告诉我们,双曲线上的每一个点到双曲线中心的距离之差等于a和b的比值。
通过给定双曲线的中心坐标和半长轴长度的信息,我们可以确定双曲线的方程。
总结起来,高中数学中的圆锥曲线方程是一个重要的概念。
圆锥曲线与方程章末归纳总结课件
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
4.中点弦问题 [例 4] 椭圆 ax2+by2=1 与直线 x+y-1=0 相交于 A、B, C 是 AB 的中点,若|AB|=2 2,OC 的斜率为 22,求椭圆的方 程.
第二章 圆锥曲线与方程
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
[解析] 设 A(x1,y1),B(x2,y2),
(1)∵O→A·O→B=0,∴OA⊥OB.∴yx11=-xy22.
∴x1x2=-y1y2①
∵yy2122= =22ppxx12, ,
② ③
∴(y1y2)2=4p2(x1x2)④
由①④得 y1y2=-4p2 且 x1x2=4p2.∴结论成立.
第二章 圆锥曲线与方程
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
已知椭圆的长轴长 2a=100(m),短轴长 2b=60(m),则椭 圆的方程为5x022+3y022=1.
设顶点 A 的坐标为(x0,y0),x0>0,y0>0,则 5x0202+3y0022=1,因此 y20=295(502-x20). 根据矩形 ABCD 的对称性,可知它的面积 S=4x0y0. 由于 x20y20=x20·295(502-x20) =295(-x40+502x20)=295-x20-52022+5402,
第二章 圆锥曲线与方程
成才之路 ·高中新课程 ·学习指导 ·人教A版 ·数学 ·选修2-1
5.实际应用问题 [ 例 5] 有 一 椭 圆 形 溜 冰 场 , 长 轴 长 100m , 短 轴 长 60m.现要在这溜冰场上划定一个各顶点都在溜冰场边界上的 矩形区域,且使这个区域的面积最大,应把这个矩形的顶点定 位在何处?这时矩形的周长是多少? [分析] 因为椭圆和矩形都是中心对称图形,又矩形的各 顶点在椭圆上,所以他们有同一个对称中心.同时,椭圆关于 长轴、短轴所在的直线都对称,可知此矩形也关于这两条直线 都对称.因此,以这两条直线建立平面直角坐标系,可利用椭 圆的方程及矩形所满足的条件来解决问题.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 13 页 九、《圆锥曲线与方程》变式试题 命题人:广州市教育局教研室 曾辛金
1.(人教A版选修1-1,2-1第39页例2) 如图,在圆224xy上任取一点P,过点P作X轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?
变式1:设点P是圆224xy上的任一点,定点D的坐标为(8,0).当点P在圆上运动时,求线段PD的中点M的轨迹方程.
解:设点M的坐标为,xy,点P的坐标为00,xy,
则082xx,02yy.即028xx,02yy. 因为点P 00,xy在圆224xy上,所以 22004xy.
即222824xy, 即2241xy,这就是动点M的轨迹方程. 变式2:设点P是圆224xy上的任一点,定点D的坐标为(8,0),若点M满足2PMMD.当点P在圆上运动时,求点M的轨迹方程.
解:设点M的坐标为,xy,点P的坐标为00,xy,由2PMMD,得 00,28,xxyyxy,
即0316xx,03yy. 因为点P00,xy在圆224xy上,所以 22004xy.
即2231634xy,
即2216439xy,这就是动点M的轨迹方程.
X Y P
O D M 第 2 页 共 13 页 变式3:设点P是曲线,0fxy上的任一点,定点D的坐标为,ab,若点M满足(,1)PMMDR.当点P在曲线,0fxy上运动时,求点M的轨迹方程.
解:设点M的坐标为,xy,点P的坐标为00,xy,由PMMD,得 00,,xxyyaxby,
即01xxa,01yyb. 因为点P00,xy在圆,0fxy上,所以 00,0fxy.
即1,10fxayb,这就是动点M的轨迹方程.
2.(人教A版选修1-1,2-1第40页练习第3题) 已知经过椭圆2212516xy的右焦点2F作垂直于x轴的直线A B,交椭圆于A,B两点,
1F是椭圆的左焦点.
(1)求1AFB的周长; (2)如果AB不垂直于x轴,1AFB的周长有变化吗?为什么? 变式1(2005年全国卷Ⅲ):设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是
A.22 B.212 C.22 D.21
解一:设椭圆方程为22221xyab,依题意,显然有212PFFF,则22bca,即222acca,即2210ee,解得21e.选D.
解二:∵△F1PF2为等腰直角三角形,∴cPFcFFPF22,21212. ∵aPFPF221,∴acc222,∴12121ac.故选D. 第 3 页 共 13 页
变式2:已知双曲线22221,(0,0)xyabab的左,右焦点分别为12,FF,点P在双曲线的右支上,且12||4||PFPF,则此双曲线的离心率e的最大值为 . 解一:由定义知12||||2PFPFa,又已知12||4||PFPF,解得183PFa,
223PFa,在12PFF中,由余弦定理,得2222218981732382494964coseaacaaPFF,
要求e的最大值,即求21cosPFF的最小值,当1cos21PFF时,解得53e.即e的最大值为53. 解二:设),(yxP,由焦半径公式得aexPFaexPF21,,∵214PFPF,∴)(4)(aexaex,∴xae35,∵ax,∴35e,∴e的最大值为53. 变式3(2005年全国卷Ⅰ):已知椭圆的中心为坐标原点O,焦点在x轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,OAOB与(3,1)a共线. (Ⅰ)求椭圆的离心率; (Ⅱ)设M为椭圆上任意一点,且 (,)OMOAOBR,证明22为定值.
解:(Ⅰ)设椭圆方程为)0,(),0(12222cFbabyax,
则直线AB的方程为cxy,代入12222byax,化简得 02)(22222222bacacxaxba.
设A(11,yx),B22,(yx),则22222121222222,.acacabxxxxabab
由1212(,),(3,1),OAOBxxyyaOAOB与a共线,得 ,0)()(32121xxyy又cxycxy2211,,
.23,0)()2(3212121cxxxxcxx
即232222cbaca,所以36.32222abacba, 故离心率.36ace (Ⅱ)证明:由(Ⅰ)知223ba,所以椭圆12222byax可化为.33222byx 设(,)OMxy,由已知得),,(),(),(2211yxyxyx
.,2121yyyxxx
),(yxM在椭圆上,.3)(3)(2221221byyxx
即.3)3(2)3()3(221212222221212byyxxyxyx① 第 4 页 共 13 页
由(Ⅰ)知.21,23,23222221cbcacxx 222221222
3,8acabxxcab
1212121221212
222
33()()43()33930.22xxyyxxxcxcxxxxccccc
又222222212133,33byxbyx,代入①得.122 故22为定值,定值为1.
3.(人教A版选修1-1,2-1第47页习题2.1A组第6题) 已知点P是椭圆22154xy上的一点,且以点P及焦点1F,2F为顶点的三角形的面积等于1,求点P的坐标. 变式1(2004年湖北卷理):已知椭圆191622yx的左、右焦点分别为F1、F2,点P在椭圆上,若P、F1、F2是一个直角三角形的三个顶点,则点P到x轴的距离为 A.59 B.3 C.779 D.49
解:依题意,可知当以F1或F2为三角形的直角顶点时,点P的坐标为97,4,则点P到x轴的距离为49,故选D.(可以证明不存在以点P为直角顶点的三角形) 变式2(2006年全国卷Ⅱ):已知ABC的顶点B、C在椭圆2213xy上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则ABC的周长是 A.23 B.6 C.43 D.12
解:由于椭圆2213xy的长半轴长3a,而根据椭圆的定义可知ABC的周长为
443a,故选C. 第 5 页 共 13 页
4.(人教A版选修1-1,2-1第47页习题2.1B组第3题) 如图,矩形ABCD中,2ABa,2BCb,E,F,G,H分别是矩形四条边的中点,R,S,T是线段OF的四等分点,R,S,T是线段CF的四等分点.请证明直线ER与GR、ES与GS、ET与GT的交点L,M,N在同一个椭圆上.
变式1:直线:1lykx与双曲线22:21Cxy的右支交于不同的两点A、B.若双曲线C的右焦点F在以AB为直径的圆上时,则实数k . 解:将直线:1lykx代入双曲线C的方程2221xy整理,得
.022)2(22kxxk ……①
依题意,直线L与双曲线C的右支交于不同两点,故 222
22
20,(2)8(2)0,20,220.2kkkkkk
解得22k.
设A、B两点的坐标分别为),(11yx、),(22yx,则由①式得
.22,22222221kxxkk
xx
……②
∵双曲线C的右焦点F ,0c在以AB为直径的圆上,则由FA⊥FB得: .0)1)(1())((.0))((21212121kxkxcxcxyycxcx即 整理,得.01))(()1(221212cxxckxxk……③
把②式及26c代入③式化简,得.066252kk 解得))(2,2(566566舍去或kk,故566k.
NMLT/S/R/
TSROHGFE
DC
BA
