漳州双语实验学校高三文科上学期第三次月考
福建省部分学校2024-2025学年高三上学期第三次联考数学试题(含答案)

2024-2025学年度第一学期福建省部分学校高中毕业班第三次联考数学试卷(考试时间:120分钟;满分:150分)一、单项选择题(本题共8小题,每小题5分,共40分。
每小题只有一个选项是符合题意的。
)1.已知集合A ={―2,―1,0,1,2},B ={x |2x ≤12},则A ∩B =()A .{―1}B .{―2,―1}C .{1}D .{―1,0,1}2.已知非零向量a ,b 满足3|→a |=|→b |,向量a 在向量b 方向上的投影向量是―,则a 与b 夹角的余弦值为( )A .33B .13C .―33D .―133.(2―x )5展开式中x 3项的系数是( )A .―40B .40C .―80D .804.如图,在平行六面体ABCD ―A 1B 1C 1D 1中,以顶点A 为端点的三条棱长均为3,且它们彼此的夹角都是60°,则对角线AC 1长为( )A .36B .32C .33D .65.若一个圆锥底面半径为1,高为22,则该圆锥表面积为( )A .πB .2πC .4πD .6π6.已知sin(α+β)=7210,sin(α―β)=210,则sin2αsin2β=( )A .625B .1225C .45D .24257.把液体A 放在冷空气中冷却,如果液体A 原来的温度是θ1℃,空气的温度是θ0℃,则t min 后液体A 的温度θ℃可由公式θ=θ0+(θ1―θ0)e ―0.3t 求得.现把温度是60℃的液体A 放在13℃的空气中冷却,液体A 的温度冷却到37℃和25℃所用的时间分别为t 1min ,t 2min ,则t 2―t 1的值约为( )(参考数据:ln2≈0.69,ln3≈1.10)A .2.3B .2.7C .3.7D .4.78.对于函数y =f (x ),若存在x 0,使f (x 0)=―f (―x 0),则称点(x 0,f (x 0))与点(―x 0,f (―x 0))是函数f (x )的一对“隐对称点”.若函数f (x )={x 2+4x ,x >0mx +2,x ≤0的图象存在“隐对称点”,则实数m 的取值范围是( )A .(0,4―22]B .[4―22,+∞)C .[4+22,+∞)D .(0,4+22]二、多项选择题(本题共3小题,每小题6分,共18分。
漳州三中2018-2019学年高三上学期第三次月考试卷数学含答案
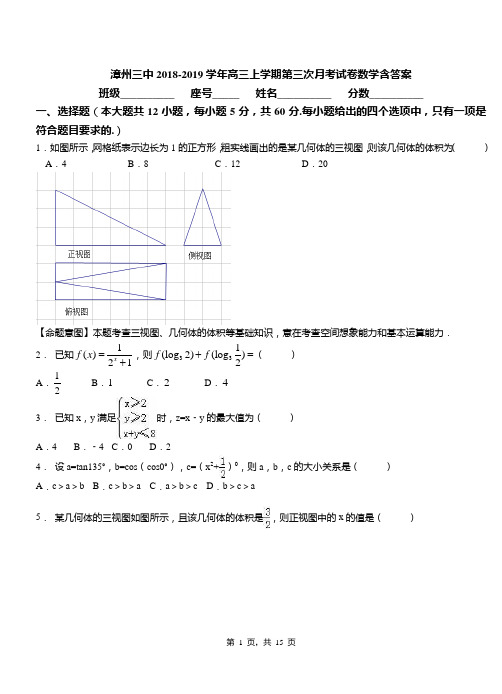
漳州三中2018-2019学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 如图所示,网格纸表示边长为1的正方形,粗实线画出的是某几何体的三视图,则该几何体的体积为( ) A .4 B .8 C .12 D .20【命题意图】本题考查三视图、几何体的体积等基础知识,意在考查空间想象能力和基本运算能力. 2. 已知1()21xf x =+,则331(log 2)(log )2f f +=( ) A .12B .1C .2D .43. 已知x ,y 满足时,z=x ﹣y 的最大值为( ) A .4B .﹣4C .0D .24. 设a=tan135°,b=cos (cos0°),c=(x 2+)0,则a ,b ,c 的大小关系是( ) A .c >a >b B .c >b >a C .a >b >c D .b >c >a5. 某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x 的值是( )A .2B .C .D .36. 设集合M={1,2},N={a 2},则“a=1”是“N ⊆M ”的( ) A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件7. 已知向量(1,2)a =,(1,0)b =,(3,4)c =,若λ为实数,()//a b c λ+,则λ=( ) A .14 B .12C .1D .2 8. 已知全集I={1,2,3,4,5,6},A={1,2,3,4},B={3,4,5,6},那么∁I (A ∩B )等于( ) A .{3,4} B .{1,2,5,6} C .{1,2,3,4,5,6} D .∅9. 定义运算:,,a a ba b b a b≤⎧*=⎨>⎩.例如121*=,则函数()sin cos f x x x =*的值域为( )A .22⎡-⎢⎣⎦ B .[]1,1- C .2⎤⎥⎣⎦ D .1,2⎡-⎢⎣⎦ 10.若某程序框图如图所示,则该程序运行后输出的值是( ) A.7B.8C. 9D. 10【命题意图】本题考查阅读程序框图,理解程序框图的功能,本质是循环语句循环终止的条件. 11.某空间几何体的三视图如图所示,则该几何体的体积为( )A .B .8C .D .1612.已知抛物线C :y x 82=的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FQ PF 2=,则=QF ( ) A .6B .3C .38D .34 第Ⅱ卷(非选择题,共100分)二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.直线l 1和l 2是圆x 2+y 2=2的两条切线,若l 1与l 2的交点为(1,3),则l 1与l 2的夹角的正切值等于 _________ 。
高三数学上学期第三次月考试题(解析版) 文 湘教版

ABC P高三上学期第三次月考数学(文)试题(解析版)一.选择题:(本大题共10小题,每小题5分,共50分)1.若集合{1,0,1},{2,}x A B y y x A =-==∈则A B = ( ) A.{0} B. {1}C.{0,1}D.{1,01}-答案:B解析:111,22x y -=-==;0110,21;1,22,1,22x y x y B ⎧⎫=======⎨⎬⎩⎭则 1{1,0,1}{,1,2}{1}2A B B =-= 故选2.已知等差数列}{n a 中,1,16497==+a a a ,则12a 的值是( ) A .15 B .30 C .31D .64答案:A解析:79412a a a a +=+ ,1279416115a a a a =+-=-=,故选A3.设P 是△ABC 所在平面内的一点,2BC BA BP +=,则( ) A.0PA PB += B. 0PB PC += C. 0PC PA += D.0PA PB PC ++=答案:C20,.BC BA BP P AC PA PC C +=+=解:由得为中点,则故选 4.下面四个条件中,使b a >成立的充分而不必要的条件是( )A.1+>b aB.1->b aC.22b a > D.33b a >答案:A解:110,,1a b a b a b a b a b >+⇒->>>>+>则即是的充分条件a b >⇒1,1a b a b a b >+>+>即是的不必要条件,故选A5.在△ABC 中,若cos A =45,cos B =513,则cos C 的值是( )7.同时具有性质:“①最小正周期为π;②图像关于直线3x π=对称;③在(,)63ππ-上是增函数.”的一个函数是 ( ) A.sin()26x y π=+B.cos()26x y π=-C.cos(2)3y x π=+ D.sin(2)6y x π=-答案:D解:由①②得C 、D ,由③D 故选D.8.函数)(x f 的定义域为R ,2)1(=-f ,对任意2)(,'>∈x f R x ,则42)(+>x x f 的解集为( )A.)1,1(-B.),1(+∞-C.)1,(--∞D.R 答案:B解:令()()24g x f x x =--,则()()2g x f x ''=-因为()2f x '>所以()0g x '>则()g x 在R 递增,1,()(1)(1)2(1)40x g x g f >->-=----=即()24f x x >+9.函数)0,0)(cos(3πϕωϕω<<>+=x y 为奇函数,该函数的部分图像如右图 所表示,A 、B 分别为最高点与最低点,并且两点间的距离为4,则该函数的一条对称轴为( ) A .2π=x B .2π=xC . 1x =D .2x =答案:C解: 最高点与最低点两点间的距离为4,则44T=⇒=,又2T πω=所以2ωπ=函数)y x ωϕ=+为奇函数,所以2πϕ=,函数的对称轴22812k x k πππ+==+函数的一条对称轴为1x =10.已知定义在R 上的偶函数()f x 满足)()4(x f x f =-,且在区间[0,2]上x x f =)(.若关于x 的方程x x f m log )(=有三个不同的根,则m 的范围为( ). A.)4,2( B.)22,2( C.)22,6( D.)10,6( 答案:D解: (4)()4f x f x T -==由得,[0,10]x ∈的图象如图(2)(6)(10)2f f f ===则log 62log 102m mm <⎧⇒<<⎨>⎩二.填空题:(本大题共7小题,每小题4分,共28分) 11.函数()()()a x x x f +-=1为奇函数,则=a ; 答案:0解析:(0)0(0)100f f a a =⇒=-⨯=⇒=12.已知等比数列{}n a 为递增数列,且373a a +=,282a a ⋅=,则117a a =___; 答案:2解析: 2837372,3a a a a a a ==+= 又3371177731222211a a a a a a a a ==⎧⎧∴===⎨⎨==⎩⎩或(舍去),13.已知3()|log |f x x =,若)()(b f a f =,则b a +的取值范围是 ; 答案:(2,)+∞sin sin 2,2sin cos ,A B B B B ∴== 又A=2B,即 16.若{}n a 是等差数列,,,m n p 是互不相等的正整数,则有:()()()0p m n m n a n p a p m a -+-+-=,类比上述性质,相应地,对等比数列{}n b ,有 . 答案:1m nn pp m pm n a a a ---⋅⋅=解:等比数列的指数相当于等差数列的差式1m nn pp m pm n a a a ---⋅⋅=17.已知函数()ln xf x e a x =+的定义域是D=(0,)+∞,关于函数)(x f 给出下列命题:①对于任意),0(+∞∈a ,函数)(x f 是D 上的减函数; ②对于任意)0,(-∞∈a ,函数)(x f 存在最小值;[来③对于任意),0(+∞∈a ,使得对于任意的D x ∈,都有)(x f >0成立;④存在)0,(-∞∈a ,使得函数)(x f 有两个零点。
高三数学上学期第三次月考试题解析文试题

〔2〕
因为t≠0,以下分两种情况讨论:
①假设 的变化情况如下表:
x
〔-t,∞〕
+
-
+
所以, 的单调递增区间是 ,〔-t,∞〕; 的单调递减区间是 。
②假设 的变化情况如下表:
所以, 的单调递增区间是〔-∞,t〕, ; 的单调递减区间是 。
综上可得:
当t<0时, 的单调递增区间是 ,〔-t,∞〕; 的单调递减区间是
三、解答题〔一共75分〕
16、〔12分〕 ,
〔1〕求 的值;
〔2〕求β。
解析:该题通过 求 的值,考察三角函数的同角关系式及其符号判断和正切的二倍角公式;通过 求β,考察考察三角函数的同角关系式、三角函数符号判断、变角和余弦的差角公式以及知值求角;考察转化才能和运算才能,是中档题。
〔1〕
〔2〕
17、〔12分〕设函数 是奇函数〔a,b,c都是整数〕,且 ,
15、 是定义在R上的不恒为零的函数,且对任意实数a、b满足 ,有以下结论:
① ② 为偶函数;③数列{an}为等比数列;④数列{bn}为等差数列。其中正确结论的序号是。
答案:①③④
解析:因为 获得 获得 获得 获得
由 得 代入〔1〕得
。该题通过函数方程考察函数性质与递推数列求数列通项公式,既考察函数方程问题一般的研究方法:赋值,又考察转化化归,对才能要求较高,是难题。
解析:该题考察简单的二次不等式求解和集合的交运算,是简单题.
2.复数z= 〔 为虚数单位〕在复平面内对应的点所在象限为〔〕
A.第一象限B.第二象限C.第三象限D.第四象限
答案:D
解析: 简单考察乘除复数运算及复数的几何意义,是简单题.
3.假设点〔a,9〕在函数 的图象上,那么tan =的值是〔〕
高三数学上学期第三次月考试题文含解析A试题

县一中2021届高三第三次月考文科数学试卷【试卷综述】本套试卷注重对数学根底知识、根本技能、根本思想和方法的考察,突出了对数学的计算才能、逻辑思维才能等方面的考察。
突出考察数学主干知识 ,侧重于中学数学学科的根底知识和根本技能的考察;侧重于知识交汇点的考察。
注重双基和数学思想数学方法的复习,注重运算才能思维才能的培养。
在考察学生根底知识的同时,考察学生的才能。
一、选择题:(本大题一一共10小题,每一小题5分,一共50分.在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的) 【题文】1. 3x >是2560x x -+>的 〔 A 〕A .充分不必要条件 B.必要不充分条件C .充分必要条件 D .既不充分又不必要条件 【知识点】充分、必要、充要条件的判断.A2【答案】【解析】A 解析:由2560x x -+>得:3x >或者2x ,所以3x >能推出3x >或者2x,但3x >或者2x ,不能推出3x >,故3x >是2560x x -+>的充分不必要条件,应选A 。
【思路点拨】先由2560x x -+>得:3x >或者2x,再做出双向判断即可。
【题文】2.设x Z ∈,集合A 是奇数集,集合B :,2p x A x B ∀∈∈,那么〔 D 〕A .:,2p x A xB ⌝∃∈∈ B .:,2p x A x B ⌝∃∉∈ C.:,2p x A x B ⌝∀∉∉C .D . :,2p x A x B ⌝∃∈∉【知识点】全称命题;命题的否认.A2【答案】【解析】D 解析:因为全称命题的否认是特称命题,所以设x ∈Z ,集合A 是奇数集,集合B 是偶数集.假设命题:,2p x A x B ∀∈∈,那么:,2p x A x B ⌝∃∈∉,应选D 。
【思路点拨】直接利用全称命题的否认是特称命题,写出命题的否认命题即可.【题文】3. 全集R U =,集合{}{}3|,5,4,3,2,1≥∈==x R x B A ,以下图中阴影局部所表示的集合为( B ) A . {}1 B . {}2,1 C . {}32,1,D . {}21,0,【知识点】Venn 图表达集合的关系及运算.A1【答案】【解析】B 解析:图中阴影局部表示的集合中的元素是在集合A 中,但不在集合B 中.由韦恩图可知阴影局部表示的集合为〔C U B 〕∩A,又{}{}3|,5,4,3,2,1≥∈==x R x B A ,∵C U B={x|x <3},∴〔C U B 〕∩A={1,2}. 那么图中阴影局部表示的集合是:{}2,1.应选B .【思路点拨】先观察Venn 图,图中阴影局部表示的集合中的元素是在集合A 中,但不在集合B 中,得出图中阴影局部表示的集合,再结合条件即可求解.【题文】4.数列{a n }是等差数列,假设a 1+a 5+a 9=π,那么cos(a 2+a 8)=( A )A .-12B .-32 C.12 D.32【知识点】等差数列的性质.D2【答案】【解析】A 解析:∵数列{a n }是等差数列,159a a a ,52852a ,a a 2a 33,2821cos a a cos32(),应选A . 【思路点拨】利用等差数列的性质,求得5a 3,2852a a 2a 3,从而可得结论.【题文】5.假设1a <1b<0,那么以下结论不.正确的选项是( D ) A .22a b < B .2ab b < C .0a b +< D .||||||a b a b +>+ 【知识点】不等关系与不等式.E1【答案】【解析】D 解析:由于1a <1b<0,不妨令1,2ab ,可得a 2<b 2,故A 正确.22,2abb ,故B 正确.1,2a b ,30a b ,故C 正确,1,2ab,||||3a b ,||3a b ,||||||a b a b ,所以D 不正确.应选D .【思路点拨】不妨令a=-1,b=-2,代入各个选项进展验证,找出符合条件的选项. 【题文】6.将函数y=3cosx+sinx 〔x ∈R 〕的图象向左平移m 〔m >0〕个单位长度后,所得到的图象关于y 轴对称,那么m 的最小值是〔 B 〕 A.12π B. 6π C. 3π D 65π【知识点】两角和与差的正弦函数;函数y=Asin 〔ωx+φ〕的图象变换.C4 C5 【答案】【解析】B 解析:由1sin )2sin(),23y x x x π=+=+当m 6π=时,平移后函数为2sin()2cos 2y x x π=+=,其图象关于y 轴对称,且此时m 最小。
福建省四地六校高三上学期第三次月考试卷语文试卷

【精品】福建省四地六校高三上学期第三次月考试卷语文试卷学校:___________姓名:___________班级:___________考号:___________一、句子默写1.补写出下列名句名篇中的空缺部分(10分)(1)舸舰弥津,____________。
(《滕王阁序》)(2)________,响穷彭蠡之滨。
(《滕王阁序》)(3)层峦耸翠,________。
(《滕王阁序》)(4)外无期功强近之亲,_______________。
(《陈情表》)(5)今臣亡国贱俘,________。
(《陈情表》)(6)______________,听臣微志。
(《陈情表》)(7)________,流入宫墙。
(《阿房宫赋》)(8)瓦缝参差,______________。
(《阿房宫赋》)(9)小楼昨夜又东风,__________________。
(《虞美人》)(10)______________,只是朱颜改。
(《虞美人》)二、文言文阅读阅读下面的文言文,完成后面问题(15分)张安世字子孺,少以父任为郎。
用善书给事尚书,精力于职,休沐未尝出。
上行幸河东,尝亡书三箧,诏问莫能知,唯安世识.之,具作其事。
后购求得书,以相校无所遗失。
上奇其材,擢为尚书令,迁光禄大夫。
昭帝即位,大将军霍光秉政,以安世笃行,光亲重之。
久之,天子下诏曰:“右将军光禄勋安世辅政宿卫,肃敬不怠,十有三年,咸以康宁。
夫亲亲任贤,唐、虞之道也,其.封安世为富平侯。
”大将军光薨后数月,御史大夫魏相上封事曰:“车骑将军安世事孝武皇帝三十余年,忠信谨厚,勤劳政事,国家重臣也,宜尊其位,以为大将军。
”上亦欲用之。
安世闻之,惧不敢当。
请闻求见,免冠顿首曰:“老臣诚自量不足以居大位,继大将军后,唯天子财哀,以全老臣之命。
”上笑曰:“君言太谦。
君而.不可,尚谁可者!”安世深辞弗能得。
尝有所荐,其人来谢,安世大恨.,以为举贤达能,岂有私谢邪?绝勿复为通.。
有郎功高不调,自言,安世应曰:“君之功高,明主所知。
福建省高三上学期第三次月考数学试题(解析版)
一、单选题1.已知集合,,若,,则( ) M N {}1,1M =-{}1,0,1M N =- A . B . C . D .M N ⊆N M ⊆M N ⋂=∅0N ∈【答案】D【分析】根据集合N 中所含元素的可能性逐一判断即可.【详解】对于A ,当集合时,不是的子集,故A 错误; {}0N =M N 对于B ,当集合时,不是的子集,故B 错误; {}0N =N M 对于C ,当集合时,,故C 错误;{}0,1N ={}1M N =≠∅ 对于D ,因为,,且,所以,故D 正确. {}1,0,1M N =- {}01,0,1∈-0M ∉0N ∈故选:D.2.已知复数满足,则( ) z (2i)62i z -=+z=A .B .4C .D .【答案】D【分析】根据复数的除法运算求出,则可求得.z z 【详解】解:. ()()()()62i 2i 62i 1010i22i 2i 2i 2i 5z ++++====+--+=故选:D.3.若,则( )tan 3cos()2αα⎛⎫-=-π ⎪⎝⎭πcos 2=αA . B .C .或D .或1-790791-79【答案】D【解析】用诱导公式结合同角间的商的关系,从已知等式可求出,即可求解.sin ,cos αα【详解】由得,tan 3cos()2αα⎛⎫-=-π ⎪⎝⎭πsin 23cos cos 2αααπ⎛⎫- ⎪⎝⎭=-π⎛⎫- ⎪⎝⎭所以,所以或,cos 3cos sin ααα=-cos 0α=1sin 3α=-故或.2cos 22cos 11αα=-=-2cos 21279sin αα=-=故选:D .【点睛】本题主要考查三角恒等变换等基础知识,意在考查逻辑推理、数学运算的数学核心素养,属于基础题.4.对于正项数列中,定义:为数列的“匀称值”已知数列{}n a 12323nn a a a na G n+++⋅⋅⋅+={}n a {}n a 的“匀称值”为,则该数列中的( ) 2n G n =+10a =A .B .C .D .83125942110【答案】D【分析】确定,取和带入式子,相减得到答案. ()123223n n nG n n a a a na =+=+++⋅⋅⋅+10n =9n =【详解】,即,123232nn a a a na G n n+++⋅⋅⋅+==+()123223n n nG n n a a a na =+=+++⋅⋅⋅+故;; ()12310231010102a a a a +++⋅⋅⋅+=⨯+()1239239992a a a a +++⋅⋅⋅+=⨯+两式相减得,所以. 101021a =102110a =故选:D5.函数的图象大致是( )322--=-x xy x xA .B .C .D .【答案】B【分析】根据函数的奇偶性,结合特殊值法进行判断即可. 【详解】,解得且,30x x -≠0x ≠1x ≠±令,则, 322()x xf x x x--=-3322()()()(2)2x x x x f x f x x x x x -----===----故函数为偶函数,其图象关于轴对称,排除C 选项;322()x xf x x x--=-y,排除D 选项; 0.50.51(0.5)02220.150.5f -=<-,故可排除A 选项. 10101221(10)100010f -=>-故选:B6.已知△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,且,a =30B =︒ABC S = 则△ABC 的外接圆的直径为( ) AB .C .D【答案】C【分析】先由面积公式求出c,利用余弦定理求出b ,利用正弦定理求出外接圆的直径. 【详解】因为,a =30B =︒ABC S = 所以,解得:. 111sin222ABC S ac B c ==⨯=V 4c =由余弦定理得:.b==由正弦定理得:. 2sin b R B===故选:C7.在△ABC 中,∠ACB 为钝角,AC =BC =1,,且.若函数f (m )CO xCA yCB =+1x y+=(m ∈R),则的最小值为( )CA mCB =-CO A .1 B . C .D 3412【答案】C【分析】由题意可得||的最小值为AB边上的高,由函数f (m )=|-m |CO CA CB点A 到BC ∠ACB =120°,即可求出||的最小值.CO 【详解】法一:由=x +y , 且x +y =1,可知A ,O ,B 三点共线,CO CACB 所以||的最小值为AB 边上的高,又AC =BC =1,即O 为AB 的中点, CO且函数f (m )=|-m |A 到BC CA CB 又AC =1,所以∠ACB =120°,在中,, ABC min 1sin 302CO AC =︒=从而可得||的最小值为. CO 12故选:C.法二:由=x +y , 且x +y =1,可知A ,O ,B 三点共线,CO CACB 所以||的最小值为AB 边上的高. CO设的夹角为,所以CA CB,θ ()2222222212cos cos sin CA mCB CA m CB mCA CB m m m θθθ-=+-⋅=+-=-+ 依题,可得,因为是钝角,所以. 23sin ,sin 4θθ==θ23πθ=在中,,ABC min 1sin 302CO AC =︒= 从而可得||的最小值为.CO 12 故选:C.8.已知函数,则函数的零点个数是( ) ()333,13log (1),1x x f x x x ⎧+≤⎪=⎨⎪->⎩()()()132F x f f x f x =--⎡⎤⎣⎦A . B .C .D .6543【答案】B【分析】确定函数的值域,利用换元法令 ,则,则将()333,13log (1),1x x f x x x ⎧+≤⎪=⎨⎪->⎩()t f x =[0,)t ∈+∞函数的零点问题转化为函数的图象的交点问题,作函()()()132F x f f x f x =--⎡⎤⎣⎦1(),32y f t y t ==+数图象,确定其交点以及其横坐标范围,再结合的图象,即可确定1(),32y f t y t ==+()f x 的零点个数.()()()132F x f f x f x =--⎡⎤⎣⎦【详解】已知,当时, ,()333,13log (1),1x x f x x x ⎧+≤⎪=⎨⎪->⎩1x ≤133)13(3x x f x -+=+=当时,, 1x >3()|log (1)|f x x =-作出其图象如图示:可知值域为,设 ,则,()f x [0,)+∞()t f x =[0,)t ∈+∞则函数的零点问题即为函数的图象的交点问题, ()()()132F x f f x f x =--⎡⎤⎣⎦1(),32y f t y t ==+而,作出函数的图象如图示:()333,013log(1),1t t f t t t ⎧+≤≤⎪=⎨⎪->⎩1(),32y f t y t ==+可知:的图象有两个交点,横坐标分别在之间,1(),32y f t y t ==+(0,1),(1,2)不妨设交点横坐标为,12(0,1),(1,2)t t ∈∈当时,由图象和直线可知,二者有两个交点,()1t f x =()f x11,(0,1)y t t =∈即此时有两个零点; ()()()132F x f f x f x =--⎡⎤⎣⎦当时,由图象和直线可知,二者有3个交点,()2t f x =()f x 22,(1,2)y t t =∈即此时有3个零点, ()()()132F x f f x f x =--⎡⎤⎣⎦故函数的零点个数是5, ()()()132F x f f x f x =--⎡⎤⎣⎦故选:B.【点睛】本题考查了复合函数的零点个数的确定问题,综合性较强,涉及到函数的值域以及分段函数的性质的应用和数形结合的思想方法,解答的关键是采用换元法将函数的零点问题转化为函数图象的交点问题.二、多选题9.如图,在直三棱柱中,,,,侧面的对111ABC A B C -12AA =1AB BC ==120ABC ∠=︒11AAC C 角线交点,点是侧棱上的一个动点,下列结论正确的是( )O E 1BBA .直三棱柱的侧面积是 4+B .直三棱柱的外接球表面积是8πC .三棱锥的体积与点的位置有关 1E AA O -ED .的最小值为1AE EC +【答案】ABD【分析】由题意画出图形,计算直三棱柱的侧面积即可判断A ;讲直棱柱放在圆柱中,求出直棱柱底面外接圆半径,进而求出外接球半径,利用球的表面积公式即可判断B ;由棱锥底面积与高为定值判断C ;将侧面展开即可求出最小值判断D .【详解】在直三棱柱中,,,, 111ABC A B C -12AA =1AB BC ==120ABC ︒∠=则,底面和是等腰三角形,侧面全是矩形, AC =ABC 111A B C所以其侧面积为1×2×,故A 正确; 24=+设底面外接圆半径为,即,即,r 2r =1r =所以直棱柱的外接球半径R 直三棱柱的外接球表面积为,故B 正确; 248S R ππ==由BB 1∥平面AA 1C 1C ,且点E 是侧棱上的一个动点,1BB 三棱锥的高为定值,∴1E AA O -122,故C 错误; 114AA O S =∴1E AA O V -=1312把侧面和侧面展开在一个平面上,当为的中点时,11AAC C 11CC B B E 1BB取最小值,,故D 正确.1AE EC +()min1AEEC ==+故选:ABD .10.已知平面向量,,则下列说法正确的是( ) ()1,0a =(1,b = A .B .||16a b +=()2a b a +⋅= C .向量与的夹角为D .向量在上的投影向量为+a b a 30°+a b a 2a 【答案】BD【分析】根据向量模长的坐标计算即可判断A ,根据数量积的坐标运算可判断B,由夹角公式可判断C ,由投影向量的求解公式可判断D.【详解】,所以,故A 错误;((11,02,a b +=++=4a b +==,故B 正确;()1202a a b ⋅+=⨯+⨯=, ()1cos ,2a a b a a b aa b⋅+<+>==+,,,故C 错误;(),0,πa a b <+>∈ a ∴< π3a b +>=向量在上的投影向量为,故D 正确. +a b a ()2·21a ab a a a a a ⋅+=⨯=故选:BD11.设数列是以d 为公差的等差数列,是其前n 项和,,且,则下列结论正确{}n a n S 10a >69S S =的是( ) A . B .C .D .或为的最大值0d >80a =56S S >7S 8S n S 【答案】BD【分析】由及前n 项和公式可得,即可判断A 、B 的正误,进而得到69S S =17a d =-判断C ,结合二次函数的性质判断D 的正误. 2152n dn dnS -=【详解】由,即,则,又, 69S S =1165986922a d a d ⨯⨯+=+17a d =-10a >所以,,则A 错误,B 正确;0d <8170a a d =+=且,故,C 错误; 21(1)1522n n n d dn dnS na --=+=525S d =-<627S d =-由的二次函数性质:开口向下且,易知为的最大值,D 正确. n S 69S S =78S S =n S 故选:BD12.函数的部分图像如图所示, 则下列说法中, 正确的有())0,||2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭( )A .的最小正周期为 ()f x T πB .向左平移个单位后得到的新函数是偶函数 ()f x 38πC .若方程在上共有 6 个根, 则这 6 个根的和为()1f x =(0,)m 338πD .图像上的动点到直线的距离最小时, 的横坐标为5()0,4f x x π⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭M 240x y -+=M 4π【答案】ABD【分析】选项A ,把图像上的点代入函数解析式,可以求出,再算出最小正周期进行判断; ω选项B ,利用图像的平移,得到新函数解析式,再判断奇偶性; 选项C ,方程的根转化为两个函数图像的交点问题,再根据对称性求和; 选项D ,点到直线距离的最小问题,转化成曲线的切线问题解决.【详解】因为经过点,所以, ()f x 5π08⎛⎫⎪⎝⎭,5π5π088f ωϕ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭又在的单调递减区间内,所以①; 5π8()f x 5ππ2π()8k k ωϕ+=+∈Z又因为经过点,所以,, ()f x 5π14⎛⎫⎪⎝⎭,5π5π144f ωϕ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭5πsin 4ωϕ⎛⎫+= ⎪⎝⎭又是在时最小的解,所以②. 5π4x =()1f x =5π8x >5π9π2π()44k k ωϕ+=+∈Z 联立①、②,可得,即,代入①,可得,又,所以5π5π84ω=2ω=π2π()4k k ϕ=-+∈Z π||2ϕ<,则.的最小正周期为,A 正确. π4ϕ=-π()24f x x ⎛⎫=- ⎪⎝⎭()f x 2ππ2=向左平移个单位后得到的新函数是,为()f x 3π83πππ()222842f x x x x ⎡⎤⎛⎫⎛⎫+-=+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦偶函数,B 正确.设在上的6个根从小到大依次为.令,则,根据的()1f x =(0)m ,126x x x ,,,ππ242x -=3π8x =()f x 对称性,可得,则由的周期性可得,,所以123π28x x +=()f x 342x x +=3π8T +11π8=563π19π2288x x T +=+=,C 错误. 613π11π19π33π28884ii x=⎛⎫=++=⎪⎝⎭∑作与平行的直线,使其与有公共点,则在运动的过程中,只有当直线240l x y -+=:5π()04f x x ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭,与相切时,直线与l 存在最小距离,也是点M 到直线的最小距离,5π()04f x x ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭,240x y -+=令,则,π()224f x x ⎛⎫'=-= ⎪⎝⎭ππ22π44x k -=±+()k ∈Z 解得或,又,所以(舍去),πx k =()k ∈Z ππ()4x k k =+∈Z 5π04x ⎡⎤∈⎢⎥⎣⎦,π5π044x =,,又,令,,到直线的距离大(0)1f =-1(01)M -,π14f ⎛⎫= ⎪⎝⎭2π14M ⎛⎫⎪⎝⎭,1M l 于到直线的距离,所以到直线的距离最小时,的横坐标为,D 正确 2M l M 240x y -+=M π4故选:ABD .三、填空题13.已知曲线的一条切线的斜率为,则该切线的方程为______. 23ln y x x =-1-【答案】20x y +-=【解析】设出切点坐标,利用函数在切点处的斜率为即可求出切点,进而求出切线方程. 1-【详解】设切点为,()00,x y ,,解得(舍去)或,, 32y x x'=-0321x x ∴-=-032x =-01x =01y ∴=故切线方程为,即. ()111y x -=-⨯-20x y +-=故答案为:.20x y +-=14.把正整数以下列方法分组:,其中每组都比它的前一组多一个数,设表()()()1,2,3,4,5,6, n S 示第组中所有各数的和,那么等于___________. n 10S 【答案】505【分析】根据数的排列规律,可求得第组的最后一个数字,再求得第组的第一个数字,即可1010由等差数列求和公式求解.【详解】由数字排列规律可知,每组的最后一个数字为, 123n +++⋅⋅⋅+所以第组的最后一个数字为, 10()1011012310552⨯++++⋅⋅⋅+==第组共有个数字,所以第组第一个数字为, 1010105510146-+=由等差数列前n 项和公式可得,()101046555052S ⨯+==故答案为:.50515.已知三棱锥中,,,,,若三棱锥A BCD -AB AC =AB AC ⊥BD DC ⊥6DBC π∠=A BCD-的最大体积为,则三棱锥外接球的表面积为_____. 32A BCD -【答案】12π【分析】取中点,说明为三棱锥外接球球心,记外接球半径为,用表示各线段BC O O A BCD -r r 长,易知面面时,三棱锥体积最大,由此列方程求解半径,即可得到外接ABC ⊥BCD A BCD -r 球表面积.【详解】解:如图,取中点,连结、,BC O AO DO,,为中点,BD DC ⊥6DBC π∠=O BC,,,∴12OD OB OC BC ===12CD BC ==BD ,,为中点,AB AC =AB AC ⊥O BC ,, ∴AO BC ⊥OA OB OC ==,∴OA OD OB OC ===为三棱锥外接球球心,∴O A BCD -记三棱锥外接球半径为,A BCD -r则,,OA OD OB OC CD r =====BD ==易知面面时,三棱锥体积最大, ABC ⊥BCD A BCD -故当三棱锥体积最大时,面面, A BCD -ABC ⊥BCD 又面与面交于直线,在面上,ABC BCD BC AO ABC 面,∴AO ⊥BCD 此时三棱锥的体积为,∴A BCD -13BCD AO S ⋅ 三棱锥的最大体积为, A BCD -32,即, ∴1332BCD AO S ⋅= 1332r =解得,r =三棱锥外接球的表面积.∴A BCD -244312S r πππ==⨯=故答案为:12π【点睛】本题考查了三棱锥的外接球表面积的求法,考查了面面垂直的性质定理,考查了空间想象能力和推理能力,属于中档题.16.如图,在中,若面积的最大值为__________.ABC ,,AB AC AD DC BD ===ABC【答案】2【分析】先求得面积的的表达式,再对其求最大值即可解决. ABC【详解】中,令,则 ABD △AD m ==2AB m m <又,则有,则 BD =22223=44cos BD m m m A =+-2253cos =4m A m -则 2122sin 2sin =22ABCS m m A m A m =⨯⨯⋅=又,(当且仅当时等号成立) 2133m <<2≤m 则面积的最大值为2ABC故答案为:2四、解答题17.已知函数()sin 2cos 22sin cos .36f x x x x x ππ⎛⎫⎛⎫=+++- ⎪ ⎪⎝⎭⎝⎭(1)求函数的最小正周期及对称轴方程; ()f x (2)将函数的图象向左平移个单位,再将所得图象上各点的纵坐标不变、横坐标伸长为原()y f x =12π来的2倍,得到函数的图象,求在[0,2π]上的单调递减区间. ()y g x =()y g x =【答案】(1)最小正周期为,对称轴方程为, π122k x ππ=-+Z k ∈(2) 250,,,233πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦【分析】(1)利用两角和差的正余弦公式与辅助角公式化简可得,再根据周()2cos 26f x x π⎛⎫=+ ⎪⎝⎭期的公式与余弦函数的对称轴公式求解即可;(2)根据三角函数图形变换的性质可得,再根据余弦函数的单调区间求解即()2cos 3g x x π⎛⎫=+ ⎪⎝⎭可.【详解】(1),()11sin2sin2sin222f x x x x x x =--()1sin22sin22f x x x x x ⎫=-=-⎪⎪⎭,2cos2cos sin2sin 2cos 2666x x x πππ⎛⎫⎛⎫=-=+ ⎪ ⎪⎝⎭⎝⎭所以函数的最小正周期为, ()f x π令,,得函数的对称轴方程为, 26x k ππ+=Z k ∈()f x 122k x ππ=-+Z.k ∈(2)将函数的图象向左平移个单位后所得图象的解析式为()y f x =12π,2cos 22cos 21263y x x πππ⎡⎤⎛⎫⎛⎫=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦所以,()12cos 22cos 233g x x x ππ⎛⎫⎛⎫=⨯+=+ ⎪ ⎪⎝⎭⎝⎭令,223k x k ππππ++……所以.又, 222,Z 33k x k k ππππ-++∈……[]0,2x π∈所以在上的单调递减区间为.()y g x =[]0,2π250,,,233πππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦18.中,sin 2A -sin 2B -sin 2C =sin B sin C . ABC (1)求A ;(2)若BC =3,求周长的最大值. ABC【答案】(1);(2)23π3+【分析】(1)利用正弦定理角化边,配凑出的形式,进而求得;cos A A (2)方法一:利用余弦定理可得到,利用基本不等式可求得的()29AC AB AC AB +-⋅=AC AB +最大值,进而得到结果.【详解】(1)由正弦定理可得:,222BC AC AB AC AB --=⋅,2221cos 22AC AB BC A AC AB +-∴==-⋅,.()0,A π∈ 23A π∴=(2)[方法一]【最优解】:余弦+不等式由余弦定理得:, 2222cos BC AC AB AC AB A =+-⋅229AC AB AC AB =++⋅=即.()29AC AB AC AB +-⋅=(当且仅当时取等号),22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭AC AB =,()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭解得:(当且仅当时取等号),AC AB +≤AC AB =周长周长的最大值为ABC ∴ 3L AC AB BC =++≤+ABC ∴ 3+[方法二]:正弦化角(通性通法)设,则,根据正弦定理可知,所以,66ππαα=+=-B C 66ππα-<<sin sin sin a b cA B C===,即sin )b c B C +=+sin sin 66ππαα⎤⎛⎫⎛⎫=++- ⎪ ⎪⎥⎝⎭⎝⎭⎦α=≤0α=时,等号成立.此时周长的最大值为6B C π==ABC 3+[方法三]:余弦与三角换元结合在中,角A ,B ,C 所对的边分别为a ,b ,c .由余弦定理得,即ABC 229b c bc =++.令,得2213924⎛⎫++= ⎪⎝⎭b cc 13sin ,20,2b c c θπθθ⎧+=⎪⎛⎫∈⎨ ⎪⎝⎭⎪=⎩3sin b c θθ+=时,6πθ⎛⎫+≤ ⎪⎝⎭6C π=max ()b c +=所以周长的最大值为ABC 3+【整体点评】本题考查解三角形的相关知识,涉及到正弦定理角化边的应用、余弦定理的应用、三角形周长最大值的求解问题;方法一:求解周长最大值的关键是能够在余弦定理构造的等式中,结合基本不等式构造不等关系求得最值.方法二采用正弦定理边化角,利用三角函数的范围进行求解最值,如果三角形是锐角三角形或有限制条件的,则采用此法解决.方法三巧妙利用三角换元,实现边化角,进而转化为正弦函数求最值问题. 19.已知函数. ()()32312132623,57f x x x ax g a a a a =+--=+--(1)时,求函数的单调递增区间;1a =()f x (2)若函数在区间上不单调,且时,不等式恒成立,求实数a ()f x []2,0-[]2,0x ∈-()()f x g a <的取值范围.【答案】(1);(2).(,1),(2,)-∞-+∞()1,2【分析】(1)求导函数,利用导数大于0,可得函数的单调递增区间;()f x (2)利用在上不单调,确定,时,不等式恒成立,等价于()f x []2,0-02a <<[]2,0x ∈-()()f x g a <,从而可求实数的取值范围.()()f a g a -<a 【详解】(1)当时,,定义域为R , 1a =()32113223f x x x x =---,()()()2221f x x x x x ∴'=--=-+令,得,或, ()0f x >′1x <-2x >函数的单调递增区间是;∴()f x (,1),(2,)-∞-+∞(2),()()()()2222f x x a x a x a x '=+--=+-令,得,或,()0f x '=2x =x a =-∵函数在区间上不单调,()f x []2,0-,即,()2,0a ∴-∈-02a <<又∵在上,,在上,, ()2,a --()0f x >′(),0a -()0f x <′在上的最大值为,()f x \[]2,0-()f a -∴当时,不等式恒成立,等价于, []2,0x ∈-()()f x g a <()()f a g a -<,3221223()32a a a a g a -∴-+⨯+-<, 3231135766a a a a ∴+-<+-,解得,2540a a ∴-+<14a <<综上所述,a 的取值范围是.()1,2【点睛】本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.20.已知数列的各项均为正数,其前n 项和为,且 {}n a n S 22n n S a =-(1)求数列的通项公式;{}n a (2)若,设数列的前n 项和为,当对任意都成立时,求实数21·log n n n b a a +={}n b n T 0n T k -≥*N n ∈k 的取值范围.【答案】(1);(2).2n n a =(],4-∞【分析】(1)由,当时,,解得,当时,,利用等22n n S a =-1n =1122a a =-1a 2n …1n n n a s s -=-比数列的通项公式即可得出.(2),利用错位相减法即可得出. 1212log 2log 2(1)2n n n n n n b a a n ++=⋅=⋅=+【详解】解:(1),22n n S a =- 当时,,解得,∴1n =1122a a =-12a =当时,,2n …111(22)(22)22n n n n n n n a S S a a a a ---=-=---=-,12n n a a -∴=数列是以2为首项,以2为公比的等比数列,∴{}n a .2n n a ∴=(2),1212log 2log 2(1)2n n n n n n b a a n ++=⋅=⋅=+数列的前项和为,{}n b n 23223242(1)2n n T n =⨯+⨯+⨯+⋯⋯++,231222322(1)2n n n T n n +∴=⨯+⨯+⋯⋯+⋅++⋅相减可得:, 23112(12)4222(1)22(1)212n n n n n T n n ++--=+++⋯⋯+-+⋅=+-+⋅-化为:.12n n T n +=⋅,min ()4n T ∴=当对任意都成立时,0n T k -…N*n ∈,min ()4n k T =…实数的取值范围是,.∴k (-∞4]21.如图,四棱锥的底面是菱形,,.P ABCD -2AB AC ==PA =PB PD =(1)证明:平面平面;PAC ⊥ABCD (2)若,点在棱上,且,求二面角的余弦值. PA AC ⊥M PC BM MD ⊥B AM C --【答案】(1)证明见解析;(2【分析】(1)连接与相交于,根据,得到平面,得到证明. BD AC E PE BD ⊥AC BD ⊥BD ⊥PAC (2)以为轴建立空间直角坐标系,设,根据,,AN AD AP ,,x y z (,,),,01M a b M c P PC λλ=≤≤得到,计算平面的法向量为,平面的法向量为BM MD ⊥12M ABM n = ACM,计算夹角得到答案.3,0)m =-【详解】(1)如图所示:连接与相交于,,故, BD AC E PB PD =PE BD ⊥四棱锥的底面是菱形,故,,故平面, P ABCD -AC BD ⊥AC PE E = BD ⊥PAC 平面,故平面平面.PD ⊂ABCD PAC ⊥ABCD (2),故平面,取中点,连接,故.PA AC ⊥PA ⊥ABCD BC N AN AN AD ⊥以为轴建立空间直角坐标系,如图所示:,,AN AD AP ,,x y z 则,设,1,0),(0,2,0),(0,0,B D C P -(,,),,01M a b M c P PC λλ=≤≤,解得,,. (,,a b c λ∴-=-a =b λ=c =-,,,)M λ∴,,,1,,)BM λ=+),2,DM λ=-- BM DM ⊥故,(1)(2))0BM DM λλ⋅=++-+=解得或(舍去),. 12λ=54λ=12M ∴设平面的法向量为, ABM (),,n x y z =则,取,1020n AM x y n AB y ⎧⋅+=⎪⎨⎪⋅=-=⎩x n == 设平面的法向量为,ACM (),,m a b c = 则,取,1020m AM b m AC b ⎧⋅=+=⎪⎨⎪⋅=+=⎩ a =3,0)m =- 设二面角的平面角为,则B AM C --θcos m n m nθ⋅===⋅【点睛】本题考查了面面垂直,二面角,意在考查学生的空间想象能力和计算能力. 22.已知函数. ()()ln ,tf x x s s t R x=+-∈(1)讨论的单调性;()f x(2)当时,若函数恰有两个零点,证明:. 1t =()f x ()1212,0x x x x <<122x x +>【答案】(1)答案见解析;(2)证明见解析.【分析】(1)求出的导数,讨论和时导数正负即可得出单调性; ()f x 0t ≤0t >(2)令,则由题可得,将题目转化为证明大于0()1201x m m x =<<11ln m x m -=()12ln g m m m m=--恒成立,利用导数即可证明. 【详解】解:(1). ()221()0t x tf x x x x x-'=-=>当时,在上恒成立,所以在上单调递增;0t ≤()0f x '>()0,∞+()f x ()0,∞+当时,令得;令得;所以在上单调递减,在0t >()0f x '>x t >()0f x '<0x t <<()f x ()0,t (),t +∞上单调递增.(2)证明:当时,在上单调递减,在上单调递增.所以,解得1t =()f x ()0,1()1,+∞()110f s =-<.1s >由条件有,整理得,121211ln ln x s x s x x +-=+-1112221211ln x x x x x x x x x --==令,则,. ()1201x m m x =<<11ln m m x -=11ln m x m-=所以, 2212111l 1ln 111n m x m m x x m x x m m ⎛⎫--⎛⎫+=+=+=⎪ ⎪⎝⎭⎝⎭所以, 2212ln ln ln 12ln 112ln 22m mm m m m m mm m mx x m-----+-=-==令,则,()12ln g m m m m =--()2221111m m g m m m m -+'=+-=当时,,所以单调递增,, 01m <<()0g m '>()g m ()()10g m g <=又当时,,所以,即.01m <<ln 0m <1220x x +->122x x +>【点睛】关键点睛:本题考查与双变量有关的不等式证明,解题的关键是将其转化为证明大于0恒成立. ()12ln g m m m m=--。
高三第三次月考数学(文科)试卷答案
银川一中2020届高三年级第三次月考(文科)参考答案一、选择题:二、填空题:13. 2x-y-2=0 14. 7 15. 4(1)21(2)n n a n n =⎧=⎨+≥⎩ 16. 4三、简答题:17、解: (1)证明 连接OE ,如图所示. ∵O 、E 分别为AC 、PC 的中点,∴OE ∥P A.∵OE ⊂面BDE ,P A ⊄面BDE , ∴P A ∥面BDE ............................................6分 (2)证明 ∵PO ⊥面ABCD ,∴PO ⊥BD .在正方形ABCD 中,BD ⊥AC ,又∵PO ∩AC =O ,∴BD ⊥面P AC . 又∵BD ⊂面BDE ,∴面P AC ⊥面BDE ......................12分18.试题解析:(1)411=+n n a a ,∴数列}{n a 是首项为41,公比为41的等比数列,∴*)()41(N n a n n ∈=. 因为2log 341-=n n a b ,所以232)41(log 341-=-=n b n n .(2)由(1)知,23,)41(-==n b a n n n , 所以,)41()23(n n n c +-=所以,)41()23()41)53()41(7)41(4411132n n n n n S +-+(+-+++++++=-])41()41)41()41(41[)]23()53(741[132n n n n +(++++++-+-++++=-n n n n n n )41(313123411])41(1[412)231(2⋅-+-=--+-+=.19.()()()2222211,sin sin ,sin 1sin,0,,2362,366521,652cos6133AD BDABD BD B BAD BD B BAD BAD BAD AD ADB ABD ADC ACD AD CD AD CD CD CD CD ππππππππ∆==∠⨯∠==<∠<∴∠=∴∠=--=∴∆∠=∆=+-⎛=+-⨯ ⎝⎭+证明:在中由正弦定理是等腰三角形由知,AB=BD=1,在中,AC 3100,5(1.311sin 1322ABC CD CD S AB BC B λ∆-==-∴∴=⨯⨯=⨯⨯=解得舍去), CD=2 BC=BD+CD=3, =20.解析:(Ⅰ)因为1AA ABC ⊥平面,所以⊥1CC 平面ABC .而⊂1CC 平面11B BCC ,所以平面⊥ABC 平面11B BCC . ………2分因为线段BC 的中点为D ,且.ABC AD BC ∆⊥是等腰三角形,所以 而BC C CBB ABC ABC AD =⋂⊂11,平面平面平面,11AD CBB C ⊥所以平面. 111C E CBB C ⊂又因为面,1.AD CE ⊥所以(Ⅱ)1AA ABC ⊥平面,1AA AC ⊥则.90BAC ∠=,即AC AB ⊥.又AB AC A ⋂=,所以11AC ABB A ⊥平面,故1111AC ABB A ⊥平面,所以11A EC ∆是直角三角形.在三棱柱111ABC A B C -中,11//AC A C ,直线1AC C E 、所成角的余弦为12, 则在11EC A Rt ∆中,111cos 2AC E ∠=,112AC AC ==,所以1A E =………7分 在E B A Rt 11∆中,112A B =,所以1B E =.因为1AA =E 是线段1BB 的靠近点B 的三等分点.因为,324222221313111111=⨯⨯⨯⨯=⋅=∆-CA S V E B A E B A C 所以11B A DE V -=11D A B E V -=1112C A B E V -.322=21.(1)由题意,函数()()211ln 1(0)22f x x x m x m x =+-+++>, 则()11f x x m x'=+--, 因为2x =是函数()f x 的极值点,所以()122102f m +'=--=,故32m =,即()152f x x x =+-',令()215252022x x f x x x x -+'=+-=>,解得102x <<或2x >.令()225202x x f x x'-+=<,解得122x <<,所以()f x 在10,2⎛⎫ ⎪⎝⎭和()2,+∞上单调递增,在1,22⎛⎫⎪⎝⎭上单调递减. (2)由()11f x x m x'=+--, 当1m ≤时,()0f x '>,则()f x 在()1,+∞上单调递增,又()10f =,所以()211ln 1022x x m x m +-+++>恒成立; 当1m >时,易知()11f x x m x'=+--在()1,+∞上单调递增,故存在()01,x ∈+∞,使得()00f x '=,所以()f x 在()01,x 上单调递减,在()0,x +∞上单调递增, 又()10f =,则()00f x <,这与()0f x >恒成立矛盾. 综上,1m ≤.22.(1)曲线C 的普通方程为22(1)1x y -+= ,极坐标方程为2cos ρθ= ------4分(2)设11(,)P ρθ,则有2cos 3ρθπθ=⎧⎪⎨=⎪⎩解得111,3πρθ== --6分设22(,)Q ρθ,则有2sin()33πρθπθ⎧+=⎪⎪⎨⎪=⎪⎩解得223,3πρθ==--8分所以2PQ = . --10分23.解:(1)f (x )+f (x +4)=|x -1|+|x +3|=⎩⎪⎨⎪⎧-2x -2,x <-3,4,-3≤x ≤1,2x +2,x >1.当x <-3时,由-2x -2≥8,解得x ≤-5; 当-3≤x ≤1时,f (x )≤8不成立;当x >1时,由2x +2≥8,解得x ≥3.……………………………………………4分 所以,不等式f (x )≤4的解集为{x |x ≤-5,或x ≥3}.……………………………5分 (2)f (ab )>|a |f ( ba ),即|ab -1|>|a -b |. …………………………………………6分∵因为|a |<1,|b |<1,∴|ab -1|2-|a -b |2=(a 2b 2-2ab +1)-(a 2-2ab +b 2)=(a 2-1)(b 2-1)>0, 所以,|ab -1|>|a -b |.故所证不等式成立.…………………………………10分。
2024届福建省漳州市高三第三次质量检测三模生物试题(解析版)
【解析】
【分析】原核细胞与真核细胞的本质区别是有无核膜包被的细胞核。
图示O~a阶段米根霉细胞可进行产生乳酸的无氧呼吸,所以无CO2释放。
【详解】A、酒精跨膜运输方式为自由扩散,该过程不消耗ATP,A错误;
B、米根霉与酵母菌均是真核生物,均有核膜包被的细胞核,B错误;
C、O~a阶段米根霉细胞可进行产生乳酸的无氧呼吸,所以无CO2释放,C错误;
【详解】A、由图可知,第2天时小球藻的种群增长速率最快,A正确;
B、温度、营养物质等非密度制约因素能制约小球藻种群的增长,第4天后浓度下降可能是因为营养不足,B正确;
C、由图可知,小球藻第5天的相对浓度值大于第3天的,即第5天的小球藻数量大于第3天的,故第5天小球藻红光吸收量大于第3天,C正确;
D、实验结果显示小球藻种群数量在第4天以D错误。
B、该激素为分泌蛋白,与溶酶体酶的合成加工途径相似,均是在核糖体上合成,经内质网初加工,高尔基体再加工,B正确;
C、由题意可知,相关激素含量过高时发生粒溶,使体液中激素含量维持动态平衡,C正确;
D、粒溶是将多余的激素降解的过程,该过程可为细胞提供有用的物质和能量,D正确。
故选A。
2.小球藻是单细胞绿色藻类,大约10h分裂一次,其死亡个体叶绿素a含量降低。研究人员吸取小球藻培养液,统计其种群数量变化如图所示。下列分析错误的是( )
A.皮质醇的分泌及调节血糖的过程仅存在体液调节
B.糖皮质激素升血糖 原理与胰高血糖素相同
C.个体的内质网功能受损可导致血液中游离型皮质醇含量增加
D.长期服用糖皮质激素类药物可治疗炎症并增强机体的免疫功能
【答案】C
【解析】
【分析】神经调节和体液调节共同协调、相辅相通成,但神经调节占主导地位。两种调节方式的特点:神经调节是以反射的形式来实现的,需要的结构基础是反射弧,作用过程表现为迅速、作用时间短,作用范围有限;体液调节的特点主要是激素随着血液循环送到全身各处并在靶器官、靶细胞部位发挥调节作用的,其作用特点为作用时间长、作用范围广,速度慢。神经调节与体液调节之间的关系:一方面大多数内分泌腺都受中枢神经系统的控制;另一方面内分泌腺分泌的激素也可以影响神经系统的功能。
范文高三文科数学第三次月考试卷及答案
池州一中2012-2013学年度高三月考数学试卷(文科)第Ⅰ卷 (选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,选出符合题目要求的一项.⒈ 已知{2,3,4}U =,集合{|(1)(4)0,}A x x x x Z =--<∈,则 U A =ð( ) A . {}1,4 B .{}2,3,4 C .{}2,3 D . {4}⒉ 已知函数4log 0()3 0x x x f x x >⎧=⎨≤⎩,则1[()]16f f =( )A .9B .19 CD⒊ 设[]x 为表示不超过x 的最大整数,则函数lg[]y x =的定义域为 ( )A .(0,)+∞B .[1,)+∞C . (1,)+∞D . (1,2) ⒋ 设0.5323,log 2,cos3a b c π===,则( ) A .c b a << B .a b c << C .c a b << D .b c a <<⒌ 已知函数2n y a x =(*0,n a n N ≠∈)的图象在1x =处的切线斜率为121n a -+(*2,n n N ≥∈),且当1n =时,其图象经过()2,8,则7a =( )A .12 B .5 C .6 D .7⒍ 命题“函数()()y f x x M =∈是奇函数”的否定是( )A .x M ∃∈,()()f x f x -≠-B .x M ∀∈, ()()f x f x -≠-C .x M ∀∈,()()f x f x -=-D .x M ∃∈,()()f x f x -=- ⒎ 把函数sin()(0,||)2y A x πωφωφ=+><的图象向左平移3π个单位得到()y f x =的图象 (如图),则2A ωϕ-+=( ) A .6π-B .6π C . 3π- D . 3π⒏ Direchlet 函数定义为: 1()0Rt Q D t t Q ∈⎧=⎨∈⎩ð,关于函数()D t 的性质叙述不正确...的是( )A .()D t 的值域为{}0,1B .()D t 为偶函数C .()D t 不是单调函数 D .()D t 不是周期函数⒐ 函数()=lg cos 2f x x x π⎛⎫-⎪⎝⎭的零点个数是( ) A .3 B .4 C .5 D .6⒑ 已知向量a 、b 的夹角为θ,+=a b 2-=a b ,则θ的取值范围是( )A .03πθ≤≤B .32ππθ≤<C .62ππθ≤<D .203πθ<<第II 卷(非选择题,共100分)二、填空题:共5小题,每小题5分,计25分. ⒒ 函数()f x =的定义域为 .⒓ 已知322ππα⎛⎫∈ ⎪⎝⎭,,()3tan 74απ-=-,则sin cos αα=+ .⒔ 函数()()x f x e x R =∈可表示为奇函数()h x 与偶函数()g x 的和 ,则()h x = .⒕ 给出下列命题: ⑴ 1y =是幂函数;⑵“1x <”是“2x <”的充分不必要条件;⑶ 2)0x -≥的解集是[)2,+∞;⑷ 函数tan y x =的图象关于点,0()2k k Z π⎛⎫∈ ⎪⎝⎭成中心对称;⑸ 命题“若x y =,则sin sin x y =”的逆否命题为真命题.其中真命题的序号是 (写出所有正确命题的序号)⒖ 对于三次函数32()(0)f x ax bx cx d a =+++≠,给出定义:设()f x '是函数()y f x =的导数,()f x ''是()f x '的导数,若方程()0f x ''=有实数解0x ,则称点00(,())x f x 为函数()y f x =的“拐点”,某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数32115()33212f x x x x =-+-,请你根据上面探究结果,解答以下问题: (1)函数32115()33212f x x x x =-+-的对称中心为 ; (2)计算1232012()()()()2013201320132013f f f f ++++= . 三、解答题:本大题共6小题,计75分.解答应写出必要的文字说明,证明过程或演算步骤. ⒗(本小题满分12分)已知向量()2cos ,2x x =m ,(cos ,1)x =n ,设函数()f x =⋅m n ,x R ∈. (Ⅰ)求函数()f x 的最小正周期和单调递减区间;(Ⅱ)若方程()0f x k -=在区间π0,2⎡⎤⎢⎥⎣⎦上有实数根,求k 的取值范围.⒘(本小题满分12分)已知命题p :实数x 满足12123x --≤-≤;命题q :实数x 满足222(1)0(0)x x m m -+-≤>,若p ⌝是q ⌝的必要不充分条件,求实数m 的取值范围.⒙(本小题满分13分)已知()x f x m =(m 为常数,0m >且1m ≠).设1()f a ,2()f a ,…,()n f a ,…(*n N ∈)是首项为m 2,公比为m 的等比数列.(Ⅰ)求证:数列{}n a 是等差数列;(Ⅱ)若()n n n b a f a =⋅,且数列{}n b 的前n 项和为n S ,当2m =时,求n S . ⒚ (本小题满分12分)已知ABC ∆的内角,,A B C 所对的边分别是,,a b c ,设向量(,)a b =m ,(sin ,sin )B A =n ,(2,2)b a =--p .(Ⅰ)若m //n ,求证:ABC ∆为等腰三角形; (Ⅱ)若m ⊥p ,边长2c =,3C π∠=,求ABC ∆的面积.⒛(本小题满分12分)如图,在ABC ∆中,设AB =a ,AC =b ,AP 的中点为Q ,BQ 的中点为R ,CR 的中点恰为P . (Ⅰ)若=+AP λμa b ,求λ和μ的值;(Ⅱ)以AB ,AC 为邻边, AP 为对角线,作平行四边形ANPM ,求平行四边形ANPM 和三角形ABC 的面积之比ANPMABCS S ∆. 21.(本小题满分14分)已知0()x f x x e =⋅,10()()f x f x '=,21()()f x f x '=,…,*(1)()()()n n f x f x n N -'=∈.(Ⅰ)请写出的()n f x 表达式(不需证明); (Ⅱ)求()n f x 的极小值()n n n y f x =;(Ⅲ)设2()2(1)88n g x x n x n =--+-+,()n g x 的最大值为a ,()n f x 的最小值为b ,试求a b -的最小值.池州一中2013届高三第三次月考(10月)数学(文科)答案一、 选择题: 题号 1 2 3 4 5 6 7 8 9 10 答案D BCA B AC DC A二、填空题题号 11121314 15答案⑵⑷⑸1,12⎛⎫⎪⎝⎭,2012 11. 解:由21011141340x x x x x x +>>-⎧⎧⇒⇒-<<⎨⎨-<<--+>⎩⎩,即定义域为(1,1)- 三、解答题16. 解: (Ⅰ)由题意知:f(x) = 22cos21cos2212cos(2)3x x x x x π=+=++∴f(x)的最小正周期 T = π (4)∴f(x)的单调递减区间 [,],63k k k z ππππ-+∈ ......................6分 17.解:令{}12122103x A xx x ⎧-⎫=-≤-≤=-≤≤⎨⎬⎩⎭P ε∴⌝⌝则的逆否命题为“P ε若则”而P ε⌝⌝是的必要不充分条件,∴P ε是的必要不充分条件故A B ∴0129101m m m m >⎧⎪-≤-⇒≥⎨⎪≤+⎩18. 解:(1)由题意f (a n )=211n n m m m -+⋅=,即1na n m m +=.∴a n =n +1,(2分) ∴a n +1-a n =1, ∴数列{a n }是以2为首项,1为公差的等差数列. (2)由题意()n n n b a f a =⋅=(n +1)·m n+1,当m =2时,b n =(n +1)·2n +1∴S n =2·22+3·23+4·24+…+(n +1)·2n +1 ① ①式两端同乘以2,得2S n =2·23+3·24+4·25+…+n·2n +1+(n +1)·2n +2 ② ②-①并整理,得S n =-2·22-23-24-25-…-2n +1+(n +1)·2n +2 =-22-(22+23+24+…+2n +1)+(n +1)·2n +2=-22-22(1-2n)1-2+(n +1)·2n +2=-22+22(1-2n )+(n +1)·2n +2=2n +2·n .19. 【解析】证明:(Ⅰ)//,sin sin ,m n a A b B ∴=u v v Q 即22a ba b R R⋅=⋅, 其中R 是ABC ∆外接圆半径,a b = --------(5分)ABC ∴∆为等腰三角形 -----(6分)解(Ⅱ)由题意可知m ⊥p 0,(2)(2)0m p a b b a =-+-=u v u v 即,a b ab ∴+= --------(8分)由余弦定理可知, 2224()3a b ab a b ab =+-=+-2()340ab ab --=即 4(1)a b a b ∴==-舍去---------(10分)11sin 4sin 223S ab C π∴==⋅⋅= ………………………(12分)20.(1)解:∵Q 为AP 中点,∴1a b 222uQP AP λ==+⋅ P 为CR 中点,∴a (1)b PR CP AP AC u λ==-=+- 同理:11()22RQ BR BQ AQ AB ===- 11(a b a)(1)a b 222224λμλμ=+-=-+ 而0QP PR RQ ++= ∴1a b a (1)b (1)a b 022224λμλμλμ+++-+-+=即21(1)0722*******λλλλμμμμ⎧⎧=++-=⎪⎪⎪⎪⇒⎨⎨⎪⎪+-+==⎪⎪⎩⎩(2)sin ANPMSAN AM A =⋅⋅ 1sin 2ABCSAB AC A =⋅⋅ ∴sin 24162217749sin 2ANPM ABC AN AM A AN AM S S AB AC AB AC A ⋅⋅==⋅⋅=⨯⨯=⋅⋅ 21. 【解析】本小题主要考查函数的概念、导数应用、函数的单调区间和极值等知识,考查运用数学知识解决问题及推理的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
漳州双语实验学校高三文科上学期第三次月考历史试卷06.12.5
一、选择题。(每小题2分,共50分) 文明的传承、交融为和谐社会的构建奠定了坚实的基础。据此回答1~2题。 1.春秋战国作为一个社会大变革时期,同时也是一个思想流派纷呈的时期。下列春秋战国时期提出的思想,至今对构建和谐社会仍产生着积极影响的是 ①“绝圣弃智,绝仁弃义” ②“己所不欲,勿施与人” ③“兼相爱,交相利” ④人贵贱有“序” A.①②③④ B.①②③ C.②③ D.①④ 2.洪秀全创立拜上帝教的根本目的是 A.进行反洋教斗争 B.在中国宣传基督教 C.推翻清政府的统治 D.反对儒家思想 国家统一是社会稳定发展的前提。回答第3~4题。 3.关于我国古代自秦汉以来中央与地方关系演变趋势的叙述,错误的一项是 A.强化中央对地方的控制和监视 B.地方权力愈来愈小,中央权力愈来愈大 C.地方权力增强,中央集权削弱 D.中央对边疆地区治理渐趋严密 4.新中国为完成国家统一,巩固新生的人民政权,采取了一系列积极措施,主要体现在 ①开展剿匪作战 ②和平解放西藏 ③开展“三反”“五反”运动 ④镇压反革命运动 A.①②③ B.①③④ C.③④ D.①②④ 领导经济建设工作,是中共作为执政党的重要职责。回答5~6题。 5.在下列党的会议中最早提出要把经济建设作为党的工作重心的是
6.中共“十三大”提出的“一个中心,两个基本点”的本质是 A.发扬社会主义民主 B.建立社会主义制度 C.发展社会主义生产力 D.坚持党的正确领导 一切从实际出发,政党与政府在政治实践中不断走向成熟。回答第7~8题。 7.经过第一次国内革命战争的洗礼,土地革命战争时期中国共产党政治上趋于成熟,表现在 ①开始正确认识中国社会的性质 ②纠正右倾机会主义错误 ③进行农村包围城市的革命道路的探索 ④根据社会主要矛盾的变化及时调整革命策略 A.①② B.③④ C.②③④ D.①②③④ 8.毛泽东说:“„„使阶级斗争服从于今天抗日的民族斗争,这是统一战线的根本原则。”体现了这一“根本原则”的中共政策有 ①和平解决西安事变的方针 ②减租减息的土地政策 ③有理有利有节地反击国民党掀起的反共高潮 ④“三三制”原则 A.①②③ B.①③ C.③④ D.①②③④ 实行专制主义中央集权制度是中国古代史的广大特点;也是中国封建社会持续时间较长的一个重要原因.回答9—10
题. 9.秦朝建立了专制主义中央集权制度。中央集权指 A.帝位终身制 B.皇位世袭制 C.地方服从并受制于中央 D.中央各部门相互制约与监督 10.在中国近代史上的下列人物中,反对君主专制制度的有①林则徐 ②曾国藩 ③康有为 ④孙中山 A.①② B.①②③ C.③④ D.④ 2005年9月28日是中国古代思想家、教育家孔子诞辰2556年,该日全球30多家孔庙联合举行祭祀大典。回答11-13题。 11.孔子的思想中自相矛盾的一组是①知之为知之 ②因材施教 ③贵贱有序 ④有教无类 A.①② B.②③ C.①③ D.③④ 12. 孟子是继孔子之后的儒学大师,被尊称为“亚圣”。亚圣的核心思想是 A.民贵君轻 B.政在得民 C.已所不欲,勿施于人 D.仁者爱人 13. 今天我党大力倡导“以德治国”,对此,我们可以继承和发扬儒家学说中的主要是 A.“和为贵”与“仁”的思想 B.农本思想 C.“有教无类”的思想 D.“民为贵,君为轻”的思想 近代以来,关注、解决农民问题是赢得革命成功和实现现代化的关键问题。回答14~16题。
14.在江苏吴县,太平天国“监军(官名)提各乡卒长(官名)给田凭,每亩钱360文,领凭后租田概作自产,农民窃喜,陆续完纳。”这反映出太平天国在其占领区 A.没有能够触动旧的土地所有制 B.实现了土地和产品的平均分配 C.一定程度上满足农民的土地要求 D.领导农民进行反封建的抗税斗争 15.孙中山领导的资产阶级革命派提出的解决土地问题的方案是 A.用暴力手段夺取地主土地归国家所有 B.核定全国地价,革命后增长地价归国家所有 C.废除小土地所有制,建立资本主义大农业 D.没收地主土地,建立农民土地所有制 16.1922年,中共“二大”在宣言中指出“中国三万万的农民,乃是革命中的最大要素。 农民因为土地缺乏、人口稠密、天灾流行、战争和土匪的扰乱、军阀的额外征税和剥削、 外国商品的压迫、生活程度的增高等原因,以至日趋穷困和痛苦”。这表明中国共产党 A.以发动农民运动作为党的中心工作 B.提出了由国民革命转向土地革命的方针 C.认识到农民阶级在民主革命中的重要地位 D.决定建立农村革命根据地实行工农武装割据 人类社会自产生以来,改革就与社会进步相伴而生。据此回答17—18题。
17. 公元前338年,秦惠王听信谗言下令逮捕商鞅。商鞅在逃亡途中投宿旅店遭到拒绝。店主说:“商君定有法律,谁让没有凭证的旅客住宿,谁就要连坐。”无处可去的商鞅最后被逮捕处死。这个“作法自毙”的故事说明秦国 A. 变法深入人心 B. 法治代替人治 C. 变法违背民意 D. 变法最终失败 18. 中国当前的改革开放与晚清的开埠通商最本质的区别是 A. 关税的税率不同 B. 国家行使主权的权限不同 C. 对外开放的地区不同 D. 对意识形态的影响不同 “逆子孤臣一稚儒,填膺大义抗强胡。丰功岂在尊明朔,确保台湾入版图。”这是张学良将军歌颂郑成功历史功绩的诗。回答第19~21题。 19.中国中央政府最早正式管辖台湾的机构是 A.福建省 B.澎湖巡检司 C.宣政院 D.理藩院 20.张学良将军类同郑成功“确保台湾入版图”的爱国义举是 A.宣布东北易帜 B.组织察哈尔民众抗日同盟军 C.发动西安事变 D.建立“中华共和国人民革命政府” 21.中国政府最早提出和平解决台湾问题是在 A. 1954年一届全国人民代表大会召开时 B.1978年中共十一届三中全会召开时 C.1979年元旦全国人大常委会发表《告台湾同胞书》 D.1982年邓小平接见英国首相撒切尔夫人时 在近现代历史上,中国人民经过长期艰苦卓绝的抗争和努力,终于实现了国家的独立和 富强,国际地位日益提高。回答22~25题。 22.洋务运动对中国近代化进程的主要影响是 A.开始了中国早期的工业化进程 B.实践了“师夷长技以制夷”的思想 C.建立了中国近代第一支海军 D.抵制了西方列强对中国的经济侵略 23.中国人民取得抗日战争胜利的各种原因中,最主要的是 A.世界人民的支援 B.国共合作与全民族团结抗战 C.中国地大、物博、人众、兵多 D.美国向日本投掷了原子弹 24.20世纪中叶,毛泽东宣告,中国人民从此站立起来了。下列各项中与这一结论相符的是 A.抗战胜利洗雪百年国耻 B.半殖民地半封建社会结束 C.抗美援朝取得胜利 D.社会主义改造基本完成 25.随着综合国力的增强,我国的国地地位不断提高。下列各项中最能体现我国在国际社会长期发挥重要作用的是 A.在亚非会议倡导求同存异方针 B.坚持独立自主和平外交政策 C.成为世界贸易组织的成员国 D.担任联合国安理会常任理事国 二、非选择题。(16分+18分+16分,共50分) 26.(16分)在推进区域经济协调发展的过程中,我国提出中部崛起的重大战略。湖北武汉是中部地区最重要的中心城市和发展基地,在促进中部地区崛起中肩负着重要的历史使命。 材料一:湖北是楚文化的发源地,堪称古代世界青铜冶炼技术高峰的铜绿山古矿冶炼遗址和越王匀践剑等分别出土于鄂东及江汉平原,秦代竹简首次在云梦出土。 (1) 结合所学知识,列举出代表中国古代楚文化的其他成就(举出三例)。(3分) 材料二:1889年8月8日,张之洞任湖广总赞,在湖北开始新政,下列四幅图片反映其新政的部分成果。
方言学堂 湖北兵工厂 汉阳铁厂 湖北新军 (2)读以上四副图片。回答: ①概括指出张之洞“湖北新政”的主要措施。(3分) ②1911年,“敢为天下先”的武汉革命党人打响了辛亥革命的第一枪,结合所学知识分析张之洞“湖北新政”与武昌起义爆发之间的关系。(6分) 材料三:建国之初,得力于新中国产业布局,武汉独揽国家重点投资项目的四分之一,一跃成为新中国的工业重镇.然而这座大都市却在上个世纪90年代后渐渐失去光彩。 (3)请列举出新中国成立初期,武汉所取得的经济建设成就(至少两例)。(2分) (4)简要分析武汉“渐渐失去光彩”的原因。(2分) 27. (18分)中国共产党十六届五中全会把以人为本作为“十一五”时期科学发展的核心内容和根本目标。阅读下列材料,回答问题: 材料一 “天之生民,非为君也;天之立君,以为民也。”(《大略篇》)“故有社稷者而不能爱民,不能利民,则求民之亲爱己,不可得也。”(《君道篇》) ——《荀子》 材料二 “礼者,贵贱有等,长幼有差,贫富轻重皆有称者也。……由士以上,则必以礼乐节之;众庶百姓,则必以法数制之。” ——《荀子〃富国篇》 材料三 (一)在权利方面,人们生来是而且始终是自由平等的。……(二)任何政治结合的目的都在于保存人的自然的和不可动摇的权利。这些权利就是自由、财产、安全和反抗压迫。(三)整个主权的本原主要是寄托于国民。任何团体、任何个人都不得行使主权所未明白授予的权力。……(六)法律是公共意志的表现。全国公民都有权亲身或经由其代表参与法律的制定……在法律面前,所有的公民都是平等的,故他们都能平等地按其能力担任一切官职。 材料四 近世各国所谓民权制度,往往为资产阶级所专有,使成为压迫平民之工具。若国民党之民权主义,则为一般平民所共有,非少数人所得而私也。 ——孙中山《中国国民党第一次全国代表大会宣言》 材料五 “人们支持人权,但不要忘记还有一个国权。”“中国人民珍惜同其他国家和人民的友谊和合作,更加珍惜自己经长期奋斗而得来的独立自主的权利。” ——《邓小平文选》 请回答: (1)据材料一、二,指出荀子在对待人民的态度上的两种观点。结合当时的背景,分析产生这些观点的原因。(5分) (2)材料三的观念与材料二有何不同?(3分)请举出国际上两个19世纪以前把这种理论制度化、法制化的实例,说明其进步意义。(4分) (3)据材料四指出孙中山先生晚年民权思想的主要特征是什么?(1分)其产生的历史原因是什么?(2分) (4)据材料五指出邓小平在人权问题上更注重什么?(1分)结合所学知识简单说明邓小平注重的内容与人权的关系?(2分) 28、(16分)阅读下列材料: 材料一:近代实业家张謇认为,中国要振兴实业就必须以建立和发展棉纺织业和钢铁业作为中心,以此来带动其他经济部门的发展。建立起独立的民族工业体系,这样才“可以操经济界之主权”,以抵制外来的经济侵略而获得国家的经济独立。 他曾说:“至于铁矿需本(资本)尤重,非用开放主义,无可措手,但使条约正当,权限分明。”“现在世界以大企业立国,而中国以公司法、破产法不备,故逐将昙花一现之基础……我无法律为之防,其危险将视无可得资为尤甚,故农林工商部第一计划即在立法。” -----据《张褰传》等编 材料二:(建国初期)落后的经济状况只能靠优先发展重工业才能改变,只有钢铁等基础工业发展了,机器制造业的原材料增多了,轻工业的装备才能保证。…… 同时,当时的国际环境也极需要我们尽快建立强大的军事工业,以增强国防力量。 ---何沁主编《中华人民共和国史》 请回答: 1.根据材料一,概括张謇的主张。(3分) 2.张謇的主张在当时是否得以实现(1分),你认为其主要原因有哪些?(2分) 3.在实业方面,以上材料都强调发展什么?(1分)请根据材料概述其理由。(2分) 4.为把我国建成为社会主义工业化国家,建国初期我党采取了哪些重要措施?(3分)其结果如何?(2分)简述产生这一结果的主要原因。(2分)
