最全三角函数的图像与性质知识点总结
三角函数和反三角函数图像性质知识点总结

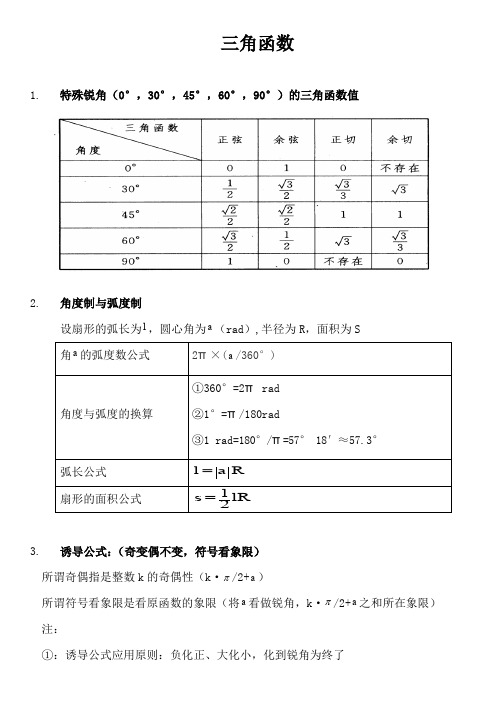
三角函数1.特别锐角( 0°, 30°, 45°, 60°, 90°)的三角函数值2.角度制与弧度制设扇形的弧长为l,圆心角为a(rad ), 半径为 R,面积为 S角a的弧度数公式2π×(a /360 °)①360°=2π rad角度与弧度的换算②1°=π/180rad③1 rad= 180°/π=57° 18′≈ 57.3 °弧长公式l a R扇形的面积公式s 1 lR23.引诱公式:(奇变偶不变,符号看象限)所谓奇偶指是整数 k 的奇偶性( k· /2+ a)所谓符号看象限是看原函数的象限(将a看做锐角, k·/2+a之和所在象限)注:①:引诱公式应用原则:负化正、大化小,化到锐角为终了4.三角函数的图像和性质:(其中 k z )①:三角y sinx 函数函数图象定义域R值域[-1,1]周期 2奇偶性奇单2k , 2 k2 2调2k , 2 k2 2性对对称轴 : x k2 称性对称中心 : ( k , 0) 零值点x k最x k , y max 12值x k , y min 12y cosxR[-1,1]2偶2k,2 k2k,2 k对称轴: x k对称中心:( k+ 2 , 0)x k2x 2k , y max 1 ;y 2k, y min1y tanx y cotxx k x k2R R奇非奇非偶k, k k , k2 2k对称中心: (2, 0)x kx2k点②:函数 y Asin( x) 的图像与性质:(1)函数y Asin( x) 和 y Acos( x) 的周期都是T 2 (2)函数y A tan( x) 和 y Acot( x) 的周期都是T5.三角函数尺度变换y sin x 经过变换变为 y Asin( x )的步骤(先平移后伸缩):1y sinx 横坐标变为原来的倍y sin x向左或向右(x)纵坐标不变平移个单位y sin纵坐标变为原来A的倍 A (x )横坐标不变y sin6.三角函数的对称变换:① y f ( x) y f ( x) )将 y f (x) 图像绕y轴翻折180°(整体翻折)(对三角函数来说:图像关于x 轴对称)② y f ( x) y f (x) 将 y f ( x) 图像绕 x 轴翻折180°(整体翻折)(对三角函数来说:图像关于y 轴对称)③ y f ( x) y f ( x) 将y f (x) 图像在y轴右侧保留,并把右侧图像绕y 轴翻折到左侧(偶函数局部翻折)④ y f ( x)y f ( x) 保留y f ( x) 在 x 轴上方图像,x 轴下方图像绕x 轴翻折上去(局部翻动)7.反三角函数的图像与性质:名称y=arsinx y=arccosx y=arctanxy=sinx y=cosx y=tanx(x ( , ))的( x (0, )) 的反(x ( , ))的反定义 2 2 2 2反函数,叫做反函数,叫做反余函数,叫做反正切正弦函数弦函数函数图像性质定义域[-1,1][-1,1](-∞,+∞)值域[- ,][0,π](- , )2 2 2 2单调性1,1 增函数1,1 减函数, 增函数奇偶性 arcsin( )arccos( ) arccosarctanarcsin arctan( )y=arccotxy=cotx ( x(0,))的反函数,叫做反余切函数(-∞,+∞)(0,π),减函数arccot()arccot周期性非周期函数非周期函数非周期函数非周期函数7. 三角函数公式:(1)倒数关系:(2)平方关系:22tan cot 1 sincos122sin csc 11tanseccossec1221 cot csc(3)三角和与差公式:sin( ) sin cos cos sinsin( ) sin cos cos sin cos( ) cos cos sinsincos( ) cos cossin sintan()tan tantan()tan tan1 tan tan1 tan tan(4)二倍角公式:sin2 2sin cos21 cos2sin1 cos2 2cos2 cos 2sin 22cos 21 1 2sin 2升幂公式22sin (降幂公式) 1 1 cos22cos 22cos2tan2 2tancos221 tan(5)三角函数的和差化积公式(6)三角函数的积化和差公式sinsin 2sincossin cos1 sin() sin()2221sinsin2cossin cos sinsin() sin()22 21cos(coscos 2coscoscos cos) cos()222coscos2sinsinsin sin1cos( ) cos()222六边形记忆法:图形结构“上弦中切下割,左正右余中间 1”;记忆方法“对角线上两个函数的积为 1;阴影三角形上两极点的三角函数值的平方和等于下极点的三角函数值的平方;任意一极点的三角函数值等于相邻两个极点的三角函数值的乘积。
三角函数与反三角函数图像性质、知识点总结
三角函数 1. 特殊锐角(0°,30°,45°,60°,90°)的三角函数值2.角度制与弧度制设扇形的弧长为l ,圆心角为a (rad ),半径为R ,面积为S 角a 的弧度数公式 2π×(a /360°)角度与弧度的换算①360°=2π rad ②1°=π/180rad③1 rad=180°/π=57° 18′≈57.3°弧长公式 l a R =扇形的面积公式 12s lR =3.诱导公式:(奇变偶不变,符号看象限)所谓奇偶指是整数k 的奇偶性(k ·π/2+a )所谓符号看象限是看原函数的象限(将a 看做锐角,k ·π/2+a 之和所在象限) 注:①:诱导公式应用原则:负化正、大化小,化到锐角为终了4. 三角函数的图像和性质:(其中z k ∈)①:三角函数 x y sin = x y cos =x y tan = cot y x=函 数 图 象定义域 R R 2x k ππ≠+x k π≠值域 [-1,1][-1,1]RR周期 2π2πππ奇偶性 奇偶奇非奇非偶单 调 性 2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦[]2,2k k πππ-↑ []2,2k k πππ+↓,22k k ππππ⎡⎤-+↑⎢⎥⎣⎦[],k k πππ+↓对 称 性 :2x k ππ=+对称轴对称中心:(,0)k π:x k π=对称轴:对称中心(+,0)2k ππ:对称中心(,0)2k π零值点 πk x =2ππ+=k xπk x =2ππ+=k x最 值 点2ππ+=k x ,1max=y2ππ-=k x ,1min-=yπk x 2=,1max =y ;2y k ππ=+,1min -=y②:函数)sin(ϕω+=x A y 的图像与性质:(1) 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T(2) 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A ()的步骤(先平移后伸缩): 1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变()A ()6.三角函数的对称变换:① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°(整体翻折) (对三角函数来说:图像关于x 轴对称)② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°(整体翻折) (对三角函数来说:图像关于y 轴对称)③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留,并把右侧图像绕y 轴翻折到左侧(偶函数局部翻折)④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像,x 轴下方图像绕x 轴翻折上去(局部翻动)7.反三角函数的图像与性质:名称y=arsinx y=arccosx y=arctanx y=arccotx定义y=sinx((,))22xππ∈-的反函数,叫做反正弦函数y=cosx((0,))xπ∈的反函数,叫做反余弦函数y=tanx((,))22xππ∈-的反函数,叫做反正切函数y=cotx((0,))xπ∈的反函数,叫做反余切函数性质图像定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性[]1,1-增函数[]1,1-减函数(),-∞+∞增函数(),-∞+∞减函数奇偶性arcsin()arcsinθθ-=-arccos()arccosθπθ-=-arctan()arctanθθ-=-arccot()arccotθπθ-=-周期性非周期函数非周期函数非周期函数非周期函数7.三角函数公式:(1)倒数关系: (2)平方关系:tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=(3)三角和与差公式:sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+(4)二倍角公式:()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式 22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式) (5)三角函数的和差化积公式 (6)三角函数的积化和差公式sin sin 2sin cos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
(完整版)三角函数知识点总结

(完整版)三角函数知识点总结三角函数知识点总结正弦函数(Sine Function)正弦函数是一个周期函数,其值在区间[-1, 1]之间波动。
它的图像是一条连续的曲线,描述了角度和其对应的正弦值之间的关系。
* 正弦函数的定义域为所有实数。
* 正弦函数的最大值是1,最小值是-1。
* 正弦函数以360度或2π为周期。
余弦函数(Cosine Function)余弦函数也是一个周期函数,与正弦函数非常相似。
它的图像是一条连续的曲线,描述了角度和其对应的余弦值之间的关系。
* 余弦函数的定义域为所有实数。
* 余弦函数的最大值是1,最小值是-1。
* 余弦函数以360度或2π为周期。
正切函数(Tangent Function)正切函数是三角函数中最常用的函数之一。
它的定义域为除去所有余弦函数的零点的实数集合。
* 正切函数的值在整个数轴上都有定义。
* 正切函数的值没有上限或下限。
三角函数的性质三角函数有几个重要的性质:* 正弦函数是奇函数,即对于任何实数x,有sin(-x)=-sin(x)。
* 余弦函数是偶函数,即对于任何实数x,有cos(-x)=cos(x)。
* 正弦函数和余弦函数的关系可以通过三角恒等式sin²(x)+cos²(x)=1来表示。
* 正切函数是奇函数,即对于任何实数x,有tan(-x)=-tan(x)。
* 正切函数和正弦函数/余弦函数的关系可以通过三角恒等式tan(x)=sin(x)/cos(x)来表示。
总结三角函数是数学中重要的一部分,它们在几何、物理、工程等领域中有着广泛的应用。
本文介绍了正弦函数、余弦函数和正切函数的定义、性质以及其在数轴上的范围。
通过熟练掌握三角函数的相关知识,我们能够更好地理解和解决与角度和曲线相关的问题。
三角函数知识点归纳总结

三角函数知识点归纳总结三角函数是数学中的一个重要分支,它与直角三角形的边长和角度有关。
在高中数学课程中,三角函数是解决几何问题和物理问题中不可或缺的工具。
以下是三角函数的知识点归纳总结:1. 三角函数的定义在直角三角形中,对于任意一个锐角,我们可以用三角函数来表示这个角与直角三角形的边长之间的关系。
三角函数主要有正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc)六种。
- 正弦(sin):对于锐角θ,sinθ 定义为对边长度与斜边长度的比值。
- 余弦(cos):cosθ 定义为邻边长度与斜边长度的比值。
- 正切(tan):tanθ 定义为对边长度与邻边长度的比值。
- 余切(cot):cotθ 定义为邻边长度与对边长度的比值。
- 正割(sec):secθ 定义为斜边长度与邻边长度的比值。
- 余割(csc):cscθ 定义为斜边长度与对边长度的比值。
2. 三角函数的基本性质- 正弦和余弦函数的值域是[-1, 1]。
- 正切和余切函数的值域是所有实数,除了cotθ = 0(θ = π/2 +kπ)和tanθ = 0(θ = kπ)。
- 三角函数是周期函数,正弦、余弦和正切函数的最小正周期是2π,而余切、正割和余割函数的最小正周期是π。
3. 三角函数的图像- 正弦函数的图像是波形图,周期为2π,振幅为1。
- 余弦函数的图像与正弦函数类似,但相位偏移了π/2。
- 正切函数的图像是周期性的,周期为π,且在每个周期的π/2和3π/2处有垂直渐近线。
4. 三角恒等式- 基本恒等式:sin²θ + cos²θ = 1。
- 双角恒等式:sin2θ = 2sinθcosθ,cos2θ = cos²θ -sin²θ。
- 和差化积:s in(α + β) = sinαcosβ + cosαsinβ,sin(α - β) = sinαcosβ - cosαsinβ,cos(α + β) = cosαcosβ - sinαsinβ,cos(α - β) = cosαcosβ + sinαsinβ。
三角函数的图像和性质

三角函数的图像和性质三角函数是数学中的一类特殊函数,以其图像的周期性和性质的多样性而被广泛研究和应用。
本文将介绍三角函数的图像特点和基本性质。
一、正弦函数的图像和性质正弦函数是最基本的三角函数之一,用sin(x)表示。
其图像为周期性曲线,其周期为2π。
在一个周期内,正弦函数的值在[-1,1]之间变化。
图像在x轴上的零点是正弦函数的特殊点,记为x=kπ,其中k为整数。
正弦函数的图像在x=kπ时经过极大值或极小值。
正弦函数的性质:1. 周期性:sin(x+2π)=sin(x),即正弦函数在过一周期后会重复。
2. 奇偶性:sin(-x)=-sin(x),即正弦函数关于原点对称。
3. 对称性:sin(π-x)=sin(x),即正弦函数关于y轴对称。
二、余弦函数的图像和性质余弦函数是另一个常见的三角函数,用cos(x)表示。
余弦函数的图像也是周期性曲线,其周期同样为2π。
在一个周期内,余弦函数的值同样在[-1,1]之间变化。
与正弦函数不同的是,余弦函数的图像在x=kπ时经过极大值或极小值。
余弦函数的性质:1. 周期性:cos(x+2π)=cos(x),即余弦函数在过一周期后会重复。
2. 奇偶性:cos(-x)=cos(x),即余弦函数关于y轴对称。
3. 对称性:cos(π-x)=-cos(x),即余弦函数关于原点对称。
三、正切函数的图像和性质正切函数是三角函数中另一个常见的函数,用tan(x)表示。
正切函数的图像为周期性曲线,其周期为π。
正切函数的图像在x=kπ+π/2时会出现无穷大的间断点,即tan(x)在这些点是无界的。
正切函数的性质:1. 周期性:tan(x+π)=tan(x),即正切函数在过一个周期后会重复。
2. 奇偶性:tan(-x)=-tan(x),即正切函数关于原点对称。
四、其他三角函数除了正弦函数、余弦函数和正切函数,还有其他与它们密切相关的三角函数。
1. 反正弦函数:用arcsin(x)表示,表示一个角的正弦值等于x,返回值在[-π/2, π/2]之间。
三角函数知识点归纳总结

三角函数是高中数学中的重要内容,涉及到三角函数的定义、性质、图像、公式等方面的知识。
下面是对三角函数知识点的归纳总结:一、三角函数的定义1. 正弦函数(sin):在直角三角形中,对边与斜边的比值。
2. 余弦函数(cos):在直角三角形中,邻边与斜边的比值。
3. 正切函数(tan):在直角三角形中,对边与邻边的比值。
4. 余切函数(cot):在直角三角形中,邻边与对边的比值。
5. 正割函数(sec):在直角三角形中,斜边与邻边的比值。
6. 余割函数(csc):在直角三角形中,斜边与对边的比值。
二、三角函数的性质1. 奇偶性:sin和cos函数是奇函数,tan和cot函数是偶函数。
2. 周期性:sin和cos函数的周期为2π,tan和cot函数的周期为π。
3. 值域:sin和cos函数的值域为[-1, 1],tan和cot函数的值域为实数集。
4. 单调性:sin和cos函数在每个周期内单调递增或递减,tan和cot函数在每个周期内单调递增。
5. 对称性:sin和cos函数关于原点对称,tan和cot函数关于坐标轴对称。
三、三角函数的图像1. 正弦函数的图像:在直角坐标系中,以x轴为始边,以角θ为终边的一条线段。
2. 余弦函数的图像:在直角坐标系中,以x轴为始边,以角θ为终边的一条线段。
3. 正切函数的图像:在直角坐标系中,以x轴为始边,以角θ为终边的一条线段。
4. 余切函数的图像:在直角坐标系中,以x轴为始边,以角θ为终边的一条线段。
5. 正割函数的图像:在直角坐标系中,以x轴为始边,以角θ为终边的一条线段。
6. 余割函数的图像:在直角坐标系中,以x轴为始边,以角θ为终边的一条线段。
四、三角函数的基本公式1. 和差公式:sin(a+b) = sina * cosb + cosa * sinb;cos(a+b) = cosa * cosb - sina * sinb;tan(a+b) = (tana + tanb) / (1 - tana * tanb);cot(a+b) = (1 / tana + 1 / tanb) / (1 / tana * 1 / tanb - 1);sec(a+b) = secab / (cosa * cosb - sina * sinb);csc(a+b) = cscab / (cosa * cosb + sina * sinb)。
三角函数与反三角函数图像性质、知识点总结
三角函数 1. 特殊锐角(0°,30°,45°,60°,90°)的三角函数值2.角度制与弧度制设扇形的弧长为l ,圆心角为a (rad ),半径为R ,面积为S 角a 的弧度数公式 2π×(a /360°)角度与弧度的换算①360°=2π rad ②1°=π/180rad③1 rad=180°/π=57° 18′≈57.3°弧长公式 l a R =扇形的面积公式 12s lR =3.诱导公式:(奇变偶不变,符号看象限)所谓奇偶指是整数k 的奇偶性(k ·π/2+a )所谓符号看象限是看原函数的象限(将a 看做锐角,k ·π/2+a 之和所在象限) 注:①:诱导公式应用原则:负化正、大化小,化到锐角为终了4. 三角函数的图像和性质:(其中z k ∈)①:三角函数 x y sin = x y cos =x y tan = cot y x=函 数 图 象定义域 R R 2x k ππ≠+x k π≠值域 [-1,1][-1,1]RR周期 2π2πππ奇偶性 奇偶奇非奇非偶单 调 性 2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦[]2,2k k πππ-↑ []2,2k k πππ+↓,22k k ππππ⎡⎤-+↑⎢⎥⎣⎦[],k k πππ+↓对 称 性 :2x k ππ=+对称轴对称中心:(,0)k π:x k π=对称轴:对称中心(+,0)2k ππ:对称中心(,0)2k π零值点 πk x =2ππ+=k xπk x =2ππ+=k x最 值 点2ππ+=k x ,1max=y2ππ-=k x ,1min-=yπk x 2=,1max =y ;2y k ππ=+,1min -=y②:函数)sin(ϕω+=x A y 的图像与性质:(1) 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T(2) 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A ()的步骤(先平移后伸缩): 1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变()A ()6.三角函数的对称变换:① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°(整体翻折) (对三角函数来说:图像关于x 轴对称)② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°(整体翻折) (对三角函数来说:图像关于y 轴对称)③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留,并把右侧图像绕y 轴翻折到左侧(偶函数局部翻折)④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像,x 轴下方图像绕x 轴翻折上去(局部翻动)7.反三角函数的图像与性质:名称y=arsinx y=arccosx y=arctanx y=arccotx定义y=sinx((,))22xππ∈-的反函数,叫做反正弦函数y=cosx((0,))xπ∈的反函数,叫做反余弦函数y=tanx((,))22xππ∈-的反函数,叫做反正切函数y=cotx((0,))xπ∈的反函数,叫做反余切函数性质图像定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性[]1,1-增函数[]1,1-减函数(),-∞+∞增函数(),-∞+∞减函数奇偶性arcsin()arcsinθθ-=-arccos()arccosθπθ-=-arctan()arctanθθ-=-arccot()arccotθπθ-=-周期性非周期函数非周期函数非周期函数非周期函数7.三角函数公式:(1)倒数关系: (2)平方关系:tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=(3)三角和与差公式:sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+(4)二倍角公式:()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式 22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式) (5)三角函数的和差化积公式 (6)三角函数的积化和差公式sin sin 2sin cos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
三角函数的性质知识点总结
三角函数的性质知识点总结三角函数是数学中非常重要的一部分,它在几何、物理、工程等领域都有着广泛的应用。
本文将对三角函数的性质进行详细的总结。
一、正弦函数(sin)1、定义域正弦函数的定义域为实数集 R。
2、值域值域为-1, 1。
即-1 ≤ sin x ≤ 1 。
3、周期性正弦函数是周期函数,其最小正周期为2π 。
即 sin(x +2π) = sin x 。
4、奇偶性正弦函数是奇函数,即 sin(x) = sin x 。
5、单调性在区间π/2 +2kπ, π/2 +2kπ (k ∈ Z)上单调递增;在区间π/2+2kπ, 3π/2 +2kπ (k ∈ Z)上单调递减。
6、对称轴对称轴方程为 x =π/2 +kπ (k ∈ Z)。
7、对称中心对称中心为(kπ, 0) (k ∈ Z)。
二、余弦函数(cos)1、定义域余弦函数的定义域也是实数集 R。
2、值域值域同样为-1, 1 。
即-1 ≤ cos x ≤ 1 。
3、周期性余弦函数也是周期函数,最小正周期为2π 。
即 cos(x +2π) = cos x 。
4、奇偶性余弦函数是偶函数,即 cos(x) = cos x 。
5、单调性在区间2kπ π, 2kπ (k ∈ Z)上单调递增;在区间2kπ, 2kπ +π (k ∈ Z)上单调递减。
6、对称轴对称轴方程为 x =kπ (k ∈ Z)。
7、对称中心对称中心为(π/2 +kπ, 0) (k ∈ Z)。
三、正切函数(tan)1、定义域正切函数的定义域为{ x |x ≠ π/2 +kπ, k ∈ Z }。
2、值域值域为实数集 R。
3、周期性正切函数的最小正周期为π 。
即 tan(x +π) = tan x 。
4、奇偶性正切函数是奇函数,即 tan(x) = tan x 。
5、单调性在区间(π/2 +kπ, π/2 +kπ )(k ∈ Z)上单调递增。
四、余切函数(cot)1、定义域余切函数的定义域为{ x |x ≠ kπ, k ∈ Z }。
三角函数的图像与性质知识点及题型归纳总结
三角函数的图像与性质知识点及题型归纳总结知识点讲解1.五点法”作图原理在确定正弦函数y Sinx(x [0,2 ])的图像时,起关键作用的5个点是3(0,0),( ,1),( ,0),( , 1),(2 ,0).2 2在确定余弦函数y COSX(X [0,2 ])的图像时,起关键作用的5个点是3(0,1),^-,0),( , 1),( ,0),(2 ,1).2 22•三角函数的图像与性质ASin(wx )与y ACoS(WX )(A 0, W 0)的图像与性质3. y(1)最小正周期:T .W(2)定义域与值域:y ASin(wx ) , y ACOS(WX )的定义域为R 值域为[-A,A].(3)最值假设A 0, W 0.①对于y ASin(wx ),当WX — 2k (k Z)时,函数取得最大值A当WX — 2k (k Z)时,函数取得最小值A;②对于y ACOS(WX ),当WX 2k (k Z)时,函数取得最大值A;当WX 2k (k Z)时,函数取得最小值A;(4)对称轴与对称中心假设A 0, W 0.①对于y ASin(wx ),当 WX O k — (k Z),即卩 Sin(wx 0 )1时,y Sin(wx )的对称轴为X X 0当WX ok (k Z),即Sin(WX o ) 0 时,y Sin(WX )的对称中心为(X 0,0).②对于yACOS(WX ),当WX 0k (k Z),即卩 CQS(WX O ) 1时,y CQS(WX )的对称轴为X X 0 当WX ok (k Z),即卩 CQS(WX O)时,y CQS(WX)的对称中心为(X 0,0).正、余弦曲线的对称轴是相应函数取最大(小)值的位置 •正、余弦的对称中心是相应函数与 X 轴交点的位置. (5)单调性. 假设A 0, W 0.①对于yASi n(wx)WX[二 2k,2 2k ](k Z) 增区间;2WX[ 2k 2 3,22k ](k Z) 减区间. ②对于yACQS(WX )WX [ 2k ,2k ](k Z)增区间;WX[2k ,2k](k Z)减区间.(6)平移与伸缩由函数y Sinx 的图像变换为函数 y 2sin(2x—) 3的图像的步骤; 3方法(XX -2x -)23'先相位变换,后周期变换,再振幅变换,不妨采用谐音记忆:我们 想欺负 ”(相一期一幅) 三角函数图像,使之变形y Sin X 的图像向左平移一个单位3y Sin (X护图像1所有点的横坐标变为原来的 -2纵坐标不变y Sin(2X捫图像所有点的纵坐标变为原来的 2倍横坐标不变y 2Sin(2X3)的图像方法二:(XXΞ 2xT ).先周期变换,后相位变换,再振幅变换向上平移3个单位y 2 Si n(2x —) 3y Si nx 的图像1所有点的横坐标变为原来的 -2纵坐标不变y sin 2x 的图像向左平移—个单位6y Si n2(x) Sin (2x )的图像6 2向上平移3各单位y 2 Si n(2x )的图像y 2 Si n(2x ) 33 3注:在进行图像变换时,提倡先平移后伸缩(先相位后周期,即想欺负”,但先伸缩后平移(先周期后相位)在题目中也经常出现,所以必须熟练掌握,无论哪种变化,切记每一个变换总是对变量 X 而言的,即图像变换要看 变量X ”发生多大变化,而不是 角WX移一个单位,得到的图像表达式是 y Sin 2(x) Sin(2x ),而不是y Sin(2x );再如,将 66 3 6图像y Sin(X -)上各点的横坐标扩大到原来的2倍(纵坐标不变),得到的函数图像表达式是61X 1 y Sin(—X),而不是y Sin (X )•此点要引起同学们的的别注意 •26 26题型归纳及思路提示思路提示一般将所给函数化为 y ASin(WX)或y ACOS(WZ ), A 0.w O ,然后依据y Sin X, y CoSX 的性质整体求解•题型1 三角函数性质的应用 一、函数的奇偶性 例4.16函数y Sin(X )(0)是R 上的偶函数,贝U 等于( )A. 0 B . — C. — D.4 2解析 因为函数y Sin(X )是R 上的偶函数,所以其图像关于 y 轴对称,有正弦函数的对称性知,当X 0时,Sin 1 ,又0 ,所以 -.故选C.2评注 由y Sinx 是奇函数和y cosx 是偶函数可拓展得到关于三角函数奇偶性的重要结论:(1)若 y ASi n(x )为奇函数, 则k (k Z);(2) 若 y ASi n(x )为偶函数,则 k(k 2Z); (3) 若 y ACOS(X )为奇函数, 则 k(k2Z);(4) 若 y ACOS(X)为偶函数, 则k (k Z);k若y Atan(x )为奇函数,则 (k Z),该函数不可能为偶函数.所有点的纵坐标变为原来的 2倍横坐标不变”变化多少•例如,函数y Sin2x 的图像向右平2变式1已知a R,函数f (X) Sinx a(x R)为奇函数,则a等于( )A.0B.1 C.-1D. 1变式2 设 R ,则“O ”是“f(x) CoS(X )(x R)为偶函数”的( )),其中W 0 ,则f (x)是偶函数的充要条件是(A. f (0) 1B. f(0)0 C. f (0)1 D. f (0)例 4.17 设函数 f(χ) Sin(2x -)(x R),则 f(x)是()2A. 最小正周期为 的奇函数B. 最小正周期为的偶函数C. 最小正周期为一的奇函数2 D. 最小正周期为一的偶函数2解析 f(x) sin(2x -) cos2x ,所以是最小正周期为 X 的偶函数•故选B.2 2 1变式1 若函数f(χ) Sin X -(X R),则f(x)是()2 A. 偶函数且最小正周期为 B. 奇函数且最小正周期为 C. 偶函数且最小正周期为 2 D. 奇函数且最小正周期为 2二、函数的周期性Tw.A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不比哟啊条件 (2)函数 ASi n(wx ),y ACOS(WX ), y Ata n(wx )的周期均为T(3)函数ASi n(wx )b(b 0),y2ACOS(WX ) b(b 0)的周期均 T -变式 3 设 f (x) Sin(WX 变式2F 列函数中,既是(0,—)上的增函数,又是以2为周期的偶函数的是(A. y cos 2xB. y sin 2xc ∙y COSXD.ySin X例4.18函数ySin (2x )COS (2X 6S)的最小正周期为( A.—2B.—4C. 2D.解析 函数ySin (2x 评注 —)Cos(2x 关于三角函数周期的几个重要结论:1) sin(4x 62•故选A(1) 函数ASin (WX )b, y A COS(WX ) b, y A tan(wx2)b 的周期分别为TI Wl变式1函数y Sin(2x —) cos(2x —)的最小正周期和最大值分别为( )A. ,1 B ∙ ,、2 C. 2 ,1 D.2 ,,2 变式2 已知函数f(x) Sin X(Sinx COSX)(X R),贝U f(x)的最小正周期为 变式3 设函数 f(x) sin3x Sin3x ,贝U f (x)为( ) A. 周期函数,最小正周期为 B . 周期函数,最小正周期为 周期函数,最小正周期为 非周期函数 一、函数的单调性C. D. 3 2 3 2 例4.19函数y 2si n( 2x)( x 6 7 B ∙[,]12 12 [0,])为增函数的区间是( )解析因为y 2si n( — 2x) 6 2sin(2x 6), 所以y 2sin(6 2X)的递增区间实际上是 y 2 si n(2x 2 6 2解得 k X k (k Z). 3 5 X 6 令k 0 ,得 —— ,又因为X [0,], 3 6所以 X 5 .即函数 y 2sin(- 2x)(x [0, 5 ])的增区间为[,].故选C 3 66 3 6 评注 三角函数的单调性, 需将函数y ASi n(wx )看成由一次函数和正弦函数组成的复合函数,复合函数单调区间的单调方法转化为解一兀- 次不等式 令2k Z), 2x 如函数y ASi n( wx -)的递减区间. 2kx —(k )(A 0,w 0)的单调区间的确定基本思想是吧 WX 看做是一个整体,如由 利用 2k2 WX2k 2WX2kx (k Z)解出X 的范围,所得区间即为增区间;由2 3 2kx (k Z)解出X 的范围,所得区间即为减区间 若函数y ASin(wx )中2A 0, w 0 ,可用诱导公式将函数变为 y ASin( WX ),则y ASin( WX )的增区间为原函数的减区间,减区间为原函数的的增区间.如y sin( x) Sin(X ),令44232kX 2k ,即 2k X 2k(k Z),可得[2k,2k 2 4244 4为原函数的减区间•对于函数y ACoS(WX ),y Atan(wx)的单调性的讨论与以上类似处理即可3 变式1若函数y Sinx f (x)在[,]内单调递增,则f (x)可以是( )4 4A.1B.cosxC.sinXD. cosx变式2 已知W 0 ,函数f(χ) Sin(WX 1 5 1 3 1A ∙[亍匚]B ∙[;,;] C.(0j2 4 2 4 2 -)在(一,)上单调递减,则 W 的取值范围是(4 2D.(0,2] 变式 3 已知函数 f (x) . 3Sin wx COS(WX ) COS(WX ), X R, (W 0).3 3(1)求函数f (x)的值域; (2)若f (X)的最小正周期为,χ [0,—],求f (x)的单调递减区间2 2四、函数的对称性(对称轴、对称中心) 例4.30函数y Sin(2x-)图像的对称轴方程可能是(A. XB.C. XD.X6 12 6 12解析解法一:已知y Si nx 的对称轴方程是X k -(k Z)2 k令 2x 3 k (k Z),得 X(k Z),2 2 12当k 0时,X ,故选D.12解法当 X时, 2x0.其正弦值为 0;63当X 时,2x123 6 ,其正弦值不等于1或-1当X时,2x -2 其正弦值不等于 1 或-1633当X时,2x—, 这时Sin 1.12 322(1)函数y Sin X 的对称轴为X k(k 2Z),对称中心为(k .0)(k Z);(2)函数y cosx 的对称轴为X k (k Z) ,对称中心为(k ,0)(k Z ); (3)函数yta nx 函数无对称轴,对称中心为k(―,0)(k Z);故选D评注 关于三角函数对称的几个重要结论;24A.关于点(一,0)对称3 B.关于直线X—对称4C.关于点(一,0)对称D .关于直线X -对称43变式2 y Sin(X)的图像的一个对称中心是( )43 A.( ,0)B.(4,O)3C. (4 ,O)D⑺2x 2x变式3 yCOST SinT 的图像中,相邻两条对称轴之间的距离是变式4 将函数y Sinx3CoSX 的图像沿X 轴向右平移a 个单位(a 0),所得图像关于y 轴对称,则a 的最小值是( ).A. 7B. C. D.—62 6 3五、三角函数性质的综合思路提示三角函数的性质(如奇偶性、周期性、单调性、对称性)中,尤为重要的是对称性 因为对称性奇偶性(若函数图像关于坐标原点对称,则函数f (X)为奇函数;若函数图像关于 y 轴对称,则函数f(x)为偶函数);对称性 周期性(相邻的两条对称轴之间的距离是T;相邻的对称中心之间的距离为 T;相邻的对称轴2 2与对称中心之间的距离为 T);对称性 单调性(在相邻的对称轴之间,函数 f(x)单调,特殊的,若4(4)求函数y ASin(WX) b(w 0)的对称轴的方法;令 WXk (k Z),得k X 2 ---------- (k Z);对称中心的求取方法;令 WXW为( ------ ,b).Wk (k Z),得 X,即对称中心k (5)求函数y ACOS(WX ) b(W 0)的对称轴的方法; 令WX k (k Z)得X Z --------------------------W k即对称中心为( ----------- ,b)(k Z)W变式1已知函数f (X) Sin(WX )(W 30)的最小正周期为,则该函数的图像(24f (x) ASin(wx), A 0, w 0 ,函数 f (x)在[I , ?]上单调,且 0 [1,2],设 max 1,2,则T深刻体现了三角函数的单调性与周期性、对称性之间的紧密联系)6 3 6 3例 4.21 设 f(x) asin 2x bcos2x ,其中 a, b R,ab 0,若 f (X )11 ① f (IT ) 0;③f (X)既不是奇函数也不是偶函数;④ f (X)的单调递增区间是[k - k —](k Z);6,3⑤ 存在经过点(a,b)的直线与函数f (x)的图像不相交. 以上结论正确的是 ________ (写出所有正确命题的序号)分析 函数f(χ) ,a 2b 2sin(2χ ),tan -,其中一条对称轴为 X ―,函数的最小正周期 a 6T ,通过对称轴 对称中心(对称轴与零点相距 T 的奇数倍)通过对称轴奇偶性(若函数f(x)为4奇函数,则一等于T的奇数倍;若函数f (X)为偶函数,则一等于T的偶数倍);通过对称性单调性(在6 46 4相邻的两条对称轴之间,f(x)单调递增或单调递减).是f (X)的对称轴,又f (X)的最小正周期为关于y 轴对称,所以函数 f(x)既不是奇函数也不是偶函数,故③正确2 2对于④:依题意,函数 f(x)相邻两条对称轴x 1 -,x 2,在区间[k -,k](k Z)上函数f (X)单调,不能确定是单调递增,还是单调递减,故④不正确f (―)对一切X R 恒成立,则 6② f(7F )解析 f (x) a 2b 2Sin(2x),其中 tanb,f(xaf (O ))对一切 XR 恒成立,知直线X -11对于①:f(—)123)可看做X3,加了 -个周期所对应的函数值,所以 6 4 11 f(IT) 0.故①正对于②:函数y f (X)周期T77—,因为 ——一一,所以f ()f(—)2 10 5 2105对于③:因为一既不是T的奇倍数,也不是 64 T的偶倍数,所以函数4f(x)的图像既不关于原点对称,也不因此咱错误,故②不正确K(其中tan —),所以af (x) a 2 b 2 ,又 ab⑤不正确,应填①③.(1)求f (X)的值域;3⑵若y f (X)在区间[亍R 上为增函数,求W的最大值.解析(1)f (x) 4 COS(WX —)sin wx cos2wx4(CoSWXCos & Sinwxsinfsin wx cos2wx 2 -. 3 Sin WXCOSWX 2sin 2WX cos2wx .3sin 2wx 1 cos2wx cos2wx .3sin2wx 1[1,1]所以函数f (X)的值域为[1 .. 3,1 ... 3].f(X) 3sin2wx 1,由y f(X)在区间[3T2]上为增函数,的例 4.22 设 f (χ) 4COS(WX )Sin WX 6 cos(2wx ),其中 W评注一般的,若f (x)(x R)为奇函数,在【1,2】上为增函数,其中2 ,若令max{ 1, 2},则T,即可求出W 的范围. 4变式1已知函数f (x)2sin(wx),其中常数 W 0,若y f(x)在[2]上单调递增,求W 的取 3变式2 已知函数f (x) 2sin(wx)(w 0),f (―) f (—)在[—,—]上的虽小值为-2 ,则W 的最小值对于⑤:因为 f(x) a sin 2x b cos2 X.a 2 b 2Sin(2x) ,a 2 b 2 ,因此经过点(a,b)的直线与函数f (X)的图像相交,因为Sin 2wx (2)解法一: [3w ,w[2,-](W0)3wx故WX2,得 0 W1 1 ,则W 的最大值为一. 6解法二:由 f(x),3sin 2wx 1 (W3O)在区间[32,2]上为增函数,含原点的增区间的对称型可知3 函数f (x)在[— 2 牛]上也为增函数, T 2故一3 ,即T 6 ,得—2 2w1,故0 W 6 ,则W的最44例4.23若f (X) Sin(WX-)(W O),f (—)且在( -- )上有最小值无最大值,则 3 6'3题型2根据条件确定解析式方向一: 知图求式”,即已知三角形函数的部分图像,求函数解析式 思路提示干个点代入函数式,可以求得相关特定系数 A,w,,这里需要注意的是,要认清选择的点属于五点”中的 哪一个位置点,并能正式代入式中,依据五点列表法原理,点的序号与式子的关系是:点)来确定 ;对于零点要分析向上零点还是向下零点 解析 解法一:依题意 A 2,232k-,k Z 得 2k-,k Z , 26所以 f (0) 2sin 2si n(2k-)6 1, 故选 B解法二 二:由函数f (x ) A(Sin 2x ), 得T,则相邻的零点与对称轴之间的距离为T-,因此图中向上的零点是 X 0,则满足f( ) ASin(2 ) 0所以 2k ,k Z.故12 12 12 6解析 依题意,如图4-24所示,在X8k 14.取 k 0,得 W314 32k3—,k Z 2评注 本题融汇了三角函数 f (x ) Sin (WX )的最值(对称轴)、 周期性、单调性之间的相互关系与转化f(O )已知函数图像求函数 y ASin(wx )(A 0, w 0)的解析式时,常用的解析方法是待定系数法,由图中的最大值或最小值确定 A ,由周期确定 W ,由适合解析式点的坐标确定 ,但有图像求得的y ASi n(wx)(A0,w0)的解析式一般不唯一,只有限定的取值范围,才能得出唯一解,将若第一点”(及图像 上升时与X 轴的交点)为WX 第二点”(即图像曲线的最高点)为 WX ;第三点”(及图像下降时与轴的交点),为WX ;第四点”(及图像曲线的最低点)为WX —;第五点”2(及图像上升时与 X 轴的交点) 为 WX 例 4.24 函数 f(x) A(Sin2x)(代1 A. 2B.-1C. 分析 对于y ASin (wx )的解析式的确定,通过最值确定R )的部分图像如图D.9 W127f (0) 2sin 2sin (2k) 1 ,故选 B6评注 对于三角函数问题中的 知图求式”(及其性质),应重点关注以下方面 (1) 周期(可推出 W 的值域范围) (2) 振幅(可推出 A ( A>0)) (3) 特征点(可形成三角方程,以求 的值) 对于本题代入零点(X o ,o ),( X o 为上零点),则满足AS in (WX o ) 0,所以 2k wx 0, k Z, f (0) ASin Asin( wx 0) ASi n(wx 0) 2Sin(2 石) 1,对于正弦型函数f (X ) ASin(wx )(w 0, R),若已知上零点 X 0 ,则 f(0)ASin (WX 0) •同理,若已知下零 点x °,则 f (0) ASin(WX 0). 变式一 函数 f(x) ASin(wx )(A,w,是常数,A f(0) 0,w变式二 已知函数f(x) ACOS(WXA. C. 2 3 12 2B.-3 1 D.—2)的部分图像如图 ()例4.25已知函数 y ASi n(wx )(A 0,w 0, 式. 分析有最小值为-2确定A , 不易求解,我们可抓住 — 12 由周期确定W ,但本题的周期 T 3T 7 T ,,且3T —,建立周期2 4 12 T 的不等关系, 系(根据零点) (0,1)得到. 从而得到 W 的取值范围,在建立 W 的等量关 ,最终建立求得 W ,而 的确定可通过特征点4-28所示,求函数f (x )的解析 解析有图知 A 2 ,将点(0,1),代入y ASin (WX )中,得12sin ,即 Sin 1 ,又22 ,又因为T—, 6WT_,又—6 2712 18 7,故 W ,又点( ,0)在函数图像上,且 6 7 712 2410 12 2k ,k Z ,解得 W 24k 10,k Z ,因此777(0,1)点在函数的单调增区间上,故7T 为函数f (X )的下零点,所 12迢k W 里,得7 7 75 sin (X3-k 11 ,又k Z ,因此k 1,此时W 2.6 12所以 f(x) 2sin(2x)• 6变式一已知f(x) cos 2(wx )(w,为常数), 点(1,0)如图4-29所示,求W 的值.方向二:知性质(如奇偶性、单调性、对称性、最值) 求解函数解析式(即 A,w,的值的确定)例 4.26 已知函数 f(x) Sin(wx)(w 0,0心,且在区间[0,—]上为单调函数,求函数 f(x)的解析式.2评注 根据函数必关于 y 轴对称,在三角函数中联想到 y coswx 的模型,从图象、对称轴、对称中心、最值点或单调性来求解(2)求函数f (x)的解析式. 题型3函数的值域(最值) 思路提示求三角函数的最值,通常要利用正、余弦函数的有界性,一般是通过三角变换化归为下列基本类型处理 .(1) y a sin X b ,设t Sinx ,化为一次函数 y at b 在[1,1]上的最值求解.b J —2 - 2(2)y a si nx bcosx c ,弓 I 入辅助角 (tan ),化为 y a bSin(X ) C ,求解方法a分析本题的目标是求w,因为y Sin(WX )为偶函数,则必关于 y 轴对称,因此化为 y coswx 的 形式,由函数在[0 -]上单调,则[0 -]最多只会是半个周期,即 T—,从而得T '2 ,2 2 2 再代入对称中心求解. 得W 的范围, 解析由函数 f (x) Sin(WX )(w 0,0 在区间[0 —]上为单调函数,得 T—,即T '2 2 2 )为R 上的偶函数,贝U —,得f(χ) coswx ,且 2 2 3 ,故— ,又W 0得0 W 2.,同时点(二,0) W 4 3 为函数f (x)的一个对称中心,的W k4,k Z ,则 w 4k 2,k Z ,因此 0 4k 2 2 , 2 33k 1,k Z 所以k 0或1得W-或2,所以函数f(x)的解析式为y CoSZX 或y33cos 2x.,0)是一个对称中变式一:已知函数 f (x) 4sin(wx )(w 0,0经过点(0,2).(1) 求 f (x)的最小正周期;,X R)图像的两条相邻对称轴的距离为 ,且23如果存在正整数 W 常数 使得函数f(x)的图像经过4同类型(1) 33y a si n2x bsinx c,设t Si nx ,化为二次函数y at2 bt C在闭区间t [ 1,1]上的最值5 sin (X3求解,也可以是 y acoWx bsinx C 或 y acoS2x bsinx C 型.(4) y a si n x cosx b(si nx cosx) C ,设 t Si nx cosx ,贝U t 21 2si n xcosx ,故t 21t 21Sin xcosx,故原函数化为二次函数 y a () bt C 在闭区间[∙λ2,ι2]上的最值求2 2(5) yasinx b与yasinx b,根据正弦函数的有界性,即可用分析法求最值,也可用不等式CSi nx d ccosx d法求最值,更可用数形结合法求最值.这里需要注意的是化为关于 Si nx 或cosx 的函数求解释务必注意SinX 或cosx 的范围.例4.27函数f (χ) Sin xcosx 的最小值是(,利用诱导公式把( x)转化为(X),化不同角为相同角, 将函数化为 263)3cos[ ( x)] 4 si n(x ) 3cos( x) 32 63 3 3)(其中tan —),所以y wax 5.故选C.分析 解析 1A.-1B. 2 1C.—2D.1将函数f (x)转化为y ASin(wx)的形式求最值、, 1 .函数 f (x) Sin xcosx Sin2χ(χ 2R)-最小值为1,故选B. 2评注 若本题改为"f(x) Sin Xcosx,X [0,] ”则最小值为 40,在解题过程中,若存在换元环节,应注意新元取值范围的限定 变式1函数f(x)Sin X cos(x )的值域为(6A.[-2,2]B.[ ,3, 3]C ∙[-1,1]D.[∙∙ 3 .. 31变式2 函数f(x) sin 2X .3Sin xcosx 在区间[ :,?]上的最大值是().1 JlA.1B.——2C .32D.1 -.3例4.28函数 y 4sin(x3sin(6 X)的最大值为()A.7B.2 3C.5D.4分析 f(x) ASin (WX)的形式.y 4sin(x解析45 sin (X 3、 2 2变式1求函数f(χ) cos(x )2 cos (X R)的值域32变式2求函数 f (x) cos(2x ) 2sin(x)sin(x )(x [ ,])的值域. 344 12 2__ 2例4.29求函数f(x) 2cos2x Sin X 4cosx 的最大值和最小值. 2a cos X bcosχ C(X R)的形式,换元转化为求二次函数在给定区间上的最值思路提示 分析 通过二倍角公式和同角公式将函数 f(x)的公式化简为y 解析 f (x)2(2 cos 2X 1)(1 cos 2x)4cos x23 cos X 4cos x 1,令 t cos X [ 1,1],则 g(t) 3t 24t 1f (t)取最大值6, 即f (x)的最大值为6;当3(tI )t -时,37(t [1,1]),因为t [ 1,1],所以当tg(t)取最小值7,即f (x)的最小值为变式1已知,求函数y cos 2X Sin X 的最小值.4变式2 求函数y sin 2x a COSX- a — (0 X —)的最大值.8 2 2 变式32右 Sin Xcos X a 0有实数解,试确定实数 a 的取值范围.变式4 若关于X 的方程cos 2x Sinx a 0在(0,§]上恒成立,求实数 a 的取值范围. 1时,例 4.30 对于函数 f(χ)Sin X 1(0 X Sin XA.有最大值无最小值C.有最大值且有最小值分析 形如yasinx b的函数的最值,CSi nx d丄,令tSin X解析解法一 :f (X) 1有最小值无最大值.故选B sin X 1ySi n x SinXSin X解法二:y得 0 Sin X 变式1 求函数y变式2题型4 ),下列结论中正确的是(B.有最小值无最大值 D .既无最大值又无最小可考虑用函数的有界性求解SinX (0,1],贝U y 1 f 在区间(0,1]上单调递减,即f(x)只1,1 ,解得y2 ,所以f (X)只有最小值无最大值.故选B■- 3 cos X的值域.2 Sin XΞ½若—X4 三角函数图像变换2,则函数y tan2xtan X 的最大值为 2由函数y Si nx的图像变换为函数y ASi n(wx ) b(代W 0)的图像.方法一:(X XWX)先相位变换,后周期变换,再振幅变换向左平移_个单位( 0))的图像向左平移个单位(0分析 利用三角函数的图像与变换求解结合选项可知,函数图像过(1,0).故选A25B.向右平移—个单位125D.向右平移—个单位6-),g(x) COS (X —),则 f(x)的图像().—)(x R, W 0)的最小正周期为 ,为了得到g (X) COS(WX)的图 4像,只要将y f (x)的图像(SinX 的图像向左平移个单位(O )个单位(0) y S 6i n (XSin(WX )的图像 所有点的纵坐标变为原 来的A 倍丿的图像 横坐标不变 ----------ASi n(wx)的图像向上平J:个单位;:0)yASin (WX ) b例4.31把函数 y COS 2X 1的图像上所有点的横坐标伸长到原来的 2倍(纵坐标不变),然后向左平移1个单位长度,在向下移 1个单位长度,得到的图像时().1Iy1、I 2/、O 1-1 22解析y cos2χ1横纵标不变2倍yCoSX 1 向左平移1个单位长度y cos(x 1)1向下平移1个单位长度y cos(x 1).变式2 已知f (χ) Sin(xA.与g(x)图像相同B.与g(x)图像关于y 轴对称C.是由g(x)的图像向左平移—个单位得到2D.是由g(x)的图像向右平移 一个单位得到2变式3已知函数f(χ) Sin(WX XA.向左平移 一个单位长度8B ∙向右平移一个单位长度81 1依题意 g (x) Sin(2 2x )Sin(4x ),2 6 2 65纵坐标不变,得到函数 y g(x)的图像,求g(x)在[0——]上的值域 ,24最有效训练题C.向左平移—个单位长度 D •向右平移—个单位长度 4 4 1 2 1例 4.32 已知函数 f(x) Sin 2xsin cos 2xcos Sin( )(0 2 2 2 (1) 求的值 1 (2)将f(x)图像上各点的横坐标缩短为原来的 -,纵坐标不变,得到函数y 2 1),其图像过点(一,).6 2g(x)的图像,求函数g(x)在[°,—]上的最大值和最小值 4 解析 由题意把点(一,1)代入函数的解析式得 6 21 . Sin- Sin2 33 1 1cos cos —4 2 2 Sin 1 COS2 sin (F ) 1(I) Sin( 6) 1, (0,), 6 -sin2x 41 . C 3 12 1 sin 2x cos X2 2 2 4 6 2 (2) f (x) -(1 COS 2X ) 41 Sin (2x 2?),当4x67,即X 时,1g (x)取最小值 一;6 44 当4x 6 , 即X时, 1 g(x)取最大值一.212 2 变式1 已知向量 m (Sin x,1), n— A (∖3Acosx, cos2x)( A2 的最大值为 6.(1)求 A 0),函数 f(x)(2)求将函数yf (x)的图像向左平移个单位,再将所的图像上各点的横坐标缩短到原来的12i 倍,1.已知函数f(x) ASi n(wx )(A 0, —0),在X —时取得最大值,则f(x)在[,0]上的2 6单调增区间是(f (x) cos 2x Sinx ,那么下列命题中假命题是(4,.已知函数f(x) Sin(6x -)的图像上各点的横坐标伸长到原来的3倍,再向右平移§个单位,).则f (x)的单调递增区间为8. 已知函数f(x) 3sin( X )(0)的图象和g(x) 2cos(2 X ) 1的图象对称轴完全相同,若6X [0,亍],贝U f(x)的取值范围为9. 定义一种运算(a 1,a 2) (a 3,a 4) a 1a 4 a 2a 3,将函数f (x) (∙∙.3,2si n x) (cosx,cos 2x)的图象向左移 n(n 0)个单位长度所得图像对应的函数为偶函数,则n 的最小值为10. 某学生对函数f (x) 2xcosx 进行研究后,得出如下四个结论: ①函数f (x)在[,0]上为单调递增,在[0,]上单调递减;②存在常数M 0,使f (x) M X 对一切实数X 均成立;③点(一,0)是函数2A ∙[B ∙[56C ∙[护2.若直线t 与函数 y Sin (2x-)和y cos(2x -)的图像分别交于 PQ 两点,则IPQ 的最大值为A.2B.1 D. 23•已知函数 A. f (x)既不是奇函数也不是偶函数 B. f(x)在[,0]上恰有一个零点 C. f (x)是周期函数D. f(x)在(一,丄)上是增函数2 6得到的A.(荷O)B.(9,O)c.q ,°)D.(畀)5.如图4-30所示,点 X 轴的A.—8y PPM PN0,则W 的值为()∖NM O/ XB.-C.4D.8∖46.已知A.[ 3,2]B.[ .3,2] C"3,2]D ∙C ∙ 3, 2) 7.已知函数 f(x) 3sin 2χ 2sin xcosX X 3 cos 2X ,其中0,且f (x)的最小正周期为,函数一个对称中心是(P 是函数y 2 sin(wx交点,若 则实数a 的取值范围为a ,有两个不同的实数解,)(x R,w 0)的图像的最高点,M,N 是该图像与(0,],关于X 的方程2sin(x -) 3y f(x)图像的一个对称中心;④函数y f(x)的图象关于直线X 对称•其中正确的.(把所有正确的命题的序号都填上)f (x) cos(2X —) sin 2x cos 2x. 所示.(1)求函数f (X)的解析式;∣S4-315A.向左平移个单位125C.向左平移个单位611.已知函数 (1)求函数 f (X)的最小正周期及图像的对称轴方程; (2)设函数 g(x) [f(x)]2f (X),求g(x)的值域. 12.已知函数 f (x) ASin( X),其中(X R, A 0,I )的部分图像如图4—31⑵已知函数f(x)图像上三点 M,N,P 的横坐标分别为一1, 1, 5,求 Sin MNP 的值.。
三角函数图象和性质(总结的很全面不看后悔)
三角函数专题辅导课程安排制作者:程国辉专题辅导一三角函数的基本性质及解题思路课时:4-5学时 学习目标:1. 掌握常用公式的变换。
2. 明确一般三角函数化简求值的思路。
第一部分 三角函数公式 1、两角和与差的三角函数:cos(α+β)=cos α·cos β-sin α·sin β cos(α-β)=cos α·cos β+sin α·sin β sin(α±β)=sin α·cos β±cos α·sin β tan(α+β)=(tan α+tan β)/(1-tan α·tan β)tan(α-β)=(tan α-tan β)/(1+tan α·tan β2、倍角公式:sin(2α)=2sin α·cos α=2/(tan α+cot α)cos(2α)=(cos α)^2-(sin α)^2=2(cos α)^2-1=1-2(sin α)^2 tan(2α)=2tan α/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cot α)3、两角和与差的正弦、余弦、正切公式及倍角公式:()sin sin cos cos sin sin 22sin cos 令αβαβαβαβααα=±=±−−−→=()()2222222cos cos cos sin sin cos 2cos sin 2cos 112sin tan tan 1+cos2tan cos 1tan tan 21cos2sin 22tan tan 21tan 令 = = αβαβαβαβααααααβααβααβααααα=±=−−−→=-↓=-=-±±=⇒-↓=-4、同角三角函数的基本关系式:(1)平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= (2)倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1, (3)商数关系:sin cos tan ,cot cos sin αααααα==第二部分:三角函数的化简、计算、证明的恒等变形的基本思路:一角二名三结构首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的图像与性质
一、 正弦函数、余弦函数的图像与性质
二、正切函数的图象与性质
定义域
{|,}2xxkkZ
值域
R
单调性
递增区间(,)()22kkkZ
奇偶性 奇函数
对称性
对称中心:(,0)()2kkZ(含原点)
最小正周期
π
函数 y=sin x y=cos x
图
象
定义域
R R
值域 [-1,1] [-1,1]
单调性
递增区间:
2,2()22kkkZ
递减区间:32,2()22kkkZ
递增区间:[2kπ-π,2kπ] (k∈Z)
递减区间:[2kπ,2kπ+π] (k∈Z)
最 值
x=2kπ+π2(k∈Z)时,ymax=1;
x=2kπ-π2(k∈Z)时,ymin=-1
x=2kπ(k∈Z)时,ymax=1;
x=2kπ+π(k∈Z) 时,ymin=-1
奇偶性 奇函数 偶函数
对称性
对称中心:(kπ,0)(k∈Z)(含原点)
对称轴:x=kπ+π2,k∈Z
对称中心:(kπ+π2,0)(k∈Z)
对称轴:x=kπ,k∈Z(含y轴)
最小正周期
2π 2π
三、三角函数图像的平移变换和伸缩变换
1. 由xysin的图象得到)sin(xAy(0,0A)的图象
xysin
方法一:先平移后伸缩 方法二:先伸缩后平移
操作 向左平移φ个单位
横坐标变为原来的1倍
结果
)sin(xy xysin
操作
横坐标变为原来的1倍
向左平移个单位
结果
)sin(xy
操作 纵坐标变为原来的A倍
结果
)sin(xAy
注意:平移变换或伸缩变换都是针对自变量x而言的,因此在用这样的变换法作图象时一
定要注意平移与伸缩的先后顺序,否则会出现错误。
2. )sin(xAy(0,0A)的性质
(1)定义域、值域、单调性、最值、对称性:
将x看作一个整体,与相应的简单三角函数比较得出;
(2)奇偶性:只有当取特殊值时,这些复合函数才具备奇偶性:
)sin(xAy
,当k时为奇函数,当2k时为偶函数;
(3)最小正周期:2T
3. y=Asin(ωx+φ), x∈[0,+∞) (0,0A)中各量的物理意义
(1) A称为振幅; (2)2T称为周期; (3)1fT称为频率;
(4)x称为相位; (5)称为初相 (6)称为圆频率.
