完整版)高三三角函数专题复习(题型全面)
高三一模复习 三角函数专题

高三一模复习 三角函数专题一、 求值1. 若 sin 4 , tan 0 ,则 cos .52. 若 是第三象限角, sin( ) 1 ,则 cos 5 , cos().223. 若角 的终边经过点 P(1 , 2) ,则 cos , tan 2 .34. 下列各式中,值为 的是2 A. 2 sin15 cos15 B. cos2 15 sin 2 15C. 2 sin 2 15 1()D. sin 2 15 cos2 155. 若 0 2 , sin 3 cos ,则 的取值范围是A.( , ) 32B.( , ) 3C.( ,4 ) 33.D.( ,3 ) 325.设 x ( 0 ,),则函数f(x)2 sin 2x 1的最小值为.2sin 2x6. 将函数 f (x) sin x 3 cos x 的图象向右平移了 n 个单位,所得图象关于 y 轴对称,则 n 的最小正值为 ( )7A.6B.3C.6D.27. 若动直线 x a 与函数 f (x) sin x 和 g(x) cos x 图象分别交于 M 、 N 两点,则| MN | 的最大值为( )A.1 B. 2 C. 3 D. 2二、最值1. 函数 f (x) sin x cos x 的最小值是.2. 函数 f (x) (1 3 tan x) cos x , 0 ,则 f (x) 的最大值为.28. 函数 f (x) sin2 x 3 sin x cos x 在区间[ , ] 上的最大值是 42A.11 3B.23C.2D.1 3()3. 函数 f (x) cos 2x 2 sin x 的最小值为,最大值为.4. 函数 f (x) 2 sin x ( 0 )在区间[ , ] 上的最小值是 2 ,则 最小值为.34三、单调性1.函数f(x) 2 sin( 2x) ( x [0 ,] )的单调递增区间是6A.[ 0 , ] B.[ ,7 ] C.[ ,5 ] D.[ 5 , ]312 12366高三一模复习 三角函数专题 第 1 页()2. 函数 f (x) | sin x | 的一个单调递增区间是A.( , ) B.( ,3 ) C.( ,3 ) D.( 3 ,2 )444422()3. 函数 f (x) sin x 3 cos x ( x [ , 0 ] )的单调递增区间是()A.[ , 5 ] B.[ 5 , ] C.[ ,0 ] D.[ ,0 ]666364. 设函数 f (x) | sin ( x ) | ( x R ),则 f (x) 3A.在区间[ 2 , 7 ] 上是增函数 B.在区间[ , ] 上是减函数362C.在区间[ , ] 上是增函数 5 D.在区间[ , ] 上是减函数8436()四、周期性1. 下列函数中,周期为 的是 ( )2A. f (x) sin x B. f (x) sin 2x C. f (x) cos x24D. f (x) cos 4x2. 函数 f (x) cos( x ) ( 0 )的最小正周期为 ,则 .653. 函数 f (x) | sin x | 的最小正周期为.24. 函数 f (x) sin x cos x 的最小正周期为.5. (1)函数 f (x) sin 2x cos 2x 的最小正周期为.5. 函数 f (x) 2 cos2 x 的一个单调递增区间是A.( , ) B.( 0 , ) C.(,3)D.( , )442442()(2)函数 f (x) (1 3 tan x) cos x 的最小正周期为6.若函数f (x) 同时具有以下两个性质:①对任意实数 x ,都有f( 4x)f( 4x) ,②f (x) 是偶函数,则 f (x) 是解析式为 ( )A. f (x) cos x B. f (x) cos(2x ) C. f (x) sin(4x ) D. f (x) cos 6x22(3)函数 f (x) (sin x cos x) sin x 的最小正周期为 (4)函数 f (x) cos 2x 2 3 sin x cos x 的最小正周期为. . .高三一模复习 三角函数专题 第 2 页6. 函数 f (x) 2 cos2 ( x ) 1是 ()4A.最小正周期为 的奇函数 B.最小正周期为 的偶函数C.最小正周期为 的奇函数 D.最小正周期为 的偶函数223. 函数 f (x) sin(2x ) 图象 3() A.关于点 (, 0 ) 对称B.关于直线 x 对称 C.关于点 (, 0 ) 对称D.关于直线 x对称34437. 函数 f (x) (sin x cos x)2 1的最小正周期是.8. 函数 f (x) 1 cos2 x ( 0 )的周期与 g(x) tan x 周期相等,则 ()32A. 2B.11C.1D.244. 如果函数 f (x) 3cos(2x ) 的图象关于点 ( 4 , 0 ) 中心对称,那么| | 的最小值为 ()3A.B.64C.3D.25. 已知函数 f (x) 2 sin x 的图象与直线 y 2 0 的相邻两个公共点之间的距离为 2 , 3则 的值为( ) A. 33B.22C.31D.3五、对称性1. 函数 f (x) sin(2x ) 图象的对称轴方程可能是 ()3A. x 6B. x 12C. x D. x 612六、图象平移与变换1. 函数 y cos x ( x R )的图象向左平移 个单位后,得到函数 y g(x) 的图象, 则 g(x) 的 2解析式为.2. 下列函数中,图象关于 x 对称的是 ()3A.f (x) sin(2x ) B.f (x) sin(2x ) C.f (x) sin(2x )366D.f (x) sin( x ) 262. 把函数 y sin x ( x R )的图象上所有点向左平移 个单位长度,再把所得图象上所有点的横 31坐标缩短到原来的 倍(纵坐标不变), 得到的图象所表示的函数是.2高三一模复习 三角函数专题 第 3 页3. 将函数 y sin 2x 图象向左平移 个单位,再向上平移1个单位,所得图象解析式是 4.3. 为了得到 y sin(2x ) 的图象,只需把 y sin(2x ) 的图象36()A.向左平移 个单位 B.向右平移 个单位 C.向左平移 个单位 D.向右平移 个单位44224. 要得到函数 y sin x 的图象,只需将函数 y cos(x ) 的图象向平移个单位.35. 将函数 y 3 cos x sin x 的图象向左平移 m 个单位,所得图象关于 y 轴对称,则 m 的最小正值为( )A.6B.325C.D.364. 已知函数 y sin(x ) cos(x ) ,则关于此函数的判断正确的是1212()A.最小正周期为 2 ,一个对称中心是 ( , 0 ) B.最小正周期为 ,一个对称中心是 ( , 0 )1212C.最小正周期为 2 ,一个对称中心是 (,0)D.最小正周期为 ,一个对称中心是 (,0)66七、图象1. 函数 f (x) sin(2x ) 在区间[ , ] 上的简图是 ()32八、综合1.定义在 R 上的函数f(x) 既是偶函数又是周期函数,若f(x) 的最小正周期是,且当x[ 0,] 时,2f (x) sin x ,则 f (5 ) 的值为.32. 函数 f (x) sin2 (x ) sin2 (x ) 是44()A.周期为 的偶函数 B.周期为 的奇函数 C.周期为 2 的偶函数 D.周期为 2 的奇函数2. 在同一平面直角坐标系中,函数 f (x) cos( x 3 ) ( x [ 0 ,2 ] )的图象和直线 y 1 的交222点个数是( ) A. 0 B.1C. 2 D. 43. 已知函数 f (x) sin(x ) ( x R ),下列结论错误的是 2()A.函数 f (x) 的最小正周期为 2 B.函数 f (x) 在区间[ 0 , ] 上是增函数2C.函数 f (x) 的图象关于 x 0 对称D.函数 f (x) 是奇函数高三一模复习 三角函数专题 第 4 页。
(完整版)高考三角函数经典解答题及答案

1在△ABC 中,角A 、B 、C 所对的边分别是a ,b ,c ,且.21222ac b c a =-+ (1)求B CA 2cos 2sin 2++的值; (2)若b=2,求△ABC 面积的最大值. 解:(1) 由余弦定理:conB=14sin22A B ++cos2B= -14(2)由.415sin ,41cos ==B B 得 ∵b=2, a2+c 2=12ac+4≥2ac,得ac ≤38,S △ABC =12acsinB ≤315(a=c 时取等号)故S △ABC 的最大值为3152在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= (I )求cosB 的值;(II )若2=⋅BC BA ,且22=b ,求c a 和b 的值.解:(I )由正弦定理得C R c B R b A R a sin 2,sin 2,sin 2===,,0sin .cos sin 3sin ,cos sin 3)sin(,cos sin 3cos sin cos sin ,cos sin cos sin 3cos sin ,cos sin 2cos sin 6cos sin 2≠==+=+-=-=A B A A B A C B B A B C C B B C B A C B B C R B A R C B R 又可得即可得故则因此.31cos =B(II )解:由2cos ,2==⋅B a 可得,,,0)(,12,cos 2,6,31cos 222222c a c a c a B ac c a b ac B ==-=+-+===即所以可得由故又 所以a =c = 63已知向量m =()B B cos 1,sin -, 向量n = (2,0),且m 与n 所成角为π3,其中A 、B 、C 是ABC ∆的内角。
(1)求角B 的大小;(2)求 C A sin sin +的取值范围。
(完整版)三角函数常考题型汇总,推荐文档
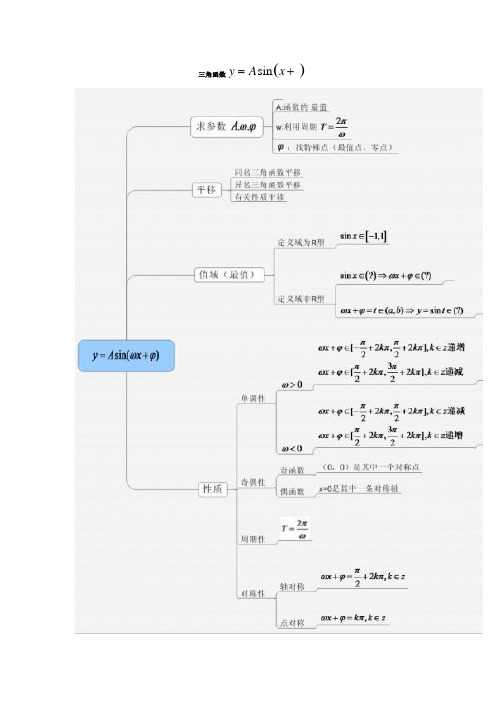
(x+) 三角函数y=A sin53 33 3 一、选择题:1. “ x =”是“函数 y = sin 2x 取得最大值”的( )4A. 充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2. 在∆ABC 中,如果sin A =3 sin C , B = 30° ,那么角 A 等于( )A . 30B . 45°C . 60°D .120° 3.函数 y = 1- 2 s in 2 (x -)是 ()4A. 最小正周期为的偶函数B. 最小正周期为的奇函数C. 最小正周期为 的偶函数D. 最小正周期为 的奇函数24. sin 225︒ = ()A.1B . -12C . 22D . - 225. 设函数 f(x )=3 sin θ x 3 +cos θ x 2 + 4x - 1 ,其中θ ∈ ⎡0∥ 5π⎤,32⎢⎣ 6 ⎥⎦则导数 f '(-1)的取值范围是( ) A . [3∥ 6]B . [3∥ 4+ C . [4- 3∥ 6D . [4-3∥ 4 + 36.∆ABC 的内角 A , B , C 的对边分别为 a , b , c ,若cos A= 2 5 2 5, bc = 5 , 则∆ABC 的面积等于( )A 、 2 5B 、4C 、D 、27.在∆ABC 中, AB = , BC = 1, AC cos B = BC cos A ,则 AC ⋅ AB = ()A.或 2B . 3 或22C . 2D . 3或 228.在∆ABC 中, AB = , BC = 1, sin A = sin B ,则 AC ⋅ AB = ( )A.2B .C .3 D . 12223 2yAOx- - - -9. 下列函数中,周期为的偶函数是 A. y = cos x B. y = sin 2xC. y = tan xD. y = sin(2x + )210. 函数 y = sin 2x cos 2x 的最小正周期是,最大值是。
高三数学二轮复习:专题一 三角函数

思维升华
函数y=Asin(ωx+φ)的性质及应用类题目的求解思路 第一步:先借助三角恒等变换及相应三角函数公式把待求函数化成y= Asin(ωx+φ)+B的形式; 第二步:把“ωx+φ”视为一个整体,借助复合函数性质求y=Asin(ωx +φ)+B的单调性及奇偶性、最值、对称性等问题.
跟踪演练 3 已知函数 f(x)=4cos ωxsinωx-π6(ω>0)的最小正周期是 π. (1)求函数f(x)在区间(0,π)上的单调递增区间;
周期为____π____,最大值为____4____.
解析
∵f(x)=2cos2x-sin2x+2=1+cos
1-cos 2x- 2
2x+2=32cos
2x+52,
∴f(x)的最小正周期为π,最大值为4.
解析 答案
2.(2018·全国Ⅱ改编 )若f(x)=cos x-sin x在[0,a]上是减函数,则a的最 3π
1 A.2
1 B.3
1 C.6
√D.-16
解析 答案
热点二 三角函数的图象及应用
函数y=Asin(ωx+φ)的图象 (1)“五点法”作图: 设 z=ωx+φ,令 z=0,π2,π,32π,2π,求出 x 的值与相应的 y 的值, 描点、连线可得. (2)图象变换: (先平移后伸缩)y=sin x―向――平左―移―φ―|>φ―0|个―或―单―向位―右―长―φ度―<―0→ y=sin(x+φ)
2
例1 (1)(2018·资阳三诊)已知角α的顶点与原点O重合,始边与x轴的非负
半轴重合,若它的终边经过点P(2,1),则tan 2α等于
√A.34
1 B.2
C.-21
D.-43
解析 因为角α的顶点与原点O重合,始边与x轴的非负半轴重合,终边
高三复习:三角函数-知识点、题型方法归纳

高三复习:三角函数-知识点、题型方法
归纳
一、知识点概述
1. 三角函数的定义和性质
- 正弦函数、余弦函数、正切函数的定义及其在数轴上的周期性;
- 三角函数的基本性质和关系:正弦函数与余弦函数的关系,正切函数与正弦函数、余弦函数的关系。
2. 三角函数的图像与性质
- 正弦函数、余弦函数的图像、特征和性质;
- 正切函数的图像、特征和性质。
3. 三角函数的基本变换
- 函数y = A · sin(Bx + C) + D的图像、特征和性质;
- 函数y = A · cos(Bx + C) + D的图像、特征和性质;
- 函数y = A · tan(Bx + C) + D的图像、特征和性质。
二、题型方法归纳
1. 计算题
- 利用三角函数的定义和性质,求解给定角的正弦、余弦、正切值;
- 利用三角函数的图像和性质,求解特定函数值。
2. 解方程和不等式
- 利用三角函数的定义和性质,解三角方程和三角不等式。
3. 图像分析题
- 分析三角函数的图像特征,如振幅、周期、对称轴等;
- 利用函数的基本变换,画出特定三角函数图像。
4. 证明题
- 利用三角函数的基本性质和关系,进行数学推导和证明。
三、总结
三角函数是高中数学的重要内容,通过复和掌握三角函数的知识点和题型方法,可以帮助学生提高解题能力和应用能力。
在复过程中,建议注重基本概念的理解、公式的记忆和方法的灵活运用,以及多做相关题目进行巩固和实践。
以上是三角函数复习的知识点和题型方法归纳,希望对你的高三复习有所帮助。
祝你学业进步,取得好成绩!。
(完整版)高考数学三角函数知识点总结及练习

三角函数总结及统练一。
教学内容:三角函数总结及统练(一)基础知识1。
与角α终边相同的角的集合},2{Z k k S ∈+==απβ2。
三角函数的定义(六种)-—三角函数是x 、y 、r 三个量的比值 3. 三角函数的符号—-口诀:一正二弦,三切四余弦。
4. 三角函数线 正弦线MP=αsin 余弦线OM=αcos 正切线AT=αtan5. 同角三角函数的关系平方关系:商数关系:倒数关系:1cot tan =⋅αα 1csc sin =⋅αα 1sec cos =⋅αα 口诀:凑一拆一;切割化弦;化异为同。
6。
α απ+k 2 α- απ- απ+απ-2 απ-2 απ+2 正弦 αsin αsin - αsin αsin - αsin - αcos αcos 余弦 αcos αcos αcos - αcos - αcos αsin αsin - 正切 αtan αtan - αtan - αtan αtan - αcot αcot - 余切 αcotαcot -αcot -αcotαcot -αtanαtan -7。
⎪⎪⎩⎪⎪⎨⎧⋅+-=-⋅-+=+⇒⎪⎪⎩⎪⎪⎨⎧⋅+⋅=-⋅-⋅=+⋅-⋅=-⋅+⋅=+βαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan(sin sin cos cos )cos(sin sin cos cos )cos(sin cos cos sin )sin(sin cos cos sin )sin( 8。
二倍角公式——代换:令αβ=⎪⎪⎩⎪⎪⎨⎧-=-=-=-=⋅=ααααααααααα22222tan 1tan 22tan sin cos sin 211cos 22cos cos sin 22sin降幂公式⎪⎪⎩⎪⎪⎨⎧+=-=22cos 1cos 22cos 1sin 22αααα半角公式:2cos 12sinαα-±=;2cos 12cos αα+±=;αααcos 1cos 12tan +-±= αααααcos 1sin sin cos 12tan+=-=9。
高三三角函数专题

三角函数专题得分点1 同角三角函数的基本关系﹑诱导公式【背一背基础知识】1. 掌握同角三角函数的基本关系式:22sin cos 1αα+=,sin tan cos ααα=. 2. 诱导公式诱导公式一:sin(2)sin k απα+=,cos(2)cos k απα+=,tan(2)tan k απα+=,其中k Z ∈诱导公式二: sin(180)α+=sin α-; cos(180)cos αα+=-,tan(180)tan αα+= 诱导公式三: sin()sin αα-=-; cos()cos αα-=,tan()tan αα-=-诱导公式四:sin(180)sin αα-=; cos(180)cos αα-=-,tan(180)tan αα-=- 诱导公式五:sin(360)sin αα-=-; cos(360)cos αα-=,tan(360)tan αα-=- 诱导公式六:sin(90)cos αα-=; cos(90)sin αα-=,tan(90)cot αα-= 诱导公式七:sin(90)cos αα+=; cos(90)sin αα+=-,tan(90)tan αα+=--α απ- απ+απ-2()Z k k ∈+απ2απ-22πα+sin-sin αsin α-sin α -sin αsin αcos αcos αcoscos α-cos α -cos α.Com]cos αcos αsin α-sin αtan -tan α-tan αtan α -tan αtan α cot α -cot α记忆方法:可用十个字概括为“奇变偶不变,符号看象限”,要把角化成形式为90k α⋅±(k 为常整数); 奇变偶不变是指:当k 为偶数时,三角函数名称不变,即前面若是正弦,后面也是正弦,名称不变,当k 为偶数时,三角函数名称变,即前面若是正弦,后面也是余弦,名称变;符号看象限是指:把α看成锐角时,为第几象限角,由原三角函数在各象限符号决定正负号,具体一二象限正弦为正,一四象限余弦为正,一三象限正切为正,其它为负. 【讲一讲基本技能】 1.必备技能:(1)同角三角函数的基本关系式包括:(1)平方关系,(2)商数关系. 解题时常用的变形措施有:大角化小,切割化弦等,应用 “弦化切”的技巧,即分子、分母同除以一个不为零的cos α,得到一个只含tan α的教简单的三角函数式。
高三数学复习《三角函数》专题复习

(1)了解任意角的概念和弧度制的概念。
(2)能进行弧度与角的互化。
2.三角函数
(1)理解任意角的三角函数(正弦、余弦、正切)的定义。 (2)能利用单位圆中的三角函数线推导出 , 的正弦、余
2
弦、正切的诱导公式,能画 y sin x, y cos x, y tan x 的图像,了
学生在三角函数部分存在的问题主要如下:
1. 三角公式记忆不到位; 2.三角变换目标意识不强; 3.角的范围考虑不到位; 4.综合应用能力差;
备考建议 三角函数是高中数学的主干知识之一,是高考重 点考查的内容.试题以中低档题为主,考查三角函数的基本 知识、方法与技能.三角函数除了具有一般函数的各种性 质外,还具有周期性和独特的对称性,再加上系统的丰富的 三角公式,使其产生的各种问题丰富多彩、变化多端
对知识的要求依次是了解、理解、掌握三个 层次。
1 、了解:要求对所列知识的含义有初步的、 感性的认识,知道这一知识内容是什么,按照 一定的程序和步骤照样模仿,并能(或会)在 有关的问题中识别和认识它。
这一层次所涉及的主要行为动词有:了解 ,知道、识别,模仿,会求、会解等。
2、理解:要求对所列知识内容有较深刻的理性认 识,知道知识间的逻辑关系,能够对所列知识做 正确的描述说明并用数学语言表达,能够利用所 学的知识内容对有关问题进行比较、判别、讨论, 具备利用所学知识解决简单问题的能力。
解三角函数的周期性。
(3)理解正弦函数,余弦函数在 0, 2 上的性质(如单调性、
最大值和最小值、图像与 x 轴的交点等),理解正切函数在
2
,
2
内的单调性。
(4)理解同角三角函数的基本关系式:sin2 x cos2 x 1, sin x tan x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完整版)高三三角函数专题复习(题型全面)三角函数考点1:三角函数的概念三角函数是以角度或弧度为自变量的函数,包括正弦函数、余弦函数、正切函数等。
考点2:三角恒等变换三角恒等变换包括两角和、差公式、倍角半角公式、诱导公式、同角的三角函数关系式等。
考点3:正弦函数、余弦函数、正切函数的图像和性质正弦函数、余弦函数、正切函数的定义域、值域、最值、单调区间、最小正周期、对称轴对称中心等性质都需要掌握。
考点4:函数y=Asin(x)(A,)的图像与性质函数y=Asin(x)(A,)的定义域、值域、最值、单调区间、最小正周期、对称轴对称中心等性质也需要掌握。
此外,该函数的图像还可以通过一定的变换得到。
一、三角函数求值问题1.三角函数的概念例1.若角的终边经过点P(4a,3a)(a0),则sin=-3/5.2.公式法例2.设(0,π/2),若sin=1/2,则2cos()=√3.练1.已知角的终边上一点的坐标为(sinθ。
cosθ)(θ∈(π/2,π)),则sin=-cosθ。
3.化简求值例3.已知为第二象限角,且sin=15/17,求sin(+π/4)的值。
练:1.已知sin=1/5,则sin4-cos4的值为-24/25.2.已知tan(θ+)=1/2,求tanθ和sin2θ-cosθ.sinθ+2cos2θ的值。
4.配凑求值例4.已知,∈(π/3,π/2),且sin(+)=-√3/2,sin(-)=1/2,求cos(+)的值。
练:1.设α∈(π/12,π/3),β∈(0,π/6),且sin(α+β)=-√3/2,sin(β-α)=-1/2,则cos(α+β)=1/2.1.已知三角函数的值,求其他三角函数的值已知 $sin\alpha = \frac{4}{5}$,$cos\beta = \frac{3}{5}$,$cos(\alpha - \beta) = \frac{1}{2}$,$sin(\beta + \theta) =\frac{3}{5}$,求 $sin(\alpha + \beta)$ 和 $tan(\alpha - 2\beta)$。
解:由 $cos(\alpha - \beta) = \frac{1}{2}$,可得 $\alpha -\beta = \frac{\pi}{3}$ 或 $-\frac{\pi}{3}$。
但由 $sin\alpha =\frac{4}{5}$,$cos\beta = \frac{3}{5}$,可知 $\alpha$ 和$\beta$ 都是第一象限角,因此$\alpha - \beta = \frac{\pi}{3}$。
由 $sin(\beta + \theta) = \frac{3}{5}$,可得 $\theta =arcsin\frac{3}{5} - \beta$。
因此,$sin(\alpha + \beta) = sin\alpha cos\beta + cos\alpha sin\beta = \frac{4}{5} \cdot \frac{3}{5} +\sqrt{1 - (\frac{4}{5})^2} \cdot \sqrt{1 - (\frac{3}{5})^2} =\frac{24}{25} + \frac{4}{5} \cdot \frac{4}{5} = \frac{56}{25}$。
又因为 $tan(\alpha - 2\beta) = \frac{tan\alpha - tan2\beta}{1+ tan\alpha tan2\beta}$,而 $tan2\beta = \frac{2tan\beta}{1 -tan^2\beta} = -\frac{24}{7}$,$tan\alpha = \frac{4}{3}$,因此$tan(\alpha - 2\beta) = \frac{\frac{4}{3} + \frac{48}{7}}{1 -\frac{4}{3} \cdot (-\frac{24}{7})} = -\frac{3}{5}$。
2.求三角函数的值求 $sin7 + cos15sin8$ 和 $cos7 - sin15sin8$ 的值。
解:$sin7 + cos15sin8 = sin7 + \frac{1}{2} (sin23 - sin7) = \frac{1}{2} sin7 + \frac{1}{2} sin23 = \frac{1}{2} (sin7 + sin23) = \frac{1}{2} sin15 = \frac{\sqrt{6} - \sqrt{2}}{4}$。
cos7 - sin15sin8 = cos7 - \frac{1}{2} (cos23 - cos7) =\frac{1}{2} cos7 + \frac{1}{2} cos23 = \frac{1}{2} (cos7 + cos23) = \frac{1}{2} cos15 = \frac{\sqrt{6} + \sqrt{2}}{4}$。
3.求三角函数的值若 $sin(\frac{2\pi}{3} + 2\alpha) = -\frac{1}{2}$,则$cos(\frac{3\pi}{2} - \alpha) =$?解:$sin(\frac{2\pi}{3} + 2\alpha) = -\frac{1}{2}$,可得$2\alpha = -\frac{\pi}{6} + k\pi$,其中 $k$ 为整数。
因此,$cos(\frac{3\pi}{2} - \alpha) = sin(\frac{\pi}{2} +\alpha) = sin(\frac{\pi}{6} + \frac{2\pi}{3} + k\pi) =sin(\frac{5\pi}{6} + k\pi) = \frac{\sqrt{3}}{2}$(当 $k$ 为偶数时),$cos(\frac{3\pi}{2} - \alpha) = sin(\frac{\pi}{2} + \alpha) = sin(\frac{\pi}{6} + \frac{2\pi}{3} + k\pi) = sin(-\frac{\pi}{6} + k\pi) = -\frac{1}{2}$(当 $k$ 为奇数时)。
因此,$cos(\frac{3\pi}{2} - \alpha) = -\frac{1}{2}$ 或$\frac{\sqrt{3}}{2}$。
1.给出简谐运动的最小正周期和相位的四组取值,分别为T=2π。
θ=0;T=6.θ=π/2;T=6π。
θ=π;T=6π。
θ=3π/2.2.给出函数y=2cos(xπ/4)的图像沿向量a=(-3,-2)平移后的解析式,即y=2cos[(xπ/4)-2]。
3.在区间[0,2π]上,函数f(x)=sin(x+π/4)有两个不等实根x1和x2,则x1+x2=5π/2.4.函数y=sin[(π/2)(2x-3)]在区间[-π/2.π/2]的简图是一条上下振荡的曲线,无法用文字简洁表达。
5.图像的一部分如右图所示的函数是y=sin(x+π/6)。
6.函数y=sin[(π/2)x-3]在区间[-π/2.π/2]的简图是一条上下振荡的曲线,无法用文字简洁表达。
7.下列函数中,图像的一部分如右图所示的是函数y=sin[(π/6)x+π/4]。
8.函数y=-4sin[(π/8)x+π/4]的部分图象如图所示,则函数表达式为y=-4sin[(π/8)x-π/4]。
9.从图中可以看出,函数y=Asin(ωx+φ)+b在6时至14时的温度变化曲线,其中A、ω、φ、b的具体值无法从图中推断出来,因此无法给出函数的解析式。
10.函数y=|sin(2x)|的最小正周期是π。
11.函数y=sin(Ax+π)/(x+π)的最小正周期为3π,因此A=2.12.函数f(x)=cos(2x)-2/3sin(x)cos(x)的最小正周期是π。
13.函数f(x)=sin(2x)-(1/2)的最小正周期是π。
由于f(-x)=-f(x),因此f(x)是一个奇函数。
D。
无单调增区间练:1.函数f(x) = sinx - 3cosx在区间[-π。
π]的单调递增区间是[-π/2.-π/6]。
2.函数y = 2cos2x的一个单调增区间是[-π/4.π/4]。
3.函数y = sinx的一个单调增区间是[0.π/2]。
四、三角函数综合问题:例1、已知函数$f(x)=\sin4x+2\sqrt{3}\sin x\cos x-\cos4x$1)求函数$f(x)$的最小正周期;(2)求函数$f(x)$的最大值和最小值及对应的$x$值;(3)求函数$f(x)$在区间$\left[\dfrac{\pi}{8},\dfrac{3\pi}{4}\right]$上的最大值和最小值及对应的$x$值;4)求函数$f(x)$的单调递增区间;(5)求函数$f(x)$在$\left[0,\pi\right]$的单调递增区间;(6)函数$f(x)$的图象可以由函数$y=\sin2x(x\in R)$的图象经过怎样的变换得到?7)求使不等式$f(x)\geq3$成立的$x$的取值集;8)若不等式$f(x)-m<2$在$x\in\left[\dfrac{\pi}{2},\pi\right]$上恒成立,求实数$m$的取值范围;9)画出函数$y=f(x)$在区间$\left[0,\pi\right]$上的图像。
练1、设函数$f(x)=3\cos\omega x+\sin\omega x\cos\omega x+a$(其中$\omega>0,a\in R$),且$f(x)$的图像在$y$轴右侧的第一个最高点的横坐标是$\dfrac{\pi}{2}$。
Ⅰ)求$\omega$的值;Ⅱ)如果$f(x)$在区间$\left[-\dfrac{\pi}{6},\dfrac{5\pi}{6}\right]$上的最小值为3,求$a$的值。
练2、已知函数$f(x)=A\sin^2(\omegax+\phi)$($A>0,\omega>0$,且$y=f(x)$的最大值为2,其图象相邻两对称轴间的距离为2,并过点$(1,2)$)Ⅰ)求$\phi$;Ⅱ)计算$f(1)+f(2)+\cdots+f(2008)$。
