加法树乘法器
各种乘法器比较
各种乘法器⽐较各种乘法器⽐较韦其敏08321050引⾔:乘法器频繁地使⽤在数字信号处理和数字通信的各种算法中,并往往影响着整个系统的运⾏速度。
如何实现快速⾼效的乘法器关系着整个系统的运算速度和资源效率。
本位⽤如下算法实现乘法运算:并⾏运算、移位相加、查找表、加法树。
并⾏运算是纯组合逻辑实现乘法器,完全由逻辑门实现;移位相加乘法器将乘法变为加法,通过逐步移位相加实现;查找表乘法器将乘积结果存储于存储器中,将操作数作为地址访问存储器,得到的输出数据就是乘法运算结果;加法树乘法器结合移位相加乘法器和查找表乘法器的优点,增加了芯⽚耗⽤,提⾼运算速度。
注:笔者使⽤综合软件为Quartus II 9.1,选⽤器件为EP2C70,选⽤ModelSim SE 6.1b进⾏仿真,对于其他的软硬件环境,需视具体情况做对应修改。
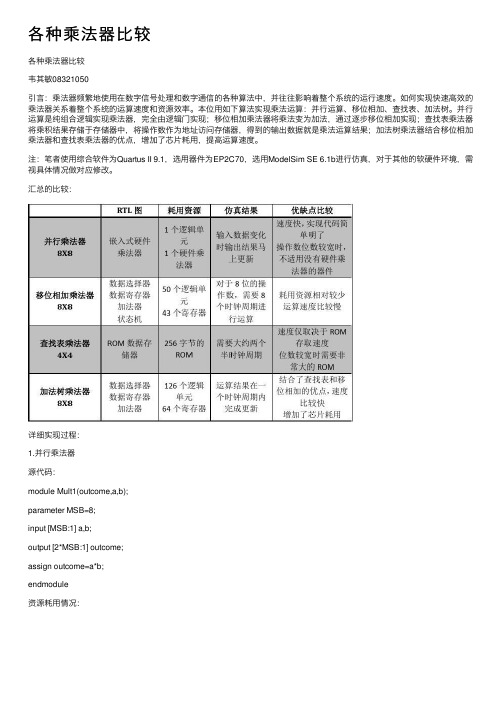
汇总的⽐较:详细实现过程:1.并⾏乘法器源代码:module Mult1(outcome,a,b);parameter MSB=8;input [MSB:1] a,b;output [2*MSB:1] outcome;assign outcome=a*b;endmodule资源耗⽤情况:ModelSim测试激励⽂件源代码:`timescale 10ns/1ns module Mult1_test();reg [8:1] a,b;wire [16:1] outcome;Mult1 u1(outcome,a,b); parameter delay=2;initialbegina=1;b=0;endinitial foreverbegin#delaya=a+1;b=b+1;if(outcome>=16'h0FFF)$stop;endendmodule仿真时序波形:DE2-70拥有300个嵌⼊式硬件乘法器单元,Quartus II综合并⾏乘法器时⾃动采⽤嵌⼊式乘法器来实现,因此中和报表中仅耗⽤了⼀个LE单元和⼀个九位的嵌⼊式乘法器单元。
8位wallace树乘法器

8位wallace树乘法器Wallace树是一种常见的乘法器,它可以用于高效地执行大数乘法运算。
它的名字来源于其发明者Wallace。
Wallace树乘法器是通过将乘法运算分解为多个部分,然后以并行的方式计算每个部分的结果来实现的。
每个部分接收两个部分乘积(Partial Product)和一个进位位(Carry-in),并计算出一个部分积(Partial Product)和一个进位位(Carry-out)。
具体来说,Wallace树乘法器由三个主要部分组成:部分乘法器(Partial Multiplier)、部分积生成器(Partial Product Generator)和部分积压缩器(Partial Product Compressor)。
部分乘法器是Wallace树乘法器的基本单元,用于计算两个二进制数的部分积。
每个部分乘法器由两个二进制数位相乘得到两个部分积和一个进位位。
部分乘法器之间通过进位位进行连接。
部分积生成器用于生成所有的部分乘积。
它接收两个输入数和多个进位位,并生成部分积。
部分积压缩器将多个部分乘积和进位位进行压缩,以得到最终的乘积。
它使用一种特殊的编码方式来表示乘积,并通过对部分积和进位位的运算进行压缩。
压缩后的结果被输出作为乘法器的最终输出。
Wallace树乘法器的优势在于它可以最大限度地提高乘法运算的并行性,从而提高乘法器的计算速度。
同时,它还可以减少乘法器所需的芯片面积和功率消耗。
然而,由于Wallace树乘法器存在部分积生成和部分积压缩的过程,因此它的面积和延迟仍然会受到影响。
为了 further enhance 实现的效率,还有一些改进的Wallace树结构,如Dadda树乘法器和Wallace树的变种。
这些改进可以进一步减少乘法器的延迟和面积。
另外,还可以使用Wallace树乘法器来实现更高位数的乘法运算,例如16位、32位甚至更高位数。
构建更高位数的Wallace树乘法器需要合理地设计其结构和逻辑电路,以确保乘法运算的正确性和高效性。
FPGA加法器乘法器

FPGA加法器设计加法作为一种基本运算,大量运用在数字信号处理和数字通信的各种算法中。
由于加法器使用频繁,因此其速度往往影响着整个系统的运行速度。
如果可以实现快速加法器的设计,则可以提高整个系统的处理速度。
加法运算是最基本的算数运算,在多数情况下,无论是乘法、除法还是减法以及FFT等运算,最终都可以分解为加法运算来实现,因此对加法运算的实现进行一些研究是非常必要的。
实现加法运算有如下一些方法:(1)级连加法器;(2)并行加法器;(3)超前进位加法器;(4)流水线加法器。
1、级连加法器级连加法器是由1位全加器级连构成的,本位的进位输出作为下一级的进位输入。
级连加法器的结构简单,但N位级连加法运算的延时是1为全加器的N倍,延时主要是由于进位信号级连造成的。
在需要高性能的设计中,这种结构不宜采用。
module add_jl(sum,cout,a,b,cin);output [3:0] sum;output cout;input [3:0] ina,inb;input cin;wire [3:1] c;full_add1 f0 (ina[0],inb[0],cin, sum[0],c[1]); //级连描述full_add1 f1 (ina[1],inb[1],c[1],sum[1],c[2]);full_add1 f2 (ina[2],inb[2],c[2],sum[2],c[3]);full_add1 f3 (ina[3],inb[3],c[3],sum[3],cout);module full_add1(ina,inb,cin,sum,cout); //1位全加器input ina,inb,cin;output sum,cout;wire s1,m1,m2,m3;and (m1,ina,inb),(m2,inb,cin),(m3,ina,cin);xor (s1,a,b),(sum,s1,cin);or (cout,m1,m2,m3);endmodule2、并行加法器并行加法器可采用Verilog语言的加法运算符直接描述,或称为数据流描述方式,实现容易,其运算速度快,但耗费资源多,尤其是当加法运算的位数较宽时,其耗用资源将会大大增加。
乘法器的工作原理

乘法器的工作原理
乘法器是一种用于实现数字乘法运算的电路或器件。
它将两个输入的数字进行相乘,并得到其乘积作为输出。
乘法器的工作原理基于逻辑门电路的组合与串联。
乘法器通常是由多个部分组成的,其中包括乘法器的位数、运算规则以及乘法器内部的逻辑门电路。
这些部分协同工作以实现精确且高效的乘法运算。
在一个典型的乘法器中,输入信号将首先被分为不同的位数。
每一位数将被独立处理,并最终合并以得到最终的乘积结果。
每个位数的处理过程包括了多个逻辑运算,例如与门、或门和异或门。
为了完成乘法运算,乘法器将两个输入位进行逐位相乘。
这里的位可以是二进制位,也可以是十进制位。
逐位相乘的方法可以通过一系列的逻辑门电路来实现。
这些逻辑门电路可以对输入位进行操作,并生成相乘位的输出。
在乘法器中,最低有效位(LSB)的运算最先进行。
在相邻的
位运算完成后,它们的结果会被以并行的方式传递给下一位的运算。
这样一直进行到最高有效位(MSB)的运算完成。
最后,所有位的乘法结果会被整合在一起,形成最终的乘积。
乘法器的性能取决于其位数和逻辑门电路的设计。
更高的位数会产生更精确的乘法结果,但也会增加乘法器的复杂性和功耗。
因此,在设计乘法器时需要权衡精确性和性能之间的关系。
总之,乘法器是一种通过组合逻辑门电路来实现数字乘法运算的电路或器件。
它将输入信号分解为不同的位数,并使用逻辑门电路逐位相乘。
最后,将每个位的乘法结果合并在一起,得到总体的乘积输出。
相加器 相乘器

相加器相乘器
相加器和相乘器是数字电路中常见的两种基本电路。
相加器用于将两个或多个二进制数相加,而相乘器则用于将两个或多个二进制数相乘。
它们都是数字电路中非常重要的组件,被广泛应用于各种数字系统中。
相加器的基本原理是将两个二进制数的每一位相加,得到一个结果和一个进位。
这个结果和进位再参与下一位的计算,直到所有位都被计算完成。
相加器可以用于实现加法器、减法器和比较器等功能。
相乘器的基本原理是将两个二进制数的每一位相乘,得到一个结果和一个进位。
这个结果和进位再参与下一位的计算,直到所有位都被计算完成。
相乘器可以用于实现乘法器、除法器等功能。
现代数字系统中常常使用带符号数、浮点数等,这些都需要更加复杂的相加器和相乘器来实现。
此外,相加器和相乘器在硬件实现上也有不同的方案,例如使用二进制加法器或绝对值器来实现加法器,使用 Booth编码或Wallace树来实现乘法器等。
总的来说,相加器和相乘器是数字电路中非常重要的基本电路,其应用广泛,其实现方式也多种多样,因此对于数字系统的学习和应用来说,了解和掌握相加器和相乘器的原理和实现方法是非常必要的。
- 1 -。
乘法器工作原理

乘法器工作原理
乘法器是一种电子设备,用于实现两个数字(或模拟)信号的乘法运算。
其工作原理可以简单地描述如下:
1. 输入信号:乘法器通常有两个输入端,分别用于接收待相乘的数字信号A和B。
2. 位展开:乘法器将输入信号A和B进行位展开操作,即将
每一个输入位(或字节)进行分离和独立处理。
这可以通过触发器、逻辑门电路等实现。
3. 部分乘积计算:对每一对输入位进行乘法运算,并将结果存储在部分乘积寄存器中。
这可以通过加法器电路来实现,其中每一个乘积被加到累加器中。
4. 乘积累加:将所有的部分乘积相加得到最终的乘积结果。
这可以通过多级加法器电路来实现。
一般来说,乘法器采用树形结构或布斯-舍乘法算法(Booth's algorithm)来提高计算效率。
5. 结果输出:输出端给出乘法运算的结果。
根据需求,这个结果可以是数字信号,模拟电压或电流等形式。
乘法器的工作原理可以根据底层电路和算法的不同而有所变化。
现代的乘法器采用复杂的电路设计和优化算法,以实现更高的运算速度和精度。
乘法器原理

乘法器原理
乘法器是一种用于执行乘法运算的数字电路。
它通常由多个逻辑门、寄存器和时钟信号组成。
乘法器的主要原理是将两个输入数(被乘数和乘数)进行相乘,然后输出它们的乘积。
乘法器的输入是一系列位(比特),每个位代表一个二进制数。
这些输入位通过逻辑门来实现不同位上的相乘。
一般来说,较高位的输入乘数与较低位的被乘数相乘后,得到的乘积需要左移若干位。
这个左移操作可以通过使用寄存器和时钟信号来完成。
乘法器可以分为多种类型,其中最常见的是布斯乘法器和Wallace树乘法器。
布斯乘法器通过将被乘数和乘数进行分割,并使用部分积和约化乘法器来实现乘法运算。
Wallace树乘法
器是一种高效的乘法器类型,它通过将乘法操作转化为加法操作来提高运算速度。
这种乘法器通常使用布斯乘法器和连锁加法器来实现。
乘法器的输出是乘法的结果,通常也是一系列位(比特)。
输出可以进一步用于其他计算或者存储在寄存器中。
同时,乘法器也可以进一步扩展为多位乘法器,用于执行更大位数的乘法操作。
综上所述,乘法器是一种将两个输入数进行相乘的数字电路。
它的原理是利用逻辑门、寄存器和时钟信号来实现乘法运算。
乘法器可以分为不同类型,其中最常见的是布斯乘法器和
Wallace树乘法器。
乘法器的输出是乘法的结果,通常用于其他计算或者存储在寄存器中。
乘法器

0
1 0 1 1
1
1
1
1
1
Company Logo
一位全加器的实现(表达式) 由真值表,可得: S=Add_1 xor Add_2 xor cin; cout=(Add_1 and Add_2) or (Add_1 and cin )or (Add_2 and cin);
所以,一位全加器的实现需要的器件有: 3输入的异或门(1个) 3输入的或门(1个);2输入的与门(3个)
Company Logo
Company Logo
串并乘法原理与步骤
假设被乘数X=1101,乘数Y=1011,步骤如下: ①1101*1=1101 ,result=1 1 0 1(放在锁存器中) ②1101*1=1101 sum=1101,把result的值左移 一位,即0 1 1 0,结果与sum相加(一位相加)
Company Logo
一位全加器的实现(电路)
Company Logo
串-并乘法器的实现
LOGO
Company Logo
加法树乘法器 加法树乘法器的基本 思想也是移位相加,不 过,它是先移位(*2), 后相乘.而且它是同时移 位。 优点:速度快 缺点:耗资源
Company Logo
混合加法器
混合加法器就是把移位相加与查找表结合起来。假设 现在把1101与1011相乘。用两位相乘实现。步骤如下: 1. 1101与11相乘,把1101看成1100+01。这样, 1101*11=(11*11)>>2+01*11; 两位乘法直接在查找表中找到,不用进行运算。所以,只 需 进行加法运算; 2.1101与10(高位)相乘,方法与1相同; 3.把2的结果移2位,再与1的结果相加。 这样,在查找表中只需保存22 *22,同样是4位的乘法 器,比单纯用查找表法( 24 * 24 ),资源少了不少。当 然在速度也要慢一下。所以混合加法器的速度与资源的利 用都是介于查找表与移位加法这两种方法之间
