插值法
计算方法第四章 插值法

4
3
xi 4 yi 2
9 16 3 4
2
0
4
7
9
16
第4章 插值法
应用背景
造函数表:三角函数、对数 预测:鸡蛋价格、城市用水量
《 计 算 方 法 》
数控加工:造船、飞机机翼骨架、服装 样片、模具加工、刀具 计算机辅助设计:潜水艇、汽车造型
服装样片
第4章 插值法
实际问题中,f (x)多样,复杂,通常只能观测到一些离散 数据;或者f (x)过于复杂而难以运算。这时我们要用近似函数 φ(x)来逼近f (x)。
《 计 算 方 法 》
φ (x)= y0
第4章 插值法
§2 线性插值与二次插值
2.1 线性插值
线性插值是代数多项式插值的最简单的形式。假设
《 计 算 方 法 》
给定了函数f (x)在两个互异点x0,x1的值,即
x x0值)
y y0 x0
y1
x1
x
第4章 插值法
现要用一线性函数
满足插值条件:
y( xi ) = yi , i = 0,1, 2
22
第4章 插值法 例:已知函数 y=f (x)的观测数据为
x
《 计 算 方 法 》
1 0
2 -5
3 -6
4 3
y
试求拉格朗日插值多项式。
第4章 插值法
《 计 算 方 法 》
( x 2)( x 3)( x 4) 解 :p3 ( x ) = 0 (1 2)(1 3)(1 4) ( x 1)( x 3)( x 4) ( 5) (2 1)(2 3)(2 4) ( x 1)( x 2)( x 4) ( 6) (3 1)(3 2)(3 4) ( x 1)( x 2)( x 3) 3 (4 1)(4 2)(4 3) = x3 4 x2 3
数值分析第五版第二章_插值法
于是
Ak
1
(x
j 0 j k
n
k
xj)
代入上式,得
(x x
l k ( x)
j 0 j k n
n
j
)
j 0 jk n
x xj xk x j
(x
j 0 j k
k
xj)
称
l k ( x) 为关于基点
x i 的n次插值基函数(i=0,1,…,n)
( x x0 )(x x2 ) ( x x0 )(x x1 ) ( x x1 )(x x2 ) P( x) y0 y1 y2 ( x0 x1 )(x0 x2 ) ( x1 x0 )(x1 x2 ) ( x2 x0 )(x2 x1 )
容易看出,P(x)满足条件
( x 0 , y0 ), ( x1 , y1 ), ( x 2 , y2 ) 的抛物线 y P( x) 近似代替曲线
y f ( x) ,如下图所示。因此也称之为抛物插值。
P(x)的参数 a0 , a1 , a 2
直接由插值条件决定, 即
y
a0 , a1 , a2满足下面
O
y=L2(x) y0 x0 y1 x1 y1 x2 y=f(x) x
( x x0 )(x x1 ) l 2 ( x) ( x2 x0 )(x2 x1 )
这样构造出来的 l0 ( x),l1 ( x),l2 ( x) 称为抛物插值的基函数 取已知数据 y0 , y1 , y 2 作为线性组合系数,将基函数
l0 ( x),l1 ( x),l2 ( x) 线性组合可得
a n x0 n a n 1 x0 n 1 a1 x0 a 0 f ( x0 ) n n 1 a n x1 a n 1 x1 a1 x1 a 0 f ( x1 ) a x n a x n 1 a x a f ( x ) n 1 n 1 n 0 n n n
第二章插值法

lk ( xk 1 ) 0
n=2的情况,假定插值节点为
xk 1 , xk , xk 1 , 要求一个二次插值多项式L2 ( x),使它满足 L2 ( x j ) y j ( j k 1, k , k 1)
y L2 ( x)在几何上就是通过三点(xk-1 , yk 1 ),(xk , yk ),(xk+1, yk 1 )的抛物线
插值法
§2.1 §2.2 §2.3 §2.4 §2.5 §2.6 §2.7 引言 拉格朗日插值 均差与牛顿插值公式 差分与等距节点插值 埃尔米特插值 分段低次插值 三次样条插值
一、插值问题
或者函数本身只是 一组实验数据,很 难对函数的性质进 行分析
对函数f (x),其函数形式可能很复杂且不利于在计算机上 ,
设函数
y f ( x ) 在区间 [a, b] 上有定义,且已知在
a x0 x1 x2 xn b
f ( xi ) yi , i 0,1,, n
如果存在一个简单函数 P ( x ),使得
P( xi ) f ( xi ) yi , i 0,1,, n
xx x x
如函数y sin x, 若给定 0, ]上5个等分点 [
其插值函数的图象如图
对于被插函数 ( x)和插值函数 ( x) f P
在节点xi处的函数值必然相等
但在节点外 ( x)的值可能就会偏离 ( x) P f 因此P( x)近似代替 ( x)必然存在着误差 f
整体误差的大小反映了插值函数的好坏
成立,则称 P ( x ) 为 f ( x ) 的插值函数
称点 xi , i 0,1,2,, n为插值节点
称区间 a , b]为插值区间 [
插值法

i 0 i j
n
x x
j
x xi
i
将 l j ( x)代入
P P
n
( x) l j ( x) y
j 0
n
j
中得
n
( x)
j 0 n
n
( x x0)(x x1)...(x x j 1)(x x j 1)...(x xn ) ( x j x0)( x j x1)...(x j x j 1)( x j x j 1)...(x j xn )y
于是
(x-x1)(x-x2) (x-x0)(x-x2) (x-x0)(x-x1) P2(x)=-----------------y0 + -----------------y1 + ------------------y2 ...(6) (x0-x1)(x0-x2) (x1-x0)(x1-x2) (x2-x0)(x2-x1)
而ai(i=0,1,2,…,n)的系数行列式是Vandermonde行 列式
1 V( x0 , x1 ,...,x n ) 1 ... 1
n i 1
x x x x
0 1
2 0 2
... ... ... ...
1
x x x
n 0 n
1
...
n
...
2 n
...
n n
x x
i
=
( x x )
0.01892 =0.314567+ ——— (0.0167) =0.330365 . 0.02
其截断误差得
其中 M 2
R1 ( x)
// 1
M
2
插值法的最简单计算公式

插值法的最简单计算公式全文共四篇示例,供读者参考第一篇示例:插值法是一种常用的数值计算方法,用于通过已知数据点推断出未知数据点的值。
在实际问题中,往往会遇到数据点不连续或者缺失的情况,这时就需要通过插值法来填补这些数据点,以便更准确地进行计算和分析。
插值法的最简单计算公式是线性插值法。
线性插值法假设数据点之间的变化是线性的,通过已知的两个数据点来推断出中间的未知数据点的值。
其计算公式为:设已知数据点为(x0, y0)和(x1, y1),需要插值的点为x,其在(x0, x1)之间,且x0 < x < x1,插值公式为:y = y0 + (y1 - y0) * (x - x0) / (x1 - x0)y为插值点x对应的值,y0和y1分别为已知数据点x0和x1对应的值。
通过这个线性插值公式,可以方便地计算出中间未知点的值。
举一个简单的例子来说明线性插值法的应用。
假设有一组数据点为(1, 2)和(3, 6),现在需要插值得到x=2时的值。
根据线性插值公式,我们可以计算出:y = 2 + (6 - 2) * (2 - 1) / (3 - 1) = 2 + 4 * 1 / 2 = 2 + 2 = 4当x=2时,线性插值法得到的值为4。
通过这个简单的例子,可以看出线性插值法的计算公式的简单易懂,适用于很多实际问题中的插值计算。
除了线性插值法,还有其他更复杂的插值方法,如多项式插值、样条插值等,它们能够更精确地拟合数据并减小误差。
在一些简单的情况下,线性插值法已经足够满足需求,并且计算起来更加直观和方便。
在实际应用中,插值法经常用于图像处理、信号处理、数据分析等领域。
通过插值法,可以将不连续的数据点连接起来,填补缺失的数据,使得数据更加完整和连续,方便后续的处理和分析。
插值法是一种简单而有效的数值计算方法,其中线性插值法是最简单的计算公式之一。
通过这个简单的公式,可以方便地推断出未知数据点的值,并在实际应用中发挥重要作用。
计算方法(2)-插值法

2
2
yk1 2
f (xk
h
2
),
y
k
1 2
f (xk
h) 2
21
3.牛顿向后插值公式
Nn (xn
th)
yn
tyn
t(t 1) 2!
2
yn
t(t
1)
(t n!
n
1)
n
yn
(t 0)
插值余项
Rn
(xn
th)
t(t
1) (t (n 1)!
Nn (x0
th)
y0
ty0
t(t 1) 2!
2
y0Leabharlann 插值余项t(t
1)
(t n!
n
1)
n
y0
Rn (x0
th)
t(t
1) (t (n 1)!
n)
h n1
f
(n1) ( ),
(x0 , xn )
20
二.向后差分与牛顿向后插值公式
杂.
根据f(x)函数表或复杂的解析表达式构
造某个简单函数P(x)作为f(x)的近似.
2
2.问题的提法
1)已知条件 设函数y f (x)在区间[a,b]上
连 续, 且 在n 1个不 同点a x0 , x1, , xn b 上 分 别 取 值y0 , y1, , yn
插值法的最简单计算公式

插值法是一种通过已知数据点来估计未知数据点值的方法。
最简单的插值方法之一是线性插值,其公式如下:
对于两个已知数据点 (x1, y1) 和 (x2, y2),要找到在 x 轴上位于 x1 和 x2 之间的某个点 x 的对应 y 值,线性插值的计算公式为:
\[ y = y1 + \frac{(x - x1)}{(x2 - x1)} \times (y2 - y1) \]
如果将这个表达式简化一下,可以得到:
\[ y = m(x - x1) + y1 \]
其中 m 是斜率,计算方式为:
\[ m = \frac{y2 - y1}{x2 - x1} \]
更一般地,对于多项式插值,比如拉格朗日插值或牛顿插值等,公式会更复杂,涉及更多的数据点和高阶多项式函数。
但在线性插值的情况下,上述公式是最基本且易于理解的插值计算方法。
插值法的最简单计算公式

插值法的最简单计算公式全文共四篇示例,供读者参考第一篇示例:插值法是数值分析领域中常用的一种方法,它可以用来估计未知函数在给定点处的值。
插值法的基本思想是基于已知数据点,构建一个多项式函数来逼近未知函数的值。
在实际应用中,插值法常常被用来对离散数据进行平滑处理,或是用来预测未来的数据。
最简单的插值方法之一是线性插值法。
线性插值法假设未知函数在两个已知数据点之间是线性变化的,即可以通过这两个点之间的直线来估计未知函数在中间点处的值。
线性插值的计算公式如下:设已知数据点为(x0, y0)和(x1, y1),要估计中间点x处的函数值y,则线性插值公式为:\[y = y0 + \frac{x - x0}{x1 - x0} * (y1 - y0)\]这个公式的推导比较简单,可以通过代入已知数据点计算出来。
如果已知数据点为(0, 1)和(2, 3),要估计在x=1处的函数值,根据线性插值公式,计算如下:在x=1处的函数值为2。
线性插值法的优点是简单易懂,计算速度快,并且可以比较精确地估计函数值。
但是线性插值法的精度受限于已知数据点之间的线性关系,如果函数在两个数据点之间发生了急剧变化,线性插值法可能无法准确估计函数值。
除了线性插值法,还有许多其他更复杂的插值方法,如拉格朗日插值、牛顿插值、三次样条插值等。
这些方法在不同的情况下可以提供更精确的函数估计值,但也需要更复杂的计算步骤。
插值法是一种常用的数值分析方法,可以帮助我们更好地处理数据和预测未知函数的值。
在实际应用中,可以根据具体情况选取合适的插值方法来进行计算。
第二篇示例:插值法是一种用于估算未知数值的方法,它基于已知数据点之间的关系进行推断。
在实际应用中,插值法经常用于数据处理、图像处理、数学建模和预测等领域。
插值法的计算公式通常比较复杂,但是我们可以通过简化的方式来理解和计算插值结果。
最简单的插值方法之一是线性插值法。
在线性插值法中,我们假设已知数据点之间的关系是线性的,然后通过线性方程来估算未知点的数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
❖
设函数关系y=f(x)在区间[a,b]
上给出一系列点的函数值
❖
(4―1)
yi=f(xi),
i=0,1,2,…,n
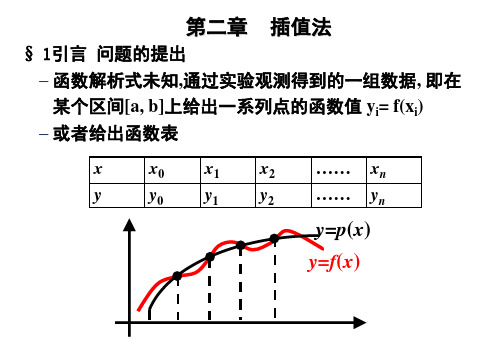
❖ 或者给出一张表函4―数1 表,如表4―1所示。
❖ 这里
❖
a≤x0<x1<x2<…<x≤b
❖ 欲选择一个函数φ(x),使得
❖
φ(xi)=yi,
(4―2)
i=0,1,2,…,n
❖
我们称Rn(x)为插值多项式Pn(x)的余
项。显然有
❖
Rn(xi)=0,i=0,1,2,…,n
❖
下面给出插值多项式Pn(x)余项的表
达式。
❖
定理设函数f(x)在区间[a,b]上具
有n+1阶导数,
❖ Pn(x)为次数不高于n的多项式,且
❖
Pn(x0)=y0
❖
Pn(x1)=y1
❖
…
❖ 则 对 插 值 区 间 上 的 任 何 x, 都 存 在
的形式。假设给定了函数f(x)在两个互异点
x0,x1的值,即
x
x0
x1
y
y0
y1
❖ 现要用一线性函数
❖
φ(x)=P1(x)=ax+b
(4―3)
❖
(4―2近)应似有地aaxx代10
替b f(yx0 )
b y1
。
按
照
插
值
原
则
,
式
因为x0≠x1,所以a,b可唯一确定,且有
a y1 y0 x1 x0
因此,a,b,c可唯一地确定。这样二次函数P2(x)也唯一地
被确定。P2(x)就是我们要求的二次插值多项式。
二次插值的几何意义是用经过三点
A(x0,y0),B(x1,y1),C(x2,y2)的抛物线来近似地代替f(x),见图 4.2。
图 4.2
§3 代数多项式插值的存在唯一 性
❖
线性插值和二次插值都属于代数多项
❖ 作为函数y=f(x)的近似表达式。
❖
由于代数多项式具有形式简单,便
于计算,且在某些情况下与给定的函数有
较好 的逼近的特性,人们很早就用它去近
似地表示复杂的函数或由表格给出的函
数。
若 个f 仅熟(x)限知 f于的(x求办0) 函 法f (数 就x0)在 是(x 将xx=0f)x(0x)附在近xf =(的nn)x(!x0近0处) (似x 展值x0成),n一
式插值。对于一般的代数插值问题,就是寻求
一个不高于n次的代数多项式
❖
Pn(x)=a0+a1x+a2x2+…+anxn
(4―9)
❖
使其在给定的n+1个互异的插值基点
上满足插值原则
❖
(4―10)
Pn(xi)=yi,
i=0,1,…,n
❖
这样的多Байду номын сангаас式是否存在并且唯一
呢?回答是肯定的。
❖
根 据 插 值 原 则 式 (4―10), 代 数 多
泰勒级数f ,(即n1)( )
(n 1)!
(
x
x0
)n1
❖ 取前n+1项的部分和Pn(x)作为f(x)的 近似式,也即
Pn (x) f (x0) f (x0)(x x0)
f
(n) ( x0 n!
)
(
x
x0
)n
f (x)
§2 线性插值与二次插值
❖
2.1 线性插值
❖
线性插值是代数多项式插值的最简单
b
y0
y1 x1
y0 x0
x0
❖
代入式(4―3)得
P1( x)
y0
y1 x1
y0 x0
( x1
x0 )
(4―4)
图 4.1
❖
因为P1(x)就是经过两点
A(x0,y0),B(x1,y1)的直线方程,所以线性插
值的几何意义为用经过两点
Ay=(xf(0x,y),0见P),1B(图x()x41.,1xyx0。1)的xx11 直y0 线 xx近1 似xx00地y1 代替曲(4线―5)
§4 代数多项式的余项
❖
代数多项式Pn(x)仅为已知函数f(x)的
一种近似表达式,用它来代替f(x)进行计算总会
带来误差。一般说来,对插值区间[a,b]上插
值基点xi(i=0,1,2,…,n)以外的点,Pn(x)≠f(x)。若 令
❖
❖则
Rn(x)=f(x)-Pn(x)
❖
f(x)=Pn(x)+Rn(x)
项 足下式PPnn列(((xx410n)―) +9a1a00)阶中 aa线11的xx10性各aa方22x个x12程02 系组数aaannxx01n0n,a1yy,1…0 ,an 应满
Pn ( xn ) a0 a1xn a2xn2 an xnn yn
❖
其中未知量a0,a1,…,an的系数行列
❖
P2(xi)=yi,
(4―7) ax02 bx0 c y0
❖
由(4―a7x)12式 b得x1 c y1
ax22 bx2 c y2
i=0,1,2,…
(4―8)
❖
则
由 于 方 程 组 (4―8) 中 x0,x1,x2 互 异 ,
x02 x0 1 x12 x1 1 0 x22 x2 1
f (t) Pn (t)
f
(x) Pn (
n1( x)
x
)
n
1
(t
)
❖
上式右端第一项f(t)有n+1阶导数,
第二项是次数不高于n的多项式,当x取某
一定 值时,第三项是变量t的n+1次多项式,
因此F(t)有n+1阶导数。又在区间[a,b]
上,F(t)有n+2个零点
❖
t=x,x0,x1,…,xn
式为范德蒙特( Vander Monde )行列
式
1 x0 x02
x0n
V ( x0, x1, , xn ) 1 x1 x12
x1n
1 xn xn2
xnn
由于插值基点xi(i=0,1,…,n)为互异,故
V(x0,x1,…,xn)≠0
因此,方程组(4―11)有唯一的一组解a0,a1,…,an,于
是Pn(x)存在且唯一。
ξ∈这(里a,bR)n,(使x) 得 f(n(n1)1()!) n1( x)
(4―12)
n1( x) ( x x0 )( x x1) ( x xn )
n
(x xi )
i0
(4―13)
证 当x=xi时,式(4―12)显然成立。
当x∈(a,b)但不等于任一个插值基点时,作辅助函数
F(t)
❖
2.2 二次插值
❖
二次插值又称为抛物线插值,也
是常用的代数多项式插值之一。设已知
函数f(x)的三个互异插值基点x0,x1,x2的函 数值分x别为y0,y1,xyo2,见下x表1 所示x:2
y
y0
y1
y2
❖ 现要构造一个二次函数
❖
(4―6)
φ(x)=P2(x)=ax2+bx+c
❖ 近似地代替f(x),并满足插值原则(4―2)
❖
应用洛尔(Rolle)定理,在(a,b)内至
少有ξ0,ξ1,…,ξn使得
❖
F′(ξi)=0,i=0,1,2,…,n
❖
如此反复应用洛尔定理,可知在
即
F (n1) ( )
f (n1) ( )
