平行四边形的底
平行四边形、三角形、梯形 面积推导过程(整理)
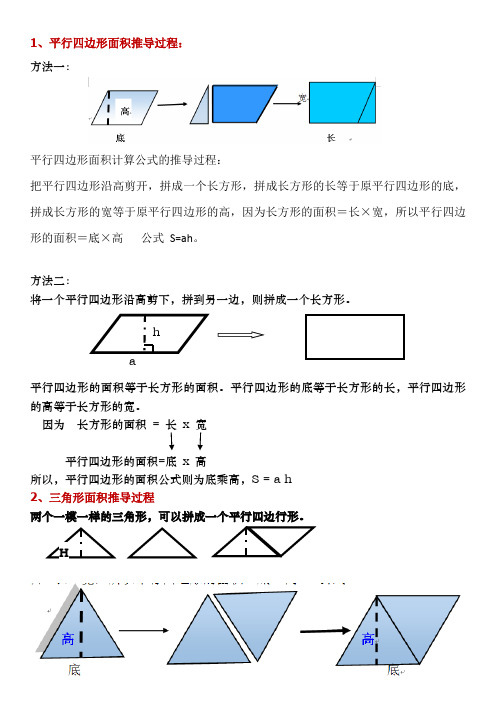
1、平行四边形面积推导过程:
方法一:
平行四边形面积计算公式的推导过程:
把平行四边形沿高剪开,拼成一个长方形,拼成长方形的长等于原平行四边形的底,拼成长方形的宽等于原平行四边形的高,因为长方形的面积=长×宽,所以平行四边形的面积=底×高公式S=ah。
方法二:
将一个平行四边形沿高剪下,拼到另一边,则拼成一个长方形。
h
a
平行四边形的面积等于长方形的面积。
平行四边形的底等于长方形的长,平行四边形的高等于长方形的宽。
因为长方形的面积= 长х宽
平行四边形的面积=底х高
所以,平行四边形的面积公式则为底乘高,S = a h
2、三角形面积推导过程
两个一模一样的三角形,可以拼成一个平行四边行形。
H
两个完全一样的三角形能拼成一个平行四边形,三角形的面积是拼成平行四边形面积的一半,三角形的高就就是这个平行四边形的高,三角形的底也是这个平行四边形的底。
平行四边形的面积=底边×高,所以三角形的面积=(同底等高的)平行四边形的面积÷2=底×高÷2 ,公式S= a×h÷2
3、梯形面积推导过程
两个完全一样的梯形可以拼成一个平行四边形,原梯形的面积是拼成平行四边形面积的一半,拼成平行四边形的底是原梯形的上底与下底的和,拼成平行四边形的高是原梯形的高,所以梯形的面积=(上底+下底)×高÷2 公式S=(a+b)×h÷2;。
平行四边形面积 的计算公式

一、平行四边形的相关计算。
1.平行四边形的面积公式:底×高(可运用割补法);用“h”表示高,“a”表示底,“S”表示平行四边形面积,则S平行四边形=a×h。
例题:一个平行四边形的底是12米,高是4米,求其面积。
解:S平行四边形=a×h=12×4=48(平方米)。
平行四边形的面积等于两组邻边的积乘以夹角的正弦值;如用“a”“b”表示两组邻边长,a表示两边的夹角,“s”表示平行四边形的面积,则S平行四边形=ab*sina。
2.平行四边形周长:四边之和。
可以二乘(底1+底2);如用“a”表示底1,“b”表示底2,“c平”表示平行四边形周长,则平行四边的周长
c=(a+b)×2。
二、平行四边形的定义。
两组对边分别平行的四边形叫作平行四边形。
平行四边形属于平面图形。
平行四边形属于四边形。
平行四边形属于中心对称图形。
三、平行四边形的性质。
1.平行四边形的两组对边分别相等。
2.平行四边形的两组对角分别相等。
3.平行四边形的邻角互补。
4.平行线间的高距离处处相等。
5.平行四边形的对角线互相平分。
四、特殊的平行四边形。
(矩形、菱形、正方形都是特殊的平行四边形)
1.矩形的定义:有一个角是直角的平行四边形是矩形。
2.菱形的定义:有一组邻边相等的平行四边形是菱形。
3.正方形的定义:一组邻边相等且有一个角是直角的平行四边形是正方形。
平行四边形的性质综合边长与面积关系以及问题应用

平行四边形的性质综合边长与面积关系以及问题应用平行四边形是一种特殊的四边形,具有一些独特的性质和特点。
在本文中,我们将综合边长与面积的关系,深入探讨平行四边形的性质,并应用到一些实际问题中。
一、平行四边形的定义和性质:平行四边形是指具有两对相对平行的边的四边形。
根据这个定义,我们可以得出以下性质:1. 对角线互相平分:平行四边形的两条对角线互相平分。
换句话说,对角线的交点将对角线等分,且将平行四边形分成两个全等的三角形。
2. 对边相等:平行四边形的对边相等。
这意味着平行四边形的相对边长相等。
3. 对角线长度关系:平行四边形的对角线长度相等。
这是因为平行四边形可以看作是由两个全等的三角形组成,对边相等,所以对角线也相等。
二、平行四边形的边长与面积关系:接下来,我们将探讨平行四边形的边长与面积之间的关系。
1. 周长与边长之间的关系:设平行四边形的边长分别为a和b,周长为P。
根据定义可知,平行四边形的对边相等,所以P = 2a + 2b。
2. 面积与边长之间的关系:设平行四边形的底边长为b,高为h,面积为S。
根据面积公式S = 底边长 ×高,可得S = b × h。
3. 通过高和底边求面积:如果已知平行四边形的底边长和高,则可以直接通过面积公式计算出面积,即S = b × h。
这个公式可以方便地用于实际问题的计算。
4. 通过对角线求面积:如果已知平行四边形的对角线长度d1和d2,则可以通过面积公式S = 0.5 × d1 × d2求出面积。
这个公式也常用于实际问题的求解。
三、平行四边形的问题应用:接下来,我们将应用平行四边形的性质和公式解决一些实际问题。
例题1:已知平行四边形的一条边长为5cm,对边的长度为8cm,求该平行四边形的面积。
解:根据平行四边形的性质可知,对边相等,所以底边长为8cm。
由于没有给出高的信息,我们无法直接计算面积。
因此,需要更多的信息来解决这个问题。
四年级上册数学教案-4.5.7平行四边形的不稳定性,底和高的概念∣人教新课标

四年级上册数学教案-4.5.7平行四边形的不稳定性,底和高的概念∣人教新课标一、教学目标1. 让学生了解平行四边形的不稳定性,理解底和高的概念。
2. 培养学生观察、分析、抽象、概括的能力。
3. 培养学生合作交流、动手操作的能力。
二、教学内容1. 平行四边形的不稳定性2. 底和高的概念3. 底和高的测量方法三、教学重点与难点1. 教学重点:平行四边形的不稳定性,底和高的概念。
2. 教学难点:底和高的测量方法。
四、教学过程1. 导入新课通过复习平行四边形的性质,引导学生思考:平行四边形具有哪些特性?当平行四边形的某个角度或边长发生变化时,会对整个平行四边形的形状产生什么影响?2. 探究平行四边形的不稳定性(1)分组讨论:让学生分组讨论平行四边形的不稳定性,引导学生从日常生活实例中寻找例子,如伸缩门、晾衣架等。
(2)展示实例:教师展示一些平行四边形的不稳定性实例,如推拉门、折叠桌等,让学生直观感受平行四边形的不稳定性。
(3)总结特点:引导学生总结平行四边形的不稳定性特点,如易变形、角度变化影响整体形状等。
3. 学习底和高的概念(1)定义:教师给出平行四边形的底和高的定义,让学生理解底和高分别指平行四边形的哪两条边。
(2)举例:教师通过举例,让学生明确底和高的位置关系,如底可以任意选取,高与底垂直。
(3)练习:让学生在平行四边形图中找出底和高,并标明。
4. 学习底和高的测量方法(1)讲解方法:教师讲解底和高的测量方法,如使用直尺、量角器等工具。
(2)演示操作:教师演示底和高的测量方法,让学生观察并模仿。
(3)分组练习:让学生分组进行底和高的测量练习,互相交流、合作。
5. 课堂小结教师引导学生回顾本节课所学内容,总结平行四边形的不稳定性、底和高的概念及测量方法。
6. 课后作业(略)五、教学反思本节课通过实例导入,让学生充分感受平行四边形的不稳定性,从而激发学生的学习兴趣。
在教学过程中,注重引导学生观察、分析、抽象、概括,培养学生的逻辑思维能力。
平行四边形和正方体的体积计算

平行四边形和正方体的体积计算平行四边形是一种具有两对平行边的四边形,而正方体是指所有的边长均相等且面为正方形的立体。
本文将讨论如何计算平行四边形和正方体的体积。
一、平行四边形的体积计算平行四边形的体积计算需要知道其底面面积和高。
下面将分别介绍如何计算平行四边形的底面面积和高,并最终得出体积的计算公式。
1.1 平行四边形的底面面积平行四边形的底面面积等于底边长度乘以高度。
设底边长度为a,高度为h,则平行四边形的底面面积S为:S = a * h1.2 平行四边形的高平行四边形的高可通过测量底边到对边的垂直距离得到。
1.3 平行四边形的体积当得到平行四边形的底面面积和高后,可以通过乘法计算得出其体积。
设底面面积为S,高为h,则平行四边形的体积V为:V = S * h二、正方体的体积计算正方体的体积计算比较简单,只需要知道其边长即可。
2.1 正方体的体积设正方体的边长为a,则正方体的体积V为:V = a * a * a三、实际问题应用举例下面举例说明如何应用以上公式计算平行四边形和正方体的体积。
例1:计算平行四边形的体积已知平行四边形的底边长为6 cm,高度为8 cm。
根据1.1和1.3的公式,可以得到:底面面积S = 6 cm * 8 cm = 48 cm²体积V = 48 cm² * 8 cm = 384 cm³因此,该平行四边形的体积为384 cm³。
例2:计算正方体的体积已知正方体的边长为10 cm。
根据2.1的公式,可以得到:体积V = 10 cm * 10 cm * 10 cm = 1000 cm³因此,该正方体的体积为1000 cm³。
综上所述,计算平行四边形和正方体的体积并不复杂,只需要知道相应的底面面积、高度或边长即可。
在实际应用中,我们可以根据具体的问题情景灵活运用这些计算方法。
通过计算体积,我们可以更好地理解并应用平行四边形和正方体这两种立体形状。
《平行四边形的性质》教案

《平行四边形的性质》教案八年级数学教案:《平行四边形》篇一教学目标1、使学生掌握平行四边形的意义及特征,了解其特性,能够正确画出底所对应的高。
2、通过观察。
动手操作,培养学生抽象概括能力和初步的空间观念。
教学重点掌握平行四边形的意义及特征。
教学难点理解平行四边形与长方形。
正方形的关系。
教学过程一、复习准备。
我们已经学过一些几何图形,观察一下这些图形有什么共同特点?在明确它们是由四条线段围成的基础上概括出:由四条线段围成的图形是四边形。
教师提问:我们学过哪些四边形呢?学生举例。
说说哪些物体表面是平行四边形?教师出示下图,让学生初步感知平行四边形。
二、学习新课。
1、理解平行四边形的意义。
首先出示一组图形。
教师提问:这些图形是什么形?它们有什么特征?(1)看到这个名称你能想到什么?(板书:平行。
四边形)教师提问:你认为什么是四边形?你学过的什么图形是四边形的?(2)动手测量。
指名到黑板上用三角板检验一下,每个图形的对边怎样。
(3)抽象概括。
根据你测量的结果,能说说什么叫平行四边形吗?小组先讨论,再让到黑板上测量的同学说出检验与测量的结果,从而引出平行四边形的确切定义。
(板书:两组对边分别平行的四边形叫做平行四边形。
)教师强调说明:只要四边形每组对边分别平行就能确定它的两组对边相等,因此平行四边形的定义是“两组对边分别平行的四边形”。
(4)反馈:判断下面图形哪些是平行四边形?演示课件“平行四边形”,出示反馈练习2、平行四边形的特征和特性。
(1)教师演示。
教师拿一个长方形木框,用两手捏住长方形的两个对角,向相反方向拉。
引导学生观察两组对边有什么变化?拉成了什么图形?什么没有变?学生明确:两组对边边长没有变,变成了平行四边形,四个直角变成了锐角和钝角。
(2)动手操作。
学生自己动手,把准备好的长方形框拉成平行四边形,并测量两组对边是否还平行。
(3)归纳平行四边形特性。
根据刚才的实验。
测量,引导学生概括出:平行四边形具有不稳定性。
平行四边形练习题
1. 填空
1、一个平行四边形, 底是1.2米, 高是底的1.5倍, 求它的面积.
2、一块平行四边形钢板, 底5米, 高3米, 如果1平方米钢重39千克, 这块钢板重多少千克?
3、下图中的正方形周长为28厘米, 求平行四边形的面积.
4一个平行四边形的底是9.6分米, 高2.5分米, 它的面积是多少平方分米?
5、一块平行四边形木板, 它的底是12分米, 高是8分米, 这块木板的面积是多少平方分米?
6、一块平行四边形的草坪, 已知它的面积是1050平方米, 高是25米, 这块草坪的底边长是多少米?
7、一块平行四边形地, 底23米, 高15米, 如果每平方米栽瓜秧9棵, 共栽多少棵?
8、平行四边形的高是70.2厘米, 是底的2倍, 平行四边形的面积是多少?
9、一个平行四边形, 高3.6分米, 比底短14厘米, 它的面积是多少平方厘米?
10、一个平行四边形的面积是72平方分米, 已知底是9分米, 高是多少?。
平行四边形体积计算公式
平行四边形体积计算公式1.平行四边形为立方体或长方体:在这种情况下,平行四边形的底面为一个矩形,其边长分别为a和b。
平行四边形的高为c。
公式:体积=长×宽×高体积=a×b×c2.平行四边形为斜柱体或斜方体:在这种情况下,平行四边形底面的边长为a和b,高为h。
平行四边形的高为c。
公式:体积=底面积×高- 公式一:底面积= a × b × sin(θ)其中,θ为平行四边形底面两条边之间的夹角。
- 公式二:底面积= 1/2 × a × b × sin(θ)其中,θ为平行四边形的对角线与底面上一条边之间的夹角,a和b是底面上两条边的长度。
以上就是平行四边形体积的计算公式。
为了更好地理解和应用这些公式,下面将通过一些具体的例子进行解析。
例子1:假设有一个平行四边形底面边长为5cm和8cm,高为6cm。
求该平行四边形的体积。
根据公式1,体积= 5cm × 8cm × 6cm = 240cm³。
例子2:假设有一个平行四边形底面边长分别为3cm和4cm,高为5cm。
该平行四边形的底面两条边之间夹角为60°。
求该平行四边形的体积。
根据公式2公式一,底面积= 3cm × 4cm × sin(60°) = 6cm²。
根据公式2体积= 6cm² × 5cm = 30cm³。
例子3:假设有一个平行四边形底面边长分别为6cm和9cm,高为10cm。
该平行四边形的对角线与底面上一条边之间夹角为45°。
求该平行四边形的体积。
根据公式2公式二,底面积= 1/2 × 6cm × 9cm × sin(45°) = 1/2 × 6cm × 9cm × √2/2 = 9√2cm²。
两个底和高分别相等的平行四边形
两个底和高分别相等的平行四边形两个底和高相等的平行四边形是一种特殊的四边形,它具有一些独特的性质和特点。
在本文中,我们将探讨这种平行四边形的定义、特征、性质以及一些相关的应用。
让我们来定义这个特殊的平行四边形。
两个底和高相等的平行四边形是指具有两对平行边和相等的底和高的四边形。
这意味着它的两对对边是平行的,且底和高的长度相等。
根据这个定义,我们可以得出一些平行四边形的性质。
首先,它的对边是平行的,这意味着任意一对相邻边都是平行的。
其次,它的底和高相等,这意味着底边的长度等于与底边垂直的高的长度。
这些性质使得两个底和高相等的平行四边形具有一些特殊的特点和应用。
一个显而易见的特点是,平行四边形的对角线相互平分。
这是因为平行四边形的两个底和高相等,所以它的对角线相等,并且相互平分。
这个特点在解决几何问题时非常有用,可以简化计算过程。
两个底和高相等的平行四边形还有一些其他的性质。
例如,它的内角和为360度。
这是因为平行四边形的对边是平行的,所以它的相邻内角和为180度,而且两个底和高相等,所以它的对角线也相等,因此两对对角角度和也为180度。
由此可见,两个底和高相等的平行四边形的内角和为360度。
除了这些性质之外,两个底和高相等的平行四边形还可以应用于许多实际问题中。
例如,在建筑设计中,我们经常会遇到需要绘制平行四边形的情况。
通过掌握两个底和高相等的平行四边形的性质,我们可以更好地进行设计和布局,确保建筑物的稳定性和美观性。
两个底和高相等的平行四边形还可以用于解决一些几何问题。
例如,我们可以利用平行四边形的对角线相互平分的性质,来证明一些几何定理。
通过运用这些性质,我们可以简化证明过程,使得问题的解决更加简单和高效。
两个底和高相等的平行四边形具有一些独特的性质和特点。
通过掌握这些性质,我们可以更好地理解和应用平行四边形的知识。
无论是在建筑设计还是在几何问题的解决中,这些性质都能为我们提供便利。
因此,我们应该深入学习和研究两个底和高相等的平行四边形,并善于运用它们解决实际问题。
平行四边形梯形平行四边形的面积计算公式
平行四边形梯形平行四边形的面积计算公式设平行四边形的底长为a,高为h,根据这个定义可以得到平行四边形的面积公式为:面积=底长×高但在实际计算时,我们往往更倾向于使用平行四边形的对角线与对角线之间的夹角来计算面积。
设平行四边形的对角线长为d1和d2,夹角为θ,则可以得到另一种计算平行四边形面积的公式:面积 = 对角线1 × 对角线2 × sin(夹角)这是因为我们可以将平行四边形分为两个相等的三角形,而三角形的面积可以使用正弦公式计算。
梯形的面积计算公式:梯形也是一种特殊的四边形,它的两条边是平行的,而另外两条边是不平行的。
梯形的面积计算公式相对较简单,设上底为a,下底为b,高为h,则梯形的面积计算公式为:面积=(上底+下底)×高÷2这是因为我们可以将梯形分为一个大三角形和一个小三角形,而两个三角形的面积之和刚好等于整个梯形的面积。
综合例题为了更好地理解平行四边形和梯形的面积计算公式,我们可以通过一个具体的例题来演示。
例题:计算以下平行四边形和梯形的面积。
1. 平行四边形的底长为8 cm,高为5 cm。
面积 = 底长× 高= 8 cm × 5 cm = 40 cm²2. 平行四边形的对角线1长为10 cm,对角线2长为6 cm,夹角为60°。
解:根据平行四边形的面积计算公式,可以计算得到面积为:面积 = 对角线1 × 对角线2 × sin(夹角) = 10 cm × 6 cm × sin(60°) ≈ 30 cm²3. 梯形的上底长为5 cm,下底长为7 cm,高为4 cm。
解:根据梯形的面积计算公式,可以计算得到面积为:面积 = (上底 + 下底) × 高÷ 2 = (5 cm + 7 cm) × 4 cm ÷ 2 = 24 cm²通过这些例题的计算,我们可以更好地理解平行四边形和梯形的面积计算公式,并灵活应用于实际问题中。
