2020年中考数学一轮专项复习提升卷——变量及函数问题(含答案)
2020届中考数学一轮复习提升练:一次函数(Word版)(有答案)

2020届中考数学一轮复习提升练:一次函数一、单选题1.下列函数①y =﹣2x +1,②y =ax ﹣b ,③y =﹣6x ,④y =x 2+2中,是一次函数的有( ) A .①② B .① C .②③D .①④ 2.已知点(x 1,y 1)和(x 2,y 2)都在函数y =﹣2x +4的图象上.则下列结论正确的是( )A .若y 1<y 2,则x 1<x 2B .若y 1﹣y 2=2,则x 1﹣x 2=﹣1C .可由直线y =2x 向上平移4个单位得到D .与坐标系围成的三角形面积为83.直线2(1)y x =-向下平移3个单位长度得到的直线是( )A .2(3)y x =-B .23y x =-C .25y x =-D .22y x =-4.如图1,将正方形ABCD 置于平面直角坐标系中,其中AD 边在x 轴上,其余各边均与坐标轴平行.直线:3l y x =-沿x 轴的负方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD 的边所截得的线段长为m ,平移的时间为t (秒),m 与t 的函数图象如图2所示,则图2中b 的值为( )A .B .C .D .5.已知函数y=(m ﹣3)x+2,若函数值y 随x 的增大而减小,则m 的值不可能是( )A .0B .1C .2D .56.下列函数: ①y=−x;②y=2x+11;③y=x 2−x+1;④y=1x 中,是一次函数的有 ( ) A .2个 B .3个 C .4个D .0个 7.一次函数y =mx +︱m -1︱的图象过点(0,3),且y 随x 的增大而增大,则m 的值为 ( ) A .4 B .2或-4 C .-2 D .-2或48.已知关于x 的一次函数y=mx+2m-7在-1≤x≤5时的函数值总是正的,则m 的取值范围是 ( ) A .m>7 B .m<1 C .1≤m≤7 D .以上都不对9.若一元二次方程x 2-2x -m =0无实数根,则一次函数y =(m +1)x +m -1的图像不经过第几象限( ) A .第四象限 B .第三象限C .第二象限D .第一象限10.已知一次函数y =kx +b ,k 从2、-3中随机取一个值,b 从1、-1、-2中随机取一个值,则该一次函数的图象经过二、三、四象限的概率为( )A .13B .23C .16D .12二、填空题11.如图,一次函数y =ax +b 的图象经过A (2,0)、B (0,﹣1)两点,则关于x 的不等式ax +b <0的解集是_____.12.若一次函数y =(1﹣2m )x +m 的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x 1<x 2时,y 1<y 2,且与y 轴相交于正半轴,则m 的取值范围是_____.13.已知等腰三角形的腰长为xcm ,顶角平分线与对边的交点到一腰的距离为4cm ,这个等腰三角形的面积为ycm 2,则y 与x 的函数关系式为____________.14.如图,已知一次函数y=kx+b 的图象如图所示,当y≤0时,x 的取值范围是_____.三、解答题15.如图,一次函数的图象交x 轴于点B (6,0),交正比例函数的图象于点A ,且点A 的横坐标为4,S △ABO =12.求一次函数和正比例函数的表达式.16.某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册0.4元.小军经常来该店租书,若每月租书数量为x 册.(1)写出零星租书方式应付金额1y (元)与租书数量x (册)之间的函数关系式.(2)写出会员卡租书方式应付金额2y (元)与租书数量x (册)之间的函数关系式.(3)小军选取哪种租书方式更合算?17.如图1,直线()20=-<y kx k k 与y 轴交于点A ,与x 轴交于点B ,AB =(1)求A B 、两点的坐标;(2)如图2,以AB为边,在第一象限内画出正方形ABCD,并求直线CD的解析式.V 18.如图,矩形OABC中,点A,点C分别在x轴,y轴上,D为边BC上的一动点,现把OCD沿OD对折,C点落在点P处.已知点B的坐标为()2.2,2时,求P点的坐标;(1) 当D点坐标为()(2) 在点D沿CB从点C运动至点B的过程中,设点P经过的路径长度为l,求l的值;=+上的次数为2次,(3) 在点D沿CB从点C运动至点B的过程中,若点P落在同一条直线y kx4请直接写出k的取值范围.参考答案1.B2.B3.C4.A5.D6.A7.A8.A9.D10.A11.x <2.12.0<m <12 13.y=4x14.x≤215.一次函数的解析式为y =﹣2x+12;正比例函数的解析式为y =x 16.见解析.17.(1)()()0,4,2,0A B ;(2)直线CD 的解析式为214=-+y x .18.(1)点 P 的坐标为 ()2,0;(2)43π;(3) k ≤<。
2020年中考数学一轮专项复习提升卷——变量及函数问题(含答案)
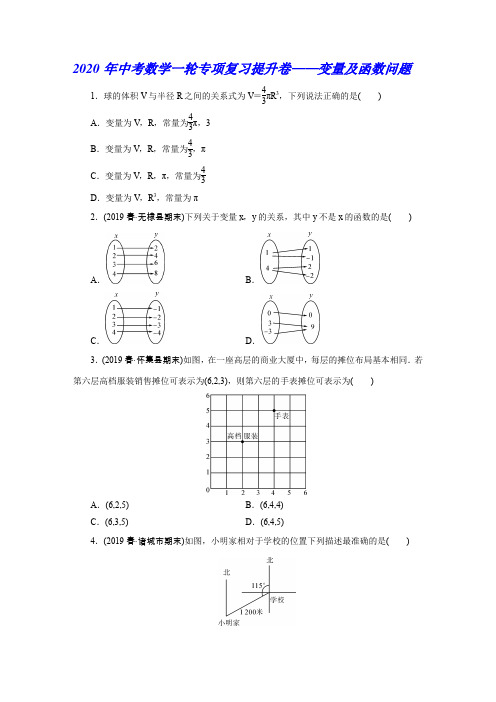
2020年中考数学一轮专项复习提升卷——变量及函数问题1.球的体积V 与半径R 之间的关系式为V =43πR 3,下列说法正确的是( )A .变量为V ,R ,常量为43π,3B .变量为V ,R ,常量为43,πC .变量为V ,R ,π,常量为43D .变量为V ,R 3,常量为π2.(2019春·无棣县期末)下列关于变量x ,y 的关系,其中y 不是x 的函数的是( )A .B .C .D .3.(2019春·怀集县期末)如图,在一座高层的商业大厦中,每层的摊位布局基本相同.若第六层高档服装销售摊位可表示为(6,2,3),则第六层的手表摊位可表示为( )A .(6,2,5)B .(6,4,4)C .(6,3,5)D .(6,4,5)4.(2019春·诸城市期末)如图,小明家相对于学校的位置下列描述最准确的是( )A .距离学校1200米处B .北偏东65°方向上的1200米处C .南偏西65°方向上的1200米处D .南偏西25°方向上的1200米处5.(2019春·庐江县期末)小明家位于公园的正东200 m 处,从小明家出发向北走300 m 就到小华家,若选取小华家为原点,分别以正东、正北方向为x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表1 m 长,则公园的坐标是( )A .(-300,-200)B .(200,300)C .(-200,-300)D .(300,200)6.(2019·内江)在函数y =1x +3+4-x 中,自变量x 的取值范围是( )A .x <4B .x ≥4且x ≠-3C .x >4D .x ≤4且x ≠-37.当实数x 的取值使得x -2有意义时,函数y =4x +1中y 的取值范围是( ) A .y ≥-7 B .y ≥9 C .y >9D .y ≤98.若函数y =⎩⎪⎨⎪⎧x 2+2(x ≤2),2x (x >2),则当函数值y =8时,自变量x 的值是( )A .±6B .4C .±6或4D .4或- 69.(2019·甘肃)已知点P (m +2,2m -4)在x 轴上,则点P 的坐标是( ) A .(4,0) B .(0,4) C .(-4,0)D .(0,-4)10.(2019·滨州)在平面直角坐标系中,将点A (1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B ,则点B 的坐标是( )A .(-1,1)B .(3,1)C .(4,-4)D .(4,0)11.(2019·青岛)如图,将线段AB 先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A ′B ′,则点B 的对应点B ′的坐标是( )A.(-4,1) B.(-1,2)C.(4,-1) D.(1,-2)12.图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则下列函数关系中正确的是()A.y=4n-4 B.y=4nC.y=4n+4 D.y=n213.(2019·齐齐哈尔)“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离s与时间t之间函数关系的是()A.B.C.D.14.(2019·绵阳)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为()A.(2,3) B.(3,2)C.(3,3) D.(3,3)15.(2019·桂林)如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐为(-4,3);(3)在(2)的条件下,直接写出点A1的坐标.16.已知:如图,矩形AOBC ,O 为坐标原点,OB ,OA 分别在x 轴、y 轴上,点A 坐标为(0,3),∠OAB =60°,以AB 为轴对折后,使C 点落在D 点处,求D 点坐标.参考答案1.球的体积V 与半径R 之间的关系式为V =43πR 3,下列说法正确的是( B )A .变量为V ,R ,常量为43π,3B .变量为V ,R ,常量为43,πC .变量为V ,R ,π,常量为43D .变量为V ,R 3,常量为π2.(2019春·无棣县期末)下列关于变量x ,y 的关系,其中y 不是x 的函数的是( B )A .B .C .D .3.(2019春·怀集县期末)如图,在一座高层的商业大厦中,每层的摊位布局基本相同.若第六层高档服装销售摊位可表示为(6,2,3),则第六层的手表摊位可表示为( D )A .(6,2,5)B .(6,4,4)C .(6,3,5)D .(6,4,5)4.(2019春·诸城市期末)如图,小明家相对于学校的位置下列描述最准确的是( C )A .距离学校1200米处B .北偏东65°方向上的1200米处C .南偏西65°方向上的1200米处D .南偏西25°方向上的1200米处5.(2019春·庐江县期末)小明家位于公园的正东200 m 处,从小明家出发向北走300 m 就到小华家,若选取小华家为原点,分别以正东、正北方向为x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表1 m 长,则公园的坐标是( C )A .(-300,-200)B .(200,300)C .(-200,-300)D .(300,200)6.(2019·内江)在函数y =1x +3+4-x 中,自变量x 的取值范围是( D )A .x <4B .x ≥4且x ≠-3C .x >4D .x ≤4且x ≠-37.当实数x 的取值使得x -2有意义时,函数y =4x +1中y 的取值范围是( B ) A .y ≥-7 B .y ≥9 C .y >9D .y ≤98.若函数y =⎩⎪⎨⎪⎧x 2+2(x ≤2),2x (x >2),则当函数值y =8时,自变量x 的值是( D )A .±6B .4C .±6或4D .4或- 69.(2019·甘肃)已知点P (m +2,2m -4)在x 轴上,则点P 的坐标是( A ) A .(4,0) B .(0,4) C .(-4,0)D .(0,-4)10.(2019·滨州)在平面直角坐标系中,将点A (1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B ,则点B 的坐标是( A )A .(-1,1)B .(3,1)C .(4,-4)D .(4,0)11.(2019·青岛)如图,将线段AB 先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A ′B ′,则点B 的对应点B ′的坐标是( D )A .(-4,1)B .(-1,2)C .(4,-1)D .(1,-2)12.图中的圆点是有规律地从里到外逐层排列的.设y 为第n 层(n 为正整数)圆点的个数,则下列函数关系中正确的是( B )A.y=4n-4 B.y=4nC.y=4n+4 D.y=n213.(2019·齐齐哈尔)“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离s与时间t之间函数关系的是(B)A.B.C.D.14.(2019·绵阳)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为(D)A.(2,3) B.(3,2)C.(3,3) D.(3,3)15.(2019·桂林)如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐为(-4,3);(3)在(2)的条件下,直接写出点A1的坐标.【解析】(1)如图,△A1B1C1为所作;(2)如图;(3)点A1的坐标为(2,6).16.已知:如图,矩形AOBC,O为坐标原点,OB,OA分别在x轴、y轴上,点A坐标为(0,3),∠OAB=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.【解析】由题意得OA=3,∠OAB=60°,∴OB=3×tan60°=3 3.∵△ACB≌△ADB,∴AD =AC =OB .过D 作DE ⊥y 轴于点E , ∵∠OAD =30° ∴ED =12AD =332,∵cos30°=OA +EO AD ,∴OE =33×32-3=32, ∴D ⎝⎛⎭⎫332,-32.。
2020年中考数学一轮复习精选题 一次函数与反比例函数(含答案)

第一象限内作正方形 ABCD,顶点 D 在双曲线 y=kx-1 上,将该正方形沿 x 轴负方向平移 a 个单位
长度后,顶点 C 恰好落在双曲线 y=kx-1 上,则 a 的值是(
)
A.3
B.4
C.5
D.6
二、填空题
17.一次函数 y=﹣3x+6 的图象不经过
象限.
18.已知点 A(0,m)和点 B(1,n)都在函数 y=﹣3x+b 的图象上,则 m
6.若函数 y=(2m+6)x2+(1-m)x 是正比例函数,则 m 的值是(
A.m=-3
B.m=1
C.m=3
) D.m>-3
7.已知一次函数 y=-0.5x+2,当 1≤x≤4 时,y 的最大值是(
A.2
B.1.5
C.2.5
D.-6
8.如图,以两条直线l1,l2 的交点坐标为解的方程组是(
). )
2020 年中考数学一轮复习精选题
一次函数与反比例函数
一、选择题
1.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问
题中因变量是( )
A.太阳光强弱
B.水的温度
C.所晒时间
D.热水器
2.一个正方形的边长为 3 cm, 它的各边边长减少x cm后,得到的新正方形的周长为y cm,y与x
A.5
B.7.5
C.10
D.25
12.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步 500 米,先到 终点的人原地休息.已 知甲先出发 2 秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间 的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
2020年数学中考第一轮复习--函数单元测试和答案

2020年数学中考第一轮复习《函数》限时检测卷(时间:60分钟 分值:100分 得分:__________)一、选择题(本大题9小题,每小题3分,共27分) 1.若点P 的坐标为(7,-6),则点P 在( ) A .第一象限 B .第二象限 C .第三象限D .第四象限2.(2019岳阳)函数y =x +2x中,自变量x 的取值范围是( ) A .x ≠0 B .x >-2 C .x >0D .x ≥-2且x ≠03.(2019上海)下列函数中,函数值y 随自变量x 的值的增大而增大的是( ) A .y =x3B .y =-x3C .y =3xD .y =-3x4.(2019赤峰)如图1,点P 是反比例函数y =kx (k ≠0)的图象上任意一点,过点P 作PM⊥x 轴,垂足为M .若△POM 的面积等于2,则k 的值等于( )图1A .-4B .4C .-2D .25.(2019百色)抛物线y =x 2+6x +7可由抛物线y =x 2如何平移得到的( ) A .先向左平移3个单位,再向下平移2个单位 B .先向左平移6个单位,再向上平移7个单位 C .先向上平移2个单位,再向左平移3个单位 D .先向右平移3个单位,再向上平移2个单位6.(2019徐州)若A (x 1,y 1),B (x 2,y 2)都在函数y =2 019x 的图象上,且x 1<0<x 2,则( )A .y 1<y 2B .y 1=y 2C .y 1>y 2D .y 1=-y 27.(2019泸州)如图2,一次函数y 1=ax +b 和反比例函数y 2=kx 的图象相交于A ,B 两点,则使y 1>y 2成立的x 取值范围是( )图2A .-2<x <0或0<x <4B .x <-2或0<x <4C .x <-2或x >4D .-2<x <0或x >48.(2019日照)如图3,是二次函数y =ax 2+bx +c 图象的一部分,下列结论中:①abc >0;②a -b +c <0;③ax 2+bx +c +1=0有两个相等的实数根;④-4a <b <-2a .其中正确结论的序号为( )图3A .①②B .①③C .②③D .①④9.(2019本溪)如图4,点P 是以AB 为直径的半圆上的动点,CA ⊥AB ,PD ⊥AC 于点D ,连接AP .设AP =x ,P A -PD =y ,则下列函数图象能反映y 与x 之间的关系的是( )图4二、填空题(本大题6小题,每小题4分,共24分)10.如果反比例函数y =a -2x(a 是常数)的图象在第一、三象限,那么a 的取值范围是____________.11.(2019白银)将二次函数y =x 2-4x +5化成y =a (x -h )2+k 的形式为____________. 12.已知一次函数y =ax (a ≠0)与反比例函数y =kx (k ≠0)的图象的一个交点的坐标为(2,4),则它们另一个交点的坐标是____________.13.(2019杭州)某函数满足当自变量x =1时,函数值y =0;当自变量x =0时,函数值y =1.写出一个满足条件的函数表达式____________.14.已知二次函数y =x 2-4x +k 的图象的顶点在x 轴下方,则实数k 的取值范围是____________.15.(2019烟台)如图5,直线y =x +2与直线y =ax +c 相交于点P (m,3),则关于x 的不等式x +2≤ax +c 的解为____________.图5三、解答题(本大题4小题,共49分)16.(10分)晨光文具店的某种毛笔每支售价30元,书法纸每本售价10元.为促销,该文具店制定了两种优惠方案:甲方案,买一支毛笔就送一本书法纸;乙方案,按购买的总金额打8折.某校欲为书法小组购买这种毛笔10支,书法纸x (x ≥10)本.(1)求甲方案实际付款金额y 甲(元)与x 的函数关系式和乙方案实际付款金额y 乙(元)与x 的函数关系式;(2)试通过计算为该校提供一种节约费用的购买方案.17.(12分)有这样一个问题:探究函数y =16x 3-2x 的图象与性质.小东根据学习函数的经验,对函数y =16x 3-2x 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:(1)函数y =16x 3-2x 的自变量x 的取值范围是____________;(2)下表是y 与x 的几组对应值:则m 的值为__________;(3)如图6,在平面直角坐标系中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象;图6(4)观察图象,写出该函数的两条性质:____________________________________. 18.(13分)(2019甘肃)如图7,一次函数y =kx +b 的图象与反比例函数y =mx 的图象相交于A (-1,n ),B (2,-1)两点,与y 轴相交于点C .图7(1)求一次函数与反比例函数的解析式;(2)若点D 与点C 关于x 轴对称,求△ABD 的面积;(3)若M (x 1,y 1),N (x 2,y 2)是反比例函数y =mx 图象上的两点,当x 1<x 2<0时,比较y 1与y 2的大小关系.19.(14分)(2019青海)如图8,在直角坐标系中,抛物线经过A (1,0),B (5,0),C (0,4)三点. (1)求抛物线的解析式和对称轴;(2)P 是抛物线对称轴上的一点,求满足P A +PC 的值为最小的点P 的坐标;(3)在第四象限的抛物线上是否存在点E ,使四边形OEBF 是以OB 为对角线且面积为12的平行四边形?若存在,请求出点E 的坐标;若不存在,请说明理由.图8 备用图参考答案1.D 2.D 3.A 4.A 5.A 6.A 7.B 8.D 9.C 10.a >2 11.y =(x -2)2+1 12.(-2,-4) 13.y =-x +1(答案不唯一)14.k <4 15.x ≤116.(1)由题意,得y 甲=30×10+10(x -10)=10x +200(x ≥10); y 乙=(30×10+10x )×0.8=8x +240(x ≥10).即甲、乙两种方案的实际付款金额与x 的关系式分别为 y 甲=10x +200(x ≥10),y 乙=8x +240(x ≥10). (2)①当y 甲=y 乙时,10x +200=8x +240,解得x =20; ②当y 甲>y 乙时,10x +200>8x +240,解得x >20; ③当y 甲<y 乙时,10x +200<8x +240,解得x <20. ∴当购买练字本少于20本时,甲方案比较节约费用; 当购买练字本等于20本时,甲、乙两种方案费用相等; 当购买练字本多于20本时,乙方案比较节约费用.图117.(1)任意实数. (2)-32.(3)函数图象如图1所示.(4)①当x <-2时,y 随x 的增大而增大;②当x >2时,y 随x 的增大而增大.(答案不唯一)18.(1)将B (2,-1)代入y =m x ,得-1=m2.解得m =-2.∴反比例函数的解析式为y =-2x.将A (-1,n )代入y =-2x ,得n =-2-1.解得n =2.∴A (-1,2).把A ,B 两点的坐标代入y =kx +b ,得⎩⎪⎨⎪⎧-k +b =2,2k +b =-1.解得⎩⎪⎨⎪⎧k =-1,b =1.∴一次函数的解析式为y =-x +1.(2)将x =0代入y =-x +1,得y =1.∴C (0,1). ∵点D 、点C 关于x 轴对称,∴D (0,-1).∵B (2,-1),∴BD ∥x 轴.∴BD =2.∴S △ABD =12×2×3=3.(3)∵-2<0,∴当x <0时,y 随x 的增大而增大. ∵x 1<x 2<0,∴y 1<y 2.19.(1)∵抛物线与x 轴交于点A (1,0),B (5,0), ∴可设抛物线的解析式为y =a (x -1)(x -5).将点C (0,4)代入y =a (x -1)(x -5),得5a =4.解得a =45.∴抛物线的解析式为y =45x 2-245x +4.图2∴抛物线的对称轴为x =--2452×45=3.(2)如图2,连接BC 交对称轴于点P ,此时P A +PC 的值最小. 设直线BC 的解析式为y =kx +b .将点B ,C 的坐标代入y =kx +b ,得⎩⎪⎨⎪⎧5k +b =0,b =4.解得⎩⎪⎨⎪⎧k =-45,b =4.∴直线BC 的解析式为y =-45x +4.当x =3时,y =85.∴点P 的坐标为⎝⎛⎭⎫3,85.(3)存在.理由如下:四边形OEBF 是以OB 为对角线且面积为12的平行四边形, 则S 四边形OEBF =2S △OEB =OB ·|y E |=5×|y E |=12. ∴|y E |=125. ∵点E 在第四象限,∴y E =-125.∴45x 2-245x +4=-125.解得x =2或4.∴点E 的坐标为⎝⎛⎭⎫2,-125或⎝⎛⎭⎫4,-125.。
2020年(通用版)中考数学一轮复习:函数 专项训练题(附答案)

2020年(通用版)中考数学一轮复习:函数专项训练题一.选择题(共15小题)1.函数y=中的自变量x的取值范围是()A.x≠B.x≥1 C.x>D.x≥2.下列曲线中不能表示y是x的函数的是()A.B.C.D.3.下列函数中,正比例函数是()A.y=﹣8x B.y=C.y=8x2D.y=8x﹣44.在平面直角坐标系中,点P(﹣2,x2+1)所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限5.如果反比例函数y=(a是常数)的图象在第一、三象限,那么a的取值范围是()A.a<0 B.a>0 C.a<2 D.a>26.如图的坐标平面上有原点O与A、B、C、D四点.若有一直线L通过点(﹣3,4)且与y 轴垂直,则L也会通过下列哪一点?()A.A B.B C.C D.D7.已知A、B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是()A.y=4x(x≥0)B.y=4x﹣3(x≥)C.y=3﹣4x(x≥0)D.y=3﹣4x(0≤x≤)8.已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为()A.3或6 B.1或6 C.1或3 D.4或69.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3 B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3 D.y=2(x+2)2﹣310.若ab<0且a>b,则函数y=ax+b的图象可能是()A.B.C.D.11.已知a,b是非零实数,|a|>|b|,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是()A.B.C.D.12.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC 的面积是()A.B.C.4 D.613.已知反比例函数y=的图象如图所示,则二次函数y=ax2﹣2x和一次函数y=bx+a 在同一平面直角坐标系中的图象可能是()A.B.C.D.14.抛物线y=ax2+bx+c的对称轴是直线x=﹣1,且过点(1,0).顶点位于第二象限,其部分图象如图4所示,给出以下判断:①ab>0且c<0;②4a﹣2b+c>0;③8a+c>0;④c=3a﹣3b;⑤直线y=2x+2与抛物线y=ax2+bx+c两个交点的横坐标分别为x1,x2,则x1+x2+x1x2=5.其中正确的个数有()A.5个B.4个C.3个D.2个15.如图,在单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,1),A3(0,0),则依图中所示规律,A2019的坐标为()A.(﹣1008,0)B.(﹣1006,0)C.(2,﹣504)D.(1,505)二.填空题(共10小题)16.已知一次函数y=kx+b的图象交y轴于负半轴,且y随x的增大而增大,请写出符合上述条件的一个解析式:.17.P(3,﹣4)到x轴的距离是.18.若抛物线y=x2+(m﹣2)x+3的对称轴是y轴,则m=.19.同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的函数关系是y=x+32,如果某一温度的摄氏度数是25℃,那么它的华氏度数是℉.20.如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是.21.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为.22.二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象不经过第象限.23.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是(3,﹣1)和(﹣3,1),那么“卒”的坐标为.24.如图,点P在函数y=的图象上,PA⊥x轴于点A,PB⊥y轴于点B,且△APB的面积为4,则k等于.25.如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形A n B n﹣1B n顶点B n的横坐标为.三.解答题(共12小题)26.如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(﹣1,a).(1)求直线l1的解析式;(2)求四边形PAOC的面积.27.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣,0),(,1),连接AB,以AB为边向上作等边三角形ABC.(1)求点C的坐标;(2)求线段BC所在直线的解析式.28.我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为x元/件(x≥6,且x是按0.5元的倍数上涨),当天销售利润为y元.(1)求y与x的函数关系式(不要求写出自变量的取值范围);(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)若每件文具的利润不超过80%,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.29.超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加x元,每天售出y件.(1)请写出y与x之间的函数表达式;(2)当x为多少时,超市每天销售这种玩具可获利润2250元?(3)设超市每天销售这种玩具可获利w元,当x为多少时w最大,最大值是多少?30.襄阳市某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜.某超市看好甲、乙两种有机蔬菜的市场价值,经调查,这两种蔬菜的进价和售价如下表所示:有机蔬菜种类进价(元/kg)售价(元/kg)甲m16乙n18(1)该超市购进甲种蔬菜10kg和乙种蔬菜5kg需要170元;购进甲种蔬菜6kg和乙种蔬菜10kg需要200元.求m,n的值;(2)该超市决定每天购进甲、乙两种蔬菜共100kg进行销售,其中甲种蔬菜的数量不少于20kg,且不大于70kg.实际销售时,由于多种因素的影响,甲种蔬菜超过60kg的部分,当天需要打5折才能售完,乙种蔬菜能按售价卖完.求超市当天售完这两种蔬菜获得的利润额y(元)与购进甲种蔬菜的数量x(kg)之间的函数关系式,并写出x的取值范围;(3)在(2)的条件下,超市在获得的利润额y(元)取得最大值时,决定售出的甲种蔬菜每千克捐出2a元,乙种蔬菜每千克捐出a元给当地福利院,若要保证捐款后的盈利率不低于20%,求a的最大值.31.如图,直角坐标系xOy中,一次函数y=﹣x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).(1)求m的值及l2的解析式;(2)求S△AOC﹣S△BOC的值;(3)一次函数y=kx+1的图象为l3,且l1,l2,l3不能围成三角形,直接写出k的值.32.长为300m的春游队伍,以v(m/s)的速度向东行进,如图1和图2,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).(1)当v=2时,解答:①求S头与t的函数关系式(不写t的取值范围);②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围)(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.33.如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).(1)求b,m的值;(2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD长为2,求a的值.34.已知抛物线y=﹣x2+bx+c经过点(1,0),(0,).(1)求该抛物线的函数表达式;(2)将抛物线y=﹣x2+bx+c平移,使其顶点恰好落在原点,请写出一种平移的方法及平移后的函数表达式.35.抛物线y=﹣x2+bx+c经过点A(3,0)和点B(0,3),且这个抛物线的对称轴为直线l,顶点为C.(1)求抛物线的解析式;(2)连接AB、AC、BC,求△ABC的面积.36.如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.(1)求二次函数与一次函数的解析式;(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.37.如图,已知点A(0,2),B(2,2),C(﹣1,﹣2),抛物线F:y=x2﹣2mx+m2﹣2与直线x=﹣2交于点P.(1)当抛物线F经过点C时,求它的表达式;(2)设点P的纵坐标为y P,求y P的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤﹣2,比较y1与y2的大小;(3)当抛物线F与线段AB有公共点时,直接写出m的取值范围.参考答案一.选择题(共15小题)1.D.2.C.3.A.4.B.5.D.6.D.7.D.8.B.9.B.10.A.11.D.12.C.13.C.14.D.15.A.二.填空题(共10小题)16.y=x﹣1(答案不唯一,k>0,b<0即可).17.4.18.2.19.77.20.x>2.21.a<c<b.22.一.23.(﹣2,﹣2).24.﹣8.25. 2n+1﹣2.三.解答题(共12小题)26.解:(1)∵点P(﹣1,a)在直线l2:y=2x+4上,∴2×(﹣1)+4=a,即a=2,则P的坐标为(﹣1,2),设直线l1的解析式为:y=kx+b(k≠0),那么,解得:.∴l1的解析式为:y=﹣x+1.(2)∵直线l1与y轴相交于点C,∴C的坐标为(0,1),又∵直线l2与x轴相交于点A,∴A点的坐标为(﹣2,0),则AB=3,而S四边形PAOC=S△PAB﹣S△BOC,∴S四边形PAOC=.27.解:(1)如图,过点B作BH⊥x轴,∵点A坐标为(﹣,0),点B坐标为(,1),∴|AB|==2,∵BH=1,∴sin∠BAH==,∴∠BAH=30°,∵△ABC为等边三角形,∴AB=AC=2,∴∠CAB+∠BAH=90°,∴点C的纵坐标为2,∴点C的坐标为(,2).(2)由(1)知点C的坐标为(,2),点B的坐标为(,1),设直线BC的解析式为:y=kx+b,则,解得,故直线BC的函数解析式为y=x+.28.解:由题意(1)y=(x﹣5)(100﹣×5)=﹣10x2+210x﹣800故y与x的函数关系式为:y=﹣10x2+210x﹣800(2)要使当天利润不低于240元,则y≥240,∴y=﹣10x2+210x﹣800=﹣10(x﹣10.5)2+302.5=240解得,x1=8,x2=13∵﹣10<0,抛物线的开口向下,∴当天销售单价所在的范围为8≤x≤13(3)∵每件文具利润不超过80%∴,得x≤9∴文具的销售单价为6≤x≤9,由(1)得y=﹣10x2+210x﹣800=﹣10(x﹣10.5)2+302.5∵对称轴为x=10.5∴6≤x≤9在对称轴的左侧,且y随着x的增大而增大∴当x=9时,取得最大值,此时y=﹣10(9﹣10.5)2+302.5=280即每件文具售价为9元时,最大利润为280元29.解:(1)根据题意得,y=﹣x+50;(2)根据题意得,(40+x)(﹣x+50)=2250,解得:x1=50,x2=10,∵每件利润不能超过60元,∴x=10,答:当x为10时,超市每天销售这种玩具可获利润2250元;(3)根据题意得,w=(40+x)(﹣x+50)=﹣x2+30x+2000=﹣(x﹣30)2+2450,∵a=﹣<0,∴当x<30时,w随x的增大而增大,∵40+x≤60,x≤2∴当x=20时,w最大=2400,答:当x为20时w最大,最大值是2400元.30.解:(1)由题意可得,,解得,,答:m的值是10,n的值是14;(2)当20≤x≤60时,y=(16﹣10)x+(18﹣14)(100﹣x)=2x+400,当60<x≤70时,y=(16﹣10)×60+(16×0.5﹣10)×(x﹣60)+(18﹣14)(100﹣x)=﹣6x+880,由上可得,y=;(3)当20≤x≤60时,y=2x+400,则当x=60时,y取得最大值,此时y=520,当60<x≤70时,y=﹣6x+880,则y<﹣6×60+880=520,由上可得,当x=60时,y取得最大值,此时y=520,∵在(2)的条件下,超市在获得的利润额y(元)取得最大值时,决定售出的甲种蔬菜每千克捐出2a元,乙种蔬菜每千克捐出a元给当地福利院,且要保证捐款后的盈利率不低于20%,∴,解得,a≤1.8,即a的最大值是1.8.31.解:(1)把C(m,4)代入一次函数y=﹣x+5,可得4=﹣m+5,解得m=2,∴C(2,4),设l2的解析式为y=ax,则4=2a,解得a=2,∴l2的解析式为y=2x;(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,y=﹣x+5,令x=0,则y=5;令y=0,则x=10,∴A(10,0),B(0,5),∴AO=10,BO=5,∴S△AOC﹣S△BOC=×10×4﹣×5×2=20﹣5=15;(3)一次函数y=kx+1的图象为l3,且l1,l2,l3不能围成三角形,∴当l3经过点C(2,4)时,k=;当l2,l3平行时,k=2;当l1,l3平行时,k=﹣;故k的值为或2或﹣.32.解:(1)①排尾从位置O开始行进的时间为t(s),则排头也离开原排头t(s),∴S头=2t+300②甲从排尾赶到排头的时间为300÷(2v﹣v)=300÷v=300÷2=150 s,此时S头=2t+300=600 m甲返回时间为:(t﹣150)s∴S甲=S头﹣S甲回=2×150+300﹣4(t﹣150)=﹣4t+1200;因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,求S的值为600m,在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=﹣4t+1200.(2)T=t追及+t返回=+=,在甲这次往返队伍的过程中队伍行进的路程为:v×=400;因此T与v的函数关系式为:T=,此时队伍在此过程中行进的路程为400m.33.解:(1)∵点P(1,b)在直线l1:y=2x+1上,∴b=2×1+1=3;∵点P(1,3)在直线l2:y=mx+4上,∴3=m+4,∴m=﹣1.(2)当x=a时,y C=2a+1;当x=a时,y D=4﹣a.∵CD=2,∴|2a+1﹣(4﹣a)|=2,解得:a=或a=.∴a的值为或.34.解:(1)把(1,0),(0,)代入抛物线解析式得:,解得:,则抛物线解析式为y=﹣x2﹣x+;(2)抛物线解析式为y=﹣x2﹣x+=﹣(x+1)2+2,将抛物线向右平移一个单位,向下平移2个单位,解析式变为y=﹣x2.35.解:(1)∵抛物线经过A、B(0,3)∴由上两式解得∴抛物线的解析式为:;(2)由(1)抛物线对称轴为直线x=把x=代入,得y=4则点C坐标为(,4)设线段AB所在直线为:y=kx+b,则有,解得∴AB解析式为:∵线段AB所在直线经过点A、B(0,3)抛物线的对称轴l于直线AB交于点D∴设点D的坐标为D将点D代入,解得m=2∴点D坐标为,∴CD=CE﹣DE=2过点B作BF⊥l于点F∴BF=OE=∵BF+AE=OE+AE=OA=∴S△ABC=S△BCD+S△ACD=CD•BF+CD•AE∴S△ABC=CD(BF+AE)=×2×=36.解:(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0),∴0=1+m,∴m=﹣1,∴抛物线解析式为y=(x+2)2﹣1=x2+4x+3,∴点C坐标(0,3),∵对称轴x=﹣2,B、C关于对称轴对称,∴点B坐标(﹣4,3),∵y=kx+b经过点A、B,∴,解得,∴一次函数解析式为y=﹣x﹣1,(2)由图象可知,写出满足(x+2)2+m≥kx+b的x的取值范围为x≤﹣4或x≥﹣1.37.解:(1)∵抛物线F经过点C(﹣1,﹣2),∴﹣2=(﹣1)2﹣2×m×(﹣1)+m2﹣2,解得,m=﹣1,∴抛物线F的表达式是:y=x2+2x﹣1;(2)当x=﹣2时,y p=4+4m+m2﹣2=(m+2)2﹣2,∴当m=﹣2时,y p取得最小值,最小值是﹣2,此时抛物线F的表达式是:y=x2+4x+2=(x+2)2﹣2,∴当x≤﹣2时,y随x的增大而减小,∵x1<x2≤﹣2,∴y1>y2;(3)m的取值范围是﹣2≤m≤0或2≤m≤4,理由:∵抛物线F与线段AB有公共点,点A(0,2),B(2,2),∴或或,解得,﹣2≤m≤0或2≤m≤4.。
中考数学一轮复习 专题三:变量与函数(2)一次函数(有答案)

中考数学一轮复习 专题三变量与函数(2)一次函数一、单选题1.若正比例函数2y x =-的图象经过点(1,4)a -,则a 的值为( )A.-1B.0C.1D.22.在平面直角坐标系中,一次函数y kx b =+的图象如图所示,则k 和b 的取值范围是( )A.00k b >>,B.00k b ><,C.00k b <>,D.00k b <<,3.如图,平面直角坐标系xOy 中,点A 的坐标为()9,6,AB y ⊥轴,垂足为B ,点P 从原点O 出发向x 轴正方向运动,同时,点Q 从点A 出发向点B 运动,当点Q 到达点B 时,点,P Q 同时停止运动,若点P 与点Q 的速度之比为1:2,则下列说法正确的是( )A.线段PQ 始终经过点()2,3B.线段PQ 始终经过点()3,2C.线段PQ 始终经过点()2,2D.线段PQ 不可能始终经过某一定点4.已知直线y kx b =+,若5k b +=-,6kb =,那么该直线不经过( )A.第一象限B.第二象限C.第三象限D.第四象限5.如图,在矩形AOBC 中,(2,0)A -,(0,1)B .若正比例函数 y kx =的图象经过点C ,则k 的值为( )A.2-B.12-C.2D.126.一条公路旁依次有,,A B C 三个村庄,甲、乙两人骑自行车分别从A 村、B 村同时出发前往C 村,甲、乙之间的距离s (km )与骑行时间t (h )之间的函数关系如图所示,下列结论:①,A B 两村相距10 km ;②出发1.25 h 后两人相遇;③甲每小时比乙多骑行8 km ;④相遇后,乙又骑行了15 min 或65 min 时两人相距2 km.其中正确的个数是( )A.1B.2C.3D.47.如图,一条直线与两坐标轴的正半轴分别交于,A B 两点,P 是线段AB 上任意一点(不包括端点),过点P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是( )A.4y x =-+B.4y x =+C.8y x =+D.8y x =-+8.某通讯公司就上宽带网推出,,A B C 三种月收费方式.这三种收费方式每月所需的费用y (元)与上网时间x (h )的函数关系如图所示,则下列判断错误的是( )A.每月上网时间不足25 h 时,选择A 方式最省钱B.每月上网费用为60元时,B 方式可上网的时间比A 方式多C.每月上网时间为35 h 时,选择B 方式最省钱D.每月上网时间超过70 h 时,选择C 方式最省钱9.如图,经过点()1,0B -的直线y kx b =+与直线22y x =-+相交于点8,3A m ⎛⎫ ⎪⎝⎭,则不等式22x kx b -+<+的解集为( )A.13x <-B.1x >C.1x <D.13x >- 10.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,设行驶的时间为x (小时),两车之间的距离为y (千米),图中的折线表示从两车出发至快车到达乙地过程中y 与x 之间的函数关系,已知两车相遇时快车比慢车多行驶40千米,快车到达乙地时,慢车还有多少千米到达甲地( )A.70B.80C.90D.100二、填空题11.如果一次函数(3)2y m x m =-+-的图象经过第三、四象限,那么m 的取值范围为______.12.已知点A 是直线1y x =+上一点,其横坐标为12-,若点B 与点A 关于y 轴对称,则点B 的坐标为___________.13.在平面直角坐标系内,一次函数11=y k x b +与22y k x b =+的图象如图所示,则关于,x y 的方程组1122y k x b y k x b -=⎧⎨-=⎩,的解是_________.14.如图,平面直角坐标系中,经过点(4,0)B -的直线y kx b =+与直线2y mx =+相交于点3,12A ⎛⎫-- ⎪⎝⎭,则连续不等式20mx kx b +<+<的解集为_________.三、解答题15.为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用y (元)与种植面积x (2m )之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.(1)直接写出当0300x ≤≤和300x >时,y 与x 的函数关系式;(2)广场上甲、乙两种花卉的种植面积共21200m ,若甲种花卉的种植面积不少于2200m ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元? 参考答案1.答案:A把点(1,4)a -代入2y x =-,得()214a --=,解得1a =-,故选A.2.答案:C由图象得,y 随x 的增大而减小,所以0k <.因为直线与y 轴交于正半轴,所以0b >.3.答案:B当OP t =时,点P 的坐标为(,0)t ,点Q 的坐标为(926)t -,.设直线PQ 的解析式为()0y kx b k =+≠,将(,0)P t ,(926)Q t -,代入y kx b =+,得0(92)6kt b t k b +=⎧⎨-+=⎩,解得2323k t t b t ⎧=⎪⎪-⎨⎪=⎪-⎩, ∴直线PQ 的解析式为2233t y x t t =+--. 当3x =时,2y =,∴直线PQ 始终经过点()3,2.故选B.4.答案:A5k b +=-,6kb =,0k ∴<,0b <,∴直线y kx b =+经过第二、三、四象限,不经过第一象限.故选A.5.答案:B(2,0)A -,(0,1)B ,21OA OB ∴==,.四边形AOBC 是矩形,1AC OB ∴==,2BC OA ==,则点C 的坐标为(2,1)-.将点(2,1)C -代入y kx =,得12k =-, 解得12k =-,故选B. 6.答案:D由图象可知A 村、B 村相距10 km ,故①正确.当出发1.25 h 时,甲、乙两人相距0 km ,故在此时相遇,故②正确.10 1.258÷=(km/h ),故甲每小时比乙多骑行8 km ,故③正确.当1.252t 时,函数图象经过点(1.25,0),(2,6),设一次函数的解析式为s mt n =+.0 1.2562m n m n =+⎧⎨=+∴⎩,解得810m n =⎧⎨=-⎩.810s t ∴=-. 当2s =时,2810t =-, 1.5t ∴=.1.5 1.250.25-=(h ),0.25h 15min =.当2 2.5t 时,设一次函数解析式为s kt b =+.将点(2,6),(2.5,0)代入得620 2.5k b k b =+⎧⎨=+⎩,解1230k b =-⎧⎨=⎩, 1230s t ∴=-+.当2s =时,21230t =-+,73t ∴=. 7131.25312-=(h ),13h 65min 12=. ∴相遇后,乙又骑行了15 min 或65 min 时两人相距2 km ,④正确.故选D.7.答案:A如图,设过点P 的两垂线分别与x 轴,y 轴的交点为,D C .设点P 的坐标为(),x y .点P 在第一象限,,PD y PC x ∴==.矩形PDOC 的周长为8,()28x y ∴+=,4x y ∴+=.∴该直线的函数表达式是4y x =-+.故选A.8.答案:D观察函数图象,可知每月上网时间不足25 h 时,选择A 方式最省钱,结论A 正确;当每月上网费用50≥元时,B 方式可上网的时间比A 方式多,结论B 正确;当25x ≥时,设A y kx b =+,将()25,30,()5,120代入A y kx b =+,得253055120k b k b +=⎧⎨+=⎩,解得345k b =⎧⎨=-⎩,()34525y x x ∴=-≥,当35x =时,3456050A y x =-=>,∴每月上网时间为35 h 时,选择B 方式最省钱,结论C 正确;当50x ≥时,设B y mx n =+,将(50,50),(55,65)代入B y mx n =+,得50505565m n m n +=⎧⎨+=⎩,解得3100m n =⎧⎨=-⎩,3100(50)B y x x ∴=-≥,当70x =时,3100110120B y x =-=<,∴结论D 错误.故选D.9.答案:D 把8,3m ⎛⎫ ⎪⎝⎭代入22y x =-+,得8223m -+=,解得13m =-,所以18,33A ⎛⎫- ⎪⎝⎭.观察图象可得,当13x >-时,22x kx b -+<+.故选D.10.答案:A设线段AB 的解析式为(0,02)y kx b k x =+≠,把()1.5,70与(2,0)代入得 1.57020k b k b +=⎧⎨+=⎩,解得140280k b =-⎧⎨=⎩, ∴线段AB 的解析式为()14028002y x x =-+.在140280y x =-+中,令0x =,得280y =,故甲、乙两地相距280千米.设两车相遇时,慢车行驶了a 千米,则快车行驶了()40a +千米,根据题意得40280a a ++=,解得120a =,故两车相遇时,慢车行驶了120千米,快车行驶了160千米,∴快车的速度为80千米/时,慢车的速度为60千米/时,根据题意得()28016080 1.5-÷=(小时),1.56090⨯=(千米),2801209070--=(千米), 则快车到达乙地时,慢车还有70千米到达甲地,故选A.11.答案:2m <一次函数(3)2y m x m =-+-的图象经过第三、四象限,∴图象一定与y 轴的负半轴有交点,202m m ∴-<∴<,.故答案为2m <.12.答案:11,22⎛⎫ ⎪⎝⎭将12x =-代入1y x =+得12y =,即1122A ⎛⎫- ⎪⎝⎭,.点,A B 关于y 轴对称,11,22B ⎛⎫∴ ⎪⎝⎭. 13.答案:21x y =⎧⎨=⎩ 由题图知一次函数11y k x b =+与22y k x b =+的图象的交点坐标为(2,1),∴关于,x y 的方程组1122y k x b y k x b -=⎧⎨-=⎩,的解是21x y =⎧⎨=⎩. 14.答案:342x -<<- 从图象上看,符合20mx kx b +<+<的x 大于点B 的横坐标且小于点A 的横坐标,所以所求连续不等式的解集是342x -<<-. 15.答案:(1)当0300x ≤≤时,设1y k x =,把点()300,39000代入得139000300k =,解得1130k =.130y x ∴=.当300x >时,设2y k x b =+,把点()300,39000,()500,55000代入得223003900050055000k b k b +=⎧⎨+=⎩,解得28015000k b =⎧⎨=⎩, 8015000y x ∴=+.130(0300)8015000(300)x x y x x ≤≤⎧∴=⎨+>⎩.(2)设甲种花卉种植3m a ,种植总费用为W 元,则乙种花卉种植2(1200)m a -,根据题意,得2002(1200)a a a ≥⎧⎨≤-⎩,解得200800a ≤≤. 当200300a ≤≤时,130100(1200)30120000W a a a =+-=+.当200a =时,126000W =最小值.当300800a <≤时, 8015000100(1200)13500020W a a a =++-=-.当800a =时,119000W =最小值.119000126000<.∴当800a =时,总费用最低,最低为19000元.此时乙种花卉种植面积为()21200800400m -=. ∴应分配甲种花卉种植面积为2800m ,乙种花卉种植面积为2400m ,才能使种植总费用最少,最少总费用为119000元.。
2020中考数学一轮专项复习《一次函数、反比例函数》能力提升卷及详细解答
2020中考数学一轮专项《一次函数、反比例函数》能力提升卷及详细解答一、选择题1.下列函数中,正比例函数是()A. y=﹣8xB. y=C. y=8x2D. y=8x﹣42.直线y=3x+1向下平移2个单位,所得直线的解析式是()A. y=3x+3B. y=3x﹣2C. y=3x+2D. y=3x﹣13.已知点是直线与双曲线(为常数)一支的交点,过点作轴的垂线,垂足为,且,则的值为()A. B. C. D.4.如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为()A. B. C. 2 D. 45.如图,点A在反比例函数y= (x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为()A. 3B. 2C.D. 16.已知ab<0,一次函数y=ax﹣b与反比例函数y=在同一直角坐标系中的图象可能()A. B. C. D.7.若、都在函数的图象上,且,则()A. B. C. D.8.如图所示,直线l1:y x+6与直线l2:y x﹣2交于点P(﹣2,3),不等式x+6 x﹣2的解集是()A. x>﹣2B. x≥﹣2C. x<﹣2D. x≤﹣29.在平面直角坐标系中,将函数的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为()A. (2,0)B. (-2,0)C. (6,0)D. (-6,0)10.如图,一次函数和反比例函数的图象相交于,两点,则使成立的取值范围是( )A. 或B. 或C. 或D. 或11.如图,正比例函数与反比例函数的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连接BC,则的面积等于()A. 8B. 6C. 4D. 212.对于反比例函数,下列说法不正确的是A. 图象分布在第二、四象限B. 当时,随的增大而增大C. 图象经过点(1,-2)D. 若点,都在图象上,且,则13.如图,直线与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是()A. (,3)B. (,)C. (2,)D. (,4)14.如图,平行于x轴的直线与函数(k1>0,x>0),y=(k2>0,x>0)的图像分别交于A,B 两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为()A. 8B. -8C. 4D. -415.如图,是函数上两点,为一动点,作轴,轴,下列说法正确的是( )① ;② ;③若,则平分;④若,则A. ①③B. ②③C. ②④D. ③④二、填空题16.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≤mx+n的解集为________.17.如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A坐标为(-4,0),点D的坐标为(-1,4),反比例函数的图象恰好经过点C,则k的值为________.18.如图,菱形ABCD顶点A在例函数y= (x>0)的图象上,函数y= (k>3,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=2,∠DAB=30°,则k的值为________.19.如图,矩形ABOC的顶点B、C分别在x轴,y轴上,顶点A在第二象限,点B的坐标为(-2,0).将线段OC绕点D逆时针旋转60°至线段OD,若反比例函数y= (k≠0)的图象经过A、D两点,则k值为________.20.如图,函数(k为常数,k>0)的图象与过原点的O的直线相交于A,B两点,点M是第一象限内双曲线上的动点(点M在点A的左侧),直线AM分别交x轴,y轴于C,D两点,连接BM分别交x轴,y轴于点E,F.现有以下四个结论:①△ODM与△OCA的面积相等;②若BM⊥AM于点M,则∠MBA=30°;③若M点的横坐标为1,△OAM为等边三角形,则;④若,则MD=2MA.其中正确的结论的序号是________.21.如图,在平面直角坐标系中,反比例y=(k>0)的图象和△ABC都在第一象限内,AB=AC=,BC∥x轴,且BC=4,点A的坐标为(3,5).若将△ABC向下平移m个单位长度,A,C两点同时落在反比例函数图象上,则m的值为________.22.如图,直线y=4﹣x与双曲线y交于A,B两点,过B作直线BC⊥y轴,垂足为C,则以OA 为直径的圆与直线BC的交点坐标是________.23.如图,和都是等腰直角三角形,,反比例函数在第一象限的图象经过点B,若,则的值为________.24.如图,反比例函数与一次函数在第三象限交于点.点的坐标为(一3,0),点是轴左侧的一点.若以为顶点的四边形为平行四边形.则点的坐标为________.25.如图,正比例函数y=kx与反比例函数y= 的图象有一个交点A(2,m),AB⊥x轴于点B,平移直线y=kx使其经过点B,得到直线l,则直线l对应的函数表达式是________ .三、解答题26.如图,已知反比例函数的图象与一次函数的图象在第一象限交于两点(1)求反比例函数和一次函数的表达式;(2)已知点,过点作平行于轴的直线,在第一象限内交一次函数的图象于点,交反比例函数上的图象于点.若,结合函数图象直接写出的取值范围.27.某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:方案一:从包装盒加工厂直接购买,购买所需的费y1与包装盒数x满足如图1所示的函数关系.方案二:租赁机器自己加工,所需费用y2(包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:(1)方案一中每个包装盒的价格是多少元?(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?(3)请分别求出y1、y2与x的函数关系式.(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由.28.如图,直线y=x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB 交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.(1)求直线AC的解析式;(2)直线l在平移过程中,请直接写出△BOF为等腰三角形时点F的坐标;(3)直线l在平移过程中,设点E到直线l的距离为d,求d与t的函数关系.29.如图,在平面直角坐标系中,O是坐标原点,平行四边形的顶点C的坐标为(8,8),顶点A的坐标为(﹣6,0),边AB在x轴上,点E为线段AD的中点,点F在线段DC上,且横坐标为3,直线EF与y轴交于点G,有一动点P以每秒1个单位长度的速度,从点A沿折线A﹣B﹣C﹣F运动,当点P到达点F时停止运动,设点P运动时间为t秒.(1)求直线EF的表达式及点G的坐标;(2)点P在运动的过程中,设△EFP的面积为S(P不与F重合),试求S与t的函数关系式;(3)在运动的过程中,是否存在点P,使得△PGF为直角三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.30.如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比例函数y=的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.(1)求一次函数y=k1x+b与反比例函数y=的解析式;(2)求△COD的面积;(3)直接写出当x取什么值时,k1x+b<.31.如图,在平面直角坐标系中,直线AB与y轴交于点,与反比例函数在第二象限内的图象相交于点.(1)求直线AB的解析式;(2)将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E,与y轴交于点D,求的面积;(3)设直线CD的解析式为,根据图象直接写出不等式的解集.32.如图所示,在平面直角坐标系中,等腰的边与反比例函数的图象相交于点,其中,点在轴的正半轴上,点的坐标为,过点作轴于点.(1)已知一次函数的图象过点,求该一次函数的表达式;(2)若点是线段上的一点,满足,过点作轴于点,连结,记的面积为,设,.①用表示(不需要写出的取值范围);②当取最小值时,求的值.33.某工厂甲、乙两车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙车间各自加工零件总数为y(件),与甲车间加工时间x(天),y与x之间的关系如图(1)所示.由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(件)与甲车间加工时间x(天)的关系如图(2)所示.(1)甲车间每天加工零件为________件,图中d值为________.(2)求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式.(3)甲车间加工多长时间时,两车间加工零件总数为1000件?34.如图1,已知矩形AOCB,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动.(1)点P到达终点O的运动时间是________s,此时点Q的运动距离是________cm;(2)当运动时间为2s时,P、Q两点的距离为________cm;(3)请你计算出发多久时,点P和点Q之间的距离是10cm;(4)如图2,以点O为坐标原点,OC所在直线为x轴,OA所在直线为y轴,1cm长为单位长度建立平面直角坐标系,连结AC,与PQ相交于点D,若双曲线y= 过点D,问k的值是否会变化?若会变化,说明理由;若不会变化,请求出k的值.35.如图,在平面直角坐标系xOy中,函数y= (m为常数,m>1,x>0)的图象经过点P(m,1)和Q (1,m),直线PQ与x轴,y轴分别交于C,D两点,点M(x,y)是该函数图象上的一个动点,过点M 分别作x轴和y轴的垂线,垂足分别为A,B.(1)求∠OCD的度数;(2)当m=3,1<x<3时,存在点M使得△OPM∽△OCP,求此时点M的坐标;(3)当m=5时,矩形OAMB与△OPQ的重叠部分的面积能否等于4.1?请说明你的理由.答案一、选择题1.解:A、y=﹣8x,是正比例函数,符合题意;B、y=,是反比例函数,不合题意;C、y=8x2,是二次函数,不合题意;D、y=8x﹣4,是一次函数,不合题意。
2020年中考数学专题复习训练第三章:变量和函数_3.2:一次函数(解析)
第三章:变量与函数 3.2:一次函数(解析)一:考点考点一:一次函数(正比例函数)的图象与性质一次函数的定义:一般地,如果y =kx +b (k ≠0,k 、b 是常数),那么y 叫做x 的一次函数。
当b =0时,一次函数y =kx 也叫做正比例函数。
一次函数的图象与性质注意:k 、b 符号的确定方法✧ 一次函数图象从左向右看呈上升趋势,k >0;呈下降趋势,k <0;✧ 一次函数图象与y 轴的交点在y 轴的正半轴上,b >0;在y 轴的负半轴上,b <0;在原点,b =0. 直线与坐标轴的交点:直线y =kx +b (k ≠0)与x 轴的交点为(kb,0),与y 轴的交点为 (0,b) 。
用待定系数法求函数解析式:步骤可归纳为“一设二列三解四还原”。
✧ 一设:设出一次函数解析式的一般式y =kx +b (k ≠0);✧ 二列:根据已知两点的坐标或已知的两个条件列出关于k 、b 的二元一次方程组; ✧ 三解:解这个方程组,求出k 、b 的值;✧ 四还原:将求得的k 、b 的值再代入y =kx +b (k ≠0)中,求得一次函数解析式。
一次函数图象的平移:✧ 一次函数y =kx +b 的图象可以看作是直线y =kx 向上(下)平移b 个单位长度得到的。
当b >0时,将直线y =kx 向上平移b 个单位长度;当b <0时,将直线y =kx 向下平移b 个单位长度。
✧ 当21k k =,21b b ≠时,直线11b x k y +=与直线22b x k y +=平行。
1. 在平面直角坐标系中,一次函数b kx y +=的图象如图所示,则k 和b 的取值范围是( C )A. k >0,b >0B. k >0,b <0C. k <0,b >0D. k <0,b <02. 一次函数y =kx -1的图象经过点P ,且y 的值随x 值的增大而增大,则点P 的坐标可以为( C )A. (﹣5,3)B. (1,﹣3)C. (2,2)D. (5,﹣1)3. 如图,在矩形AOBC 中,A(﹣2,0)、B(0,1)。
2020年中考数学一轮复习基础考点及题型专题 一次函数(解析版)
专题一次函数考点总结【思维导图】【知识要点】知识点一变量与函数变量:在一个变化过程中数值发生变化的量。
常量:在一个变化过程中数值始终不变的量。
【注意】1、变量是可以变化的,而常量是已知数,且它是不会发生变化的。
2、区分常量和变量就是在某个变化过程中该量的值是否发生变化。
函数的定义:一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x称为自变量,把y称为因变量,y是x的函数。
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
【函数概念的解读】1、有两个变量。
2、一个变量的数值随另一个变量的数值变化而变化。
3、对于自变量每一个确定的值,函数有且只有一个值与之对应。
函数定义域:一般的,一个函数的自变量x允许取值的范围,叫做这个函数的定义域。
确定函数定义域的方法:(自变量取值范围)(1)关系式为整式时,函数定义域为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零;(4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
函数值概念:如果在自变量取值范围内给定一个值a,函数对应的值为b,那么b叫做当自变量取值为a 时的函数值。
函数解析式:用来表示函数关系的数学式子叫做函数解析式或函数关系式。
函数的取值范围:使函数有意义的自变量的取值的全体,叫做自变量的取值范围。
画函数图像的一般步骤:1、列表2、描点3、连线函数图像上点的坐标与解析式之间的关系:1、将点的坐标代入到解析式中,如解析式两边成立,则点在解析式上,反之,不在。
2、两个函数图形交点的坐标就是这两个解析式所组成的方程组的解。
函数的三种表示法及其优缺点1、解析法:两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做解析法。
优:准确反映整个变化过程中自变量与函数的关系。
中考数学一轮复习 专题三:变量与函数(4)二次函数(有答案)
中考数学一轮复习 专题三 变量与函数(4)二次函数一、单选题1.二次函数2(1)3y x =-+图象的顶点坐标是( )A.()1,3B.()13-,C.()1,3-D.()13--, 2.已知点()()121,,2,A y B y 在抛物线2(1)2y x =-++上,则下列结论正确的是( ) A.122y y >>B.212y y >>C.122y y >>D.212y y >>3.若抛物线26y x x m =-+与x 轴没有交点,则m 的取值范围是( ) A.9m >B.9m ≥C.9m <-D.9m ≤-4.已知二次函数2114y x x m =-+-的图象与x 轴有交点,则m 的取值范围是( )A.5m ≤B.2m ≥C.5m <D.2m >5.在平面直角坐标系内,已知点(1,0)A -,点(1,1)B 都在直线1122y x =+上,若抛物线21(0)y ax x a =-+≠与线段AB 有两个不同的交点,则a 的取值范围是( )A.2a ≤-B.98a <C.918a ≤<或2a ≤- D.928a -≤< 6.当1a x a ≤≤+时,函数221y x x =-+的最小值为1,则a 的值为( ) A.-1B.2C.0或2D.-1或27.已知抛物线243y x x =-+与x 轴相交于点,A B (点A 在点B 左侧),顶点为M .平移该抛物线,使点M 平移后的对应点M'落在x 轴上,点B 平移后的对应点B'落在y 轴上.则平移后的抛物线解析式为( )A.221y x x =++B.221y x x =+-C.221y x x =-+D.221y x x =--8.已知反比例函数aby x=的图象如图所示,则二次函数22y ax x =-和一次函数y bx a =+在同一平面直角坐标系中的图象可能是( )A. B.C. D.9.如图,二次函数2(0)y ax bx c a =++≠的图象的顶点在第一象限,且过点(0,1)和(1,0)-.下列结论:①0ab <, ②24b a >, ③02a b c <++<, ④01b <<,⑤当1x >-时,0y >, 其中正确结论的个数是( )A.5B.4C.3D.210.对于一个函数,自变量x 取a 时,函数值y 也等于a ,我们称a 为这个函数的不动点.如果二次函数22y x x c =++有两个相异的不动点12x x ,,且121x x <<,则c 的取值范围是( )A.3c <-B.2c <-C.14c <D.1c <二、填空题11.若点(1,7),(5,7),(2,3),(,3)A B C D k ----在同一条抛物线上,则k 的值等于______. 12.当03x ≤≤时,直线y a =与抛物线2(1)3y x =--有交点,则a 的取值范围是_______________.13.二次函数2y ax bx c =++的图象如图所示,若42,M a b N a b =+=-,则,M N 的大小关系为M ______________N .(填“>”“=”或“<”)14.如图,在平面直角坐标系中,抛物线221y x x =--交y 轴于点A ,过点A 作//AB x 轴交抛物线于点B ,点P 在抛物线上,连接,PA PB ,若点P 关于x 轴的对称点恰好落在直线AB 上,则ABP △的面积是__________.三、解答题15.如图,对称轴为直线1x =-的抛物线2y x bx c =++与x 轴相交于,A B 两点,其中A 点的坐标为(3,0)-,C 为抛物线与y 轴的交点.(1)求抛物线的解析式;(2)若点P 在抛物线上,且2POC BOC S S =△△,求点P 的坐标.参考答案1.答案:A根据二次函数2()y a x m n =-+图象的顶点坐标是(),m n ,得二次函数2(1)3y x =-+图象的顶点坐标是()1,3.故选A.2.答案:A由2(1)2y x =-++知,抛物线开口向下,对称轴为直线1x =-,y 的最大值为2,在对称轴右侧y 随x 的增大而减小,又1212,2y y <∴>>,故选A.3.答案:A抛物线26y x x m =-+与x 轴没有交点,240b ac ∴∆=-<,即2(6)410m --⨯⨯<,解得9m >,m ∴的取值范围是9m >.故选A.4.答案:A二次函数2114y x x m =-+-的图象与x 轴有交点,21(1)41104m ⎛⎫∴∆=--⨯⨯-≥ ⎪⎝⎭,解得5m ≤,故选A.5.答案:C 令211122ax x x -+=+,即231022ax x -+=,若直线与抛物线有两个不同的交点,则有2314022a ⎛⎫--⨯> ⎪⎝⎭,解得98a <.若抛物线与线段AB 有两个不同的交点,则①当0a <时,110111a a ++≤⎧⎨-+≤⎩,解得2a ≤-,2a ∴≤-;②当0a >时,110111a a ++≥⎧⎨-+≥⎩,解得1a ≥,918a ∴≤<.综上所述,918a ≤<或2a ≤-,故选C.6.答案:D抛物线221y x x =-+的对称轴为直线1x =,开口向上.当1y =时,2211x x -+=,解得120,2x x ==.如图.当1a x a ≤≤+时,函数有最小值1,10a ∴+=或2a =,1a ∴=-或2a =.故选D. 7.答案:A令0y =,则2430x x -+=,解得121,3x x ==,(1,0),(3,0)A B ∴.2243(2)1y x x x =-+=--,∴点M 的坐标为(2,1)-,平移该抛物线,使点M 平移后的对应点M'落在x 轴上,点B 平移后的对应点B'落在y 轴上,∴抛物线向上平移了1个单位长度,向左平移了3个单位长度, ∴平移后的抛物线解析式为22(1)21y x x x =+=++,故选A.8.答案:C当0x =时,220y ax x =-=,即抛物线22y ax x =-经过原点,故A 错误.反比例函数aby x=的图象在第一、三象限,0ab ∴>,即,a b 同号.当0a <时,抛物线22y ax x =-的对称轴为直线10x a=<,对称轴在y 轴左侧,故D 错误;当0a >时,0b >,直线y bx a =+经过第一、二、三象限,故B 错误,C 正确.故选C.9.答案:B二次函数()20y ax bx c a =++≠的图象过点(0,1)和(1,0)-,1c ∴=,0a b c -+=.①抛物线的对称轴在y 轴右侧,02bx a∴=->,a ∴与b 异号,0ab ∴<,①正确; ②抛物线与x 轴有两个不同的交点,240b ac ∴->,1c =,240b a ∴->,即24b a >,②正确;④抛物线开口向下,0a ∴<.0ab <,0b ∴>,0a b c -+=,1c =,1a b ∴=-,0,10a b <∴-<,即1b <,01b ∴<<,④正确;③0,a b c a c b -+=∴+=,20a b c b ∴++=>,110b c a <=<,,,1112022a b c a b a a ++=++<++=+<+=∴, 02a b c ∴<++<,③正确;⑤抛物线2y ax bx c =++与x 轴的一个交点为()1,0-,设另一个交点为()0,0x ,则00x >,由题图可知,当01x x >>-时,0y >,⑤错误.综上所述,正确的结论有①②③④. 故选B. 10.答案:B根据题意,得12x x ,就是方程22x x c x ++=的两个不同的实数根,整理,得20x x c ++=.由根与系数的关系,得121x x +=-,12x x c =.121x x <<,()()120110x x ∆>⎧∴⎨--<⎩,即140110c c ->⎧⎨++<⎩,解得2c <-.故选B. 11.答案:6抛物线经过(1,7),(5,7)A B -,∴点,A B 为抛物线上关于对称轴对称的点, ∴抛物线的对称轴为直线1522x -+==, (2,3),(,3)C D k ---为抛物线上的点,且两点纵坐标相同, (2,3)C ∴--与(,3)D k -关于直线2x =对称, 222k ∴-=⨯,6k ∴=.12.答案:31a -≤≤如图,画出抛物线2(1)3y x =--在03x ≤≤范围内的图象.直线y a =与抛物线2(1)3y x =--有交点,31a ∴-≤≤.13.答案:<当1x =-时,0y a b c =-+>;当2x =时,420y a b c =++<,42()42()0M N a b a b a b c a b c ∴-=+--=++--+<,即M N <.14.答案:2在221y x x =--中,令0x =,则1y =-,(0,1)A ∴-.把1y =-代入221y x x =--得2121x x -=--,解得120,2x x ==,()21B ∴-,,2AB ∴=.点P 关于x 轴的对称点恰好落在直线AB 上,PAB ∴△的边AB 上的高为2,12222ABP S ∴=⨯⨯=△.15.答案:(1)抛物线的对称轴为直线1x =,A 点的坐标为(3,0)-,∴点B 的坐标为(1,0).将点A 和点B 的坐标代入抛物线的解析式得93010b c b c -+=⎧⎨++=⎩,解得2,3b c ==-,∴抛物线的解析式为223y x x =+-.(2)将0x =代入223y x x =+-,得3y =-,∴点(0,3),3C OC -=.易知点B 的坐标为(1,0),1OB =. 设点P 的坐标为()2,23a aa +-,则点P 到OC 的距离为a .2POC BOC S S =△△,11||222OC a OC OB ∴⋅=⨯⋅,即113||23122a ⨯⨯=⨯⨯⨯, 解得2a =±.当2a =时,点P 的坐标为(2,5);当2a =-时,点P 的坐标为(2,3)--.∴点P 的坐标为(2,5)或(2,3)--.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年中考数学一轮专项复习提升卷——变量及函数问题1.球的体积V 与半径R 之间的关系式为V =43πR 3,下列说法正确的是( )A .变量为V ,R ,常量为43π,3B .变量为V ,R ,常量为43,πC .变量为V ,R ,π,常量为43D .变量为V ,R 3,常量为π2.(2019春·无棣县期末)下列关于变量x ,y 的关系,其中y 不是x 的函数的是( )A .B .C .D .3.(2019春·怀集县期末)如图,在一座高层的商业大厦中,每层的摊位布局基本相同.若第六层高档服装销售摊位可表示为(6,2,3),则第六层的手表摊位可表示为( )A .(6,2,5)B .(6,4,4)C .(6,3,5)D .(6,4,5)4.(2019春·诸城市期末)如图,小明家相对于学校的位置下列描述最准确的是( )A .距离学校1200米处B .北偏东65°方向上的1200米处C .南偏西65°方向上的1200米处D .南偏西25°方向上的1200米处5.(2019春·庐江县期末)小明家位于公园的正东200 m 处,从小明家出发向北走300 m 就到小华家,若选取小华家为原点,分别以正东、正北方向为x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表1 m 长,则公园的坐标是( )A .(-300,-200)B .(200,300)C .(-200,-300)D .(300,200)6.(2019·内江)在函数y =1x +3+4-x 中,自变量x 的取值范围是( )A .x <4B .x ≥4且x ≠-3C .x >4D .x ≤4且x ≠-37.当实数x 的取值使得x -2有意义时,函数y =4x +1中y 的取值范围是( ) A .y ≥-7 B .y ≥9 C .y >9D .y ≤98.若函数y =⎩⎪⎨⎪⎧x 2+2(x ≤2),2x (x >2),则当函数值y =8时,自变量x 的值是( )A .±6B .4C .±6或4D .4或- 69.(2019·甘肃)已知点P (m +2,2m -4)在x 轴上,则点P 的坐标是( ) A .(4,0) B .(0,4) C .(-4,0)D .(0,-4)10.(2019·滨州)在平面直角坐标系中,将点A (1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B ,则点B 的坐标是( )A .(-1,1)B .(3,1)C .(4,-4)D .(4,0)11.(2019·青岛)如图,将线段AB 先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A ′B ′,则点B 的对应点B ′的坐标是( )A.(-4,1) B.(-1,2)C.(4,-1) D.(1,-2)12.图中的圆点是有规律地从里到外逐层排列的.设y为第n层(n为正整数)圆点的个数,则下列函数关系中正确的是()A.y=4n-4 B.y=4nC.y=4n+4 D.y=n213.(2019·齐齐哈尔)“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离s与时间t之间函数关系的是()A.B.C.D.14.(2019·绵阳)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为()A.(2,3) B.(3,2)C.(3,3) D.(3,3)15.(2019·桂林)如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐为(-4,3);(3)在(2)的条件下,直接写出点A1的坐标.16.已知:如图,矩形AOBC ,O 为坐标原点,OB ,OA 分别在x 轴、y 轴上,点A 坐标为(0,3),∠OAB =60°,以AB 为轴对折后,使C 点落在D 点处,求D 点坐标.参考答案1.球的体积V 与半径R 之间的关系式为V =43πR 3,下列说法正确的是( B )A .变量为V ,R ,常量为43π,3B .变量为V ,R ,常量为43,πC .变量为V ,R ,π,常量为43D .变量为V ,R 3,常量为π2.(2019春·无棣县期末)下列关于变量x ,y 的关系,其中y 不是x 的函数的是( B )A .B .C .D .3.(2019春·怀集县期末)如图,在一座高层的商业大厦中,每层的摊位布局基本相同.若第六层高档服装销售摊位可表示为(6,2,3),则第六层的手表摊位可表示为( D )A .(6,2,5)B .(6,4,4)C .(6,3,5)D .(6,4,5)4.(2019春·诸城市期末)如图,小明家相对于学校的位置下列描述最准确的是( C )A .距离学校1200米处B .北偏东65°方向上的1200米处C .南偏西65°方向上的1200米处D .南偏西25°方向上的1200米处5.(2019春·庐江县期末)小明家位于公园的正东200 m 处,从小明家出发向北走300 m 就到小华家,若选取小华家为原点,分别以正东、正北方向为x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表1 m 长,则公园的坐标是( C )A .(-300,-200)B .(200,300)C .(-200,-300)D .(300,200)6.(2019·内江)在函数y =1x +3+4-x 中,自变量x 的取值范围是( D )A .x <4B .x ≥4且x ≠-3C .x >4D .x ≤4且x ≠-37.当实数x 的取值使得x -2有意义时,函数y =4x +1中y 的取值范围是( B ) A .y ≥-7 B .y ≥9 C .y >9D .y ≤98.若函数y =⎩⎪⎨⎪⎧x 2+2(x ≤2),2x (x >2),则当函数值y =8时,自变量x 的值是( D )A .±6B .4C .±6或4D .4或- 69.(2019·甘肃)已知点P (m +2,2m -4)在x 轴上,则点P 的坐标是( A ) A .(4,0) B .(0,4) C .(-4,0)D .(0,-4)10.(2019·滨州)在平面直角坐标系中,将点A (1,-2)向上平移3个单位长度,再向左平移2个单位长度,得到点B ,则点B 的坐标是( A )A .(-1,1)B .(3,1)C .(4,-4)D .(4,0)11.(2019·青岛)如图,将线段AB 先向右平移5个单位,再将所得线段绕原点按顺时针方向旋转90°,得到线段A ′B ′,则点B 的对应点B ′的坐标是( D )A .(-4,1)B .(-1,2)C .(4,-1)D .(1,-2)12.图中的圆点是有规律地从里到外逐层排列的.设y 为第n 层(n 为正整数)圆点的个数,则下列函数关系中正确的是( B )A.y=4n-4 B.y=4nC.y=4n+4 D.y=n213.(2019·齐齐哈尔)“六一”儿童节前夕,某部队战士到福利院慰问儿童.战士们从营地出发,匀速步行前往文具店选购礼物,停留一段时间后,继续按原速步行到达福利院(营地、文具店、福利院三地依次在同一直线上).到达后因接到紧急任务,立即按原路匀速跑步返回营地(赠送礼物的时间忽略不计),下列图象能大致反映战士们离营地的距离s与时间t之间函数关系的是(B)A.B.C.D.14.(2019·绵阳)如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点E的坐标为(D)A.(2,3) B.(3,2)C.(3,3) D.(3,3)15.(2019·桂林)如图,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,△ABC的三个顶点均在格点上.(1)将△ABC先向右平移6个单位长度,再向上平移3个单位长度,得到△A1B1C1,画出平移后的△A1B1C1;(2)建立适当的平面直角坐标系,使得点A的坐为(-4,3);(3)在(2)的条件下,直接写出点A1的坐标.【解析】(1)如图,△A1B1C1为所作;(2)如图;(3)点A1的坐标为(2,6).16.已知:如图,矩形AOBC,O为坐标原点,OB,OA分别在x轴、y轴上,点A坐标为(0,3),∠OAB=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.【解析】由题意得OA=3,∠OAB=60°,∴OB=3×tan60°=3 3.∵△ACB≌△ADB,∴AD =AC =OB .过D 作DE ⊥y 轴于点E , ∵∠OAD =30° ∴ED =12AD =332,∵cos30°=OA +EO AD ,∴OE =33×32-3=32, ∴D ⎝⎛⎭⎫332,-32.。
