2018年全国各地中考数学真题分类汇编—矩形、菱形与正方形 精品
2012年全国中考数学试题分类解析汇编专题44:矩形、菱形、正方形

2012年全国中考数学试题分类解析汇编(159套63专题)专题44:矩形、菱形、正方形一、选择题1. (2012天津市3分)如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD 至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为【】(A1(B)3(C(D1【答案】D。
【考点】正方形的性质,勾股定理。
【分析】利用勾股定理求出CM的长,即ME的长,有DM=DE,所以可以求出DE,从而得到DG的长:∵四边形ABCD是正方形,M为边AD的中点,∴DM=12DC=1。
∴CM=1。
∵四边形EDGF1。
故选D。
2. (2012安徽省4分)为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为【】A.22a B. 32a C. 42a D.52a【答案】A 。
【考点】正多边形和圆,等腰直角三角形的性质,正方形的性质。
【分析】图案中间的阴影部分是正方形,面积是2a ,由于原来地砖更换成正八边形,四周一个阴影部分是对角线为a 的正方形的一半,它的面积用对角线积的一半来计算:222114222a a a +⨯⨯=。
故选A 。
3. (2012山西省2分)如图,已知菱形ABCD 的对角线AC .BD 的长分别为6cm 、8cm ,AE⊥BC 于点E ,则AE 的长是【 】A .B .C .48cm 5D .24cm 5 【答案】D 。
【考点】菱形的性质,勾股定理。
【分析】∵四边形ABCD 是菱形,∴CO=12AC=3,BO=12BD=,AO⊥BO,∴5=。
∴ABCD 11S BD AC 682422=⋅=⨯⨯=菱形。
又∵ABCD S BC AE =⋅菱形,∴BC·AE=24,即()24AE cm 5=。
故选D 。
4. (2012陕西省3分)如图,在菱形ABCD 中,对角线AC 与BD 相交于点O ,OE⊥AB,垂足为E ,若∠ADC=1300,则∠AOE 的大小为【 】A .75°B .65°C .55°D .50°【答案】B 。
2021年中考数学真题 矩形菱形正方形(共42题)-(原卷版)
18矩形菱形正方形(共42题)姓名:__________________ 班级:______________ 得分:_________________一、单选题1.(2021·四川成都市·中考真题)如图,四边形ABCD是菱形,点E,F分别在,BC DC 边上,添加以下条件不能判定ABE ADF≌的是()A.BE DF=B.BAE DAF∠=∠C.AE AD=D.AEB AFD∠=∠2.(2021·四川遂宁市·中考真题)如图,在矩形ABCD中,AB=5,AD=3,点E 为BC上一点,把△CDE沿DE翻折,点C恰好落在AB边上的F处,则CE的长是()A.1B.43C.32D.533.(2021·重庆中考真题)如图,正方形ABCD的对角线AC,BD交于点O,M 是边AD上一点,连接OM,过点O做ON△OM,交CD于点N.若四边形MOND的面积是1,则AB的长为()A.1B2C.2D.224.(2021·四川凉山彝族自治州·中考真题)下列命题中,假命题是()A.直角三角形斜边上的中线等于斜边的一半B.等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合C.若AB BC=,则点B是线段AC的中点D.三角形三条边的垂直平分线的交点叫做这个三角形的外心5.(2021·四川泸州市·中考真题)下列命题是真命题的是()A.对角线相等的四边形是平行四边形B.对角线互相平分且相等的四边形是矩形C.对角线互相垂直的四边形是菱形D.对角线互相垂直平分的四边形是正方形6.(2021·浙江温州市·中考真题)由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连结CG,延长BE交CG于点H.若2AE BE=,则CGBH的值为()A .32B .2C .310D .35 7.(2021·安徽中考真题)如图,在菱形ABCD 中,2AB =,120A ∠=︒,过菱形ABCD的对称中心O 分别作边AB ,BC 的垂线,交各边于点E ,F ,G ,H ,则四边形EFGH 的周长为( )A .33B .223+C .23D .123+8.(2021·重庆中考真题)如图,把含30°的直角三角板PMN 放置在正方形ABCD 中,30PMN ∠=︒,直角顶点P 在正方形ABCD 的对角线BD 上,点M ,N 分别在AB 和CD 边上,MN 与BD 交于点O ,且点O 为MN 的中点,则AMP ∠的度数为( )A.60°B.65°C.75°D.80°9.(2021·四川乐山市·中考真题)如图,已知点P是菱形ABCD的对角线AC延长线上一点,过点P分别作AD、DC延长线的垂线,垂足分别为点E、F.若120ABC∠=︒,2AB=,则PE PF-的值为()A.32B.3C.2D.5210.(2021·四川自贡市·中考真题)如图,在正方形ABCD中,6AB=,M是AD 边上的一点,:1:2AM MD=.将BMA△沿BM对折至BMN△,连接DN,则DN的长是()A.52B.958C.3D.65511.(2021·浙江绍兴市·中考真题)如图,菱形ABCD中,60B∠=︒,点P从点B 出发,沿折线BC CD-方向移动,移动到点D停止.在ABP△形状的变化过程中,依次出现的特殊三角形是()A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形12.(2021·陕西中考真题)如图,在菱形ABCD中,60ABC∠=︒,连接AC、BD,则ACBD的值为()A.12B.22C3D3二、填空题13.(2021·山东临沂市·中考真题)数学知识在生产和生活中被广泛应用,下列实例所应用的最主要的几何知识,说法正确的是___(只填写序号).△射击时,瞄准具的缺口、准星和射击目标在同一直线上,应用了“两点确定一条直线”;△车轮做成圆形,应用了“圆是中心对称图形”;△学校门口的伸缩门由菱形而不是其他四边形组成,应用了“菱形的对角线互相垂直平分”;△地板砖可以做成矩形,应用了“矩形对边相等”.14.(2021·四川泸州市·中考真题)如图,在边长为4的正方形ABCD中,点E 是BC的中点,点F在CD上,且CF=3BF,AE,BF相交于点G,则AGF的面积是________.15.(2021·四川成都市·中考真题)如图,在矩形ABCD中,4,8==,点E,AB ADF分别在边,AD BC上,且3AE=,按以下步骤操作:第一步,沿直线EF翻折,点A的对应点'A恰好落在对角线AC上,点B的对应点为'B,则线段BF的长为_______;第二步,分别在,'EF A B上取点M,N,沿直线MN继续翻折,使点F与点E重合,则线段MN的长为_______.16.(2021·江苏扬州市·中考真题)如图,在ABC中,AC BC=,矩形DEFG的顶点D、E在AB上,点F、G分别在BC、AC上,若4BF=,且2CF=,3=,DE EF则EF的长为________.17.(2021·云南中考真题)已知ABC的三个顶点都是同一个正方形的顶点,ABC∠的平分线与线段AC交于点D.若ABC的一条边长为6,则点D到直线AB的距离为__________.18.(2021·山东泰安市·中考真题)如图,将矩形纸片ABCD 折叠(AD AB >),使AB 落在AD 上,AE 为折痕,然后将矩形纸片展开铺在一个平面上,E 点不动,将BE 边折起,使点B 落在AE 上的点G 处,连接DE ,若DE EF =,2CE =,则AD 的长为________.19.(2021·江苏连云港市·中考真题)如图,菱形ABCD 的对角线AC 、BD 相交于点O ,OE AD ⊥,垂足为E ,8AC =,6BD =,则OE 的长为______.20.(2021·四川南充市·中考真题)如图,点E 是矩形ABCD 边AD 上一点,点F ,G ,H 分别是BE ,BC ,CE 的中点,3AF =,则GH 的长为________.21.(2021·四川凉山彝族自治州·中考真题)菱形ABCD 中,对角线10, 24AC BD ==,则菱形的高等于___________.22.(2021·重庆中考真题)如图,在菱形ABCD 中,对角线12AC =,16BD =,分别以点A ,B ,C ,D 为圆心,12AB 的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为__________.(结果保留π)23.(2021·四川遂宁市·中考真题)如图,正方形ABCD 中,点E 是CD 边上一点,连结BE ,以BE 为对角线作正方形BGEF ,边EF 与正方形ABCD 的对角线BD 相交于点H ,连结AF ,有以下五个结论:△ABF DBE ∠=∠;△ABF DBE ∽;△AF BD ⊥;△22BG BH BD =;△若:1:3CE DE =,则:17:16BH DH =,你认为其中正确是_____(填写序号)24.(2021·湖北十堰市·中考真题)如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为_______.25.(2021·浙江绍兴市·中考真题)图1是一种矩形时钟,图2是时钟示意图,时钟数字2的刻度在矩形ABCD的对角线BD上,时钟中心在矩形ABCD对角线的交点O上.若30cmAB=,则BC长为_______cm(结果保留根号).26.(2021·湖北黄冈市·中考真题)如图,正方形ABCD中,1∠AB=,连接AC,ACD的平分线交AD 于点E ,在AB 上截取AF DE =,连接DF ,分别交CE ,AC 于点G ,H ,点P 是线段GC 上的动点,PQ AC ⊥于点Q ,连接PH .下列结论:△CE DF ⊥;△DE DC AC +=;△3EA AH =;△PH PQ +的最小值是22.其中所有正确结论的序号是_____.27.(2021·湖南衡阳市·中考真题)如图1,菱形ABCD 的对角线AC 与BD 相交于点O ,P 、Q 两点同时从O 点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P 的运动路线为O A D O ---,点Q 的运动路线为O C B O ---.设运动的时间为x 秒,P 、Q 间的距离为y 厘米,y 与x 的函数关系的图象大致如图2所示,当点P 在A D -段上运动且P 、Q 两点间的距离最短时,P 、Q 两点的运动路程之和为__________厘米.28.(2021·湖南株洲市·中考真题)《蝶几图》是明朝人戈汕所作的一部组合家具的设计图(蜨,同“蝶”),它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,共十三只(图△中的“様”和“隻”为“样”和“只”).图△为某蝶几设计图,其中ABD △和CBD 为“大三斜”组件(“一様二隻”的大三斜组件为两个全等的等腰直角三角形),已知某人位于点P 处,点P 与点A 关于直线DQ 对称,连接CP 、DP .若24ADQ ∠=︒,则DCP∠= ___________度.29.(2021·江苏苏州市·中考真题)如图,四边形ABCD 为菱形,70ABC ∠=︒,延长BC 到E ,在DCE ∠内作射线CM ,使得15ECM∠=︒,过点D 作DF CM ⊥,垂足为F ,若5DF =,则对角线BD 的长为______.(结果保留根号)30.(2021·浙江金华市·中考真题)如图,在平面直角坐标系中,有一只用七巧板拼成的“猫”,三角形△的边BC及四边形△的边CD都在x轴上,“猫”耳尖E在y 轴上.若“猫”尾巴尖A的横坐标是1,则“猫”爪尖F的坐标是___________.三、解答题31.(2021·四川广安市·中考真题)如图,四边形ABCD是菱形,点E、F分别在边AB、AD的延长线上,且BE DF=.连接CE、CF.求证:CE CF=.32.(2021·江苏扬州市·中考真题)如图,在ABC中,BAC∠的角平分线交BC于DE AB DF AC.点D,//,//(1)试判断四边形AFDE 的形状,并说明理由;(2)若90BAC ∠=︒,且22AD =,求四边形AFDE 的面积.33.(2021·浙江金华市·中考真题)已知:如图,矩形ABCD 的对角线,AC BD 相交于点O ,120,2BOC AB ∠=︒=.(1)求矩形对角线的长.(2)过O 作OE AD ⊥于点E ,连结BE .记ABE α∠=,求tan α的值.34.(2021·江苏连云港市·中考真题)如图,点C 是BE 的中点,四边形ABCD 是平行四边形.(1)求证:四边形ACED 是平行四边形;(2)如果AB AE =,求证:四边形ACED 是矩形.35.(2021·四川凉山彝族自治州·中考真题)如图,在四边形ABCD 中,90ADC B ∠=∠=︒,过点D 作DE AB ⊥于E ,若DE BE =.(1)求证:DA DC =;(2)连接AC 交DE 于点F ,若30,6ADE AD ∠=︒=,求DF 的长.36.(2021·四川遂宁市·中考真题)如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,过点O 的直线EF 与BA 、DC 的延长线分别交于点E 、F . (1)求证:AE =CF ;(2)请再添加一个条件,使四边形BFDE 是菱形,并说明理由.37.(2021·四川自贡市·中考真题)如图,在矩形ABCD 中,点E 、F 分别是边AB 、CD 的中点.求证:DE=BF .38.(2021·浙江嘉兴市·中考真题)如图,在77⨯的正方形网格中,网格线的交点称为格点,B在格点上,每一个小正方形的边长为1.(1)以AB为边画菱形,使菱形的其余两个顶点都在格点上(画出一个即可).(2)计算你所画菱形的面积.39.(2021·浙江丽水市·中考真题)如图,在菱形ABCD中,ABC∠是锐角,E是BC 边上的动点,将射线AE绕点A按逆时针方向旋转,交直线CD于点F.(1)当AE BC EAF ABC,时,△求证:AE AF=;△连结BD EF,,若2 5EFBD=,求ABCDAEF菱形SS的值;(2)当12EAF BAD∠=∠时,延长BC交射线AF于点M,延长DC交射线AE于点N,连结AC MN,,若42AB AC==,,则当CE为何值时,AMN是等腰三角形.40.(2021·安徽中考真题)学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形AEFD为矩形,点B、C分别在EF、DF上,90ABC∠=︒,53BAD∠=︒,10AB cm=,6BC cm=.求零件的截面面积.参考数据:sin530.80︒≈,cos530.60︒≈.41.(2021·四川眉山市·中考真题)如图,在等腰直角三角形ABC中,90ACB∠=︒,25AC BC==,边长为2的正方形DEFG的对角线交点与点C重合,连接AD,BE.(1)求证:≌ACD BCE;(2)当点D在ABC内部,且90ADC∠=︒时,设AC与DG相交于点M,求AM的长;(3)将正方形DEFG绕点C旋转一周,当点A、D、E三点在同一直线上时,请直接写出AD 的长.42.(2021·浙江嘉兴市·中考真题)小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD 绕点A 顺时针旋转()090αα︒<≤︒,得到矩形'''AB C D[探究1]如图1,当90α=︒时,点'C 恰好在DB 延长线上.若1AB =,求BC 的长.[探究2]如图2,连结'AC ,过点'D 作'//'D M AC 交BD 于点M .线段'D M 与DM 相等吗?请说明理由.[探究3]在探究2的条件下,射线DB分别交'AC于点P,N(如图3),MN,AD,'PN存在一定的数量关系,并加以证明.。
2018年全国各地中考数学真题汇编:轴对称变换(含答案)-数学备课大师【全免费】

中考数学真题汇编:轴对称变换一、选择题1.下列图形中是中心对称图形的是()A. B. C. D.【答案】D2.下列图形中一定是轴对称图形的是()A. B. C. D.【答案】D3.下列图形中,既是轴对称又是中心对称图形的是()A. B. C. D.【答案】B4.如图,将一个三角形纸片沿过点的直线折叠,使点落在边上的点处,折痕为,则下列结论一定正确的是()A. B. C. D.【答案】D5.如图所示的五角星是轴对称图形,它的对称轴共有()A.1条B.3条C.5条D.无数条【答案】C6.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC 等于()A. 112°B. 110°C. 108°D. 106°【答案】D7.如图,将矩形沿对角线折叠,点落在处,交于点,已知,则的度为()A. B. C. D.【答案】D8.如图,∠AOB=60°,点P是∠AOB内的定点且OP= ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是()A. B. C. 6 D. 3【答案】D9.如图,在正方形中,,分别为,的中点,为对角线上的一个动点,则下列线段的长等于最小值的是()A. B. C. D.【答案】D10.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A. B. C. D.【答案】A二、填空题11.已知点是直线上一点,其横坐标为.若点与点关于轴对称,则点的坐标为________.【答案】(,)12.有五张卡片(形状、大小、质地都相同),正面分别画有下列图形:①线段;②正三角形;③平行四边形;④等腰梯形;⑤圆.将卡片背面朝上洗匀,从中任取一张,其正面图形既是轴对称图形,又是中心对称图形的概率是________.【答案】13.如图,在菱形中,,分别在边上,将四边形沿翻折,使的对应线段经过顶点,当时,的值为________.【答案】14.在平面直角坐标系中,点的坐标是.作点关于轴的对称点,得到点,再将点向下平移个单位,得到点,则点的坐标是(________),(________).【答案】;15.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在直线AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=________。
2024成都中考数学复习专题 矩形、菱形、正方形的性质与判定(含答案)

2024成都中考数学复习专题矩形、菱形、正方形的性质与判定基础题1. (2023上海)在四边形ABCD中,AD∥BC,AB=C D.下列说法能使四边形ABCD为矩形的是()A. AB∥CDB. AD=BCC. ∠A=∠BD. ∠A=∠D2. (2023自贡)如图,边长为3的正方形OBCD两边与坐标轴正半轴重合,点C的坐标是()A. (3,-3)B. (-3,3)C. (3,3)D. (-3,-3)第2题图3. (2022玉林)若顺次连接四边形ABCD各边的中点所得的四边形是正方形,则四边形ABCD 的两条对角线AC,BD一定是()A. 互相平分B. 互相垂直C. 互相平分且相等D. 互相垂直且相等4. (2023深圳)如图,在平行四边形ABCD中,AB=4,BC=6,将线段AB水平向右平移a 个单位长度得到线段EF,若四边形ECDF为菱形时,则a的值为()第4题图A. 1B. 2C. 3D. 45. (2023十堰)如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化.下面判断错误的是()A. 四边形ABCD由矩形变为平行四边形B. 对角线BD的长度减小C. 四边形ABCD的面积不变D. 四边形ABCD的周长不变第5题图6. 如图,菱形ABCD中,点E,F分别为AB,BC的中点,EF=2,BD=8,则该菱形的面积为()第6题图A. 12B. 16C. 20D. 327. (2023杭州)如图,矩形ABCD的对角线AC,BD相交于点O.若∠AOB=60°,则ABBC=()A. 12 B.3-12 C.32 D.33第7题图8. (2023大庆)将两个完全相同的菱形按如图方式放置,若∠BAD=α,∠CBE=β,则β=()第8题图A. 45°+12α B. 45°+32αC. 90°-12αD. 90°-32α 9. (2023河北)如图,在Rt △ABC 中,AB =4,点M 是斜边BC 的中点,以AM 为边作正方形AMEF .若S 正方形AMEF =16,则S △ABC =( ) A. 4 3 B. 8 3 C. 12 D. 16第9题图10. [新考法—条件开放](2023齐齐哈尔)如图,在四边形ABCD 中,AD =BC ,AC ⊥BD 于点O .请添加一个条件:________,使四边形ABCD 成为菱形.第10题图 11. (2023怀化)如图,点P 是正方形ABCD 的对角线AC 上的一点,PE ⊥AD 于点E ,PE =3.则点P 到直线AB 的距离为________.第11题图12. (2023绍兴)如图,在菱形ABCD 中,∠DAB =40°,连接AC ,以点A 为圆心,AC 长为半径作弧,交直线AD 于点E ,连接CE ,则∠AEC 的度数是________.第12题图13. (2023河南)矩形ABCD 中,M 为对角线BD 的中点,点N 在边AD 上,且AN =AB =1.当以点D ,M ,N 为顶点的三角形是直角三角形时,AD 的长为________.14. [新考法—条件开放](2023十堰)如图,▱ABCD 的对角线AC ,BD 交于点O ,分别以点B ,C 为圆心,12AC ,12BD 长为半径画弧,两弧交于点P ,连接BP ,CP . (1)试判断四边形BPCO 的形状,并说明理由;(2)请说明当▱ABCD 的对角线满足什么条件时,四边形BPCO 是正方形?第14题图15. 如图,在平行四边形ABCD 中,点E ,F 分别在边BC ,AD 上,且BE =DF ,连接AE ,CF ,EH ⊥CF 于点H ,FG ⊥AE 于点G .(1)判断四边形EGFH 的形状,并说明理由;(2)若AE =5,tan ∠DAE =2,EG =2GF ,求AG 的长.第15题图拔高题16. (2022青羊区模拟)我们规定菱形与正方形接近程度称为“接近度”,设菱形相邻两个内角的度数分别为α,β,将菱形的“接近度”定义为|α-β|,于是|α-β|越小,菱形越接近正方形.第16题图①若菱形的一个内角为80°,则该菱形的“接近度”为________;②当菱形的“接近度”等于________时,菱形是正方形.课时2基础题1. (2023湘潭)如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为()A. 20°B. 60°C. 70°D. 80°第1题图2. 如图,在菱形ABCD中,AC,BD为菱形的对角线,∠DBC=60°,BD=10,点F为BC 中点,则EF的长为()第2题图A. 3B. 4C. 5D. 63. 如图所示,将一张矩形纸片沿虚线对折两次,当剪刀与纸片的夹角∠ABC=45°时,已知AB=4 cm,则剪下来图形的周长为()第3题图A. 4 cmB. 4 2 cmC. 16 cmD. 16 2 cm4. (2022青岛改编)如图,O 为正方形ABCD 对角线AC 的中点,△ACE 为等边三角形.若AB =2,则OE 的长度为________.第4题图5. [新考法—数学文化](2023内江)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD 中,AB =5,AD =12,对角线AC 与BD 交于点O ,点E 为BC 边上的一个动点,EF ⊥AC ,EG ⊥BD ,垂足分别为点F ,G ,则EF +EG =________.第5题图6. (2023天津)如图,在边长为3的正方形ABCD 的外侧,作等腰三角形ADE ,EA =ED =52.第6题图(1)△ADE 的面积为________;(2)若F 为BE 的中点,连接AF 并延长,与CD 相交于点G ,则AG 的长为________.7. (2023内江)如图,在△ABC 中,D 是BC 的中点,E 是AD 的中点,过点A 作AF ∥BC 交CE 的延长线于点F .(1)求证:F A =BD ;(2)连接BF ,若AB =AC ,求证:四边形ADBF 是矩形.第7题图8. (2023兰州)如图,矩形ABCD的对角线AC与BD相交于点O,CD∥OE,直线CE是线段OD的垂直平分线,CE分别交OD,AD于点F,G,连接DE.(1)判断四边形OCDE的形状,并说明理由;(2)当CD=4时,求EG的长.第8题图拔高题9. (2023绍兴改编)如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E 在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2.当E,F,O三点重合时,当点E,F分别为OB,OD的中点时,当E,F分别运动到B,D两点时,四边形E1E2F1F2形状的变化依次是()第9题图A. 菱形→平行四边形→矩形B. 菱形→矩形→菱形C. 平行四边形→矩形→平行四边形D. 平行四边形→菱形→正方形10. (2023武侯区二诊节选)如图①,在矩形ABCD中,AD=nAB(其中n>1),点P是AD边上一动点(点P不与点A重合),点E是AB边的中点,连接PE,将矩形ABCD沿直线PE进行翻折,其顶点A翻折后的对应点为O,连接PO并延长,交BC边于点F(点F不与点C重合),过点F作∠PFC的平分线FG,交矩形ABCD的边于点G.(1)求证:PE∥FG;(2)如图②,在点P运动过程中,若E,O,G三点在同一条直线上时,点G与点D刚好重合,求n的值.图①图②第10题图参考答案与解析1. C2. C 【解析】∵正方形的边长为3,∴DC =BC =3,DC 与BC 分别垂直于y 轴和x 轴.∵点C 在第一象限,∴点C 的坐标为(3,3).3. D 【解析】如解图,E ,F ,G ,H 分别为AB ,BC ,CD ,DA 的中点,则EH ∥DB ∥GF ,HG ∥AC ∥EF ,EF =12 AC ,FG =12BD ,∴四边形EFGH 为平行四边形.要使其为正方形,即EF ⊥FG ,FE =FG ,则AC ⊥BD ,AC =BD ,即对角线一定互相垂直且相等.第3题解图4. B 【解析】∵四边形ABCD 是平行四边形,∴AB ∥CD ,CE ∥FD ,CD =AB =4.∵将线段AB 水平向右平移得到线段EF ,∴AB ∥EF ∥CD ,∴四边形ECDF 为平行四边形,当CD =CE =4时,▱ECDF 为菱形,此时a =BE =BC -CE =6-4=2.5. C 【解析】将四根木条用钉子钉成一个矩形框架ABCD ,然后向左扭动框架,∵两组对边的长度分别相等,∴四边形ABCD 是平行四边形,故A 正确,∵向左扭动框架,∴BD 的长度减小,故B 正确;∵平行四边形ABCD 的底不变,高变小了,∴平行四边形ABCD 的面积变小,故C 错误;∵平行四边形ABCD 的四条边长度不变,∴四边形ABCD 的周长不变,故D 正确.6. B 【解析】如解图,连接AC ,∵点E ,F 分别为AB ,BC 的中点,∴EF 是△ABC 的中位线,∴AC =2EF =4.∵四边形ABCD 是菱形,∴AC ⊥BD ,∴S 菱形ABCD =12 AC ·BD =12×4×8=16.第6题解图7. D 【解析】∵四边形ABCD 是矩形,∴OA =OB =OC =OD ,∠ABC =90°,∴∠OBC =∠OCB .∵∠AOB =60°,∴∠ACB =12 ∠AOB =30°,∴AB BC =tan ∠ACB =tan 30°=33. 8. D 【解析】∵四边形ABCD 和四边形BGHF 是完全相同的菱形,∴∠DBE =∠BAD =α,AB =AD ,∠ABD =∠CBD =∠CBE +∠DBE =β+α.∴∠ADB =∠ABD =β+α.∵∠BAD +∠ADB +∠ABD =180°,∴α+β+α+β+α=180°,∴β=90°-32α. 9. B 【解析】∵S 正方形AMEF =16,∴AM =4.∵M 是斜边BC 的中点,∴AM 是Rt △ABC 斜边上的中线,∴BC =2AM =8.在Rt △ABC 中,由勾股定理,得AC =BC 2-AB 2 =43 ,∴S △ABC =12 AB ·AC =12×4×43 =83 . 10. AD ∥BC (答案不唯一) 【解析】当AD ∥BC ,AD =BC 时,四边形ABCD 为平行四边形,又∵AC ⊥BD ,∴四边形ABCD 是菱形.11. 3 【解析】如解图,过点P 作PF ⊥AB 于点F ,∵四边形ABCD 是正方形,AC 是对角线,∴∠DAC =∠BAC .∵PE ⊥AD ,PF ⊥AB ,∴∠AEP =∠AFP .∵AP =AP ,∴△AEP ≌△AFP (AAS),∴PE =PF .∵PE =3,∴点P 到直线AB 的距离为PF =3.第11题解图12. 10°或80° 【解析】如解图,以点A 为圆心,AC 长为半径作弧,交直线AD 于点E 和E ′.在菱形ABCD 中,∠DAC =∠BAC ,∵∠DAB =40°,∴∠DAC =20°.∵AC =AE ,∴∠AEC =(180°-20°)÷2=80°.∵AE ′=AC ,∴∠AE ′C =∠ACE ′=10°.综上所述,∠AEC 的度数是10°或80°.第12题解图 13. 2或2 +1 【解析】分两种情况,①当∠DNM =90°时,如解图①,则MN ∥AB ,∴AN BM=AD BD.∵M 是BD 的中点,∴BD =2BM ,∴AD =2AN =2;②当∠DMN =90°时,如解图②,连接BN ,∵M 是BD 的中点,∠DMN =90°,∴BN =DN =AB 2+AN 2 =12+12 =2 ,∴AD =2 +1.综上所述,AD 的长为2或2 +1.图①图②第13题解图14. 解:(1)四边形BPCO 为平行四边形.理由如下:由作法得,BP =12 AC ,CP =12BD , ∵四边形ABCD 为平行四边形,∴OC =12 AC ,OB =12BD, ∴OC =BP ,OB =CP ,∴四边形BPCO 为平行四边形.(2)当▱ABCD 的对角线垂直且相等时,四边形BPCO 为正方形.理由:∵AC ⊥BD ,∴四边形BPCO 为矩形,∵AC =BD ,∴OB =OC ,∴四边形BPCO 为正方形.15. 解:(1)四边形EGFH 是矩形.理由如下:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC .∵BE =DF ,∴AD -DF =BC -BE ,∴AF =CE ,∴四边形AECF 是平行四边形,∴AE ∥CF ,∴∠AEH +∠FHE =180°.∵EH ⊥CF ,FG ⊥AE ,∴∠FGE =∠FHE =∠GEH =90°,∴四边形EGFH 是矩形;(2)∵FG ⊥AE ,∴∠AGF =90°.在Rt △AGF 中,tan ∠DAE =GF AG=2, ∴GF =2AG .∵EG =2GF ,∴EG =4AG .∵AE =AG +EG =5,∴AG =1,即AG 的长为1.16. 20°;0° 【解析】①∵菱形相邻两个内角的度数和为180°,∴α+β=180°,即80°+β=180,解得β=100°,∴该菱形的“接近度”为|α-β|=|80°-100°|=20°;②∵当α=β=90°时,菱形是正方形,∴|α-β|=0°时,菱形是正方形.课时21. C 【解析】∵四边形ABCD 是菱形,∴AB ∥CD ,AC ⊥BD ,∴∠DCA =∠1=20°,∴∠2=90°-∠DCA =70°.2. C 【解析】∵四边形ABCD 是菱形,∴BC =DC ,BE =DE ,∵∠DBC =60°,∴△BDC是等边三角形,∴CD =BD =10.∵点F 为BC 中点,∴EF =12CD =5. 3. D 【解析】由折叠可知,剪下的图形两条对角线互相垂直且平分,此时图形为菱形,∵∠ABC =45°,∴剪下的图形有一个角为90°,∴有一个角为90°的菱形是正方形,∵AB =4 cm ,根据勾股定理得BC =42 cm ,故剪下来图形的周长为4×42 =16 2 cm. 4. 6 【解析】∵四边形ABCD 为正方形,AB =2,∴AC =22 .∵O 为正方形ABCD 对角线AC 的中点,△ACE 为等边三角形,∴∠AOE =90°,∴AC =AE =22 ,AO =2 ,∴OE=6 .5. 6013【解析】如解图,连接OE ,∵四边形ABCD 是矩形,∴∠BAD =90°, AB =CD =5,AD =BC =12.在Rt △ABD 中,BD =AB 2+AD 2 =13.∴AC =BD =13.∵AC 与BD 交于点O ,∴AO =CO =BO =DO =132 .∵S △BCO =14 S 四边形ABCD =14×12×5=15,∴S △BCO =S △BEO +S △CEO =12 BO ·EG +12 CO ·EF =12 ×132 (EG +EF )=15,∴EF +EG =15×413 =6013.第5题解图6. (1)3 【解析】(1)如解图,过点E 作EM ⊥AD 于点M ,∵△ADE 是等腰三角形,EA =ED =52 ,AD =3,∴AM =12 AD =32,∴EM =AE 2-AM 2 =(52)2-(32)2 =2,∴S △ADE =12 AD ·EM =12 ×3×2=3. (2)13 【解析】如解图,延长EM 交AG 于点N ,∵∠BAD =∠AME =90°,∴AB ∥NE ,∴∠ABF =∠FEN ,∠BAF =∠ENF .又∵点F 为BE 中点,∴BF =EF ,∴△AFB ≌△NFE ,∴EN =BA =3.由(1)知,EM =2,∴NM =1.∵∠NMD =∠ADC =90°,且M 为AD 中点,∴NM ∥GD ,∴NM 为△AGD 的中位线,∴GD =2NM =2,∴AG =AD 2+GD 2 =13 .第6题解图7. 证明:(1)∵AF ∥BC ,∴∠AFE =∠DCE .又∵E 是AD 的中点,∴AE =DE .在△AFE 和△DCE 中,∵ ⎩⎪⎨⎪⎧∠AFE =∠DCE ,∠AEF =∠DEC ,AE =DE ,∴△AFE≌△DCE,∴AF=DC.又∵D是BC的中点,∴BD=CD,∴AF=BD;(2)∵AB=AC,∴△ABC是等腰三角形.又∵D是BC的中点,∴∠ADB=90°,由(1)知F A=BD,又∵F A∥BD,∴四边形ADBF是平行四边形.又∵∠ADB=90°,∴四边形ADBF是矩形.8. 解:(1)四边形OCDE为菱形,理由如下:∵CE是线段OD的垂直平分线,∴OF=DF,OC=DC.∵CD∥OE,∴∠EOF=∠CDF.∵∠EFO=∠CFD,∴△OFE≌△DFC,∴OE=CD,∴四边形OCDE是平行四边形.又∵OC=CD,∴四边形OCDE是菱形;(2)∵四边形ABCD是矩形,∴DO=OC=OA,由(1)可知,OC=DC,∴OC=DO=CD,∴△OCD 是等边三角形,∴∠DCO =∠CDO =60°,∴∠FDG =90°-60°=30°.∵四边形OCDE 是菱形,∴∠DEC =∠DCE =30°,∠CGD =90°-∠DCE =60°,∴∠EDG =30°,∴DG =EG .∵CD =4,∴tan ∠DCG =DG CD =DG 4, ∴DG =4·tan 30°=4×33 =433, ∴EG =433. 9. B 【解析】∵四边形ABCD 为矩形,∠ABD =60°,∴∠CDF =60°,∠EDA =∠CBD =30°.∵OE =OF ,O 为对角线BD 的中点,∴DF =EB .由对称的性质得DF =DF 2,BF =BF 1,BE =BE 2,DE =DE 1,∠F 2DC =∠CDF =60°,∠EDA =∠E 1DA =30°,∠F 1BC =∠FBC =30°,∴E 1F 2=E 2F 1,∠E 1DB =60°,∠F 1BD =60°,∴DE 1∥BF 1,∴E 1F 2∥E 2F 1,∴四边形E 1E 2F 1F 2是平行四边形,如解图①,当E ,F ,O 三点重合时,DO =BO ,∴DE 1=DF 2=AE 1=AE 2,即E 1E 2=E 1F 2,∴四边形E 1E 2F 1F 2是菱形,如解图②,当E ,F 分别为OB ,OD 的中点时,设DB =4,则DF 2=DF =1,DE 1=DE =3,在Rt △ABD 中,AB =2,AD =23 ,连接AE ,易得AE =32 AB =3 ,根据对称性可得AE 1=AE =3 ,∵AD 2=12,DE 21 =9,AE 21 =3,即AD 2=AE 21 +DE 21 ,∴△DE 1A 是直角三角形,且∠E 1=90°,∴四边形E 1E 2F 1F 2是矩形;如解图③,当F ,E 分别与D ,B 重合时,△BE 1D ,△BDF 1都是等边三角形,则四边形E 1E 2F 1F 2是菱形,∴在这三个位置时,四边形E 1E 2F 1F 2形状的变化依次是菱形→矩形→菱形.图①图②图③第9题解图10. (1)证明:由翻折知,∠APE=∠OPE,∵FG平分∠PFC,∴∠PFG=∠CFG.∵AD∥BC,∴∠APF=∠CFP,∴∠EPF=∠PFG,∴PE∥FG;(2)解:由翻折知,EA=EO,∠EOP=90°.∵E,O,D三点在同一条直线上,∴∠DOF=∠EOF=∠C=90°.又∵DF=DF,∠OFG=∠CFG,∴△DOF≌△DCF(AAS),∴DO=DC=AB.∵E是AB的中点,∴设EA=EB=EO=a,∴OD=CD=AB=2a,∴DE=OE+OD=3a.在Rt△ADE中,由勾股定理,得AD2+AE2=DE2,∴AD=(3a)2-a2=22a.∵AD=nAB,∴22a=2na,∴n=2.。
中考数学真题分类汇编及解析(二十八)菱形

(2022•武威中考)如图1,在菱形ABCD 中,∠A =60°,动点P 从点A 出发,沿折线AD →DC →CB 方向匀速运动,运动到点B 停止.设点P 的运动路程为x ,△APB 的面积为y ,y 与x 的函数图象如图2所示,则AB 的长为( )A .√3B .2√3C .3√3D .4√3【解析】选B .在菱形ABCD 中,∠A =60°,所以△ABD 为等边三角形,设AB =a ,由图2可知,△ABD 的面积为3√3,所以S △ABD =√34a 2=3√3,解得:a =2√3. (2022•自贡中考)如图,菱形ABCD 对角线交点与坐标原点O 重合,点A (﹣2,5),则点C 的坐标是( )A .(5,﹣2)B .(2,﹣5)C .(2,5)D .(﹣2,﹣5)【解析】选B.因为四边形ABCD 是菱形,所以OA =OC ,即点A 与点C 关于原点对称,因为点A (﹣2,5),所以点C 的坐标是(2,﹣5).(2022•株洲中考)如图所示,在菱形ABCD 中,对角线AC 与BD 相交于点O ,过点C 作CE ∥BD 交AB 的延长线于点E ,下列结论不一定正确的是( )A .OB =12CE B .△ACE 是直角三角形C .BC =12AE D .BE =CE 【解析】选D .因为四边形ABCD 是菱形,所以AO =CO =12,AC ⊥BD ,因为CE ∥BD ,所以△AOB ∽△ACE ,所以∠AOB =∠ACE =90°,AOAC =OBCE =ABAE =12,(2022•河南中考)如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,点E 为CD 的中点.若OE =3,则菱形ABCD 的周长为( )A .6B .12C .24D .48【解析】选C .因为四边形ABCD 为菱形,所以AC ⊥BD ,AB =BC =CD =DA ,所以△COD 为直角三角形.因为OE =3,点E 为线段CD 的中点,所以CD =2OE =6.所以C 菱形ABCD =4CD =4×6=24.(2022•赤峰中考)如图,菱形ABCD ,点A 、B 、C 、D 均在坐标轴上.∠ABC =120°,点A (﹣3,0),点E是CD 的中点,点P 是OC 上的一动点,则PD +PE 的最小值是( )A .3B .5C .2√2D .32√3【解析】选A .根据题意得,E 点关于x 轴的对称点是BC 的中点E ',连接DE '交AC 与点P ,此时PD +PE 有最小值为DE ',因为四边形ABCD 是菱形,∠ABC =120°,点A (﹣3,0),所以OA =OC =3,∠DBC =60°,所以△BCD 是等边三角形,所以DE '=OC =3,即PD +PE 的最小值是3.(2022•海南中考)如图,菱形ABCD 中,点E 是边CD 的中点,EF 垂直AB 交AB 的延长线于点F ,若BF :CE =1:2,EF =√7,则菱形ABCD 的边长是( )A .3B .4C .5D .45√7【解析】选B .过点D 作DH ⊥AB 于点H ,如图,因为四边形ABCD是菱形,所以AD=AB=CD,AB∥CD.因为EF⊥AB,DH⊥AB,所以DH∥EF,所以四边形DHFE为平行四边形,所以HF=DE,DH=EF=√7.因为点E是边CD的中点,所以DE=12CD,所以HF=12CD=12AB.因为BF:CE=1:2,所以设BF=x,则CE=2x,所以CD=4x,DE=HF=2x,AD=AB=4x,所以AF=AB+BF=5x.所以AH=AF﹣HF=3x.在Rt△ADH中,因为DH2+AH2=AD2,所以(√7)2+(3x)2=(4x)2.解得:x=±1(负数不合题意,舍去),所以x=1.所以AB=4x=4.即菱形ABCD的边长是4.A .52 B .5 C .10 D .20 【解析】选C .由作图过程可得:PQ 为BD 的垂直平分线,所以BM =MD ,BN =ND .设PQ 与BD 交于点O ,如图,则BO =DO .因为四边形ABCD 是矩形,所以AD ∥BC ,所以∠MDO =∠NBO ,∠DMO =∠BNO ,在△MDO 和△NBO 中,{∠MDO =∠NBO∠DMO =∠BNO OD =OB,所以△MDO ≌△NBO (AAS ),所以DM =BN ,所以四边形BNDM 为平行四边形,因为BM =MD ,所以四边形MBND 为菱形,所以四边形MBND 的周长=4BM .设MB =x ,则MD =BM =x ,所以AM =AD ﹣DM =4﹣x ,在Rt △ABM 中,因为AB 2+AM 2=BM 2,所以22+(4﹣x )2=x 2,解得:x =52,所以四边形MBND 的周长=4BM =10.(2022•武威中考)如图,菱形ABCD 中,对角线AC 与BD 相交于点O ,若AB =2√5cm ,AC =4cm ,则BD 的长为8 cm .【解析】因为四边形ABCD 是菱形,AC =4cm ,所以AC ⊥BD ,BO =DO ,AO =CO =2cm ,因为AB =2√5cm ,所以BO =√AB 2−AO 2=4cm ,所以DO =BO =4cm ,所以BD =8cm.答案:8.(2022•温州中考)如图,在菱形ABCD 中,AB =1,∠BAD =60°.在其内部作形状、大小都相同的菱形AENH和菱形CGMF ,使点E ,F ,G ,H 分别在边AB ,BC ,CD ,DA 上,点M ,N 在对角线AC 上.若AE =3BE ,则MN 的长为 √32 .【解析】连接DB 交AC 于点O ,作MI ⊥AB 于点I ,作FJ ⊥AB 交AB 的延长线于点J ,如图所示,因为四边形ABCD 是菱形,∠BAD =60°,AB =1,所以AB =BC =CD =DA =1,∠BAC =30°,AC ⊥BD ,因为△ABD 是等边三角形,所以OD =12,所以AO =√AD 2−DO 2=√12−(12)2=√32, 所以AC =2AO =√3,因为AE =3BE ,所以AE =34,BE =14,因为菱形AENH 和菱形CGMF 大小相同,所以BE =BF =14,∠FBJ =60°,所以FJ =BF •sin60°=14×√32=√38, 所以MI =FJ =√38,所以AM =MI sin30°=√3812=√34, 同理可得,CN =√34, 所以MN =AC ﹣AM ﹣CN =√3−√34−√34=√32. 答案:√32.DQ ﹣P 'Q 的最大值为 16√23.【解析】如图,连接BD 交AC 于点O ,过点D 作DK ⊥BC 于点B ,延长DE 交AB 于点R ,连接EP ′交AB 于点J ,作EJ 关于AC 的对称线段EJ ′,则DP ′的对应点P ″在线段EJ ′上.当点P 是定点时,DQ ﹣QP ′=AD ﹣QP ″,当D ,P ″,Q 共线时,QD ﹣QP ′的值最大,最大值是线段DP ″的长,当点P 与B 重合时,点P ″与J ′重合,此时DQ ﹣QP ′的值最大,最大值是线段DJ ′的长,也就是线段BJ 的长.因为四边形ABCD 是菱形,所以AC ⊥BD ,AO =OC ,因为AE =14.EC =18,所以AC =32,AO =OC =16,所以OE =AO ﹣AE =16﹣14=2,因为DE ⊥CD ,所以∠DOE =∠EDC =90°,因为∠DEO =∠DEC ,所以△EDO ∽△ECD ,所以DE 2=EO •EC =36,所以DE =EB =EJ =6,所以CD =√EC 2−DE 2=√182−62=12√2,所以OD =√DE 2−OE 2=√62−22=4√2,所以BD =8√2,因为S △DCB =12×OC ×BD =12BC •DK , 所以DK =12×16×8√212√212×16×8√26√2=323, 因为∠BER =∠DCK ,所以sin ∠BER =sin ∠DCK =DK CD =32312√2=4√29, 所以RB =BE ×4√29=8√23,3(2022•达州中考)如图,菱形ABCD的对角线AC,BD相交于点O,AC=24,BD=10,则菱形ABCD的周长为52.【解析】因为四边形ABCD是菱形,所以AB=BC=CD=DA,AC⊥BD,AO=CO,BO=DO,因为AC=24,BD=10,所以AO=12AC=12,BO=12BD=5,在Rt△AOB中,AB=√AO2+BO2=√122+52=13,所以菱形的周长为13×4=52.答案:52(2022•娄底中考)菱形ABCD的边长为2,∠ABC=45°,点P、Q分别是BC、BD上的动点,CQ+PQ的最小值为√2.【解析】连接AQ,作AH⊥BC于H,因为四边形ABCD是菱形,所以AB=CB,∠ABQ=∠CBQ,因为BQ=BQ,所以△ABQ≌△CBQ(SAS),(2022•天津中考)如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE的中点,AF与DE相交于点G,则GF的长等于√194.【解析】如图,过点F作FH∥CD,交DE于H,过点C作CM⊥AB,交AB的延长线于M,连接FB,因为四边形ABCD是菱形,所以AB=CD=BC=2,AB∥CD,所以FH∥AB,所以∠FHG=∠AEG,因为F是CE的中点,FH∥CD,所以H是DE的中点,所以FH是△CDE的中位线,所以FH=12CD=1,因为E是AB的中点,所以AE=BE=1,所以AE=FH,因为∠AGE=∠FGH,所以△AEG≌△FHG(AAS),所以AG=FG,因为AD∥BC,4(2022•陕西中考)如图,在菱形ABCD 中,AB =4,BD =7.若M 、N 分别是边AD 、BC 上的动点,且AM =BN ,作ME ⊥BD ,NF ⊥BD ,垂足分别为E 、F ,则ME +NF 的值为 √152.【解析】连接AC 交BD 于O ,因为四边形ABCD 为菱形,所以BD ⊥AC ,OB =OD =72,OA =OC ,由勾股定理得:OA =√AB 2−OB 2=√42−(72)2=√152,因为ME ⊥BD ,AO ⊥BD ,所以ME ∥AO ,所以△DEM ∽△DOA ,所以MEOA =DMAD ,即ME√152=4−AM 4,解得:ME =4√15−√15AM 8, 同理可得:NF =√15AM 8,所以ME +NF =√152,答案:√152.(2022•台州中考)如图,在菱形ABCD 中,∠A =60°,AB =6.折叠该菱形,使点A 落在边BC 上的点M 处,折痕分别与边AB ,AD 交于点E ,F .当点M 与点B 重合时,EF 的长为 3√3 ;当点M 的位置变化时,DF 长的最大值为 6﹣3√3 .【解析】如图1中,因为四边形ABCD 是菱形,所以AD =AB =BC =CD ,∠A =∠C =60°,所以△ADB ,△BDC 都是等边三角形,当点M 与B 重合时,EF 是等边△ADB 的高,EF =AD •sin60°=6×√32=3√3.如图2中,连接AM 交EF 于点O ,过点O 作OK ⊥AD 于点K ,交BC 于点T ,过点A 作AG ⊥CB 交CB 的延长线于点G ,取AD 的中点R ,连接OR .因为AD ∥CG ,OK ⊥AD ,所以OK ⊥CG ,所以∠G =∠AKT =∠GTK =90°,所以四边形AGTK 是矩形,所以AG =TK =AB •sin60°=3√3,因为OA =OM ,∥AOK =∠MOT ,∠AKO =∠MTO =90°,(2022•黔东南州中考)如图,矩形ABCD的对角线AC,BD相交于点O,DE∥AC,CE∥BD.若AC=10,则四边形OCED的周长是20.【解析】因为DE∥AC,CE∥BD,所以四边形OCED是平行四边形,所以OC=DE,OD=CE,因为矩形ABCD的对角线AC,BD相交于点O,所以OC=12AC=5,OD=12BD,BD=AC,所以OC=OD=5,所以OC=OD=CE=DE,所以平行四边形OCED是菱形,所以C菱形OCED=4OC=4×5=20.答案:20.(2022•哈尔滨中考)如图,菱形ABCD的对角线AC,BD相交于点O,点E在OB上,连接AE,点F为CD 的中点,连接OF.若AE=BE,OE=3,OA=4,则线段OF的长为2√5.【解析】因为四边形ABCD是菱形,所以AC⊥BD,AO=CO=4,BO=DO,所以AE=√AO2+EO2=√9+16=5,所以BE=AE=5,所以BO=8,所以BC=√BO2+CO2=√64+16=4√5,因为点F为CD的中点,BO=DO,所以OF=12BC=2√5.答案:2√5.【解析】添加的条件是AB =CD ,理由如下:因为AB ∥CD ,AB =CD ,所以四边形ABCD 是平行四边形,又因为AC ⊥BD ,所以平行四边形ABCD 是菱形.答案:AB =CD (答案不唯一).(2022•龙东中考)如图,菱形ABCD 中,对角线AC ,BD 相交于点O ,∠BAD =60°,AD =3,AH 是∠BAC的平分线,CE ⊥AH 于点E ,点P 是直线AB 上的一个动点,则OP +PE 的最小值是 32√6 .【解析】连接OE ,过点O 作OF ⊥AB ,垂足为F ,并延长到点O ′,使O ′F =OF ,连接O ′E 交直线AB 于点P ,连接OP ,所以AP 是OO ′的垂直平分线,所以OP =O ′P ,所以OP +PE =O ′P +PE =O ′E ,此时,OP +PE 的值最小,因为四边形ABCD 是菱形,所以AD =AB =3,∠BAC =12∠BAD ,OA =OC =12AC ,OD =OB =12BD ,∠AOD =90°,因为∠BAD =60°,所以△ADB 是等边三角形,所以BD =AD =3,所以OD =12BD =32,所以AO =√AD 2−DO 2=√32−(32)2=32√3,所以AC =2OA =3√3,因为CE ⊥AH ,所以∠AEC =90°,所以OE =OA =12AC =32√3,所以∠OAE =∠OEA ,因为AE 平分∠CAB ,所以∠OAE =∠EAB ,所以∠OEA =∠EAB ,所以OE ∥AB ,所以∠EOF =∠AFO =90°, 在Rt △AOF 中,∠OAB =12DAB =30°,所以OF =12OA =34√3,所以OO ′=2OF =32√3,在Rt △EOO ′中,O ′E =√EO 2+OO ′2=√(32√3)2+(32√3)2=32√6, 所以OE +PE =32√6,所以OP +PE 的最小值为32√6. 答案:32√6.(2022·安徽中考)已知四边形ABCD 中,BC =CD ,连接BD ,过点C 作BD 的垂线交AB 于点E ,连接DE .【解析】(1)证明:设CE 与BD 交于点O ,因为CB =CD ,CE ⊥BD ,所以DO =BO ,因为DE ∥BC ,所以∠DEO =∠BCO ,因为∠DOE =∠BOC ,所以△DOE ≌△BOC (AAS ),所以DE =BC ,所以四边形BCDE 是平行四边形,因为CD =CB ,所以平行四边形BCDE 是菱形;(2)(i )解:因为DE 垂直平分AC ,所以AE =EC 且DE ⊥AC ,所以∠AED =∠CED ,又因为CD =CB 且CE ⊥BD ,所以CE 垂直平分DB ,所以DE =BE ,所以∠DEC =∠BEC ,所以∠AED =∠CED =∠BEC ,又因为∠AED +∠CED +∠BEC =180°,所以∠CED =13×180°=60°;(ii )证明:由(i )得AE =EC ,又因为∠AEC =∠AED +∠DEC =120°,所以∠ACE =30°,同理可得,在等腰△DEB 中,∠EBD =30°,所以∠ACE =∠ABF =30°, 在△ACE 与△ABF 中,{∠ACE =∠ABF∠CAE =∠BAF AE =AF,所以△ABF ≌△ACE (AAS ),所以AC =AB ,又因为AE =AF ,所以AB ﹣AE =AC ﹣AF ,即BE =CF .(2022•连云港中考)如图,四边形ABCD 为平行四边形,延长AD 到点E ,使DE =AD ,且BE ⊥DC .(1)求证:四边形DBCE 为菱形;(2)若△DBC 是边长为2的等边三角形,点P 、M 、N 分别在线段BE 、BC 、CE 上运动,求PM +PN 的最小值.【解析】(1)证明:因为四边形ABCD 是平行四边形,所以AD ∥BC ,AD =BC ,因为DE =AD ,所以DE =BC ,因为E 在AD 的延长线上,所以DE ∥BC ,所以四边形DBCE是平行四边形,因为BE⊥DC,所以四边形DBCE是菱形;(2)解:作N关于BE的对称点N',过D作DH⊥BC于H,如图:由菱形的对称性知,点N关于BE的对称点N'在DE上,所以PM+PN=PM+PN',所以当P、M、N'共线时,PM+PN'=MN'=PM+PN,因为DE∥BC,所以MN'的最小值为平行线间的距离DH的长,即PM+PN的最小值为DH的长,在Rt△DBH中,∠DBC=60°,DB=2,=√3,所以PM+PN的最小值为√3.所以DH=DB•sin∠DBC=2×√32(2022•滨州中考)如图,菱形ABCD的边长为10,∠ABC=60°,对角线AC、BD相交于点O,点E在对角线BD 上,连接AE,作∠AEF=120°且边EF与直线DC相交于点F.(1)求菱形ABCD的面积;(2)求证AE=EF.【解析】(1)作AG⊥BC交BC于点G,如图所示,因为四边形ABCD是菱形,边长为10,∠ABC=60°,=5√3,所以BC=10,AG=AB•sin60°=10×√32所以菱形ABCD的面积是:BC•AG=10×5√3=50√3,即菱形ABCD的面积是50√3;(2)证明:连接EC,因为四边形ABCD是菱形,∠ABC=60°,所以EO垂直平分AC,∠BCD=120°,所以EA=EC,∠DCA=60°,所以∠EAC=∠ECA,∠ACF=120°,因为∠AEF=120°,所以∠EAC+∠EFC=360°﹣∠AEF﹣∠ACF=360°﹣120°﹣120°=120°,因为∠ECA+∠ECF=120°,所以∠EFC=∠ECF,所以EC=EF,所以AE=EF.(2022•舟山中考)小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.小惠:证明:因为AC⊥BD,OB=OD,所以AC垂直平分BD.所以AB=AD,CB=CD,所以四边形ABCD是菱形.小洁:这个题目还缺少条件,需要补充一个条件才能证明.若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.【解析】赞成小洁的说法,补充条件:OA=OC,证明如下:因为OA=OC,OB=OD,所以四边形ABCD是平行四边形,又因为AC⊥BD,所以平行四边形ABCD是菱形.(2022•凉山州中考)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.(1)求证:四边形ADBF是菱形;(2)若AB=8,菱形ADBF的面积为40.求AC的长.【解析】(1)证明:因为AF∥BC,所以∠AFC=∠FCD,∠F AE=∠CDE,因为点E是AD的中点,所以AE=DE,所以△F AE≌△CDE(AAS),所以AF=CD,因为点D是BC的中点,所以BD=CD,所以AF=BD,所以四边形AFBD是平行四边形,(2022•南充中考)如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.求证:(1)△ADE≌△CDF.(2)ME=NF.【证明】(1)因为四边形ABCD是菱形,所以DA=DC,∠DAE=∠DCF,AB=CB,因为BE=BF,所以AE=CF,在△ADE和△CDF中,{DA=DC∠DAE=∠DCF AE=CF,所以△ADE≌△CDF(SAS);(2)由(1)知△ADE≌△CDF,所以∠ADM=∠CDN,DE=DF,因为四边形ABCD是菱形,所以∠DAM=∠DCN,所以∠DMA=∠DNC,所以∠DMN=∠DNM,所以DM=DN,所以DE﹣DM=DF﹣DN,所以ME=NF.(2022•广元中考)如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB中点,连结CE.(1)求证:四边形AECD为菱形;(2)若∠D=120°,DC=2,求△ABC的面积.【解析】(1)证明:因为E为AB中点,所以AB=2AE=2BE,因为AB=2CD,所以CD=AE,又因为AE∥CD,所以四边形AECD是平行四边形,因为AC平分∠DAB,所以∠DAC=∠EAC,因为AB∥CD,所以∠DCA=∠CAB,所以∠DCA=∠DAC,所以AD=CD,所以平行四边形AECD是菱形;(2)因为四边形AECD是菱形,∠D=120°,所以AD=CD=CE=AE=2,∠D=120°=∠AEC,所以AE=CE=BE,∠CEB=60°,所以∠CAE=30°=∠ACE,△CEB是等边三角形,所以BE=BC=EC=2,∠B=60°,所以∠ACB=90°,所以AC=√3BC=2√3,所以S△ABC=12×AC×BC=12×2×2√3=2√3.【解析】(1)①证明:因为CE⊥AB,CF⊥AD,所以∠BEC=∠DFC=90°,因为四边形ABCD是菱形,所以∠B=∠D,BC=CD,所以△BEC≌△DFC(AAS),所以CE=CF;②连接AC,如图1,因为E是边AB的中点,CE⊥AB,所以BC=AC,因为四边形ABCD是菱形,所以BC=AC,所以△ABC是等边三角形,∠EAC=60°,在Rt△ACE中,AE=2,所以CE=AE•tan60°=2×√3=2√3;(2)方法一:如图2,延长FE交CB的延长线于M,因为四边形ABCD是菱形,所以AD∥BC,AB=BC,所以∠AFE=∠M,∠A=∠EBM,因为E是边AB的中点,所以AE=BE,所以△AEF≌△BEM(AAS),所以ME=EF,MB=AF,因为AE=3,EF=2AF=4,所以ME=4,BM2,BE=3,所以BC=AB=2AE=6,所以MC=8,所以MBME =24=12,MEMC=48=12,所以MBME=MEMC,因为∠M为公共角,所以△MEB∽△MCE,所以BEEC =MBME=24,因为BE=3,所以CE=6;方法二:如图3,延长FE 交CB 的延长线于M ,过点E 作EN ⊥BC 于点N ,因为四边形ABCD 是菱形,所以AD ∥BC ,AB =BC ,所以∠AFE =∠M ,∠A =∠EBM ,因为E 是边AB 的中点,所以AE =BE ,所以△AEF ≌△BEM (AAS ),所以ME =EF ,MB =AF ,因为AE =3,EF =2AF =4,所以ME =4,BM 2,BE =3,所以BC =AB =2AE =6,所以MC =8,在Rt △MEN 和Rt △BEN 中,ME 2﹣MN 2=EN 2,BE 2﹣BN 2=EN 2,所以ME 2﹣MN 2=BE 2﹣BN 2,所以42﹣(2+BN )2=32﹣BN 2,解得:BN =34,所以CN =6−34=214, 所以EN 2=BE 2﹣BN 2=32﹣(34)2=13516,在Rt △ENC 中,CE 2=EN 2+CN 2=13516+44116=57616=36,所以CE =6.(2022•娄底中考)如图,以BC 为边分别作菱形BCDE 和菱形BCFG (点C ,D ,F 共线),动点A 在以BC 为直径且处于菱形BCFG 内的圆弧上,连接EF 交BC 于点O .设∠G =θ.(1)求证:无论θ为何值,EF 与BC 相互平分;并请直接写出使EF ⊥BC 成立的θ值.(2)当θ=90°时,试给出tan ∠ABC 的值,使得EF 垂直平分AC ,请说明理由.【解析】(1)因为四边形BCFG ,四边形BCDE 都是菱形,所以CF ∥BG ,CD ∥BE ,CB =CF =CD =BG =BE ,因为D ,C ,F 共线,所以G ,B ,E 共线,所以DF ∥EG ,DF =GE ,所以四边形DEGF 是平行四边形,所以EF 与BC 互相平分.当EF ⊥FG 时,因为GF =BG =BE ,所以EG =2GF ,所以∠GEF =30°,所以θ=90°﹣30°=60°;(2)当tan ∠ABC =2时,EF 垂直平分线段AC .理由:如图(2)中,设AC 交EF 于点J .因为四边形BCFG 是菱形,所以∠G =∠FCO =90°,因为EF 与BC 互相平分,所以OC =OB ,所以CF =BC ,所以FC =2OC ,所以tan ∠FOC =tan ∠ABC ,所以∠ABC =∠FOC ,所以OJ ∥AB ,因为OC =OB ,所以CJ =AJ ,因为BC 是直径,所以∠BAC =∠OJC =90°,所以EF 垂直平分线段AC.(2022•岳阳中考)如图,点E ,F 分别在▱ABCD 的边AB ,BC 上,AE =CF ,连接DE ,DF .请从以下三个条件:①∠1=∠2;②DE =DF ;③∠3=∠4中,选择一个合适的作为已知条件,使▱ABCD 为菱形. (1)你添加的条件是 ① (填序号);(2)添加了条件后,请证明▱ABCD 为菱形.【解析】(1)添加的条件是∠1=∠2,答案:①;(2)证明:因为四边形ABCD 是平行四边形,所以∠A =∠C ,在△ADE 和△CDF 中,{∠1=∠2∠A =∠C AE =CF,所以△ADE ≌△CDF (AAS ),所以AD =CD ,所以▱ABCD 为菱形.【解析】(1)M 与B 重合时,如图1,因为PQ ⊥AB ,所以∠PQA =90°,所以PA =12AB =2,所以t =2;(2)①当0≤t ≤2时,因为AM =2t ,所以BM =4﹣2t ,因为△APQ ≌△BMF ,所以AP =BM ,所以t =4﹣2t ,所以t =43;②当2<t ≤4时,因为AM =2t ,所以BM =2t ﹣4,因为△APQ ≌△BMF ,所以AP =BM ,所以t =2t ﹣4,所以t =4;综上所述,t 的值为4或43; (3)①0≤t ≤2时,如图2,在Rt △APQ 中,PQ =√32t ,所以MQ =32t ,所以S =12PQ ⋅MQ =12×√32t ×32t =3√38t 2; ②当2<t ≤4时,如图3,因为BF =t ﹣2,MF =√3(t ﹣2),所以S △BFM =12BF •MF =√32(t −2)2,所以S =S △PQM ﹣S △BFM =−√38t 2+2√3t −2√3;所以S ={3√38t 2(0≤t ≤2)−√38t 2+2√3t −2√3(2<t ≤4); (4)连接AE ,如图4,因为△PQE 为等边三角形,所以PE =√32t ,在Rt △APE 中,tan ∠PAE =PE PA =√32t t =√32, 所以∠PAE 为定值,所以点E 的运动轨迹为直线,因为AP =t ,所以AE =√AP 2+PE 2=√t 2+(√32t)2=√72t ,当t =2时,AE =√7,(2022•荆州中考)如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中△ABC为格点三角形.请按要求作图,不需证明.(1)在图1中,作出与△ABC全等的所有格点三角形,要求所作格点三角形与△ABC有一条公共边,且不与△ABC重叠;(2)在图2中,作出以BC为对角线的所有格点菱形.【解析】(1)如图1中,△ABD1,△ABD2,△ACD3,△ACD4,△CBD5即为所求;(2)如图2中,菱形ABDC,菱形BECF即为所求.(2022•长沙中考)如图,在▱ABCD中,对角线AC,BD相交于点O,AB=AD.(1)求证:AC⊥BD;(2)若点E,F分别为AD,AO的中点,连接EF,EF=32,AO=2,求BD的长及四边形ABCD的周长.【解析】(1)因为四边形ABCD是平行四边形,AB=AD,所以▱ABCD是菱形,所以AC⊥BD;(2)因为点E,F分别为AD,AO的中点,所以EF是△AOD的中位线,所以OD=2EF=3,由(1)可知,四边形ABCD是菱形,所以AB=BC=CD=AD,AC⊥BD,BD=2OD=6,在Rt△AOD中,由勾股定理得:AD=√AO2+OD2=√22+32=√13,所以C菱形ABCD=4AD=4√13.(2)若AE=BE=2,求BF的长.【解析】(1)因为四边形ABCD是正方形,四边形HEFG是菱形,所以AD=CD,ED=GD,∠ADB=∠CDB,∠EHB=∠GHB,所以∠ADB﹣∠EHB=∠CDB﹣∠GHB,即∠ADE=∠CDG,在△ADE和△CDG中,{AD=CD∠ADE=∠CDG ED=GD,所以△ADE≌△CDG(SAS);(2)过E作EQ⊥DF于Q,则∠EQB=90°,因为四边形ABCD是正方形,所以∠A=90°,AD=AB=AE+EF=2+2=4,∠EBQ=∠CBD=45°,所以∠QEB=45°=∠EBQ,所以EQ=BQ,因为BE=2,所以2EQ2=22,所以EQ=BQ=√2(负数舍去),在Rt△DAE中,由勾股定理得:DE=√AD2+AE2=√42+22=2√5,因为四边形EFGH是菱形,所以EF=DE=2√5,所以QF=√EF2−EQ2=√(2√5)2−(√2)2=3√2,所以BF=QF﹣QB=3√2−√2=2√2.【解析】(1)作PE⊥AC于点E,在Rt△APE中,cos30°=AE AP,所以AE=AP•cos30°=√3x,因为∠APQ=120°,所以∠AQP=180°﹣120°﹣30°=30°,所以AP=PQ,所以点E为AQ中点,所以AQ=2√3x(cm),答案:2√3x.(2)如图,因为∠APQ=120°,所以∠MNB=∠PQB=60°,因为∠B=60°,所以△MNB为等边三角形,所以AP=PQ=PN=MN=NB,即AP+PN+NB=3AP=AB,所以3×2x=6,解得x=1.(3)当0≤x≤1时,作QF⊥AB于点F,因为∠A =30°,AQ =2√3x ,所以QF =12AQ =√3x ,因为PN =PQ =AP =2x ,所以y =PN •QF =2x •√3x =2√3x 2.当1<t ≤32时,QM ,NM 交BC 于点H ,K ,因为AB =6cm ,∠A =30°,所以AC =√32AB =3√3cm ,所以CQ =AC ﹣AQ =3√3−2√3x ,所以QH =2√3CQ =2√3(3√3−2√3x )=6﹣4x , 所以HM =QM ﹣QH =2x ﹣(6﹣4x )=6x ﹣6, 因为△HKM 为等边三角形,所以S △HKM =√34HM 2=9√3x 2﹣18√3x +9√3, 所以y =2√3x 2﹣(9√3x 2﹣18√3x +9√3)=﹣7√3x 2+18√3x ﹣9√3. 当32<x ≤3时,重叠图形△PQM 为等边三角形,PQ =PB =AB ﹣AP =6﹣2x ,所以y =√34PB 2=√34(6﹣2x )2=√3x 2﹣6√3x +9√3.综上所述,y ={ 2√3x 2(0≤x ≤1)−7√3x 2+18√3x −9√3(1<x ≤32)√3x 2−6√3x +9√3(32<x ≤3)。
2017年全国中考数学真题分类 矩形、菱形与正方形2017(填空题)

2017年全国中考数学真题分类矩形、菱形与正方形填空题二、填空题1.(2017山东滨州,16,4分)如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F.若AD=8,AB=6,AE=4,则△EBF周长的大小为___________.AB CDHQGFE答案:8,解析:设DH=x,则AH=8-x,由折叠的对称性,可知EH=DH=x,在Rt△AEH中,应用勾股定理,得AE2+AH2=EH2,即42+(8-x)2=x2,解得x=5.由∠GEF=90°,可证明△AHE∽△BEF,因此AE AH EHBF BE EF==,即4352BF EF==,可以求得BF=83,EF=103.所以△EBF周长为83+103+2=8.2.(2017重庆18,4分)如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将∆EFG沿EF翻折,得到∆EFM,连接DM,交EF于点N,若点F是AB边的中点,则∆EMN的周长是 .答案:21025+解析:①连接GM交EF于点H,∵将∆EFG沿EF翻折,得到∆EFM,∴EM=EG,EF垂直且平分GM,∵EF⊥ED,∴GM∥DE;②在正方形ABCD中,AD=4,∴AB=AD=CD=4,∠DAB=∠ADC =90゜,AB ∥CD ,∴AC =244422=+,∵F 是AB 的中点,∴AF =2,∴DF =522422=+;又∵AF ∥CD ,∴21===CD AF CG AG DG GF ,∴DG =354,FG =352,AG =324;③∵∠DAF =∠DEF =90゜,∴A 、D 、E 、F 四点共圆,∴∠EDF =∠EAF =45゜,∴∆DEF 是等腰直角三角形,∴()22252=+FE DE ,∴10==EF DE ,∵GH ∥DE ,∴31===EF FH DE GH DF GF ,∴310=FH ,3102=EH ;又∵GH =HM ,HM ∥DE ,∴31===EN HN DN MN DE HM ,∴21043==EH EN ,∵∠DEN =90゜,DE =10,∴DN =()2252101022=⎪⎪⎭⎫ ⎝⎛+,∴MN =625;④∵∠DGE =∠AGF ,∠EDG =∠GAF =45゜,∴∆DGE ∽∆AGF ,∴DG FG EG AG ⋅=⋅,∵DG =354,FG =352,AG =324,∴EG =325=EM ; ⑤∵210=EN ,MN =625, EM =325,∴∆EMN 的周长=210+625+325=21025+.3. (2017浙江衢州,14,4分)如图,从边长为(a +3)的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(无重叠无缝隙),则拼成的长方形的另一边长是.a +3(第14题)33a答案:a +6,解析:结合图形,长方形的另一边的长为3+a +3=a +6.4. (2017山东菏泽,11,3分)菱形ABCD 中,∠A =60°,其周长为24cm ,则菱形的面积为2cm .答案:183,解析:∵四边形ABCD 是菱形,∴AB=BC=CD=DA ,AC ⊥BD ,∵∠A =60°,∴△ABD 是等边三角形,又周长为24cm ,即BD=AB=6cm ,在Rt △AOB 中,OD=3cm ,∴AO=22226333AD OD -=-=,∴AC=2AO=63,菱形的面积=12AC BD ⋅=163618 3.2⨯⨯=5. 如图,正方形ABCD 中,BC =2,点M 是边AB 的中点,连接DM ,DM 与AC 交于点P ,点E 在DC 上,点F 在DP 上,且∠DFE =45°,若PF =65,则CE = .答案:67,解析:在Rt △ADM 中,AD =2,AM =1,由勾股定理,得DM =522=+AM AD ,由DC ∥AM ,得△DPC ~△MPA ,得2==AM DC MP DP ,∴DP =53232=DM . 又∵PF =65,所以DF =DP -PF =2565532=-.又因为∠DFE =∠DCP =45°,∠EDF =∠PDC ,所以△DFE ~△DCP ,所以DC DF DP DE =,即2521532=DE,解得DE =65. 所以CE =DC -DE =2-65=67.6. (2017山东潍坊,18,3分)如图,将一张矩形纸片ABCD 的边BC 斜着向AD 边对折,使点B 落在AD 上,记为B ′,折痕为CE ;再将CD 边斜向下对折,使点D 落在B ′C 上,记为D ′,折痕为CG ,B ′D ′=2,BE =31BC .则矩形纸片ABCD 的面积为 .2-1-c-n-j-y答案:15,解析:由折叠可知BC =B ′C ,CD =CD ′,又B ′D ′=2,故设BC =x ,则CD =x -2,EB ′=BE =31x ,∴AE =AB -BE =32x -2.由∠EB ′C =∠B =90°,易证△CDB ′∽△B ′AE ,∴CD :B ′A =B ′C :B ′E =3:1,∴B ′A =32-x .在Rt △B ′AE 中,由勾股定理,得(32-x )2+(32x -2)2=(31x )2,整理,得x 2-7x +10=0,解得x 1=5,x 2=2(不合题意,舍去).矩形纸片ABCD 的面积为BC ·CD =5×3=15.7. (2017四川宜宾,11,3分)如图,在菱形ABCD 中,若AC =8,BD =6,则菱形ABCD 的面积是 .答案:24,解析:根据菱形的面积等于对角线乘积的一半,由AC =8,BD =6,则S 等于24.DCA8. (2017湖南常德,15,3分)如图4,正方形EFGH 的顶点在边长为2的正方形的边上,若设AE=x ,正方形EFGH 的面积为y ,则y 与x 的函数关系为_______________.答案:y =2x 2-4x +4,解析:由题中条件可知,图中的四个直角三角形是全等三角形,设AE=x ,则BE =2x ,BF =x ,在Rt △EBF 中,由勾股定理可得EF 2=(2-x)2+x 2=2x 2-4x +4,即正方形的面积为2x 2-4x +4.9. (2017江苏苏州,18,3分)如图,在矩形ABCD 中,将∠ABC 绕点A 按逆时针方向旋转一定角度后,BC 的对应边B C ''交CD 边于点G .连接BB '、CC ',若AD =7,CG =4,AB B G ''=,则CC BB '='(结果保留根号).答案:74解析:根据“旋转的性质、勾股定理”,连接AG ,设DG =x ,则4AB B G x ''==+.在Rt AB G ∆'中,x 2+49=2(x +4)2,∴x =1.则AB =5,BC =7,∴254974CC BB'+=='.10. 19.(2017甘肃兰州,19,4分)在平行四边形ABCD 中,对角线AC 与DB 相交于点O 。
7.20几何压轴题(第3部分)-2018年中考数学试题分类汇编(word解析版)
第七部分专题拓展7.20 几何压轴题【一】知识点清单【二】分类试题汇编及参考答案与解析一、选择题1.(2018年贵州省遵义市-第12题-3分)如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=5,BC=10,连接AC、BD,以BD为直径的圆交AC于点E.若DE=3,则AD的长为()A.5 B.4 C.D.【知识考点】勾股定理;相似三角形的判定与性质.【思路分析】先求出AC,进而判断出△ADF∽△CAB,即可设DF=x,AD=x,利用勾股定理求出BD,再判断出△DEF∽△DBA,得出比例式建立方程即可得出结论.【解答过程】解:如图,在Rt△ABC中,AB=5,BC=10,∴AC=5过点D作DF⊥AC于F,∴∠AFD=∠CBA,∵AD∥BC,∴∠DAF=∠ACB,∴△ADF∽△CAB,∴,∴,设DF=x,则AD=x,在Rt△ABD中,BD==,∵∠DEF=∠DBA,∠DFE=∠DAB=90°,∴△DEF∽△DBA,∴,∴,∴x=2,∴AD=x=2,故选:D.【总结归纳】此题主要考查了勾股定理,相似三角形的判定和性质,平行线的性质,正确作出辅助线是解本题的关键.2.(2018年内蒙古鄂尔多斯市-第6题-3分)如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于12CD为半径作弧,两弧交于点M,N;②作直线MN,且MN恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是()A.∠ABC=60°B.S△ABE=2S△ADEC.若AB=4,则BE D.sin∠CBE【知识考点】三角形的面积;线段垂直平分线的性质;菱形的性质;作图—基本作图;解直角三角形.【思路分析】由作法得AE垂直平分CD,则∠AED=90°,CE=DE,于是可判断∠DAE=30°,∠D=60°,从而得到∠ABC=60°;利用AB=2DE得到S△ABE=2S△ADE;作EH⊥BC于H,如图,若AB=4,则可计算出CH=CE=1,EH=CH=,利用勾股定理可计算出BE=2;利用正弦的定义得sin∠CBE==.【解答过程】解:由作法得AE垂直平分CD,∴∠AED=90°,CE=DE,∵四边形ABCD为菱形,∴AD=2DE,∴∠DAE=30°,∠D=60°,∴∠ABC=60°,所以A选项的说法正确;∵AB=2DE,∴S△ABE=2S△ADE,所以B选项的说法正确;作EH⊥BC于H,如图,若AB=4,在Rt△ECH中,∵∠ECH=60°,∴CH=CE=1,EH=CH=,在Rt△BEH中,BE==2,所以C选项的说法错误;sin∠CBE===,所以D选项的说法正确.故选:C.【总结归纳】本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了菱形的性质和解直角三角形.3.(2018年江苏省无锡市-第8题-3分)如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是()A.0 B.1 C.2 D.3【知识考点】矩形的性质;切线的判定.【思路分析】连接DG、AG,作GH⊥AD于H,连接OD,如图,先确定AG=DG,则GH垂直平分AD,则可判断点O在HG上,再根据HG⊥BC可判定BC与圆O相切;接着利用OG=OG可判断圆心O不是AC与BD的交点;然后根据四边形AEFD为⊙O的内接矩形可判断AF与DE的交点是圆O的圆心.【解答过程】解:连接DG、AG,作GH⊥AD于H,连接OD,如图,∵G是BC的中点,∴AG=DG,∴GH垂直平分AD,∴点O在HG上,∵AD∥BC,∴HG⊥BC,∴BC与圆O相切;∵OG=OG,∴点O不是HG的中点,∴圆心O不是AC与BD的交点;而四边形AEFD为⊙O的内接矩形,∴AF与DE的交点是圆O的圆心;∴(1)错误,(2)(3)正确.故选:C.【总结归纳】本题考查了三角形内切圆与内心:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.也考查了矩形的性质.4.(2018年山东省潍坊市-第6题-3分)如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;(3)连接BD,BC.下列说法不正确的是()A.∠CBD=30°B.S△BDC=AB2C.点C是△ABD的外心D.sin2A+cos2D=l【知识考点】作图—基本作图;线段垂直平分线的性质;三角形的外接圆与外心;解直角三角形的应用.【思路分析】根据等边三角形的判定方法,直角三角形的判定方法以及等边三角形的性质,直角三角形的性质一一判断即可;【解答过程】解:由作图可知:AC=AB=BC,∴△ABC是等边三角形,由作图可知:CB=CA=CD,∴点C是△ABD的外心,∠ABD=90°,BD=AB,∴S △ABD =AB 2,∵AC=CD , ∴S △BDC =AB 2,故A 、B 、C 正确, 故选:D .【总结归纳】本题考查作图﹣基本作图,线段的垂直平分线的性质,三角形的外心等知识,直角三角形等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型. 5.(2018年四川省南充市-第10题-3分)如图,正方形ABCD 的边长为2,P 为CD 的中点,连结AP ,过点B 作BE ⊥AP 于点E ,延长CE 交AD 于点F ,过点C 作CH ⊥BE 于点G ,交AB 于点H ,连接HF .下列结论正确的是( )A .B .EF=2 C .cos ∠CEP=5D .HF 2=EF•CF 【知识考点】相似三角形的判定与性质;全等三角形的判定与性质;正方形的性质;解直角三角形. 【思路分析】首先证明BH=AH ,推出EG=BG ,推出CE=CB ,再证明△CEH ≌△CBH ,Rt △HFE ≌Rt △HFA ,利用全等三角形的性质即可一一判断. 【解答过程】解:连接EH .∵四边形ABCD 是正方形, ∴CD=AB═BC=AD=2,CD ∥AB , ∵BE ⊥AP ,CH ⊥BE , ∴CH ∥PA ,∴四边形CPAH 是平行四边形, ∴CP=AH , ∵CP=PD=1, ∴AH=PC=1, ∴AH=BH ,在Rt△ABE中,∵AH=HB,∴EH=HB,∵HC⊥BE,∴BG=EG,∴CB=CE=2,故选项A错误,∵CH=CH,CB=CE,HB=HE,∴△ABC≌△CEH,∴∠CBH=∠CEH=90°,∵HF=HF,HE=HA,∴Rt△HFE≌Rt△HFA,∴AF=EF,设EF=AF=x,在Rt△CDF中,有22+(2﹣x)2=(2+x)2,∴x=,∴EF=,故B错误,∵PA∥CH,∴∠CEP=∠ECH=∠BCH,∴cos∠CEP=cos∠BCH==,故C错误.∵HF=,EF=,FC=∴HF2=EF•FC,故D正确,故选:D.【总结归纳】本题考查正方形的性质、全等三角形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考选择题中的压轴题.二、填空题1.(2018年内蒙古鄂尔多斯市-第16题-3分)如图1,AF,BE是△ABC的中线,AF⊥BE,垂足为点P,设BC=a,AC=b,AB=c,则a2+b2=5c2,利用这一性质计算.如图2,在▱ABCD中,E,F,G分别是AD,BC,CD的中点,EB⊥EG于点E,AD=8,AB=则AF=.【知识考点】勾股定理;三角形中位线定理;平行四边形的性质.【思路分析】连接AC交EF于H,设BE与AF的交点为P,由点E、G分别是AD,CD的中点,得到EG是△ACD的中位线于是证出BE⊥AC,由四边形ABCD是平行四边形,得到AD∥BC,根据E,F分别是AD,BC的中点,得到AE=BF=CF=AD,证出四边形ABFE是平行四边形,证得EH=FH,推出EH,AH分别是△AFE的中线,由题目中的结论得即可得到结果.【解答过程】解:如图2,连接AC,EF交于H,AC与BE交于点Q,设BE与AF的交点为P,∵点E、G分别是AD,CD的中点,∴EG∥AC,∵BE⊥EG,∴BE⊥AC,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC=8,∴∠EAH=∠FCH,∵E,F分别是AD,BC的中点,∴AE=AD,BF=BC,∴AE=BF=CF=AD=4,∵AE∥BF,∴四边形ABFE是平行四边形,∴EF=AB=2,AP=PF,在△AEH和△CFH中,,∴△AEH≌△CFH(AAS),∴EH=FH,∴EP,AH分别是△AFE的中线,由a2+b2=5c2得:AF2+EF2=5AE2,∴AF2=5×42﹣(2)2=60,∴AF=2.故答案为:2.【总结归纳】本题考查了平行四边形的性质,勾股定理,三角形的中位线的性质,正确的作出辅助线是解题的关键.2.(2018年贵州省遵义市-第18题-4分)如图,在菱形ABCD中,∠ABC=120°,将菱形折叠,使点A恰好落在对角线BD上的点G处(不与B、D重合),折痕为EF,若DG=2,BG=6,则BE的长为.【知识考点】菱形的性质;翻折变换(折叠问题).【思路分析】作EH⊥BD于H,根据折叠的性质得到EG=EA,根据菱形的性质、等边三角形的判定定理得到△ABD为等边三角形,得到AB=BD,根据勾股定理列出方程,解方程即可.【解答过程】解:作EH⊥BD于H,由折叠的性质可知,EG=EA,由题意得,BD=DG+BG=8,∵四边形ABCD是菱形,∴AD=AB,∠ABD=∠CBD=∠ABC=60°,∴△ABD为等边三角形,∴AB=BD=8,设BE=x,则EG=AE=8﹣x,在Rt△EHB中,BH=x,EH=x,在Rt△EHG中,EG2=EH2+GH2,即(8﹣x)2=(x)2+(6﹣x)2,解得,x=2.8,即BE=2.8,故答案为:2.8.【总结归纳】本题考查的是翻转变换的性质、菱形的性质、勾股定理、解直角三角形,掌握翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.3.(2018年湖北省咸宁市-第16题-3分)如图,已知∠MON=120°,点A,B分别在OM,ON上,且OA=OB=a,将射线OM绕点O逆时针旋转得到OM′,旋转角为α(0°<α<120°且α≠60°),作点A关于直线OM′的对称点C,画直线BC交OM′于点D,连接AC,AD,有下列结论:①AD=CD;②∠ACD的大小随着α的变化而变化;③当α=30°时,四边形OADC为菱形;④△ACD2;其中正确的是.(把你认为正确结论的序号都填上).【知识考点】等边三角形的性质;菱形的判定与性质;轴对称的性质;旋转的性质.【思路分析】①根据对称的性质:对称点的连线被对称轴垂直平分可得:OM'是AC的垂直平分线,再由垂直平分线的性质可作判断;②作⊙O,根据四点共圆的性质得:∠ACD=∠E=60°,说明∠ACD是定值,不会随着α的变化而变化;③当α=30°时,即∠AOD=∠COD=30°,证明△AOC是等边三角形和△ACD是等边三角形,得OC=OA=AD=CD,可作判断;④先证明△ACD是等边三角形,当AC最大时,△ACD的面积最大,当AC为直径时最大,根据面积公式计算后可作判断.【解答过程】解:①∵A、C关于直线OM'对称,∴OM'是AC的垂直平分线,∴CD=AD,故①正确;②连接OC,由①知:OM'是AC的垂直平分线,∴OC=OA,∴OA=OB=OC,以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,则A、B、C都在⊙O上,∵∠MON=120°,∴∠BOE=60°,∵OB=OE,∴△OBE是等边三角形,∴∠E=60°,∵A、C、B、E四点共圆,∴∠ACD=∠E=60°,故②不正确;③当α=30°时,即∠AOD=∠COD=30°,∴∠AOC=60°,∴△AOC是等边三角形,∴∠OAC=60°,OC=OA=AC,由①得:CD=AD,∴∠CAD=∠ACD=∠CDA=60°,∴△ACD是等边三角形,∴AC=AD=CD,∴OC=OA=AD=CD,∴四边形OADC为菱形;故③正确;④∵CD=AD,∠ACD=60°,∴△ACD是等边三角形,当AC最大时,△ACD的面积最大,∵AC是⊙O的弦,即当AC为直径时最大,此时AC=2OA=2a,α=90°,∴△ACD面积的最大值是:AC2==,故④正确,所以本题结论正确的有:①③④故答案为:①③④.【总结归纳】本题是圆和图形变换的综合题,考查了轴对称的性质、四点共圆的性质、等边三角形的判定、菱形的判定、三角形面积及圆的有关性质,有难度,熟练掌握轴对称的性质是关键,是一道比较好的填空题的压轴题.4.(2018年江苏省无锡市-第18题-2分)如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是.【知识考点】等边三角形的性质;含30度角的直角三角形;平行四边形的判定与性质.【思路分析】作辅助线,构建30度的直角三角形,先证明四边形EODP是平行四边形,得EP=OD=a,在Rt△HEP中,∠EPH=30°,可得EH的长,计算a+2b=2OH,确认OH最大和最小值的位置,可得结论.【解答过程】解:过P作PH⊥OY交于点H,∵PD∥OY,PE∥OX,∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,∴EP=OD=a,Rt△HEP中,∠EPH=30°,∴EH=EP=a,∴a+2b=2(a+b)=2(EH+EO)=2OH,当P在AC边上时,H与C重合,此时OH的最小值=OC=OA=1,即a+2b的最小值是2;当P在点B时,OH的最大值是:1+=,即(a+2b)的最大值是5,∴2≤a+2b≤5.【总结归纳】本题考查了等边三角形的性质、直角三角形30度角的性质、平行四边形的判定和性质,有难度,掌握确认a+2b的最值就是确认OH最值的范围.5.(2018年江苏省苏州市-第18题-3分)如图,已知AB=8,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,∠DAP=60°.M,N分别是对角线AC,BE的中点.当点P在线段AB上移动时,点M,N之间的距离最短为(结果留根号).【知识考点】垂线段最短;三角形中位线定理;菱形的性质;梯形.【思路分析】连接PM、PN.首先证明∠MPN=90°设PA=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),构建二次函数,利用二次函数的性质即可解决问题;【解答过程】解:连接PM、PN.∵四边形APCD,四边形PBFE是菱形,∠DAP=60°,∴∠APC=120°,∠EPB=60°,∵M,N分别是对角线AC,BE的中点,∴∠CPM=∠APC=60°,∠EPN=∠EPB=30°,∴∠MPN=60°+30°=90°,设PA=2a,则PB=8﹣2a,PM=a,PN=(4﹣a),∴MN===,∴a=3时,MN有最小值,最小值为2,故答案为2.【总结归纳】本题考查菱形的性质、勾股定理二次函数的性质等知识,解题的关键是学会添加常用辅助线,构建二次函数解决最值问题.6.(2018年辽宁省大连市-第16题-3分)如图,矩形ABCD中,AB=2,BC=3,点E为AD上一点,且∠ABE=30°,将△ABE沿BE翻折,得到△A′BE,连接CA′并延长,与AD相交于点F,则DF 的长为.【知识考点】矩形的性质;翻折变换(折叠问题).【思路分析】如图作A′H⊥BC于H.由△CDF∽△A′HC,可得=,延长构建方程即可解决问题;【解答过程】解:如图作A′H⊥BC于H.∵∠ABC=90°,∠ABE=∠EBA′=30°,∴∠A′BH=30°,∴A′H=BA′=1,BH=A′H=,∴CH=3﹣,∵△CDF∽△A′HC,∴=,∴=,∴DF=6﹣2,故答案为6﹣2.【总结归纳】本题考查翻折变换、矩形的性质、勾股定理、直角三角形30度角性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.6.(2018年山东省潍坊市-第17题-3分)如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y 于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按A B的长是.此作法进行下去,则20192018【知识考点】弧长的计算;规律型:点的坐标;一次函数图象上点的坐标特征.【思路分析】先根据一次函数方程式求出B1点的坐标,再根据B1点的坐标求出A2点的坐标,得出B2的坐标,以此类推总结规律便可求出点A2019的坐标,再根据弧长公式计算即可求解,.【解答过程】解:直线y=x,点A1坐标为(2,0),过点A1作x轴的垂线交直线于点B1可知B1点的坐标为(2,2),以原O为圆心,OB1长为半径画弧x轴于点A2,OA2=OB1,OA2==4,点A2的坐标为(4,0),这种方法可求得B2的坐标为(4,4),故点A3的坐标为(8,0),B3(8,8)以此类推便可求出点A2019的坐标为(22019,0),则的长是=.故答案为:.【总结归纳】本题主要考查了一次函数图象上点的坐标特征,做题时要注意数形结合思想的运用,是各地的中考热点,学生在平常要多加训练,属于中档题.8.(2018年浙江省嘉兴市舟山市-第16题-4分)如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.【知识考点】矩形的性质;勾股定理.【思路分析】先根据圆周角定理确定点P在以EF为直径的圆O上,且是与矩形ABCD的交点,先确定特殊点时AF的长,当F与A和B重合时,都有两个直角三角形.符合条件,即AF=0或4,再找⊙O与AD和BC相切时AF的长,此时⊙O与矩形边各有一个交点或三个交点,在之间运动过程中符合条件,确定AF的取值.【解答过程】解:∵△EFP是直角三角形,且点P在矩形ABCD的边上,∴P是以EF为直径的圆O与矩形ABCD的交点,①当AF=0时,如图1,此时点P有两个,一个与D重合,一个交在边AB上;②当⊙O与AD相切时,设与AD边的切点为P,如图2,此时△EFP是直角三角形,点P只有一个,当⊙O与BC相切时,如图4,连接OP,此时构成三个直角三角形,则OP⊥BC,设AF=x,则BF=P1C=4﹣x,EP1=x﹣1,∵OP∥EC,OE=OF,∴OG=EP1=,∴⊙O的半径为:OF=OP=,在Rt△OGF中,由勾股定理得:OF2=OG2+GF2,∴,解得:x=,∴当1<AF<时,这样的直角三角形恰好有两个,③当AF=4,即F与B重合时,这样的直角三角形恰好有两个,如图5,综上所述,则AF的值是:0或1<AF或4.故答案为:0或1<AF或4.【总结归纳】本题考查了矩形的性质的运用,勾股定理的运用,三角形中位线定理的运用,圆的性质的运用,分类讨论思想的运用,解答时运用勾股定理求解是关键,并注意运用数形结合的思想解决问题.三、解答题1.(2018年内蒙古鄂尔多斯市-第24题-12分)(1)【操作发现】如图1,将△ABC绕点A顺时针旋转60°,得到△ADE,连接BD,则∠ABD=度.(2)【类比探究】如图2,在等边三角形ABC内任取一点P,连接PA,PB,PC,求证:以PA,PB,PC的长为三边必能组成三角形.(3)【解决问题】如图3ABC内有一点P,∠APC=90°,∠BPC=120°,求△APC 的面积.(4)【拓展应用】如图4是A,B,C三个村子位置的平面图,经测量AC=4,BC=5,∠ACB=30°,P为△ABC 内的一个动点,连接PA,PB,PC.求PA+PB+PC的最小值.【知识考点】几何变换综合题.【思路分析】(1)【操作发现】:如图1中,只要证明△DAB是等边三角形即可;(2)【类比探究】:如图2中,以PA为边长作等边△PAD,使P、D分别在AC的两侧,连接CD.利用全等三角形的性质以及三角形的三边关系即可解决问题;(3)【解决问题】:如图3中,将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,只要证明∠PP′C=90°,利用勾股定理即可解决问题;(4)【拓展应用】:如图4中,先由旋转的性质得出△APC≌△EDC,则∠ACP=∠ECD,AC=EC=4,∠PCD=60°,再证明∠BCE=90°,然后在Rt△BCE中,由勾股定理求出BE的长度,即为PA+PB+PC的最小值;【解答过程】(1)【操作发现】解:如图1中,连接BD.∵△ABC绕点A顺时针旋转60°,得到△ADE,∴AD=AB,∠DAB=60°,∴△DAB是等边三角形,∴∠ABD=60°故答案为60.(2)【类比探究】证明:如图2中,以PA为边长作等边△PAD,使P、D分别在AC的两侧,连接CD.∵∠BAC=∠PAD=60°,∴∠BAP=∠CAD,∵AB=AC,AP=AD,∴△PAB≌△ACD(SAS),∴BP=CD,在△PCD中,∵PD+CD>PC,又∵PA=PD,∴AP+BP>PC.∴PA,PB,PC的长为三边必能组成三角形.(3)【解决问题】解:如图3中,∵将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,∴△APP′是等边三角形,∠AP′C=∠APB=360°﹣90°﹣120°=150°,∴PP′=AP,∠AP′P=∠APP′=60°,∴∠PP′C=90°,∠P′PC=30°,∴PP′=PC,即AP=PC,∵∠APC=90°,∴AP2+PC2=AC2,即(PC)2+PC2=()2,∴PC=2,∴AP=,∴S△APC=AP•PC=××2=.(4)【拓展应用】解:如图4中,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD、BE.∵将△APC绕点C顺时针旋转60°,得到△EDC,∴△APC≌△EDC(旋转的性质),∴∠ACP=∠ECD,AC=EC=4,∠PCD=60°,∴∠ACP+∠PCB=∠ECD+∠PCB,∴∠ECD+∠PCB=∠ACB=30°,∴∠BCE=∠ECD+∠PCB+∠PCD=30°+60°=90°,在Rt△BCE中,∵∠BCE=90°,BC=5,CE=4,∴BE===,即PA+PB+PC的最小值为;【总结归纳】本题属于几何变换综合题,考查了旋转变换,等边三角形的性质,勾股定理等知识,解题的关键是添加常用辅助线,构造全等三角形解决问题,用转化的思想思考问题,属于中考压轴题.2.(2018年湖北省襄阳市-第24题-10分)如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:AGBE的值为:(2)探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE 之间的数量关系,并说明理由:(3)拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=BC=.【知识考点】相似形综合题.【思路分析】(1)①由GE⊥BC、GF⊥CD结合∠BCD=90°可得四边形CEGF是矩形,再由∠ECG=45°即可得证;②由正方形性质知∠CEG=∠B=90°、∠ECG=45°,据此可得=、GE∥AB,利用平行线分线段成比例定理可得;(2)连接CG,只需证△ACG∽△BCE即可得;(3)证△AHG∽△CHA得==,设BC=CD=AD=a,知AC=a,由=得AH= a、DH=a、CH=a,由=可得a的值.【解答过程】解:(1)①∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°,∵GE⊥BC、GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF是矩形,∠CGE=∠ECG=45°,∴EG=EC,∴四边形CEGF是正方形;②由①知四边形CEGF是正方形,∴∠CEG=∠B=90°,∠ECG=45°,∴=,GE∥AB,∴==,故答案为:;(2)连接CG,由旋转性质知∠BCE=∠ACG=α,在Rt△CEG和Rt△CBA中,=cos45°=、=cos45°=,∴==,∴△ACG∽△BCE,∴==,∴线段AG与BE之间的数量关系为AG=BE;(3)∵∠CEF=45°,点B、E、F三点共线,∴∠BEC=135°,∵△ACG∽△BCE,∴∠AGC=∠BEC=135°,∴∠AGH=∠CAH=45°,∵∠CHA=∠AHG,∴△AHG∽△CHA,∴==,设BC=CD=AD=a,则AC=a,则由=得=,∴AH=a,则DH=AD﹣AH=a,CH==a,∴=得=,解得:a=3,即BC=3,故答案为:3.【总结归纳】本题主要考查相似形的综合题,解题的关键是掌握正方形的判定与性质、相似三角形的判定与性质等知识点.3.(2018年湖南省湘潭市-第25题-10分)如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是AB上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.(1)若半圆的半径为10.①当∠AOM=60°时,求DM的长;②当AM=12时,求DM的长.(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.【知识考点】圆的综合题.【思路分析】(1)①当∠AOM=60°时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;②过点M作MF⊥OA于点F,设AF=x,OF=10﹣x,利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.(2)根据点M的位置分类讨论,然后利用圆周角定理以及圆内接四边形的性质即可求出答案.【解答过程】解:(1)①当∠AOM=60°时,∵OM=OA,∴△AMO是等边三角形,∴∠A=∠MOA=60°,∴∠MOD=30°,∠D=30°,∴DM=OM=10②过点M作MF⊥OA于点F,设AF=x,∴OF=10﹣x,∵AM=12,OA=OM=10,由勾股定理可知:122﹣x2=102﹣(10﹣x)2∴x=,∴AF=,∵MF∥OD,∴△AMF∽△ADO,∴,∴,∴AD=∴MD=AD﹣AM=(2)当点M位于之间时,连接BC,∵C是的中点,∴∠B=45°,∵四边形AMCB是圆内接四边形,此时∠CMD=∠B=45°,当点M位于之间时,连接BC,由圆周角定理可知:∠CMD=∠B=45°综上所述,∠CMD=45°【总结归纳】本题考查圆的综合问题,涉及圆周角定理,勾股定理,相似三角形的判定与性质,含30度角的直角三角形性质,解方程等知识,综合程度较高,需要学生灵活运用所学知识.4.(2018年湖南邵阳市-第25题-8分)如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.(1)证明:四边形OEFG是平行四边形;(2)将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.①若OG=1,求ENGM的值;②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)【知识考点】相似形综合题.【思路分析】(1)连接AC,由四个中点可知OE∥AC、OE=AC,GF∥AC、GF=AC,据此得出OE=GF、OE=GF,即可得证;(2)①由旋转性质知OG=OM、OE=ON,∠GOM=∠EON,据此可证△OGM∽△OEN得==;②连接AC、BD,根据①知△OGM∽△OEN,若要GM=EN只需使△OGM≌△OEN,添加使AC=BD 的条件均可以满足此条件.【解答过程】解:(1)如图1,连接AC,∵点O、E、F、G分别是AB、BC、CD、AD的中点,∴OE∥AC、OE=AC,GF∥AC、GF=AC,∴OE=GF,OE=GF,∴四边形OEFG是平行四边形;(2)①∵△OGE绕点O顺时针旋转得到△OMN,∴OG=OM、OE=ON,∠GOM=∠EON,∴=,∴△OGM∽△OEN,∴==.②添加AC=BD,如图2,连接AC、BD,∵点O、E、F、G分别是AB、BC、CD、AD的中点,∴OG=EF=BD、OE=GF=BD,∵AC=BD,∴OG=OE,∵△OGE绕点O顺时针旋转得到△OMN,∴OG=OM、OE=ON,∠GOM=∠EON,∴OG=OE、OM=ON,在△OGM和△OEN中,∵,∴△OGM≌△OEN(SAS),∴GM=EN.【总结归纳】本题主要考查相似形的综合题,解题的关键是熟练掌握中位线定义及其定理、平行四边形的判定、旋转的性质、相似三角形与全等三角形的判定与性质等知识点.5.(2018年江苏省淮安市-第26题-12分)如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B=°;(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.【知识考点】四边形综合题.【思路分析】(1)根据“准互余三角形”的定义构建方程即可解决问题;(2)只要证明△CAE∽△CBA,可得CA2=CE•CB,由此即可解决问题;(3)如图②中,将△BCD沿BC翻折得到△BCF.只要证明△FCB∽△FAC,可得CF2=FB•FA,设FB=x,则有:x(x+7)=122,推出x=9或﹣16(舍弃),再利用勾股定理求出AC即可;【解答过程】解:(1)∵△ABC是“准互余三角形”,∠C>90°,∠A=60°,∴2∠B+∠A=60°,解得,∠B=15°,故答案为:15°;(2)如图①中,在Rt△ABC中,∵∠B+∠BAC=90°,∠BAC=2∠BAD,∴∠B+2∠BAD=90°,∴△ABD是“准互余三角形”,∵△ABE也是“准互余三角形”,∴只有2∠A+∠BAE=90°,∵∠A+∠BAE+∠EAC=90°,∴∠CAE=∠B,∵∠C=∠C=90°,∴△CAE∽△CBA,可得CA2=CE•CB,∴CE=,∴BE=5﹣=.(3)如图②中,将△BCD沿BC翻折得到△BCF.∴CF=CD=12,∠BCF=∠BCD ,∠CBF=∠CBD , ∵∠ABD=2∠BCD ,∠BCD+∠CBD=90°, ∴∠ABD+∠DBC+∠CBF=180°, ∴A 、B 、F 共线, ∴∠A+∠ACF=90° ∴2∠ACB+∠CAB≠90°, ∴只有2∠BAC+∠ACB=90°, ∴∠FCB=∠FAC ,∵∠F=∠F , ∴△FCB ∽△FAC , ∴CF 2=FB•FA ,设FB=x , 则有:x (x+7)=122, ∴x=9或﹣16(舍弃), ∴AF=7+9=16, 在Rt △ACF 中,AC===20.【总结归纳】本题考查四边形综合题、相似三角形的判定和性质、“准互余三角形”的定义等知识,解题的关键是理解题意,学会利用翻折变换添加辅助线,构造相似三角形解决问题,学会利用已知模型构建辅助线解决问题,属于中考压轴题.6.(2018年江苏省无锡市-第27题-10分)如图,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上. (1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若11A E EC =,求nm的值.【知识考点】轨迹;旋转的性质.【思路分析】(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.解直角三角形,求出∠ABA1,得到旋转角即可解决问题;(2)由△BCE∽△BA2D2,推出==,可得CE=由=﹣1推出=,推出AC=•,推出BH=AC==•,可得m2﹣n2=6•,可得1﹣=6•,由此解方程即可解决问题;【解答过程】解:(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.∴AD=HA1=n=1,在Rt△A1HB中,∵BA1=BA=m=2,∴BA1=2HA1,∴∠ABA1=30°,∴旋转角为30°,∵BD==,∴D到点D1所经过路径的长度==π.(2)∵△BCE∽△BA2D2,∴==,∴CE=∵=﹣1∴=,∴AC=•,∴BH=AC==•,∴m2﹣n2=6•,∴m4﹣m2n2=6n4,1﹣=6•,∴=(负根已经舍弃).【总结归纳】本题考查轨迹,旋转变换、解直角三角形、弧长公式等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.7.(2018年江苏省苏州市-第27题-10分)问题1:如图①,在△ABC中,AB=4,D是AB上一点(不与A,B重合),DE∥BC,交AC于点E,连接CD.设△ABC的面积为S,△DEC的面积为S′.(1)当AD=3时,SS'=;(2)设AD=m,请你用含字母m的代数式表示SS'.问题2:如图②,在四边形ABCD中,AB=4,AD∥BC,AD=12BC,E是AB上一点(不与A,B重合),EF∥BC,交CD于点F,连接CE.设AE=n,四边形ABCD的面积为S,△EFC的面积为S′.请你利用问题1的解法或结论,用含字母n的代数式表示SS'.【知识考点】三角形中位线定理;相似三角形的判定与性质.【思路分析】问题1:(1)先根据平行线分线段成比例定理可得:,由同高三角形面积的比等于对应底边的比,则==,根据相似三角形面积比等于相似比的平方得:==,可得结论;(2)解法一:同理根据(1)可得结论;解法二:作高线DF、BH,根据三角形面积公式可得:=,分别表示和的值,代入可得结论;问题2:解法一:如图2,作辅助线,构建△OBC,证明△OAD∽△OBC,得OB=8,由问题1的解法可知:===,根据相似三角形的性质得:=,可得结论;解法二:如图3,连接AC交EF于M,根据AD=BC,可得=,得:S△ADC=S,S△ABC=,由问题1的结论可知:=,证明△CFM∽△CDA,根据相似三角形面积比等于相似比的平方,根据面积和可得结论.【解答过程】解:问题1:(1)∵AB=4,AD=3,∴BD=4﹣3=1,∵DE∥BC,∴,∴==,∵DE∥BC,∴△ADE∽△ABC,∴==,∴=,即,故答案为:;(2)解法一:∵AB=4,AD=m,∴BD=4﹣m,∵DE∥BC,∴==,∴==,∵DE∥BC,∴△ADE∽△ABC,∴==,∴===,即=;解法二:如图1,过点B作BH⊥AC于H,过D作DF⊥AC于F,则DF∥BH,∴△ADF∽△ABH,∴=,∴===,即=;问题2:如图②,解法一:如图2,分别延长BD、CE交于点O,∵AD∥BC,∴△OAD∽△OBC,∴,∴OA=AB=4,∴OB=8,∵AE=n,∴OE=4+n,∵EF∥BC,由问题1的解法可知:===,∵==,∴=,∴===,即=;解法二:如图3,连接AC交EF于M,∵AD∥BC,且AD=BC,∴=,∴S△ADC=,∴S△ADC=S,S△ABC=,由问题1的结论可知:=,∵MF∥AD,∴△CFM∽△CDA,∴===,∴S△CFM=×S,∴S△EFC=S△EMC+S△CFM=+×S=,∴=.。
2018年全国各地中考数学试题专题汇编1平行线与三角形解析版1-52题
2018年全国各地中考数学试题专题汇编1(1-52题)平行线与三角形选择题解析版1.2018年新疆5.(5分)如图,AB ∥CD ,点E 在线段BC 上,CD=CE .若∠ABC=30°,则∠D 为( )A .85°B .75°C .60°D .30°【分析】先由AB ∥CD ,得∠C=∠ABC=30°,CD=CE ,得∠D=∠CED ,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D .【解答】解:∵AB ∥CD ,∴∠C=∠ABC=30°,又∵CD=CE ,∴∠D=∠CED ,∵∠C+∠D+∠CED=180°,即30°+2∠D=180°,∴∠D=75°.故选:B .【点评】此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C ,再由CD=CE 得出∠D=∠CED ,由三角形内角和定理求出∠D .2.2018山西8. 如 图 ,在 Rt △ A BC 中 ,∠ A CB=90°,∠ A =60°,AC=6,将 △ A BC 绕 点 C 按 逆 时 针方 向 旋 转 得 到A B C ''∆,此 时 点 A ' 恰好在 AB 边 上 , 则 点 B ' 与点 B 之 间 的 距 离 是 ( )A. 12B. 6C.D.【答案】 D【考点】 旋 转 , 等 边 三 角 形 性 质【解析 】连接 BB ' ,由 旋 转 可 知AC A C '=,BC B C '=,∵ ∠ A =60°,∴ACA '∆为 等 边 三 角 形 ,∴60ACA '∠=︒, ∴60BCB '∠=︒.∴BCB '∆为 等 边 三 角 形 ,∴BB BC '== . 3.2018•海南7.(3.00分)将一把直尺和一块含30°和60°角的三角板ABC 按如图所示的位置放置,如果∠CDE=40°,那么∠BAF 的大小为( )A .10°B .15°C .20°D .25°【考点】JA:平行线的性质.【专题】1 :常规题型;551:线段、角、相交线与平行线.【分析】由DE∥AF得∠AFD=∠CDE=40°,再根据三角形的外角性质可得答案.【解答】解:由题意知DE∥AF,∴∠AFD=∠CDE=40°,∵∠B=30°,∴∠BAF=∠AFD﹣∠B=40°﹣30°=10°,故选:A.【点评】本题主要考查平行线的性质,解题的关键是掌握两直线平行同位角相等与三角形外角的性质.4.2018包头8.(3.00分)如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为()A.17.5°B.12.5° C.12°D.10°【分析】由AB=AC知∠B=∠C,据此得2∠C+∠BAC=180°,结合∠C+∠BAC=145°可知∠C=35°,根据∠DAE=90°、AD=AE知∠AED=45°,利用∠EDC=∠AED﹣∠C可得答案.【解答】解:∵AB=AC,∴∠B=∠C,∴∠B+∠C+∠BAC=2∠C+∠BAC=180°,又∵∠C+∠BAC=145°,∴∠C=35°,∵∠DAE=90°,AD=AE,∴∠AED=45°,∴∠EDC=∠AED﹣∠C=10°,故选:D.【点评】本题主要考查等腰直角三角形,解题的关键是掌握等腰直角三角形和等腰三角形的性质及三角形的内角和定理、外角的性质.5.2018天津10. 如图,将一个三角形纸片沿过点的直线折叠,使点落在边上的点处,折痕为,则下列结论一定正确的是()A. AD=BDB. AE=ACC. ED+EB=DBD.AE+CB=AB【解析】分析:由折叠的性质知,BC=BE.易得AE+CB=AB.详解:由折叠的性质知,BC=BE.∴AE+CB=AB..故选:D.6.2018重庆A卷6.下列命题正确的是A.平行四边形的对角线互相垂直平分B.矩形的对角线互相垂直平分C.菱形的对角线互相平分且相等D.正方形的对角线互相垂直平分【答案】D【解析】A.错误.平行四边形的对角线互相平分。
中考数学专项训练 矩形、菱形与正方形(含解析)(2021年整理)
2017年中考数学专项训练矩形、菱形与正方形(含解析)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017年中考数学专项训练矩形、菱形与正方形(含解析))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017年中考数学专项训练矩形、菱形与正方形(含解析)的全部内容。
矩形、菱形与正方形一、选择题1.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等2.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()A.矩形B.菱形C.正方形 D.梯形3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND 是菱形,则等于( )A.B.C.D.4.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A. cm B. cm C. cm D. cm5.如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )A.1个B.2个C.3个D.4个二、填空题6.若菱形的两条对角线分别为2和3,则此菱形的面积是.7.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= .8.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=.9.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是.10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的序号是(把你认为正确的都填上).三、解答题(共40分)11.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.12.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.13.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP 与NQ是否相等?并说明理由.14.如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,(1)的值为;(2)求证:AE=EP;(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.矩形、菱形与正方形参考答案与试题解析一、选择题1.矩形具有而菱形不具有的性质是()A.两组对边分别平行 B.对角线相等C.对角线互相平分D.两组对角分别相等【考点】矩形的性质;菱形的性质.【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.2.如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是()A.矩形B.菱形C.正方形 D.梯形【考点】旋转的性质;矩形的判定.【分析】根据旋转的性质可得AE=CE,DE=EF,再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形,然后利用等腰三角形三线合一的性质求出∠ADC=90°,再利用有一个角是直角的平行四边形是矩形解答.【解答】解:∵△ADE绕点E旋转180°得△CFE,∴AE=CE,DE=EF,∴四边形ADCF是平行四边形,∵AC=BC,点D是边AB的中点,∴∠ADC=90°,∴四边形ADCF是矩形.故选:A.【点评】本题考查了旋转的性质,矩形的判定,主要利用了对角线互相平分的四边形是平行四边形,有一个角是直角的平行四边形是矩形的判定方法,熟练掌握旋转变换只改变图形的位置不改变图形的形状与大小是解题的关键.3.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND 是菱形,则等于()A.B.C.D.【考点】勾股定理;菱形的性质;矩形的性质.【分析】首先由菱形的四条边都相等与矩形的四个角是直角,即可得到直角△ABM中三边的关系.【解答】解:∵四边形MBND是菱形,∴MD=MB.∵四边形ABCD是矩形,∴∠A=90°.设AB=x,AM=y,则MB=2x﹣y,(x、y均为正数).在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x﹣y)2,解得x=y,∴MD=MB=2x﹣y=y,∴==.故选:C.【点评】此题考查了菱形与矩形的性质,以及直角三角形中的勾股定理.解此题的关键是注意数形结合思想与方程思想的应用.4.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=()A. cm B. cm C. cm D. cm【考点】菱形的性质;勾股定理;解直角三角形.【分析】先求出菱形的边长,然后利用面积的两种表示方法求出DH,在Rt△DHB中求出BH,然后得出AH,利用tan∠HAG的值,可得出GH的值.【解答】解:∵四边形ABCD是菱形,对角线AC=8cm,BD=6cm,∴AO=4cm,BO=3cm,在Rt△AOB中,AB==5cm,∵BD×AC=AB×DH,∴DH=cm,在Rt△DHB中,BH==cm,则AH=AB﹣BH=cm,∵tan∠HAG===,∴GH=AH=cm.故选:B.【点评】本题考查了菱形的性质、解直角三角形及三角函数值的知识,注意菱形的面积等于对角线乘积的一半,也等于底乘高.5.如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有()A.1个B.2个C.3个D.4个【考点】正方形的性质.【分析】根据四边形ABCD是正方形及CE=DF,可证出△ADE≌△BAF,则得到:①AE=BF,以及△ADE和△BAF的面积相等,得到;④S△AOB=S四边形DEOF;可以证出∠ABO+∠BAO=90°,则②AE⊥BF一定成立.错误的结论是:③AO=OE.【解答】解:∵四边形ABCD是正方形,∴CD=AD∵CE=DF∴DE=AF∴△ADE≌△BAF∴AE=BF(故①正确),S△ADE=S△BAF,∠DEA=∠AFB,∠EAD=∠FBA∵S△AOB=S△BAF﹣S△AOF,S四边形DEOF=S△ADE﹣S△AOF,∴S△AOB=S四边形DEOF(故④正确),∵∠ABF+∠AFB=∠DAE+∠DEA=90°∴∠AFB+∠EAF=90°∴AE⊥BF一定成立(故②正确).假设AO=OE,∵AE⊥BF(已证),∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),∵在Rt△BCE中,BE>BC,∴AB>BC,这与正方形的边长AB=BC相矛盾,∴,假设不成立,AO≠OE(故③错误);故错误的只有一个.故选:A.【点评】本题考查了正方形的四条边都相等,每一个角都是直角的性质,全等三角形的判定与性质,综合题但难度不大,求出△ADE≌△BAF是解题的关键,也是本题的突破口.二、填空题6.若菱形的两条对角线分别为2和3,则此菱形的面积是 3 .【考点】菱形的性质.【分析】菱形的面积是对角线乘积的一半,由此可得出结果即可.【解答】解:由题意,知:S菱形=×2×3=3,故答案为:3.【点评】本题考查了菱形的面积两种求法:(1)利用底乘以相应底上的高;(2)利用菱形的特殊性,菱形面积=×两条对角线的乘积;具体用哪种方法要看已知条件来选择.7.在矩形ABCD中,对角线AC、BD相交于点O,若∠AOB=60°,AC=10,则AB= 5 .【考点】含30度角的直角三角形;矩形的性质.【分析】根据矩形的性质,可以得到△AOB是等边三角形,则可以求得OA的长,进而求得AB 的长.【解答】解:∵四边形ABCD是矩形,∴OA=OB又∵∠AOB=60°∴△AOB是等边三角形.∴AB=OA=AC=5,故答案是:5.【点评】本题考查了矩形的性质,正确理解△AOB是等边三角形是关键.8.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α=20°.【考点】旋转的性质;矩形的性质.【分析】根据矩形的性质得∠B=∠D=∠BAD=90°,根据旋转的性质得∠D′=∠D=90°,∠4=α,利用对顶角相等得到∠1=∠2=110°,再根据四边形的内角和为360°可计算出∠3=70°,然后利用互余即可得到∠α的度数.【解答】解:如图,∵四边形ABCD为矩形,∴∠B=∠D=∠BAD=90°,∵矩形ABCD绕点A顺时针旋转得到矩形AB′C′D′,∴∠D′=∠D=90°,∠4=α,∵∠1=∠2=110°,∴∠3=360°﹣90°﹣90°﹣110°=70°,∴∠4=90°﹣70°=20°,∴∠α=20°.故答案为:20°.【点评】本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了矩形的性质.9.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是10 .【考点】轴对称﹣最短路线问题;正方形的性质.【分析】由正方形性质的得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.【解答】解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小.∵四边形ABCD是正方形,∴B、D关于AC对称,∴PB=PD,∴PB+PE=PD+PE=DE.∵BE=2,AE=3BE,∴AE=6,AB=8,∴DE==10,故PB+PE的最小值是10.故答案为:10.【点评】本题考查了轴对称﹣最短路线问题,正方形的性质,解此题通常是利用两点之间,线段最短的性质得出.10.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+.其中正确的序号是①②④(把你认为正确的都填上).【考点】正方形的性质;全等三角形的判定与性质;等边三角形的性质.【专题】压轴题.【分析】根据三角形的全等的知识可以判断①的正误;根据角角之间的数量关系,以及三角形内角和为180°判断②的正误;根据线段垂直平分线的知识可以判断③的正误,利用解三角形求正方形的面积等知识可以判断④的正误.【解答】解:∵四边形ABCD是正方形,∴AB=AD,∵△AEF是等边三角形,∴AE=AF,在Rt△ABE和Rt△ADF中,,∴Rt△ABE≌Rt△ADF(HL),∴BE=DF,∵BC=DC,∴BC﹣BE=CD﹣DF,∴CE=CF,∴①说法正确;∵CE=CF,∴△ECF是等腰直角三角形,∴∠CEF=45°,∵∠AEF=60°,∴∠AEB=75°,∴②说法正确;如图,连接AC,交EF于G点,∴AC⊥EF,且AC平分EF,∵∠CAF≠∠DAF,∴DF≠FG,∴BE+DF≠EF,∴③说法错误;∵EF=2,∴CE=CF=,设正方形的边长为a,在Rt△ADF中,AD2+DF2=AF2,即a2+(a﹣)2=4,解得a=,则a2=2+,S正方形ABCD=2+,④说法正确,故答案为:①②④.【点评】本题主要考查正方形的性质的知识点,解答本题的关键是熟练掌握全等三角形的证明以及辅助线的正确作法,此题难度不大,但是有一点麻烦.三、解答题(共40分)11.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.【考点】矩形的判定;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明△AEF 和△DEC全等,根据全等三角形对应边相等可得AF=CD,再利用等量代换即可得证;(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90°,由等腰三角形三线合一的性质可知必须是AB=AC.【解答】解:(1)BD=CD.理由如下:依题意得AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD(三线合一),∴∠ADB=90°,∴▱AFBD是矩形.【点评】本题考查了矩形的判定,全等三角形的判定与性质,平行四边形的判定,是基础题,明确有一个角是直角的平行四边形是矩形是解本题的关键.12.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.【考点】菱形的判定与性质;三角形中位线定理.【分析】从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;∠BCF是120°,所以∠EBC 为60°,所以菱形的边长也为4,求出菱形的高面积就可求.【解答】(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC,又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形,又∵BE=FE,∴四边形BCFE是菱形;(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为2,∴菱形的面积为4×2=8.【点评】本题考查菱形的判定和性质以及三角形中位线定理,以及菱形的面积的计算等知识点.13.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP 与NQ是否相等?并说明理由.【考点】正方形的性质;全等三角形的判定与性质.【专题】证明题.【分析】(1)根据正方形的性质可得AB=AD,∠BAE=∠D=90°,再根据同角的余角相等求出∠ABE=∠DAF,然后利用“角边角”证明△ABE和△DAF全等,再根据全等三角形的证明即可;(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,然后与(1)相同.【解答】(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,,∴△ABE≌△DAF(ASA),∴AF=BE;(2)解:MP与NQ相等.理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,∵AB∥CD,AD∥BC,∴四边形AMPF与四边形BNQE是平行四边形,∴AF=PM,BE=NQ,∵在正方形ABCD中,AB=AD,∠BAE=∠D=90°,∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,∵在△ABE和△DAF中,,∴△ABE≌△DAF(ASA),∴AF=BE;∴MP=NQ.【点评】本题考查了正方形的性质,全等三角形的判定与性质,主要利用了正方形的四条边都相等,每一个角都是直角的性质,同角的余角相等的性质,利用三角形全等证明相等的边是常用的方法之一,要熟练掌握并灵活运用.14.如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,(1)的值为;(2)求证:AE=EP;(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.【考点】正方形的性质;全等三角形的判定与性质;平行四边形的判定.【分析】(1)由正方形的性质可得:∠B=∠C=90°,由同角的余角相等,可证得:∠BAE=∠CEF,根据同角的正弦值相等即可解答;(2)在BA边上截取BK=BE,连接KE,根据角角之间的关系得到∠AKE=∠ECP,由AB=CB,BK=BE,得AK=EC,结合∠KAE=∠CEP,证明△AKE≌△ECP,于是结论得出;(3)作DM⊥AE于AB交于点M,连接ME、DP,易得出DM∥EP,由已知条件证明△ADM≌△BAE,进而证明MD=EP,四边形DMEP是平行四边形即可证出.【解答】(1)解:∵四边形ABCD是正方形,∴∠B=∠D,∵∠AEP=90°,∴∠BAE=∠FEC,在Rt△ABE中,AE==,∵sin∠BAE==sin∠FEC=,∴=,解法二:由上得∠BAE=∠FEC,∵∠BAE=∠FEC,∠B=∠DCB,∴△ABE∽△ECF,∴=,(2)证明:在BA边上截取BK=BE,连接KE,∵∠B=90°,BK=BE,∴∠BKE=45°,∴∠AKE=135°,∵CP平分外角,∴∠DCP=45°,∴∠ECP=135°,∴∠AKE=∠ECP,∵AB=CB,BK=BE,∴AB﹣BK=BC﹣BE,即:AK=EC,由第一问得∠KAE=∠CEP,∵在△AKE和△ECP中,,∴△AKE≌△ECP(ASA),∴AE=EP;(3)答:存在.证明:作DM⊥AE交AB于点M,则有:DM∥EP,连接ME、DP,∵在△ADM与△BAE中,,∴△ADM≌△BAE(ASA),∴MD=AE,∵AE=EP,∴MD=EP,∴MD EP,∴四边形DMEP为平行四边形.【点评】此题考查了相似三角形的判定与性质,全等三角形的判定与性质以及正方形的性质等知识.此题综合性很强,图形比较复杂,解题的关键是注意数形结合思想的应用与辅助线的准确选择.。
2018-2020年安徽省中考数学复习各地区模拟试题分类(合肥专版)(12)——图形的变换及答案
2018-2020年安徽省中考数学复习各地区模拟试题分类(合肥专版)(12)——图形的变换一.选择题(共6小题) 1.(2020•包河区二模)如图,在矩形ABCD 中,点H 为边BC 的中点,点G 为线段DH 上一点,且∠BGC =90°,延长BG 交CD 于点E ,延长CG 交AD 于点F ,当CD =4,DE =1时,则DF 的长为( )A .2B .32C .√5D .952.(2020•肥东县二模)如图,正方形ABCD 的边长为2,延长AB 至E ,使得AB =BE ,连接CE ,P 为CE 上一动点,分别连接P A 、PB ,则P A +PB 的最小值为( )A .4B .5C .2√2D .2√53.(2020•肥东县二模)如图,在△ABC 中,AB =AC =6,D 是AC 中点,E 是BC 上一点,BE =52,∠AED=∠B ,则CE 的长为( )A .152B .223C .365D .6494.(2020•包河区校级一模)如图,在△ABC 中,BC =6,AA AA=AA AA,动点P 在射线EF 上,BP 交CE 于点D ,∠CBP 的平分线交CE 于点Q ,当CQ =14CE 时,EP +BP 的值为( )A .9B .12C .18D .24 5.(2020•肥东县一模)用一些完全一样的小正方体搭成一个几何体,它的主视图、俯视图与左视图都是如图所示的图形,则小正方体的个数可能是( )A .9B .8C .5D .4 6.(2020•蜀山区校级模拟)如图,等边△ABC 的边长为4,点D 是边AC 上的一动点,连接BD ,以BD 为斜边向上作等腰Rt △BDE ,连接AE ,则AE 的最小值为( )A .1B .√2C .2D .2√2−1 二.填空题(共14小题) 7.(2020•包河区二模)已知,Rt △ABC 中,∠ACB =90°,∠B =30°,AC =1,点P 是AB 上一点,连接CP ,将∠B 沿CP 折叠,使点B 落在B ′处.以下结论正确的有 . ①当AB ′⊥AC 时,AB ′的长为√2;②当点P 位于AB 中点时,四边形ACPB ′为菱形; ③当∠B 'P A =30°时,AA AA=12;④当CP ⊥AB 时,AP :AB ′:BP =1:2:3.8.(2020•长丰县一模)将一副三角尺如图所示叠放在一起,则AA AA的值是 .9.(2019•蜀山区校级三模)如图,在矩形ABCD 中,AB :BC =3:5,点E 是对角线AC 上一动点(不与点A ,C 重合),将矩形沿过点E 的直线MN 折叠,使得点A ,B 的对应点A 1,B 1分别落在直线AD 与BC 上,当△A 1CE 为直角三角形时,AN :DN 的值为 .10.(2019•庐阳区校级一模)如图,在矩形ABCD 中,AD =8,AB =14,E 为DC 上的一个点,将△ADE 沿AE 折叠,使得点D 落在D '处,若以C 、B 、D '为顶点的三角形是等腰三角形,则DE 的长为 .11.(2019•庐阳区校级模拟)如图,在Rt △ABC 中,∠C =90°,AC =8,BC =6,点D 是AB 的中点,点P 是直线AC 上一点,将△ADP 沿DP 所在的直线翻折后,点A 落在A 1处,若A 1D ⊥AC ,则点P 与点A 之间的距离为 .12.(2019•合肥模拟)在△ABC中,∠ACB=90°,AC=4,AB=5,点E、F分别在AC、AB上,连接EF,将△ABC沿EF折叠,使点A落在BC边上的点D处.若△DEF有一边垂直BC,则EF=13.(2019•瑶海区二模)在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点P为边AC上一点,且AP =5cm.点Q为边AB上的任意一点(不与点A,B重合),若点A关于直线PQ的对称点A'恰好落在△ABC的边上,则AQ的长为cm.14.(2019•合肥二模)如图,在等边△ABC中,AB=4cm,点M为边BC的中点,点N为边AB上的任意一点(不与点A,B重合).若点B关于直线MN的对称点B'恰好落在等边△ABC的边上,则BN的长为cm.15.(2019•长丰县模拟)如图,在矩形ABCD中,AB:BC=3:5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为.16.(2018•包河区一模)如图,在△ABC中,已知:AB=AC=6,BC=8,P是BC边上一点(P不与点B,C重合),∠DPE=∠B,且DP边始终经过点A,另一边PE交AC于点F,当△APF为等腰三角形时,则PB的长为.17.(2018•包河区二模)如图,在矩形ABCD中,AB=1,BC=6,将矩形折叠,使A落在BC(含端点)上点M处,这时折痕EF与AD或边CD(含端点)交于F,然后展开铺平,以A、M、F为顶点作△AMF,当△AMF的面积最大时,CM的长度为.18.(2018•长丰县一模)一个小球沿着坡度为1:3的坡面向下滚动了10米,此时小球下降的垂直高度为 米. 19.(2018•长丰县一模)如图,在△ABC 中,D 、E 分别为边AB 、AC 上的点.AA AA=AA AA,点F 为BC 边上一点,添加一个条件: ,可以使得△FDB 与△ADE 相似.(只需写出一个)20.(2018•蜀山区一模)如图示意图,A 点的坐标为(2,2),点C 在线段OA 上运动(点C 不与O 、A 重合),过点C 作CD ⊥x 轴于D ,再以CD 为一边在CD 右侧画正方形CDEF .连接AF 并延长交x 轴于B ,连接OF .若△BEF 与△OEF 相似,则点B 的坐标是 .三.解答题(共14小题) 21.(2020•肥东县二模)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC (顶点是网格线的交点)和格点O .(1)平移△ABC ,使得点A 与点O 重合,画出平移后的△A ′B ′C ′; (2)画出△ABC 关于点O 对称的△DEF ;(3)判断△A ′B ′C ′与△DEF 是否成中心对称?22.(2020•包河区一模)如图,无人机在600米高空的P 点,测得地面A 点和建筑物BC 的顶端B 的俯角分别为60°和70°,已知A 点和建筑物BC 的底端C 的距离为286√3米,求建筑物BC 的高.(结果保留整数,参考数据:√3≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)23.(2020•蜀山区一模)如图,在边长为1个单位长度的小正方形组成的12×12的网格中,已知点O 、A 、B 均为格点.(1)在给定的网格中,以点O 为位似中心将线段AB 放大为原来的2倍,得到线段A ′B ′.(点A 、B的对应点分别为点A ′、B ′),画出线段A ′B ′.(2)以线段A ′B ′为一边,作一个格点四边形A ′B ′CD ,使得格点四边形A ′B ′CD 是轴对称图形(作出一个格点四边形即可).24.(2020•庐阳区校级一模)(1)【操作发现】如图1,在△OAB 和△OCD 中,OA =OB ,OC =OD ,∠AOB =∠COD =40°,连接AC ,BD 交于点M . ①AA AA的值为 ;②∠AMB 的度数为 . (2)【类比探究】如图2,在△OAB 和△OCD 中,∠AOB =∠COD =90°,∠OAB =∠OCD =30°,连接AC 交BD 的延长线于点M .计算AA AA的值及∠AMB 的度数;(3)【实际应用】在(2)的条件下,将△OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M ,若OD =1,OB =√7,请直接写出当点C 与点M 重合时AC 的长.25.(2020•瑶海区一模)如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC 的顶点均在格点上.(1)将△ABC 向下平移5个单位再向右平移1单位后得到对应的△A 1B 1C 1,画出△A 1B 1C 1; (2)画出△A 1B 1C 1关于y 轴对称的△A 2B 2C 2;(3)P (a ,b )是△ABC 的AC 边上一点,请直接写出经过两次变换后在△A 2B 2C 2中对应的点P 2的坐标.26.(2020•包河区校级一模)如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).(1)若△ABC经过平移后得到△A1B1C1,已知点C的应点C₁的坐标为(4,﹣1),画出△A1B1C1并写出顶点A,B对应点A1,B1的坐标;(2)将△ABC绕着点O按顺时针方向旋转90°得到△A2B2C2,画出△A2B2C2.27.(2020•长丰县一模)通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=底边腰=AAAA,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:(1)can30°=;(2)如图(2),已知在△ABC中,AB=AC,canB=85,S△ABC=24,求△ABC的周长.28.(2019•包河区校级二模)如图,以AB为斜边作Rt△ABE和Rt△ACB,∠AEB=∠ACB=90°,EF⊥AB,垂足为点F,点D是线段BF上一点,连接AC分别交EF、ED、BE于P、H、Q,过点E作EG⊥DE,交BC延长线于点G,BF=6,BG=5.(1)求证:△AEH∽△BEG;(2)若EF=3,求AH的长;(3)若cos∠FBG=35,FD=43,求线段EF的长.29.(2019•包河区校级二模)在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:(1)将△ABC向左平移5个单位长度,画出平移后的△A1B1C1,并写出点A的对应点A1的坐标;(2)点O为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△A1B1C1相似,且△A2B2C2与△A1B1C1的位似比为1:1;(3)sin∠B2A2C2=(直接写出答案).30.(2019•包河区校级二模)广宇同学想测量一栋楼上竖立的旗杆的长(图中线段EF的长),已知直线EF 垂直于地面,垂足为点C,在地面A处测得点E的仰角为31°,在B处测得点E的仰角为61°、点F的仰角为45°,AB=48米,且A、B、C三点在一条直线上,请你根据以上数据帮助广宇同学求旗杆EF的长(参考数据:sin31°=0.52,cos31°=0.86,tan31°=0.60,sin61°=0.87,cos61°=0.48,tan61°=1.80)31.(2019•庐江县模拟)某校九(1)班开展数学活动,李明和张华两位同学合作用测角仪测量学校旗杆的高度,李明站在B点测得旗杆顶端E点的仰角为45°,张华站在D(D点在直线FB上)测得旗杆顶端E 点仰角为15°,已知李明和张华相距(BD)30米,李明的身高(AB)1.6米,张华的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1.参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)32.(2019•合肥二模)在10×10网格中建立如图所示的平面直角坐标系,△ABC是格点三角形(三角形的顶点是网格线的交点)(1)画出△ABC绕点O逆时针方向旋转90°得到的△A1B1C1;(2)求点A在(1)的图形变换过程中所经过的路径长.33.(2018•蜀山区一模)我们把菱形的顶点及其对称中心称作如图1所示基本图的特征点,显然这样的基本图共有5个特征点.将此基本图不断复制并按如下方式摆放,使得相邻两个基本图的一个顶点重合,这样得到图2、图3,…,…(1)观察以上图形并完成下表:图形的名称基本图的个数特征点的个数图1 1 5图2 2 9图3 3 13图4 4………猜想:在图n中,特征点的个数为(用n的式子表示);(2)如图n,将当菱形的一个锐角为60°时,将图n放在直角坐标系中(第一个基本图的两个顶点分别落在坐标轴上,且菱形较短的对角线与x轴垂直),设其中第一个基本图的对称中心O1的坐标为(x1,1),则x1=;图2018的对称中心的横坐标为.34.(2018•合肥二模)在如图所示的网格中,每个小三角形均为等边三角形,点A、B、C、D都在格点上.(1)将△ADC向左平移,使点C与点B重合,画出平移后的△EFB;(2)将△ADC绕点C逆时针旋转60°,点D的对应点为点G,画出旋转后的三角形;(3)若点P是△ABC内一点,且满足P A2+PC2=PB2,则∠APC=°.2018-2020年安徽省中考数学复习各地区模拟试题分类(合肥专版)(12)——图形的变换参考答案与试题解析一.选择题(共6小题) 1.【解答】解:如图,延长AD ,BE 相交于点M ,∵DF ∥CH ,∴△DFG ∽△HCG , ∴AA AA =AA AA ,∵DM ∥BH ,∴△DMG ∽△HBG , ∴AA AA=AA AA,∵CH =BH , ∴DF =DM ,又∵△MDE ∽△CDF , ∴AA AA =AA AA , ∴AA AA=AA AA,∴DF 2=DE •CD =1×4=4, ∴AA =√4=2. 故选:A . 2.【解答】解:作点B 关于直线EC 的对称点T ,连接PT ,AT .∵四边形ABCD 是正方形, ∴∠ABC =∠CBE =90°, ∵AB =BC =BE =2, ∴∠CEB =45°,∵EB =ET ,∠CEB =∠CET =45°, ∴∠AET =90°,∴AT =√AA 2+AA 2=√42+22=2√5, ∴PB =PT ,∴P A +PB =P A +PT ≥AT , ∴P A +PB ≥2√5,∴P A +PB 的最小值为2√5, 故选:D . 3.【解答】解:∵AB =AC , ∴∠B =∠C ,∵∠AEC =∠AED +∠DEC =∠B +∠BAE ,∠AED =∠B ,∴∠DEC =∠BAE ,∴△BAE ∽△CED ,∴AA AA=AA AA , ∵AB =AC =6,AD =DC =3,BE =52, ∴6AA =523, ∴CE =365,故选:C . 4.【解答】解:如图,延长EF 交BQ 的延长线于G . ∵AA AA =AA AA ,∴EG ∥BC ,∴∠G =∠GBC ,∵∠GBC =∠GBP ,∴∠G =∠PBG ,∴PB =PG ,∴PE +PB =PE +PG =EG ,∵CQ =14EC , ∴EQ =3CQ ,∵EG ∥BC ,∴△EQG ∽△CQB ,∴AA AA =AA AA =3,∵BC =6,∴EG =18,∴EP +PB =EG =18,故选:C .5.【解答】解:由俯视图易得最底层有4个小正方体,第二层最多有4个小正方体,那么搭成这个几何体的小正方体最多为4+2+2=8个.故选:B .6.【解答】解:如图,过点B 作BH ⊥AC 于H 点,作射线HE ,∵△ABC 是等边三角形,BH ⊥AC ,∴AH =2=CH ,∵∠BED =∠BHD =90°,∴点B ,点D ,点H ,点E 四点共圆,∴∠BHE =∠BDE =45°,∴点E 在∠AHB 的角平分线上运动,∴当AE ⊥EH 时,AE 的长度有最小值,∵∠AHE =45°,∴AH =√2AE =2,∴AE 的最小值为√2,故选:B .二.填空题(共14小题)7.【解答】解:①AC =1,∠B =30°可知BC =√3,由翻折可知:B ′C =BC =√3,因为AB '⊥AC ,由勾股定理可知:AB '=√A′A 2−AA 2=√2,正确.②当点P 位于AB 中点时,CP =PB =P A =AC =PB ′,∠B 'P A =P AC =60°,PB '∥AC ,所以四边形ACPB '是平行四边形,又PC =AC ,所以四边形ACPB '是菱形,正确.③当∠B 'P A =30°时,可知四边形BCB ′P 是菱形,BP =BC =√3;AP =2−√3,AA AA =12不成立,故不正确.④当CP ⊥AB 时,∠B '=∠B 'CA =30°,AC =AB ',∠ACP =∠B =30°,设AP =a ,则AB '=AC =2a ;AB =4a ,PB =3a ;所以:AP :AB ':BP =a :2a :3a =1:2:3,正确.故答案为:①②④.8.【解答】解:设AC =BC =x ,则CD =AA AAAA =A√33=√3x ,∵∠BAC =∠ACD =90°,∴∠BAC +∠ACD =180°,∴AB ∥CD ,∴△ABE ∽△DCE ,∴AAAA =AA AA =√3A=√33, 故答案为:√33 9.【解答】解:∵AB :BC =3:5,设AB =3x ,BC =5x ,∵四边形ABCD 是矩形,∴CD =AB =3x ,AD =BC =5x ,分两种情况:①当∠CA 1E =90°时,△A 1CE 为直角三角形,如图1所示:∵∠DCA 1+∠DA 1C =∠DA 1C +∠EA 1N =90°,∴∠DCA 1=∠EA 1N ,由折叠的性质得:AN =A 1N ,AE =A 1E ,∠EAN =∠EA 1N ,∴∠DCA 1=∠DAC ,∵∠CDA 1=∠ADC =90°,∴△CDA 1∽△ADC ,∴AA 1AA =AA AA ,即AA′3A =3A5A , ∴DA 1=95x ,∴AN =5A −95A 2=85x , DN =95x +85x =175x ,∴AN :DN =817; ②当∠A 1CE =90°时,△A 1CE 为直角三角形,如图2所示:∵∠A 1CD +∠CA 1D =∠A 1CD +∠ACD =90°,∴∠CA 1D =∠ACD ,∵∠A 1DC =∠CDA =90°,∴△A 1DC ∽△CDA ,∴A 1A AA =AA AA ,即A 1A 3A =3A 5A ,∴A 1D =95x ,由折叠的性质得:AN =A 1N ,∴DN =12(A 1A ﹣2A 1D )=12(95x +5x ﹣2×95x )=85x , AN =AD ﹣DN =5x −85x =175x ,∴AN :DN =178,综上所述,AN :DN 的值为817或178,故答案为:817或178.10.【解答】解:①:CD '=BD '时,如图,由折叠性质,得AD =AD ′,∠DAE =∠D ′AE ,∵四边形ABCD 是矩形,∴AB =CD ,∠ABC =∠DCB =90°,∵△BCD ′为等腰三角形,∴D ′B =D ′C ,∠D ′BC =∠D ′CB ,∴∠DCD ′=∠ABD ′,在△DD ′C 和△AD ′B 中,{AA =AAAAAA′=AAAA′AA′=AA′,∴△DD ′C ≌△AD ′B ,∴DD ′=AD ′,∴DD ′=AD ′=AD ,∴△ADD ′是等边三角形,∴∠DAD ′=60°,∴∠DAE =30°,∴DE =12AE , 设DE =x ,则AE =2x ,(2x )2﹣x 2=82,解得:x =8√33,即DE =8√33.②:当CD '=CB 时,如图,连接AC ,由于AD '=8,CD '=8,而AC =√142+82=2√65>8+8;故这种情况不存在.③当BD '=BC 时,如图过D '作AB 的垂线,垂足为F ,延长D 'F 交CD 于G ,由于AD '=BD ',D 'F =D 'F ;易知AF =BF ,从而由勾股定理求得D 'F =√AA′2−AA 2=√82−72=√15,又易证△AD 'F ∽△D 'EG ,设DE =x ,D 'E =x ,∴A′A AA′=A′A AA ,即A 8=8−√157; 解得x =64−8√157, 故答案为:8√33或64−8√157.11.【解答】解:分两种情况:①若点A 1在AC 左侧,如图1所示:∵∠C =90°,AC =8,BC =6,∴AB =√AA 2+AA 2=√82+62=10,∵点D 是AB 的中点,∴AD =12AB =5,∵A 1D ⊥AC ,∠C =90°∴A 1D ∥BC∴AA AA =AA AA =AA AA =12, ∴AE =EC =12AC =4,DE =12BC =3, ∵将△ADP 沿DP 所在的直线翻折得△A 1DP ,∴A 1D =AD =5,A 1P =AP ,∴A 1E =A 1D ﹣DE =5﹣3=2,∴在Rt △A 1PE 中,A 1P 2=A 1E 2+PE 2,∴AP 2=22+(4﹣AP )2,∴AP =52;②若点A 1在AC 右侧,延长A 1D 交AC 于E ,如图2所示:则A 1E =DE +A 1D =3+5=8,在Rt △EA 1P 中,A 1P 2=A 1E 2+EP 2,∴AP 2=82+(AP ﹣4)2,∴AP =10,故答案为:52或10.12.【解答】解:分两种情况:①当DF ⊥BC 时,如图1所示:则DF ∥AC ,∴∠DFE =∠AEF ,∵∠ACB =90°,AC =4,AB =5,∴BC =3,由折叠的性质得:∠DEF =∠AEF ,DE =AE ,DF =AF ,∴∠DFE =∠DEF ,∴DE =DF ,∴DE =DF =AF =AE ,设DE =DF =AF =AE =x ,∵DF ∥AC ,∴△BDF ∽△BCA ,∴AA AA =AA AA , ∴AA 3=A 4,解得:BD =34x ,在Rt △CDE 中,由勾股定理得:(4﹣x )2+(3−34x )2=x 2, 解得:x =209,或x =20(舍去), ∴AF =209,BD =53, ∴CD =BC ﹣BD =43, 作FG ⊥AE 于G ,则FG =CD =43, ∴AG =√AA 2−AA 2=169, ∴EG =AE ﹣AG =209−169=49,∴EF =√AA 2+AA 2=4√109; ②当DE ⊥BC 时,如图2所示:此时D 与C 重合,E 为AC 的中点,F 为AB 的中点,∴EF 为△ABC的中位线, ∴EF =12BC =32;综上所述,若△DEF 有一边垂直BC ,则EF 为4√109或32; 故答案为:4√109或2.13.【解答】解:在Rt △ABC 中,∠C =90°,AB =10cm ,AC =8cm ,∴BC =6cm ,①若点A '落在BC 上,如图:点A 关于直线PQ 的对称点A ',∵点A 关于直线PQ 的对称点A ',∴A 'Q =AQ ,AP =A 'P ,∵AP =5,∴PC =3,A 'C =4,A 'B =2,∴A 'A =4√5,作A 'H 垂直AB ,由勾股定理可得:{A ′A 2−AA 2=A′A 2A′A 2−AA 2=A′A 2A′A 2−AA 2=A′A 2,设AQ =AQ '=x ,BH =y ,∴{4−A 2=(4√5)2−(10−A )2A 2−(10−A −A )2=4−A 2, 解得:{A =5011A =65, 故AQ 的长为5011.②若点A '落在AB 上,如图:∵点A 关于直线PQ 的对称点A ',∴PQ ⊥AB ,∴△APQ ~△ABC ,∴AA AA =AA AA , ∴510=AA 8,∴AQ =4. 综上所述:若点A 关于直线PQ 的对称点A '恰好落在△ABC 的边上,则AQ 的长为5011或4cm .故答案为5011或4..14.【解答】解:如图1,当点B 关于直线MN 的对称点B '恰好落在等边三角形ABC 的边AB 上时, 则MN ⊥AB ,BN =B ′N ,∵△ABC 是等边三角形,∴AB =AC =BC ,∠ABC =60°,∵点M 为边BC 的中点,∴BM =12BC =12AB =2, ∴BN =12BM =1, 如图2,当点B 关于直线MN 的对称点B '恰好落在等边三角形ABC 的边AC 上时,则MN ⊥BB ′,四边形BMB ′N 是菱形,∵∠ABC =60°,点M 为边BC 的中点,∴BN =BM =12BC =12AB =2,故答案为:1或2.15.【解答】解:∵AB :BC =3:5,设AB =3x ,BC =5x ,∵四边形ABCD 是矩形,∴CD =AB =3x ,AD =BC =5x ,分两种情况:①如图所示,当∠DFE =90°时,△DEF 为直角三角形,∵∠CDF +∠CFD =∠EFN +∠CFD =90°,∴∠CDF =∠EFN ,由折叠可得,EF =EB ,∴∠EFN =∠EBN ,∴∠CDF =∠CBD ,又∵∠DCF =∠BCD =90°,∴△DCF ∽△BCD ,∴AA AA =AA AA ,即AA 3A =3A 5A ,∴CF =95x , ∴FN =5A −95A 2=8A 5, ∴CN =CF +NF =95x +85x =175x , ∴BN =5x −175x =85x ,∴CN :BN =178; ②如图所示,当∠EDF =90°时,△DEF 为直角三角形,∵∠CDF +∠CDB =∠CDF +∠CBD =90°,∴∠CDF =∠CBD ,又∵∠DCF =∠BCD =90°,∴△DCF ∽△BCD ,∴AA AA =AA AA ,即AA 3A =3A 5A ,∴CF =95x ,∴NF =5A +95A 2=175x , ∴CN =NF ﹣CF =85x ,∴BN =5x −85x =175x , ∴CN :BN =817, 综上所述,CN :BN 的值为178或817,故答案为:178或817.16.【解答】解:①当AP =PF 时,易得△ABP ≌△PCF ,则PC =AB =6,故PB =2. ②当AF =PF 时,△ABC ∽△F AP ,∴AA AA =AA AA =68,即PC =92. ∴PB =72. ③当AF =AP 时,点P 与点B 重合,不合题意.综上所述,PB 的长为2或72.故答案是:2或72. 17.【解答】解:当点F 在AD 上时,S △AMF =12AF •AB =12×1×AF ,∴当AF 取最大值时,△AMF 的面积最大,∴AF =6即点F 与点D 重合.如图所示:由翻折的性质可知:FM =AF =6.在Rt △FMC 中,MC =√AA 2−AA 2=√62−12=√35.故答案为:√35.18.【解答】解:小球沿着坡面向下前进了10m 假设到A 处,过C 作CB ⊥AB , ∵i =1:3,∴tan A =AA AA =13, 设BC =xcm ,AB =3xcm ,x 2+(3x )2=102,解得:x =√10或x =−√10(不合题意,舍去),故答案为:√10.19.【解答】解:DF ∥AC ,或∠BFD =∠A .理由:∵∠A =∠A ,AA AA =AA AA ,∴△ADE ∽△ACB ,∴①当DF ∥AC 时,△BDF ∽△BAC ,∴△BDF ∽△EAD .②当∠BFD =∠A 时,∵∠B =∠AED ,∴△FBD ∽△AED .故答案为DF ∥AC ,或∠BFD =∠A .20.【解答】解:要使△BEF 与△OFE 相似,设OD =t , ∵∠FEO =∠FEB =90°,∴只要AA AA =AA AA 或AA AA =AA AA ,即:BE =2t 或AA =12t , ①当BE =2t 时,BO =4t ,∵△BEF ~△OFE ,∴AA AA =AA AA ,∴2A 2−A =4A ,∴t 1=0(舍去)或t 2=1.5,∴B (6,0).②当AA =12t 时, (ⅰ)当B 在E 的左侧时,AA =AA −AA =32A , ∵△BEF ~△OFE ,∴AA AA =AA AA , ∴2A 2−A =32A ,∴t 1=0(舍去)或t 2=23.∴B (1,0).(ⅱ)当B 在E 的右侧时,AA =AA +AA =52A , ∵△BEF ~△OFE ,∴AA AA =AA AA , ∴2A 2−A =52A ,∴t 1=0(舍去)或t 2=65, ∴B (3,0).综上,B (1,0)(3,0)(6,0).故答案为:(1,0)(3,0)(6,0).三.解答题(共14小题)21.【解答】解:(1)如图,△A ′B ′C ′即为所求.(2)如图,△DEF 即为所求.(3)△A ′B ′C ′与△DEF 成中心对称,对称中心是线段OD 与线段FC ′的交点.22.【解答】解:如图,过B 作BE ⊥PD 于E ,在Rt △APD 中,由tan60°=600AA,得AD =600÷tan60°=200√3(米), CD =BE =286√3−200√3=86√3(米),在Rt △PBE 中,由tan70°=AA AA 得,PE =86×1.73×2.75≈409.1(米),∴BC =600﹣409.1≈191(米),答:建筑物BC 的高为191米.23.【解答】解:(1)如图,线段A ′B ′即为所求.(2)如图,矩形A ′B ′CD 即为所求(答案不唯一).24.【解答】解:(1)【问题发现】①如图1,∵∠AOB =∠COD =40°,∴∠COA =∠DOB ,∵OC =OD ,OA =OB ,∴△COA ≌△DOB (SAS ),∴AC =BD ,∴AA AA =1;②∵△COA ≌△DOB ,∴∠CAO =∠DBO ,∵∠AOB =40°,∴∠OAB +∠ABO =140°,在△AMB 中,∠AMB =180°﹣(∠CAO +∠OAB +∠ABD )=180°﹣(∠DBO +∠OAB +∠ABD )=180°﹣140°=40°,故答案为:①1;②40°;(2)【类比探究】如图2,AA AA =√3,∠AMB =90°,理由是: Rt △COD 中,∠DCO =30°,∠DOC =90°, ∴AA AA =tan30°=√33, 同理得:AA AA =tan30°=√33, ∴AA AA =AA AA ,∵∠AOB =∠COD =90°,∴∠AOC =∠BOD ,∴△AOC ∽△BOD ,∴AA AA =AA AA =√3,∠CAO =∠DBO ,在△AMB 中,∠AMB =180°﹣(∠MAB +∠ABM )=180°﹣(∠OAB +∠ABM +∠DBO )=90°;(3)【实际应用】①点C 与点M 重合时,如图3,同理得:△AOC ∽△BOD ,∴∠AMB =90°,AA AA =√3,设BD =x ,则AC =√3x ,Rt △COD 中,∠OCD =30°,OD =1,∴CD =2,BC =x ﹣2,Rt △AOB 中,∠OAB =30°,OB =√7,∴AB =2OB =2√7,在Rt △AMB 中,由勾股定理得:AC 2+BC 2=AB 2,∴(√3x )2+(x ﹣2)2=(2√7)2,x 2﹣x ﹣6=0,∴(x ﹣3)(x +2)=0,∴x 1=3,x 2=﹣2,∴AC =3√3;②点C 与点M 重合时,如图4,同理得:∠AMB =90°,AA AA =√3,设BD =x ,则AC =√3x ,在Rt △AMB 中,由勾股定理得:AC 2+BC 2=AB 2,∴(√3x )2+(x +2)2=(2√7)2,∴x 2+x ﹣6=0,∴(x +3)(x ﹣2)=0,∴x 1=﹣3,x 2=2,∴AC =2√3;综上所述,AC 的长为3√3或2√3.25.【解答】解:(1)如图所示:△A1B1C1,即为所求;(2)如图所示:△A2B2C2,即为所求;(3)∵P(a,b)是△ABC的AC边上的一点,∴将△ABC向右平移1个单位再向下平移5个单位后得到对应的点的坐标为:(a+1,b﹣5),∴(a+1,b﹣5)关于y轴对称点的坐标为:(﹣a﹣1,b﹣5).26.【解答】解:(1)△A₁B₁C₁如下图所示;A₁的坐标为(2,1),B₁的坐标为(3,﹣3).(2)△A₂B₂C₂如下图所示:27.【解答】解:(1)过点A 作AD ⊥BC 于点D ,∵∠B =30°,∴cos ∠B =AA AA =√32, ∴BD =√32AB ,∵△ABC 是等腰三角形,∴BC =2BD =√3AB ,故can 30°=AA AA =√3;(2)过点A 作AE ⊥BC 于点E ,∵canB =85,则可设BC =8x ,AB =5x ,∴AE =√AA 2−AA 2=3x ,∵S △ABC =24,∴12BC ×AE =12x 2=24, 解得:x =√2,故AB =AC =5√2,BC =8√2,从而可得△ABC 的周长为18√2.28.【解答】(1)证明:如图1,∵∠AEB =90°,EG ⊥DE ,∴∠AEB =∠DEG =90°,∴∠AEH =∠BEG ,∵BC ⊥AQ ,∴∠AEQ =∠BCQ =90°,∵∠AQE =∠BQC ,∴∠EAH =∠EBG ,∴△AEH ∽△BEG ;(2)解:∵∠BFE =∠AEB =90°,∴tan ∠EBF =AA AA =AA AA , ∵△AEH ∽△BEG , ∴AA AA =AA AA , ∴AA AA=AA AA ∵BF =6,BG =5.EF =3, ∴36=AA 5,∴AH =52:(3)如图2,延长FE 、BC ,交于点M ,作GN ⊥EF 于点N ,∵BF =6,cos ∠FBG =35,∴cos ∠FBG =AA AA =35, ∴6AA =35 ∴BM =10,∴MF =√AA 2−AA 2=8,∵BG =5,∴点G 为BM 中点∴点N 为MF 的中点,∴NG =12BF =12×6=3,NF =12MF =12×8=4, ∵∠ENG =∠DEG =∠DFE =90°,∴∠NEG +∠NGE =90°,∠NEG +∠FED =90°,∴∠NGE =∠FED ,∴△ENG ∽△DFE ,∴AA AA=AA AA 设EF =a , ∴3A =4−A AA∴DF =13A (4﹣a )=43 解得a =2∴EF =2.29.【解答】解:(1)如图所示,△A 1B 1C 1即为所求,点A 的对应点A 1的坐标为(﹣1,4)(2)如图所示,△A 2B 2C 2即为所求;(3)由题可得,△A 2B 2C 2中,A 2B 2边上的高为:√13=4√1313, ∴sin ∠B 2A 2C 2=4√1313√5=4√6565. 故答案为:4√6565.30.【解答】解:在R △BCF 中,∠CBF =45°,∴BC =FC ,在Rt △CBE 中,设BC =FC =x ,∵∠CBE =61°,∴CE =BC tan ∠CBE =1.8x ,在Rt △CAE 中,AAA ∠AAA =AAAA ,∵∠CAE =31°,AB =48,∴0.6=1.8A A +48, ∴x =24,∴EF =CE ﹣FC =0.8x =19.2(米),答:旗杆EF 的长为19.2米.31.【解答】解:过点A 作AM ⊥EF 于M ,过点C 作CN ⊥EF 于N ,∵AB =1.6米,CD =1.75米,∴MN =0.15米,∵∠EAM =45°,∴AM =ME ,设AM =ME =x 米,∵BD =30米∴CN =(x +30)米,EN =(x ﹣0.15)米,∵∠ECN =15°, ∴tan ∠ECN =AA AA =A −0.15A +30,解得:x ≈11.3,则EF =EM +MF =11.3+1.6=12.9(米). 答:旗杆的高EF 为12.9米.32.【解答】解:(1)如图所示:(2)点A 在(1)的图形变换过程中所经过的路径是一段圆弧,其半径为2√5,圆心角为90°, 所以长度为90⋅A ×2√5180=√5A .33.【解答】解:(1)图4中,特征点的个数为17,在n 个图中,特征点个数为4n +1.故答案为17.4n +1.(2)由题意可知x 1=√3,x 2=2√3,x 3=3√3,…,x n =n √3,∴图2018的对称中心的横坐标为2018√3,故答案为√3,2018√3.34.【解答】解:(1)如图所示,△EFB 即为所求;(2)如图所示,△BCG 即为所求;(3)如图所示,将△ABP 绕点A 顺时针旋转60°得到△ACD ,连接PD ,∴△ADP 是等边三角形,CD =BP ,∴∠APD =60°,AP =DP ,∵P A 2+PC 2=PB 2,∴PD 2+PC 2=CD 2,∴△CPD 是直角三角形,∴∠CPD =90°,∴∠APC =∠APD +∠CPD =60°+90°=150°.故答案为:150.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年全国各地中考数学真题分类汇编—矩形、菱形与正方形 1. (2018福建福州,21,12分)已知,矩形ABCD中,4ABcm,8BCcm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O. (1)如图10-1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长; (2)如图10-2,动点P、Q分别从A、C两点同时出发,沿AFB和CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中, ①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值. ②若点P、Q的运动路程分别为a、b(单位:cm,0ab),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.
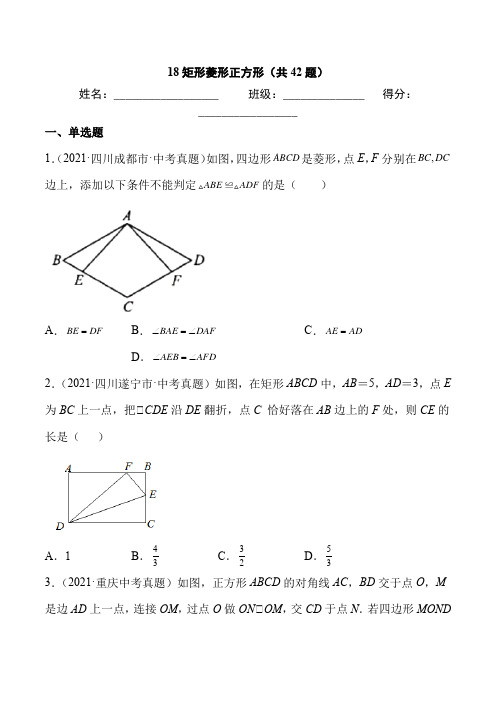
【答案】(1)证明:①∵四边形ABCD是矩形 ∴AD∥BC ∴CADACB,AEFCFE ∵EF垂直平分AC,垂足为O ∴OAOC ∴AOE≌COF ∴OEOF ∴四边形AFCE为平行四边形 又∵EFAC ∴四边形AFCE为菱形
ABC
DEF图10-1 O图10-2 ABC
DE
FPQ
备用图
A
BC
DE
FPQ ②设菱形的边长AFCFxcm,则(8)BFxcm 在RtABF中,4ABcm 由勾股定理得2224(8)xx,解得5x ∴5AFcm (2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形.因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形 ∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PCQA ∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒 ∴5PCt,124QAt ∴5124tt,解得43t ∴以A、C、P、Q四点为顶点的四边形是平行四边形时,43t秒.
②由题意得,以A、C、P、Q四点为顶点的四边形是平行四边形时,点P、Q在互相平行的对应边上. 分三种情况:
i)如图1,当P点在AF上、Q点在CE上时,APCQ,即12ab,得12ab ii)如图2,当P点在BF上、Q点在DE上时,AQCP, 即12ba,得12ab iii)如图3,当P点在AB上、Q点在CD上时,APCQ,即12ab,得12ab 综上所述,a与b满足的数量关系式是12ab(0)ab
ABC
DE
FP
Q 2. (2018广东广州市,18,9分) 如图4,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF. 求证:△ACE≌△ACF.
【答案】∵四边形ABCD为菱形 ∴∠BAC=∠DAC 又∵AE=AF,AC=AC ∴△ACE≌△ACF(SAS) 3. (2018山东滨州,24,10分)如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF。那么当点O运动到何下时,四边形AECF是矩形?并证明你的结论。
【答案】 (第24题图) FENMOCB
A
ABCDEFPQABDEFPQCABC
DE
FPQ
图1 图2 图3
A B C D
E F
图4 当点O运动到AC的中点(或OA=OC)时, 四边形AECF是矩形………………2分 证明:∵CE平分∠BCA,∴∠1=∠2,………………3分 又∵MN∥BC, ∴∠1=∠3, ∴∠3=∠2,∴EO=CO. ………………5分 同理,FO=CO………………6分 ∴EO=FO 又OA=OC, ∴四边形AECF是平行四边形………………7分 又∵∠1=∠2,∠4=∠5, ∴∠1+∠5=∠2+∠4. ………………8分 又∵∠1+∠5+∠2+∠4=180° ∴∠2+∠4=90°………………9分 ∴四边形AECF是矩形………………10分 4. (2018山东济宁,22,8分)数学课上,李老师出示了这样一道题目:如图1,正方形ABCD的边长为12,P为边BC延长线上的一点,E为DP的中点,DP的垂直平分线交边DC于M,交边AB的延长线于N.当6CP时,EM与EN的比值是多少? 经过思考,小明展示了一种正确的解题思路:过E作直线平行于BC交DC,AB分别于F,G,如图2,则可得:DFDEFCEP,因为DEEP,所以DFFC.可求出EF和EG的值,进而可求得EM与EN的比值. (1) 请按照小明的思路写出求解过程. (2) 小东又对此题作了进一步探究,得出了DPMN的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由. (1)解:过E作直线平行于BC交DC,AB分别于点F,G, 则DFDEFCEP,EMEFENEG,12GFBC. ∵DEEP,∴DFFC. ··················· 2分 ∴116322EFCP,12315EGGFEF. ∴31155EMEFENEG. ····················· 4分 (2)证明:作MH∥BC交AB于点H, ················· 5分 则MHCBCD,90MHN. ∵1809090DCP, ∴DCPMHN. ∵90MNHCMNDMECDP,90DPCCDP, ∴DPCMNH.∴DPCMNH. ············ 7分 ∴DPMN. ························ 8分
(第22题)
(第22题) H B C
D E M
N
A
P 5. (2018山东威海,24,11分)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到
△MNK.
(1)若∠1=70°,求∠MNK的度数. (2)△MNK的面积能否小于12?若能,求出此时∠1的度数;若不能,试说明理由. (3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
(备用图) 【答案】 解:∵ABCD是矩形, ∴AM∥DN, ∴∠KNM=∠1. ∵∠KMN=∠1, ∴∠KNM=∠KMN. ∵∠1=70°, ∴∠KNM=∠KMN=70°. ∴∠MNK=40°. (2)不能. 过M点作ME⊥DN,垂足为点E,则ME=AD=1, 由(1)知∠KNM=∠KMN. ∴MK=NK. 又MK≥ME, ∴NK≥1. ∴1122MNKSNKME. ∴△MNK的面积最小值为12,不可能小于12. (3)分两种情况: 情况一:将矩形纸片对折,使点B与点D重合,此时点K也与点D重合. 设MK=MD=x,则AM=5-x,由勾股定理,得 2221(5)xx,
解得,2.6x. 即2.6MDND. ∴112.61.32MNKACKSS. (情况一) 情况二:将矩形纸片沿对角线AC对折,此时折痕为AC. 设MK=AK= CK=x,则DK=5-x,同理可得 即2.6MKNK. ∴112.61.32MNKACKSS. ∴△MNK的面积最大值为1.3. (情况二) 6. (2018山东烟台,24,10分)已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC; (2)当BE⊥AD于E时,试证明:BE=AE+CD.
【答案】(1)证明:连接AC, ∵∠ABC=90°, ∴AB2+BC2=AC2. ∵CD⊥AD,∴AD2+CD2=AC2. ∵AD2+CD2=2AB2,∴AB2+BC2=2AB2, ∴AB=BC.
A B C D E (2)证明:过C作CF⊥BE于F. ∵BE⊥AD,∴四边形CDEF是矩形. ∴CD=EF. ∵∠ABE+∠BAE=90°,∠ABE+∠CBF=90°, ∴∠BAE=∠CBF,∴△BAE≌△CBF. ∴AE=BF. ∴BE=BF+EF =AE+CD.
7. (2018 浙江湖州,22,8) 如图已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF. (1) 求证:四边形AECF是平行四边形; (2) 若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长 .
【答案】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,且AD=BC,∴AF∥EC,∵BE=DF, ∴AF=EC,∴四边形AECF是平行四边形. (2)∵四边形AECF是,∴AE=CE,∴∠1=∠2,∵∠BAC=90°,∴∠3=∠90°-∠2,∠4=∠90°-∠1,∴∠3=∠4,∴AE=BE,∴BE=AE=CE=12BC=5.
8.(2018宁波市,23,8分)如图,在□ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作AGDB交CB的延长线于点G. (1)求证:DE∥BF; (2)若∠G=90,求证四边形DEBF是菱形.
