人教版八年级上册数学 12.3 角的平分线的性质 同步练习(含答案)
人教版八年级数学上册 第12章 12.3.2角的平分线的判定 培优训练(含答案)

人教版数学八年级上册12.3.2角的平分线的判定培优训练一.选择题(本大题共10小题,每小题3分,共30分)1.△ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是()A.点O一定在△ABC的内部B.∠C的平分线一定经过点OC.点O到△ABC三边的距离一定相等D.点O到△ABC三顶点的距离一定相等2.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是()A.点M B.点NC.点P D.点Q3.△ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线,如果两条平分线交于点O,那么下列说法中不正确的是( )A.点O一定在△ABC的内部B.∠C的平分线一定经过点OC.点O到△ABC的三边距离一定相等D.点O到△ABC三顶点的距离一定相等4.如图,O是△ABC内一点,且O到三边AB,BC,CA的距离OF=OD=OE,若∠BAC=70°,则∠BOC的度数是( )A.35°B.145°C.55°D.125°5.如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD与BC相交于点P,若PA=PB,则∠1与∠2的大小关系是()A.∠1=∠2 B.∠1>∠2C.∠1<∠2 D.无法确定6.如图,在△ABC中,∠ABC,∠ACB外角的平分线相交于点F,连接AF,则下列结论正确的是() A.AF平分BC B.AF平分∠BACC.AF⊥BC D.以上结论都正确7.如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是()A.在一个角的内部,且到角两边的距离相等的点在这个角的平分线上B.角的平分线上的点到这个角两边的距离相等C.三角形三条角平分线的交点到三边的距离相等D.以上均不正确8. 如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC ≌△POD的选项是()A.PC⊥OA,PD⊥OBB.OC=ODC.∠OPC=∠OPD9.△ABC是一个任意三角形,用直尺和圆规作出∠A,∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是()A.点O一定在△ABC的内部B.∠C的平分线一定经过点OC.点O到△ABC三边的距离一定相等D.点O到△ABC三顶点的距离一定相等10.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )A.有且只有1个B.有且只有2个C.组成∠E的角平分线D.组成∠E的角平分线所在的直线(E点除外)二.填空题(共8小题,3*8=24)11. 如图,PD⊥OA,PE⊥OB,点D,E为垂足,PD=6 cm,当PE=___cm时,点P在∠AOB的平分线上.12.如图,DE⊥AB于点E,DF⊥BC于点F,且DE=DF,若∠DBC=50°,则∠ABC=______°.13.如图,点P在∠AOB内部,PC⊥OA于点C,PD⊥OB于点D,PC=3 cm,当PD=____cm时,P点在∠AOB的平分线上.14.在△ABC中,点D在BC边上,DE⊥AB于点E,DF⊥AC于点F,DE=DF,∠B=50°,∠C =70°,那么∠DAF=________,∠ADE=_______.15.如图,已知△ABC的周长是20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是___.16.如图,O是△ABC内的一点,且O到△ABC的三边AB,BC,CA的距离OF=OD=OE,若∠A =70°,则∠BOC=_________.17.如图,OP平分∠MON,PE⊥OM于点E,PF⊥ON于点F,OA=OB,则图中有____对全等三角形.18.直线l1,l2,l3表示三条两两相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,则可供选择的地址有____处.三.解答题(共9小题,66分)19.(6分)如图,∠ABC的平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC 的外角平分线.20.(6分) 如图,BD=CD,BF⊥AC于点F,CE⊥AB于点E.求证:点D在∠BAC的角平分线上.21.(6分) 如图,PA=PB,∠1+∠2=180°,求证:OP平分∠AOB.22.(6分) 如图,∠ABC的角平分线与∠ACB的外角平分线相交于点D,连接AD.求证:AD是∠BAC的外角平分线.23.(6分) 如图,D,E,F分别是△ABC三边上的点,CE=BF,△DCE和△DBF的面积相等.求证:AD平分∠BAC.24.(8分) 已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.(1)如图①,若点O在边BC上,求证:∠ABC=∠ACB;(2)如图②,若点O在△ABC的内部,∠OBC=∠OCB,求证:∠ABC=∠ACB;(3)若点O在△ABC的外部,则∠ABC=∠ACB成立吗?请画图表示.25.(8分) 如图,在四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且OA平分∠BAC.(1)求证:OC平分∠ACD;(2)求证:OA⊥OC;(3)求证:AB+CD=AC.参考答案:1-5DADDA 6-10BADDD11. 612. 10013. 314. 30°,60°15. 3016. 125°17. 318. 419. 解:过点D分别作DE⊥AB,DG⊥AC,DF⊥BC,垂足分别为点E,G,F.又∵BD平分∠ABC,CD平分∠ACF,∴DE=DF,DG=DF,∴DE=DG,∴AD平分∠EAC,即AD是∠BAC的外角平分线20. 解:∵CE⊥AB于E,BF⊥AC于F,∴∠BED=∠CFD=90°,又∵∠EDB=∠CDF,BD=CD,∴△BED≌△CFD(AAS),∴ED=DF,∴点D在∠BAC的角平分线上21. 解:过点P作PE⊥AO,PF⊥OB,垂足分别为E,F,∵∠1+∠2=180°,∠2+∠PBO=180°,∴∠1=∠PBO,在△PAE和△PBF中,∠AEP=∠BFP,∠1=∠PBF,PA=PB,∴△PAE≌△PBF,∴PE=PF,∴OP平分∠AOB22. 解:过点D分别作DE⊥AB,DG⊥AC,DF⊥BC,垂足分别为E,G,F,∵BD平分∠ABC,CD平分∠ACF,∴DE=DF,DG=DF,∴DE=DG,∴AD平分∠EAC.即AD是∠BAC的外角平分线∵S △DCE =12CE·DG ,S △DBF =12BF·DH ,S △DCE =S △DBF , ∴12CE·DG =12BF·DH.又∵CE =BF ,∴DG =DH , ∴点D 在∠BAC 的平分线上,即AD 平分∠BAC24. 解:(1)过点O 分别作OE ⊥AB ,OF ⊥AC ,E ,F 分别为垂足,则OE =OF , 在Rt △OEB 和Rt △OFC 中,OB =OC ,OE =OF ,∴Rt △OEB ≌Rt △OFC(HL),∴∠ABC =∠ACB(2)过点O 分别作OE ⊥AB ,OF ⊥AC ,E ,F 分别为垂足,则OE =OF ,由HL 可证Rt △OEB ≌Rt △OFC ,∴∠OBE =∠OCF ,∵∠OBC =∠OCB ,∴∠ABC =∠ACB(3)不一定成立,如图25. 解:(1)过点O 作OE ⊥AC 于E ,∵∠B =90°,OA 平分∠BAC.∴OB =OE ,∵点O 为BD 的中点,∴OB =OD ,∴OE =OD ,∵∠D =90°,∴OC 平分∠ACD(2)在Rt △ABO 和Rt △AEO 中,∵AO =AO ,OB =OE ,∴Rt △ABO ≌Rt △AEO(HL),∴∠AOB =∠AOE.同理,∠COD =∠COE ,∴∠AOC =∠AOE +∠COE =12×180°=90°, ∴OA ⊥OC(3)∵Rt △ABO ≌Rt △AEO ,∴AB =AE ,同理可得CD =CE ,。
12 3 角的平分线的性质 期末试题分类选编 浙江省各地人教版数学八年级上册

12.3 角的平分线的性质1.(2022·浙江台州·八年级期末)如图,OP 平分∠AOB ,E 为OA 上一点,OE =4,P 到OB 的距离是2,则△OPE 的面积为( )A .2B .3C .4D .82.(2022·浙江绍兴·八年级期末)如图,AB CD ∥,BP 和CP 分别平分∠ABC 和∠BCD ,AD 过点P ,且与AB 垂直.若8AD =,10BC =,则BCP 的面积为( )A .16B .20C .40D .803.(2022·浙江杭州·八年级期末)下列语句中是命题的有( )∠线段垂直平分线上的点到线段两端的距离相等;∠作点A 关于直线l 的对称点A '∠三边对应相等的两个三角形全等吗?∠角平分线上的点到角两边的距离相等.A .1个B .2个C .3个D .4个4.(2022·浙江丽水·八年级期末)下列命题中,是真命题的是( )A .对应角相等的两个三角形是全等三角形.B .三个内角之比为3:4:5的三角形是直角三角形.C .平面直角坐标系中,点的横坐标是点到x 轴的距离.D .角平分线上的点到角两边的距离相等.5.(2022·浙江丽水·八年级期末)如图,AB CD ,点E 是AD 上的点,连接BE ,CE ,且90BEC ∠=︒,BE 平分ABC ∠.以下结论中:∠E 是AD 中点,∠AB CD BC +=,∠AE CE =,∠BCE CDE S BC S CD=△△,正确的个数为( )A.4B.3C.2D.16.(2022·浙江宁波·八年级期末)如图是用直尺和圆规作已知角∠AOB平分线OP的示意图,仔细观察,根据三角形全等的知识,说明画出OP的依据是()A.边角边,全等三角形对应角相等B.角边角,全等三角形对应角相等C.边边边,全等三角形对应角相等D.斜边直角边,全等三角形对应角相等7.(2022·浙江丽水·八年级期末)如图是用尺规作一个角的平分线,其依据正确的是()A.SAS B.SSS C.AAS D.ASA8.(2022·浙江金华·八年级期末)如图,OP平分∠MON,P A∠ON于点A,点Q是射线OM上一个动点,若P A=3,则PQ的最小值为_____.9.(2022·浙江金华·八年级期末)如图,在Rt∠ABC中,∠B=90°,以顶点C为圆心、适当长为半径画弧,EF的长为半径画弧,两弧交于点P,作分别交AC、BC于点E、F,再分别以点E、F为圆心,以大于12射线CP交AB于点D.若BD=4,AC=16,则∠ACD的面积是______.10.(2022·浙江·金华市第五中学八年级期末)如图,已知∠ABC的周长是24,OB,OC分别平分∠ABC和∠ACB,OD∠BC于D,且OD=4,∠ABC的面积是_____.11.(2022·浙江宁波·八年级期末)如图,在ABC中,CD是边AB上的高,BE平分ABC∠,交CD于点E,BC=,若BCE的面积为5,则ED的长为______.512.(2022··八年级期末)如图,点P是∠AOB平分线OC上一点,PE∠OA,PF∠OB,垂足分别是E和F,若PE=3,则PF=_____.13.(2022·浙江宁波·八年级期末)如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为_____.14.(2022·浙江台州·八年级期末)如图,在ABC 中,CD 是ACB ∠的平分线,延长CD 至点E ,使12DE CD =,连接BE ,若2AC BC =,BDE 的面积为1,则ABC 的面积是______.15.(2022·浙江·杭州外国语学校八年级期末)平面直角坐标系xOy 中有点P (x ,y ),实数x ,y ,m 满足以下两个等式:2x ﹣3m +1=0,3y ﹣2m ﹣16=0.(1)当x =1时,点P 到x 轴的距离为 ;(2)若点P 落在一、三象限的角平分线上,求点P 的坐标;(3)当x ≤4<y 时,求m 的最小整数值.16.(2022·浙江绍兴·八年级期末)如图,已知ABC .(1)请用直尺和圆规作∠ABC 的角平分线BD ,交AC 于点D .(保留作图痕迹,不写作法)(2)在(1)的条件下,若100A ∠=︒,28C ∠=︒,求∠BDA 的度数.参考答案:1.C【解析】根据角平分线上的点到角的两边距离相等,求得△OPE 的OE 边上的高,即可求得△OPE 的面积. 如图,作PH ∠OA 于点H ,∠OP 平分∠AOB ,P 到OB 的距离是2,∠PH =2∠△OPE 的面积为1142422OE PH ⨯⨯=⨯⨯=, ∠△OPE 的面积为4,故选:C本题考查了角平分线的性质定理,熟练掌握定理的内容是解答此题的关键所在.2.B【解析】过点P 作PE ∠BC 于E ,根据角平分线上的点到角的两边的距离相等可得P A =PE ,PD =PE ,那么PE =P A =PD ,又AD =8,进而求出PE =4,进而根据三角形面积公式求解即可.解:过点P 作PE ∠BC 于E ,∠AB ∠CD ,P A ∠AB ,∠PD ∠CD ,∠BP 和CP 分别平分∠ABC 和∠BCD ,∠P A =PE ,PD =PE ,∠PE =P A =PD ,∠P A +PD =AD =8,∠P A =PD =4,∠PE =4.111042022BCP S BC EP =⨯=⨯⨯= 故选:B .本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质并作辅助线是解题的关键.3.B【解析】根据命题的定义分别进行判断即可.解:∠线段垂直平分线上的点到线段两端的距离相等,是命题;∠作点A关于直线l的对称点A',不是命题;∠三边对应相等的两个三角形全等吗?不是命题;∠角平分线上的点到角两边的距离相等,是命题;故选:B.本题考查了命题与定理:判断事物的语句叫命题,命题有题设与结论两部分组成;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.4.D【解析】根据全等三角形的判定定理、三角形内角和定理、点的坐标、角平分线的性质进行判断即可.A:对应角相等的两个三角形不一定是全等三角形,本选项错误不符合题意;B:设三个内角分别为3x、4x、5x,则3x+4x+5x=180°,解得x=15°,则三个内角分别为:45°、60°、75°,∠三个内角之比为3:4:5的三角形不是直角三角形,本选项错误不符合题意;C:平面直角坐标系中,点的横坐标的绝对值是点到y轴的距离,本选项错误不符合题意;D:角平分线上的点到角两边的距离相等,本选项正确符合题意;故选:D.本题考查的是命题的真假判断,全等三角形的判定、三角形内角和定理、点的坐标、角平分线的性质,熟记这些性质是解题的关键.5.B【解析】延长BE交CD的延长线于点F,证明∆ABE≅∆DFE,得出AE=DE,AB=DF,即可判断∠和∠正确;过点E作EM∠BC于点M,EN∠CD于点N,由角平分线的性质定理即可判断∠∠.解:延长BE交CD的延长线于点F,∠AB∠CD,∠∠ABE=∠F,∠BE平分∠ABC,∠∠ABE=∠CBE,∠∠F=∠CBE,∠CF=BC,∠∠BEC=90°,∠CE∠BF,∠∠BCE=∠FCE,BE=EF,∠∠AEB=∠FED,∠∆ABE≅∆DFE,∠AE=DE,AB=DF,故∠正确;∠CF=CD+DF,∠BC=CD+AB,故∠正确;∠∠EDC≠∠ECD,∠ED≠EC,故∠错误;过点E作EM∠BC于点M,EN∠CD于点N,∠CE平分∠BCD,∠EM=EN,∠1·21·2BCE CDE BC EM SBC S CD CD EN ==,故∠正确; 故选:B .题目主要考查全等三角形的判定和性质,等腰三角形的性质,平行线的性质及角平分线的性质定理,熟练掌握运用这些知识点是解题关键.6.C【解析】结合题意,根据角平分线尺规作图、全等三角形的性质分析,即可得到答案. 根据题意,得:OD OC =,DP CP =在ODP 和OCP △中OD OC DP CP OP OP =⎧⎪=⎨⎪=⎩∠P ODP OC ≌∠DOP COP ∠=∠,即BOP AOP ∠=∠∠画出OP 的依据是:边边边,全等三角形对应角相等故选:C .本题考查了角平分线、全等三角形的知识;解题的关键是熟练掌握角平分线尺规作图、全等三角形的性质,从而完成求解.7.B【解析】利用基本作图和三角形全等的判定方法求解.解:如图,由作法得到OA OB =,AC BC =,而OC 为公共边,所以根据“SSS ”可判断OAC OBC ∆≅∆,所以AOC BOC ∠=∠,即OC 平分AOB ∠.故选:B .本题考查了作图-基本作图,解题的关键是熟练掌握5种基本作图,也考查了全等三角形的判定.8.3【解析】由垂线段最短可知,当PQ 与OM 垂直的时候,PQ 的值最小.解:由垂线段最短可知,当PQ 与OM 垂直的时候,PQ 的值最小,根据角平分线的性质可知,此时P A =PQ =3.故答案为:3.本题考查了角平分线的性质,垂线段最短,解题的关键是掌握垂线段距离最短.9.32【解析】过点D 作DQ ∠AC ,由作法可知CP 是角平分线,根据角平分线的性质知DB =DQ =3,再由三角形的面积公式计算即可.解:如图,过点D 作DQ ∠AC 于点Q ,由作图知CP 是∠ACB 的平分线,∠∠B =90°,BD =4,∠DB =DQ =4,∠AC =16,∠S △ACD =12•AC •DQ =1164322⨯⨯=, 故答案为32.本题主要考查作图-基本作图,三角形面积,解题的关键是掌握角平分线的尺规作图及角平分线的性质. 10.48【解析】过O 作OE ∠AB 于E ,OF ∠AC 于F ,连接OA ,根据角平分线的性质可得OE =OF =OD =4,再由∠ABC的面积是:AOB AOC OBC S S S ∆∆∆++,即可求解.解:过O 作OE ∠AB 于E ,OF ∠AC 于F ,连接OA ,∠OB ,OC 分别平分∠ABC 和∠ACB ,OD ∠BC ,OE ∠AB ,OF ∠AC ,∠OE =OD ,OD =OF ,即OE =OF =OD =4,∠∠ABC 的面积是:AOB AOC OBC S S S ∆∆∆++111222AB OE AC OF BC OD =⨯⨯+⨯⨯+⨯⨯ ()142AB AC BC =⨯⨯++ 14242=⨯⨯ 48=,故答案为:48.本题主要考查了角平分线的性质,熟练掌握角平分线上点到角两边的距离相等是解题的关键. 11.2【解析】过E 作EF BC ⊥于F ,根据角平分线性质求出2EF DE ==,根据三角形面积公式求出即可. 解:过E 作EF BC ⊥于F ,CD 是AB 边上的高,BE 平分ABC ∠,交CD 于点E ,DE EF ∴=,152BCE S BC EF =⨯⨯=, 1552EF ∴⨯⨯=, 2EF DE ∴==,故答案为:2.本题考查了角平分线性质的应用,能根据角平分线性质求出2EF DE ==是解此题的关键,注意:在角的内部,角平分线上的点到角的两边的距离相等.12.3.【解析】根据角平分线上的点到角两边的距离相等即可得到答案.∠点P是∠AOB平分线OC上一点,PE∠OA,PF∠OB∠PF=PE=3.本题考查了角平分线的性质:角平分线上的点到角两边的距离相等.13.2【解析】过E作EF∠BC于F,根据角平分线性质求出EF=DE=8,根据三角形面积公式求出即可.解:过E作EF∠BC于F,∠CD是AB边上的高,BE平分∠ABC,交CD于点E,∠DE=EF,×BC×EF=5,∠S△BCE=12∠1×5×EF=5,2∠EF=DE=2,故答案为:2.本题考查了角平分线性质的应用,能根据角平分线性质求出EF=DE=8是解此题的关键,注意:在角的内部,角平分线上的点到角的两边的距离相等.14.6【解析】由角平分线的性质可得DG=DH,由三角形的面积关系可求解.解:如图,过点D作DG⊥AC于G,DH⊥CB于H,∵DE12=CD,△BDE的面积为1,∴S△BCD=2S△BDE=2,∵CD是∠ACB的平分线,DH⊥CB,DG⊥AC,∴DG=DH,∵AC=2BC,12ACDS AC GD=⋅,12BCDS BC DH=⋅,∴S△ACD=2S△BCD,∴S△ACD=4,∴S△ABC=S△ACD+S△BCD=4+2=6,故答案为:6.本题考查了角平分线的性质,三角形的面积公式,添加恰当辅助线是解题的关键.15.(1)6(2)P(10,10)(3)−1【解析】(1)当x=1时,由2x﹣3m+1=0可求得m的值,再由3y﹣2m﹣16=0可求得y的值,从而可得点P的坐标,即可得点P到x轴的距离;(2)根据角平分线的性质定理及点在第一、三象限的坐标特征可得x=y,从而可得关于x与m的方程组,消去m即可求得x的值,从而可得点P的坐标;(3)由条件可得用含m的代数式表示x、y的等式,根据不等关系可得关于m的不等式组,解不等式组即可求得m的最小整数值.(1)当x=1时,由2x﹣3m+1=0,得21310m⨯-+=解得m=1由3y﹣2m﹣16=0,得321160y-⨯-=解得y=6∠点P 的坐标为(1,6)即点P 到x 轴的距离为6故答案为:6(2)∠点P 在第一、三象限的角平分线上,且在一、三象限的点的两个坐标符号相同∠x y =∠3x ﹣2m ﹣16=0由231032160x m x m -⎧⎨--=⎩+=消去m ,得x =10 ∠y =10∠点P 的坐标(10,10)(3)由2x ﹣3m +1=0,3y ﹣2m ﹣16=0可得:31216,23m m x y -+== 由题意得:314221643m m -⎧≤⎪⎪⎨+⎪>⎪⎩ 解不等式组得:23m -<≤故不等式组的整数解为:−1,0,1,2,3,最小整数值为−1.本题考查了点与坐标,角平分线的性质定理,点在各个象限的坐标特征,解二元一次方程组及解一元一次不等式组等知识,灵活运用这些知识是关键.16.(1)见解析(2)54︒【解析】(1)根据尺规作图作角平分线的步骤即可完成;(2)由三角形内角和定理可求得∠ABC 的度数,再由角平分线的性质可得∠DBC 的度数,由三角形外角的性质即可求得结果.(1)如图(2)∠∠A =100°,∠C =28°,∠180ABC A C ∠=︒-∠-∠1801002852=︒-︒-︒=︒,又∠BD 平分∠ABC ,∠∠DBC =26°,∠262854BDA DBC C ∠=∠+∠=︒+︒=︒.本题考查了角平分线的尺规作图,角平分线的性质,三角形内角和定理及外角性质,掌握这些性质是关键.。
人教版 八年级数学上册全等三角形 角平分线的性质与判定 同步练习A卷含答案

八年级数学上册全等三角形角平分线的性质与判定 A卷一、选择题1、如图,△ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于点E,且AC=7cm,则DE+BD等于()A.7cm B.6cm C.5cm D.4cm2、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC长是()A.3 B.4 C.5 D. 63、如图1,在△ABC中∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )A.2 cmB.3 cmC.4 cmD.5 cm4、如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是()A.∠ACD=∠B B.CH=CE=EF C.AC=AF D.CH=HD5、如图,MP⊥NP,MQ为∠NMP的平分线,MT=MP,连接TQ,则下列结论不正确的是()A.TQ=PQB.∠MQT=∠MQPC.∠QTN=90°D.∠NQT=∠MQT6、如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是()A.线段CD的中点B.OA与O B的中垂线的交点C.OA与CD的中垂线的交点D.CD与∠AOB的平分线的交点7、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DE=2,AC=3,则△ADC的面积是()A.3 B.4 C.5 D.68、如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=8,DE=3,则△BCE的面积等于( )A.11 B.8 C.12 D.39、如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有()A.一处 B.两处 C.三处 D.四处10、如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=144cm2,则DE的长是()A.4.8cm B.4.5cm C.4cm D.2.4cm11、如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有对全等三角形.12、如图,△ABC中,∠C=90°,AD为角平分线,若CB=8cm,BD=5cm,则D点到AB的距离为.13、如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是21cm2,AB=8cm,BC=6cm,则DE= cm.14、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,DF⊥AC于点F,S△ABC=7,DE=2,AB=4,则AC 长是.15、如图,已知BD⊥AE于点B,DC⊥AF于点C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF= .16、在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=15,且BD:DC=3:2,则D到边AB的距离是.17、如图,点D、B分别在∠A的两边上,C是∠A内一点,且AB=AD,BC=DC,CE⊥AD,CF⊥AB,垂足分别为E、F。
2021人教版八年级数学上册12.3角的平分线的性质按知识点分按题型分类易错点试题解析含答案解析
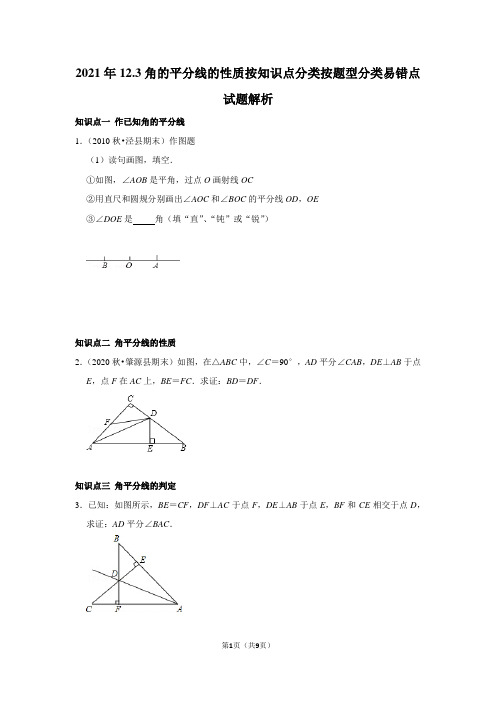
2021年12.3角的平分线的性质按知识点分类按题型分类易错点试题解析知识点一作已知角的平分线1.(2010秋•泾县期末)作图题(1)读句画图,填空.①如图,∠AOB是平角,过点O画射线OC②用直尺和圆规分别画出∠AOC和∠BOC的平分线OD,OE③∠DOE是角(填“直”、“钝”或“锐”)知识点二角平分线的性质2.(2020秋•肇源县期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.知识点三角平分线的判定3.已知:如图所示,BE=CF,DF⊥AC于点F,DE⊥AB于点E,BF和CE相交于点D,求证:AD平分∠BAC.知识点四证明几何文字命题的一般步骤4.(2019春•金水区校级期中)(1)如图1,求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;(2)如图2,若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P,连接AP,若∠BAC=62°,则∠P AC是度.题型一利用角平分线的性质解决方案设计问题5.如图,李明计划在张村、李村之间建一家超市,张、李两村坐落在两相交公路内,超市的位置应满足下列条件:①使其到两公路的距离相等;②为了方便群众,超市到两村的距离之和最短.请你通过作图确定所要建超市的位置.题型二与面积有关的角平分线的问题6.如图所示,在△ABC中,求证:(1)若AD为∠BAC的平分线,则S△ABD:S△ACD=AB:AC;(2)设D为BC上的一点,连接AD,若S△ABD:S△ACD=AB:AC,则AD为∠BAC的平分线.易错题易错点:不能正确理解角平分线的性质及判定7.(2014秋•阳谷县期末)如图,在△ABC中,BD平分∠ABC,交AC于点D,BC边上有一点E,连接DE,则AD与DE的关系为()A.AD<DE B.AD=DE C.AD>DE D.不确定8.如图,已知BE⊥AC于点E,CF⊥AB于点F,BE,CF相交于点D,连接AD,BD=CD.求证:AD平分∠BAC.王刚的做法如下:证明:∵BE⊥AC,CF⊥AB,BD=CD,∴点D在∠BAC的平分线上,∴AD平分∠BAC.王刚的做法正确吗?若不正确,请写出正确的证明过程.2021年12.3角的平分线的性质按知识点分类按题型分类易错点试题解析参考答案与试题解析一.试题(共8小题)1.(2010秋•泾县期末)作图题(1)读句画图,填空.①如图,∠AOB是平角,过点O画射线OC②用直尺和圆规分别画出∠AOC和∠BOC的平分线OD,OE③∠DOE是直角(填“直”、“钝”或“锐”)解:作图题.(1)①画出OC如图:②用圆规以O为圆心,以OA、OB为半径画圆,在线与圆的两个交点处用线连接起来找到中点,再把中点和顶点连起来即可画出OD、OE如图:③直角,2.(2020秋•肇源县期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,∴DC=DE,在△DCF 和△DEB 中,{DC =DE∠C =∠BED CF =BE,∴△DCF ≌△DEB ,(SAS ),∴BD =DF .3.已知:如图所示,BE =CF ,DF ⊥AC 于点F ,DE ⊥AB 于点E ,BF 和CE 相交于点D ,求证:AD 平分∠BAC .证明:∵BF ⊥AC 于点F ,CE ⊥AB 于点E ,∴∠BDE +∠B =∠CDF +∠C =90°,∵∠CDF =∠BDE ,∴∠B =∠C ,在△BDE 和△CDF 中,{∠B =∠C BE =CF ∠BED =∠CFD,∴△BDE ≌△CDF (ASA ),∴DE =DF ,∴AD 平分∠BAC .4.(2019春•金水区校级期中)(1)如图1,求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;(2)如图2,若∠ABC 的平分线与∠ACB 外角∠ACD 的平分线相交于点P ,连接AP ,若∠BAC =62°,则∠P AC 是 59 度.解:(1)已知:△ABC .求证:∠ABC 、∠BCA 、∠ACB 三个角的平分线相交于点F ,且点F 到三边的距离相等. 证明:如图,作∠ABC 的角平分线FB ,作∠BCA 的角平分线FC ,两条线相交于点F , 作FG ⊥AB 于点G ,FD ⊥BC 边于点D ,FE ⊥AC 于点E ,∵点F 是∠ABC 平分线上的一点,在△AGF 和△AEF 中,{∠AGF =∠AEF =90°∠GAF =∠EAF AF =AF,∴FG =FE ,同理可得,FD =FE ,∴FG =FD =FE (等量代换),∴点F 在∠BAC 的平分线上,∴三角形的三条角平分线相交于一点,并且这一点到三边的距离相等;(2)解:延长BA ,作PN ⊥BD 于N ,PF ⊥BA 于F ,PM ⊥AC 于M ,∵CP 平分∠ACD ,∴∠ACP =∠PCD ,PM =PN ,∵BP 平分∠ABC ,∴∠ABP =∠PBC ,PF =PN ,∴PF =PM ,∴∠F AP =∠P AC ,∴∠F AC =2∠P AC ,∵∠F AC+∠BAC=180°,∴2∠P AC+∠BAC=180°,∴∠P AC=12(180°﹣∠BAC)=12(180°﹣62°)=59°.故答案为:59.5.如图,李明计划在张村、李村之间建一家超市,张、李两村坐落在两相交公路内,超市的位置应满足下列条件:①使其到两公路的距离相等;②为了方便群众,超市到两村的距离之和最短.请你通过作图确定所要建超市的位置.解:(1)画出角平分线;(2)连接线段.交点P即满足条件.6.如图所示,在△ABC中,求证:(1)若AD为∠BAC的平分线,则S△ABD:S△ACD=AB:AC;(2)设D为BC上的一点,连接AD,若S△ABD:S△ACD=AB:AC,则AD为∠BAC的平分线.(1)证明:过A作AH⊥BC于H,过C作CE∥AB交AD延长线于E,则∠E=∠BAD,∵AD平分∠BAC,∴∠CAD=∠BAD,∴∠E =∠CAD ,∴AC =CE ,∵CE ∥AB ,∴△ECD ∽△ABD ,∴BD CD =AB CE , ∴BD CD =AB AC ,∴S △ABD :S △ACD =(12×BD ×AH ):(12×CD ×AH )=BD :CD =AB :AC ;(2)证明:过A 作AH ⊥BC 于H ,过C 作CE ∥AB 交AD 延长线于E∵S △ABD :S △ACD =(12×BD ×AH ):(12×CD ×AH )=BD :CD =AB :AC , 又∵CE ∥AB ,∴△ECD ∽△ABD ,∴BD CD =AB CE , ∴AB CE =AB AC ,∴CE =AC ,∴∠E =∠CAD ,∵CE ∥AB ,∴∠E =∠BAD ,∴∠BAD =∠CAD ,∴AD 平分∠BAC .7.(2014秋•阳谷县期末)如图,在△ABC 中,BD 平分∠ABC ,交AC 于点D ,BC 边上有一点E ,连接DE ,则AD 与DE 的关系为( )A .AD <DEB .AD =DEC .AD >DE D .不确定解:∵BD 平分∠ABC ,∴点D 到AB 、BC 的距离相等,∵AD 不是点D 到AB 的距离,点E 是BC 上一点,∴AD 、DE 的大小不确定.故选:D .8.如图,已知BE ⊥AC 于点E ,CF ⊥AB 于点F ,BE ,CF 相交于点D ,连接AD ,BD =CD .求证:AD 平分∠BAC .王刚的做法如下:证明:∵BE ⊥AC ,CF ⊥AB ,BD =CD ,∴点D 在∠BAC 的平分线上,∴AD 平分∠BAC .王刚的做法正确吗?若不正确,请写出正确的证明过程.解:王刚的做法不正确.证明如下:∵BE ⊥AC ,CF ⊥AB ,∴∠BFD =∠CED =90°.在△BDF 和△CDE 中,{∠BFD =∠CED ∠BDF =∠CDE BD =CD,∴△BDF ≌△CDE (AAS ),∴DF =DE .∴点D 在∠BAC 的平分线上.∴AD 平分∠BAC .。
八年级数学上册12.3角平分线的性质(讲+练)(8大题型)-【重要笔记】2022-2023学年八年级

12.3 角平分线的性质角的平分线的性质角的平分线的性质:角的平分线上的点到角两边的距离相等。
注意:用符号语言表示角的平分线的性质定理:若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.角的平分线的尺规作图角平分线的尺规作图(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.(2)分别以D、E为圆心,大于12DE的长为半径画弧,两弧在∠AOB内部交于点C.(3)画射线OC.射线OC即为所求.题型1:作已知角的平分线1.尺规作图:已知:∠CBA,求作∠CAB的平分线.【变式1-1】如图,在直线MN上求作一点P,使点P到射线OA和OB的距离相等。
(不写作法,保留作图痕迹)【变式1-2】如图,在Rt△ABC中,△C=90°.(1)作△BAC的平分线AD交边BC于点D.(尺规作图,保留作图痕迹,不写作法).(2)在(1)的条件下,若△BAC=28°,求△ADB的度数.题型2:角平分线的性质的应用-证明线段2.如图,已知OE平分△AOB,BC△OA于点C,AD△OB于点D,求证:EA=EB.【变式2-1】如图,点D、B分别在△A的两边上,C是△A内一点,AB = AD,BC = CD,CE△AD于E,CF△AF于F.求证:CE = CF.【变式2-2】已知:如图,OC是△AOB的平分线,P是OC上的一点,PD△OA,PE△OB,垂足分别为D、E,点F是OC上的另一点,连接DF,EF.求证:DF=EF.题型3:角平分线的性质的应用-和差关系3.如图,在△ABC中,△C=90°,△CAD=△BAD,DE△AB于E,点F在边AC 上,连接DF.(1)求证:AC=AE;(2)若AC=8,AB=10,求DE的长;(3)若CF=BE,直接写出线段AB,AF,EB的数量关系.【变式3-1】如图,△ABC的边BC的垂直平分线DE交△ABC的外角平分线AD于点D,DF△AB于点F,且AB>AC,试探究BF、AC、AF之间的数量关系,并说明理由.【变式3-2】题型4:角平分线的性质的应用-面积相关4.如图,BD是ΔABC的角平分线,DE⊥AB垂足为E,ΔABC的面积为70,AB= 16,BC=12,求DE的长.【变式4-1】如图,AD是△ABC的角平分线,DF△AB,垂足为F,如图DE=DG,△ADG和△AED的面积分别为50和38,求△EDF的面积【变式4-2】如图,在ΔABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,若ΔABC的面积为21cm2,AB=8cm,AC=6cm,求DE的值.角的平分线的判定角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.注意:用符号语言表示角的平分线的判定:若PE⊥AD于点E,PF⊥BD于点F,PE=PF,则PD平分∠ADB题型5:角平分线的判定5.如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,求证:AM平分∠DAB.【变式5-1】如图所示,PA=PB,△1+△2=180°.求证:OP平分△AOB.【变式5-2】如图所示,AP、CP分别是△ABC外角△MAC和△NCA的平分线,它们交于点P.求证:BP为△MBN的平分线.题型7:角平分线的性质与判定综合6.如图,已知点A、C分别在△GBE的边BG、BE上,且AB=AC,AD△BE,△GBE的平分线与AD交于点D,连接CD.求证:(1)AB=AD;(2)CD平分△ACE.【变式6-1】如图,已知△ABC中BC边的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,BG⊥AC交AC于点G.求证.(1)BF=CG.(2)若AB=6,AC=8,求AF的长度.【变式6-2】如图,在△ABC外作两个大小不同的等腰直角三角形,其中∠DAB=∠CAE=90°,AB=AD,AC=AE.连接DC、BE交于F点.(1)求证:△DAC△△BAE.(2)直线DC、BE是否互相垂直,请说明理由.(3)求证:AF平分∠DFE.【变式6-3】如图1,射线BD交△ABC的外角平分线CE于点P,已知△A=78°,△BPC=39°,BC=7,AB=4.(1)求证:BD平分△ABC;(2)如图2,AC的垂直平分线交BD于点Q,交AC于点G,QM△BC于点M,求MC的长度.题型7:角平分线的实际应用7.某地有两条相交叉的公路,计划修建一个饭馆:希望饭馆点P既在MN这条公路上,又到直线OA、OB的距离相等.你能确定饭馆应该建在什么位置吗?(保留作图痕迹)【变式7-1】如图:某地要在三条公路围成的一块平地上修建一个公园,要使公园到三条公路的距离相等,应在何处修建?(使用尺规作图,保留作图痕迹)并证明你的观点.【变式7-2】太和中学校园内有一块直角三角形(Rt △ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了月季花,在△ACD区域内种植了牡丹花,并量得两直角边AB=10m,AC=6m,分别求月季花与牡丹花两种花草的种植面积.题型8:三角形中的角平分线8.已知△ABC的三条角平分线相交于点O,过点O作OD△BC,OE△AC,OF△AB.求证:OD=OE=OF.【变式8-1】如图,△ABC中,AB=6,AC=7,BD、CD分别平分△ABC、△ACB,过点D作直线平行于BC,交AB、AC于E、F. 求△AEF的周长.【变式8-2】如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于?【变式8-3】如图①,在△ABC中,△ABC和△ACB的平分线交于点O,△A=α.(1)如图①,若△A=50°,求△BOC的度数.(2)如图②,连接OA,求证:OA平分△BAC.(3)如图③,若射线BO与△ACB的外角平分线交于点P,求证OC△PC.一、单选题1.如图,在△ABC中,△C=90°,BD平分△ABC,交AC于点D;若DC=3,AB=8则△ABD的面积是()A.8B.12C.16D.242.如图,OP平分△MON,PA△ON于点A,点Q是射线OM上的一个动点,若PA= 4,则PQ的长不可能是()A.3.5B.4C.4.5D.53.如图,已知点O是△ABC内一点,且点O到三边的距离相等,△A=40°,则△BOC=()A.110°B.120°C.130°D.140°4.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P()A.有且只有1个B.有且只有2个C.组成△E的平分线D.组成△E的平分线所在的直线(E点除外)5.如图,在Rt△ACB中,∠ACB=90°,BC=12,BD=2CD,AD平分∠BAC,则点D到AB的距离等于()A.3B.4C.5D.9二、填空题6.如图,在△ABC中,BE平分△ABC交AC于点E,AF△BC于点F,BE、AF交于点P,若AB=9,PF=3,则△ABP的面积是.7.如图,已知△COB=2△AOC,OD平分△AOB,且△COD=18°,则△AOB的度数为.8.如图,在Rt△ABC中,∠ACB=90°, AC=6, BC=8, AB=10, AD是∠BAC的平分线.若P, Q分别是AD和AC上的动点,则PC+PQ的最小值是.9.如图,OP平分△AOB,PM△OA于M,点D在OB上,DH△OP于H.若OD=4,OP=7,PM=3,则DH的长为.三、作图题10.如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?请用尺规作图标出它的位置.四、解答题11.如图,已知AD⊥BC于点D,E是延长线BA上一点,且EC⊥BC于点C,若∠ACE=∠E.求证:AD平分∠BAC.12.如图,在△ABC中,AD为△BAC的平分线,DE△AB于E,DF△AC于F,△ABC 面积是28cm2,AB=20cm,AC=8cm,求DE的长.13.如图,点P是△AOB的角平分线OC上一点,PE△OA,OE=12cm,点G是线段OP的中点,连接EG,点F是射线OB上的一个动点,若PF的最小值为4cm,求△PGE的面积.14.如图,直线AB△CD,点E在CD上,点O、点F在AB上,连接OE,过点F作FH△OE于点H.(1)尺规作图:作△EOF的角平分线OG交CD于点G;(不写作法,保留作图痕迹,并标明字母)(2)在(1)的条件下,已知△OFH=20°,求△OGD的度数.15.如图,△ABC和△EBD中,△ABC=△DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.(1)求证:AE=CD;(2)求证:AE△CD;(3)连接BM,有以下两个结论:①BM平分△CBE;②MB平分△AMD,其中正确的一个是(请写序号),并给出证明过程.。
2019-2020学年八年级上学期数学专题12.3 角平分线的性质(讲练)(解析版)

专题12.3角平分线的性质(讲练)一、知识点1、角的平分线的作法:课本第19页;2、角的平分线的性质定理:角的平分线上的点到角的两边的距离相等;3、证明一个几何中的命题,一般步骤: ①明确命题中的已知和求证;②根据题意,画出图形,并用数学符号表示已知和求证; ③经过分析,找出由已知推出求证的途径,写出证明过程;4、性质定理的逆定理:角的内部到角两边的距离相等的点在角的平分线上;(利用三角形全等来解释) 三角形的三条角平分线相交于一点,该点为内心;二、标准例题:例1:如图,OC 为AOB ∠的平分线,CM OB ⊥于M ,5OC =,4OM =,则点C 到射线OA 的距离为( )A .2B .3C .4D .5【答案】B【解析】解:如图,过C 作CF ⊥AO 于F∵OC 为∠AOB 的平分线,CM ⊥OB , ∴CM=CF , ∵OC=5,OM=4,∴CM=3, ∴CF=3, 故选:B .总结:此题主要考查了角平分线的性质,关键是掌握角的平分线上的点到角的两边的距离相等.例2:如图,在三角形ABC 中,90C =∠,AD 平分BAC ∠交BC 于点D ,且2BD CD =,6BC cm =,则点D 到AB 的距离为( )A .4cmB .3cmC .2cmD .1cm【答案】C【解析】如图,过点D 作DE ⊥AB 于E ,∵BD :DC=2:1,BC=6, ∴DC=112+×6=2, ∵AD 平分∠BAC ,∠C=90∘, ∴DE=DC=2. 故选:C .总结:本题考查角平分线的性质和点到直线的距离,解题的关键是掌握角平分线的性质.例3:如图,在Rt ABC ∆中,90B =∠,以点A 为圆心,适当长为半径画弧,分别交AB AC 、于点,D E ,再分别以点D E 、为圆心,大于12DE 为半径画弧,两弧交于点F ,作射线AF 交边BC 于点1,4BG AC ==,则ACG ∆的面积是( )A .1B .32C .2D .52【答案】C【解析】解:由作法得AG 平分BAC ∠,G ∴点到AC 的距离等于BG 的长,即G 点到AC 的距离为1,所以ACG ∆的面积14122=⨯⨯=. 故选:C .总结:本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了交平分线的性质. 例4:点D ,E 分别在△ABC 的边AC ,BD 上,BD ,CE 交于点F ,连接AF ,∠FAE =∠FAD ,FE =FD .(1)如图1,若∠AEF =∠ADF ,求证:AE =AD ;(2)如图2,若∠AEF≠∠ADF ,FB 平分∠ABC ,求∠BAC 的度数;(3)在(2)的条件下,如图3,点G 在BE 上,∠CFG =∠AFB 若AG =6,△ABC 的周长为20,求BC 长.【答案】(1)见解析;(2)60BAC ∠=︒;(3)7BC =.【解析】(1)∵FAE FAD ∠=∠,AEF ADF ∠=∠,FE FD =. ∴AEF ADF ∆≅∆,∴AE AD =.(2)过F 点分别作AB ,BC ,AC 边上的高,FP ,FQ ,FN ,点P ,Q ,N 为垂足. ∵AF ,BF 分别平分BAC ∠和ABC ∠,∴FP FQ =,FP FN =, ∴FQ FN =,且FN AC ⊥,FQ BC ⊥,∴CF 平分ACB ∠. ∴ACE BCE ∠=∠.∵2BEC BAC ACE BAF ACE ∠=∠+∠=∠+∠, ∴2EFD ABF BEC ABF BAF ACE ∠=∠+∠=∠+∠+∠1180902BAF BAF =⨯︒+∠=︒+∠. ∵FE FD =,∴Rt PEF Rt NDF ∆≅∆,∴PEF FDN ∠=∠,∴180PEF ADF ∠+∠=︒, ∴()42180BAC EFD PEF ADF ∠+∠=-⨯︒-∠-∠360180180=︒-︒=︒. ∴90180BAF BAC ︒+∠+∠=︒且2BAC BAF ∠=∠, ∴60BAC ∠=︒.(3)在BC 上取点R ,使CR CA =,∵CF CF =,FCA FCR ∠=∠,∴CAF CRF ∆≅∆. ∴30CRF CAF ∠=∠=︒,180150BRF CRF ∠=︒-∠=︒. ∵CFG AFB ∠=∠,∴CFG BFG AFB BFG ∠-∠=∠-∠, ∴18060120AFG BFC ∠=∠=︒-︒=︒,∵1302BAF BAC ∠=∠=︒, ∴30AGF ∠=︒,180150BGF AGF ∠=︒-∠=︒. ∴BGF BRF ∠=∠.∵GBF RBF ∠=∠,BF BF =,∴BGF BRF ∆≅∆. ∴BG BR =.∵AC AB BC BG AG BC AC ++=+++6220BR AG BC CR BC =+++=+=, ∴7BC =.总结:本题考查的是全等三角形的判定和性质、角平分线的性质、三角形内角和定理,正确作出辅助性、掌握全等三角形的判定定理和性质定理是解题的关键.三、练习1.如图,点O 在ABC 内,且到三边的距离相等,若∠A=60°,则∠BOC 的大小为( )A .135°B .120°C .90°D .60°【答案】B【解析】∵O 到三边的距离相等 ∴BO 平分∠ABC ,CO 平分∠ACB ∴∠OBC+∠OCB=12(∠ABC+∠ACB)=12(180°−∠A) ∵∠A=60°∴∠OBC+∠OCB=60°∴∠BOC=180°−(∠OBC+∠OCB)=180°−60°=120° 故选B.2.如图,为了促进当地旅游发展,某地要在三条公路围城的一块三角形平地ABC 上修建一个度假村。
人教版八年级数学上册12.3.1角的平分线的性质(第1课时)

E
B
C
D
A
E
B
C
D
4.如图,OC平分∠AOB, PM⊥OB于点M, PN⊥OA于点N, △POM的面积为6,OM=6, 则PN=_______ 。 2
N 0 M P
A
C B
*5.如图,△ABC中,AB=8厘米,∠C=90°, AC=BC,AD为∠BAC的平分线,DE⊥AB于 点E。求:△DBE的周长= 8厘米。
证明:连结MC,NC由作法知:
在△OMC和△ONC中 OM=ON MC=NC OC=OC ∵△OMC≌△ONC (SSS) ∴∠AOC=∠BOC 即:OC 是∠AOB的角平分线. M
A C
O
N
B
经历实验过程,发现并证明角的平分线的性质
P48 思考 利用尺规我们可以作一个角的平分线,那 么角的平分线有什么性质呢? 如图,任意作一个角∠AOB,作出∠A的平分线 OC,在OC 上任取一点P,过点 A P 画出OA,OB 的垂线,分别记 D 垂足为D,E,测量 PD,PE 并 C 作比较,你得到什么结论? P O
B
即点P到三边AB,BC,CA的距离相等
E
C
A
2. 如 图 , 在 △ ABC 中 , AC⊥BC , AD 为 ∠ BAC 的平分线,DE⊥AB,AB = 7 ㎝ , AC = 3 ㎝ , 求 BE= 4 CM. 3.如图,在△ABC中, ∠C=900,AD平分 ∠BAC交BC于点D,若 BC=8,BD=5,则点D 3 到AB的距离为_____
证明:∵ AD平分∠CAB, D是AD上一点(已知)
∵DE⊥AB,DC⊥AC(已知) ∴DC=DE(角平分线的性质) 在Rt△CDF和Rt△EDB 中 BD=FD (已知) DC=DE(已证) ∴Rt △CDF≌Rt△EDB (HL) ∴CF=EB(全等三角形对应边相等)
12.3(3)角的平分线的性质--两内角平分线

12.3(3)角的平分线的性质--两内角平分线一.【知识要点】1.两内角平分线二.【经典例题】1.如图,△ABC 的角平分线BM ,CN 交于点P .求证:试说明点P 到AB ,BC ,CA 三边的距离相等2.如图,已知ABC ∆的周长是16,MB 和MC 分别平分ABC ∠和ACB ∠,过点M 作BC 的垂线交BC 于点D ,且4MD =,则ABC ∆的面积是( )A .64B .48C .32D .423.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点O , 过点O 作EF ∥BC ,交AB 于点E ,交AC 于点F ,过点作OD ⊥AC 于点D.某班学生在一次数学活动课中,探索出如下结论:①EF= BE+CF;②点O 到△ABC 各边的距离相等;③∠BOC=90°+∠A;④设OD=m ,AE+AF=n ,则12AEF S mn =.其中正确的有( ) A.1个 B.2个 C.3个 D.4个4.(2022年绵阳期末第16题)如图,在等腰△ABC 中,AB =BC =a ,CE =b ,∠BAC 和∠ABC 的平分线分别为AD ,BE 相交于点O ,AD 交BC 于点D ,BE 交AC 于点E ,过点O 作OF ⊥AB 于F ,若OF =c ,则△ABC 的面积为 .三.【题库】【A 】1【B 】1.如图,O 是ABC ∆内的一点,且点O 到ABC ∆三边AB ,BC ,AC 的距离相等()OD OE OF ==,若70A ∠=︒,OB=OC,则=∠BOD .【C 】1.如图,∠B=∠C=90∘,AE 平分∠BAD,DE 平分∠ADC,若32CDE ABE S S ∆∆=,则:DEC ADES S ∆∆=_________.2.如图所示,已知P是△ABC三条角平分线的交点,PD⊥AB于点D,若PD=5,△ACB的周长为20,则△ABC的面积是.3.如图,四边形ABCD中,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.求证:(1)AM⊥DM;(2)M为BC的中点.【D】1.如图,△ABC的三边AB、BC、AC的长分别12,18,24,O是△ABC三条角平分线的交点,则S △OAB:S△OBC:S△OAC=().A.1︰1︰1 B.1︰2︰3 C.2︰3︰4 D.3︰4︰52.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF =PA;③AH+BD=AB;④S四边形ABDE=S△ABP,其中正确的是()A.①③B.①②④C.①②③D.②③。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.3 角的平分线的性质同步练习
一.选择题
1.如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D.若AD=2,则点D到BC的距离为()
A.1 B.C.D.2
2.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,若AC=6,BC=8,则S△ABD:S△ACD为()
A.5:3 B.5:4 C.4:3 D.3:5
3.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为()
A.6 B.5 C.4 D.3
4.如图,在CD上求一点P,使它到边OA,OB的距离相等,则点P是()
A.线段CD的中点
B.CD与过点O作CD的垂线的交点
C.CD与∠AOB的平分线的交点
D.以上均不对
5.点P在∠AOB的平分线上,点P到OA边的距离等于m,点Q是OB边上的一个动点,则PQ与m的大小关系是()
A.PQ<m B.PQ>m C.PQ≤m D.PQ≥m
6.如图,在△ABC中,∠ACB的外角平分线与∠ABC的外角平分线相交于点D.则下列结论正确的是()
A.AD平分BC B.AD平分∠CAB C.AD平分∠CDB D.AD⊥BC
7.如图在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果△ADE的周长为6cm,AC=4cm,那么AD等于()
A.2cm B.4cm C.3cm D.6cm
8.如图,点O在△ABC内,且到三边的距离相等.若∠A=40°,则∠BOC等于()
A.110°B.115°C.125°D.130°
9.如图,∠MON=60°.①以点O为圆心,2cm长为半径画弧,分别交OM、ON于点
A、C;②在分别以A、C为圆心,2cm长为半径画弧,两弧交于点B;③连结A
B、
BC,则四边形OABC的面积为()
A.4cm2B.2cm2C.4cm2D.2cm2
10.如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为()
A.54°B.50°C.48°D.46°
二.填空题
11.如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,若AB=5,DC =2,则△ABD的面积为.
12.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,若△ABC的面积为21cm2,AB=8cm,AC=6cm,则DE的长为cm.
13.如图,点E在∠BOA的平分线上,EC⊥OB,垂足为C,点F在OA上,若∠AFE =30°,EC=3,则EF=.
14.如图,若BD⊥AE于B,DC⊥AF于C,且DB=DC,∠BAC=40°,∠ADG=130°,则∠DGF=.
15.如图,已知在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB 于点E,AB=8cm,那么△DEB的周长是cm.
三.解答题
16.如图,已知CD是△ABC的角平分线,DE⊥BC,垂足为E,若AC=4,BC=10,△ABC的面积为14,求DE的长.
17.如图,点P是∠MON中一点,P A⊥OM于点A,PB⊥ON于点B,连接AB,∠P AB =∠PBA.求证:OP平分∠MON.
18.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
参考答案
1.D
2.A
3.B
4.C
5.D
6.B
7.A
8.A
9.B
10.D
11.5
12.3
13.6
14.150°
15.8
16.解:过点D作DF⊥AC交CA的延长线于点F,如图,∵CD平分∠ACB,DE⊥BC于E,
∴DF=DE.
∵△ABC的面积为14,
∴S△BCD+S△ACD=14,
∴×DE×10+×DF×4=14,
即5DE+2DE=14,
∴DE=2.
17.证明:∵∠P AB=∠PBA,
∴P A=PB,
∵P A⊥OM于点A,PB⊥ON于点B,
∴OP平分∠MON.
18.(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,∴DE=DC.
在△CDF与△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12﹣x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在△ACD与△AED中,
,
∴△ACD≌△AED(HL),
∴AC=AE,即8+x=12﹣x,
解得x=2,即CF=2.。
