几种投影的特点及分带方法
高斯投影分带说明

高斯投影分带说明
1)6度投影分带带号及投影分带中央经线经度
6度投影分带,自0度子午线起,每隔经差6度自西向东分带,带号依次编为第1、2、…、60带,6度投影分带带号用n表示。
6度投影分带中央经线经度用L0表示,计算公式有如下形式:
L0 = 6n –3 (度)(6度投影分带号n=1、2、 (60)
我国的经度范围西起73度东至135度,可分成6度带十一带,见下表:
2)3度投影分带带号及投影分带中央经线经度
3度投影分带,自度子午线起,每隔经差3度自西向东分带,带号依次编为第1、2、…、120带,3度投影分带带号用n’表示。
3度投影分带中央经线经度用L0’表示,计算公式有如下两种形式:
L0’= 3n’(度)(3度投影分带号n’=1、2、 (120)。
高斯投影6度和3度分带公式(一)

高斯投影6度和3度分带公式(一)高斯投影6度和3度分带公式介绍高斯投影是一种常用的地图投影方法,通过将地球表面上的点投影到平面上,实现地球表面的测绘和制图工作。
而在高斯投影中,存在两种常见的分带方式,即6度分带和3度分带。
下面将详细介绍这两种分带方式的相关公式和举例。
6度分带公式在6度分带方式中,地球被划分为60个纵向分带,每个分带占据经度范围为6度。
在每个分带内,利用高斯投影公式将地球上的经纬度点投影到平面上。
其公式如下:x = m0 * l * cos(B) + m0 * l^3 * cos(B)^3 * (1 - ta n(B)^2 + eta^2 * x^2) / 6 + (1)y = m0 * B + m0 * l^2 * cos(B)^2 * (1 + eta^2 * x^2) / 2 + (2)其中,x和y分别为经纬度点的投影平面坐标,B为纬度,l为经度差,eta为扁率的平方,m0为高斯投影系数。
公式(1)和(2)中的省略号表示高阶项,为了简化计算一般可以忽略。
下面以将经度为度、纬度为度的点投影为例进行说明。
首先,需要计算各个参数的值。
根据地理坐标系的定义,可以得到扁率的平方eta等于,经度差l等于度(经纬度一般采用度数表示)。
接着,根据所在纬度的带号(34度属于6度分带中的第6带),可以获得该带的高斯投影系数m0。
再根据公式(1)和(2),将以上参数代入计算即可得到该点在投影平面上的坐标。
3度分带公式与6度分带不同,3度分带将地球划分为120个纵向分带,每个分带占据经度范围为3度。
其余的计算方法和6度分带类似,公式如下:x = m0 * l * cos(B) + m0 * l^3 * cos(B)^3 * (1 - tan(B)^2 + eta^2 * x^2) / 6 + ... (1')y = m0 * B + m0 * l^2 * cos(B)^2 * (1 + eta^2 * x^2) / 2 + ... (2')需要注意的是,参数的计算方法和6度分带相同,但是高斯投影系数m0的计算会有所不同。
高斯投影6度和3度分带公式

高斯投影6度和3度分带公式
高斯投影是一种地图投影方法,它将地球的曲面投影到平面上。
高斯投影的分带是根据地球上的经度来划分的,而不是纬度。
高斯投影的6度分带公式是:
X = N * (L - L0)
Y = c1 * N * sin(2*(L - L0)) + c2 * N * sin(4*(L - L0)) + c3 * N * sin(6*(L - L0)) + c4 * N * sin(8*(L - L0))
其中,X和Y分别代表平面坐标系中的横轴和纵轴坐标,L为地点的经度,L0为分带中央经线的经度,N为真实纬度线长
度与投影纬度线长度之比的标度因子。
c1、c2、c3和c4是系数。
与之类似,高斯投影的3度分带公式如下:
X = N * (L - L0)
Y = c1 * N * sin(2*(L - L0)) + c2 * N * sin(4*(L - L0)) + c3 * N * sin(6*(L - L0)) + c4 * N * sin(8*(L - L0))
同样,X和Y分别代表平面坐标系中的横轴和纵轴坐标,L为地点的经度,L0为分带中央经线的经度,N为真实纬度线长
度与投影纬度线长度之比的标度因子。
c1、c2、c3和c4是系数。
需要注意的是,这些公式仅适用于特定的投影情况,不适用于所有高斯投影系统。
具体的参数和系数取决于使用的投影系统的设计和规范。
6度带与3度带的划分

1我国采用6度分带和3度分带1∶2.5万及1∶5万的地形图采用6度分带投影即经差为6度从零度子午线开始自西向东每个经差6度为一投影带全球共分60个带用12345�6�7�6�7表示即东经06度为第一带其中央经线的经度为东经3度东经612度为第二带其中央经线的经度为9度。
1∶1万的地形图采用3度分带从东经1.5度的经线开始每隔3度为一带用123�6�7�6�7表示全球共划分120个投影带即东经1.5 4.5度为第1带其中央经线的经度为东经3度东经4.57.5度为第2带其中央经线的经度为东经6度我省位于东经113度东经120度之间跨第38、39、40共计3个带其中东经115.5度以西为第38带其中央经线为东经114度东经115.5118.5度为39带其中央经线为东经117度东经118.5度以东到山海关为40带其中央经线为东经120度。
地形图上公里网横坐标前2位就是带号例如1∶5万地形图上的横坐标为20345486其中20即为带号345486为横坐标值。
2当地中央经线经度的计算六度带中央经线经度的计算当地中央经线经度6°×当地带号3°例如地形图上的横坐标为20345其所处的六度带的中央经线经度为6°×203°117°适用于1∶25万和1∶5万地形图。
三度带中央经线经度的计算中央经线经度3°×当地带号适用于1∶1万地形图。
不管是3度还是6度投影带每一个投影带都是一个独立的坐标系也就是说他是以0纬度即赤道为纵坐标轴的我国位于北半球故横坐标都为正以每带中央子午线为横坐标的即位与中央子午线以东纵坐标就为正位于中央子午线以西就为负为了好计算把每个纵坐标都500km成为新的都是正的纵坐标前面加上他的带号。
我国按3度投影带计算的话最大投影带是23带而按6度投影带计算的话最小投影带是24带所以根据纵坐标前的带号我们就知道是什么投影带了小于等于23带是3度投影大于等于24带是6度投影几种投影的特点及分带方法几种投影的特点及分带方法一、只谈比较常用的几种“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”1 墨卡托Mercator投影1.1 墨卡托投影简介墨卡托Mercator投影是一种等角正切圆柱投影”荷兰地图学家墨卡托Gerhardus Mercator 15121594在1569年拟定假设地球被围在一中空的圆柱里其标准纬线与圆柱相切接触然后再假想地球中心有一盏灯把球面上的图形投影到圆柱体上再把圆柱体展开这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
高斯投影分带总结
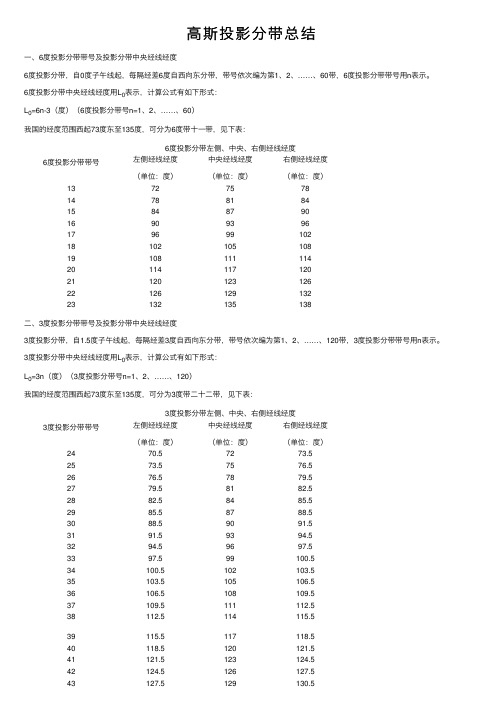
⾼斯投影分带总结⼀、6度投影分带带号及投影分带中央经线经度6度投影分带,⾃0度⼦午线起,每隔经差6度⾃西向东分带,带号依次编为第1、2、……、60带,6度投影分带带号⽤n表⽰。
6度投影分带中央经线经度⽤L0表⽰,计算公式有如下形式:L0=6n-3(度)(6度投影分带号n=1、2、 (60)我国的经度范围西起73度东⾄135度,可分为6度带⼗⼀带,见下表:6度投影分带带号6度投影分带左侧、中央、右侧经线经度左侧经线经度(单位:度)中央经线经度(单位:度)右侧经线经度(单位:度)13727578147881841584879016909396179699102181********1910811111420114117120211201231262212612913223132135138⼆、3度投影分带带号及投影分带中央经线经度3度投影分带,⾃1.5度⼦午线起,每隔经差3度⾃西向东分带,带号依次编为第1、2、……、120带,3度投影分带带号⽤n表⽰。
3度投影分带中央经线经度⽤L0表⽰,计算公式有如下形式:L0=3n(度)(3度投影分带号n=1、2、 (120)我国的经度范围西起73度东⾄135度,可分为3度带⼆⼗⼆带,见下表:3度投影分带带号3度投影分带左侧、中央、右侧经线经度左侧经线经度(单位:度)中央经线经度(单位:度)右侧经线经度(单位:度)2470.57273.5 2573.57576.5 2676.57879.5 2779.58182.5 2882.58485.5 2985.58788.5 3088.59091.5 3191.59394.5 3294.59697.5 3397.599100.5 34100.5102103.5 35103.5105106.5 36106.5108109.5 37109.5111112.5 38112.5114115.539115.5117118.5 40118.5120121.5 41121.5123124.5 42124.5126127.5 43127.5129130.544130.5132133.545133.5135136.5三、6度带带号与经度对应表带号经度左侧经线经度中央经线经度右侧经线经度1 0362 69123 121518 4182124 5242730 6303336 73639 42 84245 48 94851 54 105457 60 116063 66 126669 72 137275 78 147881 84 158487 90 169093 96 179699 102 18102105 108 19108111 114 20114117 120 21120123 126 22126129 132 ******** 138 ******** 144 25144147 150 ******** 156 ******** 162 28162165 168 29168171 174 30174177 180 ******** 186 ******** 192 33192195 198 34198 201 204 35204 207 210 36210 213 216 37216 219 222 38222225 228 39228231 234 40234237 240 41240243 246 42246249 252 43252255 258 44258261 264 45264267 270 46270273 276 47276279 282 48282285 288 49288291 294 50294297 300 51300303 30652306309 312 53312315 318 54318321 324 55324327 330 56330333 336 57336339 342 58342345 348 59348351 354 60354357 360四、3度带带号与经度对应表带号经度左侧经线经度中央经线经度右侧经线经度1 1.53 4.52 4.567.537.5910.5410.51213.5513.51516.5616.51819.5719.52122.5822.52425.5925.52728.51028.53031.51131.53334.51234.53637.51337.53940.51440.54243.51543.54546.51646.54849.51749.55152.51852.55455.51955.55758.52058.56061.52161.56364.52264.56667.52367.56970.52470.57273.52573.57576.52676.57879.52779.58182.52882.58485.52985.58788.53088.59091.53191.59394.53294.59697.53397.599100.534100.5102103.535103.5105106.536106.5108109.537109.5111112.538112.5114115.539115.5117118.540118.5120121.541121.5123124.542124.5126127.543127.5129130.544130.5132133.544130.5132133.5 45133.5135136.5 46136.5138139.5 47139.5141142.5 48142.5144145.5 49145.5147148.5 50148.5150151.5 51151.5153154.5 52154.5156157.5 53157.5159160.5 54160.5162163.5 55163.5165166.5 56166.5168169.5 57169.5171172.5 58172.5174175.5 59175.5177178.5 60178.5180181.5 61181.5183184.5 62184.5186187.5 63187.5189190.5 64190.5192193.5 65193.5195196.5 66196.5198199.5 67199.5201202.5 68202.5204205.5 69205.5207208.5 70208.5210211.5 71211.5213214.5 72214.5216217.5 73217.5219220.5 74220.5222223.5 75223.5225226.5 76226.5228229.5 77229.5231232.5 78232.5234235.5 79235.5237238.5 80238.5240241.5 81241.5243244.582244.5246247.5 83247.5249250.5 84250.5252253.5 85253.5255256.5 86256.5258259.5 87259.5261262.5 88262.5264265.5 89265.5267268.5 90268.5270271.5 91271.5273274.5 92274.5276277.5 93277.5279280.5 94280.5282283.5 95283.5285286.5 96286.5288289.5 97289.5291292.5 98292.5294295.5 99295.5297298.5 100298.5300301.5 101301.5303304.5101301.5303304.5 102304.5306307.5 103307.5309310.5 104310.5312313.5 105313.5315316.5 106316.5318319.5 107319.5321322.5 108322.5324325.5 109325.5327328.5 110328.5330331.5 111331.5333334.5 112334.5336337.5 113337.5339340.5 114340.5342343.5 115343.5345346.5 116346.5348349.5 117349.5351352.5 118352.5354355.5 119355.5357358.5 120358.5360361.5五、3度带与6度带中央经线重合3度带带号6度带带号中央经线备注113329531574219527116331373915845179511910572111632312692513752714812915873116933317993518105371911139201174121123432212945231354724141492514751261535327159552816557291715930177613118363321896533195673420169352076935207 7136213 7337219 7538225 7739231 7940237 8141243 8342249 8543255 8744261 8945267 9146273 9347279 9548285 9749291 9950297 10151303 10352309 10553315 10754321 10955327 11156333 11357339 11558345 11759351 11960357。
投影映射知识点梳理汇总

投影概念:投影指的是在两个点集之间建立一一映射关系。
长度变形:地球仪上,纬线长度不等;同一纬线上,经差相同,纬线长度相同;同一经线上,纬差相同而经线长度不同;所有经线长度相等。
面积变形:地球仪上,同一纬度带内,经差相同的网格面积相等;同一经度带内,纬度越高,面积越小。
角度变形:地球仪上,经线与纬线处处呈直角相交。
按变形性质分类:等角投影:角度变形为零。
等积投影:面积变形为零。
任意投影:长度、角度和面积都存在变形地图投影的选择中国分省(区)地图正轴等角割圆锥投影、正轴等面积割圆锥投影、正轴等角圆柱投影、高斯一克吕格投影(宽带)大比例尺地图多面体投影(北洋时期)等角割圆锥投影(兰勃特投影)(解放前)高斯一克吕格投影(解放以后)高斯一克吕格投影是横轴椭圆柱等角投影,它的中央经线和赤道为互相垂直的直线,其他经线均为凹向并对称于中央经线的曲线,其他纬线均为以赤道为对称轴的向两极弯曲的曲线,经纬线成直角相交。
角度没有变形,长度和面积均有变形,且距离中央经线愈远变形愈大。
高斯投影特征:中央经线和赤道投影为互相垂直的直线,且为投影的对称轴投影后无角度变形,即保角投影中央经线无长度变形,同一条经线上,纬度越低,变形越大,赤道处最大同一条纬线上,离中央经线越远,变形越大;为了保证地图的精度,采用分带投影方法,即将投影范围的东西界加以限制,使其变形不超过一定的限度,这样把许多带结合起来,可成为整个区域的投影。
地图投影的选择主要考虑以下因素:制图区域的范围、形状和地理位置;地图的用途、出版方式及其他要求等。
高斯投影减少误差的基本思想是什么?由于高斯一克吕格投影采用了分带方法,各带的投影完全相同,分带投影可以限制变形的程度,但也给投影带来了连续的问题。
因为两相邻投影带的公共边缘子午线在两带投影平面上的投影的弯曲方向,使得位于该边缘子午线附近,分别居于两带的地形图不能拼接。
拓扑关系:是不考虑度量(距离)和方向的空间物体之间的关系。
高斯-克吕格投影分带

该投影按照投影带中央子午线投影为直线且长度不变和赤道投影为直线的条件,确定函数的形式,从而得到高斯一克吕格投影公式。
投影后,除中央子午线和赤道为直线外,其他子午线均为对称于中央子午线的曲线。
设想用一个椭圆柱横切于椭球面上投影带的中央子午线,按上述投影条件,将中央子午线两侧一定经差范围内的椭球面正形投影于椭圆柱面。
将椭圆柱面沿过南北极的母线剪开展平,即为高斯投影平面。
取中央子午线与赤道交点的投影为原点,中央子午线的投影为纵坐标x轴,赤道的投影为横坐标y轴,构成高斯克吕格平面直角坐标系。
高斯-克吕格投影在长度和面积上变形很小,中央经线无变形,自中央经线向投影带边缘,变形逐渐增加,变形最大之处在投影带内赤道的两端。
由于其投影精度高,变形小,而且计算简便(各投影带坐标一致,只要算出一个带的数据,其他各带都能应用),因此在大比例尺地形图中应用,可以满足军事上各种需要,能在图上进行精确的量测计算。
高斯-克吕格投影分带按一定经差将地球椭球面划分成若干投影带,这是高斯投影中限制长度变形的最有效方法。
分带时既要控制长度变形使其不大于测图误差,又要使带数不致过多以减少换带计算工作,据此原则将地球椭球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。
通常按经差6度或3度分为六度带或三度带。
六度带自0度子午线起每隔经差6度自西向东分带,带号依次编为第 1、2…60带。
三度带是在六度带的基础上分成的,它的中央子午线与六度带的中央子午线和分带子午线重合,即自 1.5度子午线起每隔经差3度自西向东分带,带号依次编为三度带第 1、2…120带。
我国的经度范围西起73°东至135°,可分成六度带十一个,各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°,或三度带二十二个。
六度带可用于中小比例尺(如 1:250000)测图,三度带可用于大比例尺(如 1:10000)测图,城建坐标多采用三度带的高斯投影。
高斯克吕格投影知识总结

⾼斯克吕格投影知识总结(1)⾼斯-克吕格投影性质⾼斯-克吕格(Gauss-Kruger)投影简称“⾼斯投影”,⼜名"等⾓横切椭圆柱投影”,地球椭球⾯和平⾯间正形投影的⼀种。
德国数学家、物理学家、天⽂学家⾼斯(Carl FriedrichGauss,1777⼀ 1855)于⼗九世纪⼆⼗年代拟定,后经德国⼤地测量学家克吕格(Johannes Kruger,1857~1928)于 1912年对投影公式加以补充,故名。
该投影按照投影带中央⼦午线投影为直线且长度不变和⾚道投影为直线的条件,确定函数的形式,从⽽得到⾼斯⼀克吕格投影公式。
投影后,除中央⼦午线和⾚道为直线外,其他⼦午线均为对称于中央⼦午线的曲线。
设想⽤⼀个椭圆柱横切于椭球⾯上投影带的中央⼦午线,按上述投影条件,将中央⼦午线两侧⼀定经差范围内的椭球⾯正形投影于椭圆柱⾯。
将椭圆柱⾯沿过南北极的母线剪开展平,即为⾼斯投影平⾯。
取中央⼦午线与⾚道交点的投影为原点,中央⼦午线的投影为纵坐标x轴,⾚道的投影为横坐标y轴,构成⾼斯克吕格平⾯直⾓坐标系。
⾼斯-克吕格投影在长度和⾯积上变形很⼩,中央经线⽆变形,⾃中央经线向投影带边缘,变形逐渐增加,变形最⼤之处在投影带内⾚道的两端。
由于其投影精度⾼,变形⼩,⽽且计算简便(各投影带坐标⼀致,只要算出⼀个带的数据,其他各带都能应⽤),因此在⼤⽐例尺地形图中应⽤,可以满⾜军事上各种需要,能在图上进⾏精确的量测计算。
(2)⾼斯-克吕格投影分带按⼀定经差将地球椭球⾯划分成若⼲投影带,这是⾼斯投影中限制长度变形的最有效⽅法。
分带时既要控制长度变形使其不⼤于测图误差,⼜要使带数不致过多以减少换带计算⼯作,据此原则将地球椭球⾯沿⼦午线划分成经差相等的⽠瓣形地带,以便分带投影。
通常按经差6度或3度分为六度带或三度带。
六度带⾃0度⼦午线起每隔经差6度⾃西向东分带,带号依次编为第 1、2…60带。
三度带是在六度带的基础上分成的,它的中央⼦午线与六度带的中央⼦午线和分带⼦午线重合,即⾃ 1.5度⼦午线起每隔经差3度⾃西向东分带,带号依次编为三度带第1、2…120带。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几种投影的特点及分带方法
一、只谈比较常用的几种:“墨卡托投影”、“高斯-克吕格投影”、
“UTM投影”、“兰勃特等角投影”
1. 墨卡托(Mercator)投影
1.1 墨卡托投影简介 墨卡托(Mercator)投影,是一种"等角正切圆
柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在
1569年拟定,假设地球被围在一中空的圆柱里,其标准纬线与圆柱
相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆
柱体上,再把圆柱体展开,这就是一幅选定 标准纬线上的“墨卡托投
影”绘制出的地图。 墨卡托投影没有角度变形,由每一点向各方向的
长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相
等,纬线间隔从标准纬线向两极逐渐增大。墨卡托投影的地图上长度
和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增
大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置
关系的 正确。在地图上保持方向和角度的正确是墨卡托投影的优点,
墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两
点间的直线航行,方向不变可以一直到达 目的地,因此它对船舰在
航行中定位、确定航向都具有有利条件,给航海者带来很大方便。 “海
底地形图编绘规范”(GB/T 17834-1999,海军航保部起草)中规定1:
25万及更小比例尺的海图采用墨卡托投影,其中基本比例尺海底地
形图(1:5万,1:25万,1: 100万)采用统一基准纬线30°,非
基本比例尺图以制图区域中纬为基准纬线。基准纬线取至整度或整
分。
1.2 墨卡托投影坐标系 取零子午线或自定义原点经线(L0)与赤
道交点的投影为原点,零子午线或自定义原点经线的投影为纵坐标X
轴,赤道的投影为横坐标Y轴,构成墨卡托平面直角 坐标系。
2. 高斯-克吕格(Gauss-Kruger)投影和UTM(Universal
Transverse Mercator)投影
2.1 高斯-克吕格投影简介 高斯-克吕格(Gauss-Kruger)投影,
是一种“等角横切圆柱投影”。德国数学家、物理学家、天文学家高斯
(Carl Friedrich Gauss,1777一 1855)于十九世纪二十年代拟定,
后经德国大地测量学家克吕格(Johannes Kruger,1857~1928)于
1912年对投影公式加以补充,故名。设想用一个圆柱横切于球面上
投影带的中央经线,按照投影带中央经线投影为直线且长度不变和赤
道投影为直线的条件,将 中央经线两侧一定经差范围内的球面正形
投影于圆柱面。然后将圆柱面沿过南北极的母线剪开展平,即获高斯
一克吕格投影平面。高斯一克吕格投影后,除中央经线和赤道为直线
外,其他经线均为对称于中央经线的曲线。高斯-克吕格投影没有角
度变形,在长度和面积上变形也很小,中央经线 无变形,自中央经
线向投影带边缘,变形逐渐增加,变形最大处在投影带内赤道的两端。
由于其投影精度高,变形小,而且计算简便(各投影带坐标一致,只
要算出 一个带的数据,其他各带都能应用),因此在大比例尺地形图
中应用,可以满足军事上各种需要,并能在图上进行精确的量测计算。
按一定经差将地球椭球面划分成若干投影带,这是高斯投影中限制长
度变形的最有效方法。分带时既要控制长度变形使其不大于测图误
差,又要使带数不致过多以减 少换带计算工作,据此原则将地球椭
球面沿子午线划分成经差相等的瓜瓣形地带,以便分带投影。通常按
经差6度或3度分为六度带或三度带。六度带自0度子午线 起每隔
经差6度自西向东分带,带号依次编为第 1、2…60带。三度带是在
六度带的基础上分成的,它的中央子午线与六度带的中央子午线和分
带子午线重合,即自 1.5度子午线起每隔经差3度自西向东分带,带
号依次编为三度带第 1、2…120带。我国的经度范围西起 73°东至
135°,可分成六度带十一个,各带中央经线依次为75°、81°、87°、……、
117°、123°、129°、135°,或三度带二十二 个。 我国大于等于50
万的大中比例尺地形图多采用六度带高斯-克吕格投影,三度带高斯-
克吕格投影多用于大比例尺测图,如城建坐标多采用三度带的高斯-
克吕格 投影。
2.2 UTM投影简介 UTM投影全称为“通用横轴墨卡托投影”,是
一种“等角横轴割圆柱投影”,椭圆柱割地球于南纬80度、北纬84度
两条等高圈,投影后两条相割的经线上没有 变形,而中央经线上长
度比0.9996。UTM投影是为了全球战争需要创建的,美国于1948年
完成这种通用投影系统的计算。与高斯-克吕格投影相似,该 投影角
度没有变形,中央经线为直线,且为投影的对称轴,中央经线的比例
因子取0.9996是为了保证离中央经线左右约330km处有两条不失真
的标准经 线。 UTM投影分带方法与高斯-克吕格投影相似,是自西
经180°起每隔经差6度自西向东分带,将地球划分为60个投影带。 我
国的卫星影像资料常采用UTM投影。
2.3 高斯-克吕格投影与UTM投影异同 高斯-克吕格
(Gauss-Kruger)投影与UTM投影(Universal Transverse Mercator,通
用横轴墨卡托投影)都是横轴墨卡托投影的变种,目前一些国外的软
件或国外进口仪器的配套软件往往不支持高斯-克吕格投影,但支持
UTM投影,因此常有把UTM投影当作高斯-克吕格投影的现象。从
投影几何方式看,高斯-克吕格投影是“等角横切圆柱投影”,投影后
中央经线保持长度不 变,即比例系数为1;UTM投影是“等角横轴
割圆柱投影”,圆柱割地球于南纬80度、北纬84度两条等高圈,投
影后两条割线上没有变形,中央经线上长度比 0.9996。从计算结果
看,两者主要差别在比例因子上,高斯-克吕格投影中央经线上的比
例系数为1, UTM投影为0.9996,高斯-克吕格投影与UTM投影可
近似采用 X[UTM]=0.9996 * X[高斯],Y[UTM]=0.9996 * Y[高斯],进
行坐标转换(注意:如坐标纵轴西移了500000米,转换时必须将Y
值减去500000乘上比例因子后再加500000)。从分带方式看, 两者
的分带起点不同,高斯-克吕格投影自0度子午线起每隔经差6度自
西向东分带,第1带的中央经度为3°;UTM投影自西经180°起每隔
经差6度自西向 东分带,第1带的中央经度为-177°,因此高斯-克吕
格投影的第1带是UTM的第31带。此外,两投影的东伪偏移都是
500公里,高斯-克吕格投影北伪 偏移为零,UTM北半球投影北伪偏
移为零,南半球则为10000公里。
2.4 高斯-克吕格投影与UTM投影坐标系 高斯- 克吕格投影与
UTM投影是按分带方法各自进行投影,故各带坐标成独立系统。以
中央经线(L0)投影为纵轴X,赤道投影为横轴Y,两轴交点即为各
带的坐标原 点。为了避免横坐标出现负值,高斯- 克吕格投影与
UTM北半球投影中规定将坐标纵轴西移500公里当作起始轴,而
UTM南半球投影除了将纵轴西移500公里外,横轴南移10000公里。
由于 高斯-克吕格投影与UTM投影每一个投影带的坐标都是对本带
坐标原点的相对值,所以各带的坐标完全相同,为了区别某一坐标系
统属于哪一带,通常在横轴坐标 前加上带号,如(4231898m,
21655933m),其中21即为带号。 二、分带方法 1.我国采用6度分
带和3度分带: 1∶2.5万及1∶5万的地形图采用6度分带投影,
即经差为6度,从零度子午线开始,自西向东每个经差6度为一投影
带,全球共分60个带,用1,2, 3,4,5,……表示.即东经0~6
度为第一带,其中央经线的经度为东经3度,东经6~12度为第二带,
其中央经线的经度为9度。 1∶1万的地形图采用3度分带,从
东经1.5度的经线开始,每隔3度为一带,用1,2,3,……表示,
全球共划分120个投影带,即东经1.5~ 4.5度为第1带,其中央经
线的经度为东经3度,东经4.5~7.5度为第2带,其中央经线的经度
为东经6度.我省位于东经113度-东经120度之间, 跨第38、39、
40共计3个带,其中东经115.5度以西为第38带,其中央经线为东
经114度;东经115.5~118.5度为39带,其中央经线为 东经117度;
东经118.5度以东到山海关为40带,其中央经线为东经120度。 地
形图上公里网横坐标前2位就是带号,例如:1∶5万地形图上的横
坐标为20345486,其中20即为带号,345486为横坐标值。
2.当地中央经线经度的计算
六度带中央经线经度的计算:当地中央经线经度=6°×当地带号
-3°,例如:地形图上的横坐标为20345,其所处的六度带的
中央经线经度为:6°×20-3°=117°(适用于1∶2.5万和
1∶5万地形图);6°×49-180-3°=111°(适用于1∶50万以下
地形图)。
三度带中央经线经度的计算:中央经线经度=3°×当地带号(适
用于1∶1万地形图)。
