2017届江西省南昌市八一中学高三下学期期中考试理科综合试题
江西省南昌市高三第一次模拟考试理科综合物理试卷

江西省南昌市2017 届高三第一次模拟考试理科综合物理试卷二、选择题:本大题共8 小题,每小题 6 分.在每小题给出的四个选项中,第14~17 题只有一项符合题目要求,第18~21 题有多项符合题目要求.全部选对的得 6 分,选对但不全的得 3 分,有选错的得0 分.14.如图所示, 1887 年德国物理学家赫兹利用紫外线照射锌板后,发现与锌板连接的验电器箔片张开.关于这一现象,下列说法中正确的是()A.验电器箔片张开,是因为箔片带负电B.验电器箔片张开,是因为锌板得到了正电荷C.紫外线灯功率增大,箔片张角也增大D.换用红外线灯照射锌板,箔片也一定张开15.如图所示,在固定的斜面上,A、B 两物体通过跨过光滑的定滑轮的细线相连,物体A静止在斜面上.已知斜面倾角 30 ,A、B两物体质量分别为2m 和 m,现在 B 物体下加挂另一物体C(图中未画出),物体 A 仍静止在斜面上,则加挂物体C后()A .斜面对物体 A 的弹力增大B.细线对物体 A 的拉力不变C.斜面对物体 A 的摩擦力保持不变D.斜面对物体 A 的作用力增大16.如图甲所示是一台交流发电机的构造示意图,线圈转动产生的感应电动势随时间变化的规律如图乙所示.发电机线圈电阻为1,外接负载电阻为4,()A .线圈转速为50 r / sB.电压表的示数是 4 VC.负载电阻的电功率为 2 WD.线圈转速加倍,电压表读数变为原来的 4 倍17.火星表面很接近地球,是将来人类可能的居住地.已知火星的质量约为地球质量的1,火星的半径约9为地球半径的1,火星的自转周期约为24 h.已知地球表面重力加速度为9.8 m / s2,由此可估算出()2A .火星表面的重力加速度约为9.8 m / s2B.环绕火星运动的卫星的最大速度约为 3.7 km/ sC.火星的平均密度约为地球平均密度的一半D.火星同步卫星的运动半径等于地球同步卫星运动的半径18.一质量为m 的质点以速度v 0匀速直线运动,在t 0时开始受到恒力 F 作用,速度大小先减小后增大,其最小值为v 0.5v 0.由此可判断()A .质点受力 F 作用后一定做匀变速曲线运动B.质点受力 F 作用后可能做圆周运动C.t0时恒力F与速度v0方向间的夹角为60D. t3mv 0 时,质点速度最小19.已知均匀带电球壳内部电场强度处处为零, 电势处处相等. 如图所示, 正电荷均匀分布在半球面上, Ox为通过半球顶点与球心 O 的轴线, A 、 B 为轴上的点,且AO OB ,则下列判断正确的是()A . A 、B 两点的电势相等B . A 、B 两点的电场强度相同C .点电荷从 A 点移动到 B 点,电场力一定做正功D .同一个负电荷放在 B 点比放在 A 点的电势能大20.如图所示,质量为m 0.04 kg 、边长 l0.4 m 的正方形导体线框 abcd 放置在一光滑绝缘斜面上,线框用一平行斜面的细线系于O 点,斜面倾角为300.线框的一半处于磁场中, 磁场的磁感应强度随时间变化关系为 B 2 0.5t (T) ,方向垂直于斜面. 已知线框电阻为 R 0.5 ,重力加速度为 g 10 m / s 2 .()A .线框中的感应电流方向为 abcdaB . t0时,细线拉力大小 F 0.2 NC .线框中感应电流大小为 I 80 mAD .经过一段时间t ,线框可能沿斜面向上运动21.如图甲所示,在光滑水平面上,轻质弹簧一端固定,物体A 以速度 v 0 向右运动压缩弹簧,测得弹簧的最大压缩量为 x ;现让弹簧一端连接另一质量为m的物体 B A以 2v 0 的速度向右压缩(如图乙所示) ,物体 弹簧,测得弹簧的最大压缩量仍为 x ,则( )A . A 物体的质量为 3mB . A 物体的质量为 2mC .弹簧压缩最大时的弹性势能为3 mv 0 22D .弹簧压缩最大时的弹性势能为mv 02三、非选择题:包括必做题和选做题两部分.第 22 题~第 32 题为必做题,每个试题考生都必须做答.第33题 ~第 38 题为选做题,考生根据要求做答.(一)必做题( 11 题,共 129 分)22.( 5 分)某同学利用打点计时器测量小车做匀变速直线运动的加速度.实验器材有:电磁打点计时器、一端附有滑轮的长木板,小车、纸带、细线、钩码、刻度尺、导线、交流电源、复写纸片等.( 1)该同学在实验桌上安装好所需的器材后(如图所示)准备进行实验,下面操作必须要的是A .把附有滑轮的长木板固定打点计时器的那端适当垫高,以平衡小车运动过程中所受的摩擦力B .调节拉小车的细线使细线与长木板板面平行C .拉小车运动的钩码的质量远小于小车的质量D .实验时,先释放小车,再接通电源( 2)该同学在得到的纸带上选取七个计数点(相邻两个计数点之间还有四个点未画出) ,如图所示,图中s 1 4.81 cm , s 2 5.29 cm , s 3 5.76 cm , s 4 6.25 cm , s 5 6.71 cm , s 6 7.21 cm .已知电源频率为 50 Hz ,则加速度的大小为 ___________ m / s 2 (结果保留两位有效数字) .23.( 10 分)(1)在“测定金属丝的电阻率”实验中,某同学在一次用螺旋测微器测量金属丝的直径时,测微器计数如图甲所示,则金属丝的直径为 ___________mm.( 2)用多用电表测量金属丝的电阻R x,选择“1示,则 R x___________Ω.(3)为提高精度,现要用以下仪器再次测量金属丝的电阻①电流表 A 1(量程 150 mA ,内阻约为10)”欧姆档,并按正确步骤操作后,指针的位置如图乙所R x,实验室提供器材如下:②电压表V (量程 15V ,内阻 1 KΩ)③电流表 A 2(量程 20 mA ,内阻 r230)④定值电阻R 0100⑤滑动变阻器R,最大阻值8⑥电源 E,电动势E 6 V (内阻不计)⑦电键 S 及导线若干Ⅰ.根据上述器材完成此实验,测量时要求电表计数不得小于其量程的1,请你在虚线框内画出测量Rx的一种实验原理图(图中元件使用题中相应英文字母符号标3注).Ⅱ.实验时电流表 A 1的读数记为 I1,电压表 V 的计数记为 V ,电流表 A 2的计数记为 I 2,用已知的知你所用的仪器测得的物理量表示R x _______________ .(用字母表示)24.(14 分)在倾角37的粗糙斜面上有一质量m 2 kg 的物块,受如图甲所示的水平方向恒力 F 的作用, t0时刻物块以某一速度从斜面上 A 点沿斜面下滑,在t 4 s时滑到水平面上,此时撤去F,在这以后的一段时间内物块运动的速度随时间变化关系v-t 图像如图乙所示.已知 A 点到斜面底端的距离x 18 m,物块与各接触面之间的动摩擦因数相同,不考虑转角处机械能损失, g 10 m / s2,,.求:sin37 0.6cos37 0.8(1)物块在 A 点的速度;(2)水平恒力 F 的大小.25.( 18 分)如图所示,矩形边界 efgh 中有垂直纸面向里的匀强磁场 B 0.5 T , ef 长为 l 0.3 m , eh 长为 0.5 m ,一质量 m 8 10 26 kg、电荷量 q8 10 19 C 的粒子(重力不计)从矩形边界上某点以某个速度射入.粒子从 ef 中点 O 1 孔射出,再经小孔 O 2 进入相互正交的匀强电场和匀强磁场区域,电场强度大小E 2 105 V / m ,磁感应强度大小 B 1 0.4 T ,方向如图. 虚线 PQ 、MN 之间存在着水平向右的匀强磁场,磁感应强度大小为 B 2 0.25 T (图中未画出) .有一块折成等腰直角的硬质塑料板 abc (不带电, 宽度很窄,厚度不计) 放置在 PQ 、MN 之间(截面图如图) ,a 、c 两点恰在分别位于PQ 、MN 上, ab bc 0.3 2 m ,a 45 .粒子恰能沿图中虚线 O 2 O 3 进入 PQ 、 MN 之间的区域.( 1)求粒子射入正交电磁场时的速度大小;( 2)求粒子射入矩形边界时的速度方向和射入点的位置;( 3)假设粒子与硬质塑料相碰后,速度大小不变,方向变化遵守光的反射定律.粒子在 PQ 、MN 之间的区域中运动的时间和路程分别是多少?(二)选做题:共 45 分.请考生从给出的 2 道物理题、 2 道化学题、 2 道生物题中每科任选一题做答,并用2B 铅笔在答题卡上把所选题目的题号涂黑.注意所做题目的题号必须与所涂题目的题号一致,在答题卡选 答区域指定位置答题.如果多做,则每学科按所做的第一题计分.33.【物理 -选修 3-3】( 15 分)( 1)( 5 分)下列说法正确的是( )(填正确答案标号.选对1 个得2 分,选对 2 个得 4 分,选对3 个得 5 分;每选错 1 个扣 3 分,最低得分为 0 分)A .悬浮在水中的花粉的布朗运动反映了花粉分子的热运动B .荷叶上的水水滴呈球形是水的表面张力作用的结果C .彩色液晶显示器利用了液晶的光学性质具有各向异性的特点D .一定质量的理想气体吸收热量,其内能一定增加E .自然发生的热快递过程是向着分子热运动无序性增大的方向进行的( 2)( 10 分)如图所示,竖直放置的导热气缸,活塞横截面积为 S 0.01 m 2 ,可在气缸内无摩擦滑动.气缸侧壁有一个小孔与装有水银的U 形玻璃管相通,气缸内封闭了一段高为H70 cm的气柱( U 形管内的气 体体积 不计 ).已 知活 塞质量 m 6.8 kg ,大气 压强 p 0105 pa ,水 银密度 13.6 10 3 kg / m 3 ,g 10 m / s 2 .①求 U 形管中左管与右管的水银面的高度差h 1 ;②在活塞上加一竖直向上的拉力使U 形管中左管水银面高出右管水银面h 2 5 cm ,求活塞平衡时与气缸底部的高度.34.【物理 -选修 3-4】( 15 分) ( 1)( 5 分)图甲为一列简谐横波在 t 0时刻的波形图, P 是平衡位置在 x1.0 m处的质点, Q 是平衡位置在 x4.0 m 处的质点,图乙为质点 Q 的振动图像,则下列说法正确的是()(填正确答案标号.选对 1个得 3 分,选对 2 个得 4 分,选对 3 个得 5 分.每错选 1 个扣 3 分,最低得分为0 分)A .这列波的波长是 8 m ,周期是 0.2 s ,振幅是 10 cmB .在 t0 时,质点 Q 向 y 轴正方向运动C .从 t0 到 t 0.25 st 0 t,该波沿 x 轴负方向传播了 6 mD .从 到 0.25 s30 cm,质点 P 通过的过程为 E .质点 Q 简谐运动的表达式为 y 0.10sin10 t ( m)( 2)( 10 分)如图所示为一置于空气中用透明材料做成的圆柱体元件的横截面,AB 为通过截面圆心 O 轴线,截面图的半径为 R .一平行于 AB 的细光束从 N 点射入该元件,射出后与直线 AB 交于 P 点.现测得MN 与 AB 的距离为3R ,OP3R ,求:2①光从 N 点射入元件的入射角;②该元件材料的折射率.。
江西省南昌市八一中学、桑海中学、麻丘高中等八校2017-2018学年高二下学期期中考试数学(理)试题

江西省南昌市八一中学、桑海中学、麻丘高中等八校2017-2018学年高二下学期期中考试数学(理)试题一、单选题1 . 已知是异面直线,直线平行于直线,那么与()A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线2 . 下列命题正确的个数为()①经过三点确定一个平面;②梯形可以确定一个平面;③两两相交的三条直线最多可以确定三个平面;④如果两个平面有三个公共点,则这两个平面重合.A.B.C.D.3 . 下列命题中错误的是()A.平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行B.平行于同一个平面的两个平面平行C.若两个平面平行,则分别位于这两个平面的直线也互相平行D.若两个平面平行,则其中一个平面内的直线平行于另一个平面4 . 如图,,,,,,直线,过三点确定的平面为,则平面的交线必过()A.点B.点C.点,但不过点D.点和点5 . 如图,在正方体中,,分别是为,的中点,则下列判断错误的是()A.与垂直B.与垂直C.与平行D.与平行6 . 正方体,,,为别是,,的中点,则正方体过,,三点的截面图形是().A.三角形B.四边形C.五边形D.六边形7 . 如图是一个几何体的平面展开图,其中四边形是正方形,分别是的中点,在此几何体中,给出下面四个结论:①直线与直线是异面直线;②直线与直线异面③直线平面;④平面平面其中正确的有()A.①②B.②③C.①④D.②④8 . 侧棱长都都相等的四棱锥中,下列结论正确的有()个① 为正四棱锥;②各侧棱与底面所成角都相等;③各侧面与底面夹角都相等;④四边形可能为直角梯形()A.1B.2C.3D.49 . 如图,四边形中,,,.将四边形沿对角线折成四面体,使平面平面,则下列结论正确的是A.B.C.与平面所成的角为D.四面体的体积为10 . 如图,在棱长为1的正方体中,点分别是棱的中点,是侧面内一点,若平面,则线段长度的取值范围是()A.B.C.D.11 . 某几何体三视图如图所示,若这个几何体的各顶点都在同一个球面上,则这个球的体积为()A.B.C.D.12 . 已知是平面的斜线段,为斜足,若与平面成角,过定点的动直线与斜线成角,且交于点,则动点的轨迹是( )A.圆B.椭圆C.双曲线D.抛物线二、填空题13 . 在正方体中,分别为棱的中点,则异面直线与所成角的余弦值为__________.14 . 的三个顶点分别是,,,则边上的高长为__________.15 . 已知圆锥的母线长为,高为,则该圆锥的外接球的表面积是__________.16 . 如图,在边长为1的正方体中,动点在线段上运动,则的最小值为_____________.三、解答题17 . 如图,在空间四边形中,,分别为,的中点,在上,在上,且有,求证:、、交于一点.18 . 如图,分别是正方体的棱的中点,求证:平面∥平面19 . 如图,四棱锥中,底面是边长为1的菱形,,,,为的中点.(1)求异面直线与所成角的余弦值;(2)求点到平面的距离.20 . 如图所示,四棱锥的底面是边长为1的正方形,侧棱底面,在侧面内,有于,且,求直线与平面所成角的正弦值.21 . 如图,在正方形中,点,分别是,的中点,将分别沿,折起,使两点重合于.(1)求证:平面;(2)求二面角的余弦值.22 . 如图,在等腰梯形中,,,,四边形为矩形,平面平面,.(1)求证:平面;(2)点在线段上运动,设平面与平面二面角的平面角为,试求的取值范围.。
江西省南昌市八一中学高三下册第二学期期中考试数学文试卷(含答案)【推荐】

2016~2017学年度第二学期南昌市八一中学期中考试试卷高三文科数学考试用时:120分 全卷满分:150分一、选择题:本大题共12个小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 是虚数单位,若复数132z =-,则21z z ++的值为( ) A . -1 B .1 C. 0 D .i2.集合1,2n M x x n Z ⎧⎫==+∈⎨⎬⎩⎭,1,2N y y m m Z ⎧⎫==+∈⎨⎬⎩⎭,则两集合,M N 的关系为( ) A.M N ⋂=∅B.M N = C. M N ⊂ D.N M ⊂ 3.下列说法正确的是( )A. 命题””的否定是““0,0,20200≥-∈∀<-∈∃-+x x R x x x R x B. ”则”的否命题是“若则命题“若2222,,b a b a b a b a =≠≠≠ C. .2112121>+>>x x x x 的充要条件是且D.q p ,为两个命题,若q p ∨为真且q p ∧为假,则q p ,两个命题中必有一个为真,一个为假.4.已知向量a ρ,b ρ的夹角为3π,且2a =r ,1b =r ,则向量a r 与向量2a b +r r 的夹角为( )A.6π B. 3π C. 4π D.2π 5.已知集合{}3,2,1,2,,A m A n A =--∈∈方程122=+ny mx 表示的图形记为“W ”,则W 表示双曲线的概率为( ) A .12 B .14 C .18 D .386.右边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序 (第6题图) 框图(图中“m MOD n ”表示m 除以n 的余数), 若输入的m ,n 分别为72,15,则输出的m =( ) A .12 B .3 C .15 D .457.如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )A .π)528(+B .310πC .π)5210(+D .83π 8.已知定义在R 上的函数xex f -=)(,记)3(log 5.0f a =,)5(log 2f b =,)0(f c =,则c b a ,,的大小关系为( )A . c a b <<B .b a c <<C .b c a <<D .a b c <<9.如图在正方体ABCD-A 1B 1C 1D 1中,P 是上底面A 1B 1C 1D 1内一动点,PM 垂直AD 于M,PM=PB , 则点P 的轨迹为( )A.线段B.椭圆一部分C.抛物线一部分D.双曲线一部分10.偶函数)(x f 是定义域为R 上的可导函数,当0≥x 时,都有x x f 2)(<'成立,则不等式1)(2)1(+>+-x f x x f 的解集是( ) A. 12x x ⎧⎫<⎨⎬⎩⎭ B. ⎭⎬⎫⎩⎨⎧>21x x C. 12x x ⎧⎫≠⎨⎬⎩⎭D.实数集R11.今有苹果m 个(+∈N m ),分给10个同学,每个同学都分到苹果,恰好全部分完.第一个人分得全部苹果的一半还多一个,第二个人分得第一个人余下苹果的一半还多一个,以此类推,后一个人分得前一个人余下的苹果的一半还多一个,则苹果个数m 为( ) A.2046 B.1024 C.2017 D.201812.当m 变化时,不在直线0232212=--+-m my x m )(上的点构成区域G,),(y x P 是区域G 内的任意一点,则 2233223x y x y++ 的取值范围是( )()=m f x n ⋅r rA.(1,2)B.[112, ] C .(112, ) D.(2,3) 二、填空题:本大题共4小题,每小题5分,共20分.13.函数)>(0)6sin()(ωπω+=x x f 与)θ+=x x g 2sin()(对称轴完全相同,将)(x f 图象向右平移3π 个单位得到)(x h ,则)(x h 的解析式是。
江西省南昌市八一中学高三下学期期中考试——数学文数
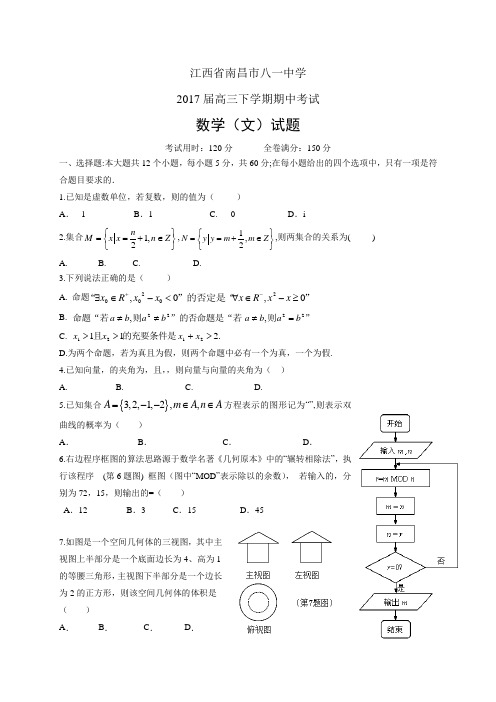
江西省南昌市八一中学 2017届高三下学期期中考试数学(文)试题考试用时:120分 全卷满分:150分一、选择题:本大题共12个小题,每小题5分,共60分;在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知是虚数单位,若复数,则的值为( )A . -1B .1 C. 0 D .i2.集合1,2n M x x n Z ⎧⎫==+∈⎨⎬⎩⎭,1,2N y y m m Z ⎧⎫==+∈⎨⎬⎩⎭,则两集合的关系为( ) A. B. C. D.3.下列说法正确的是( )A. 命题””的否定是““0,0,20200≥-∈∀<-∈∃-+x x R x x x R x B. ”则”的否命题是“若则命题“若2222,,b a b a b a b a =≠≠≠ C. .2112121>+>>x x x x 的充要条件是且D.为两个命题,若为真且为假,则两个命题中必有一个为真,一个为假. 4.已知向量,的夹角为,且,,则向量与向量的夹角为( ) A. B. C. D.5.已知集合{}3,2,1,2,,A m A n A =--∈∈方程表示的图形记为“”,则表示双曲线的概率为( )A .B .C .D . 6.右边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序 (第6题图) 框图(图中“MOD ”表示除以的余数), 若输入的,分别为72,15,则输出的=( )A .12B .3C .15D .457.如图是一个空间几何体的三视图,其中主视图上半部分是一个底面边长为4、高为1的等腰三角形,主视图下半部分是一个边长为2的正方形,则该空间几何体的体积是( )A .B .C .D .8.已知定义在R 上的函数,记,,,则的大小关系为( ) A .B .C .D .9.如图在正方体ABCD-A 1B 1C 1D 1中,P 是上底面A 1B 1C 1D 1内一动点,PM 垂直AD 于M,PM=PB , 则点P 的轨迹为( )A.线段B.椭圆一部分C.抛物线一部分D.双曲线一部分10.偶函数是定义域为R 上的可导函数,当时,都有成立,则不等式1)(2)1(+>+-x f x x f 的解集是( )A. B.C. D.实数集R11.今有苹果个(),分给10个同学,每个同学都分到苹果,恰好全部分完.第一个人分得全部苹果的一半还多一个,第二个人分得第一个人余下苹果的一半还多一个,以此类推,后一个人分得前一个人余下的苹果的一半还多一个,则苹果个数为( )A.2046B.1024C.2017D.201812.当变化时,不在直线0232212=--+-m my x m )(上的点构成区域G,是区域G 内的任意一点,则3x y 的取值范围是( )A.(1,2)B.[] C .() D.(2,3) 二、填空题:本大题共4小题,每小题5分,共20分.13.函数)>(0)6sin()(ωπω+=x x f 与对称轴完全相同,将图象向右平移 个单位得到,则的解析式是 。
江西省南昌市八一中学2017届高三下学期期中考试英语试卷(含答案)

2016~2017学年度第二学期南昌市八一中学期中考试试卷高三英语考试用时:120分全卷满分:150分第Ⅰ卷第一部分听力(共两节,满分30分)第一节(共5小题,每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What happened to the man?A. He got a parking ticket.B. He lost his ticket.C. He got a permit to park in the red zone.2. What is the man doing now?A. Drinking a cup of tea.B. Washing clothes.C. Going to the bank.3. Where was the computer used last week?A. In a lab.B. In a theater.C. In a classroom.4. What day is it today?A. Friday.B. Wednesday.C. Tuesday.5. Why does Mary call the man?A. To cancel an appointment.B. To confirm an appointment.C. To reschedule an appointment. 第二节(共15小题,每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各个小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
江西省南昌市八一中学2017-2018学年高一下学期期中考

2017-2018学年度第二学期南昌市八一中学期中考试卷高一物理一、选择题 (每小题4分,其中1-6题只有一个选项正确) (40分)1.牛顿总结前人的观点, 得出著名的万有引力定律后, 并未能计算出万有引力常量G, 请问是下列哪位科学家通过扭秤实验测量出了万有引力常量 ( )A 伽利略B 胡克C 开普勒D 卡文迪许2.已知汽车以10 m/s 的速度通过拱桥顶部时,对桥面的压力为汽车所受重力的3/4。
那么若要使汽车由粗糙桥面行驶至拱桥顶部时不受摩擦力的作用,那么汽车在到达拱桥顶部时的速度至少为()A 15 m/sB 20 m/sC 25 m/sD 30 m/s3.在空间某一点以大小相等的速度分别竖直向上、竖直向下、水平抛出质量相等的小球,不计空气阻力,经过相等的时间(设小球均未落地)( )A.做竖直下抛运动的小球加速度最大B.三个小球的速度变化相同C.做平抛运动的小球速度变化最小D.做竖直下抛的小球速度变化最小4.一名宇航员来到一个星球上,如果该星球的质量是地球质量的一半,它的直径也是地球直径的一半,那么这名宇航员在该星球上所受的万有引力大小是它在地球上所受万有引力的( )A.0.25倍B.0.5倍C.2.0倍D.4.0倍5.如图所示,当正方形薄板绕着过其中心O并与板垂直的转动轴转动时,板上A、B两点( )A.角速度之比ωA∶ωB=2∶1B.角速度之比ωA∶ωB=1∶ 2C.线速度之比v A∶v B=2∶1D.线速度之比v A∶v B=1∶ 26 .如图,可视为质点的小球,位于半径为 3 m半圆柱体左端点A的正上方某处,以一定的初速度水平抛出小球,其运动轨迹恰好能与半圆柱体相切于B点.过B点的半圆柱体半径与水平方向的夹角为60°,则初速度为(不计空气阻力,重力加速度g取10 m/s2)( )A.553 m/s B .4 3 m/sC .3 5 m/s D.152 m/s 7. “飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m ,做圆周运动的半径为r ,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )A .人和车的速度为gr tan θB .人和车的速度为gr sin θC .桶面对车的弹力为mg cos θD .桶面对车的弹力为mgsin θ8. 如图所示为赛车场的一个水平“U”形弯道,转弯处为圆心在O 点的半圆,内外半径分别为r 和2r .一辆质量为m 的赛车通过AB 线经弯道到达A ′B ′线,有如图所示的①、②、③三条路线,其中路线③是以O ′为圆心的半圆,OO ′=r .赛车沿圆弧路线行驶时,路面对轮胎的最大径向静摩擦力为F max .选择路线,赛车以不打滑的最大速率通过弯道(所选路线内赛车速率不变,发动机功率足够大),则( )A .选择路线①,赛车经过的路程最短B .选择路线②,赛车的速率最小C .选择路线③,赛车所用时间最短D .①、②、③三条路线的圆弧上,赛车的向心加速度大小相等9. )如图所示,做匀速直线运动的小车A 通过一根绕过定滑轮的长绳吊起一重物B ,设重物和小车速度的大小分别为v B 、v A ,则( )A .v A >v BB .v A <v BC .绳的拉力等于B 的重力D .绳的拉力大于B 的重力10. 发射地球同步卫星时,先将卫星发射至近地圆轨道1上,然后经点火,使其沿椭圆轨道2运行,然后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q 点,轨道2、3相切于P 点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )A.卫星在轨道1上的速率大于在轨道3上的速率B.卫星在轨道1上的周期大于在轨道3上周期C.卫星在轨道2上的周期小于在轨道3上周期D.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度二、填空题(18分)11.人造卫星的发射应该充分利用地球的自转向(填“东”或“南”或“西”或“北”)发射, 第一宇宙速度是人造地球卫星发射的(填“最大”或“最小”)速度,是人造卫星运行的(填“最大”或“最小”)速度。
江西省南昌市八一中学高三下册第二学期期中考试数学文试卷(含答案)【精校】.doc
高三文科数学
考试用时: 120 分
全卷满分: 150 分
一、选择题 : 本大题共 12 个小题,每小题 5 分,共 60 分 ; 在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知 i 是虚数单位,若复数 z
1
3 i ,则 z2 z 1 的值为(
)
22
A. -1
B
.1
C. 0
D
.i
2. 集合 M
x x n 1,n Z , N 2
yy
m
1 ,m
Z , 则两集合 M , N 的关系为 (
)
2
A. M N B. M N C. M N D. N M
3. 下列说法正确的是(
)
A. 命题“ x0 R , x0 2 x0 0”的否定是“ x R , x2 x 0” B. 命题“若 a b, 则 a2 b 2”的否命题是“若 a b,则 a 2 b 2”
, 3)
13. 函数 f (x) sin( x () > 0)与 g ( x) sin(2 x )对称轴完全相同,将 f ( x) 图象向右平移 6
3 个单位得到 h( x) ,则 h( x) 的解析式是。
14. 点 P 是椭圆上任意一点, F1, F2 分别是椭圆的左右焦点 ,
率的值是 .
F1PF2 的最大值是 60o ,则椭圆的离心
o
o
(0 ,60 ) ,
3x 3 y
2
2 =cos
3 x2 y2
( 1 ,1) 2
16. 令 x2 x1,得 f(x) 为奇函数
三、解答题
17.( 1)由题意知 f x cos2 x 1 3 sin x cos x sin 2x
2020届江西省南昌市2017级高三第一次模拟测试(全国I卷)理科综合化学试卷及解析
2020届江西省南昌市2017级高三第一次模拟测试(全国I卷)理科综合化学试卷★祝考试顺利★(解析版)一、选择题1.下列说法正确的是( )A. 国庆70周年大典放飞的气球由可降解材料制成,主要成分是聚乙烯B. 歼- 20上用到的氮化镓材料是一种金属合金材料C. 我国发射的“嫦娥三号”卫星所使用的碳纤维,是一种无机非金属材料D. “绿水青山就是金山银山”。
推广聚氯乙烯代替木材,生产快餐盒等,以减少术材的使用【答案】C【详解】A.聚乙烯材料不可降解,A错误;B.氮化镓,化学式GaN,是氮和镓的化合物,并不属于合金,B错误;C.碳纤维是碳的单质,是一种无机非金属材料,C正确;D.聚氯乙烯是塑料,不可降解,且不可于用于食品包装,D错误。
答案选C。
2.设N A为阿伏加德罗常数的值,下列说法正确的是A. 28g晶体硅中含有N A个Si-Si键B. 叠氮化铵(NH4N3)发生爆炸反应:NH4N3=2N2↑+2H2↑,当产生标准状况下22.4L气体时,转移电子的数目为N AC. pH=1的H3PO4溶液中所含H+的数目为0.1N AD. 200mL1mol/LAl2(SO4)3溶液中A13+和SO42-的数目总和是NA【答案】B【详解】A.1个Si原子周围有4个Si-Si,而1个Si-Si周围有2个Si原子,则Si和Si-Si的比例为2:4=1:2,28gSi其物质的量为1mol,则含有的Si-Si的物质的量为2mol,其数目为2N A,A错误;B.叠氮化铵发生爆炸时,H的化合价降低,从+1降低到0,1mol叠氮化铵发生爆炸时,生成4mol 气体,则总共转移4mol电子;现生成22.4:L,即1mol气体,则转移的电子数为N A,B正确;C.不知道磷酸溶液的体积,无法求出其溶液中的H+数目,C错误;D.200mL1mol·L-1Al2(SO4)3溶液中,如果Al3+不水解,则Al3+和SO42-的物质的量=0.2L×1mol·L-1×2+0.2L×1mol·L-1×3=1mol,其数目为NA,但是Al3+为弱碱的阳离子,在溶液中会水解,因此Al3+数目会减少,Al3+和SO42-的总数目小于NA,D错误。
江西省南昌市八一中学2018届高三第三次模拟考试理科综合试题
2017—2018学年度南昌市八一中学高三第三次模拟测试卷理科综合能力测试第I卷(选择题包括21小题,每小题6分,共126分)可能用到的相对分子质量: H-1 C-12 N-14 O-16 Na-23 Al-27 P-31 S-32 Cl-35.5一、选择题(本大题包括13小题,每小题6分,共78分,每小题的四个选项中,只有一项符合题目要求。
)1.下列关于生命系统中信息传递的叙述,正确的是A.生物体内细胞之间的信息传递必须依赖细胞膜上的受体的识别B.生物体内的信息传递一般都具有双向性C.无论生物体内还是生物体外,传递每一种信息都必须依赖具体的信息分子D.人体产生的能降低血糖浓度的胰岛素分子不属于生态系统信息传递中的化学信息2.下列关于实验描述正确的是A.科学家一般采用同位素标记法研究光合作用和细胞呼吸的化学反应过程B.探究2,4—D促进植物扦插枝条生根的最适浓度时需先做预实验,目的是让结果更精确C.萨顿推论出基因在染色体上运用的是假说—演绎法,沃森和克里克运用模型法研究DNA的复制方式D.提取色素时选用层析液的原因是不同色素在层析液中溶解度不同3.关于内环境稳态,以下说法正确的是A.下丘脑滲透压感受器能感受细胞外液渗透压升高并产生渴觉B.正常情况下生成与回流的组织液中氧气含量相等C.血液中C02增多引起呼吸频率加快,是由体液和神经共同调节的D.毛细血管处血浆和组织液之间相互转化的量总是平衡的4.百日咳、白喉和破伤风是三种常见传染病,分别由三种致病菌导致。
我国政府在儿童中推广“百白破”三联体疫苗的免费接种,大大降低了发病率,接种后A.吞噬细胞产生三类相应的淋巴因子B.效应T细胞对疫苗进行摄取、处理和呈递C.成功的标志是相应记忆细胞和抗体的产生D.体内出现一种能抑制上述三类致病菌的抗体5.兔的长毛(由基因HL控制)与短毛(由基因Hs控制)是由一对等位基因控制的相对性状。
某生物育种基地利用纯种兔进行如下杂交实验,产生了大量的F1与F2个体,统计结果如下表,下列说法正确的是A.B.控制兔长毛、短毛的等位基因位于Y染色体上C. F2雌雄个体的基因型相同D. F2中短毛雄兔的基因型为HsHs6.下面有关生态系统的叙述不正确的是A.生产者、消费者和分解者中都有细菌B.—条蛇吃了一条蜥蜴,可获得该蜥蜴同化能量的10%~20%C.抵抗力稳定性很低的生态系统其恢复力稳定性也可能很低D.一棵树上不同高度的喜鹊巢,不能反映动物群落的垂直结构7.化学在生活中发挥着重要的作用,下列说法正确的是A.食用油脂饱和程度越大,熔点越高B.棉、麻、丝、毛及合成纤维完全燃烧都只生成CO2和H2OC.纯铁易被腐蚀,可以在纯铁中混入碳元素制成“生铁”,以提高其抗腐蚀能力D.光纤通信是现代化的通信手段,光导纤维的主要成分是晶体硅8.设N A为阿伏加德罗常数的值。
江西省南昌一中、十中、南铁一中三校联考2017届高三下
2016-2017学年江西省南昌一中、十中、南铁一中三校联考高三(下)第四次月考数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内,复数(i是虚数单位)对应的点位于()A.第四象限B.第三象限C.第二象限D.第一象限2.设集合U={0,1,2,3,4,5},A={1,2},B={x∈Z|x2﹣5x+4<0},则∁U(A ∪B)=()A.{0,1,2,3}B.{5}C.{1,2,4}D.{0,4,5}3.等比数列{a n}的前n项和为S n,已知a2a5=2a3,且a4与2a7的等差中项为,则S5=()A.29 B.31 C.33 D.364.如图是一个几何体的三视图,其中俯视图中的曲线为四分之一圆,则该几何体的表面积为()A.3 B.C.4 D.5.执行如图所示的算法,则输出的结果是()A .1B .C .D .26.如图,在△OMN 中,A ,B 分别是OM ,ON 的中点,若=x+y (x ,y ∈R ),且点P 落在四边形ABNM 内(含边界),则的取值范围是( )A .[,]B .[,]C .[,]D .[,]7.已知函数f (x )=sin (ωx +φ)(ω>0,|φ|<)的最小正周期为π,且其图象向左平移个单位后得到函数g (x )=cosωx 的图象,则函数f (x )的图象( )A .关于直线x=对称B .关于直线x=对称C .关于点(,0)对称D .关于点(,0)对称8.若二项式()6的展开式中的常数项为m ,则=( )A .B .﹣C .D .﹣9.已知函数f (x )=|lgx |,a >b >0,f (a )=f (b ),则的最小值等于( )A.2 B.C.2+D.210.已知定义在(0,)上的函数f(x),f′(x)为其导函数,且f(x)<f′(x)•tanx恒成立,则()A.f()>f()B.f()<f()C.f()>f()D.f(1)<2f()•sin111.在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)不等式t<e1+e2恒成立,则t的最大值为()A.B.C.2 D.12.已知函数f(x)=,则函数g(x)=f(x)﹣cosπx在区间[0,8]内所有零点的和为()A.16 B.30 C.32 D.40二、填空题:本大题共4小题,每小题5分,共20分.13.已知f(x)为偶函数,当x<0时,f(x)=ln(﹣x)+3x,则曲线y=f(x)在点(1,f(1))处的切线方程是.14.已知不等式组则z=的最大值为.15.冬季供暖就要开始,现分配出5名水暖工去3个不同的居民小区检查暖气管道,每名水暖工只去一个小区,且每个小区都要有人去检查,那么分配的方案共有种.16.如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:①函数y=sinx具有“P(a)性质”;②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f(x)是周期函数.其中正确的是(写出所有正确命题的编号).三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.17.某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,但可见部分,如图,据此解答下列问题:(1)求分数在[50,60]的频率及全班人数;(2)求分数在[80,90]之间的频数,并计算频率分布直方图中[80,90]间的矩形的高.18.在等比数列{a n}中,a1=1,且a2是a1与a3﹣1的等差中项.(1)求数列{a n}的通项公式;(2)若数列{b n}满足.求数列{b n}的前n项和.19.已知函数f(x)=sin(﹣2x)﹣2sin(x﹣)cos(x+).(1)求函数f(x)的最小正周期和单调递增区间;(2)若x∈[,],且F(x)=﹣4λf(x)﹣cos(4x﹣)的最小值是﹣,求实数λ的值.20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.(1)证明:AB⊥平面BEF;(2)若,求二面角E ﹣BD ﹣C 的大小;( 3)求点C 到平面DEB 的距离.21.已知抛物线E :y 2=2px (p >0),直线x=my +3与E 交于A 、B 两点,且•=6,其中O 为坐标原点. (1)求抛物线E 的方程;(2)已知点C 的坐标为(﹣3,0),记直线CA 、CB 的斜率分别为k 1,k 2,证明+﹣2m 2为定值.22.已知函数f (x )=xe 2x ﹣lnx ﹣ax .(1)当a=0时,求函数f (x )在[,1]上的最小值; (2)若∀x >0,不等式f (x )≥1恒成立,求a 的取值范围;(3)若∀x >0,不等式f ()﹣1≥e +恒成立,求a 的取值范围.2016-2017学年江西省南昌一中、十中、南铁一中三校联考高三(下)第四次月考数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.在复平面内,复数(i是虚数单位)对应的点位于()A.第四象限B.第三象限C.第二象限D.第一象限【考点】复数代数形式的乘除运算.【分析】由复数代数形式的乘除运算化简复数,求出在复平面内,复数对应的点的坐标,则答案可求.【解答】解:=,在复平面内,复数对应的点的坐标为:(,),位于第四象限.故选:A.2.设集合U={0,1,2,3,4,5},A={1,2},B={x∈Z|x2﹣5x+4<0},则∁U(A ∪B)=()A.{0,1,2,3}B.{5}C.{1,2,4}D.{0,4,5}【考点】交、并、补集的混合运算.【分析】求出集合B中不等式的解集,找出解集中的整数解确定出B,求出A与B 的并集,找出全集中不属于并集的元素,即可求出所求.【解答】解:集合B中的不等式x2﹣5x+4<0,变形得:(x﹣1)(x﹣4)<0,解得:1<x<4,∴B={2,3},∵A={1,2},∴A∪B={1,2,3},∵集合U={0,1,2,3,4,5},(A∪B)={0,4,5}.∴∁∪故选D.3.等比数列{a n}的前n项和为S n,已知a2a5=2a3,且a4与2a7的等差中项为,则S5=()A.29 B.31 C.33 D.36【考点】等比数列的前n项和.【分析】利用a2•a3=2a1,且a4与2a7的等差中项为,求出数列的首项与公比,再利用等比数列的求和公式,即可得出结论.【解答】解:∵数列{a n}是等比数列,a2•a3=2a1=a1q•=a1•a4,∴a4=2.∵a4与2a7的等差中项为,∴a4 +2a7 =,故有a7 =.∴q3==,∴q=,∴a1==16.∴S5==31.故选:B.4.如图是一个几何体的三视图,其中俯视图中的曲线为四分之一圆,则该几何体的表面积为()A.3 B.C.4 D.【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.【分析】由已知可得该几何体是一个以俯视图这底面的柱体,根据柱体表面积公式,可得答案.【解答】解:由已知可得该几何体是一个以俯视图这底面的柱体,底面积为1﹣,底面周长为:2+,柱体的高为1,故该几何体的表面积S=2×(1﹣)+2+=4,故选:C5.执行如图所示的算法,则输出的结果是()A.1 B.C.D.2【考点】程序框图.【分析】模拟执行程序框图,依次写出每次循环得到的n,M,S的值,当S=1时,满足条件S∈Q,退出循环,输出S的值为1.【解答】解:模拟执行程序框图,可得S=0,n=2n=3,M=,S=不满足条件S∈Q,n=4,M=,S=+不满足条件S∈Q,n=5,M=,S=++=1满足条件S∈Q,退出循环,输出S的值为1.故选:A.6.如图,在△OMN中,A,B分别是OM,ON的中点,若=x+y(x,y∈R),且点P落在四边形ABNM内(含边界),则的取值范围是()A.[,]B.[,] C.[,] D.[,]【考点】平面向量的基本定理及其意义.【分析】若P在线段AB上,设=λ,则有=,由于=x+y,则有x+y=1,由于在△OMN中,A,B分别是OM,ON的中点,P落在线段MN上,则x+y=2.即可得到取值范围.【解答】解:若P在线段AB上,设=λ,则有==,∴=,由于=x+y(x,y∈R),则x=,y=,故有x+y=1,若P在线段MN上,设=λ,则有=,故x=1,y=0时,最小值为,当x=0,y=1时,最大值为故范围为[]由于在△OMN中,A,B分别是OM,ON的中点,则=x+y=x+y(x,y∈R),则x=,y=,故有x+y=2,当x=2,y=0时有最小值,当x=0,y=2时,有最大值故范围为[]若P在阴影部分内(含边界),则∈.故选:C.7.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,且其图象向左平移个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象()A.关于直线x=对称B.关于直线x=对称C.关于点(,0)对称D.关于点(,0)对称【考点】函数y=Asin(ωx+φ)的图象变换.【分析】利用正弦函数的周期性、函数y=Asin(ωx+φ)的图象变换规律、诱导公式,求得f(x)的解析式,再利用正弦函数的图象的对称性,得出结论.【解答】解:∵函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,∴=π,∴ω=2.把其图象向左平移个单位后得到函数g(x)=cosωx=sin(2x++φ)的图象,∴+φ=kπ+,k∈Z,∴φ=﹣,∴f(x)=sin(2x﹣).由于当x=时,函数f(x)=0,故A不满足条件,而C满足条件;令x=,求得函数f(x)=sin=,故B、D不满足条件,故选:C.8.若二项式()6的展开式中的常数项为m,则=()A.B.﹣ C.D.﹣【考点】二项式定理.【分析】运用二项式展开式的通项公式,化简整理,令x的次数为0,求出m,再由定积分的运算法则,即可求得.=,【解答】解:二项式()6的展开式的通项公式为:T r+1令12﹣3r=0,则r=4.即有m==3.则=(x2﹣2x)dx=(x3﹣x2)=.故选:C.9.已知函数f(x)=|lgx|,a>b>0,f(a)=f(b),则的最小值等于()A.2 B.C.2+D.2【考点】对数函数图象与性质的综合应用.【分析】根据对数的运算性质,可得ab=1(a>b>0),进而可将=(a﹣b)+,进而根据基本不等式,可得答案.【解答】解:∵f(x)=|lgx|,a>b>0,f(a)=f(b),则lga=﹣lgb,则a=,即ab=1(a>b>0)==(a﹣b)+≥2故的最小值等于2故选A10.已知定义在(0,)上的函数f(x),f′(x)为其导函数,且f(x)<f′(x)•tanx恒成立,则()A.f()>f()B.f()<f()C.f()>f()D.f(1)<2f()•sin1【考点】导数在最大值、最小值问题中的应用.【分析】把给出的等式变形得到f′(x)sinx﹣f(x)cosx>0,由此联想构造辅助函数g(x)=,由其导函数的符号得到其在(0,)上为增函数,则g()<g()<g(1)<g(),整理后即可得到答案.【解答】解:解:因为x∈(0,),所以sinx>0,cosx>0,由f(x)<f′(x)tanx,得f(x)cosx<f′(x)sinx,即f′(x)sinx﹣f(x)cosx>0.令g(x)=,x∈(0,),则g′(x)=>0.所以函数g(x)=在x∈(0,)上为增函数,则g()<g()<g(1)<g(),即,对照选项,A.应为>,C.应为<f(),D.应为f(1)2f()sin1,B正确.故选B.11.在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,若对任意x∈(0,1)不等式t<e1+e2恒成立,则t的最大值为()A.B.C.2 D.【考点】椭圆的简单性质.【分析】根据余弦定理表示出BD,进而根据双曲线的定义可得到a1的值,再由AB=2c1,e=可表示出e1,同样的在椭圆中用c2和a2表示出e2,然后利用换元法即可求出e1+e2的取值范围,即得结论•【解答】解:在等腰梯形ABCD中,BD2=AD2+AB2﹣2AD•AB•cos∠DAB=1+4﹣2×1×2×(1﹣x)=1+4x,由双曲线的定义可得a1=,c1=1,e1=,由椭圆的定义可得a2=,c2=x,e2=,则e1+e2=+=+,令t=∈(0,﹣1),则e1+e2=(t+)在(0,﹣1)上单调递减,所以e1+e2>×(﹣1+)=,故选:B.12.已知函数f(x)=,则函数g(x)=f(x)﹣cosπx在区间[0,8]内所有零点的和为()A.16 B.30 C.32 D.40【考点】根的存在性及根的个数判断;函数的零点与方程根的关系.【分析】在同一个坐标系中作出函数f(x)和y=cosπx的图象,由图象的局部对称可得结果.【解答】解:当0≤x≤1时,f(x)=x,当1<x<2时,f(x)=﹣x+2,当2≤x≤3时,f(x)=3f(x﹣2)=3(x﹣2),当3<x<4时,f(x)=3f(x﹣2)=3[﹣(x﹣2)+2]=﹣3(x﹣4),当4≤x≤5时,f(x)=3f(x﹣2)=3(3x﹣6)=9(x﹣2),当5<x<6时,f(x)=3f(x﹣2)=﹣9(x﹣6),当6≤x≤7时,f(x)=3f(x﹣2)=27(x﹣6),当7<x≤8时,f(x)=﹣27(x﹣8),在同一坐标系中画出函数f(x)与函数y=cosπx的图象,如图:由图可知点A,B关于x=1对称,点C,D关于x=3对称,点E,F关于x=5对称,点G,H关于x=7对称,设A,B,C,D,E,F,G,H的横坐标分别为a,b,c,d,e,f,g,h,则a+b=2,c+d=6,e+f=10,g+h=14,∴a+b+c+d+e+f+g+h=32.故选:C.二、填空题:本大题共4小题,每小题5分,共20分.13.已知f(x)为偶函数,当x<0时,f(x)=ln(﹣x)+3x,则曲线y=f(x)在点(1,f(1))处的切线方程是2x+y+1=0.【考点】利用导数研究曲线上某点切线方程.【分析】由偶函数的定义,可得f(﹣x)=f(x),即有x>0时,f(x)=lnx﹣3x,求出导数,求得切线的斜率,由点斜式方程可得切线的方程.【解答】解:f(x)为偶函数,可得f(﹣x)=f(x),当x<0时,f(x)=ln(﹣x)+3x,即有x>0时,f(x)=lnx﹣3x,f′(x)=﹣3,可得f(1)=ln1﹣3=﹣3,f′(1)=1﹣3=﹣2,则曲线y=f(x)在点(1,﹣3)处的切线方程为y﹣(﹣3)=﹣2(x﹣1),即为2x+y+1=0.故答案为:2x+y+1=0.14.已知不等式组则z=的最大值为3.【考点】简单线性规划.【分析】画出满足条件的平面区域,结合的几何意义求出z的最大值即可.【解答】解:画出满足条件的平面区域,如图示:,的几何意义表示平面区域内的点与点A(﹣1,1)的直线的斜率,结合图象直线过AB时,斜率最大,此时z==3,故答案为:3.15.冬季供暖就要开始,现分配出5名水暖工去3个不同的居民小区检查暖气管道,每名水暖工只去一个小区,且每个小区都要有人去检查,那么分配的方案共有150种.【考点】计数原理的应用.【分析】依题意,可分两类:①(3,1,1);②(2,2,1);利用排列组合的知识解决即可.【解答】解:根据题意,分配5名水暖工去3个不同的小区,要求5名水暖工都分配出去,且每个小区都要有人去检查,5人可以分为(2,2,1),(3,1,1),分组方法共有+C53=25种,分别分配到3个不同的小区,有A33种情况,由分步计数原理,可得共25A33=150种不同分配方案,故答案为:150.16.如果y=f(x)的定义域为R,对于定义域内的任意x,存在实数a使得f(x+a)=f(﹣x)成立,则称此函数具有“P(a)性质”.给出下列命题:①函数y=sinx具有“P(a)性质”;②若奇函数y=f(x)具有“P(2)性质”,且f(1)=1,则f具有“P(4)性质”,图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,则y=f(x)在(﹣2,﹣1)上单调递减,在(1,2)上单调递增;④若不恒为零的函数y=f(x)同时具有“P(0)性质”和“P(3)性质”,函数y=f(x)是周期函数.其中正确的是①③④(写出所有正确命题的编号).【考点】抽象函数及其应用.【分析】根据新定义,得出f(x)的周期,结合函数奇偶性的性质即可判断.【解答】解:①∵sin(x+π)=﹣sin(x)=sin(﹣x),∴函数y=sinx具有“P(a)性质”;故①正确;②∵若奇函数y=f(x)具有“P(2)性质”,∴f(x+2)=f(﹣x)=﹣f(x),∴f(x)=f(2﹣x)=﹣f(x﹣2),∴f(x+2)=f(x﹣2),∴f(x)是周期为4的函数,∴f=﹣f(1)=﹣1,故②不正确;③∵若函数y=f(x)具有“P(4)性质”,∴f(x+4)=f(﹣x),∴f(x+2)=f(2﹣x),∴f(x)关于x=2对称,∵图象关于点(1,0)成中心对称,∴f(2﹣x)=﹣f(x),即f(2+x)=﹣f(﹣x),又f(x+2)=f(2﹣x),∴f(x)=f(﹣x),∴f(x)为偶函数,∵图象关于点(1,0)成中心对称,且在(﹣1,0)上单调递减,∴图象也关于点(﹣1,0)成中心对称,且在(﹣2,﹣1)上单调递减,根据偶函数的对称得出:在(1,2)上单调递增;故③正确;④∵f(x)具有“P(0)性质”和“P(3)性质”,∴f(x)=f(﹣x),f(x+3)=f(﹣x)=f(x),∴f(x)为偶函数,且周期为3,故④正确.故答案为:①③④.三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.17.某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,但可见部分,如图,据此解答下列问题:(1)求分数在[50,60]的频率及全班人数;(2)求分数在[80,90]之间的频数,并计算频率分布直方图中[80,90]间的矩形的高.【考点】频率分布直方图;茎叶图.【分析】(1)由直方图在得到分数在[50,60)的频率,求出全班人数;(2)由茎叶图求出分数在[80,90)之间的人数,进一步求出频率分布直方图中[80,90]间的矩形的高【解答】解:(1)分数在[50,60]的频率为0.008×10=0.08.由茎叶图知,分数在[50,60]之间的频数为2,所以全班人数为=25.(2)分数在[80,90]之间的频数为25﹣2﹣7﹣10﹣2=4,频率分布直方图中[80,90]间的矩形的高为÷10=0.016.18.在等比数列{a n}中,a1=1,且a2是a1与a3﹣1的等差中项.(1)求数列{a n}的通项公式;(2)若数列{b n}满足.求数列{b n}的前n项和.【考点】数列的求和;等比数列的通项公式.【分析】(1)设等比数列{a n}的公比为q,运用等差数列的性质和等比数列的通项公式,解方程可得公比q,即可得到所求通项公式;(2)化简b n=2n﹣1+(﹣),运用分组求和和裂项相消求和,化简即可得到所求和.【解答】解:(1)设等比数列{a n}的公比为q,a2是a1与a3﹣1的等差中项,即有a1+a3﹣1=2a2,即为1+q2﹣1=2q,解得q=2,即有a n=a1q n﹣1=2n﹣1;(2)=a n+=2n﹣1+(﹣),数列{b n}的前n项和=(1+2+22+…+2n﹣1)+(1﹣+﹣+﹣+…+﹣)=+1﹣=2n﹣.19.已知函数f(x)=sin(﹣2x)﹣2sin(x﹣)cos(x+).(1)求函数f(x)的最小正周期和单调递增区间;(2)若x∈[,],且F(x)=﹣4λf(x)﹣cos(4x﹣)的最小值是﹣,求实数λ的值.【考点】三角函数的周期性及其求法;正弦函数的单调性.【分析】(1)先利用两角和余差和二倍角等基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,最后将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;(2)x∈[,]时,化解F(x),求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的最小值,可得实数λ的值.【解答】解:函数f(x)=sin(﹣2x)﹣2sin(x﹣)cos(x+).化简可得:f(x)=sin cos2x﹣cos sin2x﹣2sin(x﹣)cos(π﹣+x)=cos2x+sin2x+sin(2x﹣)=sin2x﹣cos2x=sin(2x﹣)(1)函数f(x)的最小正周期T=,∵2x﹣∈[,],k∈Z单调递增区间;即≤2x﹣≤,解得:≤x≤,∴函数f(x)的单调递增区间为[,],k∈Z.(2)由F(x)=﹣4λf(x)﹣cos(4x﹣)=﹣4λsin(2x﹣)﹣cos(4x﹣)=﹣4λsin(2x﹣)﹣1+2sin2(2x﹣)令t=sin(2x﹣),x∈[,],∴2x﹣∈[0,]∴0≤t≤1那么F(x)转化为g(t)=﹣4λt+2t2﹣1,其对称轴t=λ,开口向上,当t=λ时,取得最小值为,由,解得:λ=.故得实数λ的值为.20.如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.(1)证明:AB⊥平面BEF;(2)若,求二面角E﹣BD﹣C的大小;(3)求点C到平面DEB的距离.【考点】二面角的平面角及求法;点、线、面间的距离计算.【分析】(1)证明AB⊥BF.推出平面PAD⊥平面ABCD,证明AB⊥PD,AB⊥EF.然后证明AB⊥平面BEF.(2)以A为原点,以AB,AD,AP为x轴,y轴,z轴正向建立空间直角坐标系,求出平面CDB的法向量为=(0,0,1),平面EBD的法向量,设二面角E﹣BD ﹣C的大小为θ,利用空间向量的数量积求解即可.(3)由(2)知,然后求解点C到平面DEB的距离.【解答】解:(1)证:由已知DF∥AB且∠DAB为直角,故ABFD是矩形,从而AB⊥BF.又PA⊥底面ABCD,∴平面PAD⊥平面ABCD,∵AB⊥AD,故AB⊥平面PAD,∴AB⊥PD,在△PCD内,E、F分别是PC、CD的中点,EF∥PD,∴AB⊥EF.由此得AB⊥平面BEF…(2)以A为原点,以AB,AD,AP为x轴,y轴,z轴正向建立空间直角坐标系,则设平面CDB的法向量为=(0,0,1),平面EBD的法向量为=(x,y,z),则可取设二面角E﹣BD﹣C的大小为θ,则=,所以,…(3)由(2)知,所以,点C到平面DEB的距离为…21.已知抛物线E:y2=2px(p>0),直线x=my+3与E交于A、B两点,且•=6,其中O为坐标原点.(1)求抛物线E的方程;(2)已知点C的坐标为(﹣3,0),记直线CA、CB的斜率分别为k1,k2,证明+﹣2m2为定值.【考点】抛物线的简单性质.(1)由题意可知:将直线方程代入抛物线方程,由韦达定理可知:y1+y2=2pm,【分析】y1•y2=﹣6p,•=x1•x2+y1•y2=+y1•y2,求得9﹣6p=6,求得p的值,即可求得抛物线E的方程;(2)由直线的斜率公式可知:k1==,k2==, +﹣2m2=(m+)2+(m+)2﹣2m2=2m2+12m×+36×﹣2m2,由(1)可知:y1+y2=2pm=m,y1•y2=﹣6p=﹣3,代入即可求得+﹣2m2=24.【解答】解:(1)设A(x1,y1),B(x2,y2),,整理得:y2﹣2pmy﹣6p=0,由韦达定理可知:y1+y2=2pm,y1•y2=﹣6p,则x 1•x 2=由•=x 1•x 2+y 1•y 2=+y 1•y 2=9﹣6p=6,解得:p=,∴y 2=x ;(2)证明:由直线CA 的斜率k 1,k 1==,CB 的斜率k 2,k 2==,∴=m +, =m +,∴+﹣2m 2=(m +)2+(m +)2﹣2m 2,=2m 2+12m (+)+36×(+)﹣2m 2,=2m 2+12m ×+36×﹣2m 2,由(1)可知:y 1+y 2=2pm=m ,y 1•y 2=﹣6p=﹣3,∴+﹣2m 2=2m 2+12m ×()+36×﹣2m 2=24,∴+﹣2m 2为定值.22.已知函数f (x )=xe 2x ﹣lnx ﹣ax .(1)当a=0时,求函数f (x )在[,1]上的最小值; (2)若∀x >0,不等式f (x )≥1恒成立,求a 的取值范围;(3)若∀x >0,不等式f ()﹣1≥e +恒成立,求a 的取值范围.【考点】利用导数求闭区间上函数的最值;利用导数研究函数的单调性.【分析】(1)a=0时,,,由此利用导数性质能求出函数f(x)在[,1]上的最小值.(2),函数f(x)在区间(0,x0)上递减,在(x0,+∞)上递增,由∀x>0,不等式f(x)≥1恒成立,得lnx0+2x02≤0,由此能求出a的取值范围.(3)由f()﹣1≥,得a对任意x>0成立,令函数g(x)=xlnx﹣x﹣,则,由此利用导数性质能求出a的取值范围.【解答】解:(1)a=0时,f(x)=xe2x﹣lnx,∴,,∴函数f′(x)在(0,+∞)上是增函数,又函数f′(x)的值域为R,故∃x0>0,使得f′(x0)=(2x0+1)e﹣=0,又∵,∴,∴当x∈[]时,f′(x)>0,即函数f(x)在区间[,1]上递增,∴.(2),由(1)知函数f′(x)在(0,+∞)上是增函数,且∃x0>0,使得f′(x0)=0,进而函数f(x)在区间(0,x0)上递减,在(x0,+∞)上递增,﹣lnx0﹣ax0,由f′(x0)=0,得:(2x0+1)e﹣﹣a=0,∴,∴f(x0)=1﹣lnx0﹣2x02,∵∀x>0,不等式f(x)≥1恒成立,∴1﹣lnx0﹣2x02e≥1,∴lnx0+2x02≤0,设h(x0)=lnx0+2x e,则h(x0)为增函数,且有唯一零点,设为t,则h(t)=lnt+2t2e2t=0,则﹣lnt=2t2e2t,即,令g(x)=xe x,则g(x)单调递增,且g(2t)=g(),则2t=ln,即,∵a=(2x0+1)﹣在(0,t]为增函数,则当x0=t时,a有最大值,=,∴a≤2,∴a的取值范围是(﹣∞,2].(3)由f()﹣1≥,得,∴xlnx﹣x﹣a≥,∴a对任意x>0成立,令函数g(x)=xlnx﹣x﹣,∴,当x>1时,g′(x)>0,当0<x<1时,g′(x)<0,∴当x=1时,函数g(x)取得最小值g(1)=﹣1﹣=﹣1﹣,∴a≤﹣1﹣.∴a的取值范围是(﹣∞,﹣1﹣).2017年4月27日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1页 2017届江西省南昌市八一中学高三下学期期中考试理科综合试题 考试用时:150分 全卷满分:300分 可能用到的相对原子质量: H-1 C -12 O-16 Br-80 Cl-35.5 第Ⅰ卷 (选择题 共126分) 一、选择题(本大题共13小题,每小题6分,共78分。每小题给出的四个选项中,只有一个选项正确,有选错或不答的得0分。) 1.下列关于生物体结构与功能的叙述正确的是( ) A.细菌代谢速率极快,细胞膜以及其他的膜结构所构成的生物膜系统为其提供了结构基础 B.胰岛A细胞分泌胰岛素的过程,需消耗ATP,体现了细胞膜具有一定的流动性 C.衰老的细胞内多种酶的活性降低,细胞核的体积增大 D.在电镜下观察分裂间期的真核细胞,可以看到细胞核的主要结构有核膜、核仁和染色体 2. 图甲所示为原核细胞基因表达过程,图乙为生物的中心法则,①~⑤表示生理过程。下列叙述不正确的是( )
A.图甲中存在DNA、RNA、蛋白质等生物大分子 B.图甲中合成的多肽还需经内质网和高尔基体的加工才具有生物活性 C.图乙中过程③在核糖体中完成 D. 在人体内浆细胞和效应T细胞能发生图乙中的生理过程②③而不能发生过程① 3. 下列有关实验方法或检测的叙述,正确的是( ) A.观察植物细胞的质壁分离和复原必需使用高倍镜观察 B. 胡萝卜素处于滤纸最上方,是因为其在提取液中的溶解度最高 C.探究低温诱导植物细胞染色体数目变化的实验中,需用体积分数95%的酒精冲洗卡诺氏液 D.在用过氧化氢酶、过氧化氢为原料来探究酶的最适温度的实验中,常用单位时间内氧气释放量来检测实验结果 4. 下列有关种群、群落和生态系统的叙述,不正确...的是( ) A.雌螳螂在交配后将雄螳螂吃掉属于捕食关系 B.生态系统的信息传递不都是沿着食物链进行的 C. 捕食者的存在有利于增加物种多样性 D.丰富度能够反映群落在一定时期的物种数目,但不能反映群落的演替趋势
核糖体
聚合酶 蛋白质 2页
5.将与生物学有关的内容依次填入图中各框中,其中包含关系正确的选项是( ) 6.下图甲、乙表示某二倍体动物细胞不同分裂时期的图像,丙为该动物细胞正常分裂时有关物质或结构数量变化的部分曲线图,下列分析不正确...的是( )
A.由图甲可知该二倍体动物应为雄性个体 B.图乙中的染色体数是该生物体细胞染色体数的两倍 C.若图丙曲线表示有丝分裂中染色体组数数目变化的部分曲线,则n等于2 D.若图丙曲线表示减数第一次分裂核DNA分子数目变化的部分曲线,则n等于2 7.下列说法正确的是 ( ) A.铅蓄电池是常见的二次电池,性能优良,比能量高,缺点是废弃电池铅污染严重 B.用玻璃棒蘸取KMnO4(H+)溶液,滴在pH试纸上,然后与标准比色卡对照,测定其pH C.石油的分馏、蛋白质的盐析、焰色反应、煤的液化与气化都是物理变化 D.在元素周期表的金属和非金属分界线附近可寻找锗、硅、硒等半导体材料 8.中国药学家屠呦呦因发现青蒿素及其抗疟疗效,荣获诺贝尔 生理学或医学奖。青蒿素结构式如右图所示,下列有关青蒿素 研究的说法不正确的是 ( ) A.提取过程中为防止破坏青蒿素结构,应避免高温,故采用低沸点溶剂乙醚进行萃取 B.可使用质谱仪测出这个分子的相对分子质量,也可用紫外光谱确定这个分子的环状结构 C.青蒿素是脂溶性的,既可看作是醚类也可看作是酯类,既有氧化性又有还原性 D.元素分析仪可以确定青蒿素中是否含有C、H、O等元素 9. 下列相关家庭实验能达到预期目的的是 ( ) 3页
相关实验 预期目的 A. 在少量食用碱中一次性加入过量食醋 探究食用碱是碳酸钠还是碳酸氢钠
B. 在食用盐中滴加少量淀粉液 探究食用盐是否为加碘盐
C. 用激光笔照射淀粉液 探究淀粉液是胶体还是溶液
D 将鸡蛋白溶于水后,滴加AgNO3溶液 验证蛋白质中含有氯元素
10.下列离子方程式书写正确的是 ( ) A.含0.1molFeI2的溶液中滴加含0.125molCl2的氯水:2Fe2++8I-+5Cl2=2Fe3++4I2+10Cl- B.足量CO2通入饱和Na2CO3溶液中:CO2 + CO32-+ H2O = 2HCO3- C.向饱和的Ca(HCO3)2溶液中加入足量的NaOH: Ca2++ HCO3-+OH- = CaCO3 + H2O D.新制氯水中滴加澄清石灰水,黄绿色褪去: Cl2+Ca(OH)2=Ca2++Cl-+ClO-+H2O 11. 锂-铜空气燃料电池容量高、成本低,具有广阔的发展前
景。该电池通过一种复杂的铜腐蚀“现象”产生电力,其中放电过程为2Li+Cu2O+H2O=2Cu+2Li++2OH-,下列说法不正确的是( ) A.放电时,正极的电极反应式为Cu2O+H2O+2e-=2Cu+2OH-
B.放电时,电子透过固体电解质向Li极移动 C.通空气时,铜电极被腐蚀,表面产生Cu2O D.整个反应过程中,氧化剂为O2
12.如表所示的五种元素中,W、X、Y、Z为短周期元素,这四种元素的原子最外层电子数之和为22。下
列说法正确的是 ( ) A.X、Y、Z三种元素最低价氢化物的沸点依次升高 B.由X、Y和氢三种元素形成的化合物中只有共价键 C.物质WY2、W3X4、WZ4均有熔点高、硬度大的特性 D.T元素的单质具有半导体的特性,T与Z元素可形成化合物TZ4 13.已知草酸为二元弱酸:H2C2O4HC2O4-+H+ 1aK; HC2O4-C2O42-+H+ 2aK; 常温下,向某浓度的草酸溶液中逐滴加入一定量浓度的KOH溶液,所得溶液中H2C2O4、HC2O4-、C2O42-三种微粒的物质的量分数(δ)与溶液pH的关系如图所示,则下列说法中不正确的是 ( )
A.pH=1.2溶液中:c(K+)+c(H+) = c(OH-)+c(H2C2O4)
X Y W Z T 4页
B.pH=2.7溶液中:224222424(HCO)1000(HCO)(CO)ccc- C.将相同物质的量KHC2O4和K2C2O4固体完全溶于水可配得pH为4.2的混合液 D.向pH=1.2的溶液中加KOH溶液将pH增大至4.2的过程中水的电离程度一直增大 二、选择题(本大题共8小题,每小题6分,在每小题给出的四个选项中,第14至18题只有一项符合题目要求,第19至21题有多项符合题目要求. 全部选对的得6分,选对但不全的得3分,有选错的得0分) 14.一种比飞机还要快的旅行工具即将诞生,称为“第五类交通方式”,它就是“Hyperloop(超级高铁)”。如果乘坐Hyperloop从北京到上海,1400公里的路程约需要80分钟,Hyperloop先匀加速,达到最大速度1200 km/h后匀速运动,快进站时再匀减速运动,且加速与减速的加速度大小相等,则下列关于Hyperloop的说法正确的是( ) A.加速与减速的时间相等,加速时间为12分钟 B.中途匀速时间为60分钟 C.加速时加速度大小为1 m/s2 D.如果加速度大小为10 m/s2,题中所述运动最短需要65分钟 15. 2016年8月16日01时40分,由我国研制的世界首颗量子科学试验卫星“墨子号”在酒泉卫星发射中心用长征二号丁运载火箭成功发射升空.它的成功发射和在轨运行,不仅将有助于我国广域量子通信网络的构建,服务于国家信息安全,它将开展对量子力学基本问题的空间尺度试验检验,加深人类对量子力学自身的理解,关于量子和量子化,下列说法错误..的是 ( ) A.玻尔在研究原子结构中引进了量子化的概念 B.普朗克把能量子引入物理学,破除了“能量连续变化”的传统观念 C.光子的概念是爱因斯坦提出的 D.光电效应实验中的光电子,也就是光子 16.钳形电流表(可看成理想变压器)的外形和结构如图(a)所示.图(a)中电流表的读数为1 A,图(b)中用同一电缆线绕了3匝,则 ( ) A.这种电流表能测直流电流,图(b)的读数为2.4 A B.这种电流表能测交流电流,图(b)的读数为3 A C.若测量时导线中交流电流频率增大,图(b)的读数小于3 A D.若测量时导线中交流电流频率增大,图(b)的读数大于3 A 17.女航天员王亚平在“天宫一号”目标飞行器里通过一个实验成功展示了失重状态下液滴的表面张力引起的效应。在视频中可观察到漂浮的液滴处于相互垂直的两个椭球之间不断变化的周期性“脉动”中。假设液滴处于完全失重状态,液滴的上述“脉动”可视为液滴形状的周期性微小变化(振动),如图所示。已知
液滴振动的频率表达式为2121xkrf,其中k为一个无单位的比例系数,r为液滴半径,ρ为液体密度,σ为液体表面张力系数(其单位为N/m),x是待定常数。对于待定常数x的大小, 5页
x y O A B P
β v0
下列说法中可能正确的是( ) A.23 B.-3 C.12 D. 23- 18.已知质量分布均匀的球壳对壳内物体的万有引力为零.假设地球是质量分布均匀的球体.如图若在地球内挖一球形内切空腔。有一小球自切点A自由释放,则小球在球形空腔内将做 ( ) A.匀速直线运动 B.加速度越来越大的直线运动 C.匀加速直线运动 D.加速度越来越小的直线运动 19. 在水滑的水平面内建立如图所示的直角坐标系,长为L的光滑细杆AB 的两个端点A、B被分别约束在x轴和y轴上运动,现让A沿x轴正方向以速度v0匀速运动,已知P点为杆的中点,杆AB与x轴的夹角为β。关于P点的运动轨迹和P点的运动速度大小v表达式正确的是( ) A.P点的运动轨迹是圆的一部分 B.P点的运动轨迹是椭圆的一部分
C.P点的运动速度大小0tanvv D.P点的运动速度大小02sinvv 20. 如图所示,不带电物体A和带电的物体B用跨过定滑轮的绝缘轻绳连接,A、B的质量分别为2m和m,劲度系数为k的轻弹簧一端固定在水平面上,另一端与物体A相连,倾角为θ的斜面处于沿斜面向上的匀强电场中,整个系统不计一切摩擦.开始时,物体B在一沿斜面向上的外力F=3mgsinθ的作用下保持静止且轻绳恰好伸直,然后撤去外力F,直到物体B获得最大速度,且弹簧未超过弹性限度,则在此过程中( ) A.物体A受到的电场力大小为mgsinθ B.物体B的速度最大时,弹簧的伸长量为
kmgsin3
C.撤去外力F的瞬间,物体B的加速度为gsinθ D.物体A、弹簧和地球所组成的系统机械能增加量等于物体B和地球组成的系统的机械能的减少量 21. 如图所示的光滑水平面上,水平条形区域Ⅰ和Ⅱ内有方向垂直纸面向里的匀强磁场,其宽度均为s,区域Ⅰ和Ⅱ之间有一宽度为L=3s的无磁场区域,一质量为m、边长为s的正方形线框在水平恒定外力作用下从距区域Ⅰ左边界s处由静止开始做匀加速直线运动,假设线框能匀速地通过磁场区域Ⅰ和Ⅱ,则下列说法正确的是( ) A. 线框通过区域Ⅰ和区域Ⅱ时的速度大小之比为l:3 B.区域Ⅰ与区域Ⅱ内磁场的磁感应强度大小之比为3:1 C.线框通过区域Ⅰ和区域Ⅱ过程产生的热量相等 D.线框右边通过区域Ⅰ和区域Ⅱ过程通过线框某一横截面的电荷量相等
