梁的弯曲正应力实验报告总结
弯曲正应力实验报告

弯曲正应力实验报告弯曲正应力实验报告引言:弯曲正应力实验是材料力学中的一项重要实验,通过对材料在受力情况下的变形和应力分布进行观察和分析,可以了解材料的力学性质和强度。
本实验旨在通过对不同材料的弯曲试样进行加载,测量其变形和应力分布,从而探究材料的弯曲性能。
实验原理:弯曲正应力实验是利用悬臂梁的弯曲变形来研究材料的力学性质。
在实验中,我们采用了一根长条形试样,将其固定在一端,然后在另一端施加一个力。
通过测量试样的挠度和应力,可以得到弯曲试样的力学性能。
实验步骤:1. 准备工作:选择合适的试样和装置,确保试样的尺寸和几何形状符合实验要求。
2. 安装试样:将试样固定在支架上,并调整好试样的位置和方向。
3. 施加力:通过加载装置施加一个力,使试样发生弯曲变形。
4. 测量挠度:使用测量仪器(如游标卡尺或激光测量仪)测量试样在不同位置的挠度。
5. 记录数据:将测量到的挠度数据记录下来,并与施加的力进行对应。
6. 计算应力:根据试样的几何形状和力的大小,计算出试样不同位置处的应力。
7. 绘制应力-挠度曲线:将应力和挠度的数据绘制成曲线图,分析试样的弯曲性能。
实验结果:通过实验我们得到了一组应力-挠度曲线数据。
根据这些数据,我们可以观察到试样在受力作用下的变形情况,并得到试样在不同位置处的应力分布情况。
根据应力-挠度曲线的形状,可以判断材料的强度和韧性。
讨论与分析:根据实验结果,我们可以对不同材料的弯曲性能进行比较和分析。
通过观察应力-挠度曲线的形状,我们可以判断材料的强度和韧性。
对于强度较高的材料,其应力-挠度曲线会表现出较高的刚性,即挠度随应力的增加变化较小;而对于韧性较好的材料,其应力-挠度曲线会表现出较大的变形能力,即挠度随应力的增加变化较大。
结论:通过对弯曲正应力实验的进行,我们可以得到材料的弯曲性能数据,并通过分析这些数据来了解材料的力学性质。
实验结果可以为工程设计和材料选择提供参考依据,以确保材料的使用安全性和可靠性。
梁的纯弯曲正应力实验报告

梁的纯弯曲正应力实验报告梁的纯弯曲正应力实验报告一、实验目的本实验旨在通过对实验材料进行纯弯曲加载,测量其正应力和弯曲角度,从而掌握材料在纯弯曲状态下的应力特性,并探究材料性能的影响因素。
二、实验原理当梁在纯弯曲时,受到的载荷可以分解为一个弯矩和一个剪力。
由于实验中去除了外部作用力,剪力为零,因此我们只需要考虑弯矩作用下的应力情况。
在梁的截面上,由于受到弯曲,不同位置的应变不同,因此会形成不同大小的应力。
在正常情况下,当梁未发生破坏时,梁的内部应力呈线性分布,即受到的弯矩越大,所受到的应力也会相应增大。
三、实验设备本实验所使用的设备包括:1.纯弯曲实验台2.测力仪3.梁材料(一定长度的圆形钢管或方管)四、实验步骤1. 选择一段合适材质的梁进行实验。
2. 将梁固定在纯弯曲实验台上。
3. 在梁的一端加上一定荷载。
4. 通过测力仪测量在梁部位不同位置受到的正应力。
5. 在梁的另一端加上一定数量的荷载,并重复步骤4,记录正应力。
6. 重复以上操作,直到梁发生破坏。
五、实验结果在实验过程中,我们记录了梁不同位置受到的正应力,并根据实验数据分析了不同弯矩下的应力分布曲线。
实验结果表明,在纯弯曲状态下,梁的内部应力呈线性分布,随着弯矩的增大,所受应力也会逐渐增大,直到梁发生破坏。
六、实验分析根据实验结果,我们可以发现梁的性能会受到材料的影响。
不同的材料具有不同的弯曲特性,不同的性能和抗断性能。
而在实验中,我们也可以通过调整材料的材质和长度来控制弯曲的程度,从而控制梁的应力分布和破坏点位置。
七、实验结论本实验通过纯弯曲实验台对梁进行弯曲测试,得到了不同弯矩下的应力分布曲线。
实验结论表明,梁在纯弯曲状态下,其内部应力呈线性分布,随着弯矩的增大,所受应力也会逐渐增大,直到梁发生破坏。
同时,不同材质和长度的材料在弯曲状态下具有不同的弯曲特性和抗断性能。
纯弯曲梁的正应力实验参考书报告
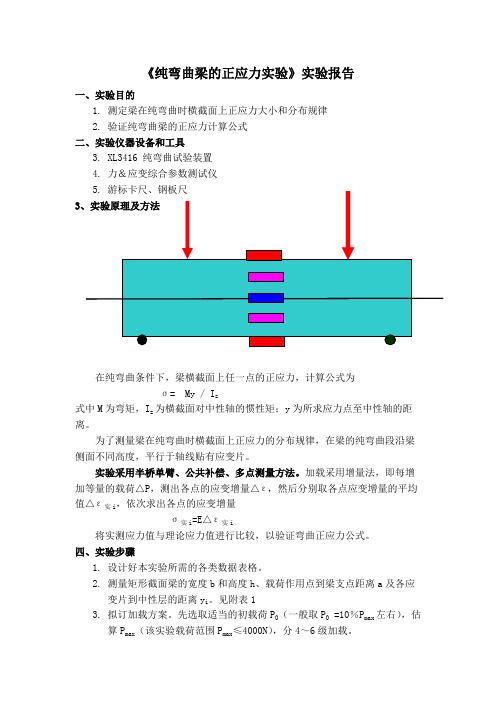
《纯弯曲梁的正应力实验》实验报告一、实验目的1.测定梁在纯弯曲时横截面上正应力大小和分布规律2.验证纯弯曲梁的正应力计算公式二、实验仪器设备和工具3.XL3416 纯弯曲试验装置4.力&应变综合参数测试仪5.游标卡尺、钢板尺3、实验原理及方法在纯弯曲条件下,梁横截面上任一点的正应力,计算公式为σ= My / I z式中M为弯矩,I z为横截面对中性轴的惯性矩;y为所求应力点至中性轴的距离。
为了测量梁在纯弯曲时横截面上正应力的分布规律,在梁的纯弯曲段沿梁侧面不同高度,平行于轴线贴有应变片。
实验采用半桥单臂、公共补偿、多点测量方法。
加载采用增量法,即每增加等量的载荷△P,测出各点的应变增量△ε,然后分别取各点应变增量的平均值△ε实i,依次求出各点的应变增量σ实i=E△ε实i将实测应力值与理论应力值进行比较,以验证弯曲正应力公式。
四、实验步骤1.设计好本实验所需的各类数据表格。
2.测量矩形截面梁的宽度b和高度h、载荷作用点到梁支点距离a及各应变片到中性层的距离y i。
见附表13.拟订加载方案。
先选取适当的初载荷P0(一般取P0 =10%P max左右),估算P max(该实验载荷范围P max≤4000N),分4~6级加载。
4.根据加载方案,调整好实验加载装置。
5. 按实验要求接好线,调整好仪器,检查整个测试系统是否处于正常工作状态。
6.加载。
均匀缓慢加载至初载荷P 0,记下各点应变的初始读数;然后分级等增量加载,每增加一级载荷,依次记录各点电阻应变片的应变值εi ,直到最终载荷。
实验至少重复两次。
见附表27.作完实验后,卸掉载荷,关闭电源,整理好所用仪器设备,清理实验现场,将所用仪器设备复原,实验资料交指导教师检查签字。
附表1 (试件相关数据)附表2 (实验数据)P 50010001500200025003000载荷N △P 500500500500500εP -33-66-99-133-166△εP -33-33-34-334平均值-33.25εP -16-33-50-67-83△εP -17-17-17-162平均值16.75εP 00000△εP 00001平均值0εP 1532476379△εP 171516163平均值16εP 326597130163△εP 33323333 各 测点电阻应变仪读数µε5平均值32.75五、实验结果处理1.实验值计算根据测得的各点应变值εi 求出应变增量平均值△εi ,代入胡克定律计算应变片至中性层距离(mm )梁的尺寸和有关参数Y 1-20宽 度 b = 20 mm Y 2-10高 度 h = 40 mm Y 30跨 度 L = 620mm (新700 mm )Y 410载荷距离 a = 150 mm Y 520弹性模量 E = 210 GPa ( 新206 GPa )泊 松 比 μ= 0.26惯性矩I z =bh 3/12=1.067×10-7m 4 =106667mm 4。
梁的纯弯曲正应力实验报告

梁的纯弯曲正应力实验报告一、实验目的。
本实验旨在通过对梁的纯弯曲正应力实验,了解梁在纯弯曲状态下的受力情况,掌握梁的弯曲应力分布规律,加深对梁的力学性能的理解。
二、实验原理。
梁是一种常见的结构构件,在工程中应用广泛。
梁在受外力作用下会发生弯曲变形,产生弯曲应力。
在纯弯曲状态下,梁上任意截面的应力都是正应力,弯矩对梁上任意一点的作用会引起该点产生正应力。
梁的弯曲应力分布规律受到梁的截面形状、材料性质以及外力大小和作用形式的影响。
三、实验装置与仪器。
本次实验所使用的实验装置包括,梁的支撑装置、加载装置、测力传感器、位移传感器、数据采集系统等。
测力传感器用于测量梁上各点的受力情况,位移传感器用于测量梁上各点的位移情况,数据采集系统用于采集并记录实验数据。
四、实验步骤。
1. 将梁放置在支撑装置上,并调整支撑装置,使梁处于自由悬臂梁状态。
2. 将加载装置作用在梁的中央位置,施加均匀分布的外力。
3. 通过测力传感器和位移传感器采集梁上各点的受力和位移数据。
4. 记录实验数据,并进行数据处理和分析。
五、实验数据处理与分析。
通过对实验数据的处理和分析,得到了梁在纯弯曲状态下的应力分布规律。
实验结果表明,在梁的中央位置受力最大,呈现出最大的正应力;而在梁的两端位置受力较小,呈现出较小的正应力。
梁的弯曲应力分布呈现出一定的规律性,符合理论预期。
六、实验结论。
通过本次实验,我们深入了解了梁在纯弯曲状态下的受力情况,掌握了梁的弯曲应力分布规律。
实验结果表明,在纯弯曲状态下,梁上任意截面的应力都是正应力,呈现出一定的规律性。
这对于工程结构设计和实际应用具有一定的指导意义。
七、实验心得。
通过本次实验,我们对梁的纯弯曲正应力有了更深入的了解,也增强了对力学知识的理解和应用能力。
在今后的学习和工作中,我们将继续努力,不断提高自己的实验技能和科研能力,为工程实践和科学研究做出更大的贡献。
八、参考文献。
1. 钱七虎. 结构力学实验教程[M]. 北京,中国建筑工业出版社,2008.2. 吴光辉. 结构力学[M]. 北京,高等教育出版社,2011.以上为本次梁的纯弯曲正应力实验报告的全部内容。
实验五 弯曲正应力实验报告

实验五弯曲正应力实验报告___________系____________专业__________班姓名____________ 学号_________ 1.实验目的:(1)测定梁在纯弯曲下的弯曲正应力大小及其分布规律。
(2)验证弯曲正应力计算公式。
(3)掌握电测方法。
2.实验设备:3.实验记录及计算结果:a.梁的已知数据试件材料:A3 钢弹性模量: E= GPa电阻片灵敏系数: K=试件尺寸电阻片到中性层的距离(mm)b = mm Y1= mmh = mm Y2= mmL = mm Y3= mma = mm Y4= mmI z= mm4Y5= mmb.实验记录:c.计 算:实验值计算:根据测得的应变增量平均值Δε平均,应用虎克定律算出各点对应的应力增量:平均实i i εσ∆•E =∆ (i=1,2,3,4,5)理论值计算:zii I y •∆M =∆理σ (i=1,2,3,4,5) 式中 : 123bh I z = ——惯性矩a 2∆P=∆M ——弯矩增量 y i ——各测点到中性层的距离d.正应力实验结果与理论计算值比较: 各测点正应力值(MPa )测点 1 2 3 4 5 实验值σ∆实 理论值σ∆理误差%100⨯∆∆-∆=理实理σσσe.按比例绘出(实测应力和理论计算应力)正应力分布图。
4.问题讨论:1)说明梁在纯弯曲时正应力沿梁高度的分布规律。
2)比较各测点的实测应力值与理论计算应力值,并分析产生误差的原因。
指导教师:________________________年_______月______日。
梁的弯曲正应力实验报告

一、实验目的1. 通过实验,了解梁在弯曲状态下的应力分布规律;2. 验证梁的弯曲正应力计算公式的准确性;3. 掌握应变电测法的基本原理和操作方法;4. 培养学生严谨的实验态度和科学的研究方法。
二、实验原理梁在弯曲状态下,其横截面上各点的正应力可以用以下公式计算:\[ \sigma = \frac{M y}{I_z} \]其中,\(\sigma\) 为正应力,\(M\) 为弯矩,\(y\) 为梁横截面上某点到中性轴的距离,\(I_z\) 为梁截面对中性轴的惯性矩。
实验中,通过测量梁横截面上不同位置的应变,根据虎克定律,可计算出相应位置的应力。
实验装置主要包括梁、应变片、静态数字电阻应变仪等。
三、实验仪器与设备1. 梁材料:矩形截面试件,尺寸为 \(b \times h\);2. 应变片:电阻应变片,用于测量梁横截面上的应变;3. 静态数字电阻应变仪:用于测量应变片输出的电阻变化,从而计算出应变;4. 加载装置:用于对梁施加弯矩;5. 游标卡尺:用于测量梁的尺寸;6. 计算器:用于计算实验数据。
四、实验步骤1. 准备实验装置,包括梁、应变片、应变仪等;2. 将应变片粘贴在梁的预定位置,确保应变片与梁表面紧密贴合;3. 接通应变仪电源,调整应变仪的量程和灵敏度;4. 使用游标卡尺测量梁的尺寸,记录数据;5. 在梁上施加预定的弯矩,确保梁处于弯曲状态;6. 使用应变仪测量梁横截面上不同位置的应变,记录数据;7. 根据实验数据和应变片的位置,计算出梁横截面上不同位置的应力;8. 比较实验测得的应力与理论计算值,分析误差原因。
五、实验结果与分析1. 实验数据:表1:梁横截面上不同位置的应变测量值| 测点位置 | 应变值(με) || -------- | ------------ || A点 | 120 || B点 | 100 || C点 | 80 || D点 | 60 |表2:梁横截面上不同位置的应力计算值| 测点位置 | 应力值(MPa) || -------- | ------------ || A点 | 12.00 || B点 | 10.00 || C点 | 8.00 || D点 | 6.00 |2. 结果分析:通过实验数据与理论计算值的比较,可以看出,在梁的弯曲状态下,应力在梁横截面上呈线性分布。
纯弯曲梁正应力分布规律实验报告

纯弯曲梁正应力分布规律实验报告纯弯曲正应力分布规律实验纯弯曲正应力分布规律实验一、实验目的1、用电测法测定梁纯弯曲时沿其横截面高度的正应变(正应力)分布规律;2、验证纯弯曲梁的正应力计算公式。
二、实验仪器和设备1、多功能组合实验装置一台;2、TS3860型静态数字应变仪一台;3、纯弯曲实验梁一根。
4、温度补偿块一块。
三、实验原理和方法弯曲梁的材料为钢,其弹性模量E=210GPa,泊松比μ=0.28。
用手转动实验装置上面的加力手轮,使四点弯上压头压住实验梁,则梁的中间段承受纯弯曲。
根据平面假设和纵向纤维间无挤压的假设,可得到纯弯曲正应力计算公式为:My Ix为了测量梁纯弯曲时横截面上应变分布规律,在梁纯弯曲段的侧面各点沿轴线方向布置了5片应变片(其中:b=15 mm,h=25 mm,C=124mm,梁长372mm),各应变片的分布为:1#在二分之一h处,2#、3#在上下对称于1#的四分之一h处,4#、5#在弯曲梁的上下表面。
如果测得纯弯曲梁在纯弯曲时沿横截面高度各点的轴向应变,则由单向应力状态的虎克定律公式??E?,可求出各点处的应力实验值。
将应力实验值与应力理论值进行比较,以验证弯曲正应力公式。
四、实验步骤1、对齐弯曲梁的下支座白色记号。
2、将力值调零,实验中取P0=100N,ΔP=350N,Pmax=1500N,分四次加载,在P0处将应变仪调零,实验时逐级加载,并记录各应变片在各级载荷作用下的读数应变。
3、每个测点求出应变增量的平均值??m?4i(m=1,2,···,5),算出相应的应力增量实测值??m测?E??m (MPa)。
其中,E取2.1?105MPa。
4、纯弯曲段(CD段)内的弯矩增量为:?M?bh3Iz?12。
求出各测点的理论值,式中1?MPc,由公式??m理?y 2Iz5、对每个测点列表比较??m测和??m理,并计算相对误差m测m理m理100%在梁的中性层(第1点),因??1理?0,故只需计算绝对误差。
纯弯曲梁正应力测定 工程力学实验报告

纯弯曲梁正应力测定一、 实验目的1.测定梁在纯弯曲时横截面上的正应力分布,验证平面假设理论和弯曲正应力公式。
2.学习电测应力实验方法。
二、 实验设备1.简支梁及加载装置。
2.电阻应变仪。
3.直尺,游标卡尺。
三、 实验原理根据弯曲梁的平面假设沿着梁横截面高度的正应力分布规律应当是直线。
为了验证这一假设,我们在梁的纯弯曲段内粘贴7片电阻应变片:1#、2#、3#、4#、5#、6#、7#,见指导书中图,由应变仪测出读数即知道沿着梁横面高度的正应力分布规律。
四、 实验步骤1.用游标卡尺测量梁的尺寸b 和h ,用钢尺量梁的支点至力作用点的距离d 。
2.将各点的应变片和温度补偿片以半桥的形式接入应变仪。
被测应变片接在AB 上,补偿片接在BC 上。
仪器操作步骤:1)半桥测量时将D 1DD 2接线柱用连接片连接起来并旋紧。
2)将标准电阻分别与A 、B 、C 接线柱相连。
3)接通电源开关。
4)按下“基零”键仪表显示“0000”或“-0000”(仪表内部已调好)。
5)按下“测量”键,显示测量值,将测量值调到“0000”或“-0000”。
6)按下“标定”键仪表显示-10000附近值,按照所使用应变片灵敏度K=2.17,调节灵敏度使显示为-9221。
7)将“本机、切换”开关置“切换”状态。
主机的 A 、B 、C 接线柱上的标准电阻去掉,将各被测量应变片一端分别与左上对应的各A (A 1~A 7)接线柱相连,公共输出端与一B 接线柱相连,温度补偿片接在B 、C 之间。
被测点(应变片号) 6 4 2 1 3 5 7 接线端子(通道号) 1 2 3 4 5 6 78)切换开关, 按次序所有点的平衡都调节在0000或-0000值上。
9)转动手轮,使梁加载荷,逐点测量、记录应变值。
采用增量法加载,每次0.5kN 。
注意不能超载。
0.5 kN , 初载荷调零; 1.0 kN , 1.5 kN ,2.0 kN ,2.5 kN ,读出应变值10)实验结束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梁的弯曲正应力实验报告总结
梁的弯曲正应力实验是力学实验中的一项重要实验,通过该实验可以了解梁的弯曲变形规律和弯曲正应力的计算方法。
本文将对梁的弯曲正应力实验进行总结。
一、实验原理
梁的弯曲正应力实验是通过在梁上施加一定的弯曲力,使梁发生弯曲变形,然后通过测量梁的变形量和力的大小,计算出梁的弯曲正应力。
梁的弯曲正应力可以用公式σ=M*y/I来计算,其中M为弯矩,y为梁上某一点到中性轴的距离,I为梁的截面惯性矩。
二、实验步骤
1. 准备工作:将实验室内的环境调整到稳定状态,准备好实验所需的仪器和材料。
2. 实验装置:将梁放置在实验台上,将弯曲力施加在梁的一端,另一端固定在实验台上。
3. 测量变形量:通过测量梁的变形量,确定梁上某一点到中性轴的距离y。
4. 测量力的大小:通过测量施加在梁上的力的大小,确定弯矩M。
5. 计算弯曲正应力:根据公式σ=M*y/I,计算出梁的弯曲正应力。
三、实验结果
通过实验,我们得到了梁的弯曲正应力的计算结果。
在实验中,我们可以通过改变施加在梁上的力的大小和位置,来观察梁的弯曲变形规律和弯曲正应力的变化情况。
实验结果表明,梁的弯曲正应力与施加在梁上的力成正比,与梁的截面惯性矩成反比。
四、实验分析
通过梁的弯曲正应力实验,我们可以了解到梁的弯曲变形规律和弯曲正应力的计算方法。
在实际工程中,梁的弯曲正应力是一个非常重要的参数,它可以用来评估梁的强度和稳定性。
因此,对于工程师和设计师来说,了解梁的弯曲正应力的计算方法是非常必要的。
五、实验结论
通过本次梁的弯曲正应力实验,我们得到了梁的弯曲正应力的计算结果。
实验结果表明,梁的弯曲正应力与施加在梁上的力成正比,与梁的截面惯性矩成反比。
因此,在实际工程中,我们需要根据梁的实际情况来选择合适的材料和截面形状,以保证梁的强度和稳定性。
梁的弯曲正应力实验是力学实验中的一项重要实验,通过该实验可
以了解梁的弯曲变形规律和弯曲正应力的计算方法。
在实际工程中,了解梁的弯曲正应力的计算方法是非常必要的,可以帮助我们评估梁的强度和稳定性,从而保证工程的安全和可靠性。
