2014中考总复习第15讲函数与方程、不等式
2014年中考备考一轮复习导学案第15章二次函数及其应用
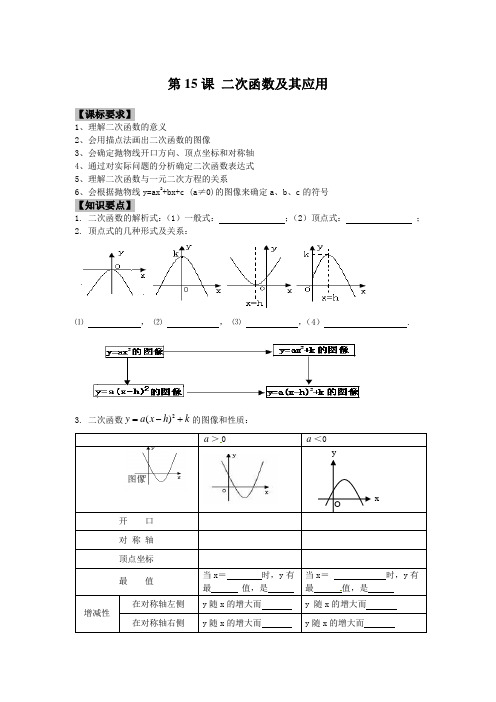
第15课 二次函数及其应用【课标要求】1、理解二次函数的意义2、会用描点法画出二次函数的图像3、会确定抛物线开口方向、顶点坐标和对称轴4、通过对实际问题的分析确定二次函数表达式5、理解二次函数与一元二次方程的关系6、会根据抛物线y=ax 2+bx+c (a ≠0)的图像来确定a 、b 、c 的符号【知识要点】1. 二次函数的解析式:(1)一般式: ;(2)顶点式: ;2. 顶点式的几种形式及关系:⑴ , ⑵ , ⑶ ,(4) .3. 二次函数2()y a x h k =-+的图像和性质:0 图像开 口 值,是4.二次函数c bx ax y ++=2通过配方可得224()24b ac b y a x a a-=++,其抛物线关于直线x = 对称,顶点坐标为( , ).⑴ 当0a >时,抛物线开口向 ,有最 (填“高”或“低”)点, 当x = 时,y 有最 (“大”或“小”)值是 ;⑵ 当0a <时,抛物线开口向 ,有最 (填“高”或“低”)点, 当x = 时,y 有最 (“大”或“小”)值是 .第一课时【典型例题】【例1】.抛物线y =2x 2-4x +5的开口方向______,顶点坐标是__________,对称轴方程是直线x =___,当x = 时,y 有最 值是 。
【例2】.二次函数 322++=x x y ,当x <-1时,y 随x 的增大而 。
【例3】抛物线y =x 2-4x +3与y 轴的交点坐标是 ,与x 轴的交点坐标是 。
当y=8时x 对应的值是 。
【例4】抛物线243y x x =-+向右平移2个单位所得抛物线的顶点坐标为( ) A 、(4,-1) B 、(0,-3) C 、(-2,-3) D 、(-2,-1)【例5】已知二次函数c bx ax y ++=2的图象如图所示,则在“①a <0,②b >0,③c < 0,④b 2-4ac >0”中,正确的判断是( )A 、①②③④B 、④C 、①②③D 、①④ 【例6一条抛物线顶点是(1,2)且经过点(-2,-4),则它的函数解析式是 ;另一抛物线经过(0,1)、(1,0)和(2,4)三点,则它的函数解析式是 。
2014年中考复习数学新课标(BS)最新复习方案---第2单元(方程与不等式)

第6课时 第7课时 第8课时
一次方程(组)及其应用 一元二次方程及其应用 分式方程及其应用
第9课时 一元一次不等式(组)及其应用
第6课时 一次方程(组)及 其应用
第6讲┃一次方程(组)及其应用
考 点 聚 焦
考点1 等式的概念与等式的性质
等式的概念
相等 表示________关系的式子,叫做等式
性 等式两边加(或减)同一个数或同一个整式 质 所得的结果仍相等.如果 a=b,那么 a±c 1 =b±c 等式的 等式两边都乘(或除以)同一个数(除数不 性质 性 为 0)所得的结果仍是等式.如果 a=b,那 质 a b 2 么 ac=bc, = (c≠0) c c
第6讲┃一次方程(组)及其应用
考点3 一元一次方程的解法 一 一元一次方程的定义:只含有________个未知数,且未知 1 数的最高次数是________次的整式方程,叫做一元一次方程. ax+b=0(a≠0) 一元一次方程的一般形式______________. 解一元一次方程的一般步骤: (1)去分母: 在方程两边都乘各分母的最小公倍数, 注意别 漏乘. (2)去括号:注意括号前的系数与符号. (3)移项: 把含有未知数的项移到方程的一边, 其他项移到 另一边,注意移项要改变符号. (4)合并同类项:把方程化成 ax=b(a≠0)的形式.
图6-1
考点聚焦 归类探究 回归教材 中考预测
第6讲┃一次方程(组)及其应用
考点聚焦
归类探究
回归教材
中考预测
第6讲┃一次方程(组)及其应用
探究二 一元一次方程的解法
命题角度: 1.一元一次方程及其解的概念; 2.解一元一次方程的一般步骤.
0.3x+0.5 2x-1 = 的过 例2 [2011· 滨州] 依据下列解方程 0.2 3 程,请在前面的括号内填写变形步骤,在后面的括号 内填写变形依据.
2014届高考人教A版数学(理)一轮复习讲义15不等式选讲

选修4-5 不等式选讲考点梳理1.绝对值不等式的解法(1)含绝对值的不等式|x |<a 与|x |>a 的解法(2)|①|ax +b |≤c ⇔-c ≤ax +b ≤c ; ②|ax +b |≥c ⇔ax +b ≥c 或ax +b ≤-c .(3)|x -a |+|x -b |≥c (c >0)和|x -a |+|x -b |≤c (c >0)型不等式的解法 法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想; 法二:利用“零点分段法”求解,体现了分类讨论的思想;法三:通过构造函数,利用函数的图象求解,体现了函数与方程的思想. 2.绝对值的三角不等式(1)定理1:若a ,b 是实数,则|a +b |≤|a |+|b |,当且仅当ab ≥0时,等号成立. (2)定理2:设a ,b ,c 是实数,则|a -c |≤|a -b |+|b -c |,当且仅当(a -b )(b -c )≥0时,等号成立. 推论1:||a |-|b ||≤|a +b |. 推论2:||a |-|b ||≤|a -b |.考点自测1.不等式|x -8|-|x -4|>2的解集为________.解析令:f (x )=|x -8|-|x -4|=⎩⎨⎧4,x ≤4,-2x +12,4<x ≤8,-4,x >8,当x ≤4时,f (x )=4>2;当4<x ≤8时,f (x )=-2x +12>2,得x <5, ∴4<x <5;当x >8时,f (x )=-4>2不成立. 故原不等式的解集为:{x |x <5}. 答案 {x |x <5}2.(2012·湖南)不等式|2x +1|-2|x -1|>0的解集为________.解析 可根据绝对值不等式的性质进行变换,化绝对值不等式为一元一次不等式求解.原不等式即|2x +1|>2|x -1|,两端平方后解得12x >3,即x >14.答案 ⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x >143.已知关于x 的不等式|x -1|+|x |≤k 无解,则实数k 的取值范围是________. 解析 ∵|x -1|+|x |≥|x -1-x |=1,∴当k <1时,不等式|x -1|+|x |≤k 无解,故k <1. 答案 (-∞,1)4.若不等式|3x -b |<4的解集中的整数有且仅有1,2,3,则b 的取值范围为________.解析 由|3x -b |<4,得b -43<x <b +43, 即⎩⎪⎨⎪⎧0≤b -43<1,3<b +43≤4,解得5<b <7.答案 (5,7)5.(2012·陕西)若存在实数x 使|x -a |+|x -1|≤3成立,则实数a 的取值范围是________.解析 ∵|x -a |+|x -1|≥|(x -a )-(x -1)|=|a -1|, 要使|x -a |+|x -1|≤3有解,可使|a -1|≤3,∴-3≤a -1≤3,∴-2≤a ≤4. 答案 [-2,4]对应学生213考向一 含绝对值不等式的解法【例1】►设函数f (x )=|2x +1|-|x -4|. (1)解不等式f (x )>2; (2)求函数y =f (x )的最小值.解 (1)f (x )=|2x +1|-|x -4|=⎩⎪⎨⎪⎧-x -5 ⎝ ⎛⎭⎪⎫x <-12,3x -3 ⎝ ⎛⎭⎪⎫-12≤x <4,x +5 (x ≥4).当x <-12时,由f (x )=-x -5>2得,x <-7.∴x <-7;当-12≤x <4时,由f (x )=3x -3>2,得x >53, ∴53<x <4;当x ≥4时,由f (x )=x +5>2,得x >-3,∴x ≥4.故原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x <-7或x >53. (2)画出f (x )的图象如图:∴f (x )min =-92.(1)用零点分段法解绝对值不等式的步骤:①求零点;②划区间、去绝对值号;③分别解去掉绝对值的不等式;④取每个结果的并集,注意在分段时不要遗漏区间的端点值.(2)用图象法,数形结合可以求解含有绝对值的不等式,使得代数问题几何化,即通俗易懂,又简洁直观,是一种较好的方法.【训练1】 (2012·新课标全国)已知函数f (x )=|x +a |+|x -2|. (1)当a =-3时,求不等式f (x )≥3的解集;(2)若f (x )≤|x -4|的解集包含[1,2],求a 的取值范围.解(1)当a =-3时,f (x )=⎩⎨⎧-2x +5,x ≤2,1,2<x <3,2x -5,x ≥3.当x ≤2时,由f (x )≥3得-2x +5≥3,解得x ≤1; 当2<x <3时,f (x )≥3无解;当x ≥3时,由f (x )≥3得2x -5≥3,解得x ≥4. 所以f (x )≥3的解集为{x |x ≤1}∪{x |x ≥4}. (2)f (x )≤|x -4|⇔|x -4|-|x -2|≥|x +a |.当x ∈[1,2]时,|x -4|-|x -2|≥|x +a |⇔4-x -(2-x )≥|x +a |⇔-2-a ≤x ≤2-a .由条件得-2-a ≤1且2-a ≥2,即-3≤a ≤0. 故满足条件的a 的取值范围是[-3,0].考向二 绝对值不等式的证明【例2】►已知函数f (x )=ax 2+x -a (-1≤x ≤1),且|a |≤1,求证:|f (x )|≤54. 证明 ∵-1≤x ≤1,∴|x |≤1. 又∵|a |≤1,∴|f (x )|=|a (x 2-1)+x |≤|a (x 2-1)|+|x | ≤|x 2-1|+|x |=1-|x |2+|x | =-⎝ ⎛⎭⎪⎫|x |-122+54≤54. 证明绝对值不等式主要有三种方法:(1)利用绝对值的定义脱去绝对值符号,转化为普通不等式再证明;(2)利用三角不等式||a |-|b ||≤|a ±b |≤|a |+|b |进行证明;(3)转化为函数问题,数形结合进行证明.【训练2】 设函数f (x )=x 2-2x ,实数a 满足|x -a |<1. 求证:|f (x )-f (a )|<2|a |+3.证明 |f (x )-f (a )|=|x 2-a 2+2(a -x )| =|(x -a )(x +a )+2(a -x )| =|x -a ||x +a -2|<|x +a -2|=|x -a +2a -2|<|x -a |+2|a |+2<2|a |+3.考向三 含绝对值的恒成立问题【例3】►已知函数f (x )=|x -a |.(1)若不等式f (x )≤3的解集为{x |-1≤x ≤5},求实数a 的值;(2)在(1)的条件下,若f (x )+f (x +5)≥m 对一切实数x 恒成立,求实数m 的取值范围.解 法一 (1)由f (x )≤3得|x -a |≤3, 解得a -3≤x ≤a +3.又已知不等式f (x )≤3的解集为{x |-1≤x ≤5}, 所以⎩⎨⎧a -3=-1,a +3=5,解得a =2.(2)当a =2时,f (x )=|x -2|. 设g (x )=f (x )+f (x +5),于是g (x )=|x -2|+|x +3|=⎩⎨⎧-2x -1,x <-3;5,-3≤x ≤2;2x +1,x >2.所以当x <-3时,g (x )>5; 当-3≤x ≤2时,g (x )=5; 当x >2时,g (x )>5.综上可得,g (x )的最小值为5.从而,若f (x )+f (x +5)≥m 即g (x )≥m 对一切实数x 恒成立,则m 的取值范围是(-∞,5]. 法二 (1)同法一.(2)当a =2时,f (x )=|x -2|.设g (x )=f (x )+f (x +5).由|x -2|+|x +3|≥|(x -2)-(x +3)|=5(当且仅当-3≤x ≤2时等号成立)得,g (x )的最小值为5.从而,若f (x )+f (x +5)≥m 即g (x )≥m 对一切实数x 恒成立,则m 的取值范围是(-∞,5].(1)研究含有绝对值的函数问题时,根据绝对值的定义,分类讨论去掉绝对值符号,转化为分段函数,然后利用数形结合解决,是常用的思想方法. (2)f (x )<a 恒成立⇔f (x )max <a ;f (x )>a 恒成立⇔f (x )min >a .【训练3】 (2012·辽宁)已知f (x )=|ax +1|(a ∈R ),不等式f (x )≤3的解集为{x |-2≤x ≤1}. (1)求a 的值;(2)若⎪⎪⎪⎪⎪⎪f (x )-2f ⎝ ⎛⎭⎪⎫x 2≤k 恒成立,求k 的取值范围.解 (1)由|ax +1|≤3得-4≤ax ≤2. 又f (x )≤3的解集为{x |-2≤x ≤1}, 所以当a ≤0时,不合题意. 当a >0时,-4a ≤x ≤2a ,得a =2.(2)记h (x )=f (x )-2f ⎝ ⎛⎭⎪⎫x 2,则h (x )=⎩⎪⎨⎪⎧1,x ≤-1,-4x -3,-1<x <-12,-1,x ≥-12,所以|h (x )|≤1,因此k ≥1. 故k 的取值范围是[1,+∞).(时间:30分钟 满分:60分)一、填空题(每小题5分,共40分) 1.不等式|2x -1|<3的解集为________.解析 ①当2x -1≥0,即x ≥12时,不等式变为2x -1<3,得x <2,∴12≤x <2.②当2x -1<0即x <12时,不等式变为-(2x -1)<3即x >-1,∴-1<x <12,综上不等式解集为{x |-1<x <2}. 答案 (-1,2)2.已知x >0,则函数y =x (1-x 2)的最大值为________.解析 ∵y =x (1-x 2),∴y 2=x 2(1-x 2)2=2x 2(1-x 2)(1-x 2)·12.∵2x 2+(1-x 2)+(1-x 2)=2,∴y 2≤12⎝⎛⎭⎪⎫2x 2+1-x 2+1-x 233=427. 当且仅当2x 2=1-x 2,即x =33时取等号. ∴y ≤239.∴y 的最大值为239. 答案2393.(2011·江西)对于x ∈R ,不等式|x +10|-|x -2|≥8的解集为________. 解析 法一 (零点分段法)由题意可知,⎩⎨⎧ x ≤-10,-x -10+x -2≥8或⎩⎨⎧ -10<x <2,x +10+x -2≥8或⎩⎨⎧x ≥2,x +10-x +2≥8, 解得x ≥0,故原不等式的解集为{x |x ≥0}.法二 (几何意义法)如图,在数轴上令点A 、B 的坐标分别为-10,2,在x 轴上任取一点P ,其坐标设为x ,则|P A |=|x +10|,|PB |=|x -2|,观察数轴可知,要使|P A |-|PB |≥8,则只需x ≥0.故原不等式的解集为{x |x ≥0}.答案 {x |x ≥0}4.(2011·陕西)若不等式|x +1|+|x -2|≥a 对任意x ∈R 恒成立,则a 的取值范围是________.解析 由于|x +1|+|x -2|≥|(x +1)-(x -2)|=3.所以只需a ≤3即可. 答案 (-∞,3]5.若不等式|x +1|+|x -3|≥a +4a 对任意的实数x 恒成立,则实数a 的取值范围是________.解析 当a <0时,显然成立;当a >0时,∵|x +1|+|x -3|的最小值为4, ∴a +4a ≤4.∴a =2.综上可知a 的取值范围是(-∞,0)∪{2}.答案 (-∞,0)∪{2}6.设x ,y ,z ∈R ,若x 2+y 2+z 2=4,则x -2y +2z 的最小值为________时,(x ,y ,z )=________.解析 ∵(x -2y +2z )2≤(x 2+y 2+z 2)[12+(-2)2+22]=4×9=36,∴x -2y +2z 最小值为-6,此时x 1=y -2=z2.又∵x 2+y 2+z 2=4,∴x =-23,y =43,z =-43. 答案 -6 ⎝ ⎛⎭⎪⎫-23,43,-437.若对任意x >0,xx 2+3x +1≤a 恒成立,则a 的取值范围是________.解析 ∵a ≥xx 2+3x +1=1x +1x +3对任意x >0恒成立,设u =x +1x +3, ∴只需a ≥1u 恒成立即可.∵x >0,∴u ≥5(当且仅当x =1时取等号). 由u ≥5,知0<1u ≤15,∴a ≥15.答案 ⎣⎢⎡⎭⎪⎫15,+∞8.已知h >0,a ,b ∈R ,命题甲:|a -b |<2h :命题乙:|a -1|<h 且|b -1|<h ,则甲是乙的________条件.解析 |a -b |=|a -1+1-b |≤|a -1|+|b -1|<2h ,故由乙能推出甲成立,但甲成立不能推出乙成立,所以甲是乙的必要不充分条件. 答案 必要不充分 二、解答题(共20分)9.(10分)对于任意实数a (a ≠0)和b ,不等式|a +b |+|a -2b |≥|a |(|x -1|+|x -2|)恒成立,试求实数x 的取值范围. 解 原不等式等价于|a +b |+|a -2b ||a |≥|x -1|+|x -2|,设ba =t ,则原不等式变为|t +1|+|2t -1|≥|x -1|+|x -2|对任意t 恒成立.因为|t +1|+|2t -1|=⎩⎪⎨⎪⎧3t ,t ≥12,-t +2,-1<t <12,-3t ,t ≤-1,在t =12时取到最小值为32.所以有32≥|x -1|+|x -2|=⎩⎨⎧2x -3,x ≥2,1,1<x <2,3-2x ,x ≤1,解得x ∈⎣⎢⎡⎦⎥⎤34,94.10.(10分)(2012·福建)已知函数f (x )=m -|x -2|,m ∈R ,且f (x +2)≥0的解集为[-1,1]. (1)求m 的值;(2)若a ,b ,c ∈R +,且1a +12b +13c =m ,求证:a +2b +3c ≥9. 解 (1)因为f (x +2)=m -|x |,所以f (x +2)≥0等价于|x |≤m , 学.科.网Z.X.X.K] 由|x |≤m 有解,得m ≥0,且其解集为{x |-m ≤x ≤m }. 又f (x +2)≥0的解集为[-1,1],故m =1.(2)由(1)知1a +12b +13c =1,又a ,b ,c ∈R +,由柯西不等式得 a +2b +3c =(a +2b +3c )⎝ ⎛⎭⎪⎫1a +12b +13c≥⎝⎛⎭⎪⎫a ·1a +2b ·12b +3c ·13c 2=9.。
2014年中考数学方程与不等式总复习(4)全面版

1
4.只含有一个未知数,并且未知数的次数是__1__, 系数_不__等__于__0__的不等式,叫做一元一次不等式.
5.关于_同__一__未__知__数___的几个一元一次不等式合在一 起,就组成一个一元一次不等式组。
((23))若90绿%化x+村9道5的%总(1费00用0-不超x)过=39120500.元解,得则最x=多5可0购0(买棵B种)树,
苗则多购少买棵B?种树苗500棵.
(y=3)35(02品00项0种+-目51)x0单+x=价(33(00+元005/0棵)(()10元00)成-.活x率)≤3植10树0费0,(解元得/棵x)≥400.
数学电子教案
专题8:一次不等式(组)
考点
课标要求
不等式 基本性 质及其 解的概
念
1.了解不等式的意义; 2.探索不等式的基本性质; 3.理解一元一次不等式(组)及 其解的有关概念.
1.熟练解一元一次不等式及一元
一元一 次不等 式(组) 的解法
一次不等式组; 2.会求某些一元一次不等式及一 元一次不等式组的特殊解(如正整 数解); 3.会一元一次不等式的应用(考查频率:★★☆☆☆) 命题方向:(1)列一元一次不等式解决获利最大和获利最小问 题;(2)其它用不等式解决为应用问题.
8解.:((201)13湖设北商十场堰应)购某 进商A型场台计灯划x购盏进,A则,BB型两台种灯新为型(节10能0-台x灯)共
1盏00,盏根,据这题两意种得台,灯3的0x+进5价0(、10售0-价x如)=下3表50所0,示解:得x=75,所以100
(完整)中考数学方程与不等式知识结构图

方程(组)与不等式(组) 知识结构表 方程: 含有未知数的等式叫做方程.有关概念 方程的解:能使方程两边的值相等的未知数的值,叫做方程的解.解方程: 求方程的解的过程叫做解方程.定义: 只含有一个未知数,且未知数的次数是1的整式方程叫做一元一次方程。
(1) 一元一次方程 解法: 去分母、去括号、移项、合并同类项、系数化为1.定义: 含有两个未知数,且未知项的次数都是1的整式方程,叫做二元一次方程.由这样的几个方(2) 二元一次方程(组) 程所组成的方程组叫做二元一次方程组.方程组里各个方程的公共解叫做这个方程组的解.分类 解法: 基本思想是消元,基本方法是代入消元法、加减消元法.方程(组) 定义:只含有一个未知数,且未知数的最高次数是2的整式方程叫做一元二次方程.它的一般形式为02=++c bx ax (0≠a )。
(3)一元二次方程 解法; 直接开平方法、配方法、因式分解法、求根公式法.根的判别式(ac b 42-=∆):当0>∆时,一元二次方程有两个不相等的实数根;当0=∆时,一元二次方程有两个相等的实数根;当0<∆时,一元二次方程没有实数根.以上结论,反之亦成立.方 定义:分母中含有未知数的方程叫做分式方程.程 (4)分式方程 解法:其基本思想是将分式方程转化为整式方程,其方法是运用等式性质在方程两边同乘以最简公分母.解与 分式方程必须要验根.有时也可采用换元法.不 应用: 一般步骤:①审清题意,找出等量关系;②设未知数;③列出方程(组);④解方程(组);⑤检验方程(组)的根;⑥作答.等式 不等式:用不等号表示不等关系的式子叫做不等式.不等式的解: 使不等式成立的未知数的值叫做不等式的解.有关概念不等式的解集:一个不等式的所有解,组成这个不等式的解的集合,简称为这个不等式的解集.解不等式:求不等式的解集的过程,叫做解不等式.性质1:如果a>b,那么a+c>b+c,a-c>b-c.不等式的性质性质2:如果a>b,并且c>0,那么ac>bc.性质3:如果a>b,并且c<0,那么ac<bc.定义: 只含有一个未知数,且未知数的最高次数是1的不等式.不等式(组) 一元一次不等式解法:基本步骤是:去分母、去括号、移项、合并同类项、系数化为1.特别要注意当系数化为1时,不等式两边同乘以(或除以)同一个负数,不等号的方向必须改变.分类定义:几个未知数相同的一元一次不等式所组成的不等式组叫做一元一次不等式组.一元一次不等式组解法:求出不等式组中每一个不等式的解集,再求出解集的公共部分.解集有如下规律: 同大取大;同小取小;大小小大取中间;大大小小题无解.应用: 解不等式(组)在实际问题中的应用,关键是使学生能从实际问题中抽象出数量关系,列出不等式(组),建立不等式模型,通过转化为纯数学问题来解决实际应用问题.在列不等式时还要密切关注题中的不等关系,如“至少”,“至多”,“不大于”,“不小于"等等.。
2014届中考总复习——一元一次不等式(组)及其应用

知识点一、不等式的基本概念1、不等式:用连接起来的式子叫做不等式2、不等式的解:使不等式成立的值,叫做不等式的解3、不等式的解集:一个含有未知数的不等的解的叫做不等式的解集【谈重点】1、常用的不等号有等2、不等式的解与解集是不同的两个概念,不等式的解是单独的未知数的值,而解集是一个范围的未知数的值组成的集合,一般由无数个解组成3、不等式的解集一般可以在数轴上表示出来。
注意“>”“<”在数轴上表示为,而“≥”“≤”在数轴上表示为。
知识点二、不等式的基本性质基本性质1:不等式两边都加上(或减去)同一个或同一个不等号的方向,即:若a<b,则a+c b+c(或a-c b-c)基本性质2:不等式两边都乘以(或除以)同一个不等号的方向,即:若a<b,c>0则a c b c(或acbc)基本性质3:不等式两边都乘以(或除以)同一个不等号的方向,即:若a<b ,c <0则a c b c(或acbc)知识点三、一元一次不等式及其解法2014年中考总复习一元一次不等式(组)1、定义:只含有一个未知数,并且未知数的次数是 且系数 的不等式叫一元一次不等式,其一般形式为 或 。
2、一元一次不等式的解法步骤和一元一次方程的解法相同,即包含 、 、 、 、 五个步骤。
知识点四、一元一次不等式组及其解法1、定义:把几个含有相同未知数的 合起来,就组成了一个一元一次不等式组2、解集:几个不等式解集的 叫做由它们所组成的不等式组的解集3、解法步骤:先求出不等式组中各个不等式的 再求出他们的 部分,就得到不等式组的解集4、一元一次不等式组解集的四种情况(a<b )1、 2、3、4、【谈重点】1、求不等式的解集,一般要体现在数轴上,这样不容易出错。
2、一元一次不等式组求解过程中往常出现求特殊解的问题,比如:整数解、非负数解等,这时要注意不要漏了解,特别当出现“≥”或“≤”时要注意两头的数值是否在取值的范围内。
全效学习(浙江专版)中考数学总复习第15课时一次函数的应用课件
解:(1)A 比 B 晚出发 1 h,B 的速度是630=20(km/h). 图15-6
第二十二页,共44页。
(2)由图知,A 的速度是39-01=45(km/h).设在 B 出发后 x h, 两人相遇,则 20x=45(x-1). 解得 x=1.8. 答:在 B 出发后 1.8 h,两人相遇.
第二十九页,共44页。
类型之三 方案选择 [2015·广安]为了贯彻落实市委市政府提出的“精准扶贫”
精神.某校特制定了一系列关于帮扶A,B两贫困村的计 划.现决定从某地运送152箱鱼苗到A,B两村养殖,若用大小 货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小 货车的载货能力(nénglì)分别为12箱/辆和8箱/辆,其运往A,B 两村的运费如下表 [2015·德州]某商店以40元/千克的单价(dānjià)新进一批茶叶,经
调查发现,在一段时间内,销售量y(kg)与销售单价(dānjià)x(元/千克) 之间的函数关系如图15-3所示. (1)根据图象求y与x的函数关系式; (2)商店想在销售成本不超过3 000元的情况下,使销售利润达到2 400 元,销售单价(dānjià)应定为多少?
车型
目的地
大货车
小货车
A村(元/辆)
800 400
B村(元/辆)
900 600
第三十页,共44页。
(1)求这15辆车中大小(dàxiǎo)货车各多少辆? (2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A 村的大货车为x辆,前往A,B两村总费用为y元,试求出y与x 的函数解析式. (3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出 使总费用最少的货车调配方案,并求出最少费用.
2014届中考数学复习专题二 方程与不等式《2.1一元一次方程与二元一次方程(组)》课件
10、(09牡丹江)五一期间,百货大楼推出全 场打八折的优惠活动,持贵宾卡可在八折基 础上继续打折,小明妈妈持贵宾卡买了标价 为10000元的商品,共节省2800元,则用贵宾 卡又享受了
9 折优惠.
解:设用贵宾卡又享受了x折优惠, x 依题意得:10000-10000×80%× =2800 10 解之得:x=9 即用贵宾卡又享受了9折优惠.
专题二 方程与不等式
§2.1一元一次方程 与二元一次方程(组)
等式的基本性质: ①等式的两边同时加上(或减去)同一个 代数式,所的结果仍是等式.若a=b,则 a±m=b±m. ②等式的两边同时乘同一个数(或除以同一 不为0的数),所的结果仍是等式。 若a=b,则am=bm;或如果a=b,m ≠ 0,那 么a/c=b/c . 等式具有传递性,若a=b,b=c,则a=c.
14、(09达州) 将一种浓度为15℅的溶液 30㎏, 配制成浓度不低于20℅的同种溶液, 则至少需要浓度为35℅的该种溶液 ______㎏. 10 解:设35%溶液为x则得:
35%x+30×15%=(x+30)×20%
解得x=10kg,故至少需要35%的溶液
10kg.
相信你能行
步骤
去分 母
去括 号 移项
1)移动的项一定要变号, 不移的项不变号 2)注意移项较多时不要漏项
合并 同类 项 系数 化1
合并同类项 法则
1)把系数相加 2)字母和字母的指数不变
将方程两边都除以未知数系 数a,得解x=b/a
等式性 质2
解的分子,分母位置不要颠 倒
音乐能激发或抚慰情怀,绘画使人赏心悦目,诗 歌能动人心弦,哲学使人获得智慧,科学可改善 物质生活,但数学能给予以上的一切。--克莱因.
2014年中考专题复习不等式组
1、解不等式4(x ﹣1)+3≥3x ,并把解集在数轴上表示出来.2、解不等式组:;并把解集在数轴上表示出来.3、“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石. (1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.4、实数,,a b c 在数轴上对应的点如图所示,则下列式子中正确的是( ) A .a c b c ->- B . a c b c +<+ C .ac bc > D . a c b b<5、解不等式组23120x x +>⎧⎨-⎩?,并把解集在数轴上表示出来.6、一元一次不等式组的解集是 .7、解不等式:,并把解集表示在数轴上.8、设A 是由2×4个整数组成的2行4列的数表,如果某一行(或某一列)各数之和为负数,则改变该行(或该列)中所有数的符号,称为一次“操作”. (1) 数表A 如表1所示,如果经过两次“操作”, 使得到的数表每行的各数之和与每列的各数之和 均为非负整数,请写出每次“操作”后所得的数 表;(写出一种方法即可)(2)数表A 如表2所示,若经过任意..一次“操作”以后,便可使得到的数表每行的各数之和与每列的各数之和均为非负整数,求整数a 的值abc x()5第题图22221212a a a a a a a a ------表2表19、若a>b,则下列不等式变形错误..的是A.a+1 > b+1B. a2>b2C. 3a-4 > 3b-4 D.4-3a > 4-3b10、已知关于x、y的方程组的解满足不等式组,求满足条件的m的整数值。
11、已知x=3是关于x的不等式的解,求a的取值范围.12、设“▲”、“●”、“■”分别表示三种不同的物体,现用天平秤两次,情况如图所示,那么▲、●、■这三种物体按质量从大到小排列应为()A.■、●、▲ B.▲、■、● C.■、▲、● D.●、▲、■13、“低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具。
2014中考总复习 数与式、方程(组)不等式(组)
九年级第8讲 2014中考总复习 数与式、方程(组)不等式(组) 一、基础知识、期末考点分析:1、有理数,相反数,倒数,绝对值,数轴,无理数,实数及大小比较,实数的分类.2、平方根,算术平方根,立方根,乘方运算,开方运算,科学记数法,实数的运算.3、幂的运算,整式的运算,乘法公式,因式分解4、分式的概念,分式有意义、无意义、值为0的条件,分式的基本性质,分式的运算.5、二次根式的概念,二次根式的性质,最简二次根式,同类二次根式,二次根式的加、减、乘、除运算.6、一元一次方程的概念及解法,二元一次方程(组)及其解法,解方程组的基本思想.7、一元二次方程的概念及解法,根的判别式,根与系数的关系9、等式的性质,一元一次不等式(组)的解法及应用.能够根据具体问题中的数量关系,建立不等式(组)模型解决实际问题.10、分式方程的概念及解法,增根的概念,分式方程的应用. 11、一元一次方程、二元一次方程组、一元二次方程的应用. 二、经典例题例1、(2013•资阳)16的平方根是( ) A 、2 B 、±2 C 、4 D 、±4跟踪训练1:(2012•资阳)-(2-)的相反数是( ) A .2B .12-C .2-D .12跟踪训练2:(2011•资阳)-4的相反数是( )A. 4B. -4C. 14D. 14-跟踪训练3:(2010•资阳) -3的绝对值是( ) A. 3B. -3C. 13D. 13-跟踪训练4:(2010•资阳)9的平方根为____________.例2、(2013•资阳)(﹣a 2b )2•a= .跟踪训练1:(2012•成都七中)设n 为正整数,记n !=1×2×3×4×…….. ×n(n ≥2),1!=1,则!21+!32+!43+…….+!98+!109=( ) A.1-!101 B.1+!101 C.1-!91 D.1+!91例3、(2013•资阳)如图4( ) A. 点M B. 点N C. 点PD. 点Q图4例4、(2013•资阳)在函数y=中,自变量x 的取值范围是( )跟踪训练1:(2012•资阳)下列计算或化简正确的是( )A .235a a a += B =C 3=±D .1111x x -=-+-跟踪训练2:(2011•资阳)下列计算中,正确的是( )A. =B. =3= 3=-跟踪训练3:(2012•成都七中)计算:12014201320122011+⨯⨯⨯-20122=( ) A.2011 B.2012 C.2013 D.2014跟踪训练4:已知x 、y 为实数,且实数m 满足关系式m y x --+253+m y x -+32=y x +-1999·y x --1999,求m 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【答案】 5
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
7. (2011·江苏南京)已知函数 y= m x2- 6x+ 1( m 是常数) . ( 1) 求证: 不论 m 为何值, 该函数的图象都经过 y 轴上的一个定点; ( 2) 若该函数的图象与 x 轴只有一个交点, 求 m 的值. 【解析】 ( 1) 证明: ∵当 x= 0 时, y= 1. ∴不论 m 为何值, 函数 y= m x2- 6x+ 1 的图象都经过 y 轴上一个定点(0, 1); (2)①当 m = 0 时, 函数 y= - 6x+ 1 的图象与 x 轴只有一个交点; ②当 m ≠0 时, 若函数 y= m x2- 6x+ 1 的图象与 x 轴只有一个交点, 则方程 m x2- 6x+ 1= 0 有两个相等的实数根, ∴Δ= (- 6)2- 4m = 0, m = 9. 综上, 若函数 y= m x- 6x+ 1 的图象与 x 轴只有一个交点, 则 m 的值为 0 或 9.
3. (2013·龙岩质检)若一次函数 y= kx+ b( k, b 为常数, 且 k≠0) 的图象如图所示, 根据图象信息, 则关于 x 的不等式 kx+ b> 3 的解为 .
【答案】 x> 2.
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
4.(2012·黔西南)某工厂计划生产 A、B 两种产品共 10 件,其生 产成本和利润如下表: A 种产品 B 种产品 成本(万元/件) 2 5 利润(万元/件) 1 3 (1)若工厂计划获利 14 万元,问 A、 B 两种产品应分别生产多少件? (2)若工厂计划投入资金不多于 44 万元,且获利多于 14 万元,问 工厂有哪几种生产方案? (3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
【解析】 ( 1) 设生产 A 种产品 x 件, 则生产 B 种产品( 10- x) 件, 于是有 x+ 3( 10- x) = 14, 解得 x= 8, 则 10- x= 10- 8= 2( 件) ∴应生产 A 种产品 8 件, B 种产品 2 件. ( 2) 设应生产 A 种产品 x 件, 则生产 B 种产品( 10- x) 件, 由题意有:
k 2 解这个方程组, 得 b 8 .
6 ∴一次函数的解析式为 y1= - 2x+ 8, 反比例函数的解析式为 y2= x .
(2)1≤x≤3.
第一部分
复习目标
Байду номын сангаас
知识回顾
重点解析
探究拓展
真题演练
知识考点 0 2 一次函数与一元一次不等式
从函数值的角度看, 不等式 kx+ b> 0 的解集为使函数值大于零( 即 kx+ b> 0) 的 x 的取值范围; 从图象的角度看, 由于一次函数的图象在 x 轴上方 时, y> 0, 因此 kx+ b> 0 的解集为一次函数在 x 轴上方的图象所对应的 x 的取值 范围.
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
例2
k2 (2012·咸宁)如图, 直线 y= k1x+ b 与双曲线 y= x 交
于 A 、B 两点, 它们的横坐标分别为 1 和 5, 则不等式
k2 k1x< x - b 的解集是
.
【思路点拨】 根据不等式与直线和双曲线解析式的关系, 找出直线在双曲线 下方的自变量 x 的取值范围即可. 【自主解答】
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
一、一次函数与方程( 组) 、不等式 1. 解一元一次方程可以转化为: 当一次函数值为 自变量的值. 从图象上看, 这相当于已知直线 y= kx+ b, 确定它与 x 轴交点的 坐标. 2. 解一元一次不等式可以看作: 当一次函数值大于( 或小于) 0 时, 求 相应的取值范围. 时, 求相应的
k2 k2 由 k1x< x - b, 得, k1x+ b< x ,
当 0< x< 1 或 x> 5 时, 双曲线图象在直线图象上方,
k2 ∴不等式 k1x< x - b 的解集是 0< x< 1 或 x> 5.
故答案为: 0< x< 1 或 x > 5.
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
b , a
c x1•x2= a .
第一部分
复习目标
知识回顾
重点解析
探究拓展
2 2
真题演练
例3
(娄底中考)已知关于 x 的二次函数 y=x -(2m-1)x+m +3m+4.
探究 m 满足什么条件时,二次函数 y 的图象与 x 轴的交点的个数. 【思路点拨】 令 y=0,得到一个关于 x 的一元二次方程,讨论判 别式Δ 的大小,得到二次函数 y 的图象与 x 轴的交点的个数. 【自主解答】 令 y=0,得 x2-(2m-1)x+m2+3m+4=0, 2 2 Δ =(2m-1) -4(m +3m+4)=-16m-15. 当Δ >0 时,方程有两个不相等的实数根,
A 2 ( 3) 由已知可得, B 产品生产越多, 获利越大, ∴当 B 8 时可获得最大利润, 其最
大利润为 2×1+ 8×3= 26 万元.
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
5. (2011·湖北宜昌)某市实施“限塑令”后, 2008 年大约减少塑料消耗约 4 万 吨. 调查分析结果显示, 从 2008 年开始, 五年内该市因实施 “限塑令” 而减少的 塑料消耗量 y( 万吨) 随着时间 x( 年) 逐年成直线上升, y 与 x 之间的关系如图所 示.
15 即-16m-15>0,∴m<- 16 ,
此时,y 的图象与 x 轴有两个交点;
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
当Δ =0 时,方程有两个相等的实数根, 即-16m-15=0,∴m=- 16 , 此时,y 的图象与 x 轴只有一个交点; 当Δ <0 时,方程没有实数根, 即-16m-15<0,∴m>15 15 , 16 15
2 x 5(10 x) ≤ 44 ∴可以采用的方案有: x 3(10 x) >14 解得 2≤x< 8;
A 2 A 3 A 4 A 5 A 6 A 7 , , , , , 共 6 种方案; B 8 B 7 B 6 B 5 B 4 B 3
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
知识考点 0 3 二次函数与一元二次方程 1. 二次函数 y= ax2+ bx+ c( a≠0) , 当 y= 0 时, 就变成了 ax2+ bx+ c= 0( a ≠ 0) . 2. ax2+ bx+ c= 0( a≠0) 的解是抛物线与 x 轴交点的横坐标. 3. 当Δ= b2- 4ac> 0 时, 抛物线与 x 轴有两个不同的交点; 当Δ = b2- 4ac= 0 时, 抛物线与 x 轴有一个交点; 当Δ= b2- 4ac< 0 时, 抛物线与 x 轴 没有交点. 4 . 设抛物线 y= a x2+ bx+ c 与 x 轴两交点坐标分别为 A ( x1, 0 ) , B ( x2, 0 ) , 则 x1+ x2=
此时,y 的图象与 x 轴没有交点. ∴当 m<- 16 时,y 的图象与 x 轴有两个交点; 当 m=- 16 时,y 的图象与 x 轴只有一个交点; 当 m>- 16 时,y 的图象与 x 轴没有交点.
15 15
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
6. (2012·营口)二次函数 y= x2- 6x+ n 的部分图象如图所示, 若关于 x 的一元二 次方程 x2- 6x+ n= 0 的一个解为 x1= 1, 则另一个解 x2= .
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
【思路点拨】 (1)把 P (1, b)代入 y= x+ 1 可求出 b 的值.
y x 1 (2)点 P (1, b)的坐标就是方程组 y mx n 的解.
(3)由 P 点在直线 y= m x+ n 上, 代入验证可知点 P 是否在直线 y= nx+ m 上. 【自主解答】 (1) ∵P (1, b) 在直线 y= x+ 1 上, ∴当 x= 1 时, b= 1+ 1= 2.
( 1) 求 y 与 x 之间的关系式; ( 2) 请你估计, 该市 2011 年因实施“限塑令”而减少的塑料消耗量为多少?
第一部分
复习目标
知识回顾
重点解析
探究拓展
真题演练
【解析】 ( 1) 设 y= kx+ b. 由题意, 得
2008k b 4 2010k b 6 ,
解得 k= 1, b= - 2004, ∴y= x- 2004. ( 2) 当 x= 2011 时, y= 2011- 2004= 7. ∴该市 2011 年因“限塑令”而减少的塑料消耗量约为 7 万吨.
