【南方凤凰台】(江苏专用)高考数学大一轮复习 第九章 第42课 数列的综合应用要点导学
高考数学文(江苏)一轮练习:专题6 第42练 Word含解析

[基础保分练] 1.数列23,-45,67,-89,…的第5项是________.
2.在数列{an}中,an+1=an+2-an,a1=2,a2=5,则a5=________.
3.已知数列{an}满足an+1= 2an,0≤an<12,2an-1,12≤an<1,若a1=67,则a2 019的值为________. 4.设数列{an}的通项公式为an=1n+n+1,10-3是数列的第________项. 5.数列{an}满足a1=1,且an+1-an=n+1(n∈N*),a3=________. 6.已知数列{an}中,an=nn-15.6(n∈N*),则数列{an}的最大项为第________项. 7.数列{an}的通项公式an=-n2+10n+11,则该数列前________项的和最大. 8.已知数列{an}的前n项和为Sn,a1=a,a2=a2,an+2=an+1-an,S56=6,则a=________. 9.若数列{an}的前n项和Sn=n2-10n(n=1,2,3,…),则此数列的通项公式为____________. 10.已知数列{an}的通项公式为an=n-98n-99(n∈N*),给出下列说法: ①数列{an}中的最大项和最小项分别是a10,a9; ②数列{an}中的最大项和最小项分别是a9,a10; ③数列{an}中的最大项和最小项分别是a1,a9; ④数列{an}中的最大项和最小项分别是a1,a10. 其中,说法正确的是________.(填序号)
[能力提升练] 1.已知数列:21,12,31,22,13,41,32,23,14,…,根据它的前9项的规律,这个数列的第30项为________.
2.已知数列{an},an=-2n2+λn,若该数列是递减数列,则实数λ的取值范围是________. 3.已知数列{an}的前n项和Sn=2an-2n+1,若不等式2n2-n-3<(5-λ)an对∀n∈N*恒成立,则整数λ的最大值为________
【南方凤凰台】(江苏专用)高考数学大一轮复习 第二章 第15课 函数的综合应用检测评估

第15课函数的综合应用一、填空题1. 设函数f(x)是定义在R上的周期为2的偶函数,当x∈[0,1]时,f(x)=x+1,则f32⎛⎫⎪⎝⎭= .2. 设f(x)=log 3(3x+1)+12ax是偶函数,则实数a的值为.3. 方程4x-2x+1-3=0的解是.4. 设函数D(x)=1,,0,,xx⎧⎨⎩为有理数为无理数则下列结论中正确的是.(填序号)①D(x)的值域为{0,1};②D(x)是偶函数;③D(x)不是周期函数;④D(x)不是单调函数.5. (2014·皖南八校模拟)已知函数f(x)=ax2+ax和g(x)=x-a,其中a∈R且a≠0.若函数f(x)与g(x)的图象的一个公共点恰好在x轴上,则a的值为.6. (2014·天津卷)函数f(x)=12log(x2-4)的单调增区间是.7. (2014·重庆卷)函数f(x)=log(2x)的最小值为.8. (2014·佛山模拟)已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,在(0,+∞)上单调递减,且f12⎛⎫⎪⎝⎭那么方程f(x)=0的根的个数为.二、解答题9. 一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社.一个月(以30天计算)有20天每天可卖出400份,其余10天只能卖250份,但每天从报社买进报纸的份数都相同,问:应该从报社买多少份才能使每月所获得的利润最大? 并求每月最大利润.10. (2014·安庆模拟)已知函数f(x)=21axx b++(a≠0)是奇函数,且函数f(x)的图象经过点(1,3),求实数a,b的值.11. (2014·南京模拟)已知函数f(x)=x2-2ax+5(a>1).(1) 若f(x)的定义域和值域均是[1,a],求实数a的值;(2) 若f(x)在区间(-∞,2]上是减函数,且对任意的x1,x2∈[1,a+1],总有|f(x1)-f(x2)|≤4,求实数a的取值范围.第15课函数的综合应用1. 32解析:由题意知f32⎛⎫⎪⎝⎭=f3-22⎛⎫⎪⎝⎭=f1-2⎛⎫⎪⎝⎭=f12⎛⎫⎪⎝⎭=12+1=32.2. -1 解析:由题意可得f(-1)=f(1),即log3(3-1+1)-12a=log3(3+1)+12a,解得a=-1.3. log23 解析:考虑换元t=2x.4. ①②④5. -1 解析:由题意知函数g(x)的图象与x轴的交点坐标为(a,0),又因为点(a,0)也在函数f(x)的图象上,所以a3+a2=0,而a≠0,所以a=-1.6. (-∞,-2) 解析:函数f(x)=lo12g(x2-4)的定义域为(-∞,-2)∪(2,+∞),由于外层函数为减函数,由复合函数的单调性可知,只需求u(x)=x2-4(x<-2或x>2)的单调减区间,所以f(x)=lo12g(x2-4)的单调增区间为(-∞,-2).7. -14解析:f(x)=12log2x·[2(log2x+1)]=(log2x)2+log2x=221log x2⎛⎫+⎪⎝⎭-14,所以当log2x=-12,即x=时,f(x)取得最小值-1 4.8. 2 解析:由于函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且)>0,故有因为函数f(x)在区间(0,+∞)上单调递减,且f12⎛⎫⎪⎝⎭>0,由零点存在定理知,存在c∈12⎛⎝,使得f(c)=0,即函数f(x)在(0,+∞)上有唯一零点,由奇函数图象的特点知,函数f(x)在(-∞,0)上也有一个零点,故方程f(x)=0的根的个数为2.9. 设每天从报社买进x份(250≤x≤400).则每月所获利润y=[(6x+750)+(0.8x-200)]-6x=0.8x+550(250≤x≤400). y在[250,400]上是一次函数,所以当x=400时,y取得最大值870.所以从报社买400份才能使每月所获得的利润最大,每月最大利润为870元.10. 因为函数f(x)=21axx b++是奇函数,所以f(-x)=-f(x),即21ax-x b++=-21axx b++,因为a≠0,所以-x+b=-x-b,所以b=0.又函数f(x)的图象经过点(1,3),所以f(1)=3,1a1b++=3,因为b=0,所以a=2.11. (1) 因为f(x)=(x-a)2+5-a2(a>1), 所以f(x)在[1,a]上是减函数,又定义域和值域均为[1,a],所以f(1)a, f(a)1,=⎧⎨=⎩即221-2a5a,a-2a51,+=⎧⎨+=⎩解得a=2.(2) 因为f(x)在区间(-∞,2]上是减函数,所以a≥2, 又x=a∈[1,a+1],且(a+1)-a≤a-1,所以f(x)max=f(1)=6-2a,f(x)min=f(a)=5-a2,因为对任意的x1,x2∈[1,a+1],总有|f(x1)-f(x2)|≤4,所以f(x)max-f(x)min≤4,即(6-2a)-(5-a2)≤4,解得-1≤a≤3, 又a≥2,所以2≤a≤3.综上,实数a的取值范围是[2,3].。
【南方新课堂】高考数学一轮总复习 (基础轻过关+考点巧突破)第九章 第4讲 数列的求和 理 新人教

(2)等比数列{an}的前n项和Sn:①当q=1时,Sn=__n_a_1_;
a11-qn
a1-an___=____1_-__q__.
2.分组求和法 把一个数列分成几个可以直接求和的数列. 3.错位相减法 适用于一个等差数列和等比数列对应项相乘构成的数列求 和. 4.裂项相消法 有时把一个数列的通项公式分成两项差的形式,相加过程消 去中间项,只剩有限项再求和.
∵2a1+3a2=1,∴2a1+3a1q=1,代入解得:a1=13. 故数列{an}的通项公式为 an=31n. (2)bn=log3a1+log3a2+log3a3+…+log3an =-(1+2+3+…+n)=-nn2+1.
故b1n=-nn2+1=-21n-n+1 1.
b11+b12+…+b1n= 2
思想与方法 14.分类讨论思想在数列中的应用
例题:已知点 Pn(an,bn)都在直线 l:y=2x+2 上,P1 为直线 l 与 x 轴的交点,数列{an}成等差数列,公差为 1(n∈N*).
(1)求数列{an}、{bn}的通项公式; (2)若 f(n)=abnnnn为 为奇 偶数 数, ,问是否存在 k∈N*,使得 f(k+ 5)=2f(k)-2 成立;若存在,求出 k 的值,若不存在,说明理由; (3)求证:|P11P2|2+|P11P3|2+…+|P11Pn|2<25(n≥2,n∈N*).
求 k 的值要分为偶数和奇数两种情况讨论.求和 P11P22+P11P32+…+P11Pn2一般都是从等比数列或裂项相消法两 种途径去思考,如果两种方法都行不通,考虑利用放缩法进行适 当变形转化.
1.对于一般数列的求和,通常化归为等差、等比数列的求和, 以考查公式为主.由于数列求和是由通项公式决定的,因此,从 寻找数列的通项公式入手,通过研究它的特点确定使用的方法是
高考(江苏专版)大一轮数学(文)复习检测:第43课 数列的综合应用 Word版含答案

第43课数列的综合应用A 应知应会1.已知f1(x)=,f n+1(x)=f1(f n(x)),且a n=,其中n∈N*,则a2 014=.2.下列有关于公差d>0的等差数列{a n}的四个命题:①数列{a n}是递增数列;②数列{na n}是递增数列;③数列是递增数列;④数列{a n+3nd}是递增数列.其中真命题为.(填序号)3.设等差数列{a n}的前n项和为S n,若=a1+a200,且A,B,C三点共线(该直线不过原点O),则S200=.4.将正奇数排成如图所示的三角形数阵(第k行有k个奇数),其中第i行第j个数表示为a ij(i,j∈N*),例如a42=15.若a ij=2 017,则i-j=.(第4题)5.设等差数列{a n}的前n项和为S n,已知a1=2,S6=22.(1)求S n;(2)若从{a n}中抽取一个公比为q的等比数列{},其中k1=1,且k1<k2<…<k n<…,k n∈N*,当q取最小值时,求{k n}的通项公式.6.已知数列{a n}满足a1=2,对一切正整数n,都有a n+1+a n=3×2n.(1)探讨数列{a n}是否为等比数列,并说明理由;(2)若b n=,求证:b1+b2+…+b n<n+4.B 巩固提升1.若数列{a n}满足a1=2,a n=(n=2,3,4,…),且有一个形如a n=sin(ωn+φ)+的通项公式,其中ω,φ均为实数,且ω>0,|φ|<,则ω=,φ=.2.在各项均为正数的等比数列{a n}中,若a1≥1,a2≤2,a3≥3,则a4的取值范围是.3.已知数列{a n}的通项公式为a n=7n+2,数列{b n}的通项公式为b n=n2.若将数列{a n},{b n}中相同的项按从小到大的顺序排列后记作数列{c n},则c9的值为.4.(2016·盐城三模)若数列{a n}满足:对任意的n∈N*,只有有限个正整数m使得a m<n成立,记这样的m的个数为b n,则得到一个新数列{b n}.例如,若数列{a n}是1,2,3,…,n,…,则数列{b n}是0,1,2,…,n-1,….现已知数列{a n}是等比数列,且a2=2,a5=16,则数列{b n}中满足b i=2 016的正整数i的个数为.5.设数列{a n}的前n项和为S n.若对任意的正整数n,总存在正整数m,使得S n=a m,则称{a n}是“H 数列”.(1)若数列{a n}的前n项和S n=2n,求证:数列{a n}是“H数列”;(2)已知数列{a n}是等差数列,其首项a1=1,公差d<0,若{a n}是“H数列”,求d的值.6.(2016·前黄中学)在数列{a n}中,已知a2=1,前n项和为S n,且S n=.(1)求a1的值.(2)证明数列{a n}为等差数列,并写出其通项公式.(3)若lg b n=,试问:是否存在正整数p,q(其中1<p<q),使得b1,b p,b q成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,请说明理由.第43课数列的综合应用A 应知应会1.【解析】因为a n+1====-a n,所以{a n}是公比为-的等比数列,a1==,所以a2 014=.2.①④【解析】①因为d>0,显然{a n}为递增数列,故①正确;②因为(n+1)a n+1-na n=a1+2nd 不一定大于0,所以②错误;③因为==+d,a1-d的值不能确定,所以③错误;④因为数列{3nd}也是递增数列,故{a n+3nd}是递增数列,所以④正确.3. 100【解析】由题意知a1+a200=1,S200=×200=100.4.26【解析】前k行共有奇数1+2+3+…+k=个,所以第k行的最后一个数为2·-1=k2+k-1,第k+1行的第一个数为k(k+1)+1.当k+1=45时,k(k+1)+1=44×45+1=1 981,即第45行的第一个数为1981.因为=18,所以2 017是第45行的第19个数,即i=45,j=19,所以i-j=45-19=26.5.【解答】(1)设等差数列{a n}的公差为d,则S6=6a1+×6×5d=22,解得d=,所以S n=.(2)由(1)得a n=(n+2).因为数列{a n}是正项递增的等差数列,所以数列{}的公比q>1.若k2=2,则由a2=,得q==,此时=2×=,由=(n+2),解得n=∉N*,所以k2>2.同理,k2>3.若k2=4,则由a4=4,得q=2,此时=2·2n-1,因为=(k n+2),所以(k n+2)=2n,即k n=3·2n-1-2.所以最小的公比q=2,此时k n=3·2n-1-2.6.【解答】(1)假设{a n}是等比数列,由a1+a2=6,得a2=4,所以a n=2n.此时a n+1+a n=2n+1+2n=3×2n,满足题意.所以{a n}可以为等比数列.(2)由(1)知b n===1+.因为=<=2-,所以b n<1+4-,所以b1+b2+…+b n<n+4=n+4-<n+4.B 巩固提升1.0【解析】由题意得a2=-1,a3=,a4=2=a1,所以数列{a n}是周期为3的周期数列.又因为a n=sin(ωn+φ)+是该数列的一个通项公式,所以T==3⇒ω=.当n=1时,a1=sin+φ+=2⇒sin=.又|φ|<,所以φ=0或φ=-.当φ=-时,a2=sin+=≠-1,不符合题意,舍去;当φ=0时,满足题意.综上,ω=,φ=0. 2.【解析】设等比数列{a n}的公比为q.由a2=a1q≤2,得q≤,由a3=a1q2≥3,得q≥,故≤q≤,所以≤,解得a1≤,故1≤a1≤,所以a4=a1q3≤a1=≤8,且a4=a1q3≥a1=≥=,所以a4的取值范围是,8.3.961【解析】令a n=b m,则7n+2=m2,即7(n-1)=(m-3)(m+3),易知m+3或m-3是7的整数倍,所以当m=3,4,10,11,17,18,24,25,31,32…时满足等式,故c9=312=961.4. 22 015【解析】设数列{a n}的公比为q.由题意知==8=q3,所以q=2,所以a n=2n-1.由数列{b n}的定义可知b1=0,b2=1,b3=2,b4=2,b5=3,b6=3,b7=3,b8=3,b9=4,…,则当n≥1时,b i=n的i共有2n-1个,所以满足b i=2 016的正整数i的个数为22 015.5.【解答】(1)当n≥2时,a n=S n-S n-1=2n-2n-1=2n-1.当n=1时,a1=S1=2,所以当n=1时,S1=a1,当n≥2时,S n=a n+1,所以{a n}是“H数列”.(2)S n=na1+d=n+d,对任意的n∈N*,存在m∈N*,使得S n=a m,即n+=1+(m-1)d.取n=2,得1+d=(m-1)d,则m=2+.因为d<0,所以m<2,又m∈N*,所以m=1,所以d=-1.当d=-1时,a m=2-m,S n=是小于2的整数,n∈N*.于是对任意的正整数n,总存在正整数m=2-S n=2-,使得S n=2-m=a m,所以{a n}是“H数列”,因此d的值为-1.6.【解答】(1)令n=1,得a1=S1==0.(2)由S n=,得S n=,①得S n+1=.②②-①得(n-1)a n+1=na n,③所以na n+2=(n+1)a n+1.④④-③得na n+2+na n=2na n+1,即a n+2+a n=2a n+1.又a1=0,a2=1,a2-a1=1,所以数列{a n}是以0为首项、1为公差的等差数列,所以a n=n-1.(3)假设存在正整数数组(p,q),使得b1,b p,b q成等比数列,则lg b1,lg b p,lg b q成等差数列,所以=+,所以q=3q.(*)易知(p,q)=(2,3)为方程(*)的一组解.当p≥3,且p∈N*时,-=<0,故数列(p≥3)为递减数列,所以-≤-<0,所以此时方程(*)无正整数解.综上,存在唯一正整数数组(p,q)=(2,3),使得b1,b p,b q成等比数列.。
高考数学大一轮复习 第九章 第50课 线面平行与面面平行要点导学

【南方凤凰台】(江苏专用)2016届高考数学大一轮复习第九章第50课线面平行与面面平行要点导学要点导学各个击破线面平行的判定与证明如图(1),在等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图(2)所示的三棱锥A-BCF,求证:DE∥平面BCF.图(1) 图(2)(例1)[思维引导]将平面图形折成空间图形要弄清折前折后不变的关系,如ADDB=AEEC.[证明]在等边三角形ABC中,AD=AE,所以ADDB=AEEC,在折叠后的三棱锥A-BCF中也成立,所以DE∥BC.因为DE⊄平面BCF,BC平面BCF, 所以DE∥平面BCF.(2014·山东卷)如图,在四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=12AD,E,F分别为线段AD,PC的中点,求证:AP∥平面BEF.(变式1) [证明]设AC∩BE=O,连接OF,CE.由于E为AD的中点,AB=BC=12AD,AD∥BC.所以AE∥BC,AE=AB=BC,因此四边形ABCE为菱形,所以O为AC的中点.又F为PC的中点,因此在△PAC中,AP∥OF.又OF平面BEF,AP⊄平面BEF,所以AP∥平面BEF.如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AD⊥AB,CD∥AB,AB=2,CD=3,点M,N分别是PA,PB的中点.(变式2)(1) 求证:MN∥平面PCD;(2) 求证:四边形MNCD是直角梯形.[证明](1) 因为点M,N分别是PA,PB的中点,所以MN∥AB.因为CD∥AB,所以MN∥CD.又因为CD 平面PCD,MN ⊄平面PCD,所以MN∥平面PCD.(2) 因为MN=12AB=1,ED=3,所以MN≠CD,又MN∥CD,所以四边形MNCD是梯形.因为AD⊥AB,CD∥AB,所以CD⊥AD,又因为PD⊥底面ABCD,CD平面ABCD, 所以CD⊥PD,又AD∩PD=D,所以CD⊥平面PAD.因为MD平面PAD,所以CD⊥MD,所以四边形MNCD是直角梯形.线面平行的性质的应用(2014·泰州模拟改编)如图,在四棱锥P-ABCD中,底面ABCD是正方形,E是PC的中点,F为线段AC上一点.若EF∥平面PBD,求AFFC的值.(例2)[思维引导]通过线面平行的性质,将空间的问题转化到一个平面PAC中,通过EF∥PO来确定点F的位置,求出AFFC的值.[解答]设AC∩BD=O,连接PO.因为EF∥平面PBD,底面ABCD是正方形,平面PBD∩平面PAC=PO,且EF平面PAC,所以EF∥PO,又E是PC的中点,所以OF=FC,AF=3FC,即AFFC=3.在空间四边形ABCD中,点E,F,G,H分别在AB,BC,CD,DA上,且四边形EFGH为平行四边形,求证:AC∥平面EFGH.(变式) [证明]如图,因为四边形EFGH是平行四边形,所以EF∥HG.又HG平面ACD,EF⊄平面ACD,所以EF∥平面ACD.又EF平面ABC,平面ABC∩平面ADC=AC,所以EF∥AC.又EF平面EFGH,AC⊄平面EFGH,所以AC∥平面EFGH.面面平行的判定(2014·江苏模拟)如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,且AB⊥BC,M,N分别为线段AE,AB的中点,求证:平面DMN∥平面BEC.(例3)[思维引导]分别证MN∥平面BCE和BC∥平面BCE,再利用面面平行的性质定理进行证明.[证明]因为N是AB的中点,△ABD为正三角形,所以DN⊥AB.因为BC⊥AB,所以DN∥BC.因为BC平面BCE,DN⊄平面BCE,所以BC∥平面BCE.又因为M为AE的中点,所以MN∥BE.因为MN⊄平面BCE,BE平面BCE,所以MN∥平面BCE,因为MN∩DN=N,所以平面MND∥平面BCE.[精要点评]在利用面面平行的性质定理进行证明时,不能直接根据DN∥BC 和MN∥BE得出平面DMN∥平面BEC.如图,在三棱柱ABC-A1B1C1中,M,N,Q分别是AA1,BB1,B1C1的中点,求证:平面ABC1∥平面MNQ.(变式)[证明]在△B1BC1中,因为N,Q分别为B1B,B1C1的中点,所以QN∥BC1,又因为QN⊄平面ABC1,BC1平面ABC1,所以QN∥平面ABC1.在矩形A1B1BA中,因为M,N分别为AA1,BB1的中点,所以MN∥AB,又MN⊄平面ABC1,AB平面ABC1,所以MN∥平面ABC1.又因为QN∩MN=N,QN,MN平面MNQ,所以平面MNQ∥平面ABC1.直线与平面平行的探索问题(2014·四川卷)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.(例4)[思维引导]对于求某个特殊位置上的点这类问题,一种办法是由猜想定下点的位置,后证明;另一种办法是可先假定存在这个点,然后再根据点的特点找到这个点所满足的条件.[解答]线段AB上存在点M,且M为AB的中点,使得直线DE∥平面A1MC.证明如下:取线段AB的中点M,连接A1M,MC,A1C,AC1,连接MD,OE,OM.设O为A1C,AC1的交点,则MD,OE分别为△ABC,△ACC1的中位线,所以MD∥AC,且MD=12AC,OE∥AC,且OE=12AC,所以MD OE.从而四边形MDEO为平行四边形,所以DE∥MO.因为直线DE⊄平面A1MC,MO平面A1MC,所以直线DE∥平面A1MC.即线段AB上存在点M,使得直线DE∥平面A1MC.[精要点评]“探索”在于由未知到已知,由变化到确定.找平行关系时多借助中点、中位线、平行四边形等图形,此题的本质仍是线与面的平行关系.(2014·蚌埠模拟)在如图所示的几何体中,平面CDEF为正方形,平面ABCD为等腰梯形,AB ∥CD,AC=3,AB=2BC=2,AC⊥FB.(变式)(1) 求证:AC⊥平面FBC.(2) 线段AC上是否存在点M,使EA∥平面FDM?并证明你的结论.[解答](1) 在△ABC中,AC=3,AB=2,BC=1,所以AC⊥BC.又因为 AC⊥FB,BC∩FB=B,所以AC⊥平面FBC.(2) 线段AC上存在点M,且M为AC中点时,有EA∥平面FDM.证明如下:连接CE,与DF交于点N,连接MN.因为CDEF为正方形,所以N为CE中点,所以 EA∥MN.因为MN平面FDM,EA⊄平面FDM,所以EA∥平面FDM.所以线段AC上存在点M,使得EA∥平面FDM.在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABC,EF∥AB,FG ∥BC,EG∥AC,AB=2EF.若M是线段AD的中点,求证:GM∥平面ABFE.(范题赏析)[思维引导]要证明直线GM与平面ABFE平行,就要在平面ABFE内找到一条直线与GM平行.本题可以考虑构造四边形AMGF,然后再证明其为平行四边形即可.[规范答题]连接AF,因为EF∥AB,FG∥BC,EG∥AC,所以△ABC∽△EFG.(4分)由AB=2EF,得BC=2FG.所以FG∥BC,则FG=12BC. (6分)在平行四边形ABCD中,M是线段AD的中点,所以AM∥BC,且AM=12BC. (8分)所以FG∥AM,且FG=AM,所以四边形AFGM为平行四边形,所以GM∥FA.(10分)又FA平面ABFE,GM⊄平面ABFE,所以GM∥平面ABFE.(14分)1. 平面α内的两条直线a,b都平行于平面β,则α和β的位置关系是. [答案]平行或相交2. 若直线a∥b,a∥平面α,则直线b与平面α的位置关系为.[答案]b∥α或bα[解析]很容易漏掉bα的情况,这一点很值得注意.3. (2014·泰州中学模拟)给出下列命题:①如果一个平面经过另一个平面的垂线,那么这两个平面相互垂直;②如果一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;③如果两条平行直线中的一条垂直于直线m,那么另一条直线也与直线m垂直;④如果两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,真命题有.(填序号)[答案]①③④[解析]由面面垂直的判定定理可知①正确;如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面相互平行,但若是两条平行直线,得不到平面平行,故②错误;根据空间直线夹角的定义,可得两条平行直线与第三条直线的夹角相等,故若两条平行直线中的一条垂直于直线m,那么另一条直线也与直线m垂直,即③正确;根据面面垂直的性质定理,若两个平面垂直,那么一个平面内与它们的交线垂直的直线与另一个平面也垂直,则一个平面内与它们的交线不垂直的直线与另一个平面也不垂直,故④正确.4. (2014·济南期末)在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2,点E是线段AB上的动点,点M为D1C 的中点.若点E是AB的中点,求证:直线ME∥平面ADD1A1.(第4题)[证明]取DD1的中点N,连接MN,AN,则MN∥CD,且MN=12CD,AE∥CD,且AE=12CD,所以MN AE,所以四边形MNAE为平行四边形,故ME∥AN. 因为AN平面ADD1A1,ME⊄平面ADD1A1,所以ME∥平面AD1.[温馨提醒]趁热打铁,事半功倍.请老师布置同学们完成《配套检测与评估》中的练习(第99-100页).。
2020江苏高考数学(理)(提高版)大一轮复习课件:第7章 第42课 推理与证明

反证法 若 x,y 都是正实数,且 x+y>2,求证:1+y x<2 与1+x y<2 中至少有一 个成立. 【思维引导】对于直接难以证明或含否定词或含至多至少的命题的证明,通常考 虑使用反证法证明.本题中含有“至少”,所以本题的证明采用反证法证明较好.先 假设原命题的结论不正确,即原命题结论的反面成立,即1+y x≥2,1+x y≥2 同时成 立,因为 x,y 均为正实数,进而可得 1+x≥2y,1+y≥2x,再由同向不等式的可加性 得到 x+y≤2,这与已知矛盾,进而可得假设不正确,从而肯定原命题的结论成立.
【解析】第 n 个等式左边共有 2n 项且等式左边分母分别为 1,2,…,2n,分子为 1,正负交替出现,即为 1-12+13-14+…+2n1-1-21n;等式右边共有 n 项且分母分 别为 n+1,n+2,…,2n,分子为 1,即为n+1 1+n+1 2+…+21n.所以第 n 个等式可 为 1-12+13-14+…+2n1-1-21n=n+1 1+n+1 2+…+21n.
3. 证明分直接证明和间接证明. 直接证明又有综合法、分析法等. 常用的间接证明方法是 反证法.
4. 综合法是从 已知条出件发,经过逐步的推理,达到待证的 结论. 分析法是从待证的结出论发,寻求结论成立的充分条件,达到题设的已知条件或 已被证明的事. 实 反证法是从假设结论不成入手立,推出与已知条件、公理、或定显然理成立的事 实等矛盾的结果,从而判定假设错误,结论成立.一般步骤为反设、归谬、 存真.
第七章 数列、推理与证明 第42课 推理与证明
栏
目 导
链教材 ·夯基固本 研题型 ·技法通关
航
链教材 ·夯基固 本
激活思维 1. (选修 1-2P31 例 1 改编)前提:蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是 用肺呼吸的,蜥蜴是用肺呼吸的.蛇、鳄鱼、海龟、蜥蜴都是爬行动物. 则结论是 __所__有___的___爬__行___动___物__都___是___用__肺___呼___吸__的_______________________________. 2. (选修 1-2P32 例 3 改编)由23<34,23<45,23<56,…,猜想:若 m>0,则32++mm与23之
2023年高考数学一轮复习(新高考地区专用)4-2 等比数列(精讲)(含详解)
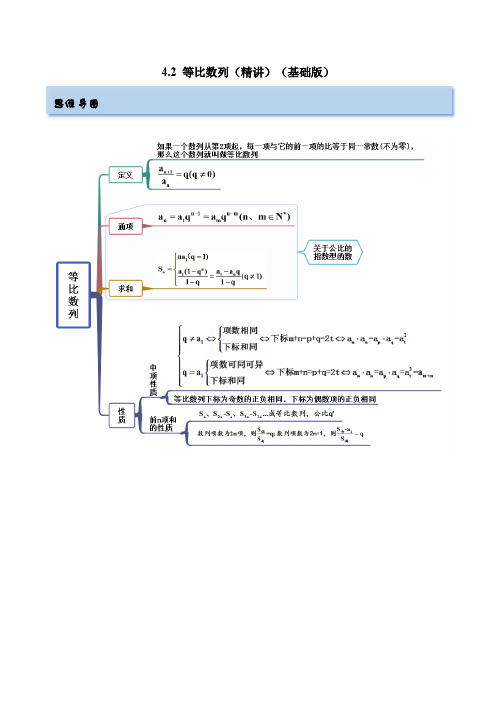
4.2 等比数列(精讲)(基础版)思维导图考点一 等比数列基本量的计算【例1】(1)(2022·北京丰台·一模)若数列{}n a 满足12n n a a +=,且41a =,则数列{}n a 的前4项和等于( )考点呈现例题剖析A .15B .14C .158 D .78(2)(2022·重庆·模拟预测)已知等比数列{}n a 的前n 项和为n S ,且2a ,53a ,89a 成等差数列,则63S S =( ) A .13B .43C .3D .4【一隅三反】1.(2022·江西·新余四中)已知n S 为等比数列{}n a 的前n 项和,若38a =,324S =,则公比q =( ) A .12-B .13-C .12-或1D .13-或12.(2022·河北廊坊·高三阶段练习)已知n S 为等比数列{}n a 的前n 项和,且公比1q >,则“51a a >”是“40S >”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.(2022·全国·高三专题练习)已知{}n a 为等比数列,n S 为其前n 项和,若213S a =,223a a =,则4S =( )A .7B .8C .15D .314.(2022·河北石家庄·高三期末)等比数列{}n a 的前n 项和为n S ,33S =,69S =,则公比q =( )A .3B .2C .33D .325(2022·四川·三模(理))已知n S 是各项均为正数的等比数列{}n a 的前n 项和,若2481a a ⋅=,313S =,则6a =( ).A .21B .81C .243D .729考点二 等比中项【例2-1】(2022·江西·上饶市第一中学二模)等比数列{}n a 中,若59a =,则3436log log a a +=( ) A .2B .3C .4D .91.等比数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)便可迎刃而解.2.等比数列的前n 项和公式涉及对公比q 的分类讨论,当q =1时,{a n }的前n 项和S n =na 1;当q ≠1时,{a n }的前n 项和S n =a 1(1-q n )1-q =a 1-a n q1-q.温馨提示【例2-2】(2022·福建·模拟预测)已知数列{}n a 为等比数列,则“5a ,7a 是方程2202210x x ++=的两实根”是”61a =,或61a =-”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【一隅三反】1.(2022·安徽黄山·一模)在等比数列{}n a 中,1a ,13a 是方程21390x x -+=的两根,则2127a a a 的值为( ) AB .3 C.D .3±2.(2022·吉林吉林)已知各项均为正数的等比数列{}n a 中,23a =,93453a a a =,则3a =( ) A .6B .9C .27D .813.(2022·全国·高三专题练习)设a ,b ,c ,d 是非零实数,则“a ,b ,c ,d 成等比数列”是“ad bc =”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件4.(2022·广西柳州)在等比数列{}n a 中,已知22a =,8462a a =,则公比q =( ) A .2-BC .2D .2±考点三 等比数列前n 项和的性质【例3-1】(2022·全国·高三专题练习)已知等比数列{an }的前n 项和为Sn ,S 10=1,S 30=13,S 40=( ) A .﹣51B .﹣20C .27D .40【例3-2】(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为n S ,若121n n S t -=⋅-,则t =( )A .2B .-2C .1D .-1【例3-3】(2022·全国·高三专题练习)已知数列}{n a 的前n 项和121n n S -=+,则数列}{n a 的前10项中所有奇数项之和与所有偶数项之和的比为( ) A .12B .2C .172341D .341172【例3-4】(2022·全国·高三专题练习)数列{}n a 中,12a =,对任意 ,,m n m n m n N a a a ++∈=,若155121022k k k a a a ++++++=-,则 k =( )A .2B .3C .4D .5【例3-5】(2022·全国·高三专题练习)各项均为正数的等比数列{}n a 的前n 项和n S ,若264a a =,31a =,则29()42n n S a +的最小值为( )A .4B .6C .8D .12【一隅三反】1.(2022·湖南·长沙一中)一个等比数列的前7项和为48,前14项和为60,则前21项和为( ) A .180 B .108 C .75D .632.(2022·全国·高三专题练习)已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的项数为( ) A .2B .4C .8D .163.(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为213n n S r -=+,则r 的值为 A .13B .13-C .19D .19-4.(2021·全国·高三专题练习)已知等比数列{}n a 中,11a =,132185k a a a ++++=,24242k a a a +++=,则k =( ) A .2B .3C .4D .55.(2022·四川绵阳·一模)已知正项等比数列{}n a 的前n 项和为n S ,若5-,3S ,6S 成等差数列,则96S S -的最小值为( )A .25B .20C .15D .10考点四 等比数列定义及其运用【例4】(2022·全国·高三专题练习)已知数列{}n a 满足12a =,121nn n a a a +=+,则下列结论正确的是( )A .数列1n a ⎧⎫⎨⎬⎩⎭是公差为12的等差数列 B .数列1n a ⎧⎫⎨⎬⎩⎭是公差为2的等差数列C .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列 D .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为2的等比数列 【一隅三反】1.(2021·江苏盐城)(多选)设等比数列{}n a 的前n 项和为n S ,则下列数列一定是等比数列的有( )A .12a a +,23a a +,34a a +,…B .13a a ,35a a +,57a a +,…C .2S ,42S S -,64S S -,…D .3S ,63S S -,96S S -,…2.(2022·广东·佛山一中)已知数列{n a }满足:11232n n a a a +==+, (1)求证:数列{1n a +}是等比数列;(2)()3log 1n n b a =+,求数列{n a ·n b }的前n 项和n S .3.(2022·全国·高三专题练习)已知数列{}n a 的前n 项和为n S ,且112a =,11()*2n n n a a N n n ++=∈. (1)证明数列{}n an为等比数列,并求数列{}n a 的通项公式;(2)设(2)n n b n S =-,求数列32{}nn b -前n 项和n T . 考点五 等比数列的实际应用【例5-1】(2022·浙江省义乌中学模拟预测)我国古代的数学名著《九章算术》中有“衰分问题”:今有女子善织,日自倍,五日织五尺,问日织几何?其意为:一女子每天织布的尺数是前一天的2倍,5天共织布5尺,问第五天织布的尺数是多少你的答案是( ) A .531B .1C .52D .8031【例5-2】(2022·江苏·沭阳如东中学模拟预测)著名的“康托三分集”是数学理性思维的构造产物,具有典型的分形特征,其操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段12,33⎛⎫⎪⎝⎭,记为第一次操作;再将剩下的两个区120,,,133⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦分别均分为三段,并各自去掉中间的区间段,记为第二次操作;…,如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使去掉的各区间长度之和不小于1415,则需要操作的次数n 的最小值为( ) 参考数据:lg2=0.3010,lg3=0.4771 A .6B .7C .8D .9【一隅三反】1.(2022·全国·模拟预测)在适宜的环境中,一种细菌的一部分不断分裂产生新的细菌,另一部分则死亡.为研究这种细菌的分裂情况,在培养皿中放入m 个细菌,在1小时内,有34的细菌分裂为原来的2倍,14的细菌死亡,此时记为第一小时的记录数据.若每隔一小时记录一次细菌个数,则细菌数超过原来的10倍的记录时间为第( )A .6小时末B .7小时末C .8小时末D .9小时末2.(2022·湖南湖南·二模)在流行病学中,基本传染数0R 是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数.0R 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定,假设某种传染病的基本传染数02R =,平均感染周期为7天,那么感染人数由1(初始感染者)增加到999大约需要的天数为( )(初始感染者传染0R 个人为第一轮传染,这0R 个人每人再传染0R 个人为第二轮传染……参考数据:lg20.3010≈) A .42B .56C .63D .703.(2022·云南·高三阶段练习(理))为了更好地解决就业问题,国家在2020年提出了“地摊经济”为响应国家号召,有不少地区出台了相关政策去鼓励“地摊经济”.老王2020年6月1日向银行借了免息贷款10000元,用于进货.因质优价廉,供不应求,据测算:每月获得的利润是该月初投入资金的20%,每月底扣除生活费1000元,余款作为资金全部用于下月再进货,如此继续,预计到2021年5月底该摊主的年所得收入为( )(取()111.27.5=,()121.29=) A .32500元 B .40000元C .42500元D .50000元4.2 等比数列(精讲)(基础版)思维导图考点一 等比数列基本量的计算【例1】(1)(2022·北京丰台·一模)若数列{}n a 满足12n n a a +=,且41a =,则数列{}n a 的前4项和等于( )考点呈现例题剖析A .15B .14C .158 D .78(2)(2022·重庆·模拟预测)已知等比数列{}n a 的前n 项和为n S ,且2a ,53a ,89a 成等差数列,则63S S =( ) A .13B .43C .3D .4【答案】(1)C (2)B【解析】(1)因为12n n a a +=,且41a =,所以数列{}n a 是以2为公比的等比数列,又3411a a q ==,得118a =,所以44141(12)(1)1581128a q S q --===--.故选:C (2)设等比数列公比为q ,由2a ,53a ,89a 成等差数列可得,47111239a q a q a q ⨯⋅=⋅+⋅,化简得639610q q -+=,解得313q =,()()61363311411311a q S q q S a q q--==+=--.故选:B. 【一隅三反】1.(2022·江西·新余四中)已知n S 为等比数列{}n a 的前n 项和,若38a =,324S =,则公比q =( )A .12-B .13-C .12-或1D .13-或1【答案】C【解析】设等比数列{}n a 的公比为q .因为38a =,324S =,所以38a =,1216a a +=,即218a q =,()1116a q +=,所以212q q +=,解得12q =-或1q =.故选:C.2.(2022·河北廊坊·高三阶段练习)已知n S 为等比数列{}n a 的前n 项和,且公比1q >,则“51a a >”是“40S >”的( )1.等比数列中有五个量a 1,n ,q ,a n ,S n ,一般可以“知三求二”,通过列方程(组)便可迎刃而解.2.等比数列的前n 项和公式涉及对公比q 的分类讨论,当q =1时,{a n }的前n 项和S n =na 1;当q ≠1时,{a n }的前n 项和S n =a 1(1-q n )1-q =a 1-a n q1-q.温馨提示A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C【解析】由40S >,得1514011a a a a q q q--=>--,因为1q >,所以510a a ->,即51a a >.故必要性满足; 1514411a a a a q S q q--==--.因为1q >,51a a >,所以40S >.故充分性满足.所以“51a a >”是“40S >”的充要条件.故选:C3.(2022·全国·高三专题练习)已知{}n a 为等比数列,n S 为其前n 项和,若213S a =,223a a =,则4S =( )A .7B .8C .15D .31【答案】C【解析】设等比数列{}n a 的公比为q ,则21213S a a a =+=,则212a a =,所以,212a q a ==, 因为223a a =,即()21124a a =,10a ≠,解得11a =,因此,()441411215112a q S q--===--.故选:C.4.(2022·河北石家庄·高三期末)等比数列{}n a 的前n 项和为n S ,33S =,69S =,则公比q =( ) ABCD【答案】D【解析】依题意,等比数列{}n a 满足,33S =,69S =,则1q ≠,()()3611113,911a q a q qq--==--,两式相除得()()3363331113,1311q q q q q q-+-==+=--,32,q q ==故选:D 5(2022·四川·三模(理))已知n S 是各项均为正数的等比数列{}n a 的前n 项和,若2481a a ⋅=,313S =,则6a =( ).A .21B .81C .243D .729【答案】C【解析】224381a a a ⋅==,因为0n a >,所以0q >,39a =,又313S =,故124a a +=,设公比是q ,则()121149a q a q ⎧+=⎨=⎩,两式相除得:2149q q +=,解得:3q =或34q =-(舍去),故336393243a a q ==⨯=.故选:C 考点二 等比中项【例2-1】(2022·江西·上饶市第一中学二模)等比数列{}n a 中,若59a =,则3436log log a a +=( )A .2B .3C .4D .9【答案】C【解析】根据等比中项得2546a a a =,所以()2434334353663log log log log log 81log 34a a a a a +=====.故选:C.【例2-2】(2022·福建·模拟预测)已知数列{}n a 为等比数列,则“5a ,7a 是方程2202210x x ++=的两实根”是”61a =,或61a =-”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【解析】在等比数列中,若5a ,7a 是方程2202210x x ++=的两实根,571a a ∴=,5720220a a +=-<,则50a <,70a <,则57661a a a a ==,则61a =或61a =-,即充分性成立,当61a =,或61a =-时,能推出57661a a a a ==,但无法推出572022a a +=-,即必要性不成立, 即“5a ,7a 是方程2202210x x ++=的两实根”是“61a =,或61a =-”的充分不必要条件,故选:A . 【一隅三反】1.(2022·安徽黄山·一模)在等比数列{}n a 中,1a ,13a 是方程21390x x -+=的两根,则2127a a a 的值为( ) AB .3 C.D .3±【答案】B【解析】因为1a 、13a 是方程21390x x -+=的两根,所以3119=a a ,11313+=a a ,所以10a >,130a >,又{}n a 为等比数列,则6710=>a q a ,所以213212719===a a a a a ,所以73a =或73a =-(舍去),所以212773==a a a a .故选:B. 2.(2022·吉林吉林)已知各项均为正数的等比数列{}n a 中,23a =,93453a a a =,则3a =( )A .6B .9C .27D .81【答案】B【解析】()3239335444,,3327a a a a a =∴==∴=,39a ∴=.故选:B 3.(2022·全国·高三专题练习)设a ,b ,c ,d 是非零实数,则“a ,b ,c ,d 成等比数列”是“ad bc =”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件D .既不充分也不必要条件【答案】A【解析】由a b c d ,,,成等比数列可得ad bc =,但当14,1,1,4a b c d ====时,a b c d ,,,不是等比数列,所以“a ,b ,c ,d 成等比数列”是“ad=bc ”的充分而不必要条件,故选:A.4.(2022·广西柳州)在等比数列{}n a 中,已知22a =,8462a a =,则公比q =( ) A.2- B C .2 D .2±【答案】D【解析】由等比数列284652a a a ==,解得452a =±,所以33522a q a ==±,所以2q =±,故选:D. 考点三 等比数列前n 项和的性质【例3-1】(2022·全国·高三专题练习)已知等比数列{an }的前n 项和为Sn ,S 10=1,S 30=13,S 40=( ) A .﹣51 B .﹣20 C .27 D .40【答案】D【解析】由{an }是等比数列,且S 10=1>0,S 30=13>0,得S 20>0,S 40>0,且1<S 20<13,S 40>13 所以S 10,S 20﹣S 10,S 30﹣S 20,S 40﹣S 30成等比数列, 即1,S 20﹣1,13﹣S 20,S 40﹣13构成等比数列,∴(S 20﹣1)2=1×(13﹣S 20),解得S 20=4或S 20=﹣3(舍去),∴(13﹣S 20)2=(S 20﹣1)(S 40﹣13),即92=3×(S 40﹣13),解得S 40=40.故选:D .【例3-2】(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为n S ,若121n n S t -=⋅-,则t =( )A .2B .-2C .1D .-1【答案】A【解析】设等比数列的公比为q ,当1q =时,1n S na =,不合题意; 当1q ≠时,等比数列前n 项和公式()1111111n n n a q a aS q qq q-==-⋅+---, 依题意()111212110,222n nn S t t t t -=⋅-=⋅-⇒+-==.故选:A【例3-3】(2022·全国·高三专题练习)已知数列}{n a 的前n 项和121n n S -=+,则数列}{n a 的前10项中所有奇数项之和与所有偶数项之和的比为( ) A .12 B .2 C .172341D .341172【答案】C【解析】当2n ≥时,212n n n n a S S --=-=,又112a S ==,即前10项分别为2,1,2,4,8,16,32,64,128,256,所以数列}{n a 的前10项中5141023341143S -===-偶,)(421451022172143S -=+=+=-奇,所以172341S S =奇偶, 故选:C .【例3-4】(2022·全国·高三专题练习)数列{}n a 中,12a =,对任意 ,,m n m n m n N a a a ++∈=,若155121022k k k a a a ++++++=-,则 k =( )A .2B .3C .4D .5【答案】C【解析】在等式m n m n a a a +=中,令1m =,可得112n n n a a a a +==,12n na a +∴=, 所以,数列{}n a 是以2为首项,以2为公比的等比数列,则1222n nn a -=⨯=,()()()()1011011105101210122122212211212k k k k k k a a a a ++++++⋅-⋅-∴+++===-=---,1522k +∴=,则15k +=,解得4k =.故选:C.【例3-5】(2022·全国·高三专题练习)各项均为正数的等比数列{}n a 的前n 项和n S ,若264a a =,31a =,则29()42n n S a +的最小值为( )A .4B .6C .8D .12【答案】C【解析】因为264a a =,且等比数列{}n a 各项均为正数,所以2444,2a a ==,公比432,a q a ==首项114a =, 所以1(1)2114n n n a q S q --==- ,通项11124n n n a a q --==,所以29()2164448242n nn n S a +=++≥=,当且仅当216,342n n n =∴=,所以当3n =时,29()42n nS a+的最小值为8.故选:C.【一隅三反】1.(2022·湖南·长沙一中)一个等比数列的前7项和为48,前14项和为60,则前21项和为( ) A .180 B .108 C .75D .63【答案】D【解析】由题意得S 7,S 14-S 7,S 21-S 14组成等比数列48,12,3,即S 21-S 14=3,∴S 21=63. 故选:D2.(2022·全国·高三专题练习)已知一个等比数列首项为1,项数是偶数,其奇数项之和为85,偶数项之和为170,则这个数列的项数为( ) A .2 B .4 C .8 D .16【答案】C【解析】设这个等比数列{}n a 共有()2k k N *∈项,公比为q ,则奇数项之和为132185k S a a a -=+++=奇,偶数项之和为()2421321170n n S a a a q a a a qS -=+++=+++==奇偶,170285S q S ∴===偶奇, 等比数列{}n a 的所有项之和为()212212211708525512kkk a S -==-=+=-,则22256k=,解得4k =,因此,这个等比数列的项数为8.故选:C.3.(2022·全国·高三专题练习)等比数列{}n a 的前n 项和为213n n S r -=+,则r 的值为A .13B .13-C .19D .19-【答案】B【解析】当1n =时,113a S r ==+,当2n ≥时,212323223221118333(31)8383393n n n n n n n n n a S S --------=-=-=-=⋅=⋅⋅=⋅ 所以81333r r +=∴=-,故选B. 4.(2021·全国·高三专题练习)已知等比数列{}n a 中,11a =,132185k a a a ++++=,24242k a a a +++=,则k =( ) A .2 B .3 C .4 D .5【答案】B【解析】设等比数列{}n a 的公比为q ,则132112285k k a a a a a a q q +++++++==,即()2285184k q a a ++=-=,因为24242k a a a +++=,所以2q,则()21123221112854212712k k k a a a a a ++⨯-+++++=+==-,即211282k +=,解得3k =,故选:B.5.(2022·四川绵阳·一模)已知正项等比数列{}n a 的前n 项和为n S ,若5-,3S ,6S 成等差数列,则96S S -的最小值为( ) A .25 B .20 C .15 D .10【答案】B【解析】因为{}n a 是正项等比数列,所以3S ,63S S -,96S S -仍然构成等比数列,所以263396()()S S S S S -=-.又5-,3S ,6S 成等差数列,所以6352S S -=,6335S S S -=+,所以()()2263396333352510S S S S S S S S S -+-===++. 又{}n a 是正项等比数列,所以30S >,3325101020S S ++≥=,当且仅当35S =时取等号.故选:B.考点四 等比数列定义及其运用【例4】(2022·全国·高三专题练习)已知数列{}n a 满足12a =,121nn n a a a +=+,则下列结论正确的是( )A .数列1n a ⎧⎫⎨⎬⎩⎭是公差为12的等差数列 B .数列1n a ⎧⎫⎨⎬⎩⎭是公差为2的等差数列C .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列 D .数列11n a ⎧⎫-⎨⎬⎩⎭是公比为2的等比数列【答案】C 【解析】∴121n n n a a a +=+,∴111111222n n n n a a a a ++==⋅+,1n a ⎧⎫∴⎨⎬⎩⎭既不是等比数列也不是等差数列; ∴1111112n n a a +⎛⎫-=- ⎪⎝⎭,∴数列11n a ⎧⎫-⎨⎬⎩⎭是公比为12的等比数列.故选:C【一隅三反】1.(2021·江苏盐城)(多选)设等比数列{}n a 的前n 项和为n S ,则下列数列一定是等比数列的有( ) A .12a a +,23a a +,34a a +,… B .13a a ,35a a +,57a a +,… C .2S ,42S S -,64S S -,… D .3S ,63S S -,96S S -,…【答案】BD【解析】设数列{}n a 的公比为q ,0q ≠,对于A 和C ,都有首项121(1)a a a q +=+,当1q =-时,120a a +=,不满足等比数列,故AC 错误;对于B ,2131(1)0a a a q +=+≠,且2235131313()a a q a a q a a a a ++==++, 同理25735a a q a a +=+,故数列13a a ,35a a +,57a a +,…为等比数列,B 正确; 对于D ,231231(1)0S a a a a q q =++=++≠,且3633S S q S -=,39663S S q S S -=-, 故数列3S ,63S S -,96S S -,…为等比数列,D 正确;故选:BD 2.(2022·广东·佛山一中)已知数列{n a }满足:11232n n a a a +==+, (1)求证:数列{1n a +}是等比数列;(2)()3log 1n n b a =+,求数列{n a ·n b }的前n 项和n S . 【答案】(1)证明见解析(2)()()12133142n nn n n S +-⨯++=-【解析】(1)因为11232n n a a a +==+,,所以1131n n a a ++=+(). 而113a +=,所以数列{1n a +}是以113a +=为首项,以3为公比的等比数列,所以13nn a +=,即31n n a =-.(2)由(1)可得()3log 1n n b a n =+=∴()31nn n a b n ⋅=-记1213233n n T n =⨯+⨯++⨯……∴所以()23131323133n n n T n n +=⨯+⨯++-⨯+⨯……∴∴-∴得:12123333nn n T n +-=+++-⨯ ()1313313n n n +-=-⨯-∴()121334n nn T +-⨯+=∴()()()1213311242n nn n n n S T n +-⨯++=-+++=-. 3.(2022·全国·高三专题练习)已知数列{}n a 的前n 项和为n S ,且112a =,11()*2n n n a a N n n ++=∈. (1)证明数列{}n an为等比数列,并求数列{}n a 的通项公式;(2)设(2)n n b n S =-,求数列32{}n n b -前n 项和n T . 【答案】(1)证明见解析;2n n na =;(2) 1(34)24(1)(2)n n n T n n ++=-++.【解析】(1)因为112n n n a a n ++=,所以1112n n a n a n++=,又因为11112a a ==,所以数列{}n a n是以首项为12,公比为12的等比数列,从而1111()()222n n n a n -=⨯=,故2n n n a =. (2)由(1)中结论可知,2311111112()3()(1)()()22222n n n S n n -=⨯+⨯+⨯++-+ ∴,所以23411111111()2()3()(1)()()222222n n n S n n +=⨯+⨯+⨯++-+ ∴,由∴-∴得,231111111()()()()222222n n n S n +=++++- 111[1()]122()1212n n n +-=-- 化简整理得,222n nn S +=-,所以222n n nn n b n S ()(), 故2232(32)22222()(2)22n n n n n n n n b n n n n n n ++--==-=--+++, 所以324351122222222222[()()()()()]132435112n n n n n T n n n n -++=--+-+-++-+--++,故1(34)24(1)(2)n n n T n n ++=-++. 考点五 等比数列的实际应用【例5-1】(2022·浙江省义乌中学模拟预测)我国古代的数学名著《九章算术》中有“衰分问题”:今有女子善织,日自倍,五日织五尺,问日织几何其意为:一女子每天织布的尺数是前一天的2倍,5天共织布5尺,问第五天织布的尺数是多少你的答案是( ) A .531B .1C .52D .8031【答案】D【解析】根据题意可知该女子每天织布的尺数成等比数列,设该等比数列为{}n a ,公比q =2, 则第1天织布的尺数为1a ,第5天织布的尺数为5a ,前5天共织布为55S =, 则()51112551231a a-=⇒=-,∴445158023131a a q =⋅=⨯=.故选:D.【例5-2】(2022·江苏·沭阳如东中学模拟预测)著名的“康托三分集”是数学理性思维的构造产物,具有典型的分形特征,其操作过程如下:将闭区间[0,1]均分为三段,去掉中间的区间段12,33⎛⎫⎪⎝⎭,记为第一次操作;再将剩下的两个区120,,,133⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦分别均分为三段,并各自去掉中间的区间段,记为第二次操作;…,如此这样,每次在上一次操作的基础上,将剩下的各个区间分别均分为三段,同样各自去掉中间的区间段.操作过程不断地进行下去,以至无穷,剩下的区间集合即是“康托三分集”.若使去掉的各区间长度之和不小于1415,则需要操作的次数n 的最小值为( ) 参考数据:lg2=0.3010,lg3=0.4771 A .6 B .7 C .8 D .9【答案】B【解析】第一次操作去掉13,设为1a ;第二次操作去掉29,设为2a ;第三次操作去掉427,设为3a , 依次类推,11233n n a -⎛⎫=⋅ ⎪⎝⎭.故0111222[()()()]3333n n S -=⨯+++ 2113121412331513n n⎡⎤⎛⎫⨯-⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=⨯=-≥ ⎪⎝⎭-, 整理,得12153n⎛⎫≥ ⎪⎝⎭,()21lg lg lg2lg3lg15315nn ⎛⎫∴≤∴-≤- ⎪⎝⎭,,()lg3lg5lg3lg5lg31lg211 6.7lg2lg3lg3lg2lg3lg2lg3lg2n -+++-∴≥===+≈----,故n 的最小值为7. 故选:B. 【一隅三反】1.(2022·全国·模拟预测)在适宜的环境中,一种细菌的一部分不断分裂产生新的细菌,另一部分则死亡.为研究这种细菌的分裂情况,在培养皿中放入m 个细菌,在1小时内,有34的细菌分裂为原来的2倍,14的细菌死亡,此时记为第一小时的记录数据.若每隔一小时记录一次细菌个数,则细菌数超过原来的10倍的记录时间为第( ) A .6小时末 B .7小时末C .8小时末D .9小时末【答案】A【解析】设n a 表示第n 小时末的细菌数,依题意有()11332242n n n a a a n --=⨯=≥,133242a m m =⨯=,则{}n a 是等比数列,首项为32m ,公比32q =,所以32nn a m ⎛⎫= ⎪⎝⎭.依题意,10n a m >,即3102n m m ⎛⎫> ⎪⎝⎭,所以3102n⎛⎫> ⎪⎝⎭, 由于563310,24372932102642⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝=⎭=<,又*N n ∈,所以6n ≥,所以第6小时末记录的细菌数超过原来的10倍, 故选:A.2.(2022·湖南湖南·二模)在流行病学中,基本传染数0R 是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均传染的人数.0R 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定,假设某种传染病的基本传染数02R =,平均感染周期为7天,那么感染人数由1(初始感染者)增加到999大约需要的天数为( )(初始感染者传染0R 个人为第一轮传染,这0R 个人每人再传染0R 个人为第二轮传染……参考数据:lg20.3010≈) A .42 B .56 C .63 D .70【答案】C【解析】设第n 轮感染的人数为n a ,则数列{}n a 是12a =,公比2q的等比数列,由()2121199912nn S ⨯-+=+=-,可得121000n +=,解得2500n =,两边取对数得lg 2lg500n =,则lg 23lg 2n =-,所以33118.979lg 20.3010n =-=-≈=, 故需要的天数约为9763⨯=. 故选:C3.(2022·云南·高三阶段练习(理))为了更好地解决就业问题,国家在2020年提出了“地摊经济”为响应国家号召,有不少地区出台了相关政策去鼓励“地摊经济”.老王2020年6月1日向银行借了免息贷款10000元,用于进货.因质优价廉,供不应求,据测算:每月获得的利润是该月初投入资金的20%,每月底扣除生活费1000元,余款作为资金全部用于下月再进货,如此继续,预计到2021年5月底该摊主的年所得收入为( )(取()111.27.5=,()121.29=)A .32500元B .40000元C .42500元D .50000元【答案】B 【解析】设010000a =,从6月份起每月底用于下月进货的资金依次记为1a ,2a ,…,12a ,()100120%1000 1.21000a a a =⨯+-=-,同理可得1 1.21000n n a a +=-, 所以()15000 1.25000n n a a +-=-, 而050005000a -=,所以数列{}5000n a -是等比数列,公比为1.2,所以50005000 1.2n n a -=⨯,12125000 1.2500050009500050000a =⨯+=⨯+=,∴总利润为500001000040000-=,故选:B .。
高考数学大一轮复习 第五节 数列的综合应用课件 理 苏教版

第十六页,共34页。
解:(1)因为 a1=a2=1,所以 b1=S1+3a1=4,b2=2S2+4a2=8,
所以 d=b2-b1=4.
(2)因为数列{bn}是等差数列,所以 bn=4n,
所以 nSn+(n+2)an=4n,即
Sn+n+n 2an=4.
第二十三页,共34页。
当 n>7 时,bbn+n 1<1,即 bn+1<bn. 所以当 n=7 或 8 时,bn 取得最大值,最大值为 b8=b7=19087. (3)由btmm<btmm++11得 tmm+1 2-9m10+t 3<0.(*) 由题意知,(*)式对任意 m∈N*恒成立. ①当 t=0 时,(*)式显然不成立,因此 t=0 不合题意; ②当 t<0 时,由m+1 2-9m10+t 3>0 可知 tm<0(m∈N*), 而当 m 为偶数时,tm>0, 因此 t<0 不合题意;
第二十六页,共34页。
角度三 数列与解析几何 3.在正项数列{an}中,a1=2,点 An( an, an+1)在双曲线 y2-
x2=1 上,数列{bn}中,点(bn,Tn)在直线 y=-12x+1 上,其 中 Tn 是数列{bn}的前 n 项和. (1)求数列{an}的通项公式; (2)求证:数列{bn}是等比数列; 解:(1)由已知点 An 在 y2-x2=1 上知,an+1-an=1, ∴数列{an}是一个以 2 为首项,以 1 为公差的等差数列. ∴an=a1+(n-1)d=2+n-1=n+1.
第五节
数列的综合应用
[典例] (2011·江苏高考)设 1=a1≤a2≤…≤a7,其中 a1,a3,a5,a7 成公比为 q 的等比数列,a2,a4,a6 成公差 为 1 的等差数列,则 q 的最小值是________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【南方凤凰台】(江苏专用)2016届高考数学大一轮复习 第九章 第42
课 数列的综合应用要点导学
要点导学 各个击破
数列与新背景、新定义的综合问题
(2014·东莞一模)如图,有一个形如六边形的点阵,它的中心是1个点(算第1层),第2层
每边有2个点,第3层每边有3个点,依次类推.
(1) 第n(n≥2)层的点数为 ;
(2) 如果一个六边形点阵共有169个点,那么它一共有 层.
(例1)
[思维引导](1) 可将第1,2,3,4,5层的点数一一列出,组成数列,然后判断数列的特点,猜出
结论;(2) 根据(1)的结果求解.
[答案](1) 6(n-1) (2) 8
[解析](1) 第1层的点数为1,第2层的点数为6,第3层的点数为12,第4层的点数为18,第5层
的点数为24,它们组成数列:1,6,12,18,24,分别记为a1,a2,a3,a4,a5.
因为a3-a2=6,a4-a3=6,a5-a4=6,猜想an-an-1=6(n≥2),
所以当n≥2时,由等差数列的通项公式可知an=a2+(n-2)d=6+(n-2)×6=6(n-1),即
an=6(n-1)(n≥2).
(2) 由(1)得(-1)(66-6)2nn+1=169,解得n=8.
[精要点评](1) 对于数列与新背景、新定义的综合问题,此类问题出题背景广、新颖,解题
的关键是读懂题意,有效地将信息转化,能较好地考查学生分析、解决问题的能力和知识的迁移
能力.一般以客观题或解答题的形式出现,属于低、中档题.
(2) 解决数列与新背景、新定义的综合问题,可通过对新数表、图象、新定义的分析、探
究,将问题转化为等差(比)数列的问题.
根据图中的5个图形及相应点的个数的变化规律,试猜测第n个图中有 个点.
(变式)
[答案]n2-n+1
[解析]序号n决定了每个图的分支数,而第n个分支有(n-1)个点,中心再加1点,故有
n(n-1)+1=n2-n+1个点.
数列与函数、不等式等综合问题
若数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
(1) 当实数t为何值时,数列{an}是等比数列?
(2) 在(1) 的结论下,设bn=log3an+1,Tn是数列11nnbb的前n项和,求T2 015的值.
[思维引导]解答本题需要掌握以下几个关键的知识点:(1) 利用前n项和与通项的关系;(2)
用裂项相消法求数列的前n项和.
[解答](1) 由题意得an+1=2Sn+1,an=2Sn-1+1(n≥2),
两式相减,得an+1-an=2an,即an+1=3an(n≥2),
所以当n≥2时,{an}是等比数列.
要使{an}是等比数列,则需21aa=21tt=3,
从而得出t=1.
(2) 由(1)知an=3n-1,bn=log3an+1=n,
11nnbb
=1(1)nn=1n-11n,
T2 015=121bb+…+201520161bb=11-2+11-23+…+11-20152016=20152016.
[精要点评]本题以函数为背景,考查数列前n项和与通项的关系、等比数列、对数知识、裂
项求前n项和等问题,内容较综合,但难度一般.
(2014·扬州模拟)设函数f(x)=233xx(x>0),数列{an}满足a1=1,an=f-11na(n∈N*,n≥
2),求数列{an}的通项公式.
[解答]因为an=f-11na=-1-112313nnaa=an-1+23(n∈N*,且n≥2),
所以an-an-1=23(n≥2).
因为a1=1,所以数列{an}是以1为首项、23为公差的等差数列,
所以an=213n.
数列型的实际应用问题
某公司一下属企业从事某种高科技产品的生产.该企业第一年年初有资金2000万元,
将其投入生产,到当年年底资金增长了50%.预计以后每年资金年增长率与第一年的相同.公司要
求企业从第一年开始,每年年底上缴资金d万元,并将剩余资金全部投入下一年生产.设第n年年
底企业上缴资金后的剩余资金为an万元.
(1) 用d表示a1,a2,并写出an+1与an的关系式;
(2) 若公司希望经过n(n≥3)年使企业的剩余资金为4000万元,试确定企业每年上缴资金d
的值(用n表示).
[解答](1)由题意得a1=2 000(1+50%)-d=3 000-d,
a2=a1(1+50%)-d=32a1-d,
an+1=an(1+50%)-d=32an-d.
(2) 由(1)得
an=32an-1-d
=232an-2-32d-d
=-233-22nad-d
=…
=-132na1-d2-23331?222n,
整理得an=-132n(3 000-d)-2d-13-12n=-132n(3 000-3d)+2d.
由题意知an=4 000,
所以-132n(3 000-3d)+2d=4 000,
解得d=3-2100023-12nn=11000(3-2)3-2nnnn.
故该企业每年上缴资金d的值为11000(3-2)3-2nnnn时,经过n(n≥3)年企业的剩余资金为4 000
元.
[精要点评]与一般应用题类似,审清题意是解决此类问题的前提.本题中出现了等差数列
与等比数列的常见问题,即求通项公式,分清类别是解题的关键.题中还出现了数列的项的值与
某数值的大小比较等,也属常规问题,仅需常规处理即可.
(2014·北京房山区模拟)2010年,我国南方省市遭遇旱涝灾害,为防洪抗旱,某地区大面
积植树造林.如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点A1(0,1),第二棵树在点
B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向,每隔一个单位种一
棵树,那么第2014棵树所在的点的坐标是 .
(变式)
[答案](10,44)
[解析]OA1B1C1设为第一个正方形,种植3棵树,依次下去,第二个正方形种植5棵树,第三个正
方形种植7棵树……它们构成一个首项为3、公差为2的等差数列,所以前n项和Sn=3n+(-1)2nn×
2=n2+2n,因为S43=1 935,S44=2 024,所以2 024-2014=10,根据图象知第2 014棵树所在的点的坐标
是(10,44).
1. 已知{an}为等差数列,若a1+a5+a9=2π,则cos(a2+a8)的值为 .
[答案]-12
[解析]a1+a5+a9=3a5=2π,则a5=23,a2+a8=2a5=43.
所以cos(a2+a8)=cos43=-12.
2. 某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵数是前一天的2倍,则
需要的最少天数n= .
[答案]6
3. (2014·盐城模拟)在数列{an}中,a1=0,111-na-11-na=1,设bn=11-nan,记Sn为数列{bn}的前n
项和,则S99= .
[答案]910
[解析]由题意可得,数列11-na是以1为首项、1为公差的等差数列,
所以11-na=n,从而有an=-1nn,
所以bn=11-nan=1-1nnn=1n-11n, [答案]23 以B=3,于是S△ABC=12×2×4×sin3=23.
所以数列{bn}的前99项的和S99=11-2+11-23+…+11-99100=1-1100=910.
4. (2014·湖北模拟)在△ABC中,三个内角A,B,C所对的边分别为a,b,c.若内角A,B,C依次成等差
数列,且不等式-x2+6x-8>0的解集为{x|a
[解析]由于不等式-x2+6x-8>0的解集为{x|2
[温馨提醒]
趁热打铁,事半功倍.请老师布置同学们完成《配套检测与评估》中的练习(第83-84页).
