等腰三角形存在性问题专项训练
等腰三角形的性质与判定综合练习 #(精选.)

1 / 3word.等腰三角形的性质与判定综合练习1、若等腰三角形的顶角为60°,则它底角的度数为( )A 、40°B 、50°C 、60°D 、70°2、如图,在△ABC 中,点D 在BC 上,AB =AD =DC ,∠B =80°,则C 的度数为( )A 、30°B 、40°C 、45°D 、60°3、如图,在△ABC 中,D 为BC 的中点,AD ⊥BC ,E 为AD 上一点,∠ABC =60°,∠ECD=40°,则∠ABE =( ) A 、10° B 、15° C 、20° D 、25°4、等腰△ABC 中,AB =AC=6cm ,∠A =150°,则△ABC 的面积为( )A 、9cm ²B 、18cm ²C 、6cm ²D 、36cm ²5、如图,在△ABC 中,AB =AC ,∠A =36°,DM 是AB 的垂直平分线,则图中的等腰三角形有( )A 、5个B 、4个C 、3个D 、2个 6、如图,在△ABC 中,∠A =60°,BE ⊥AC ,垂足为E ,CF ⊥AB , 垂足为F ,BE 、CF 交于点M 。
如果CM =4,FM =5,则BE 等于( ) A 、9 B 、12 C 、13 D 、14 7、如图,已知AB =AC ,∠A =36°,AB 的中垂线MD 交AC 于点D ,交AB 于点M 。
下列结论:①BD 是∠ABC 的平分线;②△BCD 是等腰三角形;③DC+BC=AB 。
正确的有( )A 、3个B 、2个C 、1个D 、0个8、如图,△ABC 中,AB =AC ,△DEF 为等边三角形,则γβα、、之间的关系为( )A 、2γαβ+= B 、2γβα+= C 、2γαβ—= D 、2γβα—=二、填空题9、如图,AB//CD ,CD =BD ,∠ABD =68°,则∠C 的度数为 。
(完整word版)等腰三角形存在性问题(带答案).doc

等腰三角形存在性问题(两圆一线)类型一、格点中的等腰三角形1、在如图所示的 5×5方格中,每个小方格都是边长为 1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC 有一条公共边且全等的所有格点三角形的个数是()2、 .如图,在正方形网格的格点(即最小正方形的顶点)中找一点C,使得△ABC是等腰三角形,且AB 为其中一腰.这样的 C 点有 ()个.3 、如图, A、B 是网格中的两个格点,点 C 也是网格中的一个格点,连接AB、 BC、AC,当△ ABC为等腰三角形时,格点 C 的不同位置有处,设网格中的每个小正方形的边长为1,则所有满足题意的等腰三角形ABC的面积之和等于.4、如图,在图中能画出与△ABC全等的格点三角形有几个?类型二、定边几何法讨论:两圆一线5、以线段AB 为一边的等腰直角三角形有个,请在下列图中画出来6、( 1)如图所示,线段OD 的一个端点O 在直线 AB 上,以 OD 为一边的等腰三角形ODP,并且使点P 也在 AB 上,这样的等腰三角形能画个(在图中作出点P)( 2)若∠ DOB=60°,其它条件不变,则这样的等腰三角形能画个,(只写出结果)( 3)若改变( 2)中∠ DOB的度数,其他条件不变,则等腰三角形ODP的个数和( 2)中的结果相同,则改变后∠DOB=.7、如图,南北向的公路上有一点A,东西向的公路上有一点B,若要在南北向的公路上确定点P,使得△ PAB 是等腰三角形,则这样的点P 最多能确定()个.8、线段 AB 和直线 l 在同一平面上.则下列判断可能成立的有个直线 l 上恰好只有个 1 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 2 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 3 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 4 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 5 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 6 点 P,使△ ABP为等腰三角形.9、如图AOB ,当AOB为 30 , 60 , 120 时,请在射线OA 上找点 P,使POB 为等腰三角形,并分析出当AOB 发生变化时,点P 个数的情况;类型三、三角形、长方形和正方形中的等腰三角形10、如图,在长方形ABCD中, AB=4, AD=10,点 Q 是 BC的中点,点P 在 AD 边上运动,若△ BPQ 是腰长为 5 的等腰三角形,则满足题意的点P有()个11、如图所示,在长方形ABCD 的对称轴上找一点P,使得△ PAB,△ PBC均为等腰三角形,则满足条件的点P 有()个12、如图,边长为 6 的正方形 ABCD内部有一点P,BP=4,∠ PBC=60°,点 Q 为正方形边上一动点,且△ PBQ是等腰三角形,则符合条件的Q 点有 ____个.13、在等边△ ABC所在的平面内求一点P,使△ PAB,△ PBC,△ PAC都是等腰三角形,请画出所有满足条件的点;等腰三角形存在性问题(两圆一线)答案类型一、格点中的等腰三角形1、在如图所示的 5×5方格中,每个小方格都是边长为 1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC 有一条公共边且全等的所有格点三角形的个数是(4)2、 .如图,在正方形网格的格点(即最小正方形的顶点)中找一点C,使得△ABC是等腰三角形,且AB 为其中一腰.这样的 C 点有 ( B)个.A.8B.9C.10D.113 、如图, A、B 是网格中的两个格点,点 C 也是网格中的一个格点,连接AB、 BC、AC,当△ ABC为等腰三角形时,格点 C 的不同位置有3处,设网格中的每个小正方形的边长为1,则所有满足题意的等腰三角形ABC 的面积之和等于15.【解答】解:格点 C 的不同位置分别是:C、C′、 C″,∵网格中的每个小正方形的边长为1,∴S△ABC= × 4× 3=6,S△ABC′=20﹣2× 3﹣=6.5,S△ABC″=2.5,∴S△ABC+S△ABC′+S△ABC″=6+6.5+2.5=15.故答案分别为: 3; 15.4、如图,在图中能画出与△ABC全等的格点三角形有几个?类型二、定边几何法讨论:两圆一线5、以线段AB 为一边的等腰直角三角形有个,请在下列图中画出来6、( 1)如图所示,线段OD 的一个端点O 在直线 AB 上,以 OD 为一边的等腰三角形ODP,并且使点P 也在 AB 上,这样的等腰三角形能画4个(在图中作出点P)( 2)若∠ DOB=60°,其它条件不变,则这样的等腰三角形能画2个,(只写出结果)( 3)若改变( 2)中∠ DOB的度数,其他条件不变,则等腰三角形ODP的个数和( 2)中的结果相同,则改变后∠DOB= 90 °.7、如图,南北向的公路上有一点A,东西向的公路上有一点B,若要在南北向的公路上确定点P,使得△ PAB 是等腰三角形,则这样的点P 最多能确定()个.8、线段 AB 和直线 l 在同一平面上.则下列判断可能成立的有 5 个直线 l 上恰好只有个 1 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 2 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 3 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 4 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 5 点 P,使△ ABP为等腰三角形直线 l 上恰好只有个 6 点 P,使△ ABP为等腰三角形.9、如图AOB ,当AOB为 30 , 60 , 120 时,请在射线OA 上找点 P,使POB 为等腰三角形,并分析出当AOB 发生变化时,点P 个数的情况;【结论】当AOB 为锐角,AOB60 ,有三个点,当AOB =60,只有一个点;当 AOB 为钝角或直角,只有一个点;类型三、三角形、长方形和正方形中的等腰三角形10、如图,在长方形ABCD中, AB=4, AD=10,点Q 是BC的中点,点P 在AD 边上运动,若△ BPQ 是腰长为 5 的等腰三角形,则满足题意的点P 有 ( B )A.2 个B.3 个C.4 个D.5 个11、如图所示,在长方形ABCD 的对称轴上找一点P,使得△ PAB,△ PBC均为等腰三角形,则满足条件的点P 有(C )A.1 个B.3 个C.5 个D.无数多个12、如图,边长为 6 的正方形 ABCD内部有一点P,BP=4,∠ PBC=60°,点 Q 为正方形边上一动点,且△ PBQ是等腰三角形,则符合条件的Q 点有 ____个.13、在等边△ ABC所在的平面内求一点P,使△ PAB,△ PBC,△ PAC都是等腰三角形,请画出所有满足条件的点;。
等腰三角形的性质练习(含答案)

等腰三角形的性质练习(含答案)等腰三角形的性质1.选择题:1) 等腰三角形的底角与相邻外角的关系是()A。
底角大于相邻外角 B。
底角小于相邻外角C。
底角大于或等于相邻外角 D。
底角小于或等于相邻外角2) 等腰三角形的一个内角等于100°,则另两个内角的度数分别为()A。
40°,40° B。
100°,20°C。
50°,50° D。
40°,40°或100°,20°3) 等腰三角形中的一个外角等于100°,则这个三角形的三个内角分别为()A。
50°,50°,80° B。
80°,80°,20°C。
100°,100°,20° D。
50°,50°,80°或80°,80°,20°4) 如果一个等腰三角形的一个底角比顶角大15°,那么顶角为()A。
45° B。
40° C。
55° D。
50°5) 等腰三角形一腰上的高与底边所成的角等于()A。
顶角 B。
顶角的一半C。
顶角的2倍 D。
底角的一半6) 已知:如图1所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A的度数为()A。
30° B。
45° C。
36° D。
72°2.填空题:1) 如图2所示,在△ABC中,①因为AB=AC,所以∠A=∠C;②因为AB=AC,∠1=∠2,所以BD=BC,BD⊥AC.2) 若等腰三角形的顶角与一个底角之和为110°,则顶角的度数为70°.3) 已知等腰三角形的一个角是80°,则顶角为20°.4) 在等腰三角形ABC中,一腰上的高是1cm,这条高与底边的夹角是45°,则△ABC的面积为1/2 cm².5) 如图3所示,O为△ABC内一点,且OA=OB=OC,∠ABO=20°,∠BCO=30°,则∠CAO=30°.3.等腰三角形两个内角的度数比为4:1,求其各个角的度数.设两个内角的度数为4x和x,则三角形的第三个角的度数为180°-5x.因为三角形内角和为180°,所以4x+4x+180°-5x=180°,解得x=36°,因此两个内角的度数分别为144°和36°,第三个角的度数为100°.4.如图,已知线段a和c,用圆规和直尺作等腰三角形ABC,使等腰三角形△ABC以a和c为两边,这样的三角形能作无数个.5.如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠BAC的度数.连接AD和AC,因为AD=BD,AB=AC,所以△ABD≌△ACD,故∠ABD=∠ACD.又因为AB=CD,所以△ABC为等腰三角形,所以∠BAC=180°-∠ABC=180°-2∠ABD=80°.6.如图所示,AB=AE,∠ABC=∠AED,BC=ED,点F是CD的中点.1) AF与CD不垂直.因为∠ABC=∠AED,所以△ABC≌△AED,故AB=AE,又因为BC=ED,所以AC=AD,所以AF垂直于BC的中点,而CD的中点是F,所以AF与CD不垂直.二、拓展延伸训练右下图是人字型层架的设计图,由AB、AC、BC、AD四根钢条焊接而成,其中A、B、C、D均为焊接点,且AB=AC,D为BC的中点,现在焊接所需的四根钢条已截好,且已标出BC的中点D。
初中数学专题02等腰三角形的存在性问题(原卷版)

专题二等腰三角形的存在性问题【考题研究】近几年各地的中考数学试题中,探索等腰三角形的存在性问题频频出现,这类试题的知识覆盖面较广,综合性较强,题意构思精巧,要求学生要有较高的分析问题的能力和解决问题的能力,这类问题符合课标对学生能力提高的要求。
【解题攻略】在讨论等腰三角形的存在性问题时,一般都要先分类.如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.几何法一般分三步:分类、画图、计算.哪些题目适合用几何法呢?如果△ABC的∠A(的余弦值)是确定的,夹∠A的两边AB和AC可以用含x的式子表示出来,那么就用几何法.①如图1,如果AB=AC,直接列方程;②如图2,如果BA=BC,那么;③如图3,如果CA=CB,那么.代数法一般也分三步:罗列三边长,分类列方程,解方程并检验.如果三角形的三个角都是不确定的,而三个顶点的坐标可以用含x的式子表示出来,那么根据两点间的距离公式,三边长(的平方)就可以罗列出来.【解题类型及其思路】解题类型:动态类型:1.一动点类型问题;2.双动点或多动点类型问题背景类型:1.几何图形背景;2.平面直角坐标系和几何图形背景解题思路:几何法一般分三步:分类、画图、计算;代数法一般也分三步:罗列三边长,分类列方程,解方程并检验.如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.已知腰长画等腰三角形用圆规画圆,已知底边画等腰三角形用刻度尺画垂直平分线.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.【典例指引】类型一【二次函数综合题中根据条件判定三角形的形状】典例指引1.抛物线2y x bx c =++与x 轴交于点A ,点B (1,0),与y 轴交于点C (0,﹣3),点M 是其顶点. (1)求抛物线解析式;(2)第一象限抛物线上有一点D ,满足∠DAB =45°,求点D 的坐标;(3)直线x t = (﹣3<t <﹣1)与x 轴相交于点H .与线段AC ,AM 和抛物线分别相交于点E ,F ,P .证明线段HE ,EF ,FP 总能组成等腰三角形.【举一反三】(2020·江西初三期中)如图①,已知抛物线y =ax 2+bx +3(a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1)求抛物线的解析式;(2)设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由;(3)如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.类型二【利用二次函数的性质与等腰三角形的性质确定点的坐标】典例指引2.(2019·山东初三期末)如图1,已知抛物线2()30y ax bx a =++≠与x 轴交于点(1,0)A 和点(3,0)B -,与y 轴交于点C .(l )求抛物线的表达式;(2)如图l ,若点E 为第二象限抛物线上一动点,连接,BE CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标;(3)如图2,在x 轴上是否存在一点D 使得ACD ∆为等腰三角形?若存在,请求出所有符合条件的点D 的坐标;若不存在,请说明理由.【举一反三】(2019·广东省中山市中山纪念中学三鑫双语学校初三期中)如图,已知抛物线y =ax 2+bx +c 的图象与x 轴交于A (2,0),B (﹣8,0)两点,与y 轴交于点C (0,﹣8).(1)求抛物线的解析式;(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,求出点F的坐标;(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.类型三【确定满足等腰三角形的动点的运动时间】典例指引3.(2018济南中考)如图1,抛物线平移后过点A(8,,0)和原点,顶点为B,对称轴与轴相交于点C,与原抛物线相交于点D.(1)求平移后抛物线的解析式并直接写出阴影部分的面积;(2)如图2,直线AB与轴相交于点P,点M为线段OA上一动点,为直角,边MN与AP相交于点N,设,试探求:①为何值时为等腰三角形;②为何值时线段PN的长度最小,最小长度是多少.【举一反三】如图所示,抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.(1)求此抛物线的解析式;(2)小明在探究点D运动时发现,①当点D与点C重合时,EF长度可看作O;②当点D与点O重合时,EF长度也可以看作O,于是他猜想:设点D运动到OC中点位置时,当线段EF最长,你认为他猜想是否正确,为什么?(3)连接CF、DF,请直接写出△CDF为等腰三角形时所有t的值.【新题训练】1.(2020·江西初三)如图,在平面直角坐标系中,已知点A(﹣2,﹣4),直线x=﹣2与x轴相交于点B,连接OA,抛物线y=﹣x2从点O沿OA方向平移,与直线x=﹣2交于点P,顶点M到点A时停止移动.(1)线段OA 所在直线的函数解析式是 ;(2)设平移后抛物线的顶点M 的横坐标为m ,问:当m 为何值时,线段P A 最长?并求出此时P A 的长. (3)若平移后抛物线交y 轴于点Q ,是否存在点Q 使得△OMQ 为等腰三角形?若存在,请求出点Q 的坐标;若不存在,请说明理由.2.(2018·山东中考真题)如图,在平面直角坐标系中,二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ,交y 轴于点()0,6C ,在y 轴上有一点()0,2E -,连接AE .(1)求二次函数的表达式;(2)若点D 为抛物线在x 轴负半轴上方的一个动点,求ADE ∆面积的最大值;(3)抛物线对称轴上是否存在点P ,使AEP ∆为等腰三角形,若存在,请直接写出所有P 点的坐标,若不存在请说明理由.3.(2016·广西中考真题)在平面直角坐标系中,抛物线223y x x =--+与x 轴交于A ,B 两点(A 在B 的左侧),与y 轴交于点C ,顶点为D . (1)请直接写出点A ,C ,D 的坐标;(2)如图(1),在x 轴上找一点E ,使得△CDE 的周长最小,求点E 的坐标;(3)如图(2),F 为直线AC 上的动点,在抛物线上是否存在点P ,使得△AFP 为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.4.(2019·广东广州市第二中学初三)如图(1),在平面直角坐标系中,矩形ABCO,B点坐标为(4,3),抛物线y=12-x2+bx+c经过矩形ABCO的顶点B、C,D为BC的中点,直线AD与y轴交于E点,与抛物线y=12-x2+bx+c交于第四象限的F点.(1)求该抛物线解析式与F点坐标;(2)如图,动点P从点C出发,沿线段CB以每秒1个单位长度的速度向终点B运动;同时,动点M从点A出发,沿线段AE 13个单位长度的速度向终点E运动.过点P作PH⊥OA,垂足为H,连接MP,MH.设点P的运动时间为t秒.①问EP+PH+HF是否有最小值,如果有,求出t的值;如果没有,请说明理由.②若△PMH是等腰三角形,求出此时t的值.5.(2019·湖南中考模拟)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y 轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.6.(2018·山东中考模拟)如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.7.(2019·山东中考模拟)已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C (﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△P AB的面积有最大值?(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P 使△PDE 为等腰直角三角形?若存在,求出点P 的坐标;若不存在,说明理由.8.(2018·广东中考模拟)如图,在平面直角坐标系xOy 中,二次函数24y ax bx =+-(0a ≠)的图象与x 轴交于A (﹣2,0)、B (8,0)两点,与y 轴交于点B ,其对称轴与x 轴交于点D .(1)求该二次函数的解析式;(2)如图1,连结BC ,在线段BC 上是否存在点E ,使得△CDE 为等腰三角形?若存在,求出所有符合条件的点E 的坐标;若不存在,请说明理由;(3)如图2,若点P (m ,n )是该二次函数图象上的一个动点(其中m >0,n <0),连结PB ,PD ,BD ,求△BDP 面积的最大值及此时点P 的坐标.9.(2019·四川中考模拟)如图,已知二次函数y =﹣x 2+bx +c (c >0)的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,且OB =OC =3,顶点为M .(1)求二次函数的解析式;(2)点P 为线段BM 上的一个动点,过点P 作x 轴的垂线PQ ,垂足为Q ,若OQ =m ,四边形ACPQ 的面积为S ,求S 关于m 的函数解析式,并写出m 的取值范围;(3)探索:线段BM 上是否存在点N ,使△NMC 为等腰三角形?如果存在,求出点N 的坐标;如果不存在,请说明理由.10.(2019·甘肃中考模拟)如图,已知二次函数y =ax 2+bx +c 的图象与x 轴相交于A (﹣1,0),B (3,0)两点,与y 轴相交于点C (0,﹣3). (1)求这个二次函数的表达式;(2)若P 是第四象限内这个二次函数的图象上任意一点,PH ⊥x 轴于点H ,与BC 交于点M ,连接PC . ①求线段PM 的最大值;②当△PCM 是以PM 为一腰的等腰三角形时,求点P 的坐标.11.(2019·安徽中考模拟)如图,已知直线1y x =+与抛物线2y ax 2x c =++相交于点()1,0A -和点()2,B m 两点.(1)求抛物线的函数表达式;(2)若点P 是位于直线AB 上方抛物线上的一动点,当PAB ∆的面积S 最大时,求此时PAB ∆的面积S 及点P 的坐标;(3)在x 轴上是否存在点Q ,使QAB ∆是等腰三角形?若存在,直接写出Q 点的坐标(不用说理);若不存在,请说明理由.12.(2018·江苏中考模拟)(2017南宁,第26题,10分)如图,已知抛物线2239y ax ax a =--与坐标轴交于A ,B ,C 三点,其中C (0,3),∠BAC 的平分线AE 交y 轴于点D ,交BC 于点E ,过点D 的直线l 与射线AC ,AB 分别交于点M ,N .(1)直接写出a的值、点A的坐标及抛物线的对称轴;(2)点P为抛物线的对称轴上一动点,若△P AD为等腰三角形,求出点P的坐标;(3)证明:当直线l绕点D旋转时,11AM AN均为定值,并求出该定值.13.(2019·重庆中考模拟)如图,在平面直角坐标系中,一抛物线的对称轴为直线,与y轴负半轴交于C点,与x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.(1)求此抛物线的解析式;(2)若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.(3)若平行于x轴的直线与该抛物线交于M、N两点(其中点M在点N的右侧),在x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.14.(2019·辽宁中考模拟)抛物线y=ax2+bx﹣3(a≠0)与直线y=kx+c(k≠0)相交于A(﹣1,0)、B(2,﹣3)两点,且抛物线与y轴交于点C.(1)求抛物线的解析式;(2)求出C、D两点的坐标(3)在第四象限抛物线上有一点P,若△PCD是以CD为底边的等腰三角形,求出点P的坐标.15.(2020·浙江初三期末)如图,抛物线y=﹣12x2+2x+6交x轴于A,B两点(点A在点B的右侧),交y轴于点C,顶点为D,对称轴分別交x轴、线段AC于点E、F.(1)求抛物线的对称轴及点A的坐标;(2)连结AD,CD,求△ACD的面积;(3)设动点P从点D出发,沿线段DE匀速向终点E运动,取△ACD一边的两端点和点P,若以这三点为顶点的三角形是等腰三角形,且P为顶角顶点,求所有满足条件的点P的坐标.16.(2020·湖北初三期末)如图,已知二次函数的图象经过点A(4,4),B(5,0)和原点O,P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA相较于点C.(1)求出二次函数的解析式;(2)当点P在直线OA的上方时,求线段PC的最大值;(3)当点P在直线OA的上方时,是否存在一点P,使射线OP平分∠AOy,若存在,请求出P点坐标;若不存在.请说明理由;(4)当m>0时,探索是否存在点P,使得△PCO为等腰三角形,若存在,求出P点的坐标;若不存在,请说明理由.17.(2019·吉林初三)如图1,抛物线与y =﹣211433x x ++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接AC 、BC ,点D 是线段AB 上一点,且AD =CA ,连接CD .(1)如图2,点P 是直线BC 上方抛物线上的一动点,在线段BC 上有一动点Q ,连接PC 、PD 、PQ ,当△PCD 面积最大时,求PQ +10CQ 的最小值; (2)将过点D 的直线绕点D 旋转,设旋转中的直线l 分别与直线AC 、直线CO 交于点M 、N ,当△CMN 为等腰三角形时,直接写出CM 的长.18.(2020·江苏初三期末)在平面直角坐标系xOy 中,抛物线2y x mx n =-++与x 轴交于点A ,B ( A 在B的左侧)(1)如图1,若抛物线的对称轴为直线3,4x AB =-= .①点A 的坐标为( , ),点B 的坐标为( , ); ②求抛物线的函数表达式;(2)如图2,将(1)中的抛物线向右平移若干个单位,再向下平移若干个单位,使平移后的抛物线经过点O ,且与x 正半轴交于点C ,记平移后的抛物线顶点为P ,若OCP ∆是等腰直角三角形,求点P 的坐标.。
中考数学总复习《二次函数之等腰三角形存在性问题》专项提升训练题-附答案

中考数学总复习《二次函数之等腰三角形存在性问题》专项提升训练题-附答案学校:___________班级:___________姓名:___________考号:___________ 1.已知二次函数23y ax bx a =+-经过点()1,0A -和()0,3C ,与x 轴交于另一点B ,抛物线的顶点为D .(1)求此二次函数解析式;(2)连接DC 、BC 和DB ,判断BCD △的形状并说明理由;(3)在对称轴右侧抛物线上找一点P ,使得P 、D 、C 构成以PC 为底边的等腰三角形,求出点P 的坐标及此时四边形PBCD 的面积.2.如图,抛物线2y x bx c =-++过点(1,0)A -和(3,0)B ,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 为抛物线对称轴上一动点,当PCB 是以BC 为底边的等腰三角形时,求P 的坐标;(3)在(2)条件下,是否存在点M 为抛物线上的点,使得2BCM BCP S S =△△?若存在,求出点M 的横坐标;若不存在,请说明理由.3.如图,已知抛物线2y ax bx c =++经过点()3,0A -,()0,4C 两点,且与x 轴的另一个交点为B ,对称轴为直线=1x -.(1)求抛物线的表达式;(2)已知点M 是抛物线对称轴上一点,当MBC 的周长最小时,求M 点的坐标.(3)D 是第二象限内抛物线上的动点,设点D 的横坐标为m ,求四边形ABCD 面积S 的最大值及此时D 点的坐标;(4)若点P 在抛物线对称轴上,是否存在点P ,使以点B ,C 和P 为顶点的三角形是等腰三角形?若存在,请求出P 点的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系中,抛物线24y ax bx =+-与x 轴交于()40A ,、()30B -,两点,与y 轴交于点C .(1)求这条抛物线所对应的函数表达式.(2)如图①,点D 是x 轴下方抛物线上的动点,且不与点C 重合.设点D 的横坐标为m ,以O 、A 、C 、D 为顶点的四边形面积为S ,求S 与m 之间的函数关系式.(3)如图①,连结BC ,点M 为线段AB 上一点,点N 为线段BC 上一点,且BM CN n ==,直接写出当n 为何值时BMN 为等腰三角形.5.抛物线24y x x =-与直线y x =交于原点O 和点B ,与x 轴交于点A ,顶点为D .(1)填空:点B 的坐标为 ,点D 的坐标为 .(2)如图1,连结OD ,P 为x 轴上的动点,当以O ,D ,P 为顶点的三角形是等腰三角形时,求点P 的坐标;(3)如图2,M 是点B 关于抛物线对称轴的对称点,Q 是抛物线上的动点,它的横生标为m (05)m <<,连结MQ ,BQ 和MQ 与直线OB 交于点E .设BEQ 和BEM △的面积分别为1S 和2S ,设12S t S =己,试求t 关于m 的函数解析式并求出t 的最值6.如图,在平面直角坐标系中,二次函数2y x bx c =-+-的图象与x 轴交于点(3,0)A -和点(1,0)B ,与y 轴交于点C .(1)求这个二次函数的表达式;(2)如图①,二次函数图象的对称轴与直线AC 交于点D ,若E 是直线AC 上方抛物线上的一个动点,求ECD 面积的最大值;(3)如图①,P 是直线AC 上的一个动点,是否存在点P ,使PBC 是等腰三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.7.如图1,抛物线23432363y x x =++与x 轴交于点A ,B (A 在B 左边),与y 轴交于点C ,连AC ,点D 与点C 关于抛物线的对称轴对称,过点D 作DE AC ∥交抛物线于点E ,交y 轴于点P .(1)点F 是直线AC 下方抛物线上点一动点,连DF 交AC 于点G ,连EG ,当EFG 的面积的最大值时,直线DE 上有一动点M ,直线AC 上有一动点N ,满足MN AC ⊥,连GM 和NO ,求GM MN NO ++的最小值;(2)如图2,在(1)的条件下,过点F 作FH x ⊥轴于点H 交AC 于点L ,将AHL 沿着射线AC 平移到点A 与点C 重合,从而得到A H L '''(点A ,H ,L 分别对应点A ',H '和L '),再将A H L '''绕点H '逆时针旋转(0180)αα︒<<︒,旋转过程中,边A L ''所在直线交直线DE 于Q ,交y 轴于点R ,求当PQR 为等腰三角形时,直接写出PR 的长.8.如图,在平面直角坐标系中,抛物线2y ax bx c =++与x 轴交于()4,0B ,()2,0C -两点,与y 轴交于点()0,2A -.(1)求该抛物线的函数表达式;(2)若点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点K ,过点P 作y 轴的平行线交x 轴于点D ,求12PK PD +的最大值及此时点P 的坐标; (3)在抛物线的对称轴上是否存在一点M ,使得MAB △是以AB 为腰的等腰三角形;若存在,请求出点M 的坐标,若不存在,请说明理由.9.如图,抛物线23y ax bx =++与x 轴相交于点(1,0)A -,B ,对称轴是1x =,与y 轴相交于点C .(1)求抛物线的函数表达式;(2)点P 为抛物线对称轴上一动点,当PCB 是以BC 为底边的等腰三角形时,求点P 的坐标;(3)在(2)的条件下,在第一象限内,抛物线上是否存在点M ,使得BCM BCP S S =△△?若存在,求出点M 的横坐标;若不存在,请说明理由.10.如图,抛物线2y x bx c =++的图象与x 轴交于(3,0)A -、(1,0)B 两点,与y 轴交于点C ,点P 是抛物线上位于第三象限内的一点.(1)求抛物线的解析式.(2)连接AP 、PC 和CB ,求四边形APCB 面积的最大值及此时P 点的坐标.(3)点D 为抛物线对称轴上的一点,当以点A 、C 、D 为顶点的三角形为等腰三角形时,请写出所有符合条件的点D 的坐标,并把求其中一个点D 的过程写出来.11.已知拋物线2y ax bx c =++经过点()120B ,和()06C -,,对称轴为直线2x =.(1)求该拋物线的解析式;(2)点D 在线段AB 上,且AD AC =,若动点P 从A 点出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一动点Q 以某一速度从C 点出发沿线段CB 匀速运动,问是否存在某一时刻t ,使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t (秒)和点Q 的运动速度,若不存在,请说明理由;(3)在(2)的条件下,在x 轴上是否存在点M ,使MPQ 为等腰三角形?若存在,请求出所有点M 的坐标,若不存在,请说明理由.12.已知抛物线与x 轴交于1030A C -(,)、(,),与y 轴交于点03B -(,).(1)求抛物线对应的函数解析式;(2)在x 轴上是否存在点P ,使PBC 为等腰三角形?若存在,求出P 点坐标;若不存在,请说明理由;(3)点M 为抛物线上一动点,在直线BC 上是否存在点Q ,使以点O 、B 、Q 、M 为顶点的四边形为平行四边形?若存在,求出Q 点的坐标;若不存在,请说明理由.13.如图,抛物线212y x mx n =-++与x 轴交于A B 、两点,与y 轴交于点C ,拋物线的对称轴交x 轴于点D ,已知()()1,0,0,2A C -.(1)求抛物线的解析式;(2)点E 是线段BC 上的一个动点(不与B C 、重合),过点E 作x 轴的垂线与抛物线相交于点F ,当点E 运动到什么位置时,四边形CDBF 的面积最大?求出四边形CDBF 的最大面积及此时点E 的坐标.(3)在抛物线的对称轴上是否存在点P ,使PCD 为等腰三角形?如果存在,直接写出P 点的坐标;如果不存在,请说明理由.14.如图,已知抛物线与x 轴交于1,0A 和()5,0B -两点,与y 轴交于点C .直线33y x =-+过抛物线的顶点P .(1)求抛物线的函数解析式;(2)若直线()50x m m =-<<与抛物线交于点E ,与直线BC 交于点F . ①当EF 取得最大值时,求m 的值和EF 的最大值; ①当EFC 是等腰三角形时,求点E 的坐标.15.如图1,在平面直角坐标系中,抛物线23y ax bx =+-与x 轴交于点()60A ,和()10B -,,与y 轴交于点C ,连接BC ,过点A 、C 作直线AC .(1)求抛物线的函数解析式.⊥交AC于点F,过点P作(2)点P为直线AC下方抛物线上一动点,过点P作PF AC∥交x轴于点E,求AE PFPE AC+的最大值及此时点P的坐标.(3)在(2)问的条件下,将抛物线23=+-沿射线CB方向平移10个单位长度得y ax bx到新抛物线y',新抛物线y'与原抛物线交于点M;连接CP,把线段CP沿直线AC平移,记平移后的线段为C P'',当以C'、P'和M为顶点的三角形是等腰三角形时,请直接写出所有符合条件的P'点的坐标.参考答案: 1.(1)223y x x =-++(2)BCD △为直角三角形(3)点P 的坐标为()2,3,四边形PBCD 的面积为42.(1)223y x x =-++(2)()1,1P(3)M 点横坐标为3172+或3172-或1或23.(1)248433y x x =--+ (2)81,3M ⎛⎫- ⎪⎝⎭ (3)252S =,3,52D ⎛⎫- ⎪⎝⎭(4)P 的坐标为:()1,0-或()1,13-或()1,13--或131,8⎛⎫- ⎪⎝⎭4.(1)211433=--y x x (2)当30m -<<时28S m =-+;当04m <<时228833S m m =-++. (3)52n =,2511n =和3011n = 5.(1)(5,5) ()2,4-(2)点P 的坐标为()()()()25,025,04,05,0-或或或(3)()21525056224t m m ⎛⎫=--+<< ⎪⎝⎭,t 的最大值为25246.(1)223y x x =--+(2)98ECD S =最大△(3)点P 的坐标为()535--,或()535+,或5122⎛⎫- ⎪⎝⎭,或()21-,.7.(1)239745+(2)17333-或8338.(1)211242y x x =-- (2)存在,12PK PD +的最大值为258 335,216P ⎛⎫- ⎪⎝⎭(3)存在,M 的坐标为()111,或()111-,或()1219-+,或()1219--,.9.(1)223y x x =-++(2)点P 的坐标为(1,1)(3)存在,点M 的横坐标为352+或35210.(1)223y x x =+-(2)点P 坐标为315,24⎛⎫-- ⎪⎝⎭ max 758ABCP S =四边形 (3)1(1,14)D - 2(1,14)D -- 3(1,173)D -- 4(1,173)D --- 5(1,1)D --;11.(1)2116164y x x =--; (2)存在5t =时线段PQ 被直线CD 垂直平分,点Q 的运动速度每秒355单位长度; (3)1(2,0)M 2(33,0)10M -+ 3(33,0)10M -- 4(15,0)M ;12.(1)2=23y x x --(2)3,0-()或(323,0)+,或(323,0)-+,或0,0() (3)存在Q 1Q :321213(,)22+- 2321213,)22(Q -+- 3)213(,22192Q --4)321(,29212Q +-+-13.(1)213222y x x =-++ (2)当2x =时,四边形CDBF 的面积最大,最大值为132,此时()2,1E (3)存在,满足条件的P 点坐标为35353325,,,4,22222216⎛⎫⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,,14.(1)245y x x =--+(2)①当52m =-时,EF 有最大值,最大值为254;①()38-,或()45-,或()25622--,15.(1)215322y x x =-- (2)AE +PF 的最大值为:9595+;此时()3,6P - (3)点P '的坐标为:172112911,55⎛⎫--- ⎪ ⎪⎝⎭或172412911,55⎛⎫+-+ ⎪ ⎪⎝⎭或()11,13--。
等腰三角形存在性问题专项训练

等腰三⾓形存在性问题专项训练lBA第讲:等腰三⾓形存在性问题专题训练⼀、等腰三⾓形4⼤性质(1)等边对等⾓、等⾓对等边;(2)三线合⼀;(3)含有60°⾓的等腰三⾓形是等边三⾓形;(4)等腰三⾓形底边上任意⼀点到两腰的距离等于腰上的⾼;⼆、构造等腰三⾓形⼆、特殊的等腰三⾓形(1)等边三⾓形;(2)等腰直⾓三⾓形;(3)底⾓为30°的等腰三⾓形;(4)黄⾦三⾓形⼀、模型引⼊引⼊:如图,已知线段AB ,在过A 点的直线l 上求作点P ,使△ABP 为等腰三⾓形.思维提升:在平⾯直⾓坐标系内,已知点A (2,1),O 为坐标原点.请你在坐标轴上确定点P ,使得ΔAOP 为等腰三⾓形.在给出的坐标系中把所有这样的点P 都找出来,画上实⼼点,并在旁边标上P 1,P 2,……,P k ,(有k 个就标到P K 为⽌,不必写出画法)【答案】⼆、典型分析例1.如图,在等腰梯形ABCD 中,AD //BC ,BC =4AD =24,∠B =45°.直⾓三⾓板含45°⾓的顶点E 在边BC 上移动,⼀直⾓边始终经过点A ,斜边与CD 交于点F .若△ABE 为等腰三⾓形,则CF 的长等于.【答案】,2,.例2.如图,四边形OABC 是⼀张放在平⾯直⾓坐标系中的正⽅形纸⽚.点O 与坐标原点重合,点A 在x 轴上,点C 在y 轴上,OC =4,点E 为BC 的中点,点N 的坐标为(30),,过点N 且平⾏于y 轴的直线MN 与EB 交于点M .现将纸⽚折叠,使顶点C 落在MN 上,并与MN 上的点G 重合,折痕为EF ,点F 为折痕与y 轴的交点.(1)求点G 的坐标;(2)求折痕EF 所在直线的解析式;(3)设点P 为直线EF 上的点,是否存在这样的点P ,使得以P 、F 、G 为顶点的三⾓形为等腰三⾓形,若存在,请直接写出点P 的坐标;若不存在,请说明理由.523 y xCF OEMBGNAF【答案】解:(1)四边形ABCO 是正⽅形,4BC OA ∴==,E 为CB 中点,2EB ∴=MN y ∥轴,(30)N ,,MN EB ∴⊥且1MB NA ==1EM ∴=⽽2EG EC ==,1sin 2EM EGM EG ∴∠==30EGM ∴∠=cos303MG EG ∴==· (34G ∴,(2)30EGM ∠=60MEG FEG CEF ∴∠=∠=∠=tan 6023CF CE ∴==·4FO∴=-(04F ∴-,,(24)E ,设直线EF 的解析式:(0)y kx b k =+≠244k b b +=??∴?=-??4k b ?=?∴?=-??∴折痕EF所在直线解析式:4y =+-(3)12((14P P -,,,34(34P P -,,综合训练yxCOEMBGNA4P3P2P1PEM BCN AOFGyx(2011湖南)如图(11)所⽰,在平⾯直⾓坐标系Oxy 中,已知点A (94-,0),点C (0,3),点B 是x 轴上⼀点(位于点A 的右侧),以AB 为直径的圆恰好经过....点C .(1)求∠ACB 的度数;(2)已知抛物线y =ax 2+bx +3经过A 、B 两点,求抛物线的解析式;(3)线段BC 上是否存在点D ,使△BOD 为等腰三⾓形.若存在,则求出所有符合条件的点D 的坐标;若不存在,请说明理由.【答案】(1)∵以AB 为直径的圆恰好经过....点C ∴∠ACB =090(2)∵△AOC ∽△ABC∴OB AO OC ?=2∵A (-94,0),点C (0,3),∴49=AO 3=OC ∴OB 4932=∴ 4=OB ∴B (4,0) 把 A 、B 、C 三点坐标代⼊得 3127312++-=x x y (3)①OD =OB , D 在OB 的中垂线上,过D 作DH ⊥OB ,垂⾜是H ,则H 是OB 中点.DH =OC 21 OB OH 21= ∴D )23,2( ② BD =BO 过D 作DG ⊥OB ,垂⾜是G ∴OG :OB =CD :CB DG :OC =1:5 ∴ OG :4=1:5 DG :3=1:5 ∴OG =54 DG =53∴D (54,53)⼀、模型引⼊xO⼆、典例分析例3(济南)如图,在梯形ABCD 中,AD //BC ,AD =3,DC =5,AB =24,∠B =45°.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒.(1)求BC 的长.(2)试探究:t 为何值时,△MNC 为等腰三⾓形.【答案】(1)如图①,过A 、D 分别作AK BC ⊥于K ,DH BC ⊥于H ,则四边形ADHK 是矩形∴3KH AD ==.在Rt ABK △中,sin 4542AK AB =??==cos 4542BK AB =??== 在Rt CDH △中,由勾股定理得,3HC == ∴43310BC BK KH HC =++=++= (2)分三种情况讨论:①当NC MC =时,如图②,即102t t =- ∴103t =CADCB MN(图②)(题图③)AD CBM NH E(图①)A DCBK H②当MN NC =时,如图③,过N 作NE MC ⊥于E 解法⼀:由等腰三⾓形三线合⼀性质得()11102522EC MC t t ==-=- 在Rt CEN △中,5cos EC t c NC t -==⼜在Rt DHC △中,3cos 5CH c CD ==∴535t t -= 解得258t =解法⼆:∵90C C DHC NEC =∠=∠=?∠∠,∴NEC DHC △∽△∴NC ECDC HC =即553t t -= ∴258t = ③当MN MC =时,如图④,过M 作MF CN ⊥于F 点.11 22FC NC t == 解法⼀:(⽅法同②中解法⼀)132cos 1025tFC C MC t ===- 解得6017t =解法⼆:∵90C C MFC DHC =∠=∠=?∠∠,∴MFC DHC △∽△∴FC MCHC DC =即1102235tt -=∴6017t = 综上所述,当103t =、258t =或6017t =时,MNC △为等腰三⾓形.同类训练:平⾯直⾓坐标系中,四边形OABC 为矩形,点A 、B 的坐标分别为(3,0),(3,4).动点M 、N 分别从O 、B 同时出发,以每秒1个单位的速度运动.其中,点M 沿OA 向终(图④)ADCBH NMF点A 运动,点N 沿BC 向终点C 运动.过点N 作NP ⊥BC ,交AC 于P ,连结MP .已知动点运动了x 秒.1.P 点的坐标为( ______,_____ );(⽤含x 的代数式表⽰).2.试求三⾓形MPA ⾯积的最⼤值,并求此时x 的值.3.探索:当x 为何值时,三⾓形MPA 是⼀个等腰三⾓形?你发现了⼏种情况?写出你的研究成果.【答案】解:(1)由题意可知C (0,4),⼜A (3,0),所以直线AC 解析式为:443y x =-+,因为P 点的横坐标与N 点的横坐标相同为3﹣x ,代⼊直线AC 中得43y x =,所以P 点坐标为(43,3x x -);(2)设△MP A 的⾯积为S ,在△MP A 中,MA =3﹣x ,MA 边上的⾼为4 3x ,其中,0≤x ≤3 ∴214233(3)()23322S x x x =-=--+ S =(3﹣x )·x =(﹣x 2+6x )=﹣(x ﹣3)2+6 ∴S 的最⼤值为32,此时32x =;(3)延长NP 交x 轴于Q ,则有PQ ⊥OA ①若MP =P A∵PQ ⊥MA ∴MQ =QA =x .∴3x =3,∴x =1②若MP =MA ,则MQ =3﹣2x ,43PQ x =,PM =MA =3﹣x 在Rt △PMQ 中,∵PM 2=MQ 2+PQ 2∴2224(3)(32)()3x x x -=-+ ∴5443x =③若P A=AM,∵53PA x=,AM=3﹣x∴533x x=-∴98x=综上所述,x=1,或5443x=或98x=.第四模块:其它类型例4如图,在直⾓梯形ABCD中,AD∥BC,∠C=900,BC=16,DC=12,AD=21,动点P从D出发,沿射线DA的⽅向以每秒2个单位长度的速度运动,动点Q从点C出发,经线段CB上以每秒1个单位长度的速度向点B运动,点P、Q分别从D、C同时出发,当点Q运动到点B时,点P随之停⽌运动.设运动时间为t秒.(1)设△BPQ的⾯积为S,求S与t之间的函数关系式.(2)当t为何值时,以B、P、Q三点为项点的三⾓形是等腰三⾓形?【答案】解:(1)如图,过点P作PM⊥BC,垂⾜为M,则四边形PDCM为矩形.∴PM=DC=12.∵QB=16﹣t,∴S=12×12×(16﹣t)=96﹣6t(0≤t<16);(2)由图可知:CM=PD=2t,CQ=t.以B、P、Q三点为顶点的三⾓形是等腰三⾓形,可以分三种情况:①若PQ=BQ.在Rt△PMQ中,PQ2=t2+122,由PQ2=BQ2得t2+122=(16﹣t)2,解得72t=;②若BP=BQ.在Rt△PMB中,BP2=(16﹣2t)2+122.由BP2=BQ2得:(16﹣2t)2+122=(16﹣t)2即3t2﹣32t+144=0.由于△=﹣704<0,BACQDPM∴3t 2﹣32t +144=0⽆解,∴PB ≠BQ .③若PB =PQ .由PB 2=PQ 2,得t 2+122=(16﹣2t )2+122 整理,得3t 2﹣64t +256=0.解得1163t =,t 2=16(不合题意,舍去)综合上⾯的讨论可知:当72t =秒或163t =秒时,以B 、P 、Q 三点为顶点的三⾓形是等腰三⾓形.综合训练:(江苏)如图,已知⼀次函数y =-x +7与正⽐例函数y =43x 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停⽌运动.在运动过程中,设动点P 运动的时间为t 秒.① t 为何值时,以A 、P 、R 为顶点的三⾓形的⾯积为8?②是否存在以A 、P 、Q 为顶点的三⾓形是等腰三⾓形?若存在,求t 的值;若不存在,请说明理由.【答案】(1)根据题意,得743y x y x =-+??=,解得 34x y =??=?,∴A (3,4) . 令y =-x +7=0,得x =7.∴B (7,0). (2)①当P 在OC 上运动时,0≤t <4.由S △APR =S 梯形COBA -S △ACP -S △PQR -S △ARB =8,得 12(3+7)×4-12×3×(4-t )- 12t (7-t )- 12t ×4=8 整理,得t 2-8t +12=0, 解之得t 1=2,t 2=6(舍)当P 在CA 上运动,4≤t <7.由S △APR = 12×(7-t ) ×4=8,得t =3(舍)∴当t =2时,以A 、P 、R 为顶点的三⾓形的⾯积为8. ②当P 在OC 上运动时,0≤t <4. ∴AP=(4-t )2+32,AQ=2t ,PQ =7-t 当AP =AQ 时,(4-t )2+32=2(4-t )2,整理得,t 2-8t +7=0. ∴t =1, t =7(舍) 当AP=PQ 时,(4-t )2+32=(7-t )2, 整理得,6t =24. ∴t =4(舍去) 当AQ=PQ 时,2(4-t)2=(7-t )2 整理得,t 2-2t -17=0 ∴t =1±3 2 (舍)当P 在CA 上运动时,4≤t <7. 过A 作AD ⊥OB 于D ,则AD =BD =4. 设直线l 交AC 于E ,则QE ⊥AC ,AE =RD =t -4,AP =7-t . 由cos ∠OAC= AE AQ = ACAO ,得AQ = 53(t -4).当AP=AQ 时,7-t = 53(t -4),解得t = 418.当AQ=PQ 时,AE =PE ,即AE = 12AP得t -4= 12(7-t ),解得t =5.当AP=PQ 时,过P 作PF ⊥AQ 于F AF = 12AQ = 12×53(t -4).在Rt△APF中,由cos∠P AF=AFAP=35,得AF=35AP即12×53(t-4)=35×(7-t),解得t=22643.∴综上所述,t=1或418或5或22643时,△APQ是等腰三⾓形.。
专题二:一次函数中等腰直角三角形存在性问题方法总结
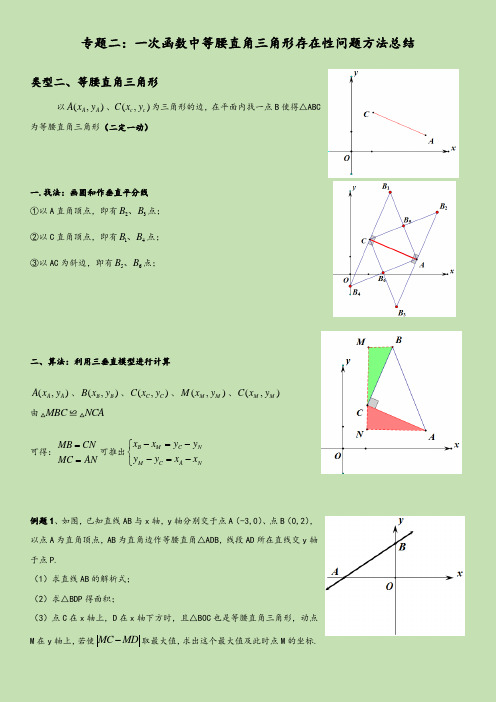
专题二:一次函数中等腰直角三角形存在性问题方法总结类型二、等腰直角三角形以(,)A A A x y 、(,)c c C x y 为三角形的边,在平面内找一点B 使得△ABC为等腰直角三角形(二定一动)一.找法:画圆和作垂直平分线①以A 直角顶点,即有23B B 、点;②以C 直角顶点,即有14B B 、点;③以AC 为斜边,即有56B B 、点;二、算法:利用三垂直模型进行计算(,)A A A x y 、(,)B B B x y 、(,)C C C x y 、(,)M M M x y 、(,)M M C x y由MBC ≌NCA可得:MB CN MC AN ==可推出B M C N M C A Nx x y y y y x x -=-⎧⎨-=-⎩例题1、如图,已知直线AB 与x 轴,y 轴分别交于点A (-3,0)、点B (0,2),以点A 为直角顶点,AB 为直角边作等腰直角△ADB ,线段AD 所在直线交y 轴于点P.(1)求直线AB 的解析式;(2)求△BDP 得面积;(3)点C 在x 轴上,D 在x 轴下方时,且△BOC 也是等腰直角三角形,动点M 在y 轴上,若使MC MD -取最大值,求出这个最大值及此时点M 的坐标.【答案】(1)AB 解析式:2+23y x = (2)①1(1,3)D -- 算法:利用1AOB AID ≅ 设1(,)D m n 20(3)0(3)0m n -=--⎧⎨--=-⎩解得13m n =-⎧⎨=-⎩ 则1(1,3)D -- 同理2(5,3)D -(3)根据题意,如图:12(2,0)(2,0)C C -、(两种情况答案一样,自行分类分析)当11,,C D M 三点共线时,MC MD -取最大值,最大值为11C D 11C D 解析式:36y x =--则M (0,-6)11max 10MC MD C D -==练习:1.已知直线1:l y x b =-+与x 轴交于点A ,直线2416:33l y x =-与x 轴交于点B ,直线12l l 、交于点C ,且C 点的横坐标为1.(1)求直线1l 的解析式和点A 的坐标.(2)直线1l 与y 轴交于点D ,将1l 向上平移9个单位得3l ,3l 与x 轴、y 轴分别交于点E 、F ,点P 为3l 上一动点,连接AP 、BP ,当△ABP 的周长最小时,求△ABP 的周长和点P 的坐标.(3)将1l 绕点C 逆时针旋转,使旋转后的直线4l 过点G (-2,0),过点C 作5l 平行于x 轴,点M 、N 分别为直线4l 、5l 上两个动点,是否存在点M 、点N ,使△BMN 是以点M 为直角顶点的等腰直角三角形,若存在,求出点M 的坐标,若不存在,请说明理由.【答案】解:(1)将1x =代入直线41633y x =-,得4161433y =⨯-=-, 故点C 的坐标为(1,4)-,将C 的坐标(1,4)-代入直线y x b =-+得,41b -=-+, 解得3b =-,∴直线1:3l y x =--,令0y =,则30x --=,解得3x =-,故点A 的坐标为(3,0)-,(2)直线3l 为1l 向上平移9个单位所得,故直线3l 的解析式为:6y x =-+,令0x =,得6y =,令0y =,得6x =,故点E ,点F 的坐标分别为(6,0),(0,6), 直线2416:33l y x =-与x 轴交于点B , 令0y =,得4x =,故B 点的坐标为(4,0),取点B 关于3l 的对称点Q ,设点Q 的坐标为(,)a b ,则线段BQ 的中点坐标为(2a b +,)2b 在直线3l , ∴622b a b +=-+,(1) 且(1)14b a ⋅-=--即14b a =-,(2) 联立(1)(2)得622b a b b +⎧=-+⎪⎪⎨⎪,解得:62a b =⎧⎨=⎩, (6,2)Q ∴,直线AQ 的解析式:2293y x =+, 当ABP ∆的周长最小时,即AP BP +最小, 连接AQ ,交直线3l 于点P ,此时AP BP +最小,最小值为22(63)(20)85AQ =++-=,7AB =,此时ABP ∆的周长为785+,由22936y x y x ⎧=+⎪⎨⎪=-+⎩解得48111811x y ⎧=⎪⎪⎨⎪=⎪⎩, P ∴点坐标为48(11,18)11, (3)设4l 的解析式:y mx n =+,将(1,4)C -,(2,0)G -,代入y mx n =+得,024m n m n =-+⎧⎨-=+⎩,解得4383m n ⎧=-⎪⎪⎨⎪=-⎪⎩, 4l ∴的解析式为:4833y x =--, 1︒当点M 在直线4l 的上方时,设点(,4)N n -,点48(,)33M s s --, 过点N ,B 分别作y 轴的平行线,过点M 作x 轴的平行线,三条直线分别交于R ,S 两点,如图则R ,S 的坐标分别为48(,)33n s --,48(4,)33s --, RM s n ∴=-,48433RN s =--,4MS s =-,4833SB s =--, 90NMB ∠=︒,90NMR SMB ∴∠+∠=︒,90BMS MBS ∠+∠=︒,90S R ∠=∠=︒,MB MN =,()MNR MBS AAS ∴∆≅∆,RM SB ∴=,RN SM =, 即4833s n s -=--,484433s s --=-, 解得8s =-,16n =-,∴点M 的坐标为(8,8)-,2︒当点M 在直线4l 的下方时,设点(,4)N n -,点48(,)33M s s --, 过点N ,B 分别作y 轴的平行线,过点M 作x 轴的平行线,三条直线分别交于R ,S 两点,如图则R ,S 的坐标分别为48(,)33n s --,48(4,)33s --, RM n s ∴=-,48433RN s =+-,4MS s =-,4833SB s =+, 90NMB ∠=︒,90NMR SMB ∴∠+∠=︒,90BMS MBS ∠+∠=︒,NMR MBS ∴∠=∠,90S R ∠=∠=︒,MB MN =,()MNR MBS AAS ∴∆≅∆,RM SB ∴=,RN SM =,即4833n s s -=+,484433s s +-=-, 解得407s =,16n =, ∴点M 的坐标为40(7,72)7-, 综上点M 的坐标为(8,8)-或40(7,72)7-,练习2:7.(2020春•官渡区期末)如图,在平面直角坐标系中,直线13:4l y x =与直线2:(0)l y kx b k =+≠相交于点(,3)A a ,直线2l 与y 轴交于点(0,5)B -. (1)求直线2l 的函数解析式;(2)将OAB ∆沿直线2l 翻折得到CAB ∆,使点O 与点C 重合,AC 与x 轴交于点D .求证:四边形AOBC 是菱形;(3)在直线BC 下方是否存在点P ,使BCP ∆为等腰直角三角形?若存在,直接写出点P 坐标;若不存在,请说明理由.【答案】解:(1)直线3?:4l y x =与直线?:l y kx b =+相交于点(,3)A a , (4,3)A ∴, 直线交?l 交y 轴于点(0,5)B -,5y kx ∴=-,把(4,3)A 代入得,345k =-,2k ∴=,∴直线2l 的解析式为25y x =-;(2)22345OA =+=,OA OB ∴=,将OAB ∆沿直线?l 翻折得到CAB ∆,OB OC ∴=,OA AC =,OA OB BC AC ∴===,∴四边形AOBC 是菱形;(3)如图,过C 作CM OB ⊥于M ,则4CM OD ==,5BC OB ==,3BM ∴=,(4,2)C ∴-, 过1P 作1PN y ⊥轴于N , BCP ∆是等腰直角三角形, 190CBP ∴∠=︒,1MCB NBP ∴∠=∠, 1BC BP =,BCM ∴∆≅△1()PBN AAS , 4BN CM ∴==, 1(3,9)P ∴-;同理可得,2(7,6)P -,37(2P ,11)2-. 综上所述,点P 的坐标是(3,9)-或(7,6)-或7(2P ,11)2-.。
中考数学培优:等腰三角形存在性问题

中考数学培优:等腰三角形存在性问题【例题讲解】例题1.如图,直线l 1、12相交于点A ,点B 是直线外一点,在直线l 1、12上找一点C ,使△ABC 为一个等腰三角形.满足条件的点C 有个.【提示】①以B 为圆心,线段BA 长为半径作圆,与l 1、12交点即为满足条件点C ;②以A 为圆心,线段BA 长为半径作圆,与l 1、12交点即为满足条件点C ;③作线段AB 的垂直平分线,与l 1、12交点即为满足条件点C.(此方法简称为“两圆一线”)【巩固训练】1、一次函数y =43x +4分别交x 轴、y 轴于A 、B 两点,在坐标轴上取一点C ,使△ABC 为等腰三角形,则这样的点C 最多有个。
2、已知△ABC 的三条边长分别为3,4,6,在△ABC 所在平面内画一条直线,将△ABC 分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画()A.6条B.7条C.8条D.9条例题2.一次函数y =43x +4分别交x 轴、y 轴于A 、B 两点,在y 轴上取一点C ,使得AC =BC ,求出C 点坐标?【代数法、几何法均可解】解:如图所示,直线AB 的解析式为y =43x +4,当y =0时,x =-3,则A (-3.0);当x =0时,y =4,则B (0,4)。
设C 点坐标为(x .0),在Rt △AOB 中,由勾股定理得5==,在Rt △BOC 中,由勾股定理得BC =。
①当以AB 为底时,AC =BC ,则3+x 整理得6x =7,解得x =76,则(76,0);②当以BC 为底时,可得AC =AB ,则35x --=,解得x =2或-8,则C (2,0)或(-8,0);③当以AC 为底时,可得AB =BC ,整理得x 2=9,解得x =±3,则C (3,0)或(-3,0)(舍去)。
综上所述,满足条件的点C 的坐标是(76,0)或(2,0)或(3,0)或(-8,0)例题3.如图,直线x =-4与x 轴交于点E ,一开口向上的抛物线过原点交线段OE 于点A ,交直线x =-4于点B ,过B 且平行于x 轴的直线与抛物线交于点C ,直线OC 交直线AB 于D ,且AD :BD =1:3.(1)求点A 的坐标;(2)若△OBC 是等腰三角形,求此抛物线的函数关系式.解:(1)如图过点D 作DF ⊥x 轴于点F .由题意可知OF =AF 则2AF +AE =4①∵DF ∥BE ,∴△ADF ∽△ABE ,∴12AF AD AE AB ==,即AE =2AF ②①与②联立解得AE =2,AF =1.∴点A 的坐标为(-2,0);(2)∵抛物线过原点(0,0),∴可设此抛物线的解析式为y =ax 2+bx∵抛物线过原点(0,0)和A 点(-2,0),∴对称轴为直线x =202-+=-1∵B 、C 两点关于直线x =-1对称B 点横坐标为-4,∴C 点横坐标为2,∴BC =2-(-2)=6∵抛物线开口向上,∴∠OAB >90°,OB >AB =OC .∴当△OBC 是等腰三角形时分两种情况讨论:①当OB =BC 时设B (-4,y 1),则16+y 12=36解得y 1=±(负值舍去).将A (-2,0),B (-4,)代入y =ax 2+bx得420164a b a b -=⎧⎪⎨-=⎪⎩解得5452a b ⎧=⎪⎪⎨⎪=⎪⎩∴此抛物线的解析式为yx 2x ②当OC =BC 时设C (2,y 2),则4+y 22=36解得y 2=±负值舍去)将A (-2,0),C(2,代入y =ax 2+bx ,得42042a b a b -=⎧⎪⎨+=⎪⎩,解得2a b ⎧=⎪⎨⎪=⎩∴此抛物线的解析式为y =22x 2x 例题4.如图甲,在△ABC 中,∠ACB =90°,AC =4cm,BC =3cm.如果点P 由点B 出发沿BA 方向向点A 匀速运动,同时点Q 由点A 出发沿AC 方向向点C 匀速运动,它们的速度均为1cm /s .连接PQ ,设运动时间为t (s )(0<t <4),解答下列问题:(1)设△APQ 的面积为S ,请写出S 关于t 的函数表达式?(2)如图乙,连接PC ,将△POC 沿QC 翻折,得到四边形PQP 'C ,当四边形PQP 'C 为菱形时,求t 的值;(3)当t 为何值时,△APQ 是等腰三角形?解:(1)如图1,过点P 作PH ⊥AC 于H ,∵∠C =90°,∴AC ⊥BC ,∴PH ∥BC ,∴△APH ∽△ABC ,∴PH AP BC AB =,∵AC =4cm ,BC =3cm ,∴AB =5cm ∴535PH t -=,∴PH =3-35t ,∴△AQP 的面积为:S =12×AQ ×PH =12×t ×(3-35t )=23518()1025t --+∴当t 为52秒时,S 最大值为185cm 2.(2)如图2,连接PP ',PP '交QC 于E ,当四边形PQP 'C 为菱开时,PE 垂直平分QC ,即PE ⊥AC ,QE =EC ,∴△APE ∽△ABC ,∴AE AP AC AB =,∴AE =(5)44455AP AC t t AB ⋅-⨯==-+∴QE =AE -AQ =45t -+4-t =95t -+4,QE =12QC =12(4-t )=12-t +2∴95t -+4=12-t +2,∴解得:t =2013,∵0<2013<4.∴当四边形PQP 'C 为菱形时,t 值是2013秒;(3)由(1)知,PD =335t -+,与(2)同理得:QD =AD -AQ =945t -+∴PQ ==在△APQ 中,①当AQ =AP ,即=5-t 时,解得:t 1=52,②当PQ =AQ ,t 时,解得:t 2=2513,t 3=5.③当PQ =AP-t 时,解得:t 4=0,t 5=4013∵0<t<4,∴t 3=5,t 4=0不合题意,舍去,∴当t 为52s 或2513s 或4013s 时,△APQ 是等腰三角形.例题5.已知,如图,在Rt △ABC 中,AC =6,AB =8,D 为边AB 上一点,连接CD ,过点D 作DE ⊥DC 交BC 与E ,把△BDE 沿DE 翻折得△DE B 1,连接B 1C(1)证明:∠ADC =∠B 1DC ;(2)当B 1E /∥AC 时,求折痕DE 的长;(3)当△B 1CD 为等腰三角形时,求AD 的长.解:(1)证明由折叠的性质得:∠BDE =∠B 1DE ,∵DE ⊥DC ,∴∠ADC =180°-90°-∠BDE =90°-∠BDE ,∠B 1DC =90°-∠B 1DE ,∴∠ADC =∠B 1DC(2)解延长B 1E 交AB 于F .∵B 1E ∥AC ,∠A =90°,∴B 1F ⊥AB ,∴∠EB 1D +∠BDB 1=90°.∵∠B =∠EB 1D ,∴∠B +∠BDB 1=90°,∴∠BGD =90°,在△BDC 和△B 1FD 中,111B EB D BGD B FD BD DB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDG ≌△B 1FD .∴DF =DG ,在△ADC 和△GDC 中,90ADC CDG A DGC DC DC ∠=∠⎧⎪∠=∠=⎨⎪=⎩o ,∴△ADC ≌△GDC ,∴DG =AD .∴DF =AD =DG ,设DF =AD =DG =x ,∴BF =8-2x ,∵EF ∥AC ,∴△BFE ∽△BAC ,∴EF BF AC AB =,∴EF =1232x -,∵△EFD ∽△ACD ,∴DF EF AC AD=,∴12326x x x -=,解得:x =3,∴BF =3,EF =32,∴DE.(3)解设AD =x ,则CD,BD =8-x ,∵△B 1CD 是等腰三角形,①当B 1D =B 1C 时则∠B 1DC =∠B 1CD ,∴DB 1=BD =8-x ,如图2过B 1作B 1F ⊥CD ,则DF =CF =12CD=2,∵∠ADC =∠B 1DC ,∠B 1FD =∠A =90°,∴△CDA ∽△B 1DC ,∴1B D DF CD AD =,2x =,∴3x 2-16x +36=0,此方程无实数根.∴B 1D ≠BC .②B 1D =CD 时,∴B 1D =CD =BD =8-x .∴(8-x )2=x 2+6,∴x =74,∴AD =74.③当CD =BC 时如图2过C 作CH ⊥DB ,则DH =B 1H =12DB 1=12BD =12(8-x )在△ACD 和△CHD 中,90ADC CDH A CHD CD CD ∠=∠⎧⎪∠=∠=⎨⎪=⎩o ∴△ACD ≌△CHD ,∴AD =DH =x∴x =12(8-x ),∴x =83,∴AD =83,综上所述:当△B 1CD 是等腰三角形时AD 的长为74或83.【巩固训练】1.如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出不同的等腰三角形的个数最多为()A.4B.5C.6D.72.如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,使得△BPC是一个等腰三角形.(1)用尺规作图画出符合要求的点P.(保留作图痕迹,不要求写做法)(2)求出PA的长.3.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)4.如图,一长度为10的线段AC的两个端点A、C分别在y轴和x轴的正半轴上滑动,以A为直角顶点,AC为直角边在第一象限内作等腰直角△ABC,连接BO.(1)求OB的最大值;(2)在AC滑动过程中,△OBC能否恰好为等腰三角形?若能,求出此时点A的坐标;若不能,请说明理由.5、如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-2x+3与y轴交于点C,与x轴交于点D,点P是x轴上方的抛物线上一动点,过点P作PF⊥x.轴于点F,交直线CD于点E,设点P的横坐标为m.(1)求抛物线的解析式;(2)若△PCE为等腰三角形,求m的值.6.如图,在平面直角坐标系中,点A的坐标为(12,-8),点B、C在x轴上,tan∠ABC=43,AB=AC,AH⊥BC 于H,D为AC的中点,BD交AH于点M.(1)求过B、C、D三点的抛物线的解析式,并求出抛物线顶点E的坐标;(2)过点E且平行于AB的直线l交y轴于点G,若将(2)中的抛物线沿直线1平移,平移后的抛物线交y轴于点F,顶点为E'(点E'在y轴右侧).是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时顶点E'的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中点B坐标为(6,0),点A在第一象限,△AOB为等边三角形,OH⊥AB于点H,动点P、Q分别从B、O两点同时出发,分别沿BO、OA方向匀速移动,它们的速度都是1cm/s,当点P到达点O时,P、Q两点停止运动,设点P的运动时间为t(s),PQ交OH于点M,设四边形AQPB的面积为y.(1)求y与t之间的函数关系式;(2)设PQ的长为x(cm)试确定y与x之间的函数关系式;(3)当t为何值时,△OPM为等腰三角形;(4)线段OM有最大值吗?如果有,请求出来;如果没有,请说明理由.8.已知:如图,在矩形ABCD中,AB=5,AD=20.E为矩形外一点,且△EBA∽△ABD.3(1)求AE和BE的长;(2)将△ABE绕点B顺时针旋转一个角a(0°<α<180°),记旋转中的△ABE为△A'BE',在旋转过程中,设A'E'所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.9.如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
lBA第 讲:等腰三角形存在性问题专题训练一、等腰三角形4大性质 (1)等边对等角、等角对等边; (2)三线合一;(3)含有60°角的等腰三角形是等边三角形;(4)等腰三角形底边上任意一点到两腰的距离等于腰上的高; 二、构造等腰三角形二、特殊的等腰三角形(1)等边三角形; (2)等腰直角三角形; (3)底角为30°的等腰三角形; (4)黄金三角形 一、模型引入引入:如图,已知线段AB ,在过A 点的直线l 上求作点P ,使△ABP 为等腰三角形.思维提升:在平面直角坐标系内,已知点A (2,1),O 为坐标原点.请你在坐标轴上确定点P ,使得ΔAOP 为等腰三角形.在给出的坐标系中把所有这样的点P 都找出来,画上实心点,并在旁边标上P 1,P 2,……,P k ,(有k 个就标到P K 为止,不必写出画法)【答案】二、典型分析例1.如图,在等腰梯形ABCD 中,AD //BC ,BC =4AD =24,∠B =45°.直角三角板含45°角的顶点E 在边BC 上移动,一直角边始终经过点A ,斜边与CD 交于点F .若△ABE 为等腰三角形,则CF 的长等于 . 【答案】,2,. 例2.如图,四边形OABC 是一张放在平面直角坐标系中的正方形纸片.点O 与坐标原点重合,点A 在x 轴上,点C 在y 轴上,OC =4,点E 为BC 的中点,点N 的坐标为(30),,过点N 且平行于y 轴的直线MN 与EB 交于点M .现将纸片折叠,使顶点C 落在MN 上,并与MN 上的点G 重合,折痕为EF ,点F 为折痕与y 轴的交点.(1)求点G 的坐标;(2)求折痕EF 所在直线的解析式;(3)设点P 为直线EF 上的点,是否存在这样的点P ,使得以P 、F 、G 为顶点的三角形为等腰三角形,若存在,请直接写出点P 的坐标;若不存在,请说明理由.52423DBCAEFF【答案】解:(1)四边形ABCO 是正方形,4BC OA ∴==,E 为CB 中点,2EB ∴=MN y ∥轴,(30)N ,,MN EB ∴⊥且1MB NA ==1EM ∴=而2EG EC ==,1sin 2EM EGM EG ∴∠==30EGM ∴∠=cos303MG EG ∴==·,(343)G ∴-,(2)30EGM ∠=60MEG FEG CEF ∴∠=∠=∠=tan 6023CF CE ∴==·423FO ∴=-(0423)F ∴-,,(24)E ,设直线EF 的解析式:(0)y kx b k =+≠24423k b b +=⎧⎪∴⎨=-⎪⎩ 3423k b ⎧=⎪∴⎨=-⎪⎩ ∴折痕EF 所在直线解析式:3423y x =+-(3)12(3123)(143)P P ---,,,,34(3723)(343)P P -+,,, 综合训练(2011湖南)如图(11)所示,在平面直角坐标系Oxy 中,已知点A (94-,0),点C (0,3),点B 是x 轴上一点(位于点A 的右侧),以AB 为直径的圆恰好经过....点C . (1)求∠ACB 的度数;(2)已知抛物线y =ax 2+bx +3经过A 、B 两点,求抛物线的解析式;(3)线段BC 上是否存在点D ,使△BOD 为等腰三角形.若存在,则求出所有符合条件的点D 的坐标;若不存在,请说明理由. 【答案】(1)∵以AB 为直径的圆恰好经过....点C ∴∠ACB =090(2) ∵△AOC ∽△ABC ∴OB AO OC •=2∵A (-94,0),点C (0,3), ∴49=AO 3=OC ∴OB 4932=∴ 4=OB ∴B (4,0) 把 A 、B 、C 三点坐标代入得 3127312++-=x x y (3)①OD =OB , D 在OB 的中垂线上,过D 作DH ⊥OB ,垂足是H ,则H 是OB 中点.DH =OC 21 OB OH 21= ∴D )23,2( ② BD =BO 过D 作DG ⊥OB ,垂足是G ∴OG :OB =CD :CB DG :OC =1:5 ∴ OG :4=1:5 DG :3=1:5 ∴OG =54 DG =53∴D (54,53)第三模块:双动点情况等腰三角形存在性问题 一、模型引入xyCBA O 图11BAO二、典例分析例3(济南)如图,在梯形ABCD 中,AD //BC ,AD =3,DC =5,AB =24,∠B =45°.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒. (1)求BC 的长.(2)试探究:t 为何值时,△MNC 为等腰三角形. 【答案】(1)如图①,过A 、D 分别作AK BC ⊥于K ,DH BC ⊥于H ,则四边形ADHK 是矩形∴3KH AD ==.在Rt ABK △中,2sin 454242AK AB =•︒=•= 2cos 454242BK AB =•︒=•=在Rt CDH △中,由勾股定理得,22543HC =-= ∴43310BC BK KH HC =++=++= (2)分三种情况讨论:①当NC MC =时,如图②,即102t t =- ∴103t =OBAADCBM NOABADCB MN(图②)(题图③)AD CBM NH E(图①)A DCBK H②当MN NC =时,如图③,过N 作NE MC ⊥于E 解法一:由等腰三角形三线合一性质得()11102522EC MC t t ==-=- 在Rt CEN △中,5cos EC t c NC t -==又在Rt DHC △中,3cos 5CH c CD ==∴535t t -= 解得258t =解法二:∵90C C DHC NEC =∠=∠=︒∠∠, ∴NEC DHC △∽△∴NC ECDC HC =即553t t -= ∴258t = ③当MN MC =时,如图④,过M 作MF CN ⊥于F 点.1122FC NC t == 解法一:(方法同②中解法一)132cos 1025tFC C MC t ===- 解得6017t =解法二:∵90C C MFC DHC =∠=∠=︒∠∠, ∴MFC DHC △∽△∴FC MCHC DC =即1102235tt -=∴6017t = 综上所述,当103t =、258t =或6017t =时,MNC △为等腰三角形.同类训练:平面直角坐标系中,四边形OABC 为矩形,点A 、B 的坐标分别为(3,0),(3,4).动点M 、N 分别从O 、B 同时出发,以每秒1个单位的速度运动.其中,点M 沿OA 向终(图④)ADCBH N MF点A 运动,点N 沿BC 向终点C 运动.过点N 作NP ⊥BC ,交AC 于P ,连结MP .已知动点运动了x 秒.1.P 点的坐标为( ______,_____ );(用含x 的代数式表示).2.试求三角形MPA 面积的最大值,并求此时x 的值.3.探索:当x 为何值时,三角形MPA 是一个等腰三角形?你发现了几种情况?写出你的研究成果.【答案】解:(1)由题意可知C (0,4),又A (3,0), 所以直线AC 解析式为:443y x =-+, 因为P 点的横坐标与N 点的横坐标相同为3﹣x ,代入直线AC 中得43y x =, 所以P 点坐标为(43,3x x -); (2)设△MP A 的面积为S ,在△MP A 中,MA =3﹣x ,MA 边上的高为43x , 其中,0≤x ≤3 ∴214233(3)()23322S x x x =•-•=--+ S =(3﹣x )·x =(﹣x 2+6x )=﹣(x ﹣3)2+6 ∴S 的最大值为32,此时32x =;(3)延长NP 交x 轴于Q ,则有PQ ⊥OA ①若MP =P A∵PQ ⊥MA ∴MQ =QA =x . ∴3x =3, ∴x =1②若MP =MA ,则MQ =3﹣2x ,43PQ x =,PM =MA =3﹣x 在Rt △PMQ 中, ∵PM 2=MQ 2+PQ 2∴2224(3)(32)()3x x x -=-+ ∴5443x =③若P A=AM,∵53PA x=,AM=3﹣x∴533x x=-∴98x=综上所述,x=1,或5443x=或98x=.第四模块:其它类型例4如图,在直角梯形ABCD中,AD∥BC,∠C=900,BC=16,DC=12,AD=21,动点P从D出发,沿射线DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,经线段CB上以每秒1个单位长度的速度向点B运动,点P、Q分别从D、C同时出发,当点Q运动到点B时,点P随之停止运动.设运动时间为t秒.(1)设△BPQ的面积为S,求S与t之间的函数关系式.(2)当t为何值时,以B、P、Q三点为项点的三角形是等腰三角形?【答案】解:(1)如图,过点P作PM⊥BC,垂足为M,则四边形PDCM为矩形.∴PM=DC=12.∵QB=16﹣t,∴S=12×12×(16﹣t)=96﹣6t(0≤t<16);(2)由图可知:CM=PD=2t,CQ=t.以B、P、Q三点为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ.在Rt△PMQ中,PQ2=t2+122,由PQ2=BQ2得t2+122=(16﹣t)2,解得72t=;②若BP=BQ.在Rt△PMB中,BP2=(16﹣2t)2+122.由BP2=BQ2得:(16﹣2t)2+122=(16﹣t)2即3t2﹣32t+144=0.由于△=﹣704<0,BACQDPM∴3t 2﹣32t +144=0无解, ∴PB ≠BQ . ③若PB =PQ .由PB 2=PQ 2,得t 2+122=(16﹣2t )2+122 整理,得3t 2﹣64t +256=0.解得1163t =,t 2=16(不合题意,舍去) 综合上面的讨论可知:当72t =秒或163t =秒时,以B 、P 、Q 三点为顶点的三角形是等腰三角形. 综合训练:(江苏)如图,已知一次函数y =-x +7与正比例函数y =43x 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O —C —A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.① t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?② 是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由. 【答案】(1)根据题意,得743y x y x =-+⎧⎪⎨=⎪⎩,解得 34x y =⎧⎨=⎩,∴A (3,4) . 令y =-x +7=0,得x =7.∴B (7,0). (2)①当P 在OC 上运动时,0≤t <4.由S △APR =S 梯形COBA -S △ACP -S △PQR -S △ARB =8,得 12(3+7)×4-12×3×(4-t )- 12t (7-t )- 12t ×4=8整理,得t 2-8t +12=0, 解之得t 1=2,t 2=6(舍) 当P 在CA 上运动,4≤t <7.由S △APR = 12×(7-t ) ×4=8,得t =3(舍)∴当t =2时,以A 、P 、R 为顶点的三角形的面积为8. ②当P 在OC 上运动时,0≤t <4. ∴AP=(4-t )2+32,AQ=2t ,PQ =7-t 当AP =AQ 时, (4-t )2+32=2(4-t )2,整理得,t 2-8t +7=0. ∴t =1, t =7(舍) 当AP=PQ 时,(4-t )2+32=(7-t )2, 整理得,6t =24. ∴t =4(舍去) 当AQ=PQ 时,2(4-t )2=(7-t )2 整理得,t 2-2t -17=0 ∴t =1±3 2 (舍)当P 在CA 上运动时,4≤t <7. 过A 作AD ⊥OB 于D ,则AD =BD =4. 设直线l 交AC 于E ,则QE ⊥AC ,AE =RD =t -4,AP =7-t . 由cos ∠OAC= AE AQ = ACAO ,得AQ = 53(t -4).当AP=AQ 时,7-t = 53(t -4),解得t = 418.当AQ=PQ 时,AE =PE ,即AE = 12AP得t -4= 12(7-t ),解得t =5.当AP=PQ 时,过P 作PF ⊥AQ 于F AF = 12AQ = 12×53(t -4).在Rt△APF中,由cos∠P AF=AFAP=35,得AF=35AP即12×53(t-4)=35×(7-t),解得t=22643.∴综上所述,t=1或418或5或22643时,△APQ是等腰三角形.。
