备战中考数学二轮专题归纳提升真题二次函数存在性问题(1)—与三角形相关(解析版)
2024年中考数学二次函数中三角形面积最值及平行四边形存在性问题(必考知识点)

一、知识梳理1.三角形面积公式:S 2024年中考数学二次函数中三角形面积最值及平行四边形存在性问题(必考知识点)=21×底×高2.平行四边形的性质:对边相等、对角相等、对角线互相平分3.判别式法求最值:通过判别式判断二次方程的根的情况,进而求出最值二、问题分析1.三角形面积最值存在性问题:∙利用二次函数的性质和对称性,找到合适的底和高,计算三角形的面积;∙设置关于底和高的二次方程,利用判别式判断方程的根的情况,进而求出面积的最值。
2.平行四边形存在性问题:∙利用二次函数的对称性和性质,找到满足平行四边形性质的点;∙利用平行四边形的性质证明这些点构成平行四边形。
三、例题解析【例1】已知抛物线y=x2−2x和直线y=2x+b相交于A、B两点,且∠AOB=90°,其中O为坐标原点。
求△AOB的面积。
【答案】联立方程组:y=x2−2x,y=2x+b.消去y得:x2−4x−b=0.由于直线与抛物线有两个交点,所以判别式Δ>0:Δ=16+4b>0⇒b>−4.设交点A、B坐标分别为(x1,y1)和(x2,y2),由韦达定理得:x1+x2=4,x1x2=−b.由于∠AOB=90,所以x1x2+y1y2=0。
代入y1=2x1+b和y2=2x2+b,解得:−b+(2x1+b)(2x2+b)=0.化简得:−b−4b+8b+b2=0⇒b2+3b=0.解得:b=−3或b=0。
当b=0时,A、B坐标分别为(0,0)和(4,8),点A和点O重合,不符合条件。
因此,b =−3,代入方程组得A (1,-1),B (3,3)。
所以,△AOB 的面积为:S =21×∣O A ∣×∣O B ∣=21×2211)()(-+×2233)()(+=21×2×18=3.【例2】抛物线6221y 2--=x x 与x 轴相交于点A 、点B ,与y 轴相交于点C 。
中考数学复习---二次函数中三角形存在性问题压轴题练习(含答案解析)

中考数学复习---二次函数中三角形存在性问题压轴题练习(含答案解析)一.相似三角形的存在性1.(2022•陕西)已知抛物线y=ax2+bx﹣4经过点A(﹣2,0),B(4,0),与y 轴的交点为C.(1)求该抛物线的函数表达式;(2)若点P是该抛物线上一点,且位于其对称轴l的右侧,过点P分别作l,x 轴的垂线,垂足分别为M,N,连接MN.若△PMN和△OBC相似,求点P的坐标.【解答】解:(1)把A(﹣2,0),B(4,0)代入y=ax2+bx﹣4得:,解得,∴抛物线的函数表达式为y=x2﹣x﹣4;(2)如图:∵y=x2﹣x﹣4=(x﹣1)2﹣,∴抛物线y=x2﹣x﹣4的对称轴是直线x=1,在y=x2﹣x﹣4中,令x=0得y=﹣4,∴C(0,﹣4),∴OB=OC=4,∴△BOC是等腰直角三角形,∵△PMN和△OBC相似,∴△PMN是等腰直角三角形,∵PM⊥直线x=1,PN⊥x轴,∴∠MPN=90°,PM=PN,设P(m,m2﹣m﹣4),∴|m﹣1|=|m2﹣m﹣4|,∴m﹣1=m2﹣m﹣4或m﹣1=﹣m2+m+4,解得m=+2或m=﹣+2或m=或m=﹣,∵点P是该抛物线上一点,且位于其对称轴直线x=1的右侧,∴P的坐标为(+2,+1)或(,1﹣).2.(2022•绵阳)如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.(1)求抛物线的解析式;(2)在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°,若存在,求出点P的坐标,若不存在,请说明理由;(3)过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与△ADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.【解答】解:(1)∵顶点D的横坐标为1,∴抛物线的对称轴为直线x=1,∵A(﹣1,0),∴B(3,0),∴设抛物线的解析式为:y=a(x+1)(x﹣3),将C(0,3)代入抛物线的解析式,则﹣3a=3,解得a=﹣1,∴抛物线的解析式为:y=﹣(x+1)(x﹣3)=﹣x2+2x+3.(2)存在,P(0,﹣1),理由如下:∵∠APB+∠ACB=180°,∴∠CAP+∠CBP=180°,∴点A,C,B,P四点共圆,如图所示,由(1)知,OB=OC=3,∴∠OCB=∠OBC=45°,∴∠APC=∠ABC=45°,∴△AOP是等腰直角三角形,∴OP=OA=1,∴P(0,﹣1).(3)存在,理由如下:由(1)知抛物线的解析式为:y=﹣x2+2x+3,∴D(1,4),由抛物线的对称性可知,E(2,3),∵A(﹣1,0),∴AD=2,DE=,AE=3.∴AD2=DE2+AE2,∴△ADE是直角三角形,且∠AED=90°,DE:AE=1:3.∵点M在直线l下方的抛物线上,∴设M(t,﹣t2+2t+3),则t>2或t<0.∴EF=|t﹣2|,MF=3﹣(﹣t2+2t+3)=t2﹣2t,若△MEF与△ADE相似,则EF:MF=1:3或MF:EF=1:3,∴|t﹣2|:(t2﹣2t)=1:3或(t2﹣2t):|t﹣2|=1:3,解得t=2(舍)或t=3或﹣3或(舍)或﹣,∴M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).综上,存在点M,使以M,F,E三点为顶点的三角形与△ADE相似,此时点M的坐标为(3,0)或(﹣3,﹣12)或(﹣,).3.(2022•恩施州)在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+c与y 轴交于点P(0,4).(1)直接写出抛物线的解析式.(2)如图,将抛物线y=﹣x2+c向左平移1个单位长度,记平移后的抛物线顶点为Q,平移后的抛物线与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.判断以B、C、Q三点为顶点的三角形是否为直角三角形,并说明理由.(3)直线BC与抛物线y=﹣x2+c交于M、N两点(点N在点M的右侧),请探究在x轴上是否存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似,若存在,请求出点T的坐标;若不存在,请说明理由.(4)若将抛物线y=﹣x2+c进行适当的平移,当平移后的抛物线与直线BC最多只有一个公共点时,请直接写出抛物线y=﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标.【解答】解:(1)∵抛物线y=﹣x2+c与y轴交于点P(0,4),∴c=4,∴抛物线的解析式为y=﹣x2+4;(2)△BCQ是直角三角形.理由如下:将抛物线y=﹣x2+4向左平移1个单位长度,得新抛物线y=﹣(x+1)2+4,∴平移后的抛物线顶点为Q(﹣1,4),令x=0,得y=﹣1+4=3,∴C(0,3),令y=0,得﹣(x+1)2+4=0,解得:x1=1,x2=﹣3,∴B(﹣3,0),A(1,0),如图1,连接BQ,CQ,PQ,∵P(0,4),Q(﹣1,4),∴PQ⊥y轴,PQ=1,∵CP=4﹣3=1,∴PQ=CP,∠CPQ=90°,∴△CPQ是等腰直角三角形,∴∠PCQ=45°,∵OB=OC=3,∠BOC=90°,∴△BOC是等腰直角三角形,∴∠BCO=45°,∴∠BCQ=180°﹣45°﹣45°=90°,∴△BCQ是直角三角形.(3)在x轴上存在点T,使得以B、N、T三点为顶点的三角形与△ABC相似.∵△ABC是锐角三角形,∠ABC=45°,∴以B、N、T三点为顶点的三角形与△ABC相似,必须∠NBT=∠ABC=45°,即点T在y轴的右侧,设T(x,0),且x>0,则BT=x+3,∵B(﹣3,0),A(1,0),C(0,3),∴∠ABC=45°,AB=4,BC=3,设直线BC的解析式为y=kx+b,则,解得:,∴直线BC的解析式为y=x+3,由,解得:,,∴M(﹣,),N(,),∴BN=×=,①当△NBT∽△CBA时,则=,∴=,解得:x=,∴T(,0);②当△NBT∽△ABC时,则=,∴=,解得:x=,∴T(,0);综上所述,点T的坐标T(,0)或(,0).(4)抛物线y=﹣x2+4的顶点为P(0,4),∵直线BC的解析式为y=x+3,∴直线BC与y轴的夹角为45°,当抛物线沿着垂直直线BC的方向平移到只有1个公共点时,平移距离最小,此时向右和向下平移距离相等,设平移后的抛物线的顶点为P′(t,4﹣t),则平移后的抛物线为y=﹣(x﹣t)2+4﹣t,由﹣(x﹣t)2+4﹣t=x+3,整理得:x2+(1﹣2t)x+t2+t﹣1=0,∵平移后的抛物线与直线BC最多只有一个公共点,∴Δ=(1﹣2t)2﹣4(t2+t﹣1)=0,解得:t=,∴平移后的抛物线的顶点为P′(,),平移的最短距离为.二.直角三角形的存在性4.(2022•广安)如图,在平面直角坐标系中,抛物线y=ax2+x+m(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,﹣4),点C 坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)点P为该抛物线对称轴上的动点,使得△P AB为直角三角形,请求出点P 的坐标.【解答】解:(1)∵抛物线y=ax2+x+m(a≠0)的图象经过点B(0,﹣4),点C(2,0),∴,解得,∴抛物线的解析式为y=x2+x﹣4;(2)存在.理由:如图1中,设D (t ,t 2+t ﹣4),连接OD .令y =0,则x 2+x ﹣4=0,解得x =﹣4或2,∴A (﹣4,0),C (2,0),∵B (0,﹣4),∴OA =OB =4,∵S △ABD =S △AOD +S △OBD ﹣S △AOB =×4×(﹣﹣t +4)+×4×(﹣t )﹣×4×4=﹣t 2﹣4t =﹣(t +2)2+4,∵﹣1<0,∴t =﹣2时,△ABD 的面积最大,最大值为4,此时D (﹣2,﹣4); (3)如图2中,设抛物线的对称轴交x 轴于点N ,过点B 作BM ⊥抛物线的对称轴于点M .则N (﹣1.0).M (﹣1,﹣4);∵OA=OB=4,∠AOB=90°,∴∠OAB=∠OBA=45°,当∠P1AB=90°时,△ANP1是等腰直角三角形,∴AN=NP1=3,∴P1(﹣1,3),当∠ABP2=90°时,△BMP2是等腰直角三角形,可得P2(﹣1,﹣5),当∠APB=90°时,设P(﹣1,n),设AB的中点为J,连接PJ,则J(﹣2,﹣2),∴PJ=AB=2,∴12+(n+2)2=(2)2,解得n=﹣2或﹣﹣2,∴P3(﹣1,﹣2),P4(﹣1,﹣﹣2),综上所述,满足条件的点P的坐标为(﹣1,3)或(﹣1,﹣5)或(﹣1,﹣2)或(﹣1,﹣﹣2).5.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC 于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.(1)求抛物线的解析式;(2)当点D在第二象限且=时,求点D的坐标;(3)当△ODF为直角三角形时,请直接写出点D的坐标.【解答】解:(1)将点A(﹣4,0),C(0,4)代入y=ax2﹣3x+c,∴,解得,∴y=﹣x2﹣3x+4;(2)过点D作DG⊥AB交于G,交AC于点H,设直线AC的解析式为y=kx+b,∴,解得,∴y=x+4,设D(n,﹣n2﹣3n+4),H(n,n+4),∴DH=﹣n2﹣4n,∵DH∥OC,∴==,∵OC=4,∴DH=3,∴﹣n2﹣4n=3,解得n=﹣1或n=﹣3,∴D(﹣1,6)或(﹣3,4);(3)设F(t,t+4),当∠FDO=90°时,过点D作MN⊥y轴交于点N,过点F作FM⊥MN交于点M,∵∠DOF=45°,∴DF=DO,∵∠MDF+∠NDO=90°,∠MDF+∠MFD=90°,∴∠NDO=∠MFD,∴△MDF≌△NOD(AAS),∴DM=ON,MF=DN,∴DN+ON=﹣t,DN=ON+(﹣t﹣4),∴DN=﹣t﹣2,ON=2,∴D点纵坐标为2,∴﹣x2﹣3x+4=2,解得x=或x=,∴D点坐标为(,2)或(,2);当∠DFO=90°时,过点F作KL⊥x轴交于L点,过点D作DK⊥KL交于点K,∵∠KFD+∠LFO=90°,∠KFD+∠KDF=90°,∴∠LFO=∠KDF,∵DF=FO,∴△KDF≌△LFO(AAS),∴KD=FL,KF=LO,∴KL=t+4﹣t=4,∴D点纵坐标为4,∴﹣x2﹣3x+4=4,解得x=0或x=﹣3,∴D(0,4)或(﹣3,4);综上所述:D点坐标为(,2)或(,2)或(0,4)或(﹣3,4).三.等腰三角形的存在性6.(2022•百色)已知抛物线经过A(﹣1,0)、B(0,3)、C(3,0)三点,O 为坐标原点,抛物线交正方形OBDC的边BD于点E,点M为射线BD上一动点,连接OM,交BC于点F.(1)求抛物线的表达式;(2)求证:∠BOF=∠BDF;(3)是否存在点M,使△MDF为等腰三角形?若不存在,请说明理由;若存在,求ME的长.【解答】(1)解:设抛物线的表达式为y=ax2+bx+c,把A(﹣1,0)、B(0,3)、C(3,0)代入得:,解得,∴抛物线的表达式为:y=﹣x2+2x+3;(2)证明:∵正方形OBDC,∴∠OBC=∠DBC,BD=OB,∵BF=BF,∴△BOF≌△BDF,∴∠BOF=∠BDF;(3)解:∵抛物线交正方形OBDC的边BD于点E,∴令y=3,则3=﹣x2+2x+3,解得:x1=0,x2=2,∴E(2,3),①如图,当M在线段BD的延长线上时,∠BDF为锐角,∴∠FDM为钝角,∵△MDF为等腰三角形,∴DF=DM,∴∠M=∠DFM,∴∠BDF=∠M+∠DFM=2∠M,∵BM∥OC,∴∠M=∠MOC,由(2)得∠BOF=∠BDF,∴∠BDF+∠MOC=3∠M=90°,∴∠M=30°,在Rt△BOM中,BM=,∴ME=BM﹣BE=3﹣2;②如图,当M在线段BD上时,∠DMF为钝角,∵△MDF为等腰三角形,∴MF=DM,∴∠BDF=∠MFD,∴∠BMO=∠BDF+∠MFD=2∠BDF,由(2)得∠BOF=∠BDF,∴∠BMO=2∠BOM,∴∠BOM+∠BMO=3∠BOM=90°,∴∠BOM=30°,在Rt△BOM中,BM=,∴ME=BE﹣BM=2﹣,综上所述,ME的值为:3﹣2或2﹣.7.(2022•山西)综合与探究如图,二次函数y=﹣x2+x+4的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.点P是第一象限内二次函数图象上的一个动点,设点P的横坐标为m.过点P作直线PD⊥x轴于点D,作直线BC交PD于点E.(1)求A,B,C三点的坐标,并直接写出直线BC的函数表达式;(2)当△CEP是以PE为底边的等腰三角形时,求点P的坐标;(3)连接AC,过点P作直线l∥AC,交y轴于点F,连接DF.试探究:在点P 运动的过程中,是否存在点P,使得CE=FD,若存在,请直接写出m的值;若不存在,请说明理由.【解答】解:(1)在y=﹣x2+x+4中,令x=0得y=4,令y=0得x=8或x=﹣2,∴A(﹣2,0),B(8,0),C(0,4),设直线BC解析式为y=kx+4,将B(8,0)代入得:8k+4=0,解得k=﹣,∴直线BC解析式为y=﹣x+4;(2)过C作CG⊥PD于G,如图:设P(m,﹣m2+m+4),∴PD=﹣m2+m+4,∵∠COD=∠PDO=∠CGD=90°,∴四边形CODG是矩形,∴DG=OC=4,CG=OD=m,∴PG=PD﹣DG=﹣m2+m+4﹣4=﹣m2+m,∵CP=CE,CG⊥PD,∴GE=PG=﹣m2+m,∵∠GCE=∠OBC,∠CGE=90°=∠BOC,∴△CGE∽△BOC,∴=,即=,解得m=0(舍去)或m=4,∴P(4,6);(3)存在点P,使得CE=FD,理由如下:过C作CH⊥PD于H,如图:设P(m,﹣m2+m+4),由A(﹣2,0),C(0,4)可得直线AC解析式为y=2x+4,根据PF∥AC,设直线PF解析式为y=2x+b,将P(m,﹣m2+m+4)代入得:﹣m2+m+4=2m+b,∴b=﹣m2﹣m+4,∴直线PF解析式为y=2x﹣m2﹣m+4,令x=0得y=﹣m2﹣m+4,∴F(0,﹣m2﹣m+4),∴OF=|﹣m2﹣m+4|,同(2)可得四边形CODH是矩形,∴CH=OD,∵CE=FD,∴Rt△CHE≌Rt△DOF(HL),∴∠HCE=∠FDO,∵∠HCE=∠CBO,∴∠FDO=∠CBO,∴tan∠FDO=tan∠CBO,∴=,即=,∴﹣m2﹣m+4=m或﹣m2﹣m+4=﹣m,解得m=2﹣2或m=﹣2﹣2或m=4或m=﹣4,∵P在第一象限,∴m=2﹣2或m=4.8.(2022•东营)如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣1,0),点B(3,0),与y轴交于点C.(1)求抛物线的表达式;(2)在对称轴上找一点Q,使△ACQ的周长最小,求点Q的坐标;(3)点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当△PMB是以PB为腰的等腰直角三角形时,请直接写出所有点M的坐标.【解答】解:(1)将点A(﹣1,0),点B(3,0)代入y=ax2+bx﹣3,∴,解得,∴y=x2﹣2x﹣3;(2)连接CB交对称轴于点Q,∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线的对称轴为直线x=1,∵A、B关于对称轴x=1对称,∴AQ=BQ,∴AC+AQ+CQ=AC+CQ+BQ≥AC+BC,当C、B、Q三点共线时,△ACQ的周长最小,∵C(0,﹣3),B(3,0),设直线BC的解析式为y=kx+b,∴,解得,∴y=x﹣3,∴Q(1,﹣2);(3)当∠BPM=90°时,PM=PB,∴M点与A点重合,∴M(﹣1,0);当∠PBM=90°时,PB=BM,如图1,当P点在M点上方时,过点B作x轴的垂线GH,过点P作PH⊥GH 交于H,过点M作MG⊥HG交于G,∵∠PBM=90°,∴∠PBH+∠MBG=90°,∵∠PBH+∠BPH=90°,∴∠MBG=∠BPH,∵BP=BM,∴△BPH≌△MBG(AAS),∴BH=MG,PH=BG=2,设P(1,t),则M(3﹣t,﹣2),∴﹣2=(3﹣t)2﹣2(3﹣t)﹣3,解得t=2+或t=2﹣,∴M(1﹣,﹣2)或(1+,﹣2),∵M点在对称轴的左侧,∴M点坐标为(1﹣,﹣2);如图2,当P点在M点下方时,同理可得M(3+t,2),∴2=(3+t)2﹣2(3+t)﹣3,解得t=﹣2+(舍)或t=﹣2﹣,∴M(1﹣,2);综上所述:M点的坐标为(1﹣,﹣2)或(1﹣,2)或(﹣1,0).9.(2022•枣庄)如图①,已知抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点.(1)求抛物线的关系式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当△OPE面积最大时,求出P点坐标;(3)将抛物线L向上平移h个单位长度,使平移后所得抛物线的顶点落在△OAE 内(包括△OAE的边界),求h的取值范围;(4)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P,使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线L:y=x2+bx+c经过点A(0,3),B(1,0),∴,解得,∴抛物线的解析式为:y=x2﹣4x+3;(2)如图,过P作PG∥y轴,交OE于点G,设P(m,m2﹣4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E(3,3),∴直线OE的解析式为:y=x,∴G(m,m),∴PG=m﹣(m2﹣4m+3)=﹣m2+5m﹣3,∴S△OPE =S△OPG+S△EPG=PG•AE=×3×(﹣m2+5m﹣3)=﹣(m2﹣5m+3)=﹣(m﹣)2+,∵﹣<0,∴当m=时,△OPE面积最大,此时,P点坐标为(,﹣);(3)由y=x2﹣4x+3=(x﹣2)2﹣1,得抛物线l的对称轴为直线x=2,顶点为(2,﹣1),抛物线L向上平移h个单位长度后顶点为F(2,﹣1+h).设直线x=2交OE于点M,交AE于点N,则E(3,3),∵直线OE的解析式为:y=x,∴M(2,2),∵点F在△OAE内(包括△OAE的边界),∴2≤﹣1+h≤3,解得3≤h≤4;(4)设P(m,m2﹣4m+3),分四种情况:①当P在对称轴的左边,且在x轴下方时,如图,过P作MN⊥y轴,交y轴于M,交l于N,∴∠OMP=∠PNF=90°,∵△OPF是等腰直角三角形,∴OP=PF,∠OPF=90°,∴∠OPM+∠NPF=∠PFN+∠NPF=90°,∴∠OPM=∠PFN,∴△OMP≌△PNF(AAS),∴OM=PN,∵P(m,m2﹣4m+3),则﹣m2+4m﹣3=2﹣m,解得:m=(舍)或,∴P的坐标为(,);②当P在对称轴的左边,且在x轴上方时,同理得:2﹣m=m2﹣4m+3,解得:m1=(舍)或m2=,∴P的坐标为(,);③当P在对称轴的右边,且在x轴下方时,如图,过P作MN⊥x轴于N,过F作FM⊥MN于M,同理得△ONP≌△PMF,∴PN=FM,则﹣m2+4m﹣3=m﹣2,解得:m1=或m2=(舍);P的坐标为(,);④当P在对称轴的右边,且在x轴上方时,如图,同理得m2﹣4m+3=m﹣2,解得:m=或(舍),P的坐标为:(,);综上所述,点P的坐标是:(,)或(,)或(,)或(,).方法二:作直线DE:y=x﹣2,E(1,﹣1)是D点(2,0)绕O点顺时针旋转45°并且OD缩小倍得到,易知直线DE即为对称轴上的点绕O点顺时针旋转45°,且到O点距离缩小倍的轨迹,联立直线DE和抛物线解析式得x2﹣4x+3=x﹣2,解得x1=,x2=,同理可得x3=或x4=;综上所述,点P的坐标是:(,)或(,)或(,)或(,).10.(2023•澄城县一模)如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B,与y轴交于点C(0,3),直线l是抛物线的对称轴.(1)求抛物线的函数解析式;(2)在对称轴l上是否存在点M,使△MAC为等腰三角形,若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.【解答】解:(1)把点A(﹣1,0)、点C(0,3)分别代入y=﹣x2+bx+c,得.解得.故该抛物线解析式为:y=﹣x2+2x+3;(2)由(1)知,该抛物线解析式为:y=﹣x2+2x+3.则该抛物线的对称轴为直线x=﹣=1.故设M(1,m).∵A(﹣1,0)、点C(0,3),∴AC2=10,AM2=4+m2,CM2=1+(m﹣3)2.①若AC=AM时,10=4+m2,解得m=±.∴点M的坐标为(1,)或(1,﹣);②若AC=CM时,10=1+(m﹣3)2,解得m=0或m=6,∴点M的坐标为(1,0)或(1,6).当点M的坐标为(1,6)时,点A、C、M共线,∴点M的坐标为(1,0);③当AM=CM时,4+m2=1+(m﹣3)2,解得m=1,∴点M的坐标为(1,1).综上所述,符合条件的点M的坐标为(1,)或(1,﹣)或(1,0)或(1,1).11.(2023•碑林区校级一模)二次函数y=ax2+bx+2的图象交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,动点M从点A出发,以每秒2个单位长度的速度沿AB方向运动,过点M作MN⊥x轴交直线BC于点N,交抛物线于点D,连接AC,设运动的时间为t秒.(1)求二次函数y=ax2+bx+2的表达式;(2)在直线MN上存在一点P,当△PBC是以∠BPC为直角的等腰直角三角形时,求此时点D的坐标.【解答】解:(1)将点(﹣1,0),B(4,0)代入y=ax2+bx+2,∴a=﹣,b=,∴y=﹣x2+x+2;(2)∵BM=5﹣2t,∴M(2t﹣1,0),设P(2t﹣1,m),∵PC2=(2t﹣1)2+(m﹣2)2,PB2=(2t﹣5)2+m2,∵PB=PC,∴(2t﹣1)2+(m﹣2)2=(2t﹣5)2+m2,∴m=4t﹣5,∴P(2t﹣1,4t﹣5),∵PC⊥PB,∴×=﹣1,∴t=1或t=2,∴M(1,0)或M(3,0),∴D(1,3)或D(3,2).12.(2023•东洲区模拟)抛物线y=ax2+bx+3经过A(﹣1,0),B(3,0)两点,与y轴正半轴交于点C.(1)求此抛物线解析式;(2)如图①,连接BC,点P为抛物线第一象限上一点,设点P的横坐标为m,△PBC的面积为S,求S与m的函数关系式,并求S最大时P点坐标;(3)如图②,连接AC,在抛物线的对称轴上是否存在点M,使△MAC为等腰三角形?若存在,请直接写出符合条件的点M的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+3经过A(﹣1,0),B(3,0)两点,∴,解得:,∴抛物线解析式为y=﹣x2+2x+3;(2)点P作PF⊥x轴于点F,交BC于点E,设BC直线解析式为:y=kx+b,∵B(3,0),C(0,3),∴,解得,∴y=﹣x+3,由题意可知P(m,﹣m2+2m+3),E(m,﹣m+3),S=S△PBE+S△PCE,S=PE•OB=(﹣m2+2m+3+m﹣3)×3,,∵,∴当时,S有最大值,此时P点坐标为;(3)存在,M1(1,0),,,M4(1,1),①当AC=AM时,如图,设对称轴l与AB交于点E,则,∵AM2=AE2+EM2,∴,解得:,∴M点的坐标为或,②当AC=MC时,则OC为AM的垂直平分线.因此M与E重合,因此,M点的坐标为(1,0),③当AM=CM时,如图,设M点的坐标为(1,n),则AM2=22+n2=4+n2,CM2=12+(3﹣n)2,∴4+n2=12+(3﹣n)2,解得:n=1,∴M点的坐标为(1,1),综上可知,潢足条件的M点共四个,其坐标为M1(1,0),,,M4(1,1).13.(2023•三亚一模)如图,抛物线y=ax2+3x+c(a≠0)与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,8),顶点为D,连接AC,CD,DB,直线BC 与抛物线的对称轴l交于点E.(1)求抛物线的解析式和直线BC的解析式;(2)求四边形ABDC的面积;(3)P是第一象限内抛物线上的动点,连接PB,PC,当S△PBC =S△ABC时,求点P的坐标;(4)在抛物线的对称轴l上是否存在点M,使得△BEM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+3x+c(a≠0)过点A(﹣2,0)和C(0,8),∴,解得,∴抛物线的解析式为y=﹣x2+3x+8.令y=0,得.解得x1=﹣2,x2=8.∴点B的坐标为(8,0).设直线BC的解析式为y=kx+b.把点B(8,0),C(0,8)分别代入y=kx+b,得,解得,∴直线BC的解析式为y=﹣x+8.(2)如图1,设抛物线的对称轴l与x轴交于点H.∵抛物线的解析式为,∴顶点D的坐标为.∴S四边形ABDC =S△AOC+S梯形OCDH+S△BDH===70.(3)∵.∴.如图2,过点P作PG⊥x轴,交x轴于点G,交BC于点F.设点.∵点F在直线BC上,∴F(t,﹣t+8).∴.∴.∴.解得t1=2,t2=6.∴点P的坐标为(2,12)或P(6,8).(4)存在.∵△BEM为等腰三角形,∴BM=EM或BE=BM或BE=EM,设M(3,m),∵B(8,0),E(3,5),∴BE==5,EM=|m﹣5|,BM==,当BM=EM时,=|m﹣5|,∴m2+25=(m﹣5)2,解得:m=0,∴M(3,0);当BE=BM时,5=,∴m2+25=50,解得:m=﹣5或m=5(舍去),∴M(3,﹣5);当BE=EM时,5=|m﹣5|,解得:m=5+5或m=5﹣5,∴M(3,5+5)或(3,5﹣5),综上所述,点M的坐标为(3,0)或(3,﹣5)或(3,5+5)或(3,5﹣5).14.(2023•南海区一模)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a >0)与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P为直线BC下方抛物线上的一动点,PM⊥BC于点M,PN∥y轴交BC 于点N.求线段PM的最大值和此时点P的坐标;(3)点E为x轴上一动点,点Q为抛物线上一动点,是否存在以CQ为斜边的等腰直角三角形CEQ?若存在,请直接写出点E的坐标;若不存在,请说明理由.【解答】解:(1)将A(﹣1,0),B(3,0)代入函数y=ax2+bx﹣3(a>0)中,得,解得,∴解析式为y=x2﹣2x﹣3,故抛物线解析式为y=x2﹣2x﹣3;(2)当x=0时,y=3,∴C(0,﹣3),∵B(3,0),∴∠OCB=∠OBC=45°,∵PN∥y轴,∴∠MNP=45°,∵PM⊥BC,∴PM=PN,则当PN最大时,PM也最大,设BC的解析式为y=mx+n,∴,解得,∴BC解析式为y=x﹣3,设P(x,x2﹣2x﹣3),N(x,x﹣3),∴PN=x﹣3﹣(x2﹣2x﹣3)=﹣(x﹣)2+,当x=时,PN最大,则PM=PN=×=,∴P(,),故PM最大值为,P点坐标为(,﹣);(3)存在,点E的坐标为(﹣5,0),(,0),(0,0),(,0).∵CEQ是以CQ为斜边的等腰直角三角形,∴设Q(x,x2﹣2x﹣3),①如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,∵∠CEQ=90°,∴∠QEM+∠CEN=90°,∵∠QEM+∠MQE=90°,∴∠EQM=∠CEN,∵∠CNE=∠QME=90°,EC=EQ,∴△EMQ≌△CNE(AAS),∴CN=EM=x2﹣2x﹣3,MQ=EN=3,∴|x Q|+MQ=CN,﹣x+3=x2﹣2x﹣3,解得x=﹣2,x=3(舍去),∴OE=CM=2+3=5,E(﹣5,0),②如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,同理:△EMC≌△QNE(AAS),CM=EN=x2﹣2x﹣3,NQ=EM=3,∴﹣x+x2﹣2x﹣3=3,解得x=,x=(舍去),∴OE=CM=,E(,0),③如图,点E和点O重合,点Q和点B重合,此时E(0,0),④如图,过点E作x轴的垂线l,再分别过点C和点Q作垂线l的垂线,分别交于点M和点N,同理:△EMC≌△QNE(AAS),CM=EN=x2﹣2x﹣3,NQ=EM=3,∴x+3=x2﹣2x﹣3,解得x=,x=(舍去),∴OE=CM=,E(,0),综上所述,点E的坐标为(﹣5,0),(,0),(0,0),(,0)41。
中考数学总复习《二次函数之等腰三角形存在性问题》专项提升训练题-附答案

中考数学总复习《二次函数之等腰三角形存在性问题》专项提升训练题-附答案学校:___________班级:___________姓名:___________考号:___________ 1.已知二次函数23y ax bx a =+-经过点()1,0A -和()0,3C ,与x 轴交于另一点B ,抛物线的顶点为D .(1)求此二次函数解析式;(2)连接DC 、BC 和DB ,判断BCD △的形状并说明理由;(3)在对称轴右侧抛物线上找一点P ,使得P 、D 、C 构成以PC 为底边的等腰三角形,求出点P 的坐标及此时四边形PBCD 的面积.2.如图,抛物线2y x bx c =-++过点(1,0)A -和(3,0)B ,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 为抛物线对称轴上一动点,当PCB 是以BC 为底边的等腰三角形时,求P 的坐标;(3)在(2)条件下,是否存在点M 为抛物线上的点,使得2BCM BCP S S =△△?若存在,求出点M 的横坐标;若不存在,请说明理由.3.如图,已知抛物线2y ax bx c =++经过点()3,0A -,()0,4C 两点,且与x 轴的另一个交点为B ,对称轴为直线=1x -.(1)求抛物线的表达式;(2)已知点M 是抛物线对称轴上一点,当MBC 的周长最小时,求M 点的坐标.(3)D 是第二象限内抛物线上的动点,设点D 的横坐标为m ,求四边形ABCD 面积S 的最大值及此时D 点的坐标;(4)若点P 在抛物线对称轴上,是否存在点P ,使以点B ,C 和P 为顶点的三角形是等腰三角形?若存在,请求出P 点的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系中,抛物线24y ax bx =+-与x 轴交于()40A ,、()30B -,两点,与y 轴交于点C .(1)求这条抛物线所对应的函数表达式.(2)如图①,点D 是x 轴下方抛物线上的动点,且不与点C 重合.设点D 的横坐标为m ,以O 、A 、C 、D 为顶点的四边形面积为S ,求S 与m 之间的函数关系式.(3)如图①,连结BC ,点M 为线段AB 上一点,点N 为线段BC 上一点,且BM CN n ==,直接写出当n 为何值时BMN 为等腰三角形.5.抛物线24y x x =-与直线y x =交于原点O 和点B ,与x 轴交于点A ,顶点为D .(1)填空:点B 的坐标为 ,点D 的坐标为 .(2)如图1,连结OD ,P 为x 轴上的动点,当以O ,D ,P 为顶点的三角形是等腰三角形时,求点P 的坐标;(3)如图2,M 是点B 关于抛物线对称轴的对称点,Q 是抛物线上的动点,它的横生标为m (05)m <<,连结MQ ,BQ 和MQ 与直线OB 交于点E .设BEQ 和BEM △的面积分别为1S 和2S ,设12S t S =己,试求t 关于m 的函数解析式并求出t 的最值6.如图,在平面直角坐标系中,二次函数2y x bx c =-+-的图象与x 轴交于点(3,0)A -和点(1,0)B ,与y 轴交于点C .(1)求这个二次函数的表达式;(2)如图①,二次函数图象的对称轴与直线AC 交于点D ,若E 是直线AC 上方抛物线上的一个动点,求ECD 面积的最大值;(3)如图①,P 是直线AC 上的一个动点,是否存在点P ,使PBC 是等腰三角形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.7.如图1,抛物线23432363y x x =++与x 轴交于点A ,B (A 在B 左边),与y 轴交于点C ,连AC ,点D 与点C 关于抛物线的对称轴对称,过点D 作DE AC ∥交抛物线于点E ,交y 轴于点P .(1)点F 是直线AC 下方抛物线上点一动点,连DF 交AC 于点G ,连EG ,当EFG 的面积的最大值时,直线DE 上有一动点M ,直线AC 上有一动点N ,满足MN AC ⊥,连GM 和NO ,求GM MN NO ++的最小值;(2)如图2,在(1)的条件下,过点F 作FH x ⊥轴于点H 交AC 于点L ,将AHL 沿着射线AC 平移到点A 与点C 重合,从而得到A H L '''(点A ,H ,L 分别对应点A ',H '和L '),再将A H L '''绕点H '逆时针旋转(0180)αα︒<<︒,旋转过程中,边A L ''所在直线交直线DE 于Q ,交y 轴于点R ,求当PQR 为等腰三角形时,直接写出PR 的长.8.如图,在平面直角坐标系中,抛物线2y ax bx c =++与x 轴交于()4,0B ,()2,0C -两点,与y 轴交于点()0,2A -.(1)求该抛物线的函数表达式;(2)若点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点K ,过点P 作y 轴的平行线交x 轴于点D ,求12PK PD +的最大值及此时点P 的坐标; (3)在抛物线的对称轴上是否存在一点M ,使得MAB △是以AB 为腰的等腰三角形;若存在,请求出点M 的坐标,若不存在,请说明理由.9.如图,抛物线23y ax bx =++与x 轴相交于点(1,0)A -,B ,对称轴是1x =,与y 轴相交于点C .(1)求抛物线的函数表达式;(2)点P 为抛物线对称轴上一动点,当PCB 是以BC 为底边的等腰三角形时,求点P 的坐标;(3)在(2)的条件下,在第一象限内,抛物线上是否存在点M ,使得BCM BCP S S =△△?若存在,求出点M 的横坐标;若不存在,请说明理由.10.如图,抛物线2y x bx c =++的图象与x 轴交于(3,0)A -、(1,0)B 两点,与y 轴交于点C ,点P 是抛物线上位于第三象限内的一点.(1)求抛物线的解析式.(2)连接AP 、PC 和CB ,求四边形APCB 面积的最大值及此时P 点的坐标.(3)点D 为抛物线对称轴上的一点,当以点A 、C 、D 为顶点的三角形为等腰三角形时,请写出所有符合条件的点D 的坐标,并把求其中一个点D 的过程写出来.11.已知拋物线2y ax bx c =++经过点()120B ,和()06C -,,对称轴为直线2x =.(1)求该拋物线的解析式;(2)点D 在线段AB 上,且AD AC =,若动点P 从A 点出发沿线段AB 以每秒1个单位长度的速度匀速运动,同时另一动点Q 以某一速度从C 点出发沿线段CB 匀速运动,问是否存在某一时刻t ,使线段PQ 被直线CD 垂直平分?若存在,请求出此时的时间t (秒)和点Q 的运动速度,若不存在,请说明理由;(3)在(2)的条件下,在x 轴上是否存在点M ,使MPQ 为等腰三角形?若存在,请求出所有点M 的坐标,若不存在,请说明理由.12.已知抛物线与x 轴交于1030A C -(,)、(,),与y 轴交于点03B -(,).(1)求抛物线对应的函数解析式;(2)在x 轴上是否存在点P ,使PBC 为等腰三角形?若存在,求出P 点坐标;若不存在,请说明理由;(3)点M 为抛物线上一动点,在直线BC 上是否存在点Q ,使以点O 、B 、Q 、M 为顶点的四边形为平行四边形?若存在,求出Q 点的坐标;若不存在,请说明理由.13.如图,抛物线212y x mx n =-++与x 轴交于A B 、两点,与y 轴交于点C ,拋物线的对称轴交x 轴于点D ,已知()()1,0,0,2A C -.(1)求抛物线的解析式;(2)点E 是线段BC 上的一个动点(不与B C 、重合),过点E 作x 轴的垂线与抛物线相交于点F ,当点E 运动到什么位置时,四边形CDBF 的面积最大?求出四边形CDBF 的最大面积及此时点E 的坐标.(3)在抛物线的对称轴上是否存在点P ,使PCD 为等腰三角形?如果存在,直接写出P 点的坐标;如果不存在,请说明理由.14.如图,已知抛物线与x 轴交于1,0A 和()5,0B -两点,与y 轴交于点C .直线33y x =-+过抛物线的顶点P .(1)求抛物线的函数解析式;(2)若直线()50x m m =-<<与抛物线交于点E ,与直线BC 交于点F . ①当EF 取得最大值时,求m 的值和EF 的最大值; ①当EFC 是等腰三角形时,求点E 的坐标.15.如图1,在平面直角坐标系中,抛物线23y ax bx =+-与x 轴交于点()60A ,和()10B -,,与y 轴交于点C ,连接BC ,过点A 、C 作直线AC .(1)求抛物线的函数解析式.⊥交AC于点F,过点P作(2)点P为直线AC下方抛物线上一动点,过点P作PF AC∥交x轴于点E,求AE PFPE AC+的最大值及此时点P的坐标.(3)在(2)问的条件下,将抛物线23=+-沿射线CB方向平移10个单位长度得y ax bx到新抛物线y',新抛物线y'与原抛物线交于点M;连接CP,把线段CP沿直线AC平移,记平移后的线段为C P'',当以C'、P'和M为顶点的三角形是等腰三角形时,请直接写出所有符合条件的P'点的坐标.参考答案: 1.(1)223y x x =-++(2)BCD △为直角三角形(3)点P 的坐标为()2,3,四边形PBCD 的面积为42.(1)223y x x =-++(2)()1,1P(3)M 点横坐标为3172+或3172-或1或23.(1)248433y x x =--+ (2)81,3M ⎛⎫- ⎪⎝⎭ (3)252S =,3,52D ⎛⎫- ⎪⎝⎭(4)P 的坐标为:()1,0-或()1,13-或()1,13--或131,8⎛⎫- ⎪⎝⎭4.(1)211433=--y x x (2)当30m -<<时28S m =-+;当04m <<时228833S m m =-++. (3)52n =,2511n =和3011n = 5.(1)(5,5) ()2,4-(2)点P 的坐标为()()()()25,025,04,05,0-或或或(3)()21525056224t m m ⎛⎫=--+<< ⎪⎝⎭,t 的最大值为25246.(1)223y x x =--+(2)98ECD S =最大△(3)点P 的坐标为()535--,或()535+,或5122⎛⎫- ⎪⎝⎭,或()21-,.7.(1)239745+(2)17333-或8338.(1)211242y x x =-- (2)存在,12PK PD +的最大值为258 335,216P ⎛⎫- ⎪⎝⎭(3)存在,M 的坐标为()111,或()111-,或()1219-+,或()1219--,.9.(1)223y x x =-++(2)点P 的坐标为(1,1)(3)存在,点M 的横坐标为352+或35210.(1)223y x x =+-(2)点P 坐标为315,24⎛⎫-- ⎪⎝⎭ max 758ABCP S =四边形 (3)1(1,14)D - 2(1,14)D -- 3(1,173)D -- 4(1,173)D --- 5(1,1)D --;11.(1)2116164y x x =--; (2)存在5t =时线段PQ 被直线CD 垂直平分,点Q 的运动速度每秒355单位长度; (3)1(2,0)M 2(33,0)10M -+ 3(33,0)10M -- 4(15,0)M ;12.(1)2=23y x x --(2)3,0-()或(323,0)+,或(323,0)-+,或0,0() (3)存在Q 1Q :321213(,)22+- 2321213,)22(Q -+- 3)213(,22192Q --4)321(,29212Q +-+-13.(1)213222y x x =-++ (2)当2x =时,四边形CDBF 的面积最大,最大值为132,此时()2,1E (3)存在,满足条件的P 点坐标为35353325,,,4,22222216⎛⎫⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,,14.(1)245y x x =--+(2)①当52m =-时,EF 有最大值,最大值为254;①()38-,或()45-,或()25622--,15.(1)215322y x x =-- (2)AE +PF 的最大值为:9595+;此时()3,6P - (3)点P '的坐标为:172112911,55⎛⎫--- ⎪ ⎪⎝⎭或172412911,55⎛⎫+-+ ⎪ ⎪⎝⎭或()11,13--。
备战中考数学二轮专题归纳提升真题二次函数系数问题(解析版)

专题03 二次函数系数问题【知识点梳理】1、二次函数图象的特征与a ,b ,c 的关系2、常用公式及方法:(1)二次函数三种表达式:(2)韦达定理:若二次函数y =ax 2+bx +c 图象与x 轴有两个交点且交点坐标为(x 1,0)和(x 2,0),则x 1+x 2=−ba,x 1⋅x 2=ca。
(3)赋值法:在二次函数y =ax 2+bx +c 中,令x =1,则y =a +b +c ;令x =−1,则y =a −b +c ;令x =2,则y =4a +2b +c ;令x =−2,则y =4a −2b +c ;利用图象上对应点的位置来判断含有a 、b 、c 的关系式的正确性。
【典例分析】【例1】如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=-1,x2=3;③a+b+c<0;④当x>1时,y随x的增大而减小;⑤2a-b=0;⑥b2-4ac >0.下列结论一定成立的是【答案】①②③⑥【解析】解:①由图象可知,a>0,b<0,c<0,∴ac<0,故①正确;②由图象可知,二次函数与x轴的交点横坐标为-1和3,∴方程ax2+bx+c=0的根是x1=-1,x2=3,故②正确;③当x=1时,y<0∴a+b+c<0,故③正确;④∵方程ax2+bx+c=0的根是x1=-1,x2=3∴对称轴为x=x1+x22=−1+32=1由图象可知,当x>1时,y随x的增大而增大,故④错误;⑤∵对称轴−b2a=1∴b=-2a,2a+b=0,故⑤错误;⑥∵二次函数与x轴有两个交点,即方程ax2+bx+c=0有两个不相等的实数根,∴b2-4ac>0,故⑥正确。
故答案为:①②③⑥【练1】如图,已知二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于C 点,OA=OC.则由抛物线的特征写出如下结论:①abc>0;②4ac-b2>0;③a-b+c>0;④ac+b+1=0.其中正确的个数是()A.4个B. 3个C. 2个D. 1个【答案】B【解析】解:①由图象可知,a>0,b<0,c<0,∴abc>0,故①正确;②由图象可知,二次函数与x轴有两个交点,即方程ax2+bx+c=0有两个不相等的实数根,∴b2-4ac>0,即4ac-b2<0故②错误;③当x=-1时,y>0∴a-b+c>0,故③正确;④∵C(0,c),OA=OC,∴A(c,0)∴当x=c时,y=0,即(c)²+bc+c=0∵c≠0正确错误.故答案为:B.【练2】小明从二次函数y=ax2+bx+c的图象(如图)中观察得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0.你认为其中正确的信息是()A.①②③⑤B. ①②③④C. ①③④⑤D. ②③④⑤【答案】A【解析】解:①由图象可知,a>0,b<0,c<0,故①正确;②abc>0,故②正确;③由图象可知当x=-1时,y>0∴a-b+c>0,故③正确;④∵对称轴−b2a =13∴3b=-2a,2a+3b=0,故④错误;⑤∵当x=2时,y>0即4a+2b+c>0∵3b=-2a∴2×(-3b)+2b+c=c-4b>0,故⑤正确.故答案为:A.【例2】抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=−1,其图象如图所示.下列结论:①abc<0;②(4a+c)2<(2b)2;③若(x1,y1)和(x2,y2)是抛物线上的两点,则当|x1+1|>|x2+1|时,y1<y2;④抛物线的顶点坐标为(−1,m),则关于x的方程ax2+bx+c=m−1无实数根.其中正确结论的个数是()A.4B.3C.2D.1【答案】B【解析】解:①∵抛物线图象开口向上,∴a>0,∵对称轴在直线y轴左侧,∴a,b同号,b>0,∵抛物线与y轴交点在x轴下方,∴c<0,∴abc<0,故①正确.②(4a+c)2−(2b)2=(4a+c+2b)(4a+c−2b),当x=2时ax2+bx+c=4a+2b+c,由图象可得4a+2b+c>0,当x=−2时,ax2+bx+c=4a−2b+c,由图象可得,4a−2b+c<0∴(4a+c)2−(2b)2<0,即,(4a+c)2<(2b)2故②正确.③|x1+1|=|x1−(−1)|,|x2+1|=|x2−(−1)|,∵|x1+1|>|x2+1|∴点(x1,y1)到对称轴的距离大于点(x2,y2)到对称轴的距离,∴y1>y2,故③错误.④∵抛物线的顶点坐标为(−1,m),∴由图象知,y>m,∴ax2+bx+c>m,∴ax2+bx+c=m−1无实数根.故④正确,综上所述,①②④正确,故答案为:B.【练1】二次函数y=ax2+bx+c(a≠0)的图象的一部分如图所示.已知图象经过点(−1,0),其对称轴为直线x =1.下列结论:①abc <0;②4a +2b +c <0;③8a +c <0;④若抛物线经过点(−3,n ),则关于x 的一元二次方程()200ax bx c n a ++-=≠的两根分别为−3,5,上述结论中正确结论的个数为( )A .1个B .2个C .3个D .4个【答案】C【解析】解:①由图象可知,a <0,b >0,c >0, ∴abc <0,故①正确;②∵对称轴为直线x = −b2a =1,且图象与x 轴交于点(﹣1,0), ∴图象与x 轴的另一个交点坐标为(3,0),b=﹣2a , ∴根据图象,当x =2时,y =4a +2b +c >0,故②错误;③根据图象,当x =﹣2时,y =4a ﹣2b +c =4a +4a +c =8a +c <0,故③正确; ④∵抛物线经过点(−3,n ),∴根据抛物线的对称性,抛物线也经过点(5,n ),∴抛物线y =ax 2+bx +c 与直线y =n 的交点坐标为(﹣3,n )和(5,n ), ∴一元二次方程ax 2+bx +c −n =0(a ≠0)的两根分别为−3,5, 故④正确,综上,上述结论中正确结论有①③④, 故答案为:C .【练2】已知抛物线y =ax 2+bx +c (a,b,c 是常数,a ≠0)经过点(−1,−1),(0,1),当x =−2时,与其对应的函数值y >1.有下列结论:①0abc >;②关于x 的方程ax 2+bx +c −3=0有两个不等的实数根;③a +b +c >7.其中,正确结论的个数是( ) A .0 B .1C .2D .3【答案】D【解析】解:∵抛物线y =ax 2+bx +c (a,b,c 是常数,a ≠0)经过点(−1,−1),(0,1),当x =−2时,与其对应的函数值y >1. ∴c =1>0,a -b +c = -1,4a -2b +c >1, ∴a -b = -2,2a -b >0,∴2a-a-2>0,∴a>2>0,∴b=a+2>0,∴abc>0,∵ax2+bx+c−3=0,∴△=b2−4a(c−3)=b2+8a>0,∴ax2+bx+c−3=0有两个不等的实数根;∵b=a+2,a>2,c=1,∴a+b+c=a+a+2+1=2a+3,∵a>2,∴2a>4,∴2a+3>4+3>7,故答案为:D.【例3】抛物线y=ax2+bx+c(a,b,c为常数)开口向下且过点A(1,0),B(m,0)(−2< m<−1),下列结论:①2b+c>0;②2a+c<0;③ a(m+1)−b+c>0;④若方程a(x−m)(x−1)−1=0有两个不相等的实数根,则244ac b a-<.其中正确结论的个数是()A.4B.3C.2D.1【答案】A【解析】解:∵抛物线开口向下,∴a<0把A(1,0),B(m,0)代入y=ax2+bx+c得{a+b+c=0am2+bm+c=0,∴am2+bm=a+b∴am2+bm−a−b=0(m−1)(am+a+b)=0∵−2<m<−1∴am+a+b=0∴am=c,a(m+1)=−b∴c>0∴−1<m+1<0∵m+1<0∴−12<m+12<0∴−12<−b2a<0∴1>ba>0∴a<b<0①2b+c=2b−a−b=b−a>0,故①正确;②2a+c=2a−a−b=a−b<0,故②正确;③ a(m+1)−b+c=−2b+c=−2b−a−b=−3b−a>0,故③正确;;④若方程a(x−m)(x−1)−1=0有两个不相等的实数根,即ax2−a(m+1)x+am−1=0Δ=a2(m+1)2−4a(am−1)=a2(m+1)2−4a2m+4a=b2−4a2⋅−a−ba+4a=b2+4a2+4ab+4a=b2+4a(a+b)+4a=b2−4ac+4a>0∴4ac−b2<4a,故④正确,即正确结论的个数是4,故答案为:A.【练1】如图,抛物线y=ax2+bx+c(a≠0)的顶点为(1,n),与x轴的一个交点B(3,0),与y轴的交点在(0,﹣3)和(0,﹣2)之间.下列结论中:①abc >0;②﹣2<b<−53;③(a+c)2﹣b2=0;④2c﹣a<2n,则正确的个数为()A.1B.2C.3D.4【答案】B【解析】解:∵抛物线y=ax2+bx+c(a≠0)的开口向上,∴a>0,∵抛物线线y=ax2+bx+c(a≠0)的顶点坐标为(1,n),∴对称轴x=−b2a=1,∴b=-2a<0,∵抛物线与y轴的交点在(0,﹣3)和(0,﹣2)之间∴-3<c<-2<0,>0;故①正确;∴abc∵抛物线线x轴的一个交点B(3,0),∴9a+3b+c=0,抛物线线x轴的一个交点(-1,0),∵b=-2a,∴c=3b2<-2,∴-3<3b2∴﹣2<b<−4,故②错误;3∵抛物线线x轴的一个交点(-1,0),∴a-b+c=0,∴(a+c)2﹣b2=(a+b+c)(a-b+c)=0,故③正确;∵a>0,∴-a<0∵b=-2a∴3a+2b=-a<0∴2c﹣a>2(a+b+c),∵抛物线y=ax2+bx+c(a≠0)的顶点为(1,n),∴a+b+c=n,∴2c﹣a>2n;故④错误;故答案为:B【练2】已知二次函数y=ax2+bx+c的图像如图所示,有下列结论:①a>0;②b2−4ac >0;③4a+b=0;④不等式ax2+(b−1)x+c<0的解集为1≤x<3,正确的结论个数是()A.1B.2C.3D.4【答案】A【解析】解:∵抛物线的开口向上,∴a>0,故①正确;∵抛物线与x轴没有交点∴b2−4ac<0,故②错误∵由抛物线可知图象过(1,1),且过点(3,3){a+b+c=19a+3b+c=3∴8a+2b=2∴4a+b=1,故③错误;由抛物线可知顶点坐标为(1,1),且过点(3,3)则抛物线与直线y=x交于这两点∴ax2+(b−1)x+c<0可化为ax2+bx+c<x,根据图象,解得:1<x<3故④错误.故答案为:A.【练3】如图,已知抛物线y=ax2+bx+c的对称轴在y轴右侧,抛物线与x轴交于点A(−2,0)>0;②2b−4ac=1;和点B,与y轴的负半轴交于点C,且OB=2OC,则下列结论:①a−bc;④当−1<b<0时,在x轴下方的抛物线上一定存在关于对称轴对称的两点M,N(点③a=14M在点N左边),使得AN⊥BM.其中正确的有()A.1个B.2个C.3个D.4个【答案】B【解析】解:①从图像观察,开口朝上,所以a>0,对称轴在y轴右侧,所以b<0,图像与y轴交点在x轴下方,所以c<0<0,所以①不正确;∴a−b>0,a−bc②点A(−2,0)和点B,与y轴的负半轴交于点C(0,c),且OB=2OC设B(−2c,0)代入y=ax2+bx+c,得:4ac2−2bc+c=0∵c≠0∴2b−4ac=1,所以②正确;③∵A(−2,0),B(−2c,0)设抛物线解析式为:y=a(x+2)(x+2c)过C(0,c)∴c=4ac∴a=14,所以③正确;④如图:设AN,BM交点为P,对称轴与x轴交点为Q,顶点为D,根据抛物线的对称性,△APB是等腰直角三角形,∵A(−2,0),B(−2c,0)∴AB=2−2c,PQ=12AB=1−c又对称轴x=−2+(−2c)2=c+1∴P(c+1,c−1)由顶点坐标公式可知D(c+1,4ac−b24a)∵a=14∴D(c+1,c−b2)由题意c−b2<c−1,解得b>1或者b<−1由①知b<0∴b<−1,所以④不正确.综上所述:②③正确共2个故答案为:B.【例4】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为x=12,且经过点(2,0).下列说法:①abc<0;②−2b+c=0;③4a+2b+c<0;④若(−12,y1),(52,y2)是抛物线上的两点,则y1<y2;⑤14b+c>m(am+b)+c(其中m≠12).正确的结论有()A.2个B.3个C.4个D.5个【答案】B【解析】解:∵抛物线的开口向下,与y轴的交点位于y轴正半轴,∴a<0,c>0,∵抛物线的对称轴为x =−b 2a =12,∴b=-a >0,∴abc <0,则结论①正确;将点(2,0)代入二次函数的解析式得:4a +2b +c =0,则结论③错误;将a =−b 代入得:−2b +c =0,则结论②正确;∵抛物线的对称轴为x =12,∴x =32和x =−12时的函数值相等,即都为y 1,又∵当x ≥12时,y 随x 的增大而减小,且32<52,∴y 1>y 2,则结论④错误;由函数图象可知,当x =12时,y 取得最大值,最大值为14a +12b +c =−14b +12b +c =14b +c ,∵m ≠12, ∴14b +c >am 2+bm +c ,即14b +c >m(am +b)+c ,结论⑤正确;综上,正确的结论有①②⑤,共3个,故答案为:B .【练1】二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列结论:①0abc >,②4a −2b +c <0,③()a b x ax b -≥+,④3a +c <0,正确的有( )A .1个B .2个C .3个D .4个【答案】C【解析】解:∵抛物线开口向下,∴a <0,∵对称轴为直线x =-1,即−b 2a =−1,∴b =2a ,则b <0,∵抛物线与y轴交于正半轴,∴c>0,∴abc>0,故①正确;∵抛物线对称轴为直线x=-1,与x轴的一个交点横坐标在0和1之间,则与x轴的另一个交点在-2和-3之间,∴当x=-2时,y=4a-2b+c>0,故②错误;∵x=-1时,y=ax2+bx+c的最大值是a-b+c,∴a-b+c≥ax2+bx+c,∴a-b≥ax2+bx,即a-b≥x(ax+b),故③正确;∵当x=1时,y=a+b+c<0,b=2a,∴a+2a+c=3a+c<0,故④正确;故答案为:C.【练2】如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为x=−1,结合图象给出下列结论:①a+b+c=0;②a−2b+c<0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-3和1;④若点(−4,y1),(−2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤a−b<m(am+b)(m为任意实数).其中正确的结论有()A.1个B.2个C.3个D.4个【答案】C【解析】解:∵二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),∴当x=1时,a+b+c=0,故结论①正确;根据函数图像可知,当x =−1,y <0,即a −b +c <0,对称轴为x =−1,即−b 2a =−1,根据抛物线开口向上,得a >0,∴b =2a >0,∴a −b +c −b <0,即a −2b +c <0,故结论②正确;根据抛物线与x 轴的一个交点为(1,0),对称轴为x =−1可知:抛物线与x 轴的另一个交点为(-3,0),∴关于x 的一元二次方程ax 2+bx +c =0(a ≠0)的两根分别为-3和1, 故结论③正确;根据函数图像可知:y 2<y 1<y 3,故结论④错误;当x =m 时,y =am 2+bm +c =m(am +b)+c ,∴当m =−1时,a −b +c =m(am +b)+c ,即a −b =m(am +b),故结论⑤错误,综上:①②③正确,故答案为:C .【练3】如图,已知抛物线y =ax 2+bx +c (a ,b ,c 为常数,a ≠0)经过点(2,0),且对称轴为直线x =12,有下列结论:①0abc >;②a +b >0;③4230a b c ++<;④无论a ,b ,c 取何值,抛物线一定经过,02c a ⎛⎫ ⎪⎝⎭;⑤2440am bm b +-≥.其中正确结论有( )A .1个B .2个C .3个D .4个【答案】D 【解析】解:①图像开口朝上,故a >0 ,根据对称轴“左同右异”可知0b <, 图像与y 轴交点位于x 轴下方,可知c <0∴abc >0故①正确;②x =−b 2a =12得a =−b∴a +b =0故②错误;③∵y =ax 2+bx +c 经过(2,0)∴4a+2b+c=0又由①得c <0∴4a +2b +3c <0故③正确;④根据抛物线的对称性,得到x =2与x =−1时的函数值相等∴当x =−1时y =0,即a −b +c =0∵a=-b∴2a +c =0即c 2a =−1∴y =ax 2+bx +c 经过(c 2a ,0),即经过(−1,0)故④正确;⑤当x =12时,y =14a +12b +c , 当x =m 时,y =am 2+bm +c∵a >0∴函数有最小值14a +12b +c∴am 2+bm +c ≥14a +12b +c 化简得4am 2+4bm −b ≥0,故⑤正确.综上所述:①③④⑤正确.故选D .【练4】已知二次函数y =ax 2+bx +c(a ≠0)的图象如图所示,有下列5个结论:①0abc ;②b 2<4ac ;③2c <3b ;④a +2b >m(am +b)(m ≠1);⑤若方程|ax 2+bx +c |=1有四个根,则这四个根的和为2,其中正确的结论有( )A .2个B .3个C .4个D .5个【答案】A【解析】解:①∵抛物线开口方向向下,∴a<0,∵抛物线与y轴交于正半轴,∴c>0,∵对称轴在y轴右侧,∴b>0,∴abc<0,①错误;②∵抛物线与x轴有两个交点∴b2−4ac>0∴b2>4ac,故②错误;③∵抛物线的对称轴为直线x=1,∴−b2a=1,∴a=−12b由图象得,当x=−1时,y=a−b+c<0,∴−12b−b+c<0∴2c<3b,故③正确;④当x=1时,y=a+b+c的值最大,∴当x=m(m≠1)时,a+b+c>am2+bm+c,∴a+b>m(am+b)(m≠1),∵b>0,∴a+2b>m(am+b)(m≠1),故④正确;⑤∵方程|ax2+bx+c|=1有四个根,∴方程ax2+bx+c=1有2个根,方程ax2+bx+c=-1有2个根,∴所有根之和为2×(-ba )=2×2aa=4,所以⑤错误.∴正确的结论是③④,故选:A【例5】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.其中正确的个数为A .1B .2C .3D .4【答案】B 【解析】解∵函数y=x 2+bx+c 与x 轴无交点,∴b 2﹣4c <0;故①错误.当x=1时,y=1+b+c=1,故②错误.∵当x=3时,y=9+3b+c=3,∴3b+c+6=0.故③正确.∵当1<x <3时,二次函数值小于一次函数值,∴x 2+bx+c <x ,∴x 2+(b ﹣1)x+c <0.故④正确.综上所述,正确的结论有③④两个,故答案为:B【练1】已知抛物线y =ax 2+bx +c(a >0),且a +b +c =−12,a −b +c =−32.判断下列结论:①abc <0;②220a b c ++>;③抛物线与x 轴正半轴必有一个交点;④当2≤x ≤3时,y 最小=3a ;⑤该抛物线与直线y =x −c 有两个交点,其中正确结论的个数( ) A .2B .3C .4D .5【答案】D【解析】解:∵a +b +c =−12,a −b +c =−32,∴两式相减得b =12,两式相加得c =−1−a ,∴c <0,∵a >0,b >0,c <0,∴abc <0,故①正确;∴2a +2b +c =2a +2×12−1−a =a >0,故②正确;∵当x =1时,则y =a +b +c =−12,当x =-1时,则有y =a −b +c =−32, ∴当y =0时,则方程0=ax 2+bx +c 的两个根一个小于-1,一个根大于1, ∴抛物线与x 轴正半轴必有一个交点,故③正确;由题意可知抛物线的对称轴为直线x =−b 2a =−14a <0,∴当2≤x ≤3时,y 随x 的增大而增大,∴当x =2时,有最小值,即为y =4a +2b +c =4a +1−1−a =3a ,故④正确;联立抛物线y=ax2+bx+c及直线y=x−c可得:x−c=ax2+bx+c,整理得:ax2−1x+2c=0,2−8ac>0,∴Δ=14∴该抛物线与直线y=x−c有两个交点,故⑤正确;∴正确的个数有5个;故答案为:D.。
二次函数中考压轴题(三角形与存在性问题)解析精选
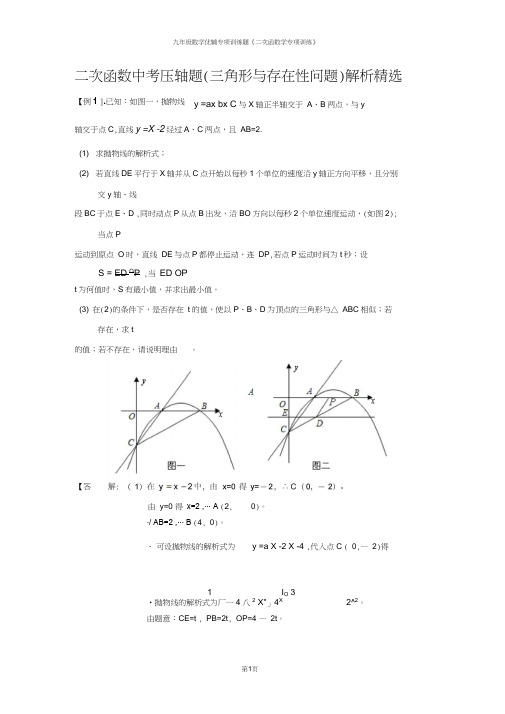
九年级数学优辅专项训练题《二次函数学专项训练》二次函数中考压轴题(三角形与存在性问题)解析精选y =ax bx C 与X 轴正半轴交于 A 、B 两点,与y 轴交于点C ,直线y =X -2经过A 、C 两点,且 AB=2. (1) 求抛物线的解析式;(2) 若直线DE 平行于X 轴并从C 点开始以每秒1个单位的速度沿y 轴正方向平移,且分别交y 轴、线段BC 于点E 、D ,同时动点P 从点B 出发,沿BO 方向以每秒2个单位速度运动,(如图2);当点P运动到原点 O 时,直线 DE 与点P 都停止运动,连 DP ,若点P 运动时间为t 秒;设S = ED O P ,当 ED OPt 为何值时,S 有最小值,并求出最小值。
(3) 在(2)的条件下,是否存在 t 的值,使以P 、B 、D 为顶点的三角形与△ ABC 相似;若存在,求t的值;若不存在,请说明理由。
∙/ AB=2 ,∙∙∙ B (4, 0)。
y =a X -2 X -4 ,代入点 C ( 0,— 2)得1I O 3•抛物线的解析式为厂一4八2 X"」4X2^2。
由题意:CE=t , PB=2t , OP=4 — 2t 。
【例1 ].已知:如图一,抛物线 ∙可设抛物线的解析式为【答案]由 y=0 得 x=2 ,∙∙∙ A (2,0)。
九年级数学优辅专项训练题《二次函数学专项训练》∙.∙ED 〃BA ,•△CED -COB o ∙O D =CO ,即E 4S o∙ED =2t oED +OP_2t+(4 —2t )_ 4 _ 1^ ED OP 2t 4 —2t -4t 2+8t _ t -1 2+12•••当t=1时,—(t —1 ) +1有最大值1。
•••当t=1时,S=ED OP 的值最小,最小值是 10ED OP(3) 存在。
设 BC 所在直线的解析式为 y=kx+b ,由B (4, 0), C (0,— 2)由题意可得:D 点的纵坐标为t — 2,贝U D 点的横坐标为2to2 2 —• BD= 4 -2t t -2 = 5 2 -t 。
二次函数-存在性问题-备战2023年中考数学考点微专题

考向3.9 二次函数-存在性问题例1、(2021·湖南湘潭·中考真题)如图,一次函数333y x =-图象与坐标轴交于点A 、B ,二次函数233y x bx c =++图象过A 、B 两点. (1)求二次函数解析式;(2)点B 关于抛物线对称轴的对称点为点C ,点P 是对称轴上一动点,在抛物线上是否存在点Q ,使得以B 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出Q 点坐标;若不存在,请说明理由.解:(1)对于33y x =:当x =0时,3y = 当y =0时,3303x -=,妥得,x =3 ∴A (3,0),B (0,3- 把A (3,0),B (0,3-23y bx c ++得: 33+3+=03b c c ⎧⎪⎨=-⎪⎩解得,233b c ⎧=⎪⎨⎪=⎩∴抛物线的解析式为:23233y =-(2)抛物线的对称轴为直线23312323b x a -=-=-=⨯故设P (1,p ),Q (m ,n ) ①当BC 为菱形对角线时,如图,∵B ,C 关于对称没对称,且对称轴与x 轴垂直, ∴∴BC 与对称轴垂直,且BC //x 轴 ∵在菱形BQCP 中,BC ⊥PQ ∴PQ ⊥x 轴 ∵点P 在x =1上, ∴点Q 也在x =1上, 当x =1时,232343113=333y =⨯-⨯--∴Q (1,433-); ②当BC 为菱形一边时,若点Q 在点P 右侧时,如图,∴BC //PQ ,且BC =PQ ∵BC //x 轴,∴令3y =23233=3y解得,120,2x x == ∴(2,3)C - ∴PQ =BC =2 ∵22(3)12+= ∴PB =BC =2 ∴迠P 在x 轴上, ∴P (1,0) ∴Q (3,0);若点Q 在点P 的左侧,如图,同理可得,Q (-1,0) 综上所述,Q 点坐标为(1,433-)或(3,0)或(-1,0)1、存在性问题的解题思路:假设存在,推理论证,得出结论;2、解決线段存在性问题的方法:将军饮马问题、垂线段问题、三角形三边关系、函数最值等;3、本题考查的知识点有用待定系数法求出二次函数的解析式,菱形的性质和判定,解一元二次方程,主要考查学生综合运用这些性质进行计算和推理的能力.同时注意用分类讨论思想解决问题。
2024年中考数学复习重难点(全国通用版):二次函数中几何存在性的问题(解析版)

专题17二次函数中几何存在性的问题【中考考向导航】目录【直击中考】 (1)【考向一二次函数中构成等腰三角形存在性问题】 (1)【考向二二次函数中构成直角三角形存在性问题】 (8)【考向三二次函数中构成三角形相似存在性问题】 (16)【考向四二次函数中构成矩形存在性问题】 (23)【考向五二次函数中构成菱形存在性问题】 (33)【考向六二次函数中构成正方形存在性问题】 (42)【直击中考】【考向一二次函数中构成等腰三角形存在性问题】(1)求抛物线的解析式;(2)求抛物线的对称轴及顶点坐标(3)在坐标轴是否存在一点明理由;设点P 的坐标为∴3PB PC n 在Rt BOP △中,∴ 2253n n 1.(2023秋·陕西商洛·九年级校考期末)如图,已知抛物线24y ax bx (0a )与x 轴交于 1,0A , 2,0B 两点,与y 轴交于点C .(1)求抛物线的解析式及点(2)若F 为抛物线上一点,连接存在,请说明理由.【答案】(1)22y x (2)存在,点F 的坐标为则BN CN ,设ON 在Rt NOB 中,2ON ∴ 2224n n ,解得:32n ,∴点N 的坐标为302 ,A (1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当(3)在直线l 上是否存在点M 不存在,请说明理由.【答案】(1)223y x x (2)点P 坐标为 1,2;PAC △(3)存在符合条件的M 点,且坐标为∵点A 与点B 关于直线l 对称,∴PA PB ,∴PC PA PC PB BC ,此时PAC △的周长最小,设直线BC 解析式为y kx b 把 3,0B , 0,3C 代入得:130k b【考向二二次函数中构成直角三角形存在性问题】(1)求该抛物线的解析式;(2)在抛物线的对称轴上是否存在一点点P 的坐标;若不存在,请说明理由.【答案】(1)2=23y x x (2)存在,坐标为 12,或 14 ,∵ 30B ,, 03C ,∴3OB OC ,∴OBC OCB ∴当190PBC 时,1PBO 当290P CB 时,同理可得2P 当90BPC 时,设点P 的坐标为1.(2023秋·山东枣庄·九年级统考期末)如图,抛物线2y x bx c 与x 轴相交于A ,B 两点,与y 轴相交于点C ,对称轴为直线2x ,顶点为D ,点B 的坐标为 3,0.(1)求抛物线的解析式;(2)连接BC、CD,判断(3)在坐标轴上是否存在一点不存在,说明理由.【答案】(1)13 y△是直角三角形;∴BCD(3)存在,点P的坐标为①当点P在x轴上时,设BD ,BP∴2162若BP 为斜边,则有 2222396162x x ,解得15x ,∴ 115,0P ,若DP 为斜边,则有 2222963162x x ,解得3x ,∴ 23,0P ;②当点P 在y 轴上时,设 0,P y ,∴2162BD , 223BP y , 22296DP y ,若BP 为斜边,则有 222396162y y ,解得15y ,∴ 30,15P ,若DP 为斜边,则有 222963162y y ,解得3y (与B 点重合舍去),综上所述,点P 的坐标为 15,0, 3,0 或 0,15 .【点睛】本题考查了二次函数的综合题,熟练掌握二次函数的图象与性质,能够利用勾股定理证明直角三角形是解题的关键.3.(2023秋·广东广州·九年级统考期末)抛物线 240y ax bx a 与x 轴交于点 2,0A 和 4,0B ,与y 轴交于点C ,连接C B .点P 是线段BC 下方抛物线上的一个动点(不与点B ,C 重合),过点P 作y 轴的平行线交BC 于M ,交x 轴于N .(1)求该抛物线的解析式;(2)过点C 作CH PN 于点H ,3BN CH ,①求点P 的坐标;②连接CP ,在y 轴上是否存在点Q ,使得CPQ 为直角三角形?若存在,求出点Q 的坐标;若不存在,请说明理由.②由题可知,显然PCQ 不能为如图,当90CPQ 时,在Rt CPH 中,14CH PH ,如图,当90CQP 时,显然,OQPN 为矩形,∴92OQ NP ,∴点Q 的坐标为90,2;(1)求抛物线的表达式;(2)求证:BOC 是直角三角形;(3)若点P 是抛物线上第一象限内的一个动点,过点M ,A 为顶点的三角形与【答案】(1)22y x x设(,)P x y ,由题意知由(2)知,BOC 为直角三角形,①若PMA COB ∽,则即223(2)x x x ,得1x ,2x (舍去)【点睛】本题考查了用待定系数法求二次函数解析式、两点间距离、勾股定理、相似三角形的判定和性质等知识点,综合性强,同时也考查数形结合的数学思想方法.【变式训练】(1)求抛物线的表达式;(2)在直线BC 上存在一点(3)在x 轴上是否存在一点标;若不存在,请说明理由.【答案】(1)2122y x【点睛】本题主要考查了二次函数综合,一次函数与几何综合,相似三角形的性质与判定,轴对称最短路径问题,勾股定理和勾股定理的逆定理,正方形的性质与判定等等,灵活运用所学知识是解题的关键.2.(2023秋·湖南邵阳·九年级统考期末)顶点 1,4D ,过点A 的直线与抛物线相交于点(1)求该抛物线解析式;AC y x ;∴直线:1二次函数的性质,清晰的分类讨论与数形结合的方法都是解本题的关键.【考向四二次函数中构成矩形存在性问题】1.(2022秋·湖北黄冈·九年级统考期末)如图,抛物线223与x轴交于A、B两点(点A在点B的y x x左边),与y轴交于点C,点D和点C关于抛物线的对称轴对称.,求线段∴FGN 为等腰直角三角形,∴22FG FN ,设2,23F x x x ,则∴2231FN x x x 当12x 时,FN 有最大值9设直线AM 的解析式为y 把 1,0A 、 1,4M 分别代入得同理可得: 2210y 解得:92y ,即90,2P 由平移的性质可得:Q综上:72,2Q 或12,2Q∴【考向五二次函数中构成菱形存在性问题】例题:(2022秋·辽宁沈阳·九年级沈阳市广全学校校考阶段练习)如图,抛物线2y ax bx c 与x 轴负半轴交于点A ,与x 轴正半轴交于点B ,与y 轴负半轴交于点C , 40A ,, 10B ,,90ACB .(1)点C 的坐标为______;抛物线的函数表达式为______;E1.(2022秋·广东汕头·九年级统考期末)如图:已知直线:22l y x 与x 轴、y 轴分别相交于A 、B 两点,∴N例题:(2022秋·辽宁抚顺·九年级校考阶段练习)如图,直线y kx 与抛物线2y x c 交于A ,B 两点,其中点B 的坐标是2,2(1)求直线AB 及抛物线的解析式;(2)C 为抛物线上的一点,ABC 的面积为3,求点C 的坐标;(3)P 在抛物线上,Q 在直线AB 上,M 在坐标平面内,当以A ,P ,Q ,M 为顶点的四边形为正方形时,直接写出点M 的坐标.【答案】(1)直线AB 的解析式为y x ,抛物线的解析式是22y x∴22 CD t t ,∴ABC DBC ADC S S S∴2CD ,∴222 t t ,解得1211712t t ,∴22 CD t t ,∴ABC BBC ADC S S S∴2CD ,∴222 t t ,∴120,1t t ,∴222 t 或1 ,∵AP AB∴直线AP 的解析式为y ∴0,2P ∴M 点与A 点关于y 轴对称∴1,1M ∵()1,1-在抛物线22y x 上,∴当 1,1P 时, 0,2M ;当M 点关于A 点对称时, 1,3M ;如图,当AQ 是正方形的对角线时,∴点P 的纵坐标为-1∴1,1P ∴2AP ∵AM AP∴1,1M 综上所述:M 点坐标为 23411,1021113M M M M ,,-,-,,-,-【点睛】本题是二次函数的综合题,涉及二次函数的图象及性质,三角形和正方形的性质,熟练掌握相关知识是解题的关键【变式训练】1.(2022秋·湖南长沙·九年级校考期末)如图,抛物线 230y ax bx a 与x 轴交于 3,0A ,D 两点,与y 轴交于点B ,抛物线的对称轴与x 轴交于点 10C ,,点E ,P 为抛物线的对称轴上的动点.∵A 、D 关于直线1x 对称,∴DE AE ,∴BE DE AE BE AB ,当A 、B 、E 三点共线时,BE DE 的值最小,∵3OA OB ,∴45OAB ,∴AC CE ,∵2AC ,∴2CE ,∴ 1,2E ;(3)解:存在点P ,M ,N ,使得以A ,P ,M ,N 为顶点的四边形为正方形,理由如下:设 1,P t ,当AM 为正方形的对角线时,如图2,PM PA ,过M 点作MG PC 交于G ,。
2023学年二轮复习解答题专题二十七:二次函数中直角三角形的存在性问题探究(解析版)

2023学年二轮复习解答题专题二十七:二次函数中直角三角形的存在性问题探究方法点睛一、构造直角三角形的一般思路:构造直角三角形,用的是“两线一圆”:分别过已知线段的两个端点作已知线段的垂线,再以已知线段为直径作圆.二、解题思路是否存在一点,使之与另外两个定点构成直角三角形的问题:首先弄清题意,注意区分直角顶点;其次借助于动点所在图形的解析式,表示出动点的坐标;然后按分类的情况,利用几何知识建立方程(组),求出动点坐标,注意要根据题意舍去不符合题意的点.方法一:利用勾股定理进行边长的计算,从而来解决问题;方法二:往往可以利用到一线等三角之K字(90°)类型和母子相似型类型,尝试建构相应的相似来进行处理;方法三:两条直线互相垂直的条件,即=-1来解决.典例剖析类型一:利用勾股定理来解决直角三角形的存在性问题例1. (2022滨州中考)如图,在平面直角坐标系中,抛物线223y x x =--与x 轴相交于点A 、B (点A 在点B 的左侧),与y 轴相交于点C ,连接,AC BC .(1)求线段AC 的长;(2)若点Р为该抛物线对称轴上的一个动点,当PA PC =时,求点P 的坐标;(3)若点M 为该抛物线上的一个动点,当BCM V 为直角三角形时,求点M 的坐标.【答案】(1(2)()11,-(3)()14-,或()25-,或-或-【解析】【分析】(1)根据解析式求出A ,B ,C 的坐标,然后用勾股定理求得AC 的长;(2)求出对称轴为x =1,设P (1,t ),用t 表示出PA 2和PC 2的长度,列出等式求解即可;(3)设点M (m ,m 2-2m -3),分情况讨论,当222CM BC BM +=,222BM BC CM +=,k 1k2222BM CM BC +=分别列出等式求解即可.【小问1详解】223y x x =--与x 轴交点:令y =0,解得121,3x x =-=,即A (-1,0),B (3,0),223y x x =--与y 轴交点:令x =0,解得y =-3,即C (0,-3),∴AO =1,CO =3,∴AC ==;【小问2详解】抛物线223y x x =--的对称轴为:x =1,设P (1,t ),∴()()22221104PA t t =++-=+,()()()222210313PC t t =-++=++,∴24t + ()213t =++∴t =-1,∴P (1,-1);【小问3详解】设点M (m ,m 2-2m -3),()()()()22222223230323BM m m m m m m =-+---=-+--,()()()222222202332CM m m m m m m =-+--+=+-,()()222300318BC =-++=,①当222CM BC BM +=时,()()()222222218323m m m m m m +-+=-+--,解得,10m =(舍),21m =,∴M (1,-4);②当222BM BC CM +=时,()()()222222323182m m m m m m -+--+=+-,解得,12m =-,23m =(舍),∴M (-2,5);③当222BM CM BC +=时,()()()222222323218m m m m m m -+--++-=,解得,m =,∴M -或-;综上所述:满足条件的M 为()14-,或()25-,或-或-.【点睛】本题是二次函数综合题,考查了与坐标轴交点、线段求值、存在直角三角形等知识,解题的关键是学会分类讨论的思想,属于中考压轴题.类型二:构造相似来解决直角三角形存在性问题例2.(2021巴中中考)已知抛物线y=ax2+bx+c与x轴交于A(﹣2,0)、B(6,0)两点,与y轴交于点C(0,﹣3).(1)求抛物线的表达式;(2)点P在直线BC下方的抛物线上,连接AP交BC于点M,当最大时,求点P的坐标及的最大值;(3)在(2)的条件下,过点P作x轴的垂线l,在l上是否存在点D,使△BCD是直角三角形,若存在,请直接写出点D的坐标;若不存在,请说明理由.【考点】二次函数综合题.【专题】二次函数图象及其性质;运算能力;应用意识.【答案】(1)y=x2﹣x﹣3;(2)P(3,﹣),有最大值;(3)D点坐标为(3,6)或(3,﹣9)或(3,﹣﹣)或(3,﹣).【分析】(1)将A(﹣2,0)、B(6,0)、C(0,﹣3)代入y=ax2+bx+c即可求解析式;(2)过点A作AE⊥x轴交直线BC于点E,过P作PF⊥x轴交直线BC于点F,由PF∥AE,可得=,则求的最大值即可;(3)分三种情况讨论:当∠CBD=90°时,过点B作GH⊥x轴,过点D作DG⊥y轴,DG与GH交于点G,过点C作CH⊥y轴,CH与GH交于点H,可证明△DBG∽△BCH,求出D(3,6);当∠BCD=90°时,过点D作DK⊥y轴交于点K,可证明△OBC∽△KCD,求出D(3,﹣9);当∠BDC=90°时,线段BC的中点T(3,﹣),设D(3,m),由DT=BC,可求D(3,﹣)或D(3,﹣﹣).【解答】解:(1)将点A(﹣2,0)、B(6,0)、C(0,﹣3)代入y=ax2+bx+c,得,解得,∴y=x2﹣x﹣3;(2)如图1,过点A作AE⊥x轴交直线BC于点E,过P作PF⊥x轴交直线BC于点F,∴PF∥AE,∴=,设直线BC的解析式为y=kx+d,∴,∴,∴y=x﹣3,设P(t,t2﹣t﹣3),则F(t,t﹣3),∴PF=t﹣3﹣t2+t+3=﹣t2+t,∵A(﹣2,0),∴E(﹣2,﹣4),∴AE=4,∴===﹣t2+t=﹣(t﹣3)2+,∴当t=3时,有最大值,∴P(3,﹣);(3)∵P(3,﹣),D点在l上,如图2,当∠CBD=90°时,过点B作GH⊥x轴,过点D作DG⊥y轴,DG与GH交于点G,过点C作CH⊥y轴,CH与GH交于点H,∴∠DBG+∠GDB=90°,∠DBG+∠CBH=90°,∴∠GDB=∠CBH,∴△DBG∽△BCH,∴=,即=,∴BG=6,∴D(3,6);如图3,当∠BCD=90°时,过点D作DK⊥y轴交于点K,∵∠KCD+∠OCB=90°,∠KCD+∠CDK=90°,∴∠CDK=∠OCB,∴△OBC∽△KCD,∴=,即=,∴KC=6,∴D(3,﹣9);如图4,当∠BDC=90°时,线段BC的中点T(3,﹣),BC=3,设D(3,m),∵DT=BC,∴|m+|=,∴m=﹣或m=﹣﹣,∴D(3,﹣)或D(3,﹣﹣);综上所述:△BCD是直角三角形时,D点坐标为(3,6)或(3,﹣9)或(3,﹣﹣)或(3,﹣).专题过关1. (2022柳州中考)已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(m,0)两点,与y轴交于点C(0,5).(1)求b,c,m的值;(2)如图1,点D是抛物线上位于对称轴右侧的一个动点,且点D在第一象限内,过点D作x轴的平行线交抛物线于点E,作y轴的平行线交x轴于点G,过点E作EF⊥x轴,垂足为点F,当四边形DEFG的周长最大时,求点D的坐标;(3)如图2,点M是抛物线的顶点,将△MBC沿BC翻折得到△NBC,NB与y轴交于点Q,在对称轴上找一点P,使得△PQB是以QB为直角边的直角三角形,求出所有符合条件的点P的坐标.【答案】(1)b=4,c=5,m=5(2)当四边形DEFG的周长最大时,点D的坐标为(3,8)(3)所有符合条件的点P的坐标为(2,233),(2,﹣9)【解析】【分析】(1)把A(﹣1,0),C(0,5)代入y=﹣x2+bx+c,利用待定系数法求解b,c即可,再令y=0,再解方程求解m即可;(2)先求解抛物线的对称轴为x=2,设D(x,﹣x2+4x+5),则E(4﹣x,﹣x2+4x+5),证明四边形DEFG 是矩形,而224,45,DE x DF x x =-=-++ 可得四边形DEFG 的周长=2(﹣x 2+4x +5)+2(2x ﹣4)=﹣2x 2+12x +2=﹣2(x ﹣3)2+20,再利用二次函数的性质可得答案;(3)过点C 作CH ⊥对称轴于H ,过点N 作NK ⊥y 轴于K ,证明△MCH ≌△NCK (AAS ),再求解N (﹣4,3),求解直线BN 的解析式为:15,33y x =-+ 可得50,,3Q æöç÷ç÷èø设P (2,p ),再利用勾股定理表示2222510612,339PQ p p p æöç÷=+-=-+ç÷èø BP 2=()222529p p -+=+,222525525,39BQ æöç÷=+=+ç÷èø再分两种情况建立方程求解即可.【小问1详解】把A (﹣1,0),C (0,5)代入y =﹣x 2+bx +c ,105b c c ì--+=ï\í=ïî ,解得:4,5b c ì=ïí=ïî∴这个抛物线的解析式为:y =﹣x 2+4x +5,令y =0,则﹣x 2+4x +5=0,解得x 1=5,x 2=﹣1,∴B (5,0),∴m =5;【小问2详解】∵抛物线的解析式为:y =﹣x 2+4x +5=﹣(x ﹣2)2+9,∴对称轴为x =2,设D (x ,﹣x 2+4x +5),∵DE x ∥轴,∴E (4﹣x ,﹣x 2+4x +5),∵过点D 作x 轴的平行线交抛物线于点E ,作y 轴的平行线交x 轴于点G ,过点E 作EF ⊥x 轴,∴四边形DEFG 是矩形,∴224,45,DE x DF x x =-=-++∴四边形DEFG 的周长=2(﹣x 2+4x +5)+2(2x ﹣4)=﹣2x 2+12x +2=﹣2(x ﹣3)2+20,∴当x =3时,四边形DEFG 的周长最大,∴当四边形DEFG 的周长最大时,点D 的坐标为(3,8);【小问3详解】过点C 作CH ⊥对称轴于H ,过点N 作NK ⊥y 轴于K ,∴∠NKC =∠MHC =90°,由翻折得CN =CM ,∠BCN =∠BCM ,∵B (5,0),C (0,5).∴OB =OC ,∴∠OCB=∠OBC=45°,∵CH⊥对称轴于H,∴CH x∥轴,∴∠BCH=45°,∴∠BCH=∠OCB,∴∠NCK=∠MCH,∴△MCH≌△NCK(AAS),∴NK=MH,CK=CH,∵抛物线的解析式为:y=﹣x2+4x+5=﹣(x﹣2)2+9,∴对称轴为x=2,M(2,9),∴MH=9﹣5=4,CH=2,∴NK=MH=4,CK=CH=2,∴N(﹣4,3),设直线BN的解析式为y=mx+n,∴43,50m nm nì-+=ïí+=ïî解得:13,53mnì=-ïïíï=ïî∴直线BN的解析式为:15,33 y x=-+∴50,,3 Qæöç÷ç÷èø设P(2,p),∴2222510612,339PQ p p p æöç÷=+-=-+ç÷èøBP 2=()222529p p -+=+,222525525,39BQ æöç÷=+=+ç÷èø分两种情况:①当∠BQP =90°时,BP 2=PQ 2+BQ 2,∴22106125925,399p p p +=-+++ 解得:23,3p = ∴232,,3P æöç÷ç÷èø②当∠QBP =90°时,P ′Q 2=BP ′2+BQ 2,∴22106125925,399p p p -+=+++ 解得:9,p =-∴点P ′的坐标为(2,﹣9).综上,所有符合条件的点P 的坐标为232,3æöç÷ç÷èø或()2,9P -.【点睛】本题考查的是利用待定系数法求解二次函数的解析式,二次函数与坐标轴的交点坐标问题,二次函数的性质,对称轴的性质,二次函数与直角三角形,勾股定理的应用,清晰的分类讨论是解本题的关键.2. (2022雅安中考)已知二次函数y =ax 2+bx +c 的图象过点A (﹣1,0),B (3,0),且与y 轴交于点C (0,﹣3).(1)求此二次函数的表达式及图象顶点D 的坐标;(2)在此抛物线的对称轴上是否存在点E ,使△ACE 为Rt △,若存在,试求点E 的坐标,若不存在,请说明理由;(3)在平面直角坐标系中,存在点P ,满足PA ⊥PD ,求线段PB 的最小值.【答案】(1)()223,1,4y x x D =--- (2)E 的坐标为:21,3æöç÷èø或81,3æö-ç÷èø或()1,1-或()1,2.- (3)BP-【解析】【分析】(1)根据题意可设抛物线为()()13,y a x x =+-再代入C 的坐标可得函数解析式,化为顶点式可得顶点坐标;(2)如图,由()()()22132314,y x x x x x =+-=--=--可得抛物线对称轴为:1,x =设()1,,E n 而A (﹣1,0),C (0,-3),再利用勾股定理分别表示210,AC = 224,AE n =+ 22610,CE n n =++ 再分三种情况讨论即可;(3)如图,连结AD ,记AD 的中点为H ,由,PA PD ⊥ 则P 在以H 为圆心,HA为半径的的圆H 上,不与A ,D 重合,连结BH ,交圆H 于P ,则PB 最短,再求解H 的坐标,结合勾股定理可得答案.【小问1详解】解:Q 二次函数y =ax 2+bx +c 的图象过点A (﹣1,0),B (3,0),∴设二次函数为:()()13,y a x x =+-把C (0,﹣3)代入抛物线可得:33,a -=-解得:1,a =∴抛物线为:()()()2213231 4.y x x x x x =+-=--=-- ()1,4.D \-【小问2详解】如图,由()()()22132314,y x x x x x =+-=--=--可得抛物线的对称轴为:1,x =设()1,,E n 而A (﹣1,0),C (0,-3),()()222100310,AC \=--++= ()2222114,AE n n =++=+ ()()2222103610,CE n n n =-++=++ 当90EAC Ð=°时,22610410n n n ++=++,解得2,3n = 即21,,3E æöç÷ç÷èø当90ACE Ð=°时,22410610,n n n +=+++ 解得:8,3n =- 即81,,3E æöç÷-ç÷èø当90AEC Ð=°时,22461010,n n n ++++=整理得:2320,n n ++=解得:121,2,n n =-=-()()1,1,1,2,E E \--综上:E 的坐标为:21,3æöç÷èø或81,3æö-ç÷èø或()1,1-或()1,2.-【小问3详解】如图,连结AD ,记AD 的中点为H ,由,PA PD ⊥则P 在以H 为圆心,HA 为半径的圆H 上,不与A ,D 重合,连结BH ,交圆H 于P ,则PB 最短,()()1,0,1,4,A D --Q()0,2,H AD HP \-= ()3,0,B QBH \==BP \即BP -【点睛】本题考查的是利用待定系数法求解抛物线的解析式,二次函数的性质,勾股定理的应用,二次函数与圆的综合,判断PB 最小时,P 的位置是解本题的关键.3. (2022广安中考)如图,在平面直角坐标系中,抛物线2y ax x m =++(a ≠0)的图象与x 轴交于A 、C 两点,与y 轴交于点B ,其中点B 坐标为(0,-4),点C 坐标为(2,0).(1)求此抛物线的函数解析式.(2)点D 是直线AB 下方抛物线上一个动点,连接AD 、BD ,探究是否存在点D ,使得△ABD 的面积最大?若存在,请求出点D 的坐标;若不存在,请说明理由.(3)点P 为该抛物线对称轴上的动点,使得△PAB 为直角三角形,请求出点P 的坐标.【答案】(1)2142y x x =+-(2)(-2,-4) (3)P 点坐标为:(-1,3),(-1,-5),(12--+,,(12---,【解析】【分析】(1)直接将B (0,-4),C (2,0)代入2y ax x m =++,即可求出解析式;(2)先求出直线AB 关系式为:4y x =--,直线AB 平移后的关系式为:4y x n =--+,当其与抛物线只有一个交点时,此时点D 距AB 最大,此时△ABD 的面积最大,由此即可求得D 点坐标;(3)分三种情况讨论,①当∠PAB =90°时,即PA ⊥AB ,则设PA 所在直线解析式为:y =x+z ,将A (-4,0)代入y =x+z 得,解得:4z =,此时P 点坐标为:(-1,3);②当∠PBA =90°时,即PB ⊥AB ,则设PB 所在直线解析式为:y x t =+,将B (0,-4)代入y x t =+得,4t =-,此时P 点坐标为:(-1,-5);③当∠APB =90°时,设P 点坐标为:()1p y -,,由于PA 所在直线斜率为:3py ,PB 在直线斜率为:41p y +-,3py g 41p y +-=-1,则此时P点坐标为:(12--+,,(12--,.【小问1详解】解:将B (0,-4),C (2,0)代入2y ax x m =++, 得:4420m a m =-ìí++=î,解得:412m a =-ìïí=ïî,∴抛物线的函数解析式为:2142y x x =+-.【小问2详解】向下平移直线AB ,使平移后的直线与抛物线只有唯一公共点D 时,此时点D 到直线AB 的距离最大,此时△ABD 的面积最大,∵21402x x +-=时,12x =,24x =-,∴A 点坐标为:(-4,0),设直线AB 关系式为:0y kx b k =+¹(),将A (-4,0),B (0,-4),代入0y kx b k =+¹(),得:404k b b -+=ìí=-î,解得:14k b =-ìí=-î,∴直线AB 关系式为:4y x =--,设直线AB 平移后的关系式为:4y x n =--+,则方程21442x n x x --+=+-有两个相等的实数根,即21202x x n +-=有两个相等的实数根,∴2n =-,即212202x x ++=的解为:x =-2,将x =-2代入抛物线解析式得,()2122442y =´---=-,∴点D 的坐标为:(-2,-4)时,△ABD 的面积最大;【小问3详解】①当∠PAB =90°时,即PA ⊥AB ,则设PA 所在直线解析式为:y =x+z ,将A (-4,0)代入y =x+z 得,40z -+=,解得:4z =,∴PA 所在直线解析式为:4y x =+,∵抛物线对称轴为:x =-1,∴当x =-1时,143y =-+=,∴P 点坐标:(-1,3);为②当∠PBA =90°时,即PB ⊥AB ,则设PB 所在直线解析式为:y x t =+,将B (0,-4)代入y x t =+得,4t =-,∴PA 所在直线解析式为:4y x =-,∴当x =-1时,145y =--=-,∴P 点坐标为:(-1,-5);③当∠APB =90°时,设P 点坐标为:()1p y -,,∴PA 所在直线斜率为:3py ,PB 在直线斜率为:41p y +-,∵PA ⊥PB ,∴3py 41p y +-=-1,解得:12p y =-22p y =--,∴P 点坐标为:(12--+,,(12--,综上所述,P 点坐标为:(-1,3),(-1,-5),(12--,,(12---,时,△PAB 为直角三角形.【点睛】本题主要考查的是二次函数图象与一次函数、三角形的综合,灵活运用所学知识是解题的关键.4. (2022呼和浩特中考)如图,抛物线212y x bx c =-++经过点(4,0)B 和点(0,2)C ,与x 轴的另一个交点为A ,连接AC 、BC .(1)求抛物线的解析式及点A 的坐标;(2)如图1,若点D 是线段AC 的中点,连接BD ,在y 轴上是否存在点E ,使得BDE V 是以BD 为斜边的直角三角形?若存在,请求出点E 的坐标;若不存在,请说明理由;(3)如图2,点P 是第一象限内抛物线上的动点,过点P 作PQ y ∥轴,分别交BC 、x 轴于点M 、N ,当PMC △中有某个角的度数等于OBC Ð度数的2倍时,请求出满足条件的点P 的横坐标.【答案】(1)213222y x x =-++;A (-1,0); (2)存在E (0,3)或(0,-1),使得BDE V 是以BD 为斜边的直角三角形; (3)2或32【解析】【分析】(1)利用待定系数法解答,即可求解;(2)先根据中点坐标公式可得点1,12D æö-ç÷èø,设点E (0,m ),再根据两点坐标公式可得()22221501224DE m m m æö=--+-=-+ç÷èø,2222181424BD m m æö=++=+ç÷èø,2216BE m =+,再由勾股定理,即可求解;(3)先求出1tan 2OC OBC OB Ð==,再求出直线BC 的解析式,然后设点213,222P a a a æö-++ç÷èø,则1,22M a a æö-+ç÷èø,CF =a ,可得2122PM a a =-+,再分三种情况讨论:若∠PCM =2∠OBC ,过点C 作CF ∥x 轴交PM 于点F ;若∠PMC =2∠OBC ;若∠CPM =2∠OBC ,过点P 作PG 平分∠CPM ,则∠MPG =∠OBC ,即可求解.【小问1详解】解:把点(4,0)B 和点(0,2)C 代入,得:1164022b c c ì-´++=ïíï=î,解得:322b c ì=ïíï=î,∴抛物线的解析式为213222y x x =-++,令y =0,则213222y x x =-++,解得:121,4x x =-=,∴点A (-1,0);【小问2详解】解:存在,理由如下:∵点A (-1,0),点(0,2)C ,点D 是线段AC 的中点,∴点1,12D æö-ç÷èø,设点E (0,m ),∴()22221501224DE m m m æö=--+-=-+ç÷èø,2222181424BD m m æö=++=+ç÷èø,2216BE m =+,∵BDE V 是以BD 为斜边的直角三角形,∴22258116244m m m m ++-+=+,整理得:2230m m --=,解得:3m =或-1,∴点E 的坐标为(0,3)或(0,-1);【小问3详解】解:∵点B (4,0),C (0,2),∴OB =4,OC =2,∴1tan 2OC OBC OB Ð==,设直线BC 的解析式为()10y kx b k =+¹,把点B (4,0),C (0,2)代入得:11402k b b +=ìí=î,解得:1122k b ì=-ïíï=î,∴直线BC 的解析式为122y x =-+,设点213,222P a a a æö-++ç÷èø,则1,22M a a æö-+ç÷èø,CF =a ,∴2213122222122PM a a a a a -æöæö=-++-=-+ç÷ç÷èøèø+,若∠PCM =2∠OBC ,过点C 作CF ∥x 轴交PM 于点F ,如图甲所示,∴∠FCM =∠OBC ,即1tan tan 2FCM OBC Ð=Ð=,∴∠PCF =∠FCM ,∵PQ y ∥轴,∴CF ⊥PQ ,∴PM =2FM ,∴214FM a a =-+,∴21142a a a -+=,解得:解得:a =2或0(舍去),∴点P 的横坐标为2;若∠PMC =2∠OBC ,∵∠PMC =∠BMN ,∴∠BMN =2∠OBC ,∵∠OBC +∠BMN =90°,∴∠OBC =30°,与1tan 2OC OBC OB Ð==相矛盾,不合题意,舍去;若∠CPM =2∠OBC ,如图乙所示,过点P 作PG 平分∠CPM ,则∠MPG =∠OBC ,∵∠PMG =∠BMN ,∴△PMG ∽△BMN ,∴∠PGM =∠BNM =90°,∴∠PGC =90°,∵PG 平分∠CPM ,即∠MPG =∠CPG ,∴∠PCM =∠PMC ,∴PC =PM ,∴2122a a -+=,解得:32a =或0(舍去),∴点P 的横坐标为32;综上所述,点P 的横坐标为2或32.图甲 图乙【点睛】本题主要考查了二次函数的综合题,解直角三角形,相似三角形的判定和性质,熟练掌握二次函数的综合题,直角三角形的性质,相似三角形的判定和性质,利用数形结合思想和分类讨论思想解答是解题的关键.5. (2022抚顺中考) 如图,抛物线23y ax x c =-+与x 轴交于(4,0)A -,B 两点,与y 轴交于点(0,4)C ,点D 为x 轴上方抛物线上的动点,射线OD 交直线AC 于点E ,将射线OD 绕点O 逆时针旋转45°得到射线OP ,OP 交直线AC 于点F ,连接DF .(1)求抛物线的解析式;(2)当点D 在第二象限且34DE EO =时,求点D 的坐标;(3)当ODF △为直角三角形时,请直接写出点D 的坐标.【答案】(1)234y x x =--+(2)(1,6)D -或(3,4)D -(3)()3,4-或(0,4)或2ö÷÷ø或2ö÷÷ø【解析】【分析】(1)利用待定系数法求解即可;(2)过点D 作DG AB ⊥于点G ,交AC 于点H ,先求出直线AC 的解析式,设()()2,34,,4D n n n H n n --++,则24DH n n =--,证明△EDH ∽△EOC 得到DH DE OC OE=,即可求出DH =3,据此求解即可;(3)分D 和F 为直角顶点进行讨论求解即可.【小问1详解】解:将(4,0),(0,4)A C -代入23y ax x c =-+得:161204a c c ++=ìí=î,解得14a c =-ìí=î,∴抛物线解析式为234y x x =--+;【小问2详解】解:过点D 作DG AB ⊥于点G ,交AC 于点H ,设过点(4,0),(0,4)A C -的直线的解析式为y kx b =+,则404k b b -+=ìí=î,解得14k b =ìí=î,∴直线AC 的解析式为4y x =+,设()()2,34,,4D n n n H n n --++,则24DH n n =--.∵DH OA OC OA ⊥,⊥,∴DG OC ∥,的∴,ECO EHD EOC EDH Ð=ÐÐ=Ð,∴EDH EOC V V ∽,∴DH DE OC OE=,∵3,44DE OC OE ==,∴3DH =,∴243n n --=解得1n =-或3n =-将1,3n n =-=-分别代入234y x x =--+得6,4y y ==∴(1,6)D -或(3,4)D -;【小问3详解】解:如图1所示,当点D 与点C 重合时,∵点A (-4,0),点C (0,4),∴OA =OC =4,∴∠OCA =∠OAC =45°,当点C 与点D 重合时,∵OP 是OD 逆时针旋转45°得到的,∴∠POD =45°,即∠FOC =45°,∴∠AOF =∠FOC =45°,又∵OA =OC ,∴OF ⊥AC ,即∠OFC =90°,∴△OFC 是直角三角形,∴此时点D 的坐标为(0,4);如图2所示,当∠DFO =90°时,连接CD ,由旋转的性质可得∠DOF =45°,∴△DOF 是等腰直角三角形,∴OF =OD ,∠FDO =∠FCO =45°,∴C 、D 、F 、O 四点共圆,∴∠FCD =∠FOD =45°,∴∠OCD =∠FCD +∠FCO =90°,∴CD ⊥OC ,∴点D 的纵坐标为4,∴当y =4时,2344x x --+=,解得3x =-或0x =(舍去),∴点D 的坐标为(-3,4);如图3所示,当∠ODF =90°时,过点D 作DH ⊥y 轴于H ,过点F 作FG ⊥DH 交HD 延长线于G ,同理可证△DOF 是等腰直角三角形,∴OD =DF ,∵FG ⊥DH ,DH ⊥y 轴,∴∠FGD =∠DHO =90°,∴∠GDF +∠GFD =90°,又∵∠GDF +∠HDO =90°,∴∠GFD =∠HDO ,∴△GDF ≌△HOD (AAS ),∴GD =OH ,GF =DH ,设点D 的坐标为(m ,234m m --+),∴234DH GF m OH GD m m ==-==--+,,∴244GH m m =--+,∴点F 的坐标为(244m m +-,224m m --+),∵点F 在直线AC :4y x =+上,∴2244424m m m m +-+=--+,∴2320m m +-=,解得m =∴点D 的坐标为2ö÷÷ø或2ö÷÷ø;综上所述,点D 的坐标为(-3,4)或(0,4)或2ö÷÷ø或2ö÷÷ø【点睛】本题主要考查了二次函数与一次函数综合,二次函数与几何综合,全等三角形的性质与判定,相似三角形的性质与判定等等,熟知相关知识是解题的关键.6. (2022恩施中考) 在平面直角坐标系中,O 为坐标原点,抛物线2y x c =-+与y 轴交于点()0,4P .(1)直接写出抛物线的解析式.(2)如图,将抛物线2y x c =-+向左平移1个单位长度,记平移后的抛物线顶点为Q ,平移后的抛物线与x 轴交于A 、B 两点(点A 在点B 的右侧),与y 轴交于点C .判断以B 、C 、Q 三点为顶点的三角形是否为直角三角形,并说明理由.(3)直线BC 与抛物线2y x c =-+交于M 、N 两点(点N 在点M 的右侧),请探究在x 轴上是否存在点T ,使得以B 、N 、T 三点为顶点的三角形与ABC V 相似,若存在,请求出点T 的坐标;若不存在,请说明理由.(4)若将抛物线2y x c =-+进行适当的平移,当平移后的抛物线与直线BC 最多只有一个公共点时,请直接写出拋物线2y x c =-+平移的最短距离并求出此时抛物线的顶点坐标.【答案】(1)24y x =-+(2)以B 、C 、Q 三点为顶点的三角形是直角三角形,理由见解析(3)存在,T ö÷÷ø或T ö÷÷ø,(4527,88æöç÷èø【解析】【分析】(1)待定系数法求二次函数解析式;(2)分别求得B 、C 、Q 的坐标,勾股定理的逆定理验证即可求解;(3)由CBA NBT Ð=Ð,故分两种情况讨论,根据相似三角形的性质与判定即可求解;(4)如图,作l BC ∥且与抛物线只有1个交点,交y 轴于点D ,过点C 作CE l ⊥于点E ,则DEC V 是等腰直角三角形,作EF DC ⊥于F ,进而求得直线l 与BC 的距离,即为所求最短距离,进而求得平移方式,将顶点坐标平移即可求解.【小问1详解】解:∵抛物线2y x c =-+与y 轴交于点()0,4P ∴4c =\抛物线解析式为24y x =-+【小问2详解】以B 、C 、Q 三点为顶点的三角形是直角三角形,理由如下:Q 24y x =-+的顶点坐标为()0,4P 依题意得,()1,4Q -\平移后的抛物线解析式为()214y x =-++令0y =,解()2140x -++=得123,1x x =-=()()1,03,0A B \-,令0x =,则3y =,即()0,3C()222222222331811231420BC CQ QB \=+==+==-++=,,222BC CQ QB \+=\以B 、C 、Q 三点为顶点的三角形是直角三角形【小问3详解】存在,T ö÷÷ø或T ö÷÷ø,理由如下,()3,0B -Q ,()03C ,,3OB OC \==\OBC V 是等腰直角三角形设直线BC 的解析式为y kx b =+,则303k b b -+=ìí=î,解得13k b =ìí=î,\直线BC 的解析式为3y x =+,联立234y x y x =+ìí=-+î解得11x y ì=ïïíïïî,22x y ì=ïïíïïîN \Q ()()1,0,3,0A B -,()0,3C ,OBC V 是等腰直角三角形\4AB =,BC ==设直线AC 的解析式为y mx n =+,03m n n +=ì\í=î33m n =-ì\í=î\直线AC 的解析式为33y x =-+当NT AC ∥时,BNT BCA V V ∽设NT 的解析式为3y x t =-+,由NT 过点N3t =-+解得1t =+\NT 的解析式为31y x =-++,令0y =解得x =T ö\÷÷ø3BT \=+=Q BNT BCA V V ∽,BT BN BA BC\==BN \=②当BNT BAC V V ∽时,则BT BN BC BA ==解得154BT =+3OB =QT ö\÷÷ø综上所述,T ö÷÷ø或T ö÷÷ø【小问4详解】如图,作l BC ∥,交y 轴于点D ,过点C 作CE l ⊥于点E ,则DEC V 是等腰直角三角形,作EF DC ⊥于FQ 直线BC 的解析式为3y x =+设与BC 平行的且与24y x =-+只有一个公共点的直线l 解析式为y x b=+则24y x y x bì=-+í=+î整理得:240x x b ++-=则()21440b D =--=解得174b =\直线l 的解析式为174y x =+175344CD \=-=,1528EF FC CD ===54CE\===即拋物线2y x c=-+EC方向()0,4PQ∴把点P先向右平移EF的长度,再向下平移FC的长度即得到平移后的坐标\平移后的顶点坐标为55,488æö-ç÷èø,即52788æöç÷èø,【点睛】本题是二次函数综合,考查了相似三角形的性质,求二次函数与一次函数解析式,二次函数图象的平移,勾股定理的逆定理,正确的添加辅助线以及正确的计算是解题的关键.7. (2022海南中考)如图1,抛物线2y ax2x c=++经过点(1,0)(0,3)A C-、,并交x 轴于另一点B,点(,)P x y在第一象限的抛物线上,AP交直线BC于点D.(1)求该抛物线的函数表达式;(2)当点P 的坐标为(1,4)时,求四边形BOCP 的面积;(3)点Q 在抛物线上,当PD AD的值最大且APQ V 是直角三角形时,求点Q 的横坐标;【答案】(1)2y x 2x 3=-++(2)152(3)点Q 的横坐标为76,113,52,1.【解析】【分析】(1)将A 、C 两点坐标代入解析式求解即可;(2)如图,连接OP ,令2230y x x =-++=,求得点B 的坐标,再根据各点的坐标确定OC 、OB 的长,然后再根据POC BOP BOCP S S S +=V V 四边形求解即可;(3)如图,作PF x ∥轴,交直线BC 于点F ,可得PFD ABD △∽△,即PD PF AD AB =,进一步说明当PF 最大时,PD PF AD AB=最大.设()2,23P m m m -++,则()222,23F m m m m --++,根据线段的核查运算求得PF 的最大值;设点()2,23Q t t t -++,若APQ V 是直角三角形,则点Q 不能与点P 、A 重合,∴3,12t t ¹¹-,再分90APQ Ð=°、90PAQ Ð=°、90AQP Ð=°三种情况解答即可.【小问1详解】解:∵抛物线2y ax 2x c =++经过点(1,0)(0,3)A C -、,∴203a c c -+=ìí=î解得13a c =-ìí=î∴该抛物线的函数表达式为2y x 2x 3=-++.【小问2详解】解:如图,连接OP ,令2230y x x =-++=,∴121,3x x =-=.∴(3,0)B ∵(0,3),(1,4)C P ,∴3,3,1,4P P OC OB x y ====.∴131,6222POC P BOP P S OC x S OB y =×==×=△△.∴152POC BOP BOCP S S S +==V V 四边形.【小问3详解】解:如图,作PF x ∥轴,交直线BC 于点F ,则PFD ABD △∽△.∴PD PF AD AB=.∵4AB =是定值,∴当PF 最大时,PD PF AD AB=最大.设BC y kx b =+,∵(0,3),(3,0)C B ,∴3BC y x =-+.设()2,23P m m m -++,则()222,23F m m m m --++.∴()222392324PF m m m m m m æö=--=-+=--+ç÷èø.∴当32m =时,PF 取得最大值94,此时315,24P æöç÷èø.设点()2,23Q t t t -++,若APQ V 是直角三角形,则点Q 不能与点P 、A 重合,∴3,12t t ¹¹-,下面分三类情况讨论:①若90APQ Ð=°,如图,过点P 作2PP x ⊥轴于点2P ,作12QP P P ⊥交2PP 的延长线于点1P ,则12PPQ AP P △∽△.∴1212QP PP PP AP =.∴23152415323142t t t -=-++-+.∵32t ¹,∴13122t =-.∴76t =.②若90PAQ Ð=°,如图,过点P 作直线1PA x ⊥轴于点1A ,过点Q 作2QA x ⊥轴于点2A ,12APA QAA ∽△△.∴1212PA AA AA QA =.∴2151432312t t t +=--+.∵1t ¹-,∴3123t =-.∴113t =.③若90AQP Ð=°,如图,过点Q 作1Q Q x ⊥轴于点1Q ,作21PQ Q Q ⊥交1Q Q 的延长线于点2Q ,则21PQQ QAQ ∽△△.∴2121PQ QQ QQ AQ =.∴()223232151234t t t t t t --++=+--++.∵3,12t t ¹¹-,∴2321t t =--.∴1251,2t t ==.综上所述,当PD AD 的值最大且APQ V 是直角三角形时,点Q 的横坐标为76,113,52,1.【点睛】本题属于二次函数综合题,主要考查了运用待定系数法求函数解析式、二次函数与几何图形的综合、相似三角形的判定与性质、直角三角形的性质以及分类讨论思想,灵活应用相关知识以及分类讨论思想成为解答本题的关键.8. (2022山西侯马二模)如图,抛物线23y ax bx =+-经过()1,0A -,()3,0B 两点,与y 轴交于点C ,P 为第四象限内抛物线上一点,过点P 作PM ⊥x 轴于点M ,连接AC ,AP ,AP 与y 轴交于点D .(1)求抛物线的函数表达式.(2)当∠MPA =2∠PAC 时,求直线AP 的函数表达式.(3)在(2)的条件下,在抛物线的对称轴上是否存在点E ,使以E ,M ,C 为顶点的三角形是直角三角形?若存在,请直接写出点E 的坐标;若不存在,请说明理由.【答案】(1)223y x x =--;(2)4433y x =--; (3)存在,点E 坐标为321,9æö-ç÷èø或101,27æöç÷èø或31,2æ-+çè或31,2æ--çè【解析】【分析】(1)把()1,0A -,()3,0B 分别代入23y ax bx =+-,解方程组即可;(2)先根据平行线的性质得到∠MPA =∠ODA ,然后再由三角形外角的性质得到△ADC 为等腰三角形,求出点D 的坐标,由A 、D 两点的坐标即可求得直线AP 的函数解析式;(3)先求出M 点坐标,设点E 的坐标为()1,n ,用含n 的代数式分别表示出2CM ,2CE ,2ME ,然后进行分类谈论依次解出点E 对应的坐标.【小问1详解】的解:把()1,0A -,()3,0B 分别代入23y ax bx =+-,得309330a b a b --=ìí+-=î.解得12a b =ìí=-î.∴抛物线的函数表达式为223y x x =--;【小问2详解】解:根据题意,得MP OD ∥.∴∠MPA =∠ODA .又∵∠MPA =2∠PAC ,∴∠ODA =2∠PAC .又∵∠ODA =∠DAC +∠ACD ,∴∠DAC =∠ACD .∴CD =AD .在223y x x =--中,令0x =,解得3y =-,∴()0,3C-.设OD =m ,则AD =CD =3-m .∵()1,0A -,∴OA =1.在Rt △AOD 中,根据勾股定理,得()22213m m +=-.解得43m =.∴40,3D æö-ç÷èø.设直线AP 的函数表达式为y kx c =+.把()1,0A -,40,3D æö-ç÷èø分别代入,得0,4.3k c c -+=ìïí=-ïî解得4,34.3k c ì=-ïïíï=-ïî∴直线AP 的函数表达式为4433y x =--;【小问3详解】解:存在,点E 的坐标为321,9æö-ç÷èø或101,27æöç÷èø或31,2æ-+çè或31,2æ--çè.令2442333x x x --=--,解得11x =-,253x =.∴点P 的横坐标为53.∵PM ⊥x 轴,∴5,03M æöç÷èø.由223y x x =--,得抛物线的对称轴为直线12b x a=-=,由(2)可得()0,3C -.设点E 的坐标为()1,n ,则2225106339CM æö=+=ç÷èø,()22213CE n =++,22254139ME n n æö=-+=+ç÷èø.若∠MCE =90°,则222CM CE ME +=,即()22210641399n n +++=+,解得329n =-.若∠CME =90°,则222CM ME CE +=,即()22210641399n n ++=++,解得1027n =.若∠CEM =90°,则222CE ME CM +=,即()22241061399n n ++++=,解得132n =-+,232n =--.综上所述,点E 的坐标为321,9æö-ç÷èø或101,27æöç÷èø或31,2æ-+çè或31,2æ--çè.【点睛】本题考查的是二次函数的综合题,熟练掌握二次函数的图像与性质,直角三角形的性质是解决问题的关键.9.(2021烟台中考)(14分)如图,抛物线y =ax 2+bx +c 经过点A (﹣2,0),B (4,0),与y 轴正半轴交于点C ,且OC =2OA ,抛物线的顶点为D ,对称轴交x 轴于点E .直线y =mx +n 经过B ,C 两点.(1)求抛物线及直线BC 的函数表达式;(2)点F 是抛物线对称轴上一点,当FA +FC 的值最小时,求出点F 的坐标及FA +FC 的最小值;(3)连接AC ,若点P 是抛物线上对称轴右侧一点,点Q 是直线BC 上一点,试探究是否存在以点E 为直角顶点的Rt △PEQ ,且满足tan ∠EQP =tan ∠OCA .若存在,求出点P 的坐标;若不存在,请说明理由.【分析】(1)用待定系数法即可求解;(2)点A 、B 关于抛物线的对称轴对称,设抛物线的对称轴交BC 于点F ,则点F 为所求点,此时,当FA +FC 的值最小,进而求解;(3)①当点Q 在点P 的左侧时,证明△QME ∽△ENP ,则=tan ∠EQP =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题04 二次函数存在性问题(1)—与三角形相关【典例分析】【例1——最值存在性问题】如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),连接AC,点P为第二象限抛物线上的动点.(1)求a、b、c的值;(2)连接PA、PC、AC,求△PAC面积的最大值;【答案】(1)a=﹣1,b=﹣2,c=3;(2)当m时,S△PAC最大.【解析】解:(1)∵抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点∴,解得:∴a=﹣1,b=﹣2,c=3;(2)如图,过点P作PE∥y轴,交AC于E,∵A(﹣3,0),C(0,3),∴直线AC的解析式为y=x+3,由(1)知,抛物线的解析式为y=﹣x2﹣2x+3,设点P(m,﹣m2﹣2m+3),则E(m,m+3),∴S△ACP PE•(x C﹣x A)[﹣m2﹣2m+3﹣(m+3)]×(0+3)(m2﹣3m)(m )2,∴当m时,S△PAC最大.【练1】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B 与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.点P为线段MB上一个动点,过点P作PD⊥x轴于点D,若OD=m.(1)求二次函数解析式;(2)设△PCD的面积为S,试判断S有最大值或最小值?若有,求出其最值,若没有,请说明理由;【答案】(1)二次函数的解析式为y=﹣x2+2x+3.(2)当m时,S最大.【解析】解:(1)把B(3,0)、C(0,3)代入y=﹣x2+bx+c,得,解得,∴二次函数的解析式为y=﹣x2+2x+3.(2)S有最大值.如图1,设直线BM的解析式为y=kx+a,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴该抛物的顶点坐标为M(1,4),把M(1,4)、B(3,0)代入y=kx+a,得,解得,∴y=﹣2x+6,∵D(m,0),∴P(m,﹣2m+6);由S△PCD PD•OD,得S m(﹣2m+6)=﹣m2+3m;∵当点P与点B重合时,不存在以P、C、D为顶点的三角形,∴1≤m<3,∴S不存在最小值;∵S=﹣m2+3m=﹣(m)2,∴当m时,S最大,∴S的最大值为.【练2】如图,已知抛物线y=ax2+bx+4(a≠0)与x轴交于点A(1,0)和B,与y轴交于点C,对称轴为直线x.(1)求抛物线的解析式;(2)如图1,若点P是线段BC上的一个动点(不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,连接OQ,当x为多少时,线段PQ长度有最值。
【答案】(1)y=x2﹣5x+4(2)当x=2时,PQ的最大值为4【解析】解:(1)由题意得:,解得,故抛物线的表达式为y=x2﹣5x+4;(2)对于y=x2﹣5x+4,令y=x2﹣5x+4=0,解得x=1或4,令x=0,则y=4,故点B的坐标为(4,0),点C(0,4),设直线BC的表达式为y=kx+t,则,解得,故直线BC的表达式为y=﹣x+4,设点P的坐标为(x,﹣x+4),则点Q的坐标为(x,x2﹣5x+4),则PQ=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x,∵﹣1<0,故PQ有最大值,当x=2时,PQ的最大值为4【练3】如图,直线y x+c与x轴交于点A(﹣3,0),与y轴交于点C,抛物线y x2+bx+c 经过点A,C,与x轴的另一个交点为B(1,0),连接BC.(1)求抛物线的函数解析式.(2)M为x轴的下方的抛物线上一动点,求△ABM的面积的最大值.【答案】(1)(2)△ABM的面积的最大值;【解析】解:(1)将A(﹣3,0),B(1,0)代入抛物线,∴解得,∴抛物线的函数解析式为:;(2)∵M是x轴的下方的抛物线上一动点,且△ABM的面积最大,∴点M为抛物线的顶点,∴M(﹣1,﹣2),∴△ABM的面积的最大值;【例2——二次函数中等腰三角形存在性问题】如图,抛物线y=ax2+4x+c经过A(﹣3,﹣4),B(0,﹣1)两点,点P是y轴左侧且位于x轴下方抛物线上一动点,设其横坐标为m.(1)直接写出抛物线的解析式;(2)过点P作PM⊥x轴交直线BD于点M,试探究是否存在点P,使△PBM是等腰三角形?若存在,求出点m的值;若不存在,说明理由.【答案】(1)y=x2+4x﹣1;(2)m的值为﹣3,﹣4,﹣5【解析】解:(1)把点A(﹣3,﹣4),B(0,﹣1)带入解析式y=ax2+4x+c,得,解得,∴y=x2+4x﹣1;(2)存在点P,∵D(﹣3,2),B(0,﹣1),∴直线BD的解析式为y=﹣x﹣1,设P(m,m2+4m﹣1),则M(m,﹣m﹣1),∵∠BMP=45°,当△PBM是等腰三角形,且45°为底角时,有∠MBP=90°或∠MPB=90°,若∠MBP=90°,则P与A重合,即m=﹣3,若∠MPB=90°,则PB∥x轴,即P的纵坐标为﹣1,∴m2+4m﹣1=﹣1,解得m=0(舍)或m=﹣4,∴m=﹣4,若45°为顶角,即MP=MB,∵MP=﹣m﹣1﹣m2﹣4m+1=﹣m2﹣5m,MB,∴﹣m2﹣5m m,解得m=﹣5(舍)或m=﹣5,∴m的值为﹣3,﹣4,﹣5.【练1】如图,抛物线y=ax2与直线y=2x在第一象限内交于点A(2,t).(1)求抛物线的解析式;(2)在x轴上是否存在一点P,使△OAP是以OA为腰的等腰三角形?若存在,请你求出点P 的坐标;若不存在,请说明理由;【答案】(1)y=x2(2)P点坐标为(-25,0)(25,0)或(4,0);【解析】解:(1)把A(2,t)代入y=2x中,得t=4,∴A(2,4),把A(2,4)代入y=ax2中,得a=1,∴抛物线的解析式为y=x2;(2)设P点的坐标为(m,0),当OA=OP时,有m2=22+42,解得,m=25,或m=-25,∴此时P点的坐标为P(-25,0),(25,0);当OA=PA时,有(m-2)2+42=22+42,解得,m=0(舍),或m=4,∴此时P点坐标为(4,0),综上,在x轴上存在一点P,使△OAP是以OA为腰的等腰三角形,其P点坐标为(-25,0)(25,0)或(4,0);【练2】如图,直线y x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(﹣1,0).(1)求B,C两点的坐标.(2)求该二次函数的解析式.(3)若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.【答案】(1)B(4,0),C(0,2).(2)y(x﹣4)(x+1)x2x+2.(3)存在P1(),P2(),P3(,4),使△PCD是以CD为腰的等腰三角形.【解析】解:(1)对直线y x+2,当x=0时,y=2,y=0时,x=4,∴B(4,0),C(0,2).(2)设二次函数为y=a(x﹣m)(x﹣n)(a≠0),∵二次函数图象经过B(4,0),A(﹣1,0),∴y=a(x﹣4)(x+1),把点C(0,2)代入y=a(x﹣4)(x+1)得:a(0﹣4)(0+1)=2,解得:a,∴y(x﹣4)(x+1)x2x+2.(3)∵二次函数图象经过B(4,0),A(﹣1,0),∴对称轴为x,∴D(,0),∵C(0,2),∴CD,①如图1,当CD=PD时,PD,∴P1(),P2(),②如图2,当CD=CP3时,过点C作CH⊥DP3于点H,∵CD=CP3,CH⊥DP3,∴DH=P3H,∵C(0,2),∴DH=2,∴P3H=2,∴P3D=4,∴P3(,4),综上所述:存在P1(),P2(),P3(,4),使△PCD是以CD为腰的等腰三角形.【练3】如图,抛物线y=ax2+4x+c经过A(﹣3,﹣4),B(0,﹣1)两点,点P是y轴左侧且位于x轴下方抛物线上一动点,设其横坐标为m.(1)直接写出抛物线的解析式;(2)将线段AB绕点B顺时针旋转90°得线段BD(点D是点A的对应点),求点D的坐标,并判断点D是否在抛物线上;(3)过点P作PM⊥x轴交直线BD于点M,试探究是否存在点P,使△PBM是等腰三角形?若存在,求出点m的值;若不存在,说明理由.【答案】(1)y=x2+4x﹣1;(2)点D不在抛物线上;(3)m的值为﹣3,﹣4,﹣5.【解析】解:(1)把点A(﹣3,﹣4),B(0,﹣1)带入解析式y=ax2+4x+c,得,解得,∴y=x2+4x﹣1;(2)如图,作AC⊥y轴于点C,作DH⊥y轴于点H,∵∠CAB+∠ABC=90°,∠HBD+∠ABC=90°,∴∠CAB=∠HBD,在△ABC和△DBH中,,∴△ABC≌△DBH(AAS),∴HB=AC=3,DH=BC=3,∴OH=2,∴D(﹣3,2),把D(﹣3,2)代入y=x2+4x﹣1中,得(﹣3)2+4×(﹣3)﹣1=﹣4≠2,∴点D不在抛物线上;(3)存在点P,∵D(﹣3,2),B(0,﹣1),∴直线BD的解析式为y=﹣x﹣1,设P(m,m2+4m﹣1),则M(m,﹣m﹣1),由(2)知:∠BMP=45°,当△PBM是等腰三角形,且45°为底角时,有∠MBP=90°或∠MPB=90°,若∠MBP=90°,则P与A重合,即m=﹣3,若∠MPB=90°,则PB∥x轴,即P的纵坐标为﹣1,∴m2+4m﹣1=﹣1,解得m=0(舍)或m=﹣4,∴m=﹣4,若45°为顶角,即MP=MB,∵MP=﹣m﹣1﹣m2﹣4m+1=﹣m2﹣5m,MB,∴﹣m2﹣5m m,解得m=﹣5(舍)或m=﹣5,∴m的值为﹣3,﹣4,﹣5.【例3——二次函数中直角三角形存在性问题】如图,已知抛物线y=﹣x2+2x+3与x轴交于点A、B,与y轴交于点C,点P是抛物线上一动点,连接PB,PC.(1)点A的坐标为,点B的坐标为;(2)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.【答案】(1)A(﹣1,0),B(3,0);(2)点P的坐标为(1,4)或(﹣2,﹣5).【解析】解:(1)令抛物线y=0,则﹣x2+2x+3=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0);故答案为:(﹣1,0),(3,0);(2)∵△PBC是以BC为直角边的直角三角形,∴有两种情况:①点C为直角顶点,如图,过点C作直线P1C⊥BC,交抛物线于点P1,连接P1B,交x轴于点D,∵B(3,0),C(0,3),∴OB=OC=3,∴∠BCO=∠OBC=45°.∵P1C⊥BC,∴∠DCB=90°,∴∠DCO=45°,又∵∠DOC=90°,∴∠ODC=45°=∠DCO,∴OD=OC=3,∴D(﹣3,0),∴直线P1C的解析式为y=x+3,联立,解得或(舍);∴P1(1,4);②点B为直角顶点,如图,过点B作直线BP2⊥BC,交抛物线于点P2,交y轴于点E,连接P2C,∵P1C⊥BC,BP2⊥BC,∴P1C∥BP2,∴设直线BP2的解析式为y=x+b,将B(3,0)代入,得0=3+b,∴b=﹣3,∴直线BP2的解析式为y=x﹣3,联立,解得或(舍),∴P2(﹣2,﹣5).综上,点P的坐标为(1,4)或(﹣2,﹣5).【练1】如图,在平面直角坐标系xOy中,已知抛物线y=ax2+bx+c与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C(0,3),连接AC,点P为第二象限抛物线上的动点.(1)求a、b、c的值;(2)在抛物线的对称轴上是否存在一点Q,使得△QAC为直角三角形,若存在,请求出所有符合条件的点Q的坐标;若不存在,请说明理由.【答案】(1)a=﹣1,b=﹣2,c=3;(2)点Q的坐标为:(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).【解析】解:(1)∵抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),C(0,3)三点∴,解得:∴a=﹣1,b=﹣2,c=3;(2)存在,点Q的坐标为:(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).如图,∵A(﹣3,0),C(0,3),∴OA=OC=3,∴AC2=OA2+OC2=32+32=18,∵y=﹣x2﹣2x+3=﹣(x+1)2+4,∴抛物线对称轴为x=﹣1,设点Q(﹣1,n),则AQ2=[﹣1﹣(﹣3)]2+n2=n2+4,CQ2=[0﹣(﹣1)]2+(n﹣3)2=n2﹣6n+10,∵△QAC为直角三角形,∴∠CAQ=90°或∠ACQ=90°或∠AQC=90°,①当∠CAQ=90°时,根据勾股定理,得:AQ2+AC2=CQ2,∴n2+4+18=n2﹣6n+10,解得:n=﹣2,∴Q1(﹣1,﹣2);②当∠ACQ =90°时,根据勾股定理,得:CQ 2+AC 2=AQ 2, ∴n 2﹣6n +10+18=n 2+4, 解得:n =4, ∴Q 2(﹣1,4);③当∠AQC =90°时,根据勾股定理,得:CQ 2+AQ 2=AC 2, ∴n 2﹣6n +10+n 2+4=18, 解得:n 1,n 2,∴Q 3(﹣1,),Q 4(﹣1,);综上所述,点Q 的坐标为:(﹣1,﹣2)或(﹣1,4)或(﹣1,)或(﹣1,).【练2】已知抛物线y =ax 2+bx +c 与x 轴交于A(-2,0)、B(6,0)两点,与y 轴交于点C(0,-3).(1)求抛物线的表达式;(2)如图,点P 在直线BC 下方的抛物线上,点P 的坐标为P ⎝⎛⎭⎫3,-154作x 轴的垂线l ,在l 上是否存在点D ,使△BCD 是直角三角形,若存在,请直接写出点D 的坐标;若不存在,请说明理由.【答案】(1)y =14x 2-x -3;(2)当△BCD 是直角三角形时,D 点坐标为(3,6)或(3,-9)或⎝⎛⎭⎫3,-352-32或⎝⎛⎭⎫3,352-32.【解析】解:(1)将点A(-2,0)、B(6,0)、C(0,-3)代入y =ax 1+bx +c , 得{4a -2b +c =0,36a +6b +c =0,c =-3,解得⎩⎨⎧a =14,b =-1,c =-3,∴y =14x 2-x -3;(2)∵P ⎝⎛⎭⎫3,-154,D 点在l 上, 如图2,当∠CBD =90°时,过点B 作BH ⊥x 轴,过点D 作DGH ⊥y 轴,DG 与GH 交于点G ,过点C 作DG ⊥y 轴,CH 与GH 交于点H ,∴∠DBG +∠GDB =90°,∠DBG +∠CBH =90°, ∴∠GDB =∠CBH , ∴△DBG ∽△BCH , ∴DG BH =BG CH ,即33=BG6, ∴BG =6,∴D(3,6); 如图3,当∠BCD =90°, 过点D 作DK ⊥y 轴交于点K ,∵∠KCD +∠OCB =90°,∠KCD +∠CDK =90°, ∴∠CDK =∠OCB , ∴△OBC ∽△KCD , ∴OB KC =OC KD ,即6KC =33, ∴KC =6,∴D(3,-9); 如图4,当∠BDC =90°时,线段BC 的中点T ⎝⎛⎭⎫3,-32,BC =35, 设D(3,m),∵DT =12BC ,∴|m +32|=352,∴m =352-32或m =-352-32, ∴D ⎝⎛⎭⎫3,352-32或D ⎝⎛⎭⎫3,-352-32; 综上所述:当△BCD 是直角三角形时,D 点坐标为(3,6)或(3,-9)或⎝⎛⎭⎫3,-352-32或⎝⎛⎭⎫3,352-32.【练3】如图,抛物线y =﹣x 2+bx +c 与x 轴相交于A 、B 两点,与y 轴相交于点C ,且点B 与点C 的坐标分别为B (3,0).C (0,3),点M 是抛物线的顶点.点P 为线段MB 上一个动点,过点P 作PD ⊥x 轴于点D ,若OD =m . (1)求二次函数解析式;(2)在MB 上是否存在点P ,使△PCD 为直角三角形?若存在,请写出点P 的坐标;若不存在,请说明理由.【答案】(1)y =﹣x 2+2x +3. (2)点P 的坐标为(,3)或(,).【解析】解:(1)把B (3,0)、C (0,3)代入y =﹣x 2+bx +c ,得,解得,∴二次函数的解析式为y=﹣x2+2x+3.(2)存在.若∠DPC=90°,如图2,则PC∥x轴,∴P(m,3),且在直线y=﹣2x+6上,∴﹣2m+6=3,解得m,∴P(,3);若∠PCD=90°,如图3,则PC2+CD2=PD2,∴m2+(﹣2m+6﹣3)2+m2+32=(﹣2m+6)2,整理得m2+6m﹣9=0,解得m1=(,m2(不符合题意,舍去);∴P(,);若∠PDC=90°,则CD2+PD2=PC2,∴m2+32+(﹣2m+6)2=m2+(﹣2m+6﹣3)2,整理得12m=36,解得m=3,此时不存在以P,C,D为顶点的三角形,∴m=3舍去.综上所述,点P 的坐标为(,3)或(,).【例4——二次函数中全等或相似三角形存在性问题】如图,抛物线y =ax 2+bx +3(a ≠0)x 轴交于点A(1,0)和点B(-3,0),与y 轴交于点C ,连接BC ,与抛物线的对称轴交于点E ,顶点为点D. (1)求抛物线的解析式;(2)点P 是对称轴左侧抛物线上的一个动点,点Q 在射线ED 上,若以点P 、Q 、E 为顶点的三角形与△BOC 相似,请直接写出点P 的坐标.【答案】(1)y =-x 2-2x +3;(2)点P 的坐标为(-1-2,2),(-2,3).【解析】解:(1)∵抛物线y =ax 2+bx +3过点A(1,0),B(-3,0), ∴{a +b +3=0,9a -3b +3=0, 解得{a =-1,b =-2,∴抛物线的解析式为:y =-x 2-2x +3; (2)令x =0,y =3,∴OC=OB =3,即△OBC 是等腰直角三角形, ∵抛物线的解析式为:y =-x 2-2x +3, ∴抛物线对称轴为:x =-1, ∵EN∥y 轴, ∴△BEN∽△BCO, ∴BN BO =ENCO , ∴23=BN 3, ∴EN=2,①若△PQE∽△OBC,如图所示,∴∠PEH=45°,过点P作PH⊥ED垂足为H,∴∠PHE=90°,∴∠HPE=∠PEH=45°,∴PH=HE,∴设点P坐标(x,-x-1+2),∴代入关系式得,-x-1+2=-x2-2x+3,整理得,x2+x-2=0,解得,x1=-2,x2=1(舍),∴点P坐标为(-2,3),②若△PEQ∽△CBO,如图所示,设P(x,2),代入关系式得,2=-x2-2x+3,整理得,x2+2x-1=0,解得,x1=-1-2,x2=-1+3(舍),∴点P的坐标为(-1-2,2)综上所述点P的坐标为(-1-2,2),(-2,3).【练1】如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-1,0),B(4,0),C(0,4)三点.(1)求抛物线的解析式及顶点D的坐标;(2)点P为线段BC上一动点(点P不与点B,C重合),过点P作x轴的垂线交(1)中的抛物线于点Q,当△PQC与△ABC相似时,求△PQC的面积.【答案】(1)解析式:y =-x 2+3x +4;D 点坐标为⎝ ⎛⎭⎪⎫32,254.(2)当△PQC 与△ABC 相似时,△PQC 的面积576125或605128.【解析】解:(1)解析式:y =-x 2+3x +4;D 点坐标为⎝ ⎛⎭⎪⎫32,254.(2)由B 、C 两点坐标易求直线BC 解析式:y =-x +4,不难得出∠CPQ=∠BCO=∠OBC,即在△CPQ 和△ABC 中,∠CPQ=∠ABC. 接下来求角两边对应成比例:表示点:设P 点坐标为(0<m<4),则Q 点坐标为(m ,-m 2+3m +4), 表示线段:PC =2m ,PQ =-m 2+4m. 如图所示,分类讨论情况一:当△CPQ∽△ABC 时,则CP AB =PQBC,代入得:2m 5=-m 2+4m 42,解得:m 1=125,m 2=0(舍),对应P 点坐标为⎝ ⎛⎭⎪⎫125,85,PQ =9625, S △PCQ =12×125×9625=576125情况二:当△CPQ∽△CBA 时,则CP CB =PQBA,代入得:2m42=-m 2+4m 5,解得:m 3=114,m 4=0(舍),对应P 点坐标为⎝⎛⎭⎪⎫114,54,PQ =5516,S △PCQ =12×114×5516=605128. 综上所述,当△PQC 与△ABC 相似时,△PQC 的面积576125或605128.【练2】如图,抛物线y =3+36x 2+bx +c 与x 轴交于A ,B 两点,点A ,B 分别位于原点的左、右两侧,BO =3AO =3,过点B 的直线与y 轴正半轴和抛物线的交点分别为C ,D ,BC =3CD.(1)求b ,C 的值;(2)求直线BD 的函数解析式;(3)点P 在抛物线的对称轴上且在x 轴下方,点Q 在射线BA 上.当△ABD 与△BPQ 相似时,请直接写出所有满足条件的点Q 的坐标.【答案】(1)b =-3+33,c (2)y =-33+ 3 (3)【解析】解:(1)∵OB=3OA =3,∴B(3,0),A(-1,0).∴{ 3+36−b +c =03+36×9+3b +c =0 解得:b =-3+33,c =-3+32(2)如图,过点D 作DE⊥y 轴于E ,∵∠ECD=∠BCO,∠DEC=∠BOC=90°∴△CDE∽△CBO∴CD BC =DE OB ∴13=DE 3,DE = 3 即D 点横坐标为-3,其坐标为D(-3,3+1)由B(3,0)得直线BD 解析式为:y =-33+ 3 (3)由A(-1,0),B(3,0),D(-3,3+1),知 S △ABD =2(3+1),BD =2(3+1),AD =2 2如图,过点A 作AH⊥BD 于H ,∴AH=2,DH =2,∴tan∠ADB=1,tan∠ABD=33, tan∠DAM=2+ 3 设Q(x ,0),P(1,m),其中m<0,x<3,①当△ABD ∽△BPQ 时,∠DAB =∠QBP(由题意知∠QBP<90°,∠DAB>90°,不存在)②当△ABD ∽△BQP 时,同理,此种情况不存在;③当△ABD∽△QBP 时,tan∠ADB=tan∠QPB=1,tan∠ABD= tan∠QBP=33, tan∠PQO=tan∠DAM=2+3, ∴-m 2=33,即m =233,-m x -1=2+3,x =43-33即Q ⎝ ⎛⎭⎪⎫43-33,0 ④当△ABD∽△QPB 时,同理,∴-m 2=1,即m =-2,-m x -1=2+3, x =5-23即Q(5-23,0)⑤当△ABD∽△PQB 时,同理,∴-m 2=1,即m =-2,-m x -1,=33, x =1-2 3即Q(5-23,0) ⑥当△ABD∽△PBQ 时,同理,∴-m 2=33,即m =233,-m 1-x =1,x =1-233即Q ⎝ ⎛⎭⎪⎫1-233,0. 综上所述:当△ABD 与△BPQ 相似时,点Q 的坐标为:Q ⎝ ⎛⎭⎪⎫43-33,0、Q(5-23,0)或Q ⎝ ⎛⎭⎪⎫1-233,0.【练3】如图,抛物线y =-x 2+bx +c 轴交于点A(-1,0),B(3,0),与y 轴交于点C ,点D 是直线BC 上方抛物线上一动点.(1)求抛物线的解析式;(2)如图1,连接BD 、CD ,设点D 的横坐标为m ,△BCD 的面积为s.试求出s 与m 的最大值;(3)如图2,设AB 的中点为E ,作DF⊥BC,垂足为F ,连接CD 、CE ,是否存在点D ,使得以C ,D ,F 三点为顶点的三角形与△CEO 相似?若存在,请直接写出点D 的坐标;若不存在,请说明理由.【答案】(1)y =-x 2+2x +3.(2)S 与m 的函数关系式为S =-32m 2+92m ,s 的最大值为278. (3)点D 的坐标为⎝⎛⎭⎫52,74或⎝⎛⎭⎫32,154.【解析】解:(1)∵抛物线y =-x 2+bx +c 与x 轴交于点A(-1,0),B(3,0), ∴y =-(x +1)(x -3)=-x 2+2x +3.∴抛物线解析式为y =-x 2+2x +3.(2)如图,过点D 作DM ∥y 轴,交BC 于点M.∵当x =0时,y =-x 2+2x +3=3,∴c(0,3).∴直线BC 解析式为y =-x +3.∴D(m ,-m 2+2m +3),M(m ,-m +3).∴DM =-m 2+2m +3-(-m +3)=-m 2+3m.∴S =S △DMB +S △DMC =12×MD(x B -x D )+12(x M -x C )=12OB·DM =32m 2+92m =-32⎝⎛⎭⎫m -322+278(0<m <3),∴S 与m 的函数关系式为S =-32m 2+92m ,s 的最大值为278. (3)存在点D ,使得以C ,D ,F 三点为顶点的三角形与△CEO 相似如图,连接BD设点D 的横坐标为m ,∵点EAB 中点,A(-1,0),B(3,0),C(0,3)∴E(1,0),OE =1,OC =3,CD 2=m 2+(-m 2+2m +3-3)2∴CE =OE 2+OC 2=12+32=10.∴sin ∠OCE =OE CE =110=1010,cos ∠OCE =OC CE =310=31010. ∴BC =OB 2+OC 2=32,DF ⊥BC.∴由(2)知,面积S =12BC·DF =-32m 2+92m. ∴DF =2S BC =-3m 2+9m 32=-m 2+m32∵以C 、D ,F 三点为顶点的三角形与△CEO 相似,∠CFD =∠COE =90° ∴△CFD ∽△COE 或△CFD ∽△EOC①若△CFD ∽△COE ,则∠FCD =∠OCE∴sin ∠FCD =DF CD =1010∴10DF 2=CD 2∴10⎝ ⎛⎭⎪⎫-m 2+3m 22=m 2+(-m 2+2m)2. 解得:m 1=4(舍去),m 2=52. ∴-m 2+2m +3=-254+5+3=74. ∴D ⎝⎛⎭⎫52,74.②若△CFD ∽△EOC ,则∠FDC =∠OCE , ∴cos ∠FDC =DF CD =31010. ∴10DF 2=9CD 2.∴10⎝ ⎛⎭⎪⎫-m 2+3m 2=9[m 2+(-m 2+2m)2]解得:m 1=0(舍去),m 2=32. ∴-m 2+2m +3=-94+3+3=154. ∴D ⎝⎛⎭⎫32,154.∴综上所述:点D 的坐标为⎝⎛⎭⎫52,74或⎝⎛⎭⎫32,154.。
