高二文科数学练习题
高二文科数学椭圆练习题

高二文科数学椭圆练习题一、选择题1. 设椭圆E的中心为O,焦点为F1,F2,焦距为2c,离心率为e。
已知2a = 6,e = 1/3,则椭圆的焦距c等于:A. 1/3B. 2/3C. 1D. 4/32. 椭圆E的长轴的长度为2a,短轴的长度为2b,离心率为e,则焦距c满足下列哪个条件?A. c = a + bB. c = a - bC. c^2 = a^2 - b^2D. c^2 = b^2 - a^23. 椭圆E的中心为O,焦点为F1,F2,离心率为e。
已知OF1 = a,OF2 = b,则a和b的关系是:A. a = bB. a > bC. a < bD. 无法确定二、填空题4. 已知椭圆E的长轴的长度为10,短轴的长度为6,则离心率e的值为________。
5. 椭圆E的中心为O,长轴的长度为2a,短轴的长度为2b,则焦距c的值为________。
6. 椭圆E的离心率为1/4,长轴的长度为12,则短轴的长度b为________。
三、解答题7. 已知点P(a, b)在椭圆E上,且OP过椭圆的焦点F,若椭圆E的长轴的长度为20,焦距为8,求椭圆E的方程。
解答:设椭圆E的中心为O(0, 0)。
由于点P(a, b)在椭圆E上,根据椭圆的定义可得:OP + PF1 = PF2(F1和F2为焦点)根据题目给出的信息,可以得到以下两个方程:√(a^2 + b^2) + √((a - 8)^2 + b^2) = √((a + 8)^2 + b^2)将上述方程两边平方,整理后可得:(a^2 + b^2) + ((a - 8)^2 + b^2) + 2√(a^2 + b^2)√((a - 8)^2 + b^2) = (a + 8)^2 + b^2化简上述方程,得:a^2 + b^2 + a^2 - 16a + 64 + 2√(a^2 + b^2)√((a - 8)^2 + b^2) = a^2 + 16a + 64将方程两边整理,得:2√(a^2 + b^2)√((a - 8)^2 + b^2) = 32a将上述方程两边平方,得:4(a^2 + b^2)((a - 8)^2 + b^2) = 1024a^2继续化简,得:4(a^2 + b^2)(a^2 - 16a + 64 + b^2) = 1024a^2将方程展开,整理,最终得到:5a^4 - 80a^3 + 64a^2 + 320a^2 - 4096a + 2560 = 0以上即为椭圆E的方程。
高二文科数学立体几何平行及垂直部分练习题
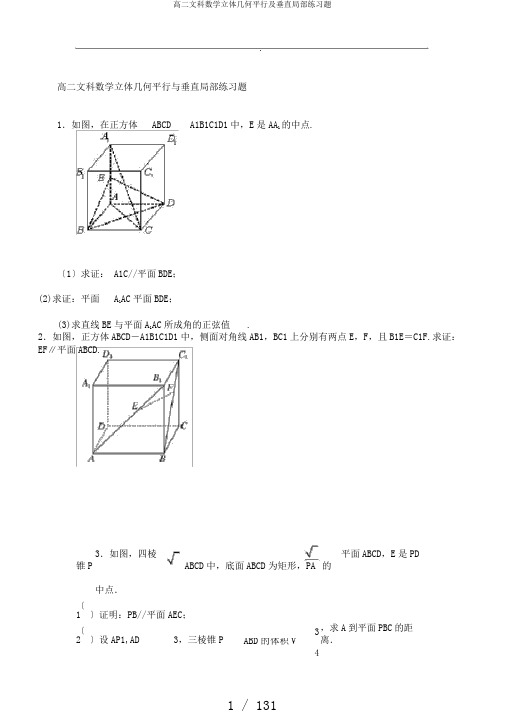
.高二文科数学立体几何平行与垂直局部练习题1.如图,在正方体ABCD A1B1C1D1中,E是AA1的中点.〔1〕求证:A1C//平面BDE;(2)求证:平面A1AC 平面BDE;(3)求直线BE与平面A1AC所成角的正弦值.2.如图,正方体ABCD-A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F.求证:EF∥平面ABCD.3.如图,四棱锥P ABCD中,底面ABCD为矩形,PA平面ABCD,E是PD 的中点.〔1〕证明:PB//平面AEC;〔2〕设AP1,AD3,三棱锥P3,求A到平面PBC的距离.ABD的体积V4..PEA DB C4.如图,四边形ABCD是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.(1)求证:MN∥平面PAD;(2)求证:MN⊥DC;PNCDA M B5.四棱锥PABCD的底面为直角梯形,AB//DC,DAB90,PA底面ABCD,且PA ADDC1,AB2,M是PB的中点.1〕求证:CMP面PAD;2〕证明:面PAD面PCD;3〕求AC与PB所成的角的余弦值;〔4〕求棱锥M PAC的体积。
6.四棱锥P-ABCD,底面ABCD为矩形,侧棱PA⊥平面ABCD,此中BC=2AB=2PA=6,M、N为侧棱PC上的两个三平分点..P NA DMBC1〕求证:AN ∥平面MBD;2〕求异面直线AN 与PD 所成角的余弦值;3〕求二面角M-BD-C 的余弦值.7.如图,ABCD 是正方形,O 是正方形的中心, P O底面ABCD ,E 是PC 的中点。
求证:〔1〕PA ∥平面BDE 2〕平面PAC 平面BDE8.在四棱锥P ABCD 中,底面ABCD 为矩形,PD底面ABCD ,AB1,BC2,PD3,G 、F 分别为AP 、CD 的中点.(1) 求证:FG//平面BCP ;(2) 求证: AD PC ;PG DF CA B9.如图,在侧棱垂直于底面的三棱柱 ABC A 1B 1C 1中,AC3,AB 5,BC 4,..AA14,点D是AB的中点.C1B1A1CBDA1〕求证:ACBC1;2〕求证:AC1//平面CDB13〕求三棱锥A1B1CD的体积.10.如图,在斜三棱柱ABC A1B1C1中,侧面AA1B1B底面ABC,BAA1600,AA12,底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE 1BC1.3A1B1C1EABGC1〕求证:GE//侧面AA1B1B;〔2〕求证:AB A1C.11.如图,在正三棱柱ABC-A1B1C1中,点D为棱AB的中点,BC=1,AA1= 3.(1)求证:BC1∥平面A1CD;(2)求三棱锥D-A1B1C的体积...12.直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=2,AA′=1,点M,N分别为A′B和B′C′的中点.(1)证明:MN∥平面A′ACC′;1(2)求三棱锥A′-MNC的体积.(锥体体积公式V=Sh,此中S为底面面积,h为高)313.如图,在直三棱柱ABCA1B1C1中,AB AC5,BB1BC6,D、E分别为AA1和B1C的中点.1〕求证:DE//平面ABC;〔5分〕2〕求三棱锥EBCD的体积.〔7分14.△ABC是边长为l的等边三角形,D、E分别是AB、AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,获得三棱锥A-BCF,此中BC2.2(1)证明:DE∥平面BCF;(2)证明:CF⊥平面ABF;(3)当AD 2F-DEG的体积V.时,求三棱锥3..15.〔本小题总分值12分〕如图,四棱锥P ABCD中,AP⊥平面PCD,AD∥BC,AB BC 1AD,E,F分别为2线段AD,PC的中点.1〕求证:AP∥平面BEF;2〕求证:BE⊥平面PAC16.如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF平面ABCD,BF=3,G、H分别是CE和CF的中点.〔Ⅰ〕求证:AF//平面BDGH;〔Ⅱ〕求VEBFH17.如图1,直角梯形ABCD中,AB//CD,BAD 900,AB AD 2,CD4,点E为线段AB上异于A,B的点,且EF//AD,沿EF将面EBCF折起,使平面EBCF..平面AEFD,如图2.〔1〕求证:AB//平面DFC;〔2〕当三棱锥F ABE体积最大时,求整个几何体的体积。
人教版高二文科数学《圆锥焦点》基础练习题

人教版高二文科数学《圆锥焦点》基础练习题题目一已知一个圆锥,下底半径为5cm,高度为10cm。
求圆锥的侧面积和体积。
解答一圆锥的侧面积可以通过以下公式计算:$$S = \pi r l$$其中,$S$表示侧面积,$r$表示圆锥的底面半径,$l$表示圆锥的斜高。
插入已知值,得到:$$S = \pi \cdot 5 \cdot 10$$计算得出,圆锥的侧面积为50π平方厘米。
圆锥的体积可以通过以下公式计算:$$V = \frac{1}{3} \pi r^2 h$$其中,$V$表示体积,$r$表示圆锥的底面半径,$h$表示圆锥的高度。
插入已知值,得到:$$V = \frac{1}{3} \pi \cdot 5^2 \cdot 10$$计算得出,圆锥的体积为250π立方厘米。
题目二已知一个圆锥的顶角为60°,底面半径为8cm。
求圆锥的侧面积和体积。
解答二圆锥的侧面积可以通过以下公式计算:$$S = \pi r l$$其中,$S$表示侧面积,$r$表示圆锥的底面半径,$l$表示圆锥的斜高。
由已知条件可知,圆锥的斜高等于底面半径,即$l = r$。
插入已知值,得到:$$S = \pi \cdot 8 \cdot 8$$计算得出,圆锥的侧面积为64π平方厘米。
圆锥的体积可以通过以下公式计算:$$V = \frac{1}{3} \pi r^2 h$$其中,$V$表示体积,$r$表示圆锥的底面半径,$h$表示圆锥的高度。
由已知条件可知,圆锥的高度等于底面半径的正弦值乘以底面半径,即$h = \sin 60° \cdot 8$。
插入已知值,得到:$$V = \frac{1}{3} \pi \cdot 8^2 \cdot \sin 60° \cdot 8$$计算得出,圆锥的体积为128π立方厘米。
以上是人教版高二文科数学《圆锥焦点》的基础练习题解答,希望能对你的学习有所帮助!。
高二数学(文科)练习(必修5 选修1-1)期末复习辅导1

高二数学(文)期末测试题第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、在等差数列}{n a 中,1a =3,93=a 则5a 的值为A . 15B . 6 C. 81 D. 92、设a R ∈,则1a >是11a< 的 A .充分但不必要条件 B .必要但不充分条件C .充要条件D .既不充分也不必要条件3、已知命题p :R x ∈∀,1cos ≤x ,则( )A 、00:,cos 1p x R x ⌝∃∈≥B 、00:,cos 1p x R x ⌝∀∈≥C 、1cos ,:00>∈∃⌝x R x pD 、00:,cos 1p x R x ⌝∀∈>4、在等比数列{}n a (n ∈N*)中,若11a =,418a =,则该数列的前10项和为 A .4122-B .9122-C .10122-D .11122-5、在ABC ∆中,60B =,2b ac =,则ABC ∆一定是A.直角三角形B.等边三角形C.锐角三角形D.钝角三角形6、函数y=2x 2+3x 在x=1时的导数为 ( )A .5B .6C .7D .87、椭圆2241x y +=的离心率为 ( ) A.22 B.43 C. 23 D.32 8、数列{}n a 的前n 项和为n S ,若1(1)n a n n =+,则5S 等于( ) A .1 B .56 C .16 D .1309、已知变量y x ,满足⎪⎩⎪⎨⎧≤-+≥≥0311y x y x ,则目标函数y x z +=2有A .5max =z ,z 无最小值B .3,5min max ==z zC .z z ,3min =无最大值D .z 既无最大值,也无最小值10、若不等式02>++a ax x 恒成立,则a 的取值范围是( )A .01<-或4>aB .40<<aC .4≥a 或0≤aD .40≤≤a11、12第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分。
高二文科数学三角函数练习

高二文科数学 三角函数练习(1)一、 选择题1.已知sin α=45,且α为第二象限角,那么tan α的值等于 ( ) (A)34 (B)43- (C)43 (D)43- 2.若θ是第三象限角,且02cos <θ,则2θ是 ( )A .第一象限角B .第二象限角C .第三象限角D .第四象限3.将分针拨快10分钟,则分针转过的弧度数是 ( ) (A)3π(B)-3π(C)6π(D)-6π4.sin (-6π19)的值是()A .21B .-21C .23D .-23 5.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角的弧度数为() (A)3π (B)32π(C)3(D)26.下列三角函数:其中函数值与sin 3π的值相同的是( )①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π];⑤sin [(2n +1)π-3π](n ∈Z ).A .①②B .①③④C .②③⑤D .①③⑤7.设是第二象限角,则sin cos αα= ( )(A) 1 (B)tan 2α (C) -tan 2α (D)1-8.已知sin(4π+α)=23,则sin(43π-α)值为() A. 21 B. —21 C. 23 D. —239、如果角θ满足2cos sin =+θθ,那么1tan tan θθ+的值是() A .1- B .2- C .1 D .210.化简:)2cos()2sin(21-∙-+ππ得()A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)11 若α是三角形的一个内角,且sin α+cos α=32,则三角形为 ( )(A)钝角三角形 (B)锐角三角形 (C)直角三角形 (D)等腰三角形12.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为() A .-36 B .36 C .-26 D .26 二、 填空题13. —1223πrad 化为角度应为. 14.已知sin αcos α=81,且4π<α<2π,则cos α-sin α的值为 ______________. 15.已知cos(4π+α)=23,则sin(43π+α)=16.cos π7 +cos 2π7 +cos 3π7 +cos 4π7 +cos 5π7 +cos 6π7=. 17.角α的终边上有一点P (m ,5),且)0(,13cos ≠=m m α,则sin α+cos α=______. 三、解答题18.若cos α=23,α是第四象限角,求sin(2)sin(3)cos(3)cos()cos()cos(4)απαπαππαπααπ-+--------的值.19.若2cos sin 2cos sin =-+αααα, (1)求tan α(2)求2sin 2α-3sin αcos α-2cos 2α20.若扇形的周长为20 cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?21 、已知51cos sin =+ββ,且πβ<<0. (1)求ββcos sin 、ββcos sin -的值;(2)求βsin 、βcos 、βtan 的值.(3)求sin 3β – cos 3β的值。
高二数学文科综合练习一

高二模块测试数学试题(文科)一、选择题:(本题共10个小题,每小题5分,共50分)1.设zz i i z 2),(12+-=则为虚数单位= (A )i --1 (B )i +-1 (C )i -1 (D )i +1 2.数列2,5,11,20,,47,x …中的x 等于(A )28 (B )32 (C )33 (D )273. 若复数12z i=+,则z 在复平面内对应的点位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限4. 若()sin cos f x x α=-,则'()f α等于 (A )sin α(B )cos α (C ) sin cos αα+ (D )2sin α5.对相关系数r ,下列说法正确的是 ( )A .||r 越大,线性相关程度越大B .||r 越小,线性相关程度越大C .||r 越大,线性相关程度越小,||r 越接近0,线性相关程度越大D .||1r ≤且||r 越接近1,线性相关程度越大,||r 越接近0,线性相关程度越小6. ()f x 与()g x 是定义在R 上的两个可导函数,若()f x ,()g x 满足''()()f x g x =, 则()f x 与()g x 满足(A) ()f x =()g x (B ) ()f x -()g x 为常数函数 (C) ()f x =()0g x =( D) ()f x +()g x 为常数函数7. 曲线x x y 43-=在点(1,3)- 处的切线倾斜角为(A )4π (B )3π (C )43π (D )2π8. 若幂函数)(x f 的图象经过点)21,41(A ,则它在A 点处的切线方程为(A ) 0144=++y x (B )0144=+-y x(C )02=-y x (D )02=+y x9. 若函数2()f x x bx c =++的图象的顶点在第四象限,则函数'()f x 的图象可能是10. 设)(x f 是定义在R 上的奇函数,2)2(=f ,当0>x 时,有)()(x f x x f >恒成立,则不等式x x f >)(的解集是 (A ) (2-,0)∪(2,∞+) (B ) (2-,0)∪(0,2)(C ) (∞-,2-)∪(2,∞+) (D ) (∞-,2-)∪(0,2)二、填空题:(本题共4个小题,每小题4分,共16分)11. 若(2)a i i b i -=-,其中a 、b R ∈,i 是虚数单位,则22a b +=_________。
高二数学文科期末测试题

高二数学文科期末测试题高二数学文科期末测试题一.选择题(每小题5分,共60分)1.以下四个命题中,真命题的序号是(。
)A。
①②。
B。
①③。
C。
②③。
D。
③④2.“x≠”是“x>”的(。
)A。
充分而不必要条件。
B。
必要而不充分条件C。
充分必要条件。
D。
既不充分也不必要条件3.若方程C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a是常数),则下列结论正确的是(。
)A。
$\forall a\in R^+$,方程C表示椭圆。
B。
$\forall a\in R^-$,方程C表示双曲线C。
$\exists a\in R^-$,方程C表示椭圆。
D。
$\exists a\in R$,方程C表示抛物线4.抛物线:$y=x^2$的焦点坐标是(。
)A。
$(0,\frac{1}{4})$。
B。
$(0,\frac{1}{2})$。
C。
$(1,\frac{1}{4})$。
D。
$(1,\frac{1}{2})$5.双曲线:$\frac{y^2}{4}-\frac{x^2}{1}=1$的渐近线方程和离心率分别是(。
)A。
$y=\pm2x$,$e=3$。
B。
$y=\pm\frac{1}{2}x$,$e=5$C。
$y=\pm\frac{1}{2}x$,$e=3$。
D。
$y=\pm2x$,$e=5$6.函数$f(x)=e^xlnx$在点$(1,f(1))$处的切线方程是(。
)A。
$y=2e(x-1)$。
B。
$y=ex-1$。
C。
$y=e(x-1)$。
D。
$y=x-e$7.函数$f(x)=ax^3+x+1$有极值的充要条件是(。
)A。
$a>$。
B。
$a\geq$。
C。
$a<$。
D。
$a\leq$8.函数$f(x)=3x-4x^3$($x\in[0,1]$)的最大值是(。
)A。
$\frac{2}{3}$。
B。
$-1$。
C。
$1$。
D。
$-\frac{2}{3}$9.过点$P(0,1)$与抛物线$y^2=x$有且只有一个交点的直线有(。
高二文科数学每日一练4

高二文科数学每日一练
1. 函数()ln f x x x =的单调递减区间是 A. 1(0,)e B. 1(,)e +∞ C. (0,)e D. (,)e +∞
2.下面几种推理是类比推理的是
(A )两条直线平行,同旁内角互补,如果∠A 和∠B 是两条平行直线的同旁内角,则∠A +∠B =1800
(B )由平面三角形的性质,推测空间四边形的性质
(C )某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员.
(D )一切偶数都能被2整除,1002是偶数,所以1002能被2整除.
3. 函数3y x bx c =++在1x =与1x =-处取得极值,则b =.
4.(几何证明选做题)如图,P A 切⊙O 于点A ,割线PBC
经过圆心O ,PB =3, P A OA 绕点O 逆时针旋转60︒
到OD ,则PD 的长为.
5.阅读下文,然后画出该章的知识结构图.
推理与证明这一章介绍了推理与证明这两个知识点. 推理这节包括合情推理和演绎推理;证明这节包括直接证明和间接证明
合情推理中有两种常用推理:归纳推理和类比推理;
直接证明有综合法和分析法;间接证明通常用反证法.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高二文科数学练习题
题一:
已知函数 $f(x) = 2x^2 - 3x + 1$,求函数 $g(x) = 3f(x) + 2$ 的零点。
解析:
首先,我们需要知道函数 $g(x)$ 的零点指的是函数 $g(x)$ 在何处取值为零。
零点的概念也可以理解为方程 $g(x) = 0$ 的解。
我们已知函数 $f(x) = 2x^2 - 3x + 1$,现在我们来求函数 $g(x) = 3f(x) + 2$ 的零点。
将函数 $f(x)$ 的表达式代入 $g(x)$ 中,得到 $g(x) = 3(2x^2 - 3x + 1) + 2$。
化简这个表达式,我们得到 $g(x) = 6x^2 - 9x + 5$。
现在,我们需要求解方程 $g(x) = 0$。
使用求根公式,我们可以得到 $x = \frac{-b \pm \sqrt{b^2 -
4ac}}{2a}$。
将 $a = 6$,$b = -9$,$c = 5$ 代入公式中,我们可以得到两个解。
$x_1 = \frac{-(-9) + \sqrt{(-9)^2 - 4 \cdot 6 \cdot 5}}{2 \cdot 6} =
\frac{9 + \sqrt{-111}}{12}$
$x_2 = \frac{-(-9) - \sqrt{(-9)^2 - 4 \cdot 6 \cdot 5}}{2 \cdot 6} =
\frac{9 - \sqrt{-111}}{12}$
由于存在负数根下,所以方程 $g(x) = 0$ 无实数根,即函数 $g(x) =
3f(x) + 2$ 没有零点。
题二:
已知函数 $f(x)$ 的定义域为实数集 $R$。
若对于所有 $x \in R$,有$f(x) + f(-x) = 4$,求函数 $f(x)$ 的表达式。
解析:
根据已知条件 $f(x) + f(-x) = 4$,我们可以推断出函数 $f(x)$ 是关于$x = 0$ 的对称函数。
设 $x = 1$,则 $f(1) + f(-1) = 4$。
设 $x = 2$,则 $f(2) + f(-2) = 4$。
可以观察到,对任意实数 $x$,我们都可以找到一个对应的 $-x$,
使得 $f(x) + f(-x) = 4$。
由于函数 $f(x)$ 是对称函数,我们知道 $f(1) = f(-1)$,$f(2) = f(-2)$,以此类推。
因此,我们可以得出结论,对于所有的实数 $x$,$f(x)$ 的值是一
个常数 $c$。
即 $f(x) = c$。
将 $f(x) = c$ 代入已知条件 $f(x) + f(-x) = 4$ 中,得到 $c + c = 4$,
即 $2c = 4$,解得 $c = 2$。
所以,函数 $f(x)$ 的表达式为 $f(x) = 2$。
综上所述,函数 $f(x)$ 的表达式为 $f(x) = 2$。
