江西省信丰中学2012-2013学年八年级数学下学期期中检测试题
江苏省江都市2012-2013学年八年级数学下学期期中试题 北师大版

110 0.5 10 0.5 10 0.5 10 0.5 A . B . C . D .2012-2013学年第二学期期中试卷八年级数学(考试时间:120分钟,满分:150分)一.选择题(每题3分,共24分)1. 不等式24x -<的解集是 ( ) A .2x >-B .2x <-C .12x >-D .12x <- 2. 下列函数中,y 是x 的反比例函数的为( ) A .12+=x yB .22x y =C . xy 51=D . x y =2 3. 下列各式中,正确的是( )A .22b b a a =B .22a b a b a b+=++C.22y y x y x y =++ D .11x y x y=--+- 4. 已知关于x 的函数y =k (x -1)和y =kx(k≠0),它们在同一坐标系内的图象大致是 ( )5. 分式2222,,,3a x y a b y a ax x y a b x a+++--+中,最简分式有 ( ) A .4个 B .3个 C .2个 D .1个 6.若把分式2xx y-中的x 和y 都扩大5倍,那么分式的值将 ( ) A .扩大5倍 B .扩大10倍 C .不变 D .缩小5倍 7. 点M(1-2m ,m -1)关于x 轴的对称点...在第一象限,则m 的取值范围在数轴上表示正确的是( )2 8.反比例函数xk y 12+=图象上有三个点)(11y x ,,)(22y x ,,)(33y x ,,其中3210x x x <<<,则1y ,2y ,3y 的大小关系是( )A .321y y y <<B .312y y y <<C .213y y y <<D .123y y y <<二.填空题(每题3分,共30分) 9. 若当x 满足条件___________,分式11x +有意义。
2012-2013 学年度北师大数学八年级下册第二学期期中考试题及参考答案

2012-2013 学年度北师大数学八年级下册第二学期期中考试题A 卷(满分100分)1.在x 1、21、212+x 、πxy 3、y x +3、ma 1+中分式的个数有( )A 、2个B 、3个C 、4个D 、5个2.下列四个从左到右的变形中,是因式分解的是( ) A 、(x+1)(x-1)= x 2-1 B 、(a-b )(m-n )=(b-a)(n-m) C 、 ab-a-b+1= (a-1)(b-1) D 、m 2-2m-3= m(m-2-m3) 3.如图表示的是不等式组的解集,则所对应的不等式组的解集是( )A 、 -1〈x 〈2B 、-12<≤xC 、-1〈x 2≤D 、21≤≤-x 4.若b a <,则下列各式中一定成立的是( )A 、11-<-b aB 、33ba > C 、b a -<- D 、 bc ac <5.分式112+-x x 的值为0,则( )A 、x=-1B 、x=1C 、x=±1D 、x=0 6.甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是( )A 、1℃~3℃B 、 3℃~5℃C 、 5℃~8℃D 、 1℃~8℃ 7.下列各式能用完全平方式进行分解因式的是( ) A 、x 2+1 B 、x 2+2x -1C 、x 2+x +1D 、x 2+4x +48.不等式-3x>12的解集是( )A 、x>-4B 、x 4-≥C 、x<-4D 、x 4-≤ 9.分式方程113=-x 的解是( ) A 、x=4 B 、x=-4 C 、x=2 D 、无解。
10.当x 为任意实数时,下列分式一定有意义的是( ) A 、212-x B 、112+x C 、||1x D 、21+x二.填空(每题2分,共30分) 1.当x 时,分式x x -+11有意义;当x 时,分式xx -+11的值为零. 2.用不等式表示“a 的3倍与16的差是一个非负数”应是 3.当x_______时,代数式2x-5的值为0,当x_______时,代数式2x-5的值不大于0. 4.一个长方形的面积是(a 2-9)平方米,其长为(a+3)米,用含有a 的整式表示它的宽为 _____ 米 5.已知一次函数y=kx+b 的图象如图,当x<0时, y 的取值范围是 .6.化简112+-x x =7.若关于x 的方程3132--=-x mx 无解,则m=__ 8.某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x 件,则根据题意,可列方程为________________.9.如果2=b a,则=++-2222ba b ab a 10.在比例尺为1:2000的地图上测得AB 两地间的图上距离为5cm ,则AB 两地间的实际距离为_____________m 。
2012—2013学年度第一学期期中考试八年级数学试卷

2012—2013学年度第一学期期中考试八年级数学试卷(100分钟,100分)2012.111、下列说法正确的是( )A.064.0-的立方根是0.4B.9-的平方根是3±C. 16的立方根是316D. 0.01的立方根是0.0000012、 如图(1):Rt △ABC 中,∠ACB=900,CD 是高,AC=4cm ,BC=3cm ,则CD=( )A. 5cmB.512cm C.125cm D.34cm3、在菱形ABCD 中,∠ADC=120°则BC:AC ( )A 、2:3B 、3:3C 、2:1D 、1:34、以下列各组数为边长,能组成直角三角形的是( )A.8、15、7B. 8、10、6C. 5、8、10D. 8、39、385)二.填空题。
(每题3分,共15分)6、算术平方根和立方根都等于本身的数是 ,81的算数平方根是 。
7、菱形有一个内角是120度,有一条对角线长为 6 cm ,此菱形的边长是 。
8、一个多边形内角和是540°,那么从一个顶点引出的对角线的条数是 。
9、 如图(2),△ABC 经过平移后到△GMN 的位置,BC 上一点D 也同时平移到点H的位置,若AB=8cm 。
∠HGN=25°,则GH= ,∠DAC= 。
10、如图(3)矩形ABCD 的对角线AC 、BD 相交于点0,过点0的直线交AB 、CD 于E 、F ,AB=6,BC=10,则图中阴影部分的面积为 。
三.解答题。
(共70分)11、计算:(每题5分,共20分)(1) 200320042)2)+ (2)()()131381672-++-(3) 40)52(2-+. (4)2101.036813-+-CBDA图(1)E12、(6分)规律探求,观察522-=58=524⨯=252,即522-=252;1033-=1027=1039⨯=3103,即1033-=3103(1)猜想2655-等于什么,并通过计算验证你的猜想;(2)写出符合这一规律的一般等式。
江西省南昌市初中十校联考八年级(下)期中数学试卷
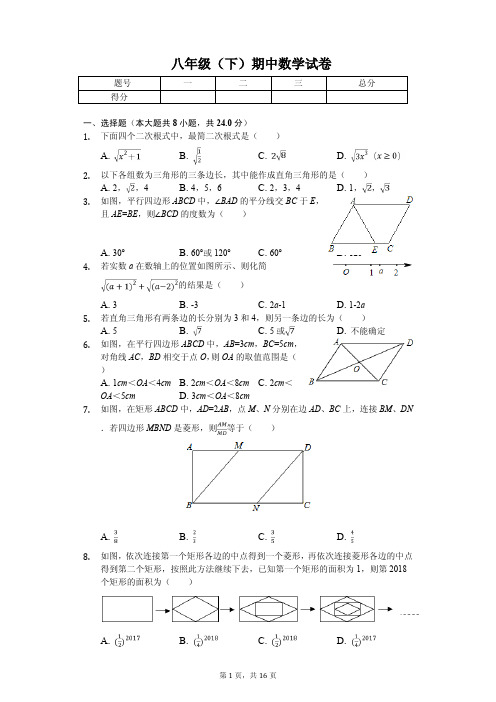
八年级(下)期中数学试卷题号一二三总分得分一、选择题(本大题共8小题,共24.0分)1.下面四个二次根式中,最简二次根式是( )A. B. C. D.2.以下各组数为三角形的三条边长,其中能作成直角三角形的是( )A.2,,4 B. 4,5,6 C. 2,3,4 D. 1,,3.如图,平行四边形ABCD中,∠BAD的平分线交BC于E,且AE=BE,则∠BCD的度数为( )A. 30°B. 60°或120°C. 60°D. 120°4.若实数a在数轴上的位置如图所示、则化简的结果是( )A. 3B. -3C. 2a-1D. 1-2a5.若直角三角形有两条边的长分别为3和4,则另一条边的长为( )A.5 B. C. 5或 D. 不能确定6.如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是( )A. 1cm<OA<4cmB. 2cm<OA<8cmC. 2cm<OA<5cm D. 3cm<OA<8cm7.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于( )A. B. C. D.8.如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去,已知第一个矩形的面积为1,则第2018个矩形的面积为( )A. B. C. D.二、填空题(本大题共6小题,共18.0分)9.若二次根式有意义,则x的取值范围是______.10.在Rt△ABC中,斜边AB=3,则AB2+BC2+CA2= ______ .11.如图,已知OA=OB,BC=1,则数轴上点A所表示的数为______.12.如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A、C分别在x轴、y轴的正半轴上,点Q在对角线OB上,若OQ=OC,则点Q的坐标为______.13.如图,在菱形ABCD中,过对角线BD上任一点P,作EF∥BC,GH∥AB,下列结论正确的是________________.(填序号)①图中共有3个菱形;②△BEP≌△BGP;③四边形AEPH的面积等于△ABD的面积的一半;④四边形AEPH的周长等于四边形GPFC的周长.14.如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为______.三、解答题(本大题共10小题,共78.0分)15.计算:(1)3-+-(2)16.先化简,再求值:(1+)÷,其中x=+1.17.如图,在△ABC中,AD⊥BC,AB=5,BD=4,CD=.(1)求AD的长.(2)求△ABC的周长.18.如图,▱ABCD的周长为26cm,AC,BD相交于点O,△BOC的周长比△AOB的周长小3cm,求AB,BC的长.19.已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于F.求证:BF=EC.20.问题背景:在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)请你利用上述方法求出△ABC的面积.(2)在图2中画△DEF,DE、EF、DF三边的长分别为、、①判断三角形的形状,说明理由.②求这个三角形的面积.(直接写出答案)21.已知四边形ABCD中,AB=10,BC=8,,∠DAC=45°,∠DCA=15°.(1)求△ADC的面积.(2)若E为AB中点,求线段CE的长.22.阅读下面的材料,解答后面提出的问题:黑白双雄,纵横江湖;双剑合壁,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也有这种相辅相成的“对子”,如:(2+)(2-)=1,(+)(-)=3,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:.像这样通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.解决问题:(1)4+的有理化因式是______,将分母有理化得______;(2)已知x=,y=,则=______;(3)利用上面所提供的解法.请化简…23.矩形ABCD中,AB=6,BC=8,E,F是对角线AC上的两个动点,分别从A,C同时出发,相向而行,速度均为1cm/s,运动时间为t秒,当其中一个动点到达后就停止运动,G,H分别是AB,DC中点.(1)求证:四边形EGFH始终是平行四边形;(2)当t为何值时,四边形EGFH为矩形.24.我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.●特例感知①等腰直角三角形______勾股高三角形(请填写“是”或者“不是”);②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若BD=2AD=2,试求线段CD的长度.●深入探究如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;●推广应用如图3,等腰△ABC为勾股高三角形,其中AB=AC>BC,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若CE=a,试求线段DE的长度.答案和解析1.【答案】A【解析】解:A、是最简二次根式;故A正确;B、被开方数含分母,可化简为,不是最简二次根式;故B错误;C、被开方数还能继续开平方,可化简为,不是最简二次根式;故C错误;D、被开方数还能继续开平方,可化简为,不是最简二次根式;故D错误;故选:A.根据最简二次根式的定义进行判断即可.本题考查最简二次根式的定义.根据最简二次根式的定义,最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.2.【答案】D【解析】解:A、∵22+()2=6≠42,故此选项错误;B、∵42+52=41≠62,故此选项错误;C、∵22+32=13≠42,故此选项错误;D、∵12+()2=3=()2,故此选项正确.故选D.由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可.本题考查直角三角形的判定,利用勾股定理的逆定理是解答此题的关键.3.【答案】D【解析】解:∵∠BAD的平分线交BC于E,∴∠EAD=∠BAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠BEA,∴AB=BE,∵AE=BE,∴△ABE是等边三角形,∴∠B=60°∴∠BCD=120°故选:D.利用∠BAD的平分线交BC于E,且AE=BE,先求出△ABE是等边三角形,再求∠BCD 的度数.主要考查了平行四边形的基本性质,并利用性质解题.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.4.【答案】A【解析】解:由数轴可得:a+1>0,a-2<0,则原式=a+1+2-a=3.故选:A.直接利用数轴结合二次根式的性质化简得出答案.此题主要考查了二次根式的性质与化简,正确化简二次根式是解题关键.5.【答案】C【解析】解:当要求的边是斜边时,则有=5;当要求的边是直角边时,则有=.故选:C.此题要分情况考虑:当另一条边是斜边时,当另一条边是直角边时.考查了勾股定理的运用,注意此题的两种情况.6.【答案】A【解析】解:∵AB=3cm,BC=5cm,∴2cm<AC<8cm,∵四边形ABCD是平行四边形,∴AO=AC,∴1cm<OA<4cm,故选:A.根据三角形的三边关系定理得到AC的取值范围,再根据平行四边形的性质即可求出OA的取值范围.本题考查了对平行四边形的性质,三角形的三边关系定理等知识点的理解和掌握,得到AO是AC的一半是解此题的关键.7.【答案】C【解析】解:∵四边形MBND是菱形,∴MD=MB.∵四边形ABCD是矩形,∴∠A=90°.设AB=x,AM=y,则MB=2x-y,(x、y均为正数).在Rt△ABM中,AB2+AM2=BM2,即x2+y2=(2x-y)2,解得x=y,∴MD=MB=2x-y=y,∴==.故选:C.首先由菱形的四条边都相等与矩形的四个角是直角,即可得到直角△ABM中三边的关系.此题考查了菱形与矩形的性质,以及直角三角形中的勾股定理.解此题的关键是注意数形结合思想与方程思想的应用.8.【答案】D【解析】解:已知第一个矩形的面积为1;第二个矩形的面积为原来的()2×2-2=;第三个矩形的面积是()2×3-2=;…故第2018个矩形的面积为:()2×2018-2=()4034=故选:D.易得第二个矩形的面积为()2,第三个矩形的面积为()4,依此类推,第2018个矩形的面积为()2×2018-2.本题考查了三角形的中位线定理及矩形、菱形的性质,是一道找规律的题目,这类题型在中考中经常出现.此题要明确矩形中点组成的四边形是菱形,并熟练掌握矩形的面积为长与宽的积,菱形的面积等于其对角线积的一半.9.【答案】x≥-1【解析】解:由题意得:x+1≥0,解得:x≥-1,故答案为:x≥-1.根据二次根式有意义的条件可得x+1≥0,再解不等式即可.此题主要考查了二次根式的意义.关键是二次根式中的被开方数必须是非负数,否则二次根式无意义.10.【答案】18【解析】解:∵△ABC为直角三角形,AB为斜边,∴AC2+BC2=AB2,又AB=3,∴AC2+BC2=AB2=9,则AB2+BC2+CA2=AB2+(BC2+CA2)=9+9=18.故答案为:18由三角形ABC为直角三角形,利用勾股定理得到斜边的平方等于两直角边的平方和,根据斜边AB的长,可得出两直角边的平方和,然后将所求式子的后两项结合,将各自的值代入即可求出值.此题考查了勾股定理,是一道基本题型.熟练掌握勾股定理是解本题的关键.11.【答案】-【解析】解:OB==,OA=OB=,A点表示的数是-.故答案为:-.根据勾股定理,可得OB的长,根据等量代换,可得答案.本题考查了实数与数轴,利用勾股定理得出OB的长是解题关键.12.【答案】(,)【解析】【分析】本题考查了正方形的性质、坐标和图形特点、等腰直角三角形的判定和性质,熟练掌握正方形的性质是关键.根据正方形的性质和等腰直角三角形的判定分别求:OD=DQ=,根据坐标特点写出点Q 的坐标.【解答】解:过Q作QD⊥OA于D,∵OQ=OC=2,∵四边形ABCO是正方形,∴∠BOA=45°,∴△ODQ是等腰直角三角形,∴OD=QD===,∴Q(,).故答案为(,).13.【答案】①②④【解析】解:∵图中有三个菱形,如菱形ABCD、菱形HOFD、菱形BEPG,∴①正确;∵四边形ABCD是菱形,∴AB∥DC,AD∥BC,∠ABD=∠CBD,∵EF∥BC,GH∥AB,∴四边形BEPG是平行四边形,∴PE=BG,PG=BE,在△BEP和△PGB中,∴△BEP≌△PGB(SSS),∴②正确;∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;∵四边形ABCD是菱形,∴AB∥CD,AD∥BC,∵EF∥BC,GH∥AB,∴AD∥EF∥BC,AB∥GH∥CD,∴四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG是平行四边形,∴AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=VG,∵四边形ABCD是菱形,∴∠EBP=∠GBP,∵PE∥BG,∴∠EPB=∠GBP,∴∠EBP=∠EPB,∴BE=PE,∴AH=PE=BG=BE=CF=PG,同理AE=HP=DF=PF=CG,∴四边形AEPH的周长=四边形GPFC的周长,∴④正确;故答案为:①②④.根据菱形的判定判断①即可;根据菱形性质求出四边形BEPG是平行四边形,推出PE=BG,PG=BE,根据全等三角形的判定推出△BEP≌△PGB,即可判断②;根据三角形面积公式即可判断③;求出四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG 是平行四边形,推出AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=VG,求出AH=PE=BG=BE=CF=PG,同理AE=HP=DF=PF=CG,即可判断④.本题考查了菱形的性质和判定,平行四边形的性质和判定,全等三角形的性质和判定的应用,主要考查学生的推理能力,题目比较好,但是比较容易出错.14.【答案】或10【解析】解:分两种情况:①如图1,当点F在矩形内部时,∵点F在AB的垂直平分线MN上,∴AN=4;∵AF=AD=5,由勾股定理得FN=3,∴FM=2,设DE为y,则EM=4-y,FE=y,在△EMF中,由勾股定理得:y2=(4-y)2+22,∴y=,即DE的长为.②如图2,当点F在矩形外部时,同①的方法可得FN=3,∴FM=8,设DE为z,则EM=z-4,FE=z,在△EMF中,由勾股定理得:z2=(z-4)2+82,∴z=10,即DE的长为10.综上所述,点F刚好落在线段AB的垂直平分线上时,DE的长为或10故答案为:或10.分两种情况讨论:点F在矩形内部;点F在矩形外部,分别根据折叠的性质以及勾股定理,列方程进行计算求解,即可得到DE的长.本题以折叠问题为背景,主要考查矩形的性质、翻折变换的性质、勾股定理等几何知识的综合应用;解决问题的关键利用直角三角形,运用勾股定理列方程求解.15.【答案】解:(1)原式=3-2+-3=-;(2)原式=50-20+3-2+1=34-2.【解析】(1)先把二次根式化为最简二次根式,然后合并即可;(2)利用平方差公式和完全平方公式计算.本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后合并同类二次根式即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.16.【答案】解:原式=(+)•,=•,=,当x=+1时,原式==1+.【解析】首先计算计算括号里面的减法,然后再计算括号外的除法,化简后,再代入x 的值,进行计算即可.此题主要考查了分式的化简求值,在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.17.【答案】解:(1)在Rt△ABD中,AD==3;(2)在Rt△ACD中,AC==2,则△ABC的周长=AB+AC+BC=5+4++2=9+3.【解析】(1)根据勾股定理求出AD;(2)根据勾股定理求出AC,计算即可.本题考查的是勾股定理,掌握直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.18.【答案】解:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OA=OC,∵△AOB的周长比△BOC的周长多3cm,∴(OA+OB+AB)-(OB+OC+BC)=8cm,即AB-BC=3cm,①∵平行四边形ABCD的周长为26cm,∴AB+BC=13cm,②由①②得到:AB=8cm,BC=5cm.【解析】由四边形ABCD是平行四边形,即可得AB=CD,AD=BC,OA=OC,然后由平行四边形ABCD的周长为26cm,△AOB的周长比△BOC的周长多3cm,可得AB-BC=3cm ,AB+BC=13cm,继而可求得AB、BC的长.此题考查了平行四边形的性质.注意掌握平行四边形对边相等与对角线互相平分的定理的应用,注意数形结合思想与方程思想的应用.19.【答案】解:如图连接AF.∵四边形ABCD是正方形,∴∠ACB=45°,∵FE⊥AC,∴∠AEF=∠CEF=∠B=90°,∴∠ECF=∠EFC=45°,∴EF=CE,在Rt△AFE和Rt△AFB中,,∴Rt△AFE≌Rt△AFB,∴BF=EF=CE,∴BF=EC.【解析】如图连接AF.只要证明△ECF是等腰直角三角形,△AFE≌△AFB即可解决问题.本题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.20.【答案】解:(1)S△ABC=3×3-×1×2-×2×3-×1×3=;(2)如图所示:∵DE=,EF=2,DF=,∴DE2+EF2=DF2,∴△DEF是直角三角形.△DEF的面积=.【解析】(1)根据题目设置的问题背景,结合图形进行计算即可;(2)根据勾股定理,找到DE、EF、DF的长分别为、、,由勾股定理的逆定理可判断△DEF是直角三角形.本题考查了勾股定理及作图的知识,解答本题关键是仔细理解问题背景,构图法求三角形的面积是经常用到的,同学们注意仔细掌握.21.【答案】解:(1)过点C作CF⊥AD,交AD延长线于点F,∵∠DAC=45°,∠DCA=15°,∴∠CDF=∠DAC+∠DCA=45°+15°=60°,在Rt△CFD中,,∴,,∴,∴==.(2)在Rt△AFC中,∵∠DAC=45°,,∴,在△ABC中,∵AC2+BC2=62+82=AB2∴△ABC是直角三角形,又∵E为AB中点,∴.【解析】(1)过点C作CF⊥AD,交AD延长线于点F,构造含有30度角的直角△CFD ,通过解该直角三角形求得DF、CF的长度,进而利用等腰直角△ACF的性质求得AD 的长度,结合三角形的面积公式解答即可;(2)由勾股定理的逆定理得到△ABC是直角三角形,由“直角三角形斜边上的中线等于斜边的一半”解答.考查了勾股定理和勾股定理的逆定理,勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.注意:辅助线的作法与目的.22.【答案】4- 10【解析】解:(1)4+的有理化因式可以是4-,分母有理化得:==;故答案为:4-;;(2)∵x=,y=,则=+=+=5-2+5+2=10;故答案为:10;(3)原式=-1+-+-+…+-+-,=-1+,=-1+10,=9.(1)找出各式的分母有理化因式即可;(2)将x与y代入原式计算即可得到结果.(3)原式各项分母有理化,合并即可得到结果.此题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.23.【答案】解:(1)证明:∵四边形ABCD是矩形,∴AB=CD,AB∥CD,AD∥BC,∠B=90°,∴AC==10,∠GAF=∠HCE,∵G、H分别是AB、DC的中点,∴AG=BG,CH=DH,∴AG=CH,∵AE=CF,∴AF=CE,在△AFG与△CEH中,∴△AFG≌△CEH(SAS),∴GF=HE同理:GE=HF∴四边形EGFH是平行四边形.(2)如下图所示,连接GH,由(1)可知四边形EGFH是平行四边形∵点G、H分别是矩形ABCD的边AB、DC的中点,∴GH=BC=8,∴当EF=GH=8时,四边形EGFH是矩形,分两种情况:①AE=CF=t,EF=10-2t=8,解得:t=1.②AE=CF=t,EF=10-2(10-t)=8解得:t=9即:当t为1秒或9时,四边形EGFH为矩形.【解析】(1)由“两组对边分别相等的四边形是平行四边形”来判定;(2)由“对角线相等的平行四边形是矩形”判定四边形EGFH为矩形时t的取值.本题考查了特殊四边形的判定、性质及综合应用,解题的关键是熟练掌握特殊四边形的性质、判定,具有应用代数的方法解决几何问题的意识.24.【答案】●特例感知:①是;②如图1中,根据勾股定理可得:CB2=CD2+4,CA2=CD2+1,于是CD2=(CD2+4)-(CD2+1)=3,∴CD=.●深入探究:如图2中,由CA2-CB2=CD2可得:CA2-CD2=CB2,而CA2-CD2=AD2,∴AD2=CB2,即AD=CB;●推广应用:过点A向ED引垂线,垂足为G,∵“勾股高三角形”△ABC为等腰三角形,且AB=AC>BC,∴只能是AC2-BC2=CD2,由上问可知AD=BC……①.又ED∥BC,∴∠ADE=∠B……②.而∠AGD=∠CDB=90°……③,∴△AGD≌△CDB(AAS),∴DG=BD.易知△ADE与△ABC均为等腰三角形,根据三线合一原理可知ED=2DG=2BD.又AB=AC,AD=AE,∴BD=EC=a,∴ED=2a.【解析】【分析】本题考查三角形综合题、勾股定理、全等三角形的判定和性质、勾股高三角形的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考创新题目.●特例感知:①根据勾股高三角形的定义即可判断;②如图1,根据勾股定理可得:CB2=CD2+4,CA2=CD2+1,于是CD2=(CD2+4)-(CD2+1)=3,即可解决问题;●深入探究:由CA2-CB2=CD2可得:CA2-CD2=CB2,而CA2-CD2=AD2,即可推出AD2=CB2;●推广应用:过点A向ED引垂线,垂足为G,只要证明△AGD≌△CDB(AAS),即可解决问题.【解答】解:●特例感知:①等腰直角三角形是勾股高三角形.故答案为是.②见答案;●深入探究:见答案;●推广应用:见答案.。
【初中数学】江西省吉安市朝宗实验学校2012-2013学年八年级上学期期中考试数学试题 人教版
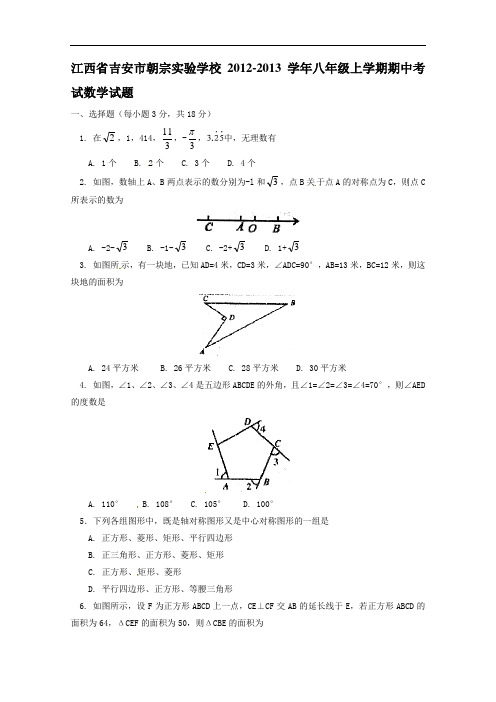
江西省吉安市朝宗实验学校2012-2013学年八年级上学期期中考试数学试题一、选择题(每小题3分,共18分) 1. 在2,1,414,311,-3,中,无理数有A. 1个B. 2个C. 3个D. 4个2. 如图,数轴上A 、B 两点表示的数分别为-l 和3,点B 关于点A 的对称点为C ,则点C 所表示的数为A. -2-3B. -1-3C. -2+3D. 1+33. 如图所示,有一块地,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为A. 24平方米B. 26平方米C. 28平方米D. 30平方米4. 如图,∠1、∠2、∠3、∠4是五边形ABCDE 的外角,且∠1=∠2=∠3=∠4=70°,则∠AED 的度数是A. 110°B. 108°C. 105°D. 100°5.下列各组图形中,既是轴对称图形又是中心对称图形的一组是 A. 正方形、菱形、矩形、平行四边形 B. 正三角形、正方形、菱形、矩形 C. 正方形、矩形、菱形D. 平行四边形、正方形、等腰三角形6. 如图所示,设F 为正方形ABCD 上一点,CE ⊥CF 交AB 的延长线于E ,若正方形ABCD 的面积为64,ΔCEF 的面积为50,则ΔCBE 的面积为A. 20B. 24C. 25D. 26二、填空题(每小题3分,共24分) 7. 若|x+2|+3-y =0,则xy=________。
8. 12-3=________。
9. 如图所示,正方形ABCD 的对角线相交于点O ,点O 是正方形A ′B ′C ′O ′的一个顶点,如果两个正方形的边长都等于1,那么正方形A ′B ′C ′O ′绕顶点O 转动,两个正方形重叠部分的面积是________。
10. 估计215-与0.5的大小关系是215-________0.5. (填“>”“=”或“<”) 11. 如图所示,菱形ABCD 中,对角线AC ,BD 相交于点O ,若再补充一个条件能使菱形ABCD 成为正方形,则这个条件是________(只写一个条件即可)。
2011-2012学年度第二学期八年级期中考试数学试题及参考答案

2011-2012学年第二学期期中考试八 年 级 数 学 试 卷(满分:100分 时间:100分钟 )一、选择题(每题3分,共30分)1.在式子1a 、2xy π、2334a b c 、56x +、78x y+、109x y +中,分式的个数有( )A 、2个B 、3个C 、4个D 、5个2.已知在□ABCD 中,AD =3cm ,AB =2 cm ,则□ABCD 的周长等于 ( ) A .10cm B .6cm C .5cm D .4cm3. 函数21-=x y 的自变量x 的取值范围是 ( ) A.x >-2 B.x <2 C.x ≠2 D.x ≠-2。
4. 下列各组数中,以a 、b 、c 为边的三角形不是直角三角形的是 ( ) A . 1.5,2,3a b c === B . 7,24,25a b c === C . 6,8,10a b c === D. 3,4,5a b c ===5. 反比例函数)0(≠=k xky 的图象经过点(2-,3),则它还经过点 ( )A. (6,1-)B.(1-,6-) C. (3,2) D.(2,3)6.下面正确的命题中,其逆命题不成立的是 ( ) A .旁内角互补,两直线平行 B.三角形的对应边相等C .对顶角相等 D.角平分线上的点到这个角的两边的距离相等 7.如图所示:数轴上点A 所表示的数为a ,则a 的值是A .+1 C 学校 班级 姓名: 学号AMNCB 8. 某单位向一所希望小学赠送1080件文具,现用A 、B 两种不同的包装箱进行包装,已知每个B 型包装箱比A 型包装箱多装15件文具,单独使用B 型包装箱比单独使用A 型包装箱可少用12个。
设B 型包装箱每个可以装x 件文具,根据题意列方程为 ( ) A .1080x =1080x -15+12 B .1080x =1080x -15-12C .1080x =1080x +15-12D .1080x =1080x +15+129.如图,点P (3a ,a )是反比例函y =kx(k >0)与⊙O 阴影部分的面积为10π,则反比例函数的解析式为 ( A .y =3x B .y =5x C .y =10x D .y =12x10. 如图,在△ABC 中,AB=AC=5,BC=6,点M 为BC 中点,MN ⊥AC 于点N ,则MN 等于 ( ) A.65 B. 95 C. 125 D. 165二、细心填一填:(每题3分,共30分)11. 根据里氏震级的定义,地震所释放出的相对能量E 与震级n 的关系为:E =10n ,那么5级地震所释放出的相对能量相当于9级地震所释放出的相对能量的 .(用科学记数法表示) 12. 解方程:xx x -=+--23123的结果是 。
2013年下八年级期中数学试卷.doc
140°80°1集里中学2013年下学期八年级期中考试数学试卷命题人:丁婧 审核人:何伟珍 满分:120分 时量:100分钟班级 姓名 得分一、填空题(每小题3分,共24分)1、点A ( a , 5 ),B ( 3 , b )关于y 轴对称,则a +b = 。
2、三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为_______;3、一个等腰三角形的周长为22cm ,若一边长为6cm ,则另外两边长为4、某商店出售下列四种形状的地砖,(1)正三角形;(2)正方形;(3)正五边形;(4)正六边形。
若只选购其中一种地砖镶嵌地面,可供选择的地砖共有 种。
5、如图,∠1=_____.6、计算)1(22 x x =7、为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是 。
8、如图,已知AB ∥CD ,OA 平分∠BAC ,OC 平分∠ACD ,OE ⊥AC 于点E ,且OE =2,则两平行线间的距离为二、选择题(每小题3分,共30分)9、下列各组线段,不能组成三角形的是 ( )A . 1,2,3B .2,3,4C .3,4,5D .5,12,13.10、下列由数字组成的图形中,是轴对称图形的是( ).11、若一个多边形的外角和与它的内角和相等,则这个多边形是( )A .三角形B .四边形C .五边形D .六边形12、下列说法:(1)全等图形的形状相同、大小相等;(2)全等三角形的对应角相等(3)两个能重合的图形一定关于某条直线对称;(4)一个轴对称图形不一定只有一条对称轴其中正确的个数是( ) A .1 B .2 C .3 D .4 13、下列选项中,不能确定△ABC 是直角三角形的是( )A.∠A +∠B =90°;B.∠A =∠B =0.5∠CC.∠A -∠B =∠CD.∠A -∠B =90°14、三角形三条高的交点一定在 ( )A 、三角形的内部B 、三角形的外部C 、三角形的内部或外部D 、三角形的内部、外部或顶点15、下列计算错误的是( ).A .104252)(b a b a =B . 2226)3(b a ab =- C .532a a a =∙ D .11243)(a a a =∙ 16、如图,某人把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,最省事的办法是( )A.带①去 B.带②去 C.带①或②去 D.带③去17、如图,已知△ABC 为直角三角形,∠B =90°,若沿图中虚线剪去∠B ,则∠1+∠2=( )A .90°B .135°C .270°D .315°18.如图所示,Rt △ABC 中,∠C =90°,AB 的垂直平分线DE 交BC 于D ,交AB 于点E .当∠B =30°时,图中一定不相等的线段有( ).A .AC =AE =BEB .AD =BDC .CD =DE D .AC =BD三、解答题(共8题,共66分)19、(本题满分8分)化简求值:),1(4)4(3)13(222x x x x x ----+-其中2-=x20、(本题满分8分)如图,是屋架设计图的一部分,点D 是斜梁AB 的中点,立柱BC 、DE 垂直于横梁AC ,AB =8 m ,∠A =30°,立柱BC 、DE 要多长。
2012-2013学年北京八中八年级(下)期中数学试卷
合,折痕为 DG,则 AG 的长为
.
20.(2 分)如图 1,正六边形 ABCDEF 的面积为 1,把它的各边延长一倍得到新正六边形
(如图 2),称为第一次扩展;则正六边形 的面积为
;把正六边形 边长按
原法延长一倍得到正六边形 A2B2C2D2E2F2(如图 3),称为第二次扩展;如此下去…,第
n 次扩展得到正六边形 AnBn∁nDnEnFn 的面积为
24.(5 分)已知,如图,在△ABC 中,∠ABC=90°,BD⊥AC 于 D,CE 平分∠BCA,交 AB 于 G,
(1)如图 1,作 EF∥AC,交 AB 于 F.求证:BE=AF; (2)如图 2,过 G 作 GM⊥AC,垂足为 M,连接 ME,判断四边形 BGME 的形状并证明.
第 6页(共 10页)
问题 1:将直线 y= x﹣1 向右平移 2 个单位,则其解析式为
;
问题 2:将直线 y= x+2 向下平移 1 个单位,再向左平移 3 个单位,其解析式为
;
问题 3:将直线 y=ax+a+1 通过向下平移
个单位可以得到直线 y=ax﹣1
知识应用:利用上述方法,我们也可以解决反比例函数的平移问题;
问题 4:反比例函数 y= 向右平移 1 个单位,其解析式为
学习是一件很有意思的事
2012-2013 学年北京八中八年级(下)期中数学试卷
一.选择题(1-9 每题 3 分,10 题 2 分,共 29 分)
1.(3 分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰直角三角形
B.平行四边形
C.菱形
D.等边三角形
2.(3 分)列数表中分别给出了变量 y 与变量 x 之间的对应关系,其中是反比例函数关系的
2012-2013学年度第一学期期中考试八年级数学试题
2012—2013学年度第一学期八年级期中数学参考答案一、选择题(本题共有12小题,每小题3分,共36分)1、B2、A3、A4、C5、B6、A7、B8、C9、D 10、C 11、B 12、A二、填空题(本题共有4题,每小题3分,共12分) 13、(2,3) 14、9 15、1, 3 16、80°,50° 三、解答题(本题共有9小题,共72分)17、解:原式=-4+2 ……4分 18、解:(a-6)+(3a-2)=0 ……4分=-2 ……6分 a =2 ……6分19、证明:在△ABO 和△CDO 中∵OA=OC, ∠AOB=∠COD, OB=OD, ……3分∴△ABO ≌△CDO, ……4分 ∴∠A=∠B, ……5分 ∴AB ∥DC. ……6分 20、解:∵∠CAN=∠C+∠A ∴∠C=∠CAN -∠A =86°-43°=43°, ……3分 ∴∠C=∠A , ……4分 ∴BC=AB , ……5分∵BC=15╳2=30(海里), ……6分 ∴AB=30海里. ……7分 21、(1)图略, A 1(1,-3);……4分 (2)S△A 1B 1C 1=8.5; ……6分 (3)略. ……7分22、(1)证明:∵△ABC 和△ADF 都是等边三角形∴AB=AC ,AD=AF , ∠BAC=∠DAF =∠ACB=60°, ……2分 ∴∠BAD=∠FAC, ……4分 在△ABD 和△ACF 中AB=AC , ∠BAD=∠FAC , AD=AF,∴△ABD ≌△ACF, ……5分 ∴BD=CF ……6分(2)解:∵△ABD ≌△ACF∴∠ACF=∠ABD=60° ……7分 ∴∠FCD=60°-(∠ACB +∠ACF )= 60° ……8分23、(1)解:∵BM 是∠ABC 的平分线,CN 是∠ACB 的平分线,∴∠ABM=∠CBM ,∠CAN=∠BCN ……1分 ∵∠A=60° ∴∠OBC+∠BCN=60°……2分 ∴∠BOC=120°……3分(2)证明:∵ OB =OC ,∴ ∠OBC=∠OCB , ……4分 又∠OBC=21∠ABC , ∠OCB=21∠ACB , ∴∠ABC =∠ACB , ∴ AB =AC , ……5分 而∠A=60°, ∴△ABC 是等边三角形 ……6分(3)在BC 上截取BD =BN,连接OD ,又∠OBD =∠OBN ,BO =BO ,∴△OBD ≌△OBN , ……7分∴∠BON =∠BOD ,而∠BOC ==120°,∴∠BON =∠BOD =∠COM =60°,∴∠COD =60°,∴∠COM =∠COD , ……8分又∠OCM =∠OCD ,CO =CO , ∴△COM ≌△COD , ……9分 ∴CM =CD , ∴CM+BN =CD+BD =BC ……10分24、(1)解:CF=MF=EB . ……2分证明如下:∵AB=BC , ∠ABC=90° , ∴∠BAC=∠C=45°,∵MF ⊥BC ,∴∠FMC=45°=∠C , ∴MF=FC ; ……3分∵EM=EA , ∴∠EAM=∠EMA , ∴ ∠EAB=∠MEC , ……4分∵∠ABE=∠EFM=90° , AE=EM ,∴△AEB ≌△EMF , ∴MF=BE. ……5分(2)过B 作BD ⊥AC 于D , ……6分∵ AB=BC , ∠ABC=90°, ∴ ∠BAC=∠C=45°,∵ME=MB, ∴∠MEB=∠MBE, ……7分 ∴∠MEF=∠BME,∵∠MEF=∠MDB=90°,∴△EMF ≌△BMD, ……8分 ∴MF=BD,∵AB=BC, ∴AC=2BD, ……9分 ∴AC=2MF. ……10分 25、(1)解:△ABO 是等腰直角三角形 ……1分 证明如下:过A 作AH ⊥OB,∵A (2,2), ∴OH=2 ,AH=2, ……2分 ∵B (4,0), ∴OB=4,∴BH=2, ∴BH=AH=OH, ……3分 ∵∠AHO=∠AHB=90°,∴∠AOH=∠OAH=∠HAB=∠ABH=45°, ……4分 ∴△ABO 是等腰直角三角形.(2)过C 作CF ⊥OB ,∵C (a ,2),∴CF=2, ……5分 ∵∠COB=30°, ∠CFO=90°, ∴CF=21OC ,OC=4 , ∴OB=OC, ……6分 ∴∠OBC=∠OCB=75°, ……7分 ∴∠ABC=∠OBC - ∠ABO =75°-45°=30°. ……8分(3)过C 作CK ⊥AB,∵A (2,2) , C (a ,2), ∴AC ∥OB, ……9分 ∴∠CAB=∠ABO=45°,∵CE ⊥AC, ∴CK=21AE , ……10分 ∵∠ABC=30°, ∴CK=21BC , ……11分∴AE=BC. ……12分。
江西省赣州市八年级下学期期中数学试卷
江西省赣州市八年级下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、单项选择题 (共10题;共20分)1. (2分)下列式子:,,,1+ ,,其中是分式个数为()A . 5B . 4C . 3D . 22. (2分) (2019·朝阳) 若点,,在反比例函数的图象上,则y1 , y2 , y3的大小关系是()A .B .C .D .3. (2分)若分式的值为0,则x的值是()A . -3B . 3C . ±3D . 04. (2分) (2015八下·宜昌期中) 三角形的三边长分别为6,8,10,它的最短边上的高为()A . 6B . 4.5C . 2.4D . 85. (2分)林老师给出一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质:甲:函数的图象经过第二象限;乙:函数的图象经过第四象限;丙:在每一个象限内,y值随x值增大而增大.根据他们的叙述,林老师给出的这个函数可能是()A . y=-3xB . y=-C . y=x-3D . y=x2-36. (2分) (2019八下·黄陂月考) △ABC在下列条件下,不是直角三角形的是()A .B .C .D .7. (2分)如果分式中的x,y都扩大到原来的3倍,那么分式的值()A . 不变B . 扩大到原来的6倍C . 扩大到原来的3倍D . 缩小到原来的倍8. (2分)下列计算正确的是()A .B .C .D .9. (2分) (2018八上·三河期末) 某工厂计划生产210个零件,由于采用新技术,实际每天生产零件的数量是原计划的1.5倍,因此提前5天完成任务.设原计划每天生产零件x个,依题意列方程为()A . ﹣ =5B . ﹣ =5C . ﹣ =5D .10. (2分)(2019·高台模拟) 关于反比例函数y= ,下列说法中错误的是()A . 它的图象是双曲线B . 它的图象在第一、三象限C . y的值随x的值增大而减小D . 若点(a,b)在它的图象上,则点(b,a)也在它的图象上二、填空题 (共10题;共11分)11. (1分) (2018九下·江都月考) 已知一粒大米的质量约为0.000021千克,该重量用科学记数法表示为________千克12. (1分) (2017八上·郑州期中) 如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________.13. (1分) (2019七上·杨浦月考) 化简: ________.14. (1分) (2016八上·港南期中) 如果分式有意义,那么x的取值范围是________.15. (1分) (2018八上·江汉期末) 若m+2=3n,则3m•27﹣n的值是________.16. (1分)如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线恰好经过点E,AB=4,AD=2,则K的值是________ .17. (2分) (2020八下·凤县月考) 用反证法证明一个三角形中不能有两个角是直角,第一步是假设这个三角形中________.“两直线平行,内错角相等”的逆命题是________.18. (1分)下列函数(其中n为常数,且n>1)① y=(x>0);② y=(n﹣1)x;③ y=(x>0);④ y=(1﹣n)x+1;⑤ y=﹣x2+2nx(x<0)中,y 的值随 x 的值增大而增大的函数有________个.19. (1分) (2019九上·海淀期中) 如图, 边长为2的正方形ABCD绕着点C顺时针旋转90°,则点A运动的路径长为________.20. (1分)要在一个长方体中放入一细直木条,现知长方体的长为2,宽为,高为,则放入木盒的细木条最大长度为________.三、解答题 (共7题;共56分)21. (10分)观察下列各式及验证过程:验证:= 验证:验证:(1)按照上述三个等式及其验证过程的基本思路,猜想的变形结果并进行验证;(2)针对上述各式反映的规律,写出用n(n≥2的自然数)表示的等式,并进行验证.22. (10分) (2018八上·港南期中)(1)解分式方程(2)在△ABC中,∠A=∠B-10°,∠C=∠B-5°,求△ABC的各个内角的度数.23. (5分) (2015八下·福清期中) 化简求值:• ,其中a=3+ ,b=3﹣.24. (5分)扬州建城2500年之际,为了继续美化城市,计划在路旁栽树1200棵,由于志愿者的参加,实际每天栽树的棵树比原计划多20%,结果提前4天完成,求实际每天栽树多少棵?25. (6分) (2018九下·厦门开学考) 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:千帕)随气体体积V(单位:立方米)的变化而变化,p随V的变化情况如表所示.P 1.52 2.534…V644838.43224…(1)写出一个符合表格数据的p关于V的函数解析式________(2)当气球内的气压大于144千帕时,气球将爆炸,依照(1)中的函数解析式,基于安全考虑,气球的体积至少为多少立方米?26. (5分)(2018·台湾) 嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B 点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1 , R2 , R3 ,其行经位置如图与表所示:路径编号图例行径位置第一条路径R1_A→C→D→B第二条路径R2…A→E→D→F→B第三条路径R3▂A→G→B 已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.27. (15分) (2017八下·淅川期末) 如图,已知双曲线y= ,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.(1)求k的值;(2)若△BCD的面积为12,求直线CD的解析式y1;(3)根据图象直接写出y≥y1时,x的取值范围.参考答案一、单项选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共10题;共11分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共7题;共56分)21-1、21-2、22-1、22-2、23-1、24-1、25-1、25-2、26-1、27-1、27-2、27-3、。
