二重积分的积分方法和积分公式
第十章第二节_二重积分的计算法

(1,1)
y x
x
y
0
1
dx sin y 2dy
x
1
(1,1)
0 dy 0 sin y dx
2
1
y
y x
(sin y ) x dy
2
1
y
x D : 0 y 1, 0 x y
o
y sin y 2dy
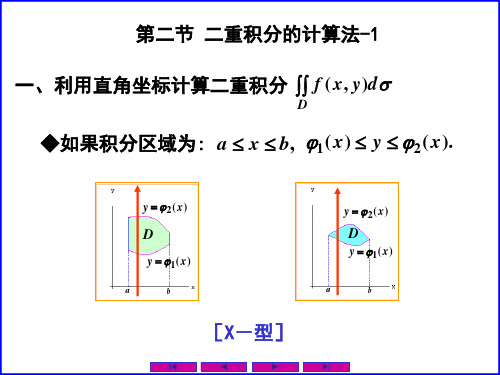
第二节 二重积分的计算法
一、利用直角坐标计算二重积分
二、极坐标系下二重积分的计算 三、小结 思考题
【复习与回顾】
回顾一元函数定积分的应用
平行截面面积为已知的立体的体积的求法
在点x处的平行截面的面积为 A( x ) 体积元素 dV A( x )dx 体积为
V A( x )dx
a b
一、利用直角坐标系计算二重积分
(( xx )0 ) 11
ff (x (x ,0 y,)dy y )dy
b
V A( x )dx
a
2 ( x )
1( x)
f ( x, y )d [
D a
f ( x , y )dy]dx.
公式1
上式称为先对 y后对x的二次积分
注意:
1)上式说明: 二重积分可化为二次定积分计算; 2)积分次序: X-型域 先Y后X; 3)积分限确定法: 后积先定限,域中做穿线; 先过为下限,后过未上线。
f ( x, y )d 的值等于以D 为底,以曲面z
D
f ( x , y ) 为顶的曲顶柱体的体积 .
【方法】根据二重积分的几何意义以及计算“平 行截面面积为已知的立体求体积”的方法来求.
二重积分的简单计算

探秘二重积分的计算方法
二重积分是高等数学中的一个重要概念,用于求解平面上某个区域内的面积,也被称为二重积分面积公式。
下面,我们将探讨二重积分的简单计算方法。
首先,二重积分的计算需要先确定被积函数和积分区域。
假设被积函数为f(x,y),积分区域为D,其在直角坐标系下的边界可以用以下公式表示:
∬f(x,y)dxdy = ∫∫f(x,y)dA
接下来,我们需要根据积分区域D的形状来确定积分的范围。
当积分区域为直角坐标系下有界区域时,我们可以采用以下方法求解:
1. 积分区域为矩形时,通常采用先对x积分后对y积分的方法,即:
∫∫f(x,y)dA = ∫ab∫cd f(x,y)dxdy
其中,积分范围为a≤x≤b,c≤y≤d。
2. 积分区域为三角形时,可采用先对y积分后对x积分的方法,即:
∫∫f(x,y)dA=∫cd∫h1(x)h2(x) f(x,y)dydx
其中,积分范围为c≤y≤d,h1(x)≤y≤h2(x)。
3. 积分区域为梯形时,可采用换元法将积分区域转化为矩形的形式,即:
∫∫f(x,y)dA=∫ab∫g1(y)g2(y) f(x,y)dxdy
其中,积分范围为g1(y)≤x≤g2(y),a≤y≤b。
以上是二重积分计算的基本方法,希望能对您有所帮助。
二重积分

0
f (r cosθ , r sinθ )r d r.
2) 如果坐标原点不在积分域 D 内部, ) 内部, 则从原点作 两条射线 θ = α 和 θ = β (α ≤ β) (如图)夹紧域 D . α, β 如图) 积分(外积分)的下限和上限, 分别是对 θ 积分(外积分)的下限和上限, 在 α 与 β 之 的边界交两点, 间作任一条射线与积分域 D 的边界交两点,它们的极 径分别为 r = r1(θ),r = r2(θ), , , 假定 r1(θ ) ≤r2(θ ), 那么 , r1(θ ) 与 r2(θ ) 分别是对 r 积分(内积分)下限与上限, 积分(内积分)下限与上限,
(2) 在D′上 雅可比行列式
y
∂(x, y) xu xv = ≠ 0; J (u, v) = 定积分换元法 , v) ∂(u yu yv
b
D
(3) 变换 f (x) d x = ∫ Df是一一对应的 ,( x = ϕ(t) ) ∫a T : D′ →α [ϕ(t)]ϕ′(t) d t
机动 目录 上页 下页 返回 结束
sinθ
∴∫∫ f (x, y) d x d y = ∫∫
D
D′
− r cosθ f (r cosθ, r sinθ ) r d r dθ
其中 0 ≤ r < +∞,0 ≤ θ < 2π (或 − π ≤ θ ≤ π ).
机动
目录
上页
下页
返回
结束
四、极系下的二重积分化为二次积分 将直系下的二重积分化为极系后, 将直系下的二重积分化为极系后,极系下的 二重积分仍然需要化为二次积分来计算。 二重积分仍然需要化为二次积分来计算
1
机动 目录 上页 下页 返回 结束
二重积分四则运算公式

二重积分四则运算公式二重积分是微积分中的一个重要概念,也是数学计算中常用的工具之一、它是对二元函数在一些区域上的求和,可以用来计算曲线下面的面积、质心、重心、弯矩等问题。
在进行二重积分的计算时,有四个基本的运算公式,分别是加法公式、乘法公式、换元公式和分部积分公式。
下面将详细介绍这四个公式以及它们的应用。
一、加法公式加法公式是用来计算两个区域上的二重积分的和的公式,具体形式如下:∬(R1∪R2)f(x,y)dA=∬R1f(x,y)dA+∬R2f(x,y)dA其中,R1和R2是两个不相交的区域,f(x,y)是定义在R1∪R2上的函数,dA表示面积元素。
加法公式的应用非常广泛,可以用于计算不规则区域上的积分,将区域分成若干个小区域,然后分别计算每个小区域上的积分再求和即可。
二、乘法公式乘法公式是用来计算两个函数的乘积的积分的公式,具体形式如下:∬Rf(x,y)g(x,y)dA=∬Rf(x,y)dA·∬Rg(x,y)dA其中,f(x,y)和g(x,y)是定义在区域R上的函数,dA表示面积元素。
乘法公式可以简化积分的计算,将二重积分分成两个单变量的积分,分别计算再相乘即可。
三、换元公式换元公式是用来进行变量替换的公式,可以将一个二元函数在坐标变换后的区域上的积分转化为原区域上的积分,具体形式如下:∬Rf(x,y) dA = ∬R'(f(g(u,v),h(u,v)) ,J(u,v), du dv其中,R是原区域,R'是通过坐标变换得到的新区域,f(x,y)是定义在R上的函数,J(u,v),是变换后的雅可比行列式。
换元公式可以简化积分的计算,通过适当的坐标变换可以将原积分转化为更简单的形式,例如将直角坐标系中的积分转化为极坐标系中的积分等。
四、分部积分公式分部积分公式是用来计算二重积分中的积分运算的公式,具体形式如下:∬R(∂f/∂x + ∂g/∂y) dA = ∮C(f dx + g dy)其中,R是区域,C是区域R的边界曲线,f(x,y)和g(x,y)是定义在R上的函数,∂f/∂x和∂g/∂y分别表示函数f和g关于x和y的偏导数。
9.2二重积分的计算(直角)

D: y ≤ x ≤ 2
2 y=x y 1
o
1 x 2x
2 2 I =∫1 d y ∫ x yd x= ∫1 y 2
[
1 2
2 x y ] dy y
2
= ∫ [ 2y −
2 1
1 2
y ]dy
3
9 = 8
例2. 计算
∫∫
D
x ydσ , 其中 是抛物线 y = x 及直线 其中D
2
所围成的闭区域. y = x − 2 所围成的闭区域 为计算简便,看成 型区域, 看成Y型区域 解: 为计算简便 看成 型区域 则
0
2
x2 2 0
2 2
2
dx∫
8− x2
0
f ( x, y)dy
y
x2 + y 2 = 8
D2
积分域由两部分组成: 解: 积分域由两部分组成
0≤ x ≤ 2 2≤ x ≤ 2 2 D : , D2 : 1 2 1 2 0≤ y ≤ 2 x 0 ≤ y ≤ 8 − x
视为Y–型区域 将D = D1 + D2 视为 型区域 , 则 0≤ y ≤ 2 D : 2 y ≤ x ≤ 8 − y2 2 I = ∫∫ f ( x, y)d xd y= ∫ dy∫
先对x 后对y的累次积分
D c ≤ y ≤ d ψ 1( y) ≤ x ≤ψ2( y)
按 , 在计算中括号中定积分 时 , 积分变量为 x , 而将 y 暂时固定 .
一、利用直角坐标计算二重积分
由曲顶柱体体积的计算可知, 由曲顶柱体体积的计算可知 若D为 X – 型区域 为 a≤ x≤b D: ϕ1( x) ≤ y ≤ ϕ2( x) 则
0902二重积分的计算法-1
b ϕ2( x) f ( x , y )dy ; = dx a ϕ1 ( x )
∫
∫∫ f ( x , y )dσ ∫
D
d ϕ2 ( y) f ( x , y )dx . = dy c ϕ1 ( y )
∫
[混合型] 混合型] (在积分过程中要正确选择积分次序) 在积分过程中要正确选择积分次序) 积分次序
y
A(x)
a
x
y = ϕ2 ( x)
b
x
D
y = ϕ1( x)
b ϕ ( x) ∴ ∫∫ f ( x , y )dσ =∫a dx ∫ϕ 2( x ) f ( x , y )dy . ……二次积分公式 ? 1 二次积分公式
D
◆如果积分区域为:c ≤ y ≤ d , ϕ1 ( y ) ≤ x ≤ ϕ 2 ( y ). 如果积分区域为:
π
练习1 练习 改变下列积分的积分次 序
∫
1 2 x− x2 2 2− x dx f ( x , y )dy + dx f ( x , y )dy . 0 0 1 0
∫
∫
∫
解 积分区域如图: 积分区域如图:
y = 2− x
原式 = ∫0 dy ∫
1
2− y
2
y = 2x − x2
1− 1− y
f ( x , y )dx.
1
o
1
x
2.设f ( x , y )在D上连续 , 其中 D是由直线 y = x , y = a及x = b (b > a )所围成的闭区域 , 证明 :
(1)∫
b x dx a a
∫ f ( x , y )dy = ∫
b b dy y a
8(2)二重积分的计算

其中函数 1 ( x )、 2 ( x )在区间 [a , b] 上连续.
y
y 2 ( x)
D
y 1 ( x)
X-型
y
y 2 ( x)
D
y 1 ( x)
x
O
a
b
O
a
b
x
X-型区域的特点: x 常数 的直线与区域D的边界 至多交于两个点.
3
二重积分的计算
用二重积分的几何意义说明其计算法
1
2 ( y )
f ( x , y )dx
二重积分的计算
注 特殊地 D为矩形域: a≤x≤b,c≤y≤d
则
f ( x , y )d a dx c D
d b c a
b
d
f ( x , y )dy
如D是上述矩形域, 且f ( x , y ) f1 ( x ) f 2 ( y ) 则
如果f ( x, y )关于x是奇函数 0, f ( x, y)dxdy 2 f ( x, y)dxdy, 如果f ( x, y)关于x是偶函数 D D 2 23 D2为D在右半平面部分.
二重积分的计算
这个性质的几何意义如图: z
z
O
y x
O
y
x 区域D关于x轴对称 f(x,y)关于坐标y为偶函数
的曲边梯形.
2 ( x0 )
1 0
z
y 2 ( x)
z f ( x, y)
x [a , b] 有:
A( x )
D
O
a
2 ( x )
*V ( x , y )f ( x , y )d f d x
b
8.2 二重积分的计算法

ϕ1(θ) ≤ r ≤ϕ2(θ),α ≤θ ≤ β
表 ( 图 来 示如 )
中 数 其 函 ϕ1(θ),ϕ2 (θ) 区 [ 在 间α, β]上 续 连 。
O
r =ϕ2(θ)
D
β
r =ϕ1(θ)
α
x
10
D:ϕ1(θ) ≤ r ≤ϕ2(θ)
α ≤θ ≤ β
D
r =ϕ2(θ)
D
r =ϕ2(θ) r =ϕ1(θ)
o x
(2)从极点出发的一族射线:θ=常数, 从极点出发的一族射线: 常数 常数, 从极点出发的一族射线 个小区域( 把D分成 n个小区域(如上图) 分成 个小区域 如上图)
8
面积元素
∆σi ∆θi ∆r i
d σ = r d rd θ
dσ
x
o
∫∫ f (x, y)dσ = ∫∫ f (r cosθ , r sinθ )r d rdθ
D
D
注意:dσ = dxdy ≠ dx ⋅ dy
9
2、如何化为两次单积分 、 积分顺序:一般是先积 后积 积分顺序:一般是先积r后积θ 定限的方法:依D的特点: 定限的方法: 的特点: 的特点
D
r =ϕ2(θ)
(1) 极 在 外 点 D
β
O
α
r =ϕ1(θ)
x
设 分 域 可 不 式 积 区 D 用 等
z
V = ∫∫ R2 − x2dσ 1
= ∫ [∫
0
R 0
D R
R2 −x2
0
R2 − x2dy] dx
2 2
o R x
y
R
y
= ∫ [ R2 − x2 y]0 R −x dx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二重积分的积分方法和积分公式二重积分是高等数学中一个重要的概念,主要用于求解平面区域上的积分问题。
在实际应用中,二重积分常常伴随着一些积分方法和积分公式,有助于简化计算过程,提高计算效率。
本文将详细介绍二重积分的积分方法和积分公式。
一、二重积分的基本概念
首先,我们需要了解二重积分的基本概念。
对于一个平面区域D,如果对于每一个区域内的点(x,y),都有一个实数f(x,y)与之对应,那么我们称f(x,y)是D上的一个二元函数。
此时,通过对区域D进行分割,我们可以得到很多个小区域,用矩形来近似表达每个小区域,使得这些小矩形的面积的和趋近于区域D的面积,这个和就可以作为表示f(x,y)在区域D上的对应二重积分。
其数学表达式为:
∬Df(x,y)dxdy
其中f(x,y)是被积函数,D是被积区域,dxdy表示在x轴和y 轴上的微小增量。
二、二重积分的积分方法
1. 变量代换法
变量代换法常用于解决被积函数较为复杂的情况。
通过建立一个新的变量,将原式中的变量替换为新的变量,并计算出新的变量的微分值,从而得到新的被积函数和被积区域。
例如,对于二重积分∬Dx^2y dxdy,如果我们令u=xy,v=y,那么在新的变量下,原式可化为∬D(u/v)dvdu。
此时,我们需要通过计算出u和v的微分值,将原被积函数与被积区域进行转化,从而得到简洁的结果。
2. 极坐标法
极坐标法常用于解决被积区域的对称性问题。
通过将二维平面
上的坐标系转化为极坐标系,可以轻松地描述出各种对称图形的
被积区域,并简化计算过程。
例如,对于二重积分∬Dxy dxdy,如果我们将被积区域D转化
为极坐标系下的区域,可以得到简化后的被积函数为
∫0^πdθ∫0^Rρ^3sinθcosθdρ。
此时,我们只需要进行简单的积分运算,就可以得到最终的结果。
3. 分部积分法
分部积分法常用于解决被积函数中的乘积项问题。
通过将乘积
项拆分成不同的部分,并对每一部分进行不同的求导和积分操作,可以简化被积函数的形式,并且可以将原式化简为更易于计算的
形式。
例如,对于二重积分∬Dxsin(xy) dxdy,如果我们将被积函数拆
分成f(x)g(y)的形式,可以得到f(x)=x,g(y)=sin(xy),然后通过对
f(x)和g(y)进行分部积分,最终化简得到∬D(sin(xy)-cos(xy))dxdy。
三、二重积分的积分公式
1. Fubini定理
Fubini定理是二重积分的一个重要定理,它表示如果f(x,y)在矩形[a,b]x[c,d]上连续,那么我们可以将二重积分f(x,y)在[a,b]与[c,d]上分别进行积分,从而得到最终的积分值。
具体表达式为:
∬Df(x,y)dxdy=∫c^d(∫a^bf(x,y)dx)dy=∫a^b(∫c^df(x,y)dy)dx
2. 对称性公式
对称性公式是通过对不同的对称性进行分析,得到的一种简化积分计算的方法。
例如,对于偶函数f(x,y)=f(-x,y),如果被积区域是在x轴左右对称的,那么二重积分的结果就可以简化为
∬Df(x,y)dxdy=2∫0^∞∫0^yl(x,y)dxdy,其中l(x,y)=f(x,y)+f(-x,y)。
3. 极限交换公式
极限交换公式是在某些特定情况下,可以将二重积分的顺序进
行交换。
它的条件是被积函数在被积区域上连续,且被积区域有界。
具体表达式为:
limₙ→∞∬Df(x,y;n)dxdy=∫a^b(∫c^df(x,y)dy)dx
其中f(x,y)是被积函数,D是被积区域,f(x,y;n)是一个逐步收
敛于f(x,y)的数列,a、b、c、d分别为被积区域D的边界。
结语
二重积分的积分方法和积分公式在实际应用中具有重要的作用,可以帮助我们简化计算过程,提高计算效率。
在掌握了基本的积
分方法和积分公式之后,我们可以更加轻松地处理二重积分问题,为更复杂的高阶积分问题打下良好的基础。
