正方体表面展开图的口诀
(完整版)展开与折叠知识点归纳

展开与折叠
知识点一:正方体的表面展开图
正方体是特殊的棱柱,它的六个面都是大小相同的正方形,将一个正方体的表面展开,可以得到11种不同的展开图,把它归为四类:一四一型,6种;二三一型,3种;三三型,1种;二二二型,一种。
正方体展开图口诀:
1、一线不过四;田凹应弃之。
2、找相对面:相间,“Z”端是对面。
3、找邻面:间二,拐角邻面知。
知识点二:棱柱的表面展开图
棱柱的表面展开图是由两个相同的多边形和一些长方形组成的。
知识点三:圆柱、圆锥的表面展开图
1、圆柱的表面展开图是由两个大小相同的圆(底面)和
一个长方形(侧面)组成,其中侧面展开图长方形的一边的长是底面圆的周长,另一边的长是圆柱的高。
2、圆锥的表面展开图是由一个(侧面)和一个圆(底面)
组成,其中扇形的半径长是圆锥母线(即圆锥底面圆周上任一点与顶点的连线)长,而扇形的弧长则是圆锥底面圆的周长。
正方体的十一种平面展开图

正方体的十一种平面展开图可记忆成下面口诀:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。
相对的两个面之间总隔着一个面正方体:中间四个面,上下各一面(6种摆法-141)中间三个面,一二隔河见(3种摆法-132/231)中间二个面,楼梯天天见(1种摆法-222)中间没有面,三三连一线(1种摆法-33)例1 在图13中(每个小四边形皆为全等的正方形),可以是一个正方体表面展开图的是( ).例2图14是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C 内分别填上适当的数,使得这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( ).A.0,-2,1B.0,1,-2C.1,0,-2D.-2,0,1例3图15所示的是一个正方体包装盒的表面展开图,各个面上标注的数字分别为1,2,3,4,5,6。
现将表面展开图复原为正方体包装盒,则标注数字1和3的两个面是互相平行的,请你写出另一组相互平行的面上所对应的数字:_______。
注:例1、例2、例3的答案分别为:C;A;2与5或4与6。
是不是有点多此一举?例4 一个无盖的正方体纸盒,将它展开成平面图形,可能情况总共有()。
A.12种 B.11种 C.9种 D.8种千万注意,你可不要选B呦!选D才对。
我又在炫耀了,不过你能很快画出这8个平面展开图吗?下面是示意图,黑方块表示展开图,白方块表示空缺。
(一)□■□■■■□■□(二)■■■■■□□□(三)■■■■□■□□(四)■■■■□□■□(五)■■■■□□□■(六)□■□■■■□□■(七)□□■■■■□□■(八)■□□■■■□□■。
正方体表面展开图的口诀

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四方连线,,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
巧记正方体11种展开图的规律

巧记正方体11种展开图的规律
老师共同研究了几条规律,希望对大家的教学有所帮助:
正方体展开11种,找规律很好记。
中间4个一连串,两边各一随便放.
二三紧连错一个,三一相连一随便。
两两相连各错一。
三个两排一对齐。
先找同层隔一面,再找异层隔二面,
剩下两面必相对,两个起头按顺序。
正方体表面展开图(一四一型:6种)口诀:中间四个一连串,两边各一随便放
(二三一型:3种)口诀:二三紧连挪一个,三一相连一随便
(二二二型:1种)口诀:两两相连各挪一
(三三型1种)口诀:三个两排一对齐。
正方体表面展开图的口诀 (1)

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四方连线,,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
七年级巧记正方体展开图口诀文档版

巧记口诀确定正方体表面展开图
6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:
正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:
四方成线两相卫,六种图形巧组合;
跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图
一、四方成线两相卫,六种图形巧组合
(1)(2)(3)(4)
(5)(6)
二、跃马失蹄四分开
(
1)
(2)
(3)(4)
123
4
5
三、两两错开一阶梯
四、对面相隔不相连
五、识图巧排“7”、“凹”、“田”。
正方形拼正方体 口诀公式

正方形拼正方体口诀公式
6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考。
正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明。
四方成线两相卫,六种图形巧组合。
跃马失蹄四分开,两两错开一阶梯。
对面相隔不相连,识图巧排“7”“凹”“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图。
五升六暑期培训正方体表面展开图口诀+练习
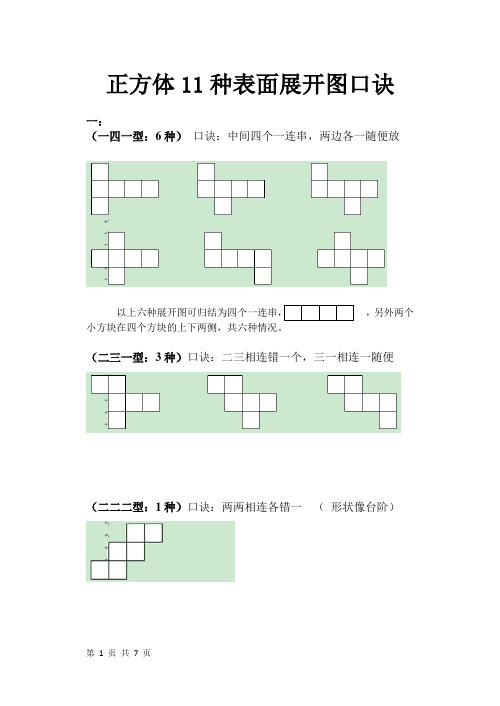
正方体11种表面展开图口诀一:(一四一型:6种)口诀:中间四个一连串,两边各一随便放,另外两个小方块在四个方块的上下两侧,共六种情况。
(二三一型:3种)口诀:二三相连错一个,三一相连一随便(二二二型:1种)口诀:两两相连各错一(形状像台阶)(三三型1种)口诀:三个两排一对齐二:识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
【例题】下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
A 、D 都有“凹”形结构,B 有“田”形结构,故应选C三:相对面特征(1)没有公共边,没有公共顶点。
(2)同行(同列)隔一个面(“I ”型图) (3)“z ”字找两端(“Z ”型图)[练习]1.请分别标出“前、后、左、右、上、下”的其中五个面。
2、下列图形中(每个小正方形的大小相同),是一个正方体表面展开图的是( )DCBA3、下列各图形中能围成正方体的是( )第4类:有1种DCBA4.如图是一个正方体的表面展开图,则图中“加”字所在面的对面所标的字是()A.北B.京C.奥D.运5.水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是 ( )A.O B. 6 C.快 D.乐6.如果有一个正方体,它的展开图可能是下面四个展开图中的()7.如图7-1是一个小正方体的侧面展开图,小正方体从如图5-2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上面的字是()A.和B.谐C.社D.会8.如图是正方体的展开图,则原正方体相对两个面上的数字和最小的是( ).A. 4B. 6C. 7D.89.有一正方体木块,它的六个面分别标上数字1——6,这是这个正方体木块从不同面所观察到的数字情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧记口诀确定正方体表面展开图
6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式
总结出来,供大家参考:
正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:
四方成线两相卫,六种图形巧组合;
跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:
一、四方成线两相卫,六种图形巧组合
(1)(2)(3)(4)
(5)(6)
以上六种展开图可归结为四方连线,即,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开
(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形
(如图),另外一个小方块的位置有四种情况,即图中四个小方块中
的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯
这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连
这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相
连,则1号面与3号面是对面,中间隔了一个2
号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”
(1) (2) (3)
这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方
体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一
顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把
该图形折叠起来将有两个面重合。
现举例说明:
例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是( )
解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
A 、D 都有“凹”形结构,B
有“田”形结构,故应选C
例2.(2004扬州)马小虎准备制作一个封闭的正方体
盒子,他先用5个大小一样的正方形制成如右图所示的拼接
图形(实线部分),经折叠后发现还少一个面,请你在右图中
的拼接图形上再接一个正方形,使新拼接成的图形经过折叠
后能成为一个封闭的正方体盒子.
(注:①只需添加一个符合要求的正方形;②添加的正方形
用阴影表示.)
解析:本题可用“跃马失蹄四分开”来解决。
图中具备了三二相连
的结构,故本题有四种答案,即小方块的位置有图中 所示的四种
情况之一。
试一试:
1.(2004浙江金华)下列图形中,不是立方体表面展开图的是( )
2.(2004镇江)如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形
1 2 3
1 2 3 4 5
和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是()
3.(2004海南)如图是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C 内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,
相对面上的两数互为相反数,则填在A、B、C内的三个数依次是
().
(A)0,-2,1(B)0,1,-2(C)1,0,-2(D)-2,0,1
(2005济南中考题)在正方体的表面上画有如图(1)中所示的粗线,图(2)是其展开图的示意图,但只在A面上画有粗线,那么将图(1)中剩余两个
面中的粗线画入图(2)中,画法正确的是(如果没有把握,还
可以动手试一试)
(正方体纸盒)
(A)(B)(C)(D)。
