高中数学圆锥曲线与方程2_3_2双曲线的简单几何性质2学案无答案新人教A版选修2_1
2014-2015学年人教A版选修2-1高中数学《2.3.2双曲线方程及性质的应用(2)》课件

2 y2 x 1 , 由 消去y并整理得x2+4x-6=0, 2 y x 2
因为Δ>0,所以直线与双曲线有两个交点,
设D(x1,y1),E(x2,y2),则x1+x2=-4,x1·x2=-6,
故|DE|=
x1 x 2 y1 y 2
2 2
2
2 x (2)①双曲线C1: y 2 1,左顶点 A( 2 ,, 0) 渐近线方程: 1 2 2 y 2x.
过点A与渐近线 y 2x 平行的直线方程为
2 ), 即 y 2x 1. 2 2 x , y 2x , 4 解方程组 得 y 1, y 2x 1 2 所求三角形的面积为 S 1 OA y 2 . 2 8 y 2(x
3 3 3
共点,经验证②④表示的直线与双曲线有交点 . 答案:②④
2 3 c2 4 (2)①由 e 可得 2 ,所以a2=3b2,故双曲线方程可化为 3 a 3 2 2 x y 2=1. 将点 代入双曲线 C 的方程,可解得 b 1 , P( 6 , 1) 3b 2 b 2 2 x 所以双曲线C的方程为 y 2 1. 3
6 3m2 6 由根与系数的关系得 x1 x 2 m, x1x 2 5 10
①
又|AB|= x1 x 2 2 y1 y 2 2 =
1 4 x1 x 2
2
4.
所以5[(x1+x2)2-4x1x2]=16 将①式代入②,解得 m 210 .
y1 y 2 标为 ( x1 x 2 , ). 2 2
2.|AB|=
x1 x 2
高中数学 第2章 圆锥曲线与方程 2.2.2 双曲线的简单几何性质 新人教A版选修1-1

解析答案
(2)与双曲线1x62 -y42=1 有公共焦点,且过点(3 2,2). 解 设所求双曲线方程为16x-2 k-4+y2 k=1(16-k>0,4+k>0), ∵双曲线过点(3 2,2), ∴136-2k2-4+4 k=1,
解得k=4或k=-14(舍去). ∴所求双曲线的标准方程为1x22 -y82=1.
∴c= a2+b2= 16=4.
∴双曲线的实轴长 2a=4,虚轴长 2b=4 3.
焦点坐标为F1(0,-4),F2(0,4),
顶点坐标为A1(0,-2),A2(0,2),
渐近线方程为 y=± 33x,离心率 e=2.
解析答案
题型二 根据双曲线的几何性质求标准方程 例2 求适合下列条件的双曲线的标准方程: (1)一个焦点为(0,13),且离心率为153; 解 依题意可知,双曲线的焦点在y轴上,且c=13,
当λ<0时,焦点在y轴上.
答案
返回
题型探究
重点突破
题型一 已知双曲线的标准方程求其几何性质
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、 离心率、渐近线方程. 解 将 9y2-4x2=-36 化为标准方程x92-y42=1,即3x22-2y22=1, ∴a=3,b=2,c= 13.
答案 不一样.椭圆的离心率0<e<1,而双曲线的离心率e>1.
(2)若双曲线确定,则渐近线确定吗?反过来呢?
答案 当双曲线的方程确定后,其渐近线方程也就确定了;
反过来,确定的渐近线却对应着无数条双曲线, 如具有相同的渐近线 y=±bax 的双曲线可设为ax22-by22=λ(λ≠0,λ∈R), 当λ>0时,焦点在x轴上,
2021_2022高中数学第二章圆锥曲线与方程3双曲线2双曲线的简单几何性质1课件新人教A版选修2

渐近线方程为
y=±
2 2 x.
典例剖析
一.已知双曲线的方程,研究其几何性质
• 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长 、离心率和渐近线方程,并作出草图.
• [分析] 将双曲线方程化成标准方程,求出a、b、c的值,然后依 据各几何量的定义作答.
[解析] 将 9y2-4x2=-36 变形为x92-y42=1, 即3x22-2y22=1,∴a=3,b=2,c= 13, 因此顶点为 A1(-3,0),A2(3,0), 焦点坐标为 F1(- 13,0),F2( 13,0), 实轴长是 2a=6,虚轴长是 2b=4,
∴双曲线的标准方程为y22-x42=1.
三.双曲线的离心率
已知 F1、F2 是双曲线ax22-by22=1(a>0,b>0)的两个焦点,PQ 是经过 F1 且垂直于 x 轴的双曲线的弦.如果∠PF2Q=90°,求 双曲线的离心率.
• [解析] 设F1(c,0),由|PF2|=|QF2|, ∠PF2Q=90°,
)
B.x42-y52=1 D.x22- y25=1
• [答案] B
[解析] e=32,c=3,∴a=2,∴b2=c2-a2=5, 即双曲线的标准方程为x42-y52=1.
4.已知双曲线ax22-y52=1 的右焦点为(3,0),则该双曲线的
离心率等于( )
A.3 1414
B.3 4 2
C.32
D.43
第二章 圆锥曲线与方程
2.3 双曲线
2.3.2 双曲线的简单几何性质
学习目标
• 1.类比椭圆的性质,能根据双曲线的标准方程,讨论它的几何性质 .
• 2.能运用双曲线的性质解决一些简单的问题.
高中数学第二章圆锥曲线与方程22双曲线222双曲线的简单几何性质课件新人教A版选修1

[类题尝试] 直线 l 在双曲线x32-y22=1 上截得的弦长 为 4,其斜率为 2,求 l 的方程.
y=2x+m, 解:设直线 l 的方程为 y=2x+m,由x32-y22=1, 得 10x2+12mx+3(m2+2)=0.(*) 设直线 l 与双曲线交于 A(x1,y1),B(x2,y2)两点,由 根与系数的关系,
切或相交,不正确.(2)求双曲线的渐近线时,先将“λ” 变成“0”,然后用因式分解即得渐近线方程,正确.(3)由 等轴双曲线的定义得 a=b,c2=a2+b2=2a2,所以 离心 率 e= 2,正确.
(4)双曲线与虚轴无交点,只与实轴有 2 个交点,不 正确.
答案:(1)× (2)√ (3)√ (4)×
(0,a),
坐标 (a,0)
(0,-a)
性质
渐近线 离心率
y=±bax
y=±abx
e=ac,e∈(1,+∞)
2.等轴双曲线 实轴和虚轴相等的双曲线叫做等轴双曲线,它的渐近 线是 y=±x,离心率为 e= 2.
1.思考判断(正确的打“√”,错误的打“×”)
(1)若直线与双曲线交于一点,则直线与双曲线相切
类型 1 双曲线的几何性质(自主研析) [典例 1] 求双曲线 9y2-4x2=-36 的顶点坐标、焦 点坐标、实轴长、虚轴长、离心率和渐近线方程. [自主解答] 将 9y2-4x2=-36 变形为x92-y42=1, 故 a=3,b=2,c= 13. 因此顶点坐标为 A1(-3,0),A2(3,0), 焦点坐标为 F1(- 13,0),F2( 13,0), 实轴长是 2a=6,
[变式训练]
(2017·天
津
卷
)
已
知
双
曲
线
高中数学 第二章 圆锥曲线与方程 2.2.2 双曲线的简单几何性质学案 新人教A版选修11
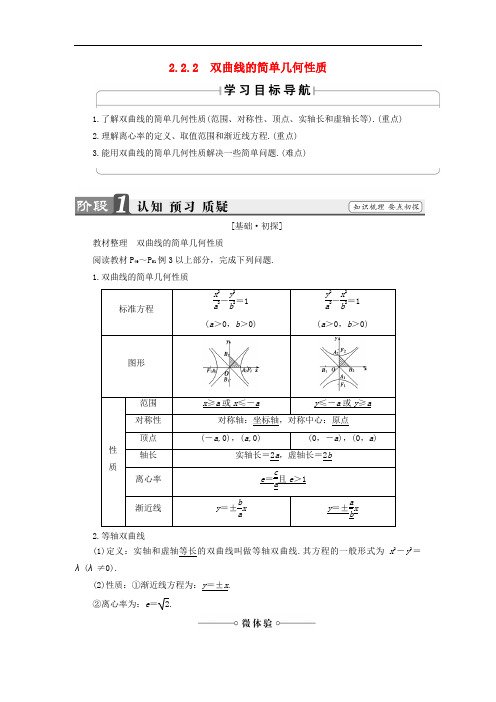
2.2.2 双曲线的简单几何性质1.了解双曲线的简单几何性质(范围、对称性、顶点、实轴长和虚轴长等).(重点)2.理解离心率的定义、取值范围和渐近线方程.(重点)3.能用双曲线的简单几何性质解决一些简单问题.(难点)[基础·初探]教材整理 双曲线的简单几何性质阅读教材P 49~P 51例3以上部分,完成下列问题. 1.双曲线的简单几何性质2.等轴双曲线(1)定义:实轴和虚轴等长的双曲线叫做等轴双曲线.其方程的一般形式为x 2-y 2=λ(λ≠0).(2)性质:①渐近线方程为:y =±x . ②离心率为:e = 2.判断(正确的打“√”,错误的打“×”) (1)双曲线是中心对称图形.( )(2)双曲线方程中a ,b 分别为实、虚轴长.( )(3)方程y 2a 2-x 2b 2=1(a >0,b >0)的渐近线方程为y =±bax .( )(4)离心率e 越大,双曲线x 2a 2-y 2b2=1的渐近线的斜率绝对值越大.( )【答案】 (1)√ (2)× (3)× (4)√[小组合作型](1)双曲线x 2-y 2=1的顶点到其渐近线的距离等于( ) A.12 B.22C.1D. 2(2)若实数k 满足0<k <5,则曲线x 216-y 25-k =1与曲线x 216-k -y 25=1的( )A.实半轴长相等B.虚半轴长相等C.离心率相等D.焦距相等(3)已知F 1,F 2分别是双曲线的两个焦点,P 为该双曲线上一点,若△PF 1F 2为等腰直角三角形,则该双曲线的离心率为( )【导学号:97792024】A.3+1B.2+1C.2 3D.2 2【自主解答】 (1)双曲线x 2-y 2=1的顶点坐标为(±1,0),渐近线为y =±x ,∴x ±y =0,∴顶点到渐近线的距离为d =|±1±0|2=22.(2)因为0<k <5,所以两曲线都表示双曲线,在x 216-y 25-k =1中a 2=16,b 2=5-k ;在x 216-k -y 25=1中a 2=16-k ,b 2=5.由c 2=a 2+b 2知两双曲线的焦距相等,故选D.(3)不妨设点P 在双曲线的右支上,则|PF 1|-|PF 2|=2a .∵△PF 1F 2是等腰直角三角形,∴只能是∠PF 2F 1=90°,∴|PF 2|=|F 1F 2|=2c , ∴|PF 1|=2a +|PF 2|=2a +2c , ∴(2a +2c )2=2·(2c )2,即c 2-2ac -a 2=0,两边同除以a 2,得e 2-2e -1=0. ∵e >1,∴e =2+1. 【答案】 (1)B (2)D (3)B由双曲线的标准方程求几何性质的四个步骤[再练一题]1.(1)已知双曲线x 2-y 2b2=1(b >0)的一条渐近线的方程为y =2x ,则b =________.【解析】 由双曲线x 2-y 2b 2=1,得a =1,∴b1=2,b =2.【答案】 2(2)求双曲线9y 2-4x 2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.【解】 将原方程转化为x 29-y 24=1,即x 232-y 222=1, ∴a =3,b =2,c =13,因此顶点坐标为A 1(-3,0),A 2(3,0), 焦点坐标为F 1(-13,0),F 2(13,0), 实轴长是2a =6,虚轴长是2b =4, 离心率e =ca =133, 渐近线方程y =±23x .分别求适合下列条件的双曲线的标准方程:(1)虚轴长为12,离心率为54;(2)顶点间距离为6,渐近线方程为y =±32x ;(3)与双曲线x 2-2y 2=2有公共渐近线,且过点M (2,-2).【精彩点拨】 用待定系数法求双曲线的标准方程时,注意先定位再定量,充分利用题中所给出的双曲线的几何性质.【自主解答】 (1)设双曲线的标准方程为x 2a 2-y 2b 2=1或y 2a 2-x 2b 2=1(a >0,b >0). 由题意知2b =12,c a =54且c 2=a 2+b 2,∴b =6,c =10,a =8. ∴双曲线的标准方程为x 264-y 236=1或y 264-x 236=1. (2)当焦点在x 轴上时,由b a =32且a =3得b =92. ∴所求双曲线的标准方程为x 29-4y 281=1.当焦点在y 轴上时,由a b =32且a =3得b =2.∴所求双曲线的标准方程为y 29-x 24=1.(3)设与双曲线x 22-y 2=1有公共渐近线的双曲线方程为x 22-y 2=k ,将点(2,-2)代入得k =222-(-2)2=-2.∴双曲线的标准方程为y 22-x 24=1.1.一般情况下,求双曲线的标准方程关键是确定a ,b 的值和焦点所在的坐标轴,若给出双曲线的顶点坐标或焦点坐标,则焦点所在的坐标轴易得.再结合c 2=a 2+b 2及e =c a列关于a ,b 的方程(组),解方程(组)可得标准方程.2.如果已知双曲线的渐近线方程为y =±b a x ,那么此双曲线方程可设为x 2a 2-y 2b2=λ(λ≠0).[再练一题]2.求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:【导学号:97792025】(1)双曲线C 的右焦点为(2,0),右顶点为(3,0); (2)双曲线过点(3,92),离心率e =103. 【解】 (1)设双曲线方程为x 2a 2-y 2b2=1(a >0,b >0).由已知得a =3,c =2, 再由a 2+b 2=c 2,得b 2=1. 故双曲线C 的方程为x 23-y 2=1.(2)由e 2=109,得c 2a 2=109,设a 2=9k (k >0),则c 2=10k ,b 2=c 2-a 2=k .于是,设所求双曲线方程为x 29k -y 2k =1, ①或y 29k -x 2k=1, ②把(3,92)代入①,得k =-161与k >0矛盾; 把(3,92)代入②,得k =9, 故所求双曲线方程为y 281-x 29=1.[探究共研型]探究1 怎样判断直线与双曲线的位置关系?【提示】 判断直线与双曲线的位置关系,一般先联立方程组,消去一个变量,转化成关于x 或y 的一元二次方程,再根据一元二次方程去讨论直线和双曲线的位置关系.这时首先要看二次项的系数是否等于0.当二次项系数等于0时,就转化成x 或y 的一元一次方程,只有一个解.这时直线与双曲线相交只有一个交点.当二次项系数不为零时,利用根的判别式,判断直线和双曲线的位置关系.探究2 直线和双曲线只有一个公共点,直线和双曲线一定相切吗?【提示】 直线和双曲线只有一个公共点时,直线不一定与双曲线相切,当直线与双曲线的渐近线平行时,直线与双曲线相交,只有一个交点.已知直线y =ax +1与双曲线3x 2-y 2=1. (1)如果直线与双曲线有两个公共点,求a 的取值范围; (2)如果直线与双曲线只有一个公共点,求a 的取值范围; (3)如果直线与双曲线没有公共点,求a 的取值范围.【精彩点拨】 将直线与双曲线方程联立用判别式Δ判断方程组解的个数,并注意对二次项系数的讨论.【自主解答】 把y =ax +1代入3x 2-y 2=1, 整理得(3-a 2)x 2-2ax -2=0. (1)∵直线与双曲线有两个公共点, ∴判别式Δ=4a 2+8(3-a 2)=24-4a 2>0, 且3-a 2≠0,得-6<a <6,且a ≠± 3.故当-6<a <6,且a ≠±3时,直线与双曲线有两个公共点. (2)∵直线与双曲线只有一个公共点,∴⎩⎪⎨⎪⎧Δ=24-4a 2=0,3-a 2≠0或3-a 2=0,∴a =±6或a =± 3.故当a =±6或a =±3时,直线与双曲线只有一个公共点. (3)∵直线与双曲线没有公共点, ∴3-a 2≠0,且Δ=24-4a 2<0. ∴a >6或a <- 6.故当a >6或a <-6时,直线与双曲线没有公共点.1.研究直线与双曲线位置关系的一般解法仍然是联立二者方程,解方程组或者转化为一元二次方程,依据根的判别式和根与系数的关系求解.2.直线与双曲线有三种位置关系(1)无公共点,此时直线有可能为双曲线的渐近线.(2)有一个公共点,分两种情况:①直线是双曲线的切线,特别地,直线过双曲线一个顶点,且垂直于实轴;②直线与双曲线的一条渐近线平行,与双曲线的一支有一个公共点.(3)有两个公共点,可能都在双曲线一支上,也可能两支上各有一点.[再练一题]3.(1)已知过点P (1,1)的直线l 与双曲线x 2-y 24=1只有一个公共点,则直线l 的斜率k的取值为________.【解析】 设直线l 的斜率为k ,则l :y =k (x -1)+1,代入双曲线方程,得到(4-k 2)x 2-(2k -2k 2)x -k 2+2k -5=0.若4-k 2=0,即k =±2,此时直线与双曲线的渐近线平行,直线与双曲线只有一个公共点;若4-k 2≠0,则Δ=[-(2k -2k 2)]2-4(4-k 2)·(-k 2+2k -5)=0,解得k =52.综上可得,直线l 的斜率k 的取值为52或±2.【答案】 52或±2(2)已知直线l :x +y =1与双曲线C :x 2a2-y 2=1(a >0).①若a =12,求l 与C 相交所得的弦长;②若l 与C 有两个不同的交点,求双曲线C 的离心率e 的取值范围. 【解】 ①当a =12时,双曲线C 的方程为4x 2-y 2=1,联立⎩⎪⎨⎪⎧x +y =1,4x 2-y 2=1,消去y 得3x 2+2x -2=0.设两个交点为A (x 1,y 1),B (x 2,y 2). 则x 1+x 2=-23,x 1x 2=-23,于是|AB |=x 1-x 22+y 1-y 22=x 1-x 22+x 2-x 12=2·x 1+x 22-4x 1x 2=2×289=2143. ②将y =-x +1代入双曲线x 2a2-y 2=1中得(1-a 2)x 2+2a 2x -2a 2=0,∴⎩⎪⎨⎪⎧1-a 2≠0,4a 4+8a 2-a 2>0,解得0<a <2且a ≠1. 又双曲线的离心率e =1+a2a=1a 2+1,∴e >62且e ≠2, 即离心率e 的取值范围是⎝⎛⎭⎪⎫62, 2∪(2,+∞).1.双曲线2x 2-y 2=8的实轴长是( ) A.2 B.2 2 C.4D.4 2【解析】 双曲线标准方程为x 24-y 28=1,故实轴长为4.【答案】 C2.下列双曲线中离心率为62的是( ) A.x 22-y 24=1 B.x 24-y 22=1 C.x 24-y 26=1 D.x 24-y 210=1 【解析】 双曲线x 24-y 22=1中a =2,b =2,∴c =6,e =62.【答案】 B3.已知双曲线中心在原点,一个顶点的坐标是(3,0)且焦距与虚轴长之比为5∶4,则双曲线的标准方程为________.【解析】 由题意得双曲线的焦点在x 轴上,且a =3,焦距与虚轴长之比为5∶4,即c ∶b =5∶4,解得c =5,b =4,∴双曲线的标准方程为x 29-y 216=1.【答案】x 29-y 216=1 4.已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)与双曲线C 2:x 24-y 216=1有相同的渐近线,且C 1的右焦点为F (5,0),则a =________,b =________.【解析】 由题意得⎩⎪⎨⎪⎧b 2a2=4,a 2+b 2=5,解得a 2=1,b 2=4.又a >0,b >0,故a =1,b =2. 【答案】 1 25.求中心在坐标原点,对称轴为坐标轴,经过点(3,-2),且一条渐近线的倾斜角为π6的双曲线的方程.【导学号:97792026】【解】 渐近线方程为y =±33x ,设双曲线方程为x 2-3y 2=λ.将(3,-2)代入求得λ=-3,所以双曲线方程为y 2-x 23=1.。
高中数学第2章圆锥曲线与方程2.3.2双曲线的几何性质1121数学

Q
B2
M(x,y)
b
(2) 在等 (yma轴ba0)x双 的 的曲 渐 下x2线 近 方 y线 2 为 m
A1
A2
o a
x
它与yybxx的. 位置的变化:趋势 B1
a
(3)利画用出逐渐双渐近曲(z线线hújià可的n)靠以 草近较图准.确的
ybx a
2021/12/8
第八页,共十五页。
y b x a
方程.。问:若将题目中“焦点在y轴上”改为(ɡǎi wéi)“焦点在坐标轴上”呢。2.若双曲线的离心率为2,则两条渐
近线的夹角为_________.
No
Image
12/8/2021
第十五页,共十五页。
x2
y2
a2 b2 1
(a b 0)
x2 a2
y2 b2
1
(a 0,b 0)
范围(fànwéi)
-a
x a
(xa或 xa)
-b y b
对称性
对称轴:x 轴 ,y轴 对称轴: x 轴,y轴 对称中心 :坐标原点 对称中心:坐标原点
顶点
(dǐngdiǎn)
(±a,0) (0,c2 a2b2
在a,b,c,e四个参数中,知二二可.求
2021/12/8
第七页,共十五页。
5.渐近线.
双曲线在第一象分 限的 内方 部程为
(1) y
b双曲 x2 线 axa222(xby2201)(a
0,b
0)
a的渐近线y为b x.
它与ybx的位置 a 关: 系
y N(x,y′)
解:由题意(tíyì)可
得
实轴长:
虚轴长:
焦点(jiāodiǎn)坐标:
高中数学第二章圆锥曲线与方程2.2.2双曲线的简单几何性质课件新人教A版选修1_1
[解析] 双曲线 C:x62-y32=1 中,c2=6+3=9,∴c=3,则 C 的右焦点的坐
标为(3,0),C 的渐近线方程为 y=± 36x,即 y=± 12x,即 x± 2y=0,则 C 的焦点
到其渐近线的距离
d=
3= 3
3.
6.已知中心在原点的双曲线的渐近线方程是 y=± 3x,且双曲线过点( 2, 3).
1.双曲线2x52 -y92=1 的顶点坐标是( A )
A.(±5,0)
B.(±5,0)或(0,±3)
C.(±4,0)
D.(±4,0)或(0,±3)
[解析] ∵双曲线的顶点在x轴上,又a=5,∴选A.
2.(2019·浙江卷,2)渐近线方程为 x±y=0 的双曲线的离心率是( C )
A.
2 2
B.1
(1)求双曲线的方程; (2)求双曲线的焦点到渐近线的距离.
[解析] (1)设双曲线的方程为:3x2-y2=λ(λ≠0),点( 2, 3)代入得 λ=3, 所以所求双曲线方程为 x2-y32=1.
(2)由于双曲线的方程为 x2-y32=1,所以它的焦点为(-2,0)、(2,0),点(- 2,0)到直线 y=± 3x 的距离为 d= |21+3|3= 3.则双曲线的焦点到渐近线的距离为
1.双曲线的简单几何性质
焦点位置
焦点在x轴上
焦点在y轴上
双曲线方程 _____ax_22_-__by_22_=__1_(a_>_0_,__b_>__0_) ____ ______ay_22-__bx_22_=__1_(_a_>_0_,__b_>_0_)____
范围
___x_≤_-__a_或__x_≥_a____
C. 2 [解析] 由题意可得ba=1,∴ e=
浙江专版高中数学第二章圆锥曲线与方程2.3.1双曲线及其标准方程课件新人教A版选修2
[典例] 已知方程k-x25-|k|y-2 2=1 对应的图形是双曲线,
那么 k 的取值范围是
()
A.k>5
B.k>5 或-2<k<2
C.k>2 或 k<-2
D.-2<k<2
[解析] ∵方程对应的图形是双曲线, ∴(k-5)(|k|-2)>0. 即k|k-|-52>>00,, 或k|k-|-52<<00,. 解得 k>5 或-2<k<2. [答案] B
设所求标准方程为1y62 -bx22=1(b>0), 把 A 点的坐标代入,得 b2=9, ∴所求双曲线的标准方程为1y62 -x92=1. (2)设双曲线的方程为 mx2+ny2=1(mn<0), ∵双曲线经过点(3,0),(-6,-3),
∴93m6m++0=9n1=,1, 解得mn==-19,13, ∴所求双曲线的标准方程为x92-y32=1.
1.双曲线标准方程的两种求法 (1)定义法:根据双曲线的定义得到相应的 a,b,c,再写出双 曲线的标准方程. (2)待定系数法:先设出双曲线的标准方程xa22-by22=1 或ay22-xb22= 1(a,b 均为正数),然后根据条件求出待定的系数代入方程即可. 2.求双曲线标准方程的两个关注点 (1)定位:“定位”是指确定与坐标系的相对位置,在“标准方 程”的前提下,确定焦点位于哪条坐标轴上,以判断方程的形式; (2)定量:“定量”是指确定 a2,b2 的具体数值,常根据条件列 方程求解.
[小试身手]
1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)
(1)平面内到两定点的距离的差等于常数(小于两定点间距离)的
点的轨迹是双曲线
【红对勾】高中数学 2-3-2-1 双曲线的简单几何性质课时作业 新人教A版选修2-1(1)
课时作业14 双曲线的简单几何性质时刻:45分钟 分值:100分一、选择题(每题6分,共36分)1.(2020·安徽高考)双曲线2x 2-y 2=8的实轴长是( )A .2B .22C .4D .4 2解析:双曲线标准方程为x 24-y 28=1,故实轴长为4.答案:C2.双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,那么m 的值为( )A .- 14B .-4C .4D .14解析:∵mx 2+y 2=1是双曲线,∴m<0,且其标准方程为y 2-x 21-m=1.又∵其虚轴长是实轴长的2倍,∴-1m =4,即m =-14.答案:A3.假设双曲线x 28-y 2m =1的渐近线方程为y =±2x,那么实数m 等于() A .4 B .8C .16D .32解析:由题意,得双曲线核心在x 轴上,且a 2=8,b 2=m ,∴a=22,b =m.又渐近线方程为y =±2x,∴m 8=4.∴m=32. 答案:D 4.假设直线x =a 与双曲线x 24-y 2=1有两个交点,那么a 的值能够是( ) A .4 B .2C .1D .-2解析:∵双曲线x 24-y 2=1中,x≥2或x≤-2, ∴假设x =a 与双曲线有两个交点, 那么a>2或a<-2,故只有A 选项符合题意.答案:A5.设a>1,那么双曲线x 2a 2-y 2a +12=1的离心率e 的取值范围是( ) A .(2,2) B .(2,5)C .(2,5)D .(2,5) 解析:e =c a =b 2+a 2a 2=1+⎝ ⎛⎭⎪⎫a +1a 2=1+⎝ ⎛⎭⎪⎫1+1a 2. ∵a>1,∴0<1a<1, ∴1<1+1a<2, ∴2<e<5,应选B .答案:B6.设F 1、F 2别离是双曲线x 2-y 29=1的左、右核心.假设P 在双曲线上,且PF 1→·PF 2→=0,那么|PF 1→+PF 2→|等于( ) A .2 5 B .5C .210D .10 解析:由题意,可知双曲线两核心的坐标别离为F 1(-10,0)、F 2(10,0).设点P(x ,y),则PF 1→=(-10-x ,-y),PF 2→=(10-x ,-y), ∵PF 1→·PF 2→=0,∴x 2+y 2-10=0,即x 2+y 2=10.∴|PF 1→+PF 2→|=|PF 1→|2+|PF 2→|2+2PF 1→·PF 2→=2x 2+y 2+20=210. 答案:C二、填空题(每题8分,共24分)7.(2020·辽宁高考)已知(2,3)在双曲线C :x 2a 2-y 2b2=1(a>0,b>0)上,C 的焦距为4,那么它的离心率为______________.解析:∵2c =4,∴c =2,那么b 2=c 2-a 2=4-a 2,故4a 2-94-a2=1得a 2=1,a =1, ∴e =c a=2. 答案:28.已知双曲线C :x 24-y 2m=1的开口比等轴双曲线的开口更开阔,那么实数m 的取值范围是________. 解析:∵等轴双曲线的离心率为2,且双曲线C 的开口比等轴双曲线更开阔,∴双曲线C :x 24-y 2m=1的离心率e>2,即4+m 4>2. ∴m>4.答案:(4,+∞)9.(2020·天津高考)已知双曲线x 2a 2-y 2b2=1(a>0,b>0)的一条渐近线方程是y =3x ,它的一个核心与抛物线y 2=16x 的核心相同,那么双曲线的方程为________.解析:由条件知双曲线的核心为(4,0),因此⎩⎪⎨⎪⎧ a 2+b 2=16,b a =3,解得a =2,b =23,故双曲线方程为x 24-y 212=1. 答案:x 24-y 212=1 三、解答题(共40分)10.(10分)(1)已知双曲线的渐近线方程为y =±34x ,求双曲线的离心率. (2)双曲线的离心率为2,求双曲线的两条渐近线的夹角.解:(1)∵双曲线的渐近线方程为y =±34x , ∴b a =34或b a =43. 当b a =34时,e =54;当b a =43时,e =53. (2)∵e =c a =2,∴a 2+b 2a =2即a =b ,∴双曲线渐近线方程为y =±x.∴双曲线两条渐近线的夹角为90°.11.(15分)设F 1、F 2别离是双曲线x 2a 2-y 2b2=1的左、右核心,假设双曲线上存在点A ,使∠F 1AF 2=90°且|AF 1|=3|AF 2|,求双曲线的离心率.解:∵AF 1⊥AF 2,∴|AF 1|2+|AF 2|2=|F 1F 2|2=4c 2.①∵|AF 1|=3|AF 2|,∴点A 在双曲线的右支上.那么|AF 1|-|AF 2|=2a ,∴|AF 2|=a ,|AF 1|=3a ,代入到①式得(3a)2+a 2=4c 2,c 2a 2=104. ∴e =c a =102. 12.(15分)中心在原点,核心在x 轴上的一椭圆与一双曲线有一起的核心F 1,F 2,且F 1F 2=213,椭圆的半长轴长与双曲线半实轴长之差为4,离心率之比为3∶7.(1)求这两曲线方程;(2)假设P 为这两曲线的一个交点,求△F 1PF 2的面积.解:(1)设椭圆方程为x 2a 2+y 2b 2=1,双曲线方程为x 2m 2-y 2n 2=1(a ,b ,m ,n>0,且a>b), 则⎩⎪⎨⎪⎧ a -m =47·13a =3·13m ,解得:a =7,m =3,∴b=6,n =2,∴椭圆方程为x 249+y 236=1,双曲线方程为x 29-y 24=1. (2)不妨设F 1,F 2别离为左、右核心,P 是第一象限的一个交点,那么PF 1+PF 2=14,PF 1-PF 2=6, ∴PF 1=10,PF 2=4,∴cos ∠F 1PF 2=PF 21+PF 22-F 1F 222PF 1·PF 2=45, ∴sin ∠F 1PF 2=35. ∴S△F 1PF 2=12PF 1·PF 2sin ∠F 1PF 2=12·10·4·35=12.。
新课标人教A版选修2-1辅导资料—双曲线的简单几何性质(含答案)
双曲线的简单几何性质一、要点精讲1.双曲线的标准方程和几何性质2.等轴双曲线实轴和虚轴等长的双曲线叫做等轴双曲线,其标准方程为()022≠=-λλy x ,离心率2=e ,渐近线方程x y ±=。
3、共渐近线的双曲线系方程:与-22a x 22b y =1有相同渐近线的双曲线系方程可设为-22ax ()022≠=λλb y ,若0>λ,则双曲线的焦点在轴上;若0<λ,则双曲线的焦点在轴上。
4、共焦点的双曲线系方程:与-22ax 22b y =1焦点相同的双曲线系方程可设为()2222221,+x y k b k a a k b k -=<<-二、基础自测1.(15安徽)下列双曲线中,渐近线方程为2y x =±的是( )(A )2214y x -= (B )2214x y -=(C )2212y x -= (D )2212x y -= 2.(2013湖北)已知π04θ<<,则双曲线1C :22221sin cos x y θθ-=与2C :22221cos sin y x θθ-=的 ( ) A .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等3.(2013课标)已知双曲线2222:1x y C a b -=(0,0)a b >>,则C 的渐近线方程为 ( )A .14y x =±B .13y x =±C .12y x =± D .y x =± 4.(15广东)已知双曲线C :12222=-b y a x 的离心率54e =,且其右焦点()25,0F ,则双曲线C 的方程为A .13422=-y x B.191622=-y x C.116922=-y x D. 14322=-y x 5.(2013湖南)设F 1、F 2是双曲线C,22221x y a b-=(a >0,b>0)的两个焦点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3.2双曲线的简单几何性质(2)
学习目标:能够根据渐近线方程求双曲线的方程;掌握直线与双曲线的位置关系并能解决简
单问题.
课前练习:双曲线14222yx的渐近线方程为_____
自主学习:
例1.根据下列条件,求双曲线的标准方程。
(1)双曲线的渐近线方程为23yx,且过点9(,1)2M
(2)已知双曲线渐近线方程为12yx,焦距为10;
(3)与双曲线1222yx有共同渐近线,且过点(2,-2)
小结:利用待定系数法求双曲线方程时,常用结论:
(1)若双曲线的渐近线方程为byxa,则双曲线方程可设为______________________
(2)与双曲线22221(0,0)xyabab有共同渐近线的双曲线方程可设为__________________
(3) 双曲线22221(0,0)xyabab与双曲线)(1222222akbkbykax有相同的______
自主探究:直线与双曲线的位置关系
联立12222byaxmkxy
消元得:02)(222222222bamamkxaxkab
(1)当0222kab时,即abk时,直线与渐近线平行,直线与双曲线有_____个交点,位置关
系是________
(2) 当0222kab时, 即abk时,
若Δ>0, 则有____个交点,位置关系是________;
若Δ=0, 则有____个交点,位置关系是________;
若Δ<0, 则_______交点,位置关系是________.
思考:直线与双曲线有一个公共点,则直线与双曲线一定相切吗?
自主学习:
例2.已知直线y=kx+1与双曲线1322yx相交于A,B两点, 当k为何值时,以AB为直径的
圆过原点, 并求此时弦长|AB|.
自主学习:自学教材P58-60例4、例5、例6
思维拓展:双曲线的第二定义(P59例5)
2.3.2双曲线的简单几何性质(2)作业
1.双曲线6x2-2y2 = -1的两条渐近线的夹角是( )
A.3 B.23 C.6 D.2
2.已知双曲线22221xyab(a>0,b>0)的一条渐近线为y=kx(k>0),离心率e=5k,则双曲
线方程为( )
A.22xa-224ya=1 B.22xa- 225ya=1
C.222214xybb D.222215xybb
3.中心在原点,离心率为35的双曲线的焦点在y轴上,则它的渐近线方程为
( )
A.xy45 B.xy54 C.xy34D.xy43
4.与双曲线1422yx有共同的渐近线,且过点(2,2)的双曲线方程为
( )
A. 112322xy B. 18222xy
C. 18222yx D. 112322yx
5.直线)2(xky与双曲线1422yx有且只有一个公共点,则k的不同取值有
( )
A.1个 B.2个 C.3个 D.4个
6.直线033yx被双曲线122yx截得的弦AB的长为___________
7.过双曲线1322yx的左焦点F1,作倾斜角为6π的弦AB,则ΔABF2的面积为_________
8.若双曲线)0(14222bbyx的渐近线为xy21,则b等于__________
9.若双曲线的渐近线方程为xy3,它的一个焦点是)0,10(,则双曲线方程是
__________________
10.求与曲线2212449xy共焦点,而与曲线2213664xy共渐近线的双曲线的方程为
_________________
11.已知双曲线22221(0,0)xyabab的两条渐近线方程为33yx,若顶点到渐近线的距离
为1,求双曲线方程。
12.过点A(6,1)作直线l与双曲线141622yx相交于B,C两点,且A为线段BC的中点,求直线
l
的方程.
13.已知双曲线C:22221(0,0)xyabab的离心率为3,虚轴长为22. (1)求双曲线C的
方程;
(2)已知直线0myx与双曲线C交于不同的两点A,B,且线段AB的中点在圆522yx上,
求m的值.
